异步时序逻辑电路的分析与设计资料
异步时序逻辑电路的分析与设计

异步时序逻辑电路的分析与设计异步时序逻辑电路是一种基于信号的到达时间和时序性的电路设计方法。
与同步时序逻辑电路不同,异步时序逻辑电路中的数据传输和处理不依赖于时钟信号,而是根据输入信号的到达顺序和时序关系来进行操作。
本文将详细介绍异步时序逻辑电路的分析与设计。
异步时序逻辑电路的分析主要包括信号流图的建立和状态表的推导。
首先,通过对输入信号的时序关系进行分析和理解,可以根据具体应用需求建立信号流图。
信号流图是一种图形化表示方式,其中包含了电路中信号的流动方式以及各个元件的逻辑功能。
在建立信号流图时,需要注意信号的输入和输出时间以及逻辑功能的实现方式,这是实现异步时序逻辑电路的关键。
在信号流图的基础上,可以根据信号的到达先后顺序推导状态表。
状态表是对电路中每个元件当前状态和下一状态的描述。
通过观察信号流图,可以确定每个元件在不同状态下的输出值,并利用这些信息进行状态表的推导。
在状态表中,可以列出元件的当前状态和下一状态的取值,并根据逻辑功能的要求来确定元件的控制信号。
异步时序逻辑电路的设计主要涉及到逻辑电路元件的选择和电路的优化。
在异步时序逻辑电路中,常用的逻辑电路元件包括触发器、门电路和编码器等。
根据实际需求,可以选择不同类型的逻辑电路元件来实现电路的逻辑功能。
在设计时,需要注意减少电路的延迟和功耗,提高电路的性能和可靠性。
可以通过选择低延迟的元件、合理布局电路和优化信号传输路径等方式来减小电路的延迟。
另外,可以采用时序检测和冗余检测等方法来增加电路的可靠性。
除了分析和设计,测试和验证是异步时序逻辑电路设计中的重要环节。
可以利用仿真软件对电路进行测试和验证,以确保电路的正确性和性能。
通过仿真可以观察电路的输入输出关系,检测是否存在冲突或错误,并进行合理的调整和优化。
总结起来,异步时序逻辑电路的分析与设计涉及到信号流图的建立、状态表的推导、元件的选择和电路的优化等方面。
通过合理的分析和设计,可以实现复杂的时序逻辑功能,并提高电路的性能和可靠性。
异步时序逻辑电路的分析与设计

异步时序逻辑电路的分析与设计异步时序逻辑电路是指电路中的各个逻辑门的输出不仅仅取决于当前的输入,还取决于先前的输入和输出状态。
与同步时序逻辑电路相比,异步时序逻辑电路具有更高的灵活性和可扩展性。
在本文中,将详细介绍异步时序逻辑电路的分析与设计方法。
首先,异步时序逻辑电路的分析是指通过对电路中各个逻辑门的输入和输出状态进行推导和分析,以获取电路所实现的具体功能和工作原理。
异步时序逻辑电路通常采用状态图或状态转换表来描述其运行过程。
状态图是一个有向图,其中每个节点表示一个状态,而边表示状态之间的转换。
状态转换表则是一种矩阵形式的表示方法,其中行表示当前状态,列表示输入,表格中的元素表示输出和下一个状态的关系。
在进行异步时序逻辑电路的设计之前,通常需要明确电路所要实现的功能和要求。
在设计过程中,需要通过一系列的步骤来完成。
第一步是确定输入和输出信号的数量和类型。
输入信号是电路用来接收外部输入的信号,而输出信号是电路的输出结果。
在这一步骤中,需要明确输入和输出信号所能取的值范围以及其对应的功能。
第二步是确定状态的数量和类型。
在异步时序逻辑电路中,状态是指电路在不同时间点的输出和输入的组合。
状态的数量和类型决定了电路的复杂程度和所能实现的功能。
第三步是绘制状态图或状态转换表。
通过绘制状态图或状态转换表,可以清晰地描述电路的工作原理和功能。
其中,状态图可以直观地表示状态之间的转换关系,而状态转换表则更加直观地表示输入输出和状态的关系。
第四步是推导逻辑表达式。
通过推导逻辑表达式,可以将电路的功能转化为逻辑门的连接方式。
在这一步骤中,可以通过布尔代数和卡诺图等方法来简化逻辑表达式,以减少电路的复杂性和成本。
第五步是选取逻辑门类型。
逻辑门是构成异步时序逻辑电路的基本元件,它决定了电路的工作速度和功耗。
在选择逻辑门类型时,需要考虑到电路的功能和性能要求,以及逻辑门的延迟时间和功耗等特性。
第六步是进行逻辑门的连接和布线。
6.2异步时序逻辑电路的分析
(2) 将驱动方程代入相应 触发器的特性方程,求出
各触发器的状态方程:
(3) 列状态表、画状态图 和时序图:
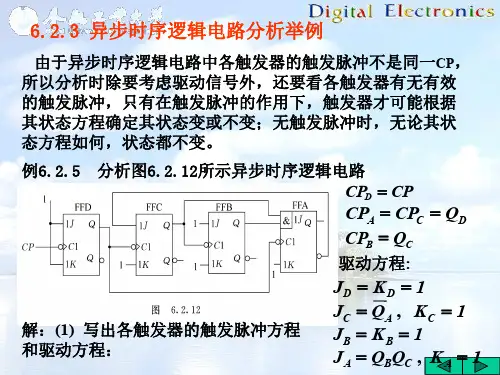
例6.2.5 分析图6.2.12所示异步时序逻辑电路
(QQAnD+负发 这1 =跳器十由Q时从个分A此Q0状0析B式态0Q可0有C是~见效每1,0)来0触1一
QBn个 一+1 C个=P异递QB步加十1,进所制以加是法
解:(1)各触发器的
触发脉冲方程:
CPD = CP
CPA = CPC = QD CPB = QC
驱动方程:
JD = KD = 1 JC = QA , KC = 1 JB = KB = 1 JA = QBQC , K A = 1
QAn+1 = QAQBQC(QD负跳时此式有效) QBn+1 = QB (QC负跳时此式有效) QCn+1 = QAQC (QD负跳时此式有效) QDn+1 = QD (CP负跳时此式有效)
例6.2.5 分析图6.2.12所示异步时序逻辑电路
CPD = CP
CPA = CPC = QD
CPB = QC
驱动方程:
解:(1) 写出各触发器的触发脉冲方程 和驱动方程:
JD = KD = 1
JC = QA , KC = 1 JB = KB = 1 JA = QBQC , K A = 1
例6.2.5 分析图6.2.12所示异步时序逻辑电路
状态图
QAQBQCQD
1111 1110
1010 1011
1100 1101
0000 0001 0010 0011 0100
10 0 0 0 0
1001 1000 0111 0110 0101
数电20(异步时序逻辑电路分析)
状态不确定
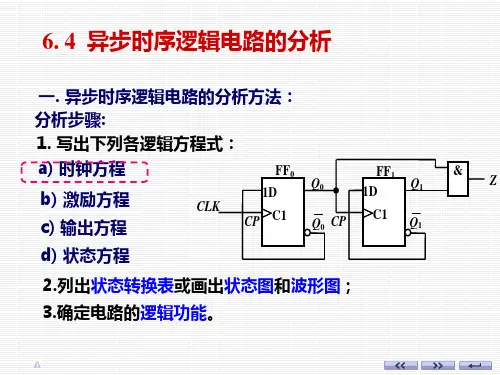
例2 分析如图所示异步时序逻辑电路.
& CLK ≥ CP0 > C FF0 Q0 CP1 >C FF1 Q1
≥ ≥ CP2 > C FF2 Q2
Q0
Q1
Q2
& CLK 何时出现触 ≥ CP0 > C FF0 Q0 CP1 >C FF1 Q1
≥ ≥ CP2 > C FF2 Q2
发沿?
解 (1) 列出各逻辑方程组 时钟方程
同步时序电路——所有触发器同时转换状态 异步时序电路——各个触发器之间的状态转换存在一定的延迟, 在此期间,电路的状态是不确定的。只有当全部触发器状态转 换完毕,电路才进入新的“稳定”状态,即次态Sn+1。
二.
异步时序逻辑电路的分析举例
FF0 CLK 1D >C1 FF1 1D >C1 & Z
例1 分析如图所示异步电路 1. 写出电路方程式 ① 时钟方程 CP0=CLK CP1=Q0 ②输出方程 ③激励方程
Q
n 2
Q
0
n 1
Q
n 0
cp2
0
cp1
0
cp0
1
Q2n 1 Q1n 1 Q0n 1
0 0 1
0
00ຫໍສະໝຸດ 0 0 1 1 101 1 0 0 1
1
0 1 0 1 0
0
0 1 1 1 1
1
0 1 0 0 0
1
1 1 0 0 0
0
0 1 0 0 0
1
1 0 0 0 1
0
1 0 0 1 0
1
1
1
1
0
0
0
1
1 0
1 0
1 0 1 0 1
5.异步时序逻辑电路

(2)输入信号的形式与约束 ① 输入信号为脉冲信号; ② 输入脉冲的宽度必须保证触发器可靠翻转; ③ 输入脉冲的间隔必须保证前一个脉冲引起的电 路响应完全结束后,后一个脉冲才能到来; ④ 不允许两个或两个以上输入端同时出现脉冲。
理由:因为客观上两个或两个以上脉冲是不可能准 确地“同时”的,在没有时钟脉冲同步的情况下, 由不可预知的时间延迟造成的微小时差,可能导致 电路产生错误的状态转移。
(2)列出电路次态真值表
输入 x 状态 y2 y1 激励函数 CP2 J2 K2 CP1 J1 K1 次态 y2n+1 y1n+1
1 1
0 0
0 1 ↓ ↓
1 1
1 1
↓ ↓
1 1
1 1
0
1
1
1 0
0
1 0
1
1
1
1
0
1
1
1
1
1
↓
↓
1
1
1
1
注意: 何时有脉冲作用? 状态发生转移的时机?
脉冲作用下,且为负跳变的瞬间!
0000 1111 0001 0010 0011 0100 0101 0110 0111 1000
第四步 功能描述 模16加1计数器
1110 1101 1100 1011 1010 1001
5.2.2 脉冲异步时序逻辑电路设计
1、设计
脉冲异步时序逻辑电路设计的方法与同步时序逻 辑电路设计大至相同。但由于在脉冲异步时序逻 辑电路中没有统一的时钟脉冲信号,以及对输入 脉冲信号的约束 ,所以在某些步骤的处理细节上 有所不同。
例如,当要使D触发器维持0不变时,可令CP为d, D为0;也可令CP为0,D为d。 显然,这将使激励函数的确定变得更加灵活,究 竟选择哪种处理方法,应看怎样更有利于电路简 化。 一般选CP为0,输入任意,因为这样显得更清晰。
异步时序逻辑电路的分析

异步时序逻辑电路的分析异步时序逻辑电路由状态元件和组合逻辑电路构成。
状态元件可以是触发器、锁存器或计数器等,用于存储和更新系统的状态信息。
组合逻辑电路用于根据输入信号和状态元件的当前状态生成输出信号。
异步时序逻辑电路使用特殊的电路元件来处理时序问题,如时序器、分频器、状态机等。
分析是指确定异步时序逻辑电路所需的状态元件和组合逻辑电路,以及它们之间的关系。
在分析过程中,需要识别系统的输入和输出信号,并建立它们之间的关联关系。
通过对系统的输入进行序列和输入/输出的波形分析,可以确定输入和输出之间的时序关系。
合成是指根据分析结果生成实际的电路布局和连接。
在合成过程中,需要选择合适的电路元件,并确定它们之间的连接方式和时序关系。
合成过程可以使用电路设计软件来自动生成电路图和布局。
1.确定系统的输入和输出信号。
根据实际需求和系统功能,确定输入和输出信号的类型和名称。
输入信号通常是一些外部事件或控制信号,输出信号则是系统的响应。
2.建立输入和输出信号之间的关联关系。
根据系统的逻辑功能和时序要求,确定输入和输出信号之间的时序关系。
可以使用状态转换图、状态转移表或状态图等形式来描述这种关系。
3.确定状态元件的类型和数量。
根据系统的状态信息和时序性能要求,选择合适的状态元件。
触发器是最常用的状态元件,可用于存储系统的状态信息。
根据状态元件的类型和数量,可以确定系统的状态变量。
4.建立状态元件和组合逻辑电路之间的关系。
根据系统的逻辑功能和时序要求,确定状态元件和组合逻辑电路之间的逻辑关系。
组合逻辑电路用于根据输入信号和当前状态元件的状态生成输出信号。
5.分析输入/输出时序波形。
通过仿真或实验,分析输入/输出时序波形以验证系统的正确性。
根据时序波形图,可以确定信号的传输延迟和时序约束等重要参数。
6.优化电路设计。
根据分析结果,对电路进行优化。
常见的优化技术包括布局优化、电路复用和逻辑优化等。
优化的目标是减少电路的延迟、功耗和面积,提高系统的性能和可靠性。
异步时序逻辑电路分析
7.2.2异步时序逻辑电路的分析方法异步时序逻辑电路的分析方法和同步时序逻辑电路的基本相同,但在异步时序逻辑电路中,只有部分触发器由计数脉冲信号源CP触发,而其它触发器则由电路内部信号触发。
在分析异步时序逻辑电路时,应考虑各个触发器的时钟条件,即应写出时钟方程。
这样,各个触发器只有在满足时钟条件后,其状态方程才能使用。
这也是异步时序逻辑电路在分析方法上与同步时序逻辑电路的根本不同点,应引起足够的重视。
分析举例例、试分析下图所示电路的逻辑功能,并画出状态转换图和时序图。
解:由上图可看出,FF1的时钟信号输入端未和输入时钟信号源CP相连,它是由FF0的Q0端输出的负跃变信号来触发的,所以是异步时序逻辑电路。
①写方程式:时钟方程:CP0=CP2=CP FF0和FF2由CP的下降沿触发。
~CP1=Q0 FF1由Q0输出的下降沿触发。
输出方程:驱动方程:状态方程:②列状态转换真值表:状态方程只有在满足时钟条件后,将现态的各种取值代入计算才是有效的。
设现态为=000,代入输出方程和状态方程中进行计算,可以得出该逻辑电路的状态转换真值表:现态次态输出`时钟脉冲Y CP2CP1$CP00000010》0010100《0100110?0111000\ 1000001…表中的第一行取值,在现态=000时,先计算次态为=01,由于CP1=Q0,其由0跃到1为正跃变,故FF1保持0态不变,这时=001。
表中的第二行取值,在现态为=001时,得=00,这时CP1=Q0由1跃到0为负跃变,FF1由0态翻到1态,这时=010。
其余依此类推。
③逻辑功能说明:由上表可看出,该电路在输入第5个计数脉冲时,返回初始的000状态,同时输出端Y 输出一个负跃变的进位信号,因此,该电路为异步五进制计数器。
④状态转换图和时序图。
根据状态转换真值表可画出该电路的状态转换图和时序图,如下图所示。
!。
数字电路逻辑设计第7章 异步时序逻辑电路
图7-8 电平异步时序逻辑电路的结构模型
①电路输出和状态的改变是由输入电位的 变化直接引起的, 由于电平异步时序逻辑电 路可以 及时地对输入信号的变化作出响应, 所以工作速度较高。 ②电路的二次状态和控制状态仅相差一个 时间延迟。即二次状态y是反馈控制状态Y 经过△t 延迟后的“重现”,因此,y被命名 为二次状态。当输入信号不变时, 反馈控 制状态与二次状态相同, 即y=Y,此时电路 处于稳定状态。
由于同步时序逻辑电路的每个状态都是稳定状 态,而电平异步时序逻辑电路有不稳定状态。 因此,其分析和设计方法也有较大的差异。 电平异步时序逻辑电路包含有稳定状态和不稳 定状态,电路从一个稳定状态转换到另一个稳 定状态,有时中间要经过一个甚至几个不稳定 的过渡状态。由于这一特点,导致了设计电平 异步时序逻辑电路时,重点注意解决的三个特 殊问题。
经卡诺图简化后, 可写出驱动方程:
D 2 = X 2Q 2Q 1 CP2 = X1Q1 + X2 D1 = X 1 CP1 = X1Q2 + X2Q2 + X3 由表7-4可得出输出函数 表达式: Z = Q 2Q 1 第五步:画出逻辑电路图
7-2* 电平异步时序逻辑电路的分析与设计方法
0 1 0 1
0 1 1 0
x 1 0 x
再由表7-4和表7-5,可建立驱动方程(控制函数) 卡诺图如图7-6所示。
图7-6 例7-2的简化卡诺图
必须指出的是:
图7-6所示卡诺图是五变量卡诺图,由于脉冲 异步时序电路不允许两个或多个输入脉冲同时 出现,也就是说,不允许输入x1x2x3出现: 011,101,110或111。而输入x1x2x3为000时, 电路保持原状态不变,故可将五变量卡诺图画 成简化形式。由于简化卡诺图的各列在完整五 变量卡诺图上是不相邻的,因此,化简时只能 在给定列中进行,并且每列只允许一个输入变 量出现。
异步时序电路分析
Q* 0 = Q′ 0clk0 ′′ Q* 1 = (Q3Q1 )clk1 Q* 2 = Q′ 2clk 2
Q* 3 = Q1Q2Q′ 3clk3
clk0 = clk0 clk1 = clk3 = Q0 clk2 = Q1
当时钟脉冲 跳变沿 到来时,方程成立 无时钟,保持原态
Q* =( JQ′ + K′ Q )CLK
′ ′ ′ clk1 = (Q′ Q* 3Q1 )clk1 1 = ( J1Q1 + K1Q1 ) ′ ′ Q* 2 = ( J 2Q2 + K 2Q2 ) clk2 = Q′ 2clk 2
′ ′ Q* 3 = ( J 3Q3 + K 3Q3 ) clk3 = Q1Q2Q′ 3clk3
(3) 输出方程
C = Q2
J1 = K1 = 1 J 2 = Q0Q1 , K 2 = 1
异步时序电路分析 例 1:
(4) 特性方程 (5) 状态方程
当时钟脉冲 跳变沿 到来时,方程成立 无时钟,保持原态
Q* =( JQ′ + K′ Q )CLK
′ ′ ′ Q* 0 = (J 0Q0 + K 0Q0 ) clk0 = (Q′ 2Q0 )CLK
J0 = K0 = 1 J1 = Q′ 3 , K1 = 1 J2 = K2 = 1
(3) 输出方程
C = Q0Q3
(2) 驱动方程
J 3 Q2Q1 ,K 3 = 1
异步时序电路分析 例 2:
(4) 特性方程 (5) 状态方程 ′ ′ Q* 0 = (J 0Q0 + K 0Q0 ) clk0 = Q′ 0clk0
计数脉冲 CLK 0 1 2 3 4 5
C = Q2
异步时序逻辑电路设计实验报告
异步时序逻辑电路的设计1.实验目的熟悉并掌握脉冲异步逻辑电路的分析方法,加深对异步时序逻辑电路的理解,掌握时序逻辑电路的设计方法及如何消除临界竞争。
2.实验器材二输入与非门74LS00反向器 74LS04三输入与非门 74LS103.实验内容用电平异步时序逻辑电路实现下沿触发的D 触发器 典型输入时间图如下:X2(CP)X1(D)Z(Q)2 6 1 5 7 1 634 3 1 67 5 58 4 54.实验步骤建立原始流程表按照输入信号的变化进行时间的划分,由题意可知设立8中不同状态,见上图画出原始流程表:状态激励状态及输出X2X100 01 11 101 ①/02/0 D/d 3/02 1/0 ②/04/0 d/d3 1/0 d/d 4/0 ③/04 d/d 5/d ④/03/05 8/1 ⑤/16/1 D/d6 d/d 5/1 ⑥/17/17 1/d d/d 6/1 ⑦/18 ⑧/15/1 d/d 7/1 化简流程表2 Y3 Y Y4 2,5 2,5 Y5 N N N N6 N N N N YY2Y10 1 01 7 N N N N Y N 8 N N N N Y Y N 12345 67画出状态合并图:选择最小闭覆盖{(231)(4)(568)(7)}并且用ABCD 分别表示:画出状态相邻图;A D BC1 2 3 8 74 56A D C BY2Y1X2X1 Y2Y1 X2X1 X2X1 Y2Y1 状态编码设二次状态用y2y1表示,用00,01,11,10分别表示A,B,C,D 四种状态,最简二进制流程表如图; 二次状态 Y2Y1 激励函数/Y2Y1和输出Z X2X1=00 X2X1=01 X2X1=11 X2X1=10 00 00/0 00/0 01/0 00/0 01 Dd/d 11/d 01/0 00/0 11 11/1 11/1 11/1 10/1 10 00/d dd/d 11/1 10/1画出卡诺图并求出激励函数和输出函数; Y2;00 01 11 10 00 0 0 0 0 01 d 1 0 0 11 1 1 1 1 10 0 d 1 1 Y2=122221y x x y x y ∙∙Y1;00 01 11 10 00 0 0 1 0 01 d 1 1 0 11 1 1 1 0 10 01Y1=212111x y x x y x ∙∙Z00 01 11 10 00 0 0 0 0 01ddZY1Y X 11 1 1 1 1 10 d 1 1 1Z=y2;根据激励函数和输出函数画出电路图:按照电路图连接号电路,并且验证结果是否与设计相符。
