学年上学期八年级期末考试美术试题(附答案)
江苏省扬州市高邮市多校联考2023-2024学年八年级上学期期末语文试题(含答案)

2023~2024学年度第一学期期末学业质量监测试题八年级语文2024.01说明:1.本试卷共6页,计22题(包含单项选择题:第3题,第7题),满分150分,考试时间150分钟。
考试结束后,请将本试卷和答题卡一并交回。
2.答题前,考生务必将本人的姓名、准考证号准确无误地填写在答题卡相应的位置上。
同时务必在试卷的装订线内将本人的姓名、准考证号、学校填好。
3.所有的试题都必须在专用的“答题卡”上作答,选择题用2B铅笔作答,非选择题在指定位置用0.5毫米黑色水笔作答,在试卷或草稿纸上答题无效。
一.积累运用(25分)学校开展“正值青春·奋斗当燃”主题活动,请你参加。
【凝聚·青春力量】阅读下面一段文字,完成1-4题。
(8分)青春是生命中最美好的时光,充满了激情、热血和无限可能。
青春是灿烂绽放的时刻。
(1)来自江苏高邮的小伙王琦获杭州亚运会男子链球冠军,他为国家赢得了荣誉,为体育事业的发展做出了巨大的贡献,他将“志存高远、自律自强、不断学习”的品质juān刻在心里。
青春是梦想追逐的时刻。
来自河北地方台的小伙杨旭获2023年中央广播电视台主持人金奖,他对主持艺术的热爱与追求,(2)不仅体现在细致入微的动作和(▲)的语调中,而且彰显于他永不满足的探索之心上,他说:因为热爱,所以执着;因为深厚,所以坚守。
青春是艰辛努力的时刻。
我们正值青春,尽管路途可能布满荆棘,但我们毫不气馁,勇往直前。
每一次失败都是一次宝贵的教训,(3)每一次努力都会使我们变得更加坚定。
1.根据拼音写汉字并给加点字注音。
(2分)juān刻(▲)气馁(▲)2.写出横线(1)句子的主干。
(2分)▲3.填入横线(2)处括号内的成语最恰当的一项是(▲)(2分)A.不折不挠B.抑扬顿挫C.惟妙惟肖D.入木三分4.将横线(3)句子改为反问句,原句意思保持不变。
(2分)▲5.根据提示,完成默写。
(9分)青春荡漾激情与活力。
热爱自然,激情永存:春爱“(1)▲,浅草才能没马蹄”;夏思“(2)▲,芳草萋萋鹦鹉洲”;秋咏“树树皆秋色,(3)▲”;冬赞“亭亭山上松,(4)▲”。
重庆市第八中学校2023-2024学年八年级上学期期末语文试题(含解析)

10.翻译下列句子。
(1)入则无法家拂士,出则无敌国外患者,国恒亡。
(2)卒然临之而不惊,无故加之而不怒。
11.下列选项中表述有误的一项是()A.甲文开头连用六个历史名人事例,论述人需要经历磨难才能担当大任。
B.甲文孟子先论证“生于忧患”,后论证“死于安乐”,篇末得出中心论点。
C.甲文第一段运用了比论证的论证方法,用来论述忧患可以激励人奋发有为。
D.乙文认为大勇者应处变不惊,能忍常人之不能忍。
12.甲乙两文都论述了成就大业者所应具备的条件,请结合文章分析两者在论证思路上有何不同。
三、现代文阅读(40分)(一)(22分)班刊创编小组在挑选适合诵读的美文时,找到如下文学类文本,请协助小组完成相应任务。
张佳玮①以前的夏天,吃完了饭,洗净碗筷,外婆便喝一声:“去乘风凉!”②——无锡话,似乎说不好“乘凉”二字,一定得“乘风凉”三个字,出口才顺。
③于是全家提了竹凳,拿了蒲扇,扶老携幼,出了门去,一路过邻居门前——夏天,大家都开着门吃晚饭——顺便呼朋引伴:“乘风凉!乘风凉!”④各家提了竹凳出来,各分一片坐了。
小孩子总是先嚷热,毕竟家里还有电风扇,乍离了风,出来一坐,觉出闷热来,立刻不高兴。
我那会儿还跟外婆抗议,什么乘凉,明明是乘热!⑤我外婆便道:“心静自然凉……”⑥我:“不懂不懂!”⑦外婆:“你数星星吧!数到一百颗,就凉了。
”⑧我那会儿数星星有个笨法子:先找到最熟悉的几颗星,以其为圆心,数周围的;左边几颗,数齐了;右边几颗,数齐了;掰着手指扒拉着,数着数着,好,一百颗了。
果然有效。
数到一百颗星星时,果然凉下来了。
⑨——现在想来,是因为心静了,是看久了幽蓝夜空,体感舒服了,是因为时候慢慢过去了,夏夜如凉水,慢慢浸下来了。
当然还有手上,轻慢摇摆的蒲扇。
14.为帮助同学们理解文章,小渝想在文段中加一些批注,请按要求帮他完成。
(1)也挺好,更舒适,只是比当年少了些风致。
(理解加点词语的含义)地阅读,这是电子书最大的优势。
河南省南阳市2023-2024学年八年级上学期期末英语试题(解析版)

2023年秋期期末调研测试试题卷八年级英语注意事项:1. 本试卷共8页,六个大题,满分120分,考试时间100分钟。
2. 本试卷分试题卷和答题卡两部分。
考生应首先阅读试题卷上的文字信息,然后在答题卡上作答,在试题卷上作答无效,交卷时只交答题卡。
一、听力理解(20小题,每小题1分,共20分)第一节听下面5段对话,每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳答案,每段对话读两遍。
1. How is the woman going there?A. By bike.B. By bus.C. On foot.2. Where could Lucy be now?A. At home.B. In the library.C. In the hospital.3. How often does the man use the computer?A. Every day.B. Every Sunday.C. Six times a week.4. What are they talking about?A. A famous museum.B. French paintings.C. A weekend plan.5. What's the woman's favorite animal?A. B. C.第二节听下面几段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳答案。
每段对话或独白读两遍。
听下面一段对话,回答第6至第7两个小题。
6. What is the girl going to draw?A. Flowers.B. Animals.C. Mountains.7 Where are the two speakers going next?A. To the park.B. To the library.C. To the art museum.听下面一段对话,回答第8至第9两个小题。
2022—2023学年度第一学期八年级上册美术期末试题

2022—2023学年度第一学期八年级上册美术期末试题学校年级姓名考号注:1.请填写清楚(学校、班级、姓名、考号)。
2.40分钟内答完全卷,满分100分一、填空题(32分,每空2分)1.中国古代仕女画重要代表作《捣练图》作者是唐代()。
2.苏州四大园林为()()()()。
3.中国画形式美:()()()()。
4.()造型运用剪、折、卷等技法,将纸制成有凹凸变化的立体艺术形象。
5.()造型运用折曲、剪刻、粘贴等方法,将纸制作成具有观赏性和实用性的立体形态的一种造型艺术。
6.柜架具有()和()的双重功能。
7.装饰布最常用的是()和()纹样。
8.( ) 指人们通过对书法作品视觉感知,运用相关知识和生活经验对书法作品进行审美判读,从而理解书法作品、书法家以及书法现象的思维活动。
二、选择题(10分,每题2分)1、彝族漆器以()色为主。
A、红白黄B、红黄黑C、红黄蓝2、《兰亭序》是书法精绝的“天下第一行书”作者是东晋( )。
A、王献之B、王羲之C、黄庭坚3、《富春山居图》是元代画家()年近80岁时创作的杰作。
A、黄公望B、梁楷C、赵孟頫4、“外师造化,中得心源”,出自唐朝画家( )。
A、倪瓒B、谢赫C、张璪5、唐代欧阳询的书法作品《九成宫醴泉铭》属于()A、楷书B、篆书C、隶书三、判断题(16分,每题2分)1、画家运用中国传统绘画泼墨泼彩技法,营造一种苍劲浑厚之美。
()2、《韩熙载夜宴图》的作者是唐寅。
()3、画家通过色彩和点、线、面这些基本造型元素来表达自己对世界的感受。
()4、徐悲鸿是中国现代杰出的画家,在艺术上主张现实主义,对中国画和西方传统的写实绘画有很高的造诣。
()5、潘天寿是中国现代杰出画家、美术教育家。
他的绘画继承传统,又大胆创新,追求壮美的表现。
()6、多宝格又称“百宝格”,专为陈设古玩器物的传统家具款式之一,以巧妙的分割和多变的造型著称。
()7、二方连续纹样是一个单位纹样向上下左右反复循环延续地排列。
江西省赣州市大余县2023-2024学年八年级上学期期末语文试题(含答案)

2023-2024学年度上学期期末检测八年级语文试题卷说明:1.全卷满分120分,考试时间150分钟。
2.请将答案写在答题卷上,否则不给分。
一、语言知识及其运用(共10分)阅读下面的文字,完成1-2题。
中国国家博物馆举行了一场名为“大唐风华”的博物展,参观者①。
此次展览的展品既有镂刻精巧的法门寺地宫珍宝,也有展现唐代风俗的壁上丹青,还有呈现胡风汉俗的三彩陶俑和多元共存的珍贵文物。
回望大唐,不禁感②,那里不仅有才华卓越的大唐诗人,有粗犷豪迈的英雄将领,也有万国衣冠拜冕旒的昂扬气象,汲取四方奇风异俗的博大胸怀。
1.文中加点字“犷”的读音和填入横线②处的字全部正确的是()(2分)A.kuǎng 嘅B.kuàng 忾C.guǎng 慨D.guāng 概2.在文中横线①处填入词语,恰当的一项是()(2分)A.连绵不断B.络绎不绝C.川流不息D.纷至沓来阅读下面的文字,完成3-5题。
江西是一片充满红色记忆的红土地,波澜壮阔的中国共产党革命史,许多源头都在江西。
星星之火在革命摇篮井冈山点燃,共和国的襁褓岁月在红都瑞金度过()人民军队的第一枪在英雄城南昌打响,工人运动的澎湃在萍乡安源发祥……_______。
只要无时无刻铭记革命先烈精神,才能不断激发中华民族的力量,凝聚起众志成城的磅礴之力,为新时代提供坚强的精神支撑,让世界的中国发展实现新的突破。
3.下列填入文章横线上的语句,衔接恰当的一项是()(1分)A.追溯雄壮史诗,传承红色精神。
B.追溯雄壮精神,传承红色史诗。
C.传承红色精神,追溯雄壮史诗。
D.传承红色史诗,追溯雄壮精神。
4.在文中括号内填入标点符号,正确的是()(1分)A.;B.,C.。
D.!5.文中画波浪线的句子有语病,下列修改正确的一项是()(2分)A.只要无时无刻铭记革命先烈精神,才能不断激发中华民族的信仰力量B.只有无时无刻铭记革命先烈精神,才能不断提高中华民族的信仰力量C.只有无时无刻铭记革命先烈精神,才能不断激发中华民族的信仰力量D.只要无时无刻铭记革命先烈精神,才能不断提高中华民族的信仰力量6.下列各句中,表达得体的一句是()(2分)A.多年不见的老同学带了许多家乡土特产来我家,我推辞不了,最后只好笑纳。
辽宁省大连市甘井子区2024-2025学年八年级上学期期中阶段性学习质量抽测数学试卷(含答案)

2024-2025学年度第一学期期中阶段性学习质量抽测八年级数学(本试卷共23道题 满分120分 考试时间共120分钟)注意:所有试题必须在答题卡上作答,在本试卷上作答无效第一部分 选择题(共30分)一、选择题(本题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.在美术字中,有些汉字是轴对称图形.下面四个汉字中,可以看作是轴对称图形的是( )A. B. C. D.2.六边形的外角和等于( )A.180°B.270°C.360°D.720°3.如图,有一池塘,要测池塘两端A ,B 的距离,可先在平地上取一个点C ,从点C 不经过池塘可以直接到达点A 和B .连接并延长到点D ,使.连接并延长到点E ,使.连接,可证,那么测量出的长就是池塘两端A ,B 的距离证明.的依据是( )(第3题)A. B. C. D.4.如图,在中,,,,点D 是的中点,,则的长度是( )(第4题)A.0.5B.1C.2D.45.如图,,若,,则的长度是()AC CD CA =BC CE CB =DE ABC DEC ≅△△DE ABC DEC ≅△△SAS AAS AAS HLRt ABC △90ACB ∠=︒30A ∠=︒2BC =AB DE AC ⊥DE EFG NMH ≅△△ 1.1EH = 3.3NH =GH(第5题)A.1.1B.2.1C.2.2D.3.36.如图,在中,,,是的角平分线,则( )(第6题)A.65°B.75°C.85°D.90°7.如图,在中,,点D 在上,且,下列结论正确的是( )(第7题)A. B. C. D.8.如图,在中,,,的高与的比是( )(第8题)A. B. C. D.9.如图,在中,以点A 为圆心,适当长为半径作弧,交于点G ,交于点H ;再分别以点G ,H为圆心,大于的长为半径作弧,两弧交于点O ;连接并延长交于点D .点P 是上的一点,过点P 分别作,,交于点E ,E 过点D 作于点M ,于点N ,交于点K ,于点L .下列线段的数量关系正确的是( )ABC △40BAC ∠=︒75B ∠=︒AD BAC ∠ADB ∠=ABC △AB AC =AC BD BC AD ==36A ∠=︒66ABC ∠=︒70C ∠=︒105ADB ∠=︒ABC △2AB =4BC =ABC △AD CE 1:11:21:32:1ABC △AB AC 12GH AO BC AD PE AB ∥PF AC ∥BC DM AB ⊥DN AC ⊥PE PF(第9题)A. B. C. D.10,如图,电信部门要在S 区修建一座电视信号发射塔.设计要求:发射塔到两个城镇A ,B 的距离相等,到两条高速公路m 和n 的距离也相等.关于发射塔应修建的位置,下列说法正确的是( )(第10题)A.线段的中点B.直线m 和n 的交角(锐角)的角平分线与线段的交点C.线段的垂直平分线和直线m 和n 的交角(锐角)的角平分线的交点D.线段的垂直平分线和线段的垂直平分线的交点第二部分 非选择题(共90分)二、填空题(本题共5小题,每小题3分,共15分)11.如图,和关于直线对称,,______°.(第11题)12.如图,,,重垂足分别为E ,F ,,若要依据证明,则需添加的一个条件是______.(第12题)13.如图,从A 处观测C 处的仰角,从B 处观测C 处的仰角,则DE DF =PE PF =2DM DL =MK NL=AB AB AB OA OB ABC △A B C '''△MN AB BC ⊥A B C '''∠=AE BC ⊥DF BC ⊥BE CF =HL BAE CDF ≅△△30CAD ∠=︒45CBD ∠=︒ACB ∠=(第13题)14.如图,五边形的内角都相等,且,,则x 的值是______.(第14题)15.如图,是等边三角形,是中线,延长至点E ,使,,垂足为F .若,,则的面积是______.(用含a 和b 的式子表示)(第15题)三、解答题(本题共8小题,共75分.解答应写出文字说明、演算步骤或推理过程)16.(本小题8分)如图,,,.求的度数.(第16题)17.(本小题8分)如图,点B ,E ,C ,F 在一条直线上,,,.求证:.ABCDE 12∠=∠34∠=∠ABC △BD BC CE CD =DF BE ⊥AB a =BD b =BDE △CD AB ⊥1A ∠=∠65B ∠=︒ACB ∠AB DE =AC DF =BE CF =A D ∠=∠18.(本小题8分)如图,在平面直角坐标系中,的顶点坐标分别为,,.(第18题)(1)请画出关于y 轴对称的图形,并直接写出顶点的坐标______;(2)关于x 轴对称的图形为.①不用画图,请直接写出三个顶点的坐标:______,______,______;②若内任意一点P 的坐标为,则点在内的对应点的坐标为______.(用含x 和y 的式子表示)(建议:先用铅笔画图,确定无误后用黑色水性笔画在答题卡上)19.(本小题8分)如图,点D 在上,点E 在上,,,和相交于点O .求证:.(第19题)20.(本小题8分)如图,中,,,平分,平分,过点O 作交,于点M ,N .求的周长.ABC △()4,1A -()1,1B --()3,2C -ABC △111A B C △1A ABC △222A B C △2A 2B 2C ABC △(),x y P 222A B C △2P AB AC AB AC =B C ∠=∠BE CD OD OE =ABC △10AB =7AC =BO ABC ∠CO ACB ∠MN BC ∥AB AC AMN △(第20题)21.(本小题10分)【课题回顾】在学习《13.4课题学习最短路径问题》时,根据“两点之间,线段最短”和“垂线段最短”探究了“将军饮马”和“造桥选址”两个问题,并初步运用探究经验解决线段和最小值的数学问题.【问题探究】如图1,在等边中,点D 为中点,点P ,Q 分别为,上的点,,,点M 是线段上的动点,连接,,求的最小值.(1)小明提出的探究思路如下:如图2,作点Q 关于直线的对称点,连接交于点M ,连接,根据“两点之间,线段最短”,可知此时的值最小.①请你运用小明的探究思路,证明此时的值最小;②求的最小值.【类比探究】(2)如图3,在平面直角坐标系中,点A 坐标为,点B 为y 轴正半轴上一点,连接,,点C 为中点,平分交边于点D ,点P 为边上的一个动点.若点M 在线段上,连接,,当的值最小时,请直接写出点P 的坐标______.(图1) (图2) (图3)(第21题)22.(本小题12分)【发现问题】在全等三角形研究“筝形”的数学活动中,学习了筝形的定义:有两组邻边分别相等的四边形叫做筝形,以及筝形的边、角、对角线的性质.小明在学完十三章《轴对称》后,将学过的角平分线的性质与判定定ABC △BC AC BC 2AP CQ ==1DQ =AD MP MQ MP MQ +AD Q 'PQ 'AD MQ MP MQ +MP MQ +MP MQ +()4,0AB 30ABO ∠=︒AB OD AOB ∠AB OB OD MC MP MC MP +理,线段垂直平分线的性质与判定定理的图形进行了整理,发现这些图形中都存在筝形,且筝形是轴对称图形.【提出问题】小明利用筝形是轴对称图形对它的面积进行了探究,得到了筝形面积与对角线的数量关系.(1)如图1,在四边形中,,,对角线与相交于点O .求证:.(图1)(图2)(第22题)【分析问题】(2)如图2,在四边形中,,,于点B ,于点D ,点M ,N 分别是,上的点,且,求的周长.(用含a 的式子表示)【解决问题】(3)①如图3,在中,点D 为内一点,平分,且.求证:.②如图4,在中,,,点D ,E 分别是边,上的动点,当四边形为筝形时,请直接写出______°.(图3)(图4)(第22题)23.(本小题13分)【活动初探】在学习等十三章《轴对称》数学活动3时,我们利用等腰三角形的轴对称性发现等腰三角形中有许多相等的线段或角,因此利用图形的轴对称性可以探究图形中边与角的数量关系.(1)如图1,在中,,点D 为中点,于点E ,于点F .求证:.ABCD AB AD =CB CD =AC BD 12ABCD S AC BD =⋅筝形ABCD AB AD a ==CB CD =AB BC ⊥AD CD ⊥AD AB MCD NCB MCN ∠+∠=∠AMN △ABC △ABC △AD BAC ∠BD CD =AB AC =ABC △80A ∠=︒30B ∠=︒BC AB AEDC BDE ∠=ABC △AB AC =BC DE AB ⊥DF AC ⊥DE DF =(图1)(图2)(第23题)【变式再探】(2)如图2,在中,,和分别为等边三角形,与相交于点G ,连接并延长,交于点D ,求证:点D 为的中点.(图3)(备用图)(第23题)【类比深探】(3)在中,,点D 为中点,,点F 为直线上一动点,点E 为射线上一动点(点E 不与点A ,C 重合),,连接.①如图3,当点F 在点A 上方,猜想并证明,,的数量关系;②若,,,请直接写出______(用含m ,n 的代数式表示).ABC △AB AC =CFA △BEA △CF BE AG BC BC ABC △AB AC =BC 30ABC ∠=︒AD CA FB FE =BE AC AE DF AC m =AE n =2m n >DF =2024-2025学年度第一学期期中阶段性学习质量抽测八年级数学参考答案第一部分 选择题(共30分)一、选择题(本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.B.2.C.3.A.4.B.5.C.6.C.7.A.8.B.9.D. 10.C.第二部分 非选择题(共90分)二、填空题(本题共5小题,每小题3分,共15分)11.90. 12.. 13.15. 14.36.15..三、解答题(本题共8小题,共75分.解答应写出文字说明、演算步骤或推理过程)16.(本小题8分)解:∵,∴.……2分∴在中,.……4分∵,∴.……6分∵在中,,∴.……8分(第16题)17.(本小题8分)证明:∵,∴.……1分∴.……2分在和中,……4分∴.……6分∴.……8分AB CD =38ab CD AB ⊥90ADC ∠=︒Rt ACD △90CAD C ∠+∠=︒1A ∠=∠145A ∠=∠=︒ABC △65B ∠=︒180ACB A B∠=︒-∠-∠1804565=︒-︒-︒70=︒BE CF =BE EC CF EC +=+BC EF =ABF △DCE △AB DE AC DF BC EF =⎧⎪=⎨⎪=⎩()SSS ABC DEF ≅△△A D ∠=∠(第17题)18.(本小题8分)解:(1);……1分图正确;……4分(第18题)(2)①,,;……7分.……8分19.(本小题8分)证明:在和中,……2分∴.……3分∴.……4分∴.∴.……5分在和中,......6分∴.......7分∴. (8)分()14,1A ()24,1A --()21,1B -()23,2C --()2,P x y -ABE △ACD △A A AB AC B C ∠=∠⎧⎪=⎨⎪∠=∠⎩()ASA ABE ACD ≅△△AE AD =AB AD AC AE -=-BD CE =OBD △OCE △BOD COE B C BD CE ∠=∠⎧⎪∠=∠⎨⎪=⎩()AAS OBD OCE ≅△△OD OE =(第19题)20.(本小题8分)证明:∵平分,平分,∴,.……1分∵,∴,.……2分∴,.……4分∴,.……6分∵…………7分∴的周长为17.……8分(第20题)21.(本小题10分)(1)①证明:如图,在上另取一点,连接,,,∵点Q 关于直线的对称点为,点M ,在上,∴,.∴.……1分在中,∵, (2)分BO ABC ∠CO ACB ∠12∠=∠34∠=∠MN BC ∥25∠=∠36∠=∠15∠=∠46∠=∠MB MO =NO NC =AMN C AM MN AN=++△AM MO NO AN=+++AM MB NC AN=+++AB AC=+17=AMN △AD M 'PM 'M Q ''M Q 'AD Q 'M 'AD MQ MQ ='M Q M Q '=''MP MQ MP MQ PQ +=+=''M PQ ''△PQ PM M Q <''+''∴.即的值最小.……3分(第21题)②解:∵是等边三角形,点D 为中点,∴,,.……4分∵,,∴.∴.……5分∵点Q 关于直线的对称点为,∴.∴.……6分∴.∵,∴是等边三角形.……7分∴.∴的最小值为4.……8分(2).……10分22.(本小题12分)(1)证明:∵,,∴垂直平分.……1分∵,∴MP MQ PM M Q '+'<'+MP MQ +ABC △BC 2AB AC BC CD ===60C ∠=︒AD BC ⊥2CQ =1DQ =3CD BD CQ DQ ==+=6AB AC BC ===AD Q '1DQ DQ ='=2BQ AP BD DQ ==-'='4CP CQ AC AP BC BQ '==-'=-=60C ∠=︒CPQ ' 4PQ CP '==MP MQ +()0,2AB AD =CB CD =AC BD ACD ABC ABCD S S S =+△△筝形()11112222ABCD S AC OD AC OB AC OD OB AC BD =⋅+⋅=+=⋅筝形即.……2分(2)如图2,延长至E ,使,连接,∵,,∴.在和中,∴.……3分∴,.∵,∴.……4分在和中,∴.……5分∴∴的周长.……6分(第22题图2)(3)①证明:如图3,过点D 作于M ,过点D 作于N ,∵平分,,,∴.……7分又∵,∴.……8分∴.12ABCD S AC BD =⋅筝形AD DE BN =CE AB BC ⊥AD CD ⊥90CDE CBN ∠=∠=︒CDE △CBN △CD CB CDE CBNDE BN =⎧⎪∠=∠⎨⎪=⎩()SAS CDE CBN ≅△△ECD NCB ∠=∠CE CN =MCD NCB MCN ∠+∠=∠MCD ECD MCN MCE ∠+∠=∠=∠MCN △MCE △CN CE MCN MCEMC MC =⎧⎪∠=∠⎨⎪=⎩()SAS MCN MCE ≅△△.MN ME =AMN △AM MN AN=++AM ME AN=++AM MD DE AN=+++AD BN AN=++2AD AB a =+=DM AB ⊥DN AC ⊥AD BAC ∠DM AB ⊥DN AC ⊥DM DN =BD CD =()Rt Rt HL BDM CDN ≅△△ABD ACD ∠=∠∵,∴.……9分∴.∴.∴.……10分(第22题图3)②100°或40°.……12分23.(本小题13分)(1)证明:∵,点D 为中点,∴平分.……1分∵,,∴.……2分(第23题图1)(2)证明:∵,∴.……3分∵和分别为等边三角形,∴.……4分∴.∴.∴.……5分∵,∴垂直平分.∴点D 为的中点 (6)分BD CD =DBC DCB ∠=∠ABD DBC ACD DCB ∠+∠=∠+∠ABC ACB ∠=∠AB AC =AB AC =BC AD BAC ∠DE AB ⊥DF AC ⊥DE DF =AB AC =ABC ACB ∠=∠CFA △BEA △60FCA EBA ∠=∠=︒ABC EBA ACB FCA ∠-∠=∠-∠GBC GCB ∠=∠GB GC =AB AC =AD BC BC(第23题图2)(3)①猜想:.证明:如图3,过点F 作于M ,过点F 作,交延长线于点N ,∴.∵,点D 为中点,∴,平分.∵,∴.∵,∴.……7分∵,∴.∴.……8分∴.在中,,∴.∴.同理.……9分∴.∴.∴.在中,,∴.……10分∴.∴.……11分(第23题图3)②或.……13分12AE AC DF =+FM AE ⊥FN BA ⊥BA 90FME FNB ∠=∠=︒AB AC =BC AD BC ⊥AD BAC ∠30ABC ∠=︒60BAD CAD FAM FAN ∠=∠=∠=∠=︒FM AE ⊥FN BA⊥FM FN =FB FE =()Rt Rt HL EFM BFN ≅△△EM BN =AE AM AB AN -=+Rt AFM △60FAM ∠=︒30AFM ∠=︒12AM AF =12AN AF =1122AE AF AB AF -=+AE AB AF =+AE AC DF AD =+-Rt ABD △30ABC ∠=︒1122AD AB AC ==12AE AC DF AC =+-12AE AC DF =+12m n +12m n -。
山西省吕梁市交城县2024-2025学年八年级上学期期中考试数学试题(含答案)
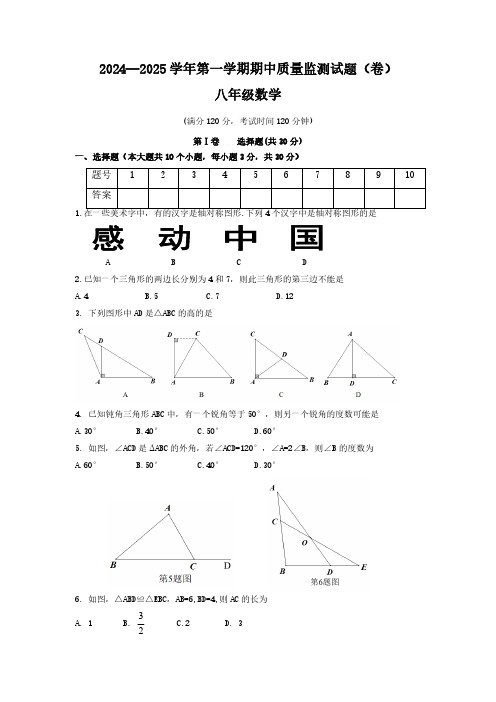
2024—2025学年第一学期期中质量监测试题(卷)八年级数学(满分120分,考试时间120分钟)第Ⅰ卷选择题(共30分)一、选择题(本大题共10个小题,每小题3分,共30分)题号12345678910答案1.在一些美术字中,有的汉字是轴对称图形.下列4个汉字中是轴对称图形的是A B C D2.已知一个三角形的两边长分别为4和7,则此三角形的第三边不能是A.4B.5C.7D.123. 下列图形中AD是△ABC的高的是4. 已知钝角三角形ABC中,有一个锐角等于50°,则另一个锐角的度数可能是A.30°B.40°C.50°D.60°5. 如图,∠ACD是ΔABC的外角,若∠ACD=120°,∠A=2∠B,则∠B的度数为A.60°B.50°C.40°D.30°6. 如图,△ABD≌△EBC,AB=6,BD=4,则AC的长为3A. 1B.C.2D. 327.在探索多边形内角和公式的过程中,多数同学采用如下表格中分割多边形的方法,并从四边形,五边形等特殊多边形的内角和计算,得到边形的内角和公式.多边形四边形五边形六边形七边形…边形图 例…内角和…以上表格中:由,,,,…,得到的结论,体现的数学思想是A. 数形结合B.类比C. 由特殊到一般D.公理化8. 如图,△ABC 与△A ′B ′C ′关于直线MN 对称,BB ′交MN 于点O ,则下列结论不一定正确的是A.∠ACB=∠A ′C ′B ′B.BO=B ′OC.AC ⊥B ′C ′D.AA ′∥ BB ′9.如图,点C 是∠AOB 的平分线上一点,CD ⊥OA ,CE ⊥OB ,垂足分别为点D ,E ,连接DE 交OC 于点F ,则下列结论中正确的个数为①CD=CE ;②DE ⊥OC ;③OD=OE ;④∠OCD=∠OCE ;⑤OF=2CFA. 2B. 3C. 4D. 510. 如图,在△ABC 中,BC 的垂直平分线分别交BC ,AB 于点D ,F.若△AFC 是等边三角形,AC=6,则DF 的长度为A.2B.3C. 4D. 6n n ︒=︒⨯-360180)24(︒=︒⨯-540180)25(︒=︒⨯-720180)26(︒=︒⨯-900180)27(︒⨯-180)2(n ︒=︒⨯-360180)24(︒=︒⨯-540180)25(︒=︒⨯-720180)26(︒=︒⨯-900180)27(︒⨯-180)2(n第Ⅱ卷 非选择题(共90分)二、填空题(本大题共5个小题,每小题3分,共15分)11. 如果一个正多边形的内角和为1620°,那么这个正多边形的一个外角的度数为 .12. A ,B 两点的坐标分别是(,)和(,4),并且A ,B 两点关于轴对称.则的值为 .13.如图,点B ,F ,C ,E 在同一条直线上,BF=CE ,AB ∥DE ,请添加一个条件,使△ABC ≌△DEF ,添加的条件可以是 .(填一个即可)14.如图,已知P 是射线ON 上一动点,∠AON=40°,当∠A=时,△AOP 为等腰三角形. 15.如图,AD 是△ABC 的中线,在AD 上取一点F ,连接BF 并延长交AC 于点E ,使AE=EF.若AC=5,AE=3,则BE 的长为 .三、解答题(本大题共8个小题,共75分)16.(6分)如图,已知△ABC ,请过点A 作一条直线,将△ABC 分成面积相等的两部分.(尺规作图,不写已知、求作、作法,只保留作图痕迹)a b c y b c a ++17.(8分)在如图所示的正方形网格中,以格点为顶点的三角形称为格点三角形,请按要求画出一个与△ABC关于某条直线对称的格点三角形.作图要求:①在四幅网格图中各画一个三角形;②所作三角形不能重复.18.(8分)如图,在△ABC中,AD⊥BC,垂足为D,BE平分∠ABC,交AD于点F,若∠BAC=70°,∠C=60°时,求∠AFB的度数19.(10分)如图,D,E是△ABC的边BC上两点,若BE=CD,∠ADB=∠AEC.求证:AB=AC.20.(10分)如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别为E,F,BE=CF.求证:AD是△ABC的角平分线.21.(10分)如图,点E是∠AOB的平分线上一点,∠MEN的两边分别与∠AOB的两边交于点M,N,且∠AOB+∠MEN=180°,EC⊥OA于点C,若△OEN和△OEM的面积分别为50和30.请求出△CEM的面积.22.(10分)如图,在等边△ABC 中,D 是AC 的中点,E 是BC 延长线上的一点,且CE=CD ,DM ⊥BC ,垂足为M.(1)求证:M 是BE 的中点;(2)若CM=2,求BE 的长度.23.(13分)综合探究:探索等腰三角形中相等的线段问题情境:数学活动课上,老师提出了一个问题:等腰三角形底边中点到两腰的距离相等吗?同学们就这个问题展开探究.问题初探:(1)希望小组的同学们根据题意画出了相应的图形,如图1.在△ABC 中,AB=AC ,D 是BC 的中点,DE ⊥AB ,DF ⊥AC ,垂足分别为点E ,F.经过合作,该小组的同学得出的结论是DE=DF.并且展示了他们的证法如下:证明:如图1,∵DE ⊥AB ,DF ⊥AC ,∴∠DEB=∠DFC=90°∵AB=AC ,∴∠B=∠C (依据1)∵D 是BC 的中点,∴BD=CD在△BDE 和△CDF 中∴△BDE ≌△CDF (依据2)∴DE=DF①请写出依据1和依据2的内容依据1: . 依据2: .⎪⎩⎪⎨⎧=∠=∠∠=∠CD BD CB DFCDEB②请你应用图2写出一种不同于希望小组的证法.问题再探:(2)未来小组的同学经过探究又有新的发现,如果在等腰三角形ABC中,作腰AB上的高CG,如图3.则CG与DE有确定的数量关系.请你直接写出这个数量关系为 .类比探究:(3)奋斗小组的同学认真研究过后,发现了以下两个正确结论:①在图4中,若DE,DF分别为△ABD和△ACD的中线,那么DE=DF仍然成立;②在图5中,若DE,DF分别为△ABD 和△ACD的角平分线,那么DE=DF仍然成立.请你选择其中一个结论,写出证明过程.2024—2025学年第一学期期中质量监测试题(卷)八年级数学答案一、选择题(本大题共10个小题,每小题3分,共30分)1—5 C D D A C 6—10 C C C C B二、填空题(本大题共5个小题,每小题3分,共15分)11. 12. 2 13. 答案不唯一,如AB=DE 14.40°或70°或100° 15. 8三、解答题(本大题共8个小题,共75分)16.(6分)图略17.(每图2分,共8分)参考答案如下:18.(8分)解:∵∠BAC=70°,∠C=60°∴∠ABC=50°………………………… 2分∵BE 平分∠ABC∴∠EBC=∠ABC=25°………………………… 4分 ∵AD ⊥BC∴∠FDB=90°………………………… 6分∴∠AFB=∠EBC+∠FDB=115°………………………… 8分19.(10分)证明:∵∠ADB=∠AEC∴∠ADE=∠AED………………………… 2分∴AD=AE………………………… 4分在△ABE 与△ACD 中………………………… 6分︒⎪⎭⎫ ⎝⎛1136021⎪⎩⎪⎨⎧=∠=∠=CD BE ADEAED AD AE∴△ABE ≌△ACD(SAS) ………………………… 8分∴AB=AC ………………………… 10分20.(10分)证明:∵D 是BC 的中点∴BD=CD………………………… 2分∵DE ⊥AB,DF ⊥AC∴∠BED=∠CFD=90° ………………………… 4分在Rt △BED 与Rt △CFD 中∴△BED ≌△CFD(HL) ……………………6分∴∠B=∠C ……………………7分∴AB=AC……………………8分∵D 是BC 的中点∴AD 是△ABC 的角平分线……………………10分21.(10分)解:过点E 作ED ⊥OB 于点D∴∠ODE=∠EDN=90°∵CE ⊥OA,OE 平分∠AOB∴∠OCE=90°,CE=DE………………………… 1分∴∠OCE=∠EDN∠AOB+∠CED=180°………………………… 2分∵∠AOB+∠MEN=180°∴∠CED=∠MEN………………………… 3分∴∠CED-∠MED=∠MEN-∠MED即∠CEM=∠DEN………………………… 4分在△CEM 和△DEN 中∴△CEM ≌△DEN(ASA)∴………………………… 5分⎩⎨⎧==CDBD CFBE ⎪⎩⎪⎨⎧∠=∠=∠=∠DEN CEM DE CE EDN OCE DEN CEM S S ∆∆=在Rt △COE 和Rt △DOE∴△COE ≌△DOE(HL)…………………………6 分∴………………………… 7分设∵∴∴………………………… 8分∵∴∴………………………… 9分∴………………………… 10分22.(第一问5分,第二问5分,共10分)证明:(1)连接BD ……………………… 1分 ∵△ABC 是等边三角形,D 是AC 的中点∴BD 平分∠ABC ,∠ABC=∠ACB=60°∴∠DBC=∠ABC=30° (2)分∵CE=CD∴∠E=∠CDE…………………………3分∴∠ACB=∠E+∠CDE∴∠E=30°∴∠E=∠DBC=30°…………………………4分∴BD=ED∵DM ⊥BE∴M 是BE 的中点…………………………5分(2)解:由(1)可知:⎩⎨⎧===OEOE DECE DOE COE S S ∆∆=xS S DEN CEM ==∆∆30=∆OEM S 30+=∆x S COE 30+=∆x S DOE 50=∆OEN S 5030=++x x 10=x 10=∆CEM S 21∠ACB=60°,M 是BE 的中点∵DM ⊥BE∴∠DME=90°…………………………6分∴∠CDM=30°∴CD=2CM…………………………7分∵CM=2∴CD=4∵CD=CE∴CE=4…………………………8分∴ME=CM+CE=6…………………………9分∵M 是BE 的中点∴BE=2ME=12…………………………10分23.(第一问6分,①各1分,②4分,第二问2分,第三问5分,共13分)(1)①依据1:等腰三角形的两个底角相等或等边对等角 ………………… 1分 依据2:两角分别相等且其中一组等角的对边相等的两个三角形全等或角角边或AAS ………………… 2分②(4分)答案不唯一,如连接AD ………………… 3分∵AB=AC,D 是BC 的中点∴AD 是∠BAC 的平分线 ………………… 5分∵DE ⊥AB,DF ⊥AC∴DE=DF ………………… 6分(2)(2分)CG=2DE …………………… 8分(3)(5分)选择①证明:∵DE ,DF 是△ABD 和△ACD 的中线∴BE=AB ,CF=AC ………………………… 9分 ∵AB=AC∴BE=CF,∠B=∠C ………………………… 10分又∵D 是BC 的中点∴BD=CD ………………………… 11分在△BDE 与△CDF 中2121⎪⎩⎪⎨⎧=∠=∠=CD BD CB CFBE∴△BDE ≌△CDF(SAS) ………………………… 12分∴DE=DF ………………………… 13分选择②证明:∵AB=AC,D 是BC 的中点∴∠B=∠C,BD=CD,AD ⊥BC∴∠ADB=∠ADC=90°………………………… 9分 又∵DE,DF 分别是△ABD 和△ACD 的平分线∴∠BDE=∠CDF=45°………………………… 10分 在△BDE 与△CDF 中∴△BDE ≌△CDF(ASA) ………………………… 12分 ∴DE=DF ………………………… 13分 ⎪⎩⎪⎨⎧∠=∠=∠=∠CDF BDE CDBD CB。
2022-2023学年天津市西青区八年级(上)期末数学试卷+答案解析(附后)

2022-2023学年天津市西青区八年级(上)期末数学试卷1. 下列等式从左到右的变形,是因式分解的是( )A. B.C. D.2. 下列计算结果正确的是( )A. B. C. D.3. 若分式有意义,则x的取值范围为( )A. B. C. D.4. KN95型口罩可以保护在颗粒物浓度很高的空间中工作的人不被颗粒物侵害,也可以帮助人们预防传染病.“KN95”表示此类型的口罩能过滤空气中的粒径约为的非油性颗粒.其中,用科学记数法表示为( )A. B. C. D.5. 如果一个多边形的内角和与外角和相等,那么这个多边形是( )A. 四边形B. 五边形C. 六边形D. 七边形6. 在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的是( )A. B. C. D.7. 下列长度的三条线段,能构成三角形的是( )A. 3,10,5B. 4,8,4C. 5,13,12D. 2,7,48.如图,≌,,,则AC的长度等于( )A.B.C.D.9. 计算的结果是( )A. B.C. D.10. 已知,,则的值为( )A. 25B. 36C. 11D. 1611. 如图,点P为内一点,过点P的线段MN分别交AB,BC于点M,N,且M,N分别在PA,PC的垂直平分线上.若,则的度数为( )A. B. C. D.12. 如图,已知点C是的平分线AC上一点,,,点E,F为垂足,点B在AE的延长线上,点D在AF上,若,,,则AE的长为( )A. 14B. 15C. 16D. 1713. 计算:______ .14. 计算:______ .15.如图,,,要使≌,则应补充条件:______ 填写一个即可16. 若,,则的值为______ .17. 如图,已知等边,过AB边上一点P作于点E,点Q为BC延长线上一点,取,连接PQ,交AC于M,已知EM的长为2,则等边三角形的边长为______ .18. 如图,在中,,,,BD是的角平分线,点P,点N分别是BD,AC边上的动点,点M在BC上,且是否存在最小值?______ 填“是”或“否”如果存在,请直接写出此时的最小值;如果不存在,请说明理由.______ .19. 分解因式:;先化简,再求值:,其中,20. 计算:;先化简,再求值:,其中21.如图,AD是的高,AE,BF是角平分线,它们相交于点O,,,求和的度数.22. 已知平面直角坐标系中,点A,B,C的坐标分别为,,作出关于x轴对称的;直接写出,,三点的坐标______ ,______ ,______ ;直接写出关于直线直线n上各点的横坐标都是对称的点的坐标______ .23. 注意:为了使同学们更好地解答本题,我们提供了一种解题思路,你可以依照这个思路,填写表格,并完成本题解答的全过程.如果你选用其他的解题方案,此时,不必填写表格,只需按照解答题的一般要求,进行解答即可.中国是最早发现并利用茶的国家,形成了具有独特魅力的茶文化,每年5月21日为国际茶日.某茶店5月份第一周绿茶、红茶的销售总额分别为1500元,900元,已知红茶每克售价是绿茶每克售价的倍,红茶的销售量比绿茶的销售量少3000克.问绿茶、红茶每克的售价分别是多少元?设绿茶每克销售价格为x元,则用含x的式子把表格补充完整;售价元/克销售量克销售总额元绿茶x______1500红茶____________900列出方程,完成本题解答.24. 如图,点C在线段AB上,,,,CF平分求证:;请你写出CF与DE的位置关系,并说明理由.25.如图,等边的边长为3,点D是AB延长线上的一个动点,以CD为边在AD 上方作等边,过点A作,连接MB并延长,交AN于点求证:;当时,求的度数;在点D的运动过程中,线段BN的长度是否会发生变化?若不变,则求出BN的长度;若变化,请说明理由.答案和解析1.【答案】C【解析】解:等式从左到右的变形是整式乘法,不是因式分解,故本选项不符合题意;B.等式从左到右的变形不是因式分解,故本选项不符合题意;C.等式从左到右的变形是因式分解,故本选项符合题意;D.等式从左到右的变形不是因式分解,故本选项不符合题意;故选:根据因式分解的定义逐个判断即可.本题考查了因式分解的定义,能熟记因式分解的定义是解此题的关键,把一个多项式化成几个整式的积的形式,叫因式分解.2.【答案】D【解析】解:,故本选项不符合题意;B.,故本选项不符合题意;C.,故本选项不符合题意;D.,故本选项符合题意;故选:先根据同底数幂的乘法,幂的乘方与积的乘方进行计算,再得出答案即可.本题考查了同底数幂的乘法法则和幂的乘方与积的乘方法则,,能熟练掌握同底数幂的乘法法则和幂的乘方与积的乘方法则是解此题的关键.3.【答案】A【解析】解:要分式有意义,则x的取值范围为,即,故选:根据分式有意义,则要求分式分母不为0,即可求得答案.本题考查了分式有意义的条件,掌握分式有意义的条件是解题的关键.4.【答案】B【解析】用科学记数法表示较小的数,一般形式为,其中,n为由原数左边起第一个不为零的数字前面的0的个数所决定.解:用科学记数法表示为:故选:本题考查了科学记数法,用科学记数法表示较小的数,一般形式为,其中,n 为由原数左边起第一个不为零的数字前面的0的个数所决定.5.【答案】A【解析】解:设多边形的边数为n,根据题意,解得故选:利用多边形的内角和与外角和公式列出方程,然后解方程即可.本题主要考查了多边形的内角和定理与外角和定理,熟练掌握定理是解题的关键.6.【答案】A【解析】解:选项B、C、D不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形,选项A能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形,故选:根据如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.本题考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.7.【答案】C【解析】解:A、,不能够组成三角形,不符合题意;B、,不能够组成三角形,不符合题意;C、,能够组成三角形,符合题意;D、,不能组成三角形,不符合题意.故选:根据“三角形任意两边之和大于第三边,任意两边之差小于第三边”对各选项进行进行逐一分析即可.本题考查了三角形的三边的关系,正确理解三边关系定理是解题关键.8.【答案】C【解析】解:≌,,,,,,,,,故选:根据全等三角形的性质得出,求出,求出DC长,再求出答案即可.本题考查了全等三角形的性质,能熟记全等三角形的性质是解此题的关键,全等三角形的对应边相等,对应角相等.9.【答案】C【解析】解:原式故选:直接利用单项式乘多项式,进而计算得出答案.此题主要考查了单项式乘多项式,正确掌握相关运算法则是解题关键.10.【答案】D【解析】解:,,故选:根据,求解即可.本题考查完全平方公式,解题的关键是熟练运用完全平方公式,属于中考常考题型.11.【答案】B【解析】【分析】本题考查的是线段的垂直平分线的性质、等腰三角形的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.根据平角的概念求出,根据线段垂直平分线的性质得到,,得到,,根据三角形的外角性质、三角形内角和定理计算,得到答案.【解答】解:,,,N分别在PA,PC的垂直平分线上,,,,,,,,12.【答案】A【解析】解:点C是的平分线AC上一点,,,,,在与中,,≌,在与中,,,设,则,,,解得:故选:欲求AE的长度,需要通过证全等三角形,利用全等三角形的对应边相等,创设条件证出线段相等,进而求得AE的长,使问题得以解决.本题考查了角平分线的性质和全等三角形的判定与性质.角平分线的性质:角的平分线上的点到角的两边的距离相等.13.【答案】1314【解析】解:,故答案为:利用乘法分配律,进行计算即可解答.本题考查了有理数的混合运算,准确熟练地进行计算是解题的关键.14.【答案】【解析】解:原式故答案为:根据负整数指数幂以及单项式乘单项式的计算方法进行计算即可.本题考查单项式乘单项式以及负整数指数幂,掌握单项式乘多项式的计算方法以及负整数指数幂的运算性质是正确解答的前提.15.【答案】或或【解析】解:,,即,又,添加时,由SAS可以判定≌;当添加时,由AAS可以判定≌;当添加时,由ASA可以判定≌;故答案为:或或由推知,已知一对边和一对角对应相等,所以根据AAS或SAS或ASA都可以推知两个三角形全等.本题考查三角形全等的判定方法;判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、添加时注意:AAA、SSA不能判定两个三角形全等,不能添加,根据已知结合图形及判定方法选择条件是正确解答本题的关键.16.【答案】15【解析】解:,故答案为:根据幂的乘方,可化成要求的形式,根据同底数幂的除法,可得答案.本题考查了同底数幂的除法,先化成要求的形式,再进行同底数幂的除法.17.【答案】4【解析】解:过P作交AC于F,如图所示:,是等边三角形,,,,,是等边三角形,,,,,,,在和中,,≌,,,,,故答案为:过P作交AC于F,得出等边三角形APF,推出,根据等腰三角形性质求出,证≌,推出,推出即可.本题考查了全等三角形的性质和判定,等边三角形的性质和判定,等腰三角形的性质,平行线的性质等知识点的应用;熟练掌握等边三角形的性质与判定,证明三角形全等是解决问题的关键.18.【答案】是【解析】解:如图所示,作点M关于BD的对称点,连接,则,,,当N,P,在同一直线上,且时,的最小值等于垂线段的长,故答案为:是;存在,理由如下:在中,,,的最小值为,故答案为:作点M关于BD的对称点,连接,则,,当N,P,在同一直线上,且时,的最小值等于垂线段的长,利用含角的直角三角形的性质,即可得到的最小值.本题主要考查了最短路线问题,凡是涉及最短距离的问题,一般要考虑线段的性质定理,结合轴对称变换来解决,多数情况要作点关于某直线的对称点.19.【答案】解:原式;原式【解析】利用提公因式法以及完全平方公式解答即可;根据平方差公式和完全平方公式化简后,再把a、b的值代入计算即可.本题考查了提公因式法分解因式以及整式的混合运算,掌握乘法公式是解答本题的关键.20.【答案】解:原式;原式,当时,原式【解析】先计算乘方,再计算乘法;先根据分式的混合运算顺序和运算法则化简原式,再将a的值代入计算即可.本题主要考查分式的化简求值,解题的关键是掌握分式的混合运算顺序和运算法则.21.【答案】解:在中,,,平分,BF平分,,是的高,,在中,,,【解析】AD是的高,利用三角形内角和定理,可求出的度数,结合角平分线的性质,可得出,的度数,在中,利用三角形内角和定理,可求出的度数,结合,可求出的度数,再在中,利用三角形内角和定理,可求出的度数.本题考查了三角形内角和定理以及角平分线的性质,牢记“三角形内角和是”是解题的关键.22.【答案】【解析】解:如图,即为所求.由图可得,,,故答案为:;;由题意可知,直线n即为直线,即点与点关于直线对称,点的坐标为故答案为:根据轴对称的性质作图即可.由图可直接得出答案.根据轴对称的性质可得答案.本题考查作图-轴对称变换,熟练掌握轴对称的性质是解答本题的关键.23.【答案】【解析】解:设绿茶每克销售价格为x元,则红茶每克销售价格为元,由题意得:绿茶的销售量为克,红茶的销售量为克,故答案为:克,,;由题意得:,解得:,经检验,是原方程的解,且符合题意,,答:绿茶每克销售价格为元,红茶每克销售价格为元.根据题意和售价销售量=销售总额即可得出结论;由题意:红茶的销售量比绿茶的销售量少3000克.列出分式方程,解方程即可.本题考查了分式方程的应用,找准等量关系,正确列出分式方程是解题的关键.24.【答案】证明:,,在和中,,≌;;解:理由:≌,,又平分,【解析】根据SAS即可证明;利用等腰三角形的三线合一的性质即可证明.本题考查全等三角形的判定和性质、等腰三角形的性质等知识,解题的关键是得到≌25.【答案】证明:,都是等边三角形,,,,,在和中,,≌,;解:≌,,,,;解:结论:BN的长度不变,理由:设CD交BM于点,,,,,,,【解析】证明≌,可得结论;利用三角形内角和定理,全等三角形的性质解决问题即可;证明,可得本题属于三角形综合题,考查了等边三角形的性质,全等三角形的判定和性质,直角三角形30度角的性质等知识,解题的关键是正确寻找全等三角形解决问题.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中八年级美术期末质量检测试题
一、单项选择。
(每题2分,共10分)
1.藏书印是(、、)三者完美结合的艺术。
A. 色彩、图形
B. 书法、章法、刀法
C. 图案、章法、刀法
D. 书法、章法
2.《朝元仙仗图》属于哪种绘画形式()
A. 版画
B. 速写
C. 白描
D. 素描
3.书籍设计狭义的是指书籍的开本、封面、()和装订形式等属于书籍外观形象的设计。
A. 造型设计
B. 封面设计
C. 护封设计
D. 内容设计
4.《自由引导人民》的构图方式是下列哪种()。
A. C. D.
5.中国山水画寄托着艺术家对大自然的热爱之情,因此()是中国山水画的灵魂所在。
A.笔墨
B. 诗书
C. 纸砚
D.意境
二、判断。
(每题2分,共10分)
1. 线是构成视觉艺术形象的唯一元素。
()
2. 色彩是绘画的强有力的语言。
()
3. 绘画中的构图要体现形式美法则。
()
4. 藏书印一般选用的文字多是篆体,分白字、红字两种。
()
5. 绘画作品是在二维的平面上表现物象,无法表现空间感。
()
三、技能题。
(10分)
请同学们设计一枚藏书票。
以动物或花卉为主,款式为方形的小品图案。
要求:图案(动物或花卉自选),拉丁文EXLIBRIS,票主名:莫言藏书,作者签名:莫言,时间:2016
注意:1、以“莫言”为作者进行签名设计,不得出现学生本人的姓名。
2、用手中的书写工具设计单色草图即可。
初中八年级美术期末质量检测试题评分标准
一、单项选择。
(每题2分,共10分)
1. B. 书法、章法、刀法
2. C. 白描
3.C. 护封设计
4.B.
5. D.意境
二、判断。
(每题2分,共10分)
1.(错)
2.(对)
3.(对)
4.(错)
5.(错)
三、技能题。
(10分)
请同学们设计一枚藏书票。
以动物或花卉为主,款式为方形的小品图案。
方形构图为2分,主要图案造型生动准确为3分,拉丁文EXLIBRIS为1分,票主名:莫言藏书为2分,作者签名:莫言为1分,时间:2016为1分。
