内方位元素(课件)讲解
合集下载
第4章 双像立体测图原理与立体测图
二、人造立体视觉
立体观察条件
①两张像片必须是从不同摄影站摄取
的。
②两眼各看一张像片，即必须分像。
③必须使同名像点的连线与眼基线平
行，以保证两视线 在同一个视平面
内。
④比例尺基本一致（比例尺的差异小
于比例尺的16%）
精选版课件ppt
A
C a1 c1 b1 c 2 P1
OL BL
C L AL
B
a2 b2 P2
航向重叠60％
精选版课件ppt
27
§4-2立体像对与立体测图原理
1、立体像对的定义（Stereo Pair）
由不同摄站获取的，具有一定影像重叠的两张像片。
o1 a1 S1
oa22 S2
A
精选版课件ppt
28
§4-2立体像对与立体测图原理
1、立体像对的定义（Stereo Pair）
精选版课件ppt
几何表面。
A
B
精选版课件ppt
1 B M B
37
§4-2立体像对与立体测图原理
三、立体像对恢复固有几何关系的过程
利用像对进行立体测图，必修重建与实地相似且符合比 例尺及空间方位的几何模型，若能恢复像片对的内、外方 位元素，就能恢复像片固有的几何关系，因此，重建立体 模型的过程是：
（1）恢复像片对的内方位元素，也称内定向。 （2）恢复像片对的外方位元素。相对定向和绝对定向。
精选版课件ppt
3
§4-1双像立体测图原理与立体测图
一、人眼的天然立体视觉 角膜
视差理论
虹膜 水晶体
瞳孔 虹膜
韧带
人眼的结构
轴视 玻璃体
视网膜
盲斑
脉络膜
武大《摄影测量》课件—第05讲 共线方程的实用形式
S
X （X ）
第五讲 共线方程的实用形式 Applied Collinearity Condition Equations
[一]用角元素表达方向余弦的共线方程
1、
x、、
x
Y
y
z
X x Y R y Z z
第五讲 共线方程的实用形式 Applied Collinearity Condition Equations
[一]用角元素表达方向余弦的共线方程
1、
x
、、
X X Y R Y Z Z
[一]用角元素表达方向余弦的共线方程
1、 x、、
Z
z y
Y
x
S
X
y x
x
N
Y
X
第五讲 共线方程的实用形式 Applied Collinearity Condition Equations
[一]用角元素表达方向余弦的共线方程
y
Y
P
X x cos y sin Y x sin y cos
X Y Z
X Y Z
X R x Y Z
X x Y R y Z z
x R x R R y z
b1 cos y sin sin y sin cos
b2 cos y cos sin y sin sin b3 sin y cos c1 sin y sin cos y sin cos
摄影测量坐标系ppt课件
像 片 外 方 位Z 角 元 素
D
像片倾角
Z zy Y
x s
o
Y
X
像片旋角
v
N
方位角
A
X
§3.6 像点的空间直角坐标变换 与中心投影构像方程
一
像
点 x x'cos y'sin 的 y x'sin y'cos
y y’
a x’
平 面
o
x
坐 标
x
y
cos sin
sin x
cos
y
变
X A
YA
Z A
Xs Ys Zs
X x a1 a2 a3 x
Y
Z
R y f
bc11
b2 c2
b3 c3
y f
x f a1 ( X A X s ) b1 (YA Ys ) c1 (Z A Z s ) a3 ( X A X s ) b3 (YA Ys ) c3 (Z A Z s )
cos
0
0 sin cos sin 0 cos 0
0 1
a1 a2 a3
b1
b2
b3
c1 c2 c3
2、以X 轴为主轴的’-’-’转角系统的坐标变换
a1 coscos a2 cossin a3 sin b1 cossin sin sin cos b2 coscos sin sin sin b3 sin cos c1 sin sin cossin cos c2 sin cos cossin sin c3 coscos
正交变换矩阵的特点
a2 1
a22
a32
1
b2 1
b2 2
无人机航测技术与应用课件：航空摄影测量基础
单眼观察景物时，人感觉到的仅是景物的中心构像，好像一 张像片，得不到景物的立体构像，无法判断远近。只有用双眼观 察景物，才能判断景物的远近，得到景物的立体效应。这种现象 称为人眼的立体视觉，即在双眼观察下能感觉出景物有远近凸凹 的视觉，称为立体视觉。正是根据这一原理，在摄影测量中要求 对同一地区在两个不同位置拍摄两张像片，构成一个立体像对， 进行立体观察与量测。
航摄像片的特点
当像片倾斜、地面起伏时，地面点在航摄像片上构像相对于理想 情况下的构像所产生的位置差异称像点位移
航摄像片与地形图的区别 1）投影方式的不同：地形图为正射投影，航摄像片为中心投影
AC B
c ab
c ba S
B
A
C
2）航片存在两项误差：像片倾斜引起的像点位移，地形起
伏引起的像点位移
s
5.2双像解析摄影测量
5.2.1共线方程 4共线方程
X
Y
Z1
X A X s YA Ys Z A Zs
X
Y
Z
1
X A
YA ZA
Xs Ys Zs
X x a1 a2 a3 x
Y Z
R y f
bc11
b2 c2
b3 c3
y f
5.2双像解析摄影测量
y
RT
Y
a2
b2
c2
Y
f Z a3 b3 c3Z
其中R是一个正交矩阵，它由9个方向余弦构成
5.2双像解析摄影测量
5.2.1共线方程 3空间直角坐标系的旋转变换
a1 a2 a3 cos Xx cos Xy cos Xz
R b1
b2
b3
c
osYx
cosYy
航摄像片的特点
当像片倾斜、地面起伏时，地面点在航摄像片上构像相对于理想 情况下的构像所产生的位置差异称像点位移
航摄像片与地形图的区别 1）投影方式的不同：地形图为正射投影，航摄像片为中心投影
AC B
c ab
c ba S
B
A
C
2）航片存在两项误差：像片倾斜引起的像点位移，地形起
伏引起的像点位移
s
5.2双像解析摄影测量
5.2.1共线方程 4共线方程
X
Y
Z1
X A X s YA Ys Z A Zs
X
Y
Z
1
X A
YA ZA
Xs Ys Zs
X x a1 a2 a3 x
Y Z
R y f
bc11
b2 c2
b3 c3
y f
5.2双像解析摄影测量
y
RT
Y
a2
b2
c2
Y
f Z a3 b3 c3Z
其中R是一个正交矩阵，它由9个方向余弦构成
5.2双像解析摄影测量
5.2.1共线方程 3空间直角坐标系的旋转变换
a1 a2 a3 cos Xx cos Xy cos Xz
R b1
b2
b3
c
osYx
cosYy
方位角PPT教学课件
陶渊明的诗歌，以歌咏田园生活的居多，后世称他为田园诗人。陶渊明的 田园诗主要见于他的组诗《饮酒》、《归园田居》、《拟古》、《和郭主簿》。 他的五言诗成就最高，诗歌的意境下平和、静穆、深远，在中国诗歌史上有着 重要的地位。他那种淡泊明志的人生态度，对读书人的影响很深。
通过虚构（
）一
个和平、美好、没有剥…削、没有压迫、人
人一薪借井徘试久 生世者问灶徊携去 死异向采有丘子山 幻朝我薪遗龚侄泽 化市言者处间辈游 ，，，，，，，， 终此死此桑依披浪 当语没人竹依榛莽 归其无皆残昔步林 空不复焉朽人荒野 无虚余知株居墟娱 。。。？。。。。
欢日漉山悔 来入我涧恨 苦室新清独 夕中熟且策 短暗酒浅还 ，，，，， 已荆只可崎 复新鸡以岖 至代招濯历 天明近我榛 旭烛局足曲 。。。。。
60°
C ●10°
●A
南
练一练
(1) 教 师 宿 舍 在 校 门 口 的 北 偏 西 15° 的 方向,试画出教师宿 舍方向的射线.
(2) 教 学 楼 在 校 门 口
的
方向.
北
学生 ● ● 宿舍 餐厅
●
综合楼
●
操场
●
办公楼
●
教学楼
●
校门
学校平面示意图
你知道他是谁?
杨利伟乘坐”神州”五号遨游太空时,我国当时 派出远望一号~四号船队,跟踪检测,其中远望一、 二号停在太平洋洋面上，某一时刻，分别测得杨 利伟在北偏东60°和北偏东30°的方向，你能 在下图中画出当时杨利伟所处的位置吗？ 另一时刻，杨利伟在“神州五号”上测得“远望 一号”“远望二号”在他的南偏西70°和南偏 西20°的方向，你能在下图中画出此时杨利伟 所处的位置吗？
练一练
北
高中化学人教版必修第一册课件：4.1原子结构与元素周期表
3.卤素单质的化学性质
(1)与氢气反应
①卤素单质与氢气反应的条件及生成物的稳定性
卤素单质 与H₂反应条件 氢化物稳定性
F₂ 暗处 很稳定
Cl加热
较稳定 不如HCl稳定 不稳定、易分解
②随原子序数的递增 ，卤 素 单质与H₂化合越来越_难，生成的氢化物 的 稳定性逐渐减弱，元素的非金属性逐渐减 弱。
二、卤族元素
(2)卤素单质间的置换反应
实验①中：试管内液体静置后分层，上层为无色，下层为橙红色，反应
的化学方程式：Cl₂+2NaBr===2NaCl+Br₂ _;
实验②中：试管内液体静置分层，上
层为无色，下层为紫红色，反应的化
学方程式：2 KI+Br₂===2KBr+I₂ ;
氯水 CCl₄
0 振荡
二、卤族元素(2)卤族元素原子结构和性质的递变性：
结构及性质
规律
原子半径 单质的氧化性
F Cl Br I 原子半径逐渐增天
F₂Cl₂Br₂I₂ 氧化性逐渐减弱
阴离子的还原性
F CI Br I 还原性逐渐增强
与H₂化合的难易程度 氢化物的稳定性
F₂Cl₂Br₂I₂ 与H₂ 化合越来越难
HF HCl HBr HI 稳定性逐渐减弱
同主族 元素 (自上 而下)
电子层数 逐渐增多
原子半径 逐渐增大
失电子能力 逐渐增强
金属性逐 渐增强
得电子能力 逐渐减弱
非金属性 逐渐减弱
【课堂回眸】
最外层电子数 电子层数 原子半径
类似性 递变性
与氧气反应 与水反应
碱金属元 素的原子 结构
碱金属单 质的物理 性质
碱金属单 质的化学 性质
无人机测绘技术 单元四 像片方位确定
单元四像片方位确定（1）教案头（2）教学内容1）概述本单元通过对摄影测量中常用的物方及像方空间坐标系的讲解，使学生认识各种坐标系的建立方法，并学会建立像片框标坐标系。
通过对航摄像片内、外方位元素的讲解，使学生能够对像片方位有一个宏观认识，并且能初步确定像片方位。
2）预备知识坐标系统是数学或物理学用语，定义为对于一个n维度系统的每一点给定唯一的n个标量，成一对一的对应之系统。
定义每一个坐标系统都应该说明坐标轴和原点。
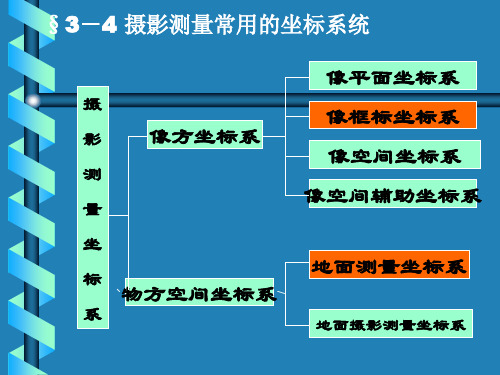
3）教学内容摄影测量几何处理的任务是根据像片上像点的位置确定相应地面点的空间位置，为此，首先必须选择适当的坐标系来定量描述像点和地面点，然后才能实现坐标系的转换，从像方测量值求出相应点在物方的坐标。
摄影测量中常用坐标系有两大类：一类是用于描述像点的位置，称为像方坐标系；另一类是描述地面点的位置，称为物方坐标系。
①像方坐标系（50分钟）像方坐标系用来表示像点的平面坐标和空间坐标。
◆像平面坐标系（25分钟）像平面坐标系是以主点为原点的右手平面坐标系，用O-xy表示。
A.作用：表示像点在像平面上的位置。
B.原点和坐标轴a.框标坐标系以像主点为坐标原点，框标连线的航线方向为x轴建立的右手系。
b.主纵线坐标系原点在主纵线上，且以主纵线为y轴，no方向为y轴正方向的右手系。
在摄影测量解析计算中，像点的坐标应采用以像主点为原点的像平面坐标系中的坐标。
为此，当像主点与框标连线交点不重合时，须将像框标坐标系原点平移至像主点。
若像主点在像框标坐标系中的坐标为x0，y0时，测量出的像点坐标x，y化算到以像主点为原点的像平面坐标系中的坐标为x-x0、y-y0。
◆像空间坐标系（15分钟）为了进行像点的空间坐标变换，需要建立起描述像点在像空间位置的坐标系，即像空间坐标系。
A.作用：表示像点在像方空间的位置。
B.原点和坐标轴以S为原点，x，y轴与框标坐标系平行，z轴由右手确定。
某像点a的像平面坐标为（x，y），则它的像空间坐标为（x，y，-f）。
《方位角问题》课件
《方位角问题》ppt课件
目录
• 方位角的基本概念 • 方位角的应用 • 方位角的计算实例 • 方位角问题解析 • 方位角问题的实际应用
01 方位角的基本概念
定义
01
02
03
方位角
指从正北方向顺时针转到 目标方向线的夹角，范围 在0°到360°之间。
真方位角
以真北方向为基准，顺时 针旋转至目标方向线的夹 角。
航海学
船舶导航
在航海学中，方位角是船舶导航 的重要参数之一，通过测量和计 算船只相对于不同地标的方位角 ，可以确定船只的位置和航向。
海上交通控制
海上交通控制中心通过监测船舶的 方位角变化，可以判断船舶的航行 轨迹和航向，确保海上交通的安全 和有序。
海洋调查
海洋调查船利用方位角来定位和测 量海洋参数，如海流、潮汐等。
掌握基本概念
了解和掌握方位角的基本 概念和计算方法是解决方 位角问题的关键。
熟练使用工具
使用量角器、罗盘等工具 进行测量和计算，可以提 高计算的准确性和效率。
实践应用
通过实践应用，如地图阅 读、导航等，可以加深对 方位角概念的理解，并提 高解决实际问题的能力。
05 方位角问题的实际应用
军事应用
1 2 3
航空学
飞机导航
航空飞行中，飞机需要精确的导 航信息来确保安全飞行，方位角 是飞机导航系统中的重要参数之
一。
机场调度
机场调度员通过监测飞机的方位 角变化，可以判断飞机的起降轨 迹和方向，确保机场的正常运行
和飞机的安全起降。
气象观测
气象观测中，方位角也被用来测 量风向、风速等气象参数。
03 方位角的计算实例
科研应用
天文学
目录
• 方位角的基本概念 • 方位角的应用 • 方位角的计算实例 • 方位角问题解析 • 方位角问题的实际应用
01 方位角的基本概念
定义
01
02
03
方位角
指从正北方向顺时针转到 目标方向线的夹角，范围 在0°到360°之间。
真方位角
以真北方向为基准，顺时 针旋转至目标方向线的夹 角。
航海学
船舶导航
在航海学中，方位角是船舶导航 的重要参数之一，通过测量和计 算船只相对于不同地标的方位角 ，可以确定船只的位置和航向。
海上交通控制
海上交通控制中心通过监测船舶的 方位角变化，可以判断船舶的航行 轨迹和航向，确保海上交通的安全 和有序。
海洋调查
海洋调查船利用方位角来定位和测 量海洋参数，如海流、潮汐等。
掌握基本概念
了解和掌握方位角的基本 概念和计算方法是解决方 位角问题的关键。
熟练使用工具
使用量角器、罗盘等工具 进行测量和计算，可以提 高计算的准确性和效率。
实践应用
通过实践应用，如地图阅 读、导航等，可以加深对 方位角概念的理解，并提 高解决实际问题的能力。
05 方位角问题的实际应用
军事应用
1 2 3
航空学
飞机导航
航空飞行中，飞机需要精确的导 航信息来确保安全飞行，方位角 是飞机导航系统中的重要参数之
一。
机场调度
机场调度员通过监测飞机的方位 角变化，可以判断飞机的起降轨 迹和方向，确保机场的正常运行
和飞机的安全起降。
气象观测
气象观测中，方位角也被用来测 量风向、风速等气象参数。
03 方位角的计算实例
科研应用
天文学