《立方根》课件5
合集下载
立方根ppt课件
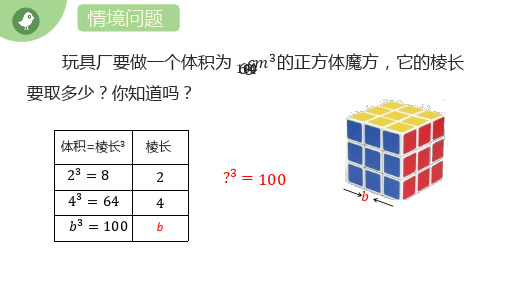
求一个数的立方根的运算,叫做开立方
。
“开立方”运算
“立方”运算
立方
8
2
开立方
小试牛刀
例1 根据立方根的意义填空:
1.因为(3 )3 = 27,
3
所以: 27 =
3;
3
所以: 0.064 = 0.4;
3
所以: 0 = 0 ;
3
所以: −27 = −3 ;
3
所以: −0.064 = −0.4 ;
2.因为(0.4 )3 = 0.064,
探究1
求下列各式的值:
3
3
23
3
= 2
(−2)3 =
−2
3
43
= 4
(−3)3 = -3
3
发现:对于任何数, 3 = .
3
03 = 0
练习
分别求下列各数的值:
3
3
−64, − −27 ,
3
3
3
7 ,(
3
解: −64=−4
3
− −27=3
3
3
73 =7
( 16)3 = 16
16)3
探究2
43 = 2x ∙ x ∙ x
4
64 = 2x 3
32 = x 3
3
x = 32
x ≈ 3.2
长方体的长:2x ≈ 2 × 3.2 ≈ 6.4
答:那么捏成的长方体橡皮泥的长大约6.4厘米。
注意变形前后方程的
定义域之间的差异。
2
作业
必做题:P114:T2、T3
选做题:P115:T7
谢谢!
开立方
性质
2.立方根的正负性与被开方数相同
。
“开立方”运算
“立方”运算
立方
8
2
开立方
小试牛刀
例1 根据立方根的意义填空:
1.因为(3 )3 = 27,
3
所以: 27 =
3;
3
所以: 0.064 = 0.4;
3
所以: 0 = 0 ;
3
所以: −27 = −3 ;
3
所以: −0.064 = −0.4 ;
2.因为(0.4 )3 = 0.064,
探究1
求下列各式的值:
3
3
23
3
= 2
(−2)3 =
−2
3
43
= 4
(−3)3 = -3
3
发现:对于任何数, 3 = .
3
03 = 0
练习
分别求下列各数的值:
3
3
−64, − −27 ,
3
3
3
7 ,(
3
解: −64=−4
3
− −27=3
3
3
73 =7
( 16)3 = 16
16)3
探究2
43 = 2x ∙ x ∙ x
4
64 = 2x 3
32 = x 3
3
x = 32
x ≈ 3.2
长方体的长:2x ≈ 2 × 3.2 ≈ 6.4
答:那么捏成的长方体橡皮泥的长大约6.4厘米。
注意变形前后方程的
定义域之间的差异。
2
作业
必做题:P114:T2、T3
选做题:P115:T7
谢谢!
开立方
性质
2.立方根的正负性与被开方数相同
《立方根》示范课教学课件【数学八年级上册北师大】

a= 2
a2=2,a= 2 ;可是x3=2该怎么求解呢?
合作探究
某化工厂使用半径为1 m的一种球形储气罐储藏气体. 现在要 造一个新的球形储气罐,如果它的体积是原来的8倍,那么它的半 径是原储气罐半径的多少倍?如果储气罐的体积是原来的4倍呢?
解:设新的球形气罐的半径为r m.
如果储气罐的体积是原来的8倍,则:
对于任何数a都有 3 a3 =a
典型例题
例2 求下列各式的值:
(1) 3 8; (2) 3 0.064 ;
(3) 3 8 ;
125
(4( ) 3 9)3.
解:(1) 3 8= 3 (2)3 = 2;
(2) 3 0.064 = 3 0.43 = 0.4;
(3) 3 8 = 3 ( 2)3 = 2; (4)(3 9)3 =9.
解:(1) x 3 0.125=0.5;
(2) (x 1)3 8 x 1 2 x3
(3) (x 1)3 64 x 1 4 x 3
随堂练习
4.若 3 x =2, y2 =4,求 x 2 y 的值.
解:∵ 3 x =2, y2 =4.
∴x = 23,y2 = 16, ∴x = 8,y = ±4. ∴x + 2y = 8 + 2×4 = 16 或 x + 2y = 8 – 2×4 = 0.
个数x就叫做a的 立平方根(也叫做 二三次方根 ).
例: 23=8
( 2)3 8 3 27
03=0
2是8的立方根 2 是 8 的立方根
3 27
0是0的立方根
做一做 2的立方等于多少?是否有其他的数,它的立方也是8? -3的立方等于多少?是否有其他的数,它的立方也是-27?
14.2 立方根课件(共24张PPT)

随堂练习
1.8的立方根为( )A.2 B.±2C.2 D.±2
2.有下列四个说法:①1的算术平方根是1;②的立方根是±;③-27没有立方根;④互为相反数的两数的立方根互为相反数.其中正确的是( )A.①② B.①③ C.①④ D.②④
C
3.已知一个正数的两个平方根分别为3a-1和-5-a,则这个正数的立方根是( )A.-2 B.2C.3 D.4
D
拓展提升
归纳小结
立方根
立方根!
授课老师:
时间:2024年9月15日
他是这样做的:因为33=27,所以,这个大正方体的棱长为3.
你认为小亮的想法和做法有没有道理?你是怎么做的?
做一做
求满足下列各式的x的值:(1)x3=-1;(2)x3=64;(3)x3=0.008;(4)x3=-.
定义:
一般地,如果一个数x的立方等于a,即x3=a,那么这个数x就叫做a的立方根,也叫做a的三次方根.
定义性质表示方法开平方
平方根
一个正数有两个平方根,它们互为相反数.0只有一个平方根,是0本身.负数没有平方根.
开平方与平方互为逆运算.
新知引入
思考
如图,已知小正方体的棱长为2,那么它的体积是多少?反过来,如果大正方体的体积V=27,你能不能求出它的棱长x呢?
小亮是这样想的:由已知小正方体的棱长为2,可以求出它的体积为23=8;同样,根据正方体的体积公式以及立方运算,由大正方体的体积,也可以求出它的棱长.
14.2 立方根
第十四章 实数
学习目标
1.了解立方根的概念,会求一个数的立方根.2.了解开立方与立方互为逆运算.3.探究立方根的性质,并能灵活运用.
学习重难点
理解并掌握立方根的性质.
1.8的立方根为( )A.2 B.±2C.2 D.±2
2.有下列四个说法:①1的算术平方根是1;②的立方根是±;③-27没有立方根;④互为相反数的两数的立方根互为相反数.其中正确的是( )A.①② B.①③ C.①④ D.②④
C
3.已知一个正数的两个平方根分别为3a-1和-5-a,则这个正数的立方根是( )A.-2 B.2C.3 D.4
D
拓展提升
归纳小结
立方根
立方根!
授课老师:
时间:2024年9月15日
他是这样做的:因为33=27,所以,这个大正方体的棱长为3.
你认为小亮的想法和做法有没有道理?你是怎么做的?
做一做
求满足下列各式的x的值:(1)x3=-1;(2)x3=64;(3)x3=0.008;(4)x3=-.
定义:
一般地,如果一个数x的立方等于a,即x3=a,那么这个数x就叫做a的立方根,也叫做a的三次方根.
定义性质表示方法开平方
平方根
一个正数有两个平方根,它们互为相反数.0只有一个平方根,是0本身.负数没有平方根.
开平方与平方互为逆运算.
新知引入
思考
如图,已知小正方体的棱长为2,那么它的体积是多少?反过来,如果大正方体的体积V=27,你能不能求出它的棱长x呢?
小亮是这样想的:由已知小正方体的棱长为2,可以求出它的体积为23=8;同样,根据正方体的体积公式以及立方运算,由大正方体的体积,也可以求出它的棱长.
14.2 立方根
第十四章 实数
学习目标
1.了解立方根的概念,会求一个数的立方根.2.了解开立方与立方互为逆运算.3.探究立方根的性质,并能灵活运用.
学习重难点
理解并掌握立方根的性质.
人教版七年级数学下册《六章 实数 6.2 立方根 用计算器求立方根、用有理数估计一个数立方根的大小》课件_5

试比较下列各数的大小:
(1) 4与 15
(2) 2 7与6
解:(1)42 16, 15 2 15 (2) ( 7 )2 7,32 9
4 15
已知非负数a、b 若a2>b2,则a>b
7 3
2 7 6
例:求 31的整数部分和小数部分。
解:31的整数六章 实数
6.1 平方根(2)
回顾
什么是算术平方根?
动手操作 合作探究
回答问题:
(1)怎样用两个面积为1的小正方形(如下图)拼成一
个大正方形?
1 1
1 1
1 1
提示:每个小 正方形面积为1,
1 两个正方形拼
成之后的总面 积变吗?
1
(2)大正方形的面积、对角线长、边长分别
为多少?
31的小数部分是 31 5
小数部分=原数-整数部分
思考:7 7的整数部分与小数部分。
2
2
2
提示:正方形面积=边长×边长
解:设大正方形的边长为x,则
x²=2
由算术平方根的意义可知 x= 2
实际问题考虑特殊情况, x为正数,x²=2正好符合 算术平方根定义
2有多大呢?
① 2 是整数吗?如果不是,你知道 2 在哪两个相邻整数范围内吗? ②能够使 2 的取值范围更加精确吗? ③你能算出 2 的近似值吗?
解答过程
1 12 1, 22 4,1 2 4,
夹值法
1 2 2;
2 1.42 1.96,1.52 2.25,1.96 2 2.25,
1.4 2 1.5;
3 1.412 1.988 1,1.422 2.016 4,1.988 1 2 2.016 4,
《立方根》课件

能够运用立方根解决实际问题
了解立方根在数学和生活中的 实际应用
未来学习建议
01
进一步学习高次方根的 概念和运算规则
02
了解数学在实际问题中 的应用,提高解决实际 问题的能力
03
学习与立方根相关的其 他数学知识,如不等式 、方程等
04
参加数学竞赛和数学实 践活动,提高数学素养 和综合能力
相关资源推荐
立方根的奇偶性:一个数是奇数或偶数,与这个数在立方时所得到的立方根没关 系。
03
立方根的计算方法
直接求解法
定义法
根据立方根的定义,如果a的立方等于b,即a³=b,那么a就是b的立方根。直 接根据定义求解立方根的方法叫做定义法。
实例
求8的立方根,根据定义8的立方根是2,因为2³=8。
迭代法
迭代法是一种通过不断逼近目标值来求得结果的方法。在求 解立方根时,可以使用迭代法不断逼近立方根的值。
建筑设计
在建筑设计时,立方根可 以用来计算建筑物的体积 和面积等。
机械设计
在机械设计中,立方根可 以用来计算物体的重量、 重心等。
水利工程
在水利工程中,立方根可 以用来计算水库的容量、 水流速度等。
05
立方根的实例
生活中的实例
药品颗粒
建筑
一些药品的颗粒是按照立方根的形式 进行包装的,比如一些儿童药品。
THANKS
感谢观看
实例:可以使用牛顿迭代法等迭代公式来求解立方根。例如 ,x₁=x²/3+x/3求解x的立方根。
近似法
近似法是一种通过近似计算来得到结 果的方法。在求解立方根时,可以使 用近似法求得近似的立方根值。
实例:可以使用近似公式来求解立方 根。例如,对于正数x,其立方根可用 下面的近似公式表示:x^(1/3) ≈ x/1.4426 + 0.13607/x + 0.01985/x² + 0.00211/x³。
《立方根》课件ppt

难点
重点难点分析
内容结构分析
介绍立方根的背景和意义,激发学生学习的兴趣和动力。
引言
概念及运算
应用
拓展
从具体实例中抽象出立方根的概念,并对其运算性质进行总结和归纳。
通过具体实例,讲解立方根在实际生活中的应用,帮助学生了解立方根的应用价值。
介绍立方根在数学文化中的地位和作用,加深学生对立方根的认识和理解。
相关链接资D%93%E5%BA%A6%E7%B1%BD%93%E8%BF%90%E7%AE%971Biblioteka 参考资料23
《数学之书》:pdf版本,立方根部分第24页起。
对数学有兴趣的学生,特别是需要提高数学思维能力的学生。
对象要求
学生需要已经掌握数学基础知识,如代数、方程等。
学生在学习立方根之前,应具备基础的运算能力和数学思维能力。
先修课程要求
02
教学内容分析
掌握立方根的概念和运算性质;能够正确求解一个数的立方根;了解立方根与平方根的区别和联系。
重点
正确理解立方根的概念;在具体情境中灵活运用立方根解决实际问题;拓展学生对立方根的认知范围,加深对立方根的深刻理解。
探究式教学法
通过小组讨论和合作完成任务,培养学生的团队合作精神和交流能力。
合作学习法
03
问题式教学
通过问题引导和启发,激发学生的学习兴趣和思维能力,促进知识意义的自主建构。
教学手段
01
多媒体辅助
利用课件、动画、视频等多种多媒体手段,增强学生的感知和认识,提高教学效率和效果。
02
实验操作法
通过实验操作和实践活动,让学生亲手操作和感知,加深对知识的理解和掌握。
学生能力培养
通过多种教学方法和手段,培养学生的分析、综合、比较、抽象等思维能力。
重点难点分析
内容结构分析
介绍立方根的背景和意义,激发学生学习的兴趣和动力。
引言
概念及运算
应用
拓展
从具体实例中抽象出立方根的概念,并对其运算性质进行总结和归纳。
通过具体实例,讲解立方根在实际生活中的应用,帮助学生了解立方根的应用价值。
介绍立方根在数学文化中的地位和作用,加深学生对立方根的认识和理解。
相关链接资D%93%E5%BA%A6%E7%B1%BD%93%E8%BF%90%E7%AE%971Biblioteka 参考资料23
《数学之书》:pdf版本,立方根部分第24页起。
对数学有兴趣的学生,特别是需要提高数学思维能力的学生。
对象要求
学生需要已经掌握数学基础知识,如代数、方程等。
学生在学习立方根之前,应具备基础的运算能力和数学思维能力。
先修课程要求
02
教学内容分析
掌握立方根的概念和运算性质;能够正确求解一个数的立方根;了解立方根与平方根的区别和联系。
重点
正确理解立方根的概念;在具体情境中灵活运用立方根解决实际问题;拓展学生对立方根的认知范围,加深对立方根的深刻理解。
探究式教学法
通过小组讨论和合作完成任务,培养学生的团队合作精神和交流能力。
合作学习法
03
问题式教学
通过问题引导和启发,激发学生的学习兴趣和思维能力,促进知识意义的自主建构。
教学手段
01
多媒体辅助
利用课件、动画、视频等多种多媒体手段,增强学生的感知和认识,提高教学效率和效果。
02
实验操作法
通过实验操作和实践活动,让学生亲手操作和感知,加深对知识的理解和掌握。
学生能力培养
通过多种教学方法和手段,培养学生的分析、综合、比较、抽象等思维能力。
