2020江苏省徐州市中考数学专题复习 函数的实际应用题
2020年江苏省徐州市中考数学试卷原卷附解析

2020年江苏省徐州市中考数学试卷原卷 学校:__________ 姓名:__________ 班级:__________ 考号:__________注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上一、选择题1.下面两个三角形一定相似的是( )A .两个等腰三角形B .两个直角三角形C .两个钝角三角形D .两个等边三角形2.下列图形中,是中心对称图形而不是轴对称图形的是( )A .平行四边形B .正三角形C .正方形D .线段AB 3.(x+a )(x-3)的积的一次项系数为零,则a 的值是( )A .1B .2C .3D .4 4.赵强同学借了一本书,共 280 页,要在两周借期内读完. 当他读了一半时,发现平均每天要多读 21 页才能在借期内读完. 他读前一半时,平均每天读多少页?如果设读前一 半时,平均每天读x 页,则下列方程中,正确的是( )A .1401401421x x +=-B .2802801421x x +=+C .1401401421x x +=+D .1010121x x +=+ 5.如果一个角等于它的余角的2倍,那么这个角是它补角的( ) A .2倍 B .12 C .5倍 D .156.为了做一个试管架,在长为cm(6cm)a a >的木板上钻3个小孔(如图),每个小孔的直径为2cm ,则x 等于( )A .34a -cmB .34a +cmC .64a -cmD .64a +cm7.把12-与 6作和、差、积、商、幂的运算,结果中为正数的有( )A . 4个B .3个C .2个D .1个 8.如图,在△ABC 与△DEF 中,给出以下六个条件中(1)AB =DE ;(2)BC =EF ;(3)AC =DF ;(4)∠A =∠D ;(5)∠B =∠E ;(6)∠C =∠F ,以其中三个作为已知条件,不.能.判断△ABC 与△DEF 全等的是( ) A .(1)(5)(2) B .(1)(2)(3)C .(4)(6)(1)D .(2)(3)(4) 二、填空题9.sin28°= ;cos36°42′= ;tan46°24′= .10.已知双曲线xk y =经过点(-1,3),如果A (11,b a ),B (22,b a )两点在该双曲线上,且1a <2a <0,那么1b 2b .11.在平面直角坐标系中,已知()24A ,,()22B -,,()62C -,,则过A ,B ,C 三点的圆的圆心坐标为______________.12.对某班同学的身高进行统计(单位:厘米),频数分布表中165.5~170.5这一组学生人数是10,频率为0.25,则该班共有_________名同学.13.已知 A ,B 的坐标分别为(-2,0),(4,0),点P 在直线2y x =+上,如果△ABP 为等腰三角形,这样的 P 点共有 个.14.已知一次函数的图象如图所示,则一次函数的解析式为 .15.对于平面内任意一个凸四边形ABCD ,现从以下四个关系式①AB=CD ;②AD=BC ;③AB ∥CD ;④∠A=∠C 中任取两个作为条件,能够得出这个四边形ABCD 是平行四边形的概率是 .16.如图是一个长方形公园,如果要从A 景点走到B 景点,至少要走 米.17.如图,AD 是ABC △的一条中线,45ADC ∠=.沿AD 所在直线把ADC △翻折,使点C 落在点C '的位置.则BC BC'= .18.如果一个三角形的三条高都在三角形的内部,那么这个三角形是 三角形(按角分类).19.下列事件中,哪些是必然事件?哪些是不确定事件?哪些是不可能事件?(1)掷一枚硬币,有国徽的一面朝上: .(2)随意翻一下日历,翻到的号数是奇数: .(3)杭州每年春季都会下雨:.20.已知线段AB长为10厘米,C是线段AB上任意一点(不与A,B重合), M是AC的中点,N是BC的中点,则MN=________厘米.21.计算:(1)48°59′55″+67°28″= ;(2)90°-78°19′40″= .三、解答题22.某产品每件成本10元,试销阶段每件产品的日销售价x(元)与产品的日销售量y (件)之间的关系如下表:x(元)15202530…y(件)25201510…⑴在草稿纸上描点,观察点的分布,建立y与x的恰当函数模型.⑵要使每日的销售利润最大,每件产品的销售价应定为多少元?此时每日销售利润是多少元?23.如图, AB是⊙O的直径,弦CD⊥AB于点M, AM = 2,BM = 10,求CD的长度.24.将进货单价为 90 元的某种商品按100 元一个售出时,能卖出 500 个,已知这种商品每涨价1 元,其销售量就要减少 10个,为了获得最大利润应怎样定价?25.已知四边形ABCD,对角线AC、BD交于点O.现给出四个条件:①AC⊥BD;②AC平分对角线BD;③AD∥BC;④∠OAD=∠ODA.请你以其中的三个条件作为命题的题设,以“四边形ABCD为菱形”作为命题的结论.(1)写出一个真命题,并证明;(2)写出一个假命题,并举出一个反例说明.26.解下列不等式组,并把臃在轴上表示出来.(1) 122(1)1x xx x -≤⎧⎨++>⎩ (2)132(2)2165()75x x x x +⎧->-⎪⎪⎨⎪--≥-⎪⎩27.如图,△ABC 的顶点A 平移到了点D ,请你作出△ABC 经平移变换后所得的像.28.若2x ax b ++能分解成(3)(4)x x +-,求a ,b 的值.29.小张把压岁钱按定期一年存入银行,当时一年定期存款的年利率为1.98%,利息税的税率为20%,到期支取时,扣除利息税后,小明实得本利和为l015.84元,问小明存入银行的压岁钱有多少元?30.在不透明的口袋中装有大小、质地完全相同的分别标有数字1,2,3的三个小球,随机摸出一个小球(不放回),将小球上的数字作为一个两位数个位上的数字,然后再摸出一个小球将小球上的数字作为这个两位数十位上的数字(利用表格或树状图解答)(1)能组成哪些两位数?(2)小华同学的学号是12,有一次试验中他摸到自己学号的概率是多少?【参考答案】学校:__________ 姓名:__________ 班级:__________ 考号:__________注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上一、选择题1.D2.A3.C4.C5.B6.C7.C8.D二、填空题9.0. 4695,0. 8018,1. 050110.<11.()41,12.40 13.414.y=-2x+215.1216.17.2218. 锐角19.(1)不确定事件;(2)不确定事件;(3)必然事件20.521.(1)116°23″ (2)11°40′20″三、解答题22.解:⑴经观察发现各点分布在一条直线上,∴设b kx y += (k ≠0), 用待定系数法求得40+-=x y .⑵设日销售利润为z ,则y xy z 10-==400502-+-x x ,当x=25时,z 最大为225.每件产品的销售价定为25元时,日销售利润最大为225元.23.54.24.设利润为 y 元,商品涨价x 元.(10090)(50010)y x x =+--,由己知得由配方法得210(20)9000y x =--+ 由二次函数的性质得当 x= 20 时,9000y =最大值∴为获得最大利润应定价120 元.25.(1)若①②③成立,则四边形ABCD 为菱形,证明略;(2)假命题:若①②④成立,则四边形ABCD 为菱形,反例略(答案不惟一). 26.(1)1x ≥-,在数轴上表示略 (2)712x -≤<,在数轴上表示略 27.略28.a=-1,b=-1229.1000元30.(1)∴能组成的两位数有21,31,12,32,13,23能组成的两位数有21,31,12,32,13,23.(2)(12)16P =学号. 开始12 3 2 3 3 2 1 1。
2020年中考数学复习专题练:《二次函数实际应用 》(含答案)

2020年中考数学复习专题练:《二次函数实际应用》1.金松科技生态农业养殖有限公司种植和销售一种绿色羊肚菌,已知该羊肚菌的成本是12元/千克,规定销售价格不低于成本,又不高于成本的两倍.经过市场调查发现,某天该羊肚菌的销售量y(千克)与销售价格x(元/千克)的函数关系如下图所示:(1)求y与x之间的函数解析式;(2)求这一天销售羊肚菌获得的利润W的最大值;(3)若该公司按每销售一千克提取1元用于捐资助学,且保证每天的销售利润不低于3600元,问该羊肚菌销售价格该如何确定.2.某超市以20元/千克的进货价购进了一批绿色食品,如果以30元/千克销售这些绿色食品,那么每天可售出400千克.由销售经验可知,每天的销售量y(千克)与销售单价x (元)(x≥30)存在如图所示的一次函数关系.(1)试求出y与x的函数关系式;(2)设该超市销售该绿色食品每天获得利润w元,当销售单价为何值时,每天可获得最大利润?最大利润是多少?3.为倡导节能环保,降低能源消耗,提倡环保型新能源开发,造福社会.某公司研发生产一种新型智能环保节能灯,成本为每件40元.市场调查发现,该智能环保节能灯每件售价y(元)与每天的销售量为x(件)的关系如图,为推广新产品,公司要求每天的销售量不少于1000件,每件利润不低于5元.(1)求每件销售单价y(元)与每天的销售量为x(件)的函数关系式并直接写出自变量x的取值范围;(2)设该公司日销售利润为P元,求每天的最大销售利润是多少元?(3)在试销售过程中,受国家政策扶持,毎销售一件该智能环保节能灯国家给予公司补贴m(m≤40)元.在获得国家每件m元补贴后,公司的日销售利润随日销售量的增大而增大,则m的取值范围是(直接写出结果).4.网络销售是一种重要的销售方式.某乡镇农贸公司新开设了一家网店,销售当地农产品.其中一种当地特产在网上试销售,其成本为每千克2元.公司在试销售期间,调查发现,每天销售量y(kg)与销售单价x(元)满足如图所示的函数关系(其中2<x≤10).(1)若5<x≤10,求y与x之间的函数关系式;(2)销售单价x为多少元时,每天的销售利润最大?最大利润是多少元?5.现代城市绿化带在不断扩大,绿化用水的节约是一个非常重要的问题.如图1、图2所示,某喷灌设备由一根高度为0.64m的水管和一个旋转喷头组成,水管竖直安装在绿化带地面上,旋转喷头安装在水管顶部(水管顶部和旋转喷头口之间的长度、水管在喷灌区域上的占地面积均忽略不计),旋转喷头可以向周围喷出多种抛物线形水柱,从而在绿化带上喷灌出一块圆形区域.现测得喷的最远的水柱在距离水管的水平距离3m处达到最高,高度为1m.(1)求喷灌出的圆形区域的半径;(2)在边长为16m的正方形绿化带上固定安装三个该设备,喷灌区域可以完全覆盖该绿化带吗?如果可以,请说明理由;如果不可以,假设水管可以上下调整高度,求水管高度为多少时,喷灌区域恰好可以完全覆盖该绿化带.(以上需要画出示意图,并有必要的计算、推理过程)6.某商家在购进一款产品时,由于运输成本及产品成本的提高,该产品第x天的成本y(元/件)与x(天)之间的关系如图所示,并连续60天均以80元/件的价格出售,第x天该产品的销售量z(件)与x(天)满足关系式z=x+15.(1)第25天,该商家的成本是元,获得的利润是元;(2)设第x天该商家出售该产品的利润为w元.①求w与x之间的函数关系式;②求出第几天的利润最大,最大利润是多少?7.某品牌服装公司经过市场调査,得到某种运动服的月销量y(件)是售价x(元/件)的一次函数,其售价、月销售量、月销售利润w(元)的三组对应值如下表:注:月销售利润=月销售量×(售价一进价)售价x(元/件)130 150 180月销售量y(件)210 150 60月销售利润w(元)10500 10500 6000(1)求y关于x的函数解析式(不要求写出自变量的取值范围);(2)当售价是多少时,月销售利润最大?最大利润是多少元?(3)为响应号召,该公司决定每售出1件服装,就捐赠a元(a>0),商家规定该服装售价不得超过200元,月销售量仍满足上关系,若此时月销售最大利润仍可达9600元,求a的值.8.“武汉加油!中国加油!”疫情牵动万人心,每个人都在为抗击疫情而努力.某厂改造了10条口罩生产线,每条生产线每天可生产口罩500个.如果每增加一条生产线,每条生产线就会比原来少生产20个口罩.设增加x条生产线后,每条生产线每天可生产口罩y 个.(1)直接写出y与x之间的函数关系式;(2)若每天共生产口罩6000个,在投入人力物力尽可能少的情况下,应该增加几条生产线?(3)设该厂每天可以生产的口罩w个,请求出w与x的函数关系式,并求出增加多少条生产线时,每天生产的口罩数量最多,最多为多少个?9.九年级孟老师数学小组经过市场调查,得到某种运动服的月销量y(件)是售价x(元/件)的一次函数,其售价、月销售量、月销售利润w(元)的三组对应值如下表:售价x(元/件)130 150 180月销售量y(件)210 150 60月销售利润w(元)10500 10500 6000注:月销售利润=月销售量×(售价﹣进价)(1)①求y关于x的函数解析式(不要求写出自变量的取值范围);②运动服的进价是元/件;当售价是元/件时,月销利润最大,最大利润是元.(2)由于某种原因,该商品进价降低了m元/件(m>0),商家规定该运动服售价不得低于150元/件,该商店在今后的售价中,月销售量与售价仍满足(1)中的函数关系式,若月销售量最大利润是12000元,求m的值.10.小明经过市场调查,整理出他妈妈商店里一种商品在第x(1≤x≤30)天的销售量的相关信息如下表:时间第x(天)1≤x≤20 20≤x≤30售价(元/件)x+30 50每天销量(件)160﹣4x已知该商品的进价为每件20元,设销售该商品的每天利润为y元.(1)求出y与x的函数关系式;(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?(3)该商品在销售过程中,共有多少天每天销售利润不低于2400元?请直接写出结果.11.我市某乡镇在“精准扶贫”活动中销售农产品,经分析发现月销售量y(万件与月份x (月)的关系为:每件产品的利润z(元)与月份x(月)的关系如表:x 1 2 3 4 5 6 7 8 9 10 11 12 z19 18 17 16 15 14 13 12 10 10 10 10 (1)请你根据表格直接写出每件产品利润z(元)与月份x(月)的函数关系式;(2)若月利润w(万元)=当月销售量y(万件)x当月每件产品的利润z(元),求月利润w(万元)与月份x(月)的关系式;(3)当x为何值时,月利润w有最大值,最大值为多少?12.某商品的进价为每件50元,售价为每件60元,每个月可卖出200件.若每件商品的售价上涨1元,则每个月少卖10件(每件售价不能高于72元),设每件商品的售价上涨x 元(x为正整数),每个月的销售量为y件.(1)求y与x的函数关系式并直接写出自变量x的取值范围;(2)设每月的销售利润为w元,每件商品的售价定为多少元时,每个月可获得最大利润?最大月利润是多少元?13.某超市销售一种高档蔬菜“莼菜”,其进价为16元/kg.经市场调查发现:该商品的日销售量y(kg)是售价x(元/kg)的一次函数,其售价、日销售量对应值如表:售价x(元/kg)20 30 40日销售量y(kg)80 60 40(1)求y关于x的函数解析式(不要求写出自变量的取值范围);(2)x为多少时,当天的销售利润w(元)最大?最大利润为多少?(3)由于产量日渐减少,该商品进价提高了a元/kg(a>0),物价部门规定该商品售价不得超过36元/kg,该商店在今后的销售中,日销售量与售价仍然满足(1)中的函数关系.若日销售最大利润是864元,求a的值.14.为满足市场需求,新生活超市在端午节前夕购进价格为3元/个的粽子,根据市场预测,该品牌粽子每个售价4元时,每天能出售500个,并且售价每上涨0.1元,其销售量将减少10个,为了维护消费者利益,物价部门规定,该品牌粽子的售价不能超过进价的200%.(1)请你利用所学知识帮助超市给该品牌粽子定价,使超市每天的销售利润为800元.(2)定价为多少时每天的利润最大?最大利润是多少?15.甲船从A处起以15km/h的速度向正北方向航行,这时乙船从A的正东方向20km的B 处起以20km/h的速度向西航行,多长时间后,两船的距离最小?最小距离是多少?16.某商场经营一种海产品,进价是每千克20元,根据市场调查发现,每日的销售量y(千克)与售价x(元/千克)是一次函数关系,如图所示:(1)求y与x的函数关系式(不求自变量取值范围);(2)某日该商场出售这种海产品获得了21000元的利润,该海产品的售价是多少?(3)若某日该商场这种海产品的销售量不少于650千克,该商场销售这种海产品获得的最大利润是多少?17.某网店专售一款电动牙刷,其成本为20元/支,销售中发现,该商品每天的销售量y(支)与销售单价x(元/支)之间存在如图所示的关系.(1)请求出y与x的函数关系式;(2)该款电动牙刷销售单价定为多少元时,每天销售利润最大?最大利润是多少元?(3)近期武汉爆发了“新型冠状病毒”疫情,该网店店主决定从每天获得的利润中抽出200元捐赠给武汉,为了保证捐款后每天剩余利润不低于550元,如何确定该款电动牙刷的售单价?18.某网店专售一品牌牙膏,其成本为22元/支,销售中发现,该商品每天的销售量y(支)与销售单价x(元/支)之间存在如图所示的关系.(1)请求出y与x之间的函数关系式;(2)该品牌牙膏销售单价定为多少元时,每天销售利润最大?最大利润是多少元?(3)在武汉爆发“新型冠状病毒”疫情期间,该网店店主决定从每天获得的利润中抽出100元捐赠给武汉,为了保证捐款后每天剩余的利润不低于350元,在抗“新型冠状病毒”疫情期间,市场监督管理局加大了对线上、线下商品销售的执法力度,对商品售价超过成本价的20%的商家进行处罚,请你给该网店店主提供一个合理化的销售单价范围.19.某工艺品厂生产一款工艺品,已知这款工艺品的生产成本为60元/件.经市场调研发现,这款工艺品每天的销售量y(件)与售价x(元/件)之间存在着如表所示的一次函数关系:售价x/(元/件)…70 90 …销售量y/件…3000 1000 …(1)求销售量y(件)与售价x(元/件)之间的函数关系式.(2)求每天的销售利润w(元)与售价x(元/件)之间的函数关系式.(3)如何定价才能使该工艺品厂每天获得的销售利润为40000元?20.如图,用一段长为30m的篱笆围成一个一边靠墙的矩形菜园,墙长为18m.设矩形菜园的边AB的长为xm,面积为Sm2.(I)写出S关于x的函数解析式,并求出x的取值范围;(Ⅱ)当该矩形菜园的面积为72m2时,求边AB的长;(Ⅲ)当边AB的长为多少时,该矩形菜园的面积最大?最大面积是多少?参考答案1.解:(1)①当12≤x≤20时,设y=kx+b.代(12,2000),(20,400),得解得∴y=﹣200x+4400②当20<x≤24时,y=400.综上,y=(2)①当12≤x≤20时,W=(x﹣12)y=(x﹣12)(﹣200x+4400)=﹣200(x﹣17)2+5000当x=17时,W的最大值为5000;②当20<x≤24时,W=(x﹣12)y=400x﹣4800.当x=24时,W的最大值为4800.∴最大利润为5000元.(3)①当12≤x≤20时,W=(x﹣12﹣1)y=(x﹣13)(﹣2000x+4400)=﹣200(x﹣17.5)2+4050令﹣200(x﹣17.5)2+4050=3600x 1=16,x2=19∴定价为16≤x≤19②当20<x≤24时,W=400(x﹣13)=400x﹣5200≥3600 ∴22≤x≤24.综上,销售价格确定为16≤x≤19或22≤x≤24.2.解:(1)设y与x的函数关系式为y=kx+b,,得,即y与x的函数关系式是y=﹣20x+1000(30≤x≤50);(2)w=(x﹣20)y=(x﹣20)(﹣20x+1000)=﹣20x2+1400x﹣20000=﹣20(x﹣35)2+4500,故当x=35时,w取得最大值,此时w=4500,答:当销售单价为35元/千克时,每天可获得最大利润4500元.3.解:(1)设每件销售单价y(元)与每天的销售量为x(件)的函数关系式为y=kx+b,把(1500,55)与(2000,50)代入y=kx+b得,,解得:,∴每件销售单价y(元)与每天的销售量为x(件)的函数关系式为y=﹣x+70,当y≥45时,﹣x+70≥45,解得:x≤2500,∴自变量x的取值范围1000≤x≤2500;(2)根据题意得,P=(y﹣40)x=(﹣x+70﹣40)x=﹣x2+30x=﹣(x ﹣1500)2+22500,∵﹣<0,P有最大值,当x<1500时,P随x的增大而增大,∴当x=1500时,P的最大值为22500元,答:每天的最大销售利润是22500元;(3)由题意得,P=(﹣x+70﹣40+m)x=﹣x2+(30+m)x,∵对称轴为x=50(30+m),∵1000≤x≤2500,∴x 的取值范围在对称轴的左侧时P 随x 的增大而增大,50(30+m )≥2500,解得:m ≥20,∴m 的取值范围是:20≤m ≤40.故答案为:20≤m ≤40.4.解:(1)设y =kx +b ,把(5,600),(10,400)代入y =kx +b , 得解得 ∴y =﹣40x +800.(2)设每天的销售利润为w 元当2<x ≤5时,w =600(x ﹣2)=600x ﹣1200当x =5时,w max =600×5﹣1200=1800(元);当5<x ≤10时,w =(﹣40x +800)(x ﹣2)=﹣40(x ﹣11)2+3240当x =10时,w max =﹣40×1+3240=3200综上所述,当x =10时,每天的销售利润最大,最大是3200元.5.解:(1)根据题意,以水管在地面安装处为坐标原点,以该处和喷的最远的水柱落地处所在直线为x 轴,建立平面直角坐标系,则喷的最远的水柱所在的抛物线顶点为(3,1),过(0,0.64).可设该抛物线对应的函数表达式是y =a (x ﹣3) 2+1,代入(0,0.64),解得,a =﹣. 所以y =﹣ (x ﹣3) 2+1.令y =0,解得x 1=﹣2(舍),x 2=8.4 分所以,喷灌出的圆形区域的半径为8 m .(2)在边长为16 m 的正方形绿化带上按如图的位置固定安装三个该设备,如图1,喷灌出的圆形区域的半径的最小值是=,8<,这样安装不能完全覆盖;如图2,设CD=x,则BC=16﹣x,DE=8,AB=16,由勾股定理得:82+x2=(16﹣x)2+162解得:x=14∴2r==∴喷灌出的圆形区域的半径的最小值是,8<,这样安装也不能完全覆盖;<,如果喷灌区域可以完全覆盖该绿化带.则一个设备喷灌出的圆形区域的半径的最小值应为m.设水管向上调整a m,则调整后喷的最远的水柱所在的抛物线函数表达式是y=﹣(x﹣3) 2+1+a.代入(,0),解得,a=.0.64+=答:水管高度为时,喷灌区域恰好可以完全覆盖该绿化带.6.解:(1)由图象可知,此时的产量为z=25+15=40(件),设直线BC的关系为y=kx+b,∴,∴,∴y=x+10,故第25天,该商家的成本是:25+10=35(元)则第25天的利润为:(80﹣35)×40=1800(元);故答案为:35,1800;(2)①当0≤x≤20时,w=(80﹣30)(x+15)=50x+750,当20<x≤60时,w=[80﹣(x+10)](x+15)=﹣x2+55x+1050 ∴w=.②当0≤x≤20时w=(80﹣30)(x+15)=50x+750,=1750元;当x=20时,w最大当20<x≤60时,w=﹣x2+55x+1050∵﹣1<0,抛物线开口向下,对称轴为x=∴当x=27或x=28时,w=﹣272+55×27+1050=1806(元)∵1806>1750∴第27天或28天的利润最大,最大为1806元.7.解:(1)设y关于x的函数解析式为:y=kx+b(k≠0)由题意得:,解得:∴y关于x的函数解析式为y=﹣3x+600;(2)运动服的进价是:130﹣10500÷210=80(元)月销售利润w=(x﹣80)(﹣3x+600)=﹣3x2+840x﹣48000=﹣3(x﹣140)2+10800∴当售价是140元时,月销售利润最大,最大利润为10800元;(3)由题意得:w=(x﹣80﹣a)(﹣3x+600)=﹣3x2+(840+3a)x﹣48000﹣600a∴当x=140+a时,w有最大值.∵a>0,且a≤140﹣80∴140<140+a≤170<200∵商家规定该服装售价不得超过200元,此时月销售最大利润仍可达9600元,∴当x=140+a时,有,解得,a=120﹣80,或a=120+80(舍去),故a=120﹣80.8.解:(1)由题意可知该函数关系为一次函数,其解析式为:y=500﹣20x;∴y与x之间的函数关系式为y=500﹣20x(0≤x≤25,且x为整数);(2)由题意得:(10+x)(500﹣20x)=6000,整理得:x2﹣15x+50=0,解得:x1=5,x2=10,∵尽可能投入少,∴x2=10舍去.答:应该增加5条生产线.(3)w=(10+x)(500﹣20x)=﹣202+300x+5000=﹣20(x﹣7.5)2+6125,∵a=﹣20<0,开口向下,∴当x=7.5时,w最大,又∵x为整数,∴当x=7或8时,w最大,最大值为6120.答:当增加7或8条生产线时,每天生产的口罩数量最多,为6120个.9.解:(1)设y关于x的函数解析式为:y=kx+b(k≠0)由题意得:解得:∴y关于x的函数解析式为y=﹣3x+600;(2)运动服的进价是:130﹣10500÷210=80(元)月销售利润w=(x﹣80)(﹣3x+600)=﹣3x2+840x﹣48000=﹣3(x﹣140)2+10800∴当售价是140元时,月销售利润最大,最大利润为10800元.故答案为:80;140;10800;(3)由题意得:w=[x﹣(80﹣m)](﹣3x+600)=﹣3x2+(840﹣3m)x﹣48000+600m对称轴为x=140﹣∵m>0∴140﹣<140<150∵商家规定该运动服售价不得低于150元/件∴由二次函数的性质,可知当x=150时,月销售量最大利润是12000元∴﹣3×1502+(840﹣3m)×150﹣48000+600m=12000解得:m=10∴m的值为10.10.(1)当1≤x<20时,y=(160﹣4x)(x+30﹣20)=﹣4x2+120x+1600;当20≤x≤30时,y=(50﹣20)(160﹣4x)=﹣120x+4800;综上:y=(2)当1≤x<20时,y=﹣4x2+120x+1600=﹣4(x﹣15)2+2500∵a=﹣4<0∴当x=15时,y有最大值,最大值为2500元;当20≤x≤30时,y=﹣120x+4800;∵k=﹣120<0∴y随x的增大而减小∴当x=20时,y有最大值,最大值为2400元,综上可知,当x=15时,当天的销售利润最大,最大利润为2500元.(3)当1≤x<20时,令y=﹣4(x﹣15)2+2500=2400,解得:x1=10,x2=20(舍)∵a=﹣4<0∴当1≤x<20时,有10天每天销售利润不低于2400元;当20≤x≤30时,令y=﹣120x+4800=2400解得:x=20由(2)可知,2400为此时间段的最大值.综上,共有11天每天销售利润不低于2400元.11.解:(1)观察表中数据可得,当1≤x≤8时,z=﹣x+20;当9≤x≤12时,z=10.∴z与x的关系式为:z=;(2)当1≤x≤6时,w=(﹣x+20)(x+8)=﹣x2+12x+160;当7≤x≤8时,w=(﹣x+20)(﹣x+20)=x2﹣40x+400;当9≤x≤12时,w=10(﹣x+20)=﹣10x+200;∴w与x的关系式为:(3)当1≤x≤6时,w=﹣x2+12x+160=﹣(x﹣6)2+196,∴x=6时,w有最大值为196;当7≤x≤8时,w=x2﹣40x+400=(x﹣20)2,w随x增大而减小,∴x=7时,w有最大值为169;当9≤x≤12时,w=﹣10x+200,w随x增大而减小,∴x=9时,w有最大值为110;∵110<169<196,∴x=6时,w有最大值为196.12.解:(1)由题意得:y=200﹣10x∵每件售价不能高于72元∴1≤x≤12,且x为正整数;(2)由题意得:w=(60+x﹣50)(200﹣10x)=(10+x)(200﹣10x)=﹣10x2+100x+2000=﹣10(x﹣5)2+2250∴当x=5时,60+x=65时,即销售单价为65元时,每个月可获得最大利润,最大月利润是2250元.13.解:(1)①依题意设y=kx+b,则有解得:∴y关于x的函数解析式为y=﹣2x+120;(2)根据题意得,w=(﹣2x+120)×(x﹣16)=﹣2x2+152x﹣1920=﹣2(x﹣38)2+968,∴当售价是38元/件时,日销售利润最大,最大利润是968元;(3)根据题意得,w=(﹣2x+120)×(x﹣16﹣a)=﹣2x2+(152+2a)x﹣1920﹣120a∵a>0,对称轴为直线x=﹣=38+>36,又∵﹣2<0,售价不得超过36元/kg,∴当x≤36时,w随x的增大而增大,∴当x=36时,w有最大值864元,∴﹣2×362+(152+2a )×36﹣1920﹣120a =864,∴解得:a =2,∴a 的值为2.14.解:(1)设每个粽子的定价为x 元时,每天的利润为800元, 根据题意得,, 解得x 1=7,x 2=5,∵售价不能超过进价的200%,∴x ≤3×200%,即x ≤6,∴x =5,∴定价为5元时,每天的利润为800元.(2)设每个粽子的定价为m 元,则每天的利润为w ,则有: w =(m ﹣3)(500﹣10×)=(m ﹣3)(500﹣100m +400)=﹣100(m ﹣3)(m ﹣9)=﹣100(m 2﹣12m +27)=﹣100[(m ﹣6)2﹣9]=﹣100(m ﹣6)2+900∵二次项系数为﹣100<0,m ≤6,∴当定价为6元时,每天的利润最大,最大的利润是900元.15.解:根据题意画出示意图如下:设x 小时后,两船相距ykm ,根据题意,得:y2=(15x)2+(20﹣20x)2=225x2+400﹣800x+400x2=(25x﹣16)2+144∴当x=时,y2有最小值144,则y的最小值为12,答:小时后,两船的距离最小,最小距离是12km.16.解:(1)设y与x之间的函数关系式为y=kx+b,将(25,950),(40,800)代入可得:解得,∴y与x之间的函数关系式为y=﹣10x+1200.(2)根据题目信息可得:(﹣10x+1200)(x﹣20)=21000,整理可得:x2﹣140x+4500=0,解得x=50或x=90.∴该海产品的售价是50元/kg或90元/kg.(3)设所获利润为W,则根据题目信息可得:W=(﹣10x+1200)(x﹣20)=﹣10(x﹣70)2+25000.∵﹣10x+1200≥650,∴x≤55.∴当x=55时,W有最大值.W的最大值为:﹣10(55﹣70)2+25000=22750(元).∴该商场销售这种海产品获得的最大利润是22750元.17.解:(1)设y与x的函数关系式为y=kx+b,将(30,100),(35,50)代入y=kx+b,得,解得,∴y与x的函数关系式为y=﹣10x+400;(2)设该款电动牙刷每天的销售利润为w 元,由题意得 w =(x ﹣20)•y=(x ﹣20)(﹣10x +400)=﹣10x 2+600x ﹣8000=﹣10(x ﹣30)2+1000,∵﹣10<0,∴当x =30时,w 有最大值,w 最大值为1000.答:该款电动牙刷销售单价定为30元时,每天销售利润最大,最大销售利润为1000 元;(3)设捐款后每天剩余利润为 z 元,由题意可得 z =﹣10x 2+600x ﹣8000﹣200=﹣10x 2+600x ﹣8200,令z =550,即﹣10x 2+600x ﹣8200=550,﹣10(x 2﹣60x +900)=﹣250,x 2﹣60x +900=25,解得x 1=25,x 2=35,画出每天剩余利润z 关于销售单价x 的函数关系图象如解图,由图象可得:当该款电动牙刷的销售单价每支不低于25元,且不高于35元时,可保证捐款后每天剩余利润不低于550 元.18.解:(1)根据题意设y =kx +b (k ≠0),将(30,100)、(35,50)代入得, 解得,∴y与x之间的关系式为y=﹣10x+400;(2)设每天的利润为W元,则W=(x﹣22)y=(x﹣22)(﹣10x+400)=﹣10x2+620x﹣8800=﹣10(x﹣31)2+810,∴销售单价定为31元时,每天最大利润为810元.(3)﹣10x2+620x﹣8800﹣100=350,解得x=25或x=37,结合图象和二次函数的特点得出25≤x≤37,又x≤22×(1+20%),综上可得25≤x≤26.4,∴按要求网店店主的销售单价范围为大于或等于25元且小于或等于26.4元.19.解:(1)设销售量y(件)与售价x(元/件)之间的函数关系式为y=kx+b,,得,即销售量y(件)与售价x(元/件)之间的函数关系式是y=﹣100x+10000;(2)由题意可得,w=(x﹣60)y=(x﹣60)(﹣100x+10000)=﹣100x2+16000x+600000,即每天的销售利润w(元)与售价x(元/件)之间的函数关系式是w=﹣100x2+16000x+600000;(3)当w=40000时,40000=﹣100x2+16000x+600000,解得,x1=x2=80,答:当定价为80元时,才能使该工艺品厂每天获得的销售利润为40000元.20.解:(Ⅰ)∵AB=CD=xm,∴BC=(30﹣2x)m,由题意得S=x(30﹣2x)=﹣2x2+30x(6≤x<15);(Ⅱ)令s=72得:﹣2x2+30x=72,解得:x=3或x=12,当x=3时,30﹣2x=24>18,∴x取12,答:AB的长为12米.(Ⅲ)∵S=﹣2x2+30x=﹣2(x﹣7.5)2+112.5,=112.5,∴当x=7.5时,S有最大值,S最大。
2020年江苏省徐州市中考数学试卷(后附答案及详尽解析)

2020年江苏省徐州市中考数学试卷一、选择题(本大题共有8小题,每小题3分,共24分.在每小题所给出的四个选项中,恰有一项是符合要求的,请将正确选项前的字母代号填涂在答题卡相应位置)1.(3分)(2020•徐州)3的相反数是()A.﹣3B.3C.−13D.132.(3分)(2020•徐州)下列垃圾分类标识的图案既是轴对称图形,又是中心对称图形的是()A.B.C.D.3.(3分)(2020•徐州)若一个三角形的两边长分别为3cm、6cm,则它的第三边的长可能是()A.2cm B.3cm C.6cm D.9cm4.(3分)(2020•徐州)在一个不透明的袋子里装有红球、黄球共20个,这些球除颜色外都相同.小明通过多次试验发现,摸出红球的频率稳定在0.25左右,则袋子中红球的个数最有可能是()A.5B.10C.12D.155.(3分)(2020•徐州)小红连续5天的体温数据如下(单位:℃):36.6,36.2,36.5,36.2,36.3.关于这组数据,下列说法正确的是()A.中位数是36.5℃B.众数是36.2°CC.平均数是36.2℃D.极差是0.3℃6.(3分)(2020•徐州)下列计算正确的是()A.a2+2a2=3a4B.a6÷a3=a2C.(a﹣b)2=a2﹣b2D.(ab)2=a2b27.(3分)(2020•徐州)如图,AB是⊙O的弦,点C在过点B的切线上,OC⊥OA,OC交AB于点P.若∠BPC=70°,则∠ABC的度数等于()A.75°B.70°C.65°D.60°8.(3分)(2020•徐州)如图,在平面直角坐标系中,函数y=4x(x>0)与y=x﹣1的图象交于点P(a,b),则代数式1a−1b的值为()A.−12B.12C.−14D.14二.填空题(本大题共10小题,每小题3分,共30分.不需要写出解答过程,请将答案直接填写在答题卡相应位置)9.(3分)(2020•徐州)7的平方根是.10.(3分)(2020•徐州)分解因式:m2﹣4=.11.(3分)(2020•徐州)若√x−3在实数范围内有意义,则x的取值范围是.12.(3分)(2020•徐州)原子很小,1个氧原子的直径大约为0.000000000148m,将0.000000000148用科学记数法表示为.13.(3分)(2020•徐州)如图,在Rt△ABC中,∠ABC=90°,D、E、F分别为AB、BC、CA的中点,若BF=5,则DE=.14.(3分)(2020•徐州)如图,在Rt△ABC中,∠C=90°,AC=4,BC=3.若以AC所在直线为轴,把△ABC旋转一周,得到一个圆锥,则这个圆锥的侧面积等于.15.(3分)(2020•徐州)方程9x =8x−1的解为.16.(3分)(2020•徐州)如图,A、B、C、D为一个正多边形的顶点,O为正多边形的中心,若∠ADB=18°,则这个正多边形的边数为.17.(3分)(2020•徐州)如图,∠MON=30°,在OM上截取OA1=√3.过点A1作A1B1⊥OM,交ON于点B1,以点B1为圆心,B1O为半径画弧,交OM于点A2;过点A2作A2B2⊥OM,交ON于点B2,以点B2为圆心,B2O为半径画弧,交OM于点A3;按此规律,所得线段A20B20的长等于.18.(3分)(2020•徐州)在△ABC中,若AB=6,∠ACB=45°.则△ABC的面积的最大值为.三、解答题(本大题共有10小题,共86分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)19.(10分)(2020•徐州)计算:(1)(﹣1)2020+|√2−2|﹣(12)﹣1;(2)(1−1a)÷a2−2a+12a−2.20.(10分)(2020•徐州)(1)解方程:2x2﹣5x+3=0;(2)解不等式组:{3x−4<52x−13>x−22.21.(7分)(2020•徐州)小红的爸爸积极参加社区抗疫志愿服务工作.根据社区的安排,志愿者被随机分到A组(体温检测)、B组(便民代购)、C组(环境消杀).(1)小红的爸爸被分到B组的概率是;(2)某中学王老师也参加了该社区的志愿者队伍,他和小红爸爸被分到同一组的概率是多少?(请用画树状图或列表的方法写出分析过程)22.(7分)(2020•徐州)某市为了解市民每天的阅读时间,随机抽取部分市民进行调查.根据调查结果绘制了如图尚不完整的统计图表:市民每天的阅读时间统计表类别A B C D 阅读时间x(min)0≤x<3030≤x<6060≤x<90x≥90频数450400m50根据以上信息解答下列问题:(1)该调查的样本容量为,m=;(2)在扇形统计图中,“B”对应扇形的圆心角等于°;(3)将每天阅读时间不低于60min的市民称为“阅读爱好者”.若该市约有600万人,请估计该市能称为“阅读爱好者”的市民有多少万人.23.(8分)(2020•徐州)如图,AC⊥BC,DC⊥EC,AC=BC,DC=EC,AE与BD交于点F.(1)求证:AE=BD;(2)求∠AFD的度数.24.(8分)(2020•徐州)本地某快递公司规定:寄件不超过1千克的部分按起步价计费:寄件超过1千克的部分按千克计费.小丽分别寄快递到上海和北京,收费标准及实际收费如下表:收费标准目的地起步价(元)超过1千克的部分(元/千克)上海a b北京a+3b+4实际收费目的地质量费用(元)上海29北京 3 22求a ,b 的值.25.(8分)(2020•徐州)小红和爸爸绕着小区广场锻炼.如图,在矩形广场ABCD 边AB 的中点M 处有一座雕塑.在某一时刻,小红到达点P 处,爸爸到达点Q 处,此时雕塑在小红的南偏东45°方向,爸爸在小红的北偏东60°方向,若小红到雕塑的距离PM =30m ,求小红与爸爸的距离PQ .(结果精确到1m ,参考数据:√2≈1.41,√3≈1.73,√6≈2.45)26.(8分)(2020•徐州)如图,在平面直角坐标系中,一次函数y =kx +b 的图象经过点A (0,﹣4)、B (2,0),交反比例函数y =mx (x >0)的图象于点C (3,a ),点P 在反比例函数的图象上,横坐标为n (0<n <3),PQ ∥y 轴交直线AB 于点Q ,D 是y 轴上任意一点,连接PD 、QD .(1)求一次函数和反比例函数的表达式; (2)求△DPQ 面积的最大值.27.(10分)(2020•徐州)我们知道:如图①,点B 把线段AC 分成两部分,如果BC AB=AB AC,那么称点B 为线段AC 的黄金分割点.它们的比值为√5−12. (1)在图①中,若AC =20cm ,则AB 的长为 cm ;(2)如图②,用边长为20cm 的正方形纸片进行如下操作:对折正方形ABCD 得折痕EF,连接CE,将CB折叠到CE上,点B对应点H,得折痕CG.试说明:G是AB的黄金分割点;(3)如图③,小明进一步探究:在边长为a的正方形ABCD的边AD上任取点E(AE >DE),连接BE,作CF⊥BE,交AB于点F,延长EF、CB交于点P.他发现当PB与BC满足某种关系时,E、F恰好分别是AD、AB的黄金分割点.请猜想小明的发现,并说明理由.28.(10分)(2020•徐州)如图,在平面直角坐标系中,函数y=﹣ax2+2ax+3a(a>0)的图象交x轴于点A、B,交y轴于点C,它的对称轴交x轴于点E.过点C作CD∥x轴交抛物线于点D,连接DE并延长交y轴于点F,交抛物线于点G.直线AF交CD于点H,交抛物线于点K,连接HE、GK.(1)点E的坐标为:;(2)当△HEF是直角三角形时,求a的值;(3)HE与GK有怎样的位置关系?请说明理由.2020年江苏省徐州市中考数学试卷参考答案与试题解析一、选择题(本大题共有8小题,每小题3分,共24分.在每小题所给出的四个选项中,恰有一项是符合要求的,请将正确选项前的字母代号填涂在答题卡相应位置)1.(3分)(2020•徐州)3的相反数是()A.﹣3B.3C.−13D.13【解答】解:根据相反数的含义,可得3的相反数是:﹣3.故选:A.2.(3分)(2020•徐州)下列垃圾分类标识的图案既是轴对称图形,又是中心对称图形的是()A.B.C.D.【解答】解:A、不是中心对称图形,不是轴对称图形,故此选项不合题意;B、不是中心对称图形,是轴对称图形,故此选项不合题意;C、既是中心对称图形,也是轴对称图形,故此选项符合题意;D、不是中心对称图形,不是轴对称图形,故此选项不合题意;故选:C.3.(3分)(2020•徐州)若一个三角形的两边长分别为3cm、6cm,则它的第三边的长可能是()A.2cm B.3cm C.6cm D.9cm【解答】解:设第三边长为xcm,根据三角形的三边关系可得:6﹣3<x<6+3,解得:3<x<9,故选:C.4.(3分)(2020•徐州)在一个不透明的袋子里装有红球、黄球共20个,这些球除颜色外都相同.小明通过多次试验发现,摸出红球的频率稳定在0.25左右,则袋子中红球的个数最有可能是()A.5B.10C.12D.15【解答】解:设袋子中红球有x个,根据题意,得:x20=0.25,解得x=5,∴袋子中红球的个数最有可能是5个,故选:A.5.(3分)(2020•徐州)小红连续5天的体温数据如下(单位:℃):36.6,36.2,36.5,36.2,36.3.关于这组数据,下列说法正确的是()A.中位数是36.5℃B.众数是36.2°CC.平均数是36.2℃D.极差是0.3℃【解答】解:把小红连续5天的体温从小到大排列得,36.2,36.2,36.3.36.5,36.6,处在中间位置的一个数是36.3℃,因此中位数是36.3℃;出现次数最多的是36.2℃,因此众数是36.2℃;平均数为:x=(36.2+36.2+36.3+36.5+36.6)÷5=36.36℃,极差为:36.6﹣36.2=0.4℃,故选:B.6.(3分)(2020•徐州)下列计算正确的是()A.a2+2a2=3a4B.a6÷a3=a2C.(a﹣b)2=a2﹣b2D.(ab)2=a2b2【解答】解:a2+2a2=3a2,因此选项A不符合题意;a6÷a3=a6﹣3=a3,因此选项B不符合题意;(a﹣b)2=a2﹣2ab+b2,因此选项C不符合题意;(ab)2=a2b2,因此选项D符合题意;故选:D.7.(3分)(2020•徐州)如图,AB是⊙O的弦,点C在过点B的切线上,OC⊥OA,OC交AB于点P.若∠BPC=70°,则∠ABC的度数等于()A.75°B.70°C.65°D.60°【解答】解:∵OC⊥OA,∴∠AOC=90°,∵∠APO=∠BPC=70°,∴∠A=90°﹣70°=20°,∵OA=OB,∴∠OBA=∠A=20°,∵BC为⊙O的切线,∴OB⊥BC,∴∠OBC=90°,∴∠ABC=90°﹣20°=70°.故选:B.8.(3分)(2020•徐州)如图,在平面直角坐标系中,函数y=4x(x>0)与y=x﹣1的图象交于点P(a,b),则代数式1a−1b的值为()A.−12B.12C.−14D.14【解答】解:法一:由题意得,{y =4x y =x −1,解得,{x =1+√172y =√17−12或{x =1−√172y =−1−√172(舍去), ∴点P (1+√172,√17−12), 即:a =1+√172,b =√17−12, ∴1a −1b=1+√17−√17−1=−14;法二:由题意得,函数y =4x (x >0)与y =x ﹣1的图象交于点P (a ,b ), ∴ab =4,b =a ﹣1, ∴1a −1b =b−a ab=−14;故选:C .二.填空题(本大题共10小题,每小题3分,共30分.不需要写出解答过程,请将答案直接填写在答题卡相应位置)9.(3分)(2020•徐州)7的平方根是 ±√7 . 【解答】解:7的平方根是±√7. 故答案为:±√7.10.(3分)(2020•徐州)分解因式:m 2﹣4= (m +2)(m ﹣2) . 【解答】解:m 2﹣4=(m +2)(m ﹣2). 故答案为:(m +2)(m ﹣2).11.(3分)(2020•徐州)若√x −3在实数范围内有意义,则x 的取值范围是 x ≥3 . 【解答】解:根据题意得x ﹣3≥0, 解得x ≥3. 故答案为:x ≥3.12.(3分)(2020•徐州)原子很小,1个氧原子的直径大约为0.000000000148m ,将0.000000000148用科学记数法表示为 1.48×10﹣10.【解答】解:0.000000000148=1.48×10﹣10.故答案为:1.48×10﹣10.13.(3分)(2020•徐州)如图,在Rt △ABC 中,∠ABC =90°,D 、E 、F 分别为AB 、BC 、CA 的中点,若BF =5,则DE = 5 .【解答】解:如图,∵在Rt△ABC中,∠ABC=90°,F为CA的中点,BF=5,∴AC=2BF=10.又∵D、E分别为AB、BC的中点,∴DE是Rt△ABC的中位线,∴DE=12AC=5.故答案是:5.14.(3分)(2020•徐州)如图,在Rt△ABC中,∠C=90°,AC=4,BC=3.若以AC所在直线为轴,把△ABC旋转一周,得到一个圆锥,则这个圆锥的侧面积等于15π.【解答】解:由已知得,母线长l=5,底面圆的半径r为3,∴圆锥的侧面积是s=πlr=5×3×π=15π.故答案为:15π.15.(3分)(2020•徐州)方程9x =8x−1的解为x=9.【解答】解:去分母得:9(x﹣1)=8x9x﹣9=8xx=9检验:把x=9代入x(x﹣1)≠0,所以x=9是原方程的解.故答案为:x=9.16.(3分)(2020•徐州)如图,A、B、C、D为一个正多边形的顶点,O为正多边形的中心,若∠ADB=18°,则这个正多边形的边数为10.【解答】解:连接OA,OB,∵A、B、C、D为一个正多边形的顶点,O为正多边形的中心,∴点A、B、C、D在以点O为圆心,OA为半径的同一个圆上,∵∠ADB=18°,∴∠AOB=2∠ADB=36°,∴这个正多边形的边数=360°36°=10,故答案为:10.17.(3分)(2020•徐州)如图,∠MON=30°,在OM上截取OA1=√3.过点A1作A1B1⊥OM,交ON于点B1,以点B1为圆心,B1O为半径画弧,交OM于点A2;过点A2作A2B2⊥OM,交ON于点B2,以点B2为圆心,B2O为半径画弧,交OM于点A3;按此规律,所得线段A20B20的长等于219.【解答】解:∵B1O=B1A1,B1A1⊥OA2,∴OA1=A1A2,∵B2A2⊥OM,B1A1⊥OM,∴B1A1∥B2A2,∴B1A1=12A2B2,∴A2B2=2A1B1,同法可得A3B3=2A2B2=22•A1B1,…,由此规律可得A20B20=219•A1B1,∵A1B1=OA1•tan30°=√3×√33=1,∴A20B20=219,故答案为219.18.(3分)(2020•徐州)在△ABC中,若AB=6,∠ACB=45°.则△ABC的面积的最大值为9√2+9.【解答】解:作△ABC的外接圆⊙O,过C作CM⊥AB于M,∵弦AB已确定,∴要使△ABC的面积最大,只要CM取最大值即可,如图所示,当CM过圆心O时,CM最大,∵CM⊥AB,CM过O,∴AM=BM(垂径定理),∴AC=BC,∵∠AOB=2∠ACB=2×45°=90°,∴OM=AM=12AB=12×6=3,∴OA=√OM2+AM2=3√2,∴CM=OC+OM=3√2+3,∴S△ABC=12AB•CM=12×6×(3√2+3)=9√2+9.故答案为:9√2+9.三、解答题(本大题共有10小题,共86分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)19.(10分)(2020•徐州)计算:(1)(﹣1)2020+|√2−2|﹣(12)﹣1;(2)(1−1a)÷a2−2a+12a−2.【解答】解:(1)原式=1+2−√2−2=1−√2;(2)原式=a−1a÷(a−1)22(a−1)=a−1a •2a−1 =2a.20.(10分)(2020•徐州)(1)解方程:2x 2﹣5x +3=0; (2)解不等式组:{3x −4<52x−13>x−22.【解答】解:(1)2x 2﹣5x +3=0, (2x ﹣3)(x ﹣1)=0, ∴2x ﹣3=0或x ﹣1=0, 解得:x 1=32,x 2=1; (2){3x −4<5①2x−13>x−22②解不等式①,得x <3. 解不等式②,得x >﹣4.则原不等式的解集为:﹣4<x <3.21.(7分)(2020•徐州)小红的爸爸积极参加社区抗疫志愿服务工作.根据社区的安排,志愿者被随机分到A 组(体温检测)、B 组(便民代购)、C 组(环境消杀). (1)小红的爸爸被分到B 组的概率是13;(2)某中学王老师也参加了该社区的志愿者队伍,他和小红爸爸被分到同一组的概率是多少?(请用画树状图或列表的方法写出分析过程)【解答】解:(1)共有3种等可能出现的结果,被分到“B 组”的有1中,因此被分到“B 组”的概率为13;(2)用列表法表示所有等可能出现的结果如下:共有9种等可能出现的结果,其中“他与小红的爸爸”在同一组的有3种, ∴P (他与小红爸爸在同一组)=39=13.22.(7分)(2020•徐州)某市为了解市民每天的阅读时间,随机抽取部分市民进行调查.根据调查结果绘制了如图尚不完整的统计图表:市民每天的阅读时间统计表类别A B C D 阅读时间x(min)0≤x<3030≤x<6060≤x<90x≥90频数450400m50根据以上信息解答下列问题:(1)该调查的样本容量为1000,m=100;(2)在扇形统计图中,“B”对应扇形的圆心角等于144°;(3)将每天阅读时间不低于60min的市民称为“阅读爱好者”.若该市约有600万人,请估计该市能称为“阅读爱好者”的市民有多少万人.【解答】解:(1)450÷45%=1000,m=1000﹣(450+400+50)=100.故答案为:1000,100;(2)360°×4001000=144°.即在扇形统计图中,“B”对应扇形的圆心角等于144°.故答案为:144;(3)600×100+501000=90(万人).答:估计该市能称为“阅读爱好者”的市民有90万人.23.(8分)(2020•徐州)如图,AC⊥BC,DC⊥EC,AC=BC,DC=EC,AE与BD交于点F .(1)求证:AE =BD ; (2)求∠AFD 的度数.【解答】解:(1)∵AC ⊥BC ,DC ⊥EC , ∴∠ACB =∠DCE =90°, ∴∠ACE =∠BCD , 在△ACE 和△BCD 中, {AC =BC∠ACE =∠BCD CE =CD, ∴△ACE ≌△BCD (SAS ), ∴AE =BD ;(2)∵∠ACB =90°, ∴∠A +∠ANC =90°, ∵△ACE ≌△BCD , ∴∠A =∠B , ∵∠ANC =∠BNF ,∴∠B +∠BNF =∠A +∠ANC =90°, ∴∠AFD =∠B +∠BNF =90°.24.(8分)(2020•徐州)本地某快递公司规定:寄件不超过1千克的部分按起步价计费:寄件超过1千克的部分按千克计费.小丽分别寄快递到上海和北京,收费标准及实际收费如下表: 收费标准 目的地 起步价(元)超过1千克的部分(元/千克)上海 a b 北京 a +3b +4实际收费 目的地 质量 费用(元)上海 2 9 北京 322求a ,b 的值.【解答】解:依题意,得:{a +(2−1)b =9a +3+(3−1)(b +4)=22,解得:{a =7b =2.答:a 的值为7,b 的值为2.25.(8分)(2020•徐州)小红和爸爸绕着小区广场锻炼.如图,在矩形广场ABCD 边AB 的中点M 处有一座雕塑.在某一时刻,小红到达点P 处,爸爸到达点Q 处,此时雕塑在小红的南偏东45°方向,爸爸在小红的北偏东60°方向,若小红到雕塑的距离PM =30m ,求小红与爸爸的距离PQ .(结果精确到1m ,参考数据:√2≈1.41,√3≈1.73,√6≈2.45)【解答】解:作PN ⊥BC 于N ,如图: 则四边形ABNP 是矩形, ∴PN =AB ,∵四边形ABCD 是矩形, ∴∠A =90°,∵∠APM=45°,∴△APM是等腰直角三角形,∴AM=√22PM=√22×30=15√2(m),∵M是AB的中点,∴PN=AB=2AM=30√2m,在Rt△PNQ中,∠NPQ=90°﹣∠DPQ=90°﹣60°=30°,∴NQ=√33PN=10√6m,PQ=2NQ=20√6≈49(m);答:小红与爸爸的距离PQ约为49m.26.(8分)(2020•徐州)如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(0,﹣4)、B(2,0),交反比例函数y=mx(x>0)的图象于点C(3,a),点P在反比例函数的图象上,横坐标为n(0<n<3),PQ∥y轴交直线AB于点Q,D是y轴上任意一点,连接PD、QD.(1)求一次函数和反比例函数的表达式;(2)求△DPQ面积的最大值.【解答】解:(1)把A(0,﹣4)、B(2,0)代入一次函数y=kx+b得,{b=−4,解得,{k=2,∴一次函数的关系式为y =2x ﹣4,当x =3时,y =2×3﹣4=2,∴点C (3,2),∵点C 在反比例函数的图象上,∴k =3×2=6,∴反比例函数的关系式为y =6x,答:一次函数的关系式为y =2x ﹣4,反比例函数的关系式为y =6x ;(2)点P 在反比例函数的图象上,点Q 在一次函数的图象上,∴点P (n ,6n ),点Q (n ,2n ﹣4), ∴PQ =6n−(2n ﹣4), ∴S △PDQ =12n [6n −(2n ﹣4)]=﹣n 2+2n +3=﹣(n ﹣1)2+4,∴当n =1时,S 最大=4,答:△DPQ 面积的最大值是4.27.(10分)(2020•徐州)我们知道:如图①,点B 把线段AC 分成两部分,如果BC AB =AB AC ,那么称点B 为线段AC 的黄金分割点.它们的比值为√5−12. (1)在图①中,若AC =20cm ,则AB 的长为 (10√5−10) cm ;(2)如图②,用边长为20cm 的正方形纸片进行如下操作:对折正方形ABCD 得折痕EF ,连接CE ,将CB 折叠到CE 上,点B 对应点H ,得折痕CG .试说明:G 是AB 的黄金分割点;(3)如图③,小明进一步探究:在边长为a 的正方形ABCD 的边AD 上任取点E (AE >DE ),连接BE ,作CF ⊥BE ,交AB 于点F ,延长EF 、CB 交于点P .他发现当PB 与BC 满足某种关系时,E 、F 恰好分别是AD 、AB 的黄金分割点.请猜想小明的发现,并说明理由.【解答】解:(1)∵点B 为线段AC 的黄金分割点,AC =20cm ,∴AB =√5−12×20=(10√5−10)cm .故答案为:(10√5−10).(2)延长EA ,CG 交于点M ,∵四边形ABCD 为正方形,∴DM ∥BC ,∴∠EMC =∠BCG ,由折叠的性质可知,∠ECM =∠BCG ,∴∠EMC =∠ECM ,∴EM =EC ,∵DE =10,DC =20,∴EC =√DE 2+DC 2=√102+202=10√5,∴EM =10√5,∴DM =10√5+10,∴tan ∠DMC =DC DH =10√5+10=√5+1=√5−12. ∴tan ∠BCG =√5−12, 即BG BC =√5−12, ∴BG AB =√5−12, ∴G 是AB 的黄金分割点;(3)当BP =BC 时,满足题意.理由如下:∵四边形ABCD 是正方形,∴AB =BC ,∠BAE =∠CBF =90°,∵BE ⊥CF ,∴∠ABE +∠CBF =90°,又∵∠BCF +∠BFC =90°,∴∠BCF =∠ABE ,∴△ABE ≌△BCF (ASA ),∴BF =AE ,∵AD ∥CP ,∴△AEF ∽△BPF ,∴AE BP =AF BF ,当E 、F 恰好分别是AD 、AB 的黄金分割点时,∵AE >DE ,∴AF BF =BF AB ,∵BF =AE ,AB =BC ,∴AF BF =BF AB =AE BC ,∴AE BP =AE BC , ∴BP =BC .28.(10分)(2020•徐州)如图,在平面直角坐标系中,函数y =﹣ax 2+2ax +3a (a >0)的图象交x 轴于点A 、B ,交y 轴于点C ,它的对称轴交x 轴于点E .过点C 作CD ∥x 轴交抛物线于点D ,连接DE 并延长交y 轴于点F ,交抛物线于点G .直线AF 交CD 于点H ,交抛物线于点K ,连接HE 、GK .(1)点E 的坐标为: (1,0) ;(2)当△HEF 是直角三角形时,求a 的值;(3)HE 与GK 有怎样的位置关系?请说明理由.【解答】解:(1)对于抛物线y=﹣ax2+2ax+3a,对称轴x=−2a−2a=1,∴E(1,0),故答案为(1,0).(2)如图,连接EC.对于抛物线y=﹣ax2+2ax+3a,令x=0,得到y=3a,令y=0,﹣ax2+2ax+3a=0,解得x=﹣1或3,∴A(﹣1,0),B(3,0),C(0,3a),∵C,D关于对称轴对称,∴D(2,3a),CD=2,EC=DE,当∠HEF=90°时,∵ED=EC,∴∠ECD=∠EDC,∵∠DCF=90°,∴∠CFD+∠EDC=90°,∠ECF+∠ECD=90°,∴∠ECF=∠EFC,∴EC=EF=DE,∵EA∥DH,∴F A=AH,∴AE=12DH,∵AE=2,∴DH=4,∵HE⊥DFEF=ED,∴FH=DH=4,在Rt △CFH 中,则有42=22+(6a )2,解得a =√33或−√33(不符合题意舍弃),∴a =√33.当∠HFE =90°时,∵OA =OE ,FO ⊥AE ,∴F A =FE ,∴OF =OA =OE =1,∴3a =1,∴a =13,综上所述,满足条件的a 的值为√33或13. (3)结论:EH ∥GK .理由:由题意A (﹣1,0),F (0,﹣3a ),D (2,3a ),H (﹣2,3a ),E (1,0), ∴直线AF 的解析式y =﹣3ax ﹣3a ,直线DF 的解析式为y =3ax ﹣3a ,由{y =−3ax −3a y =−ax 2+2ax +3a,解得{x =−1y =0或{x =6y =−21a , ∴K (6,﹣21a ),由{y =3ax −3a y =−ax 2+2ax +3a,解得{x =2y =3a 或{x =−3y =−12a , ∴G (﹣3,﹣12a ),∴直线HE 的解析式为y =﹣ax +a ,直线GK 的解析式为y =﹣ax ﹣15a ,∵k 相同,∴HE ∥GK .。
2020年中考数学复习专题之二次函数的综合应用问题
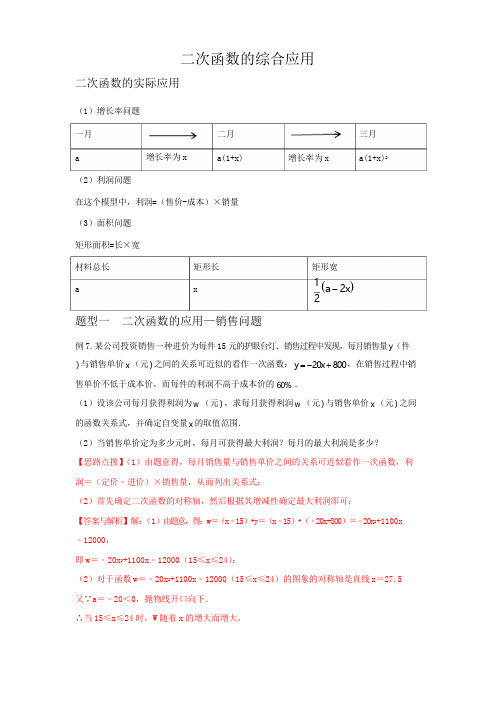
二次函数的综合应用二次函数的实际应用(1)增长率问题一月a增长率为x 二月a(1+x)增长率为x三月a(1+x)2(2)利润问题在这个模型中,利润=(售价-成本)×销量(3)面积问题矩形面积=长×宽材料总长a 矩形长x矩形宽1(a-2x)2题型一二次函数的应用—销售问题例7.某公司投资销售一种进价为每件15元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:y=-20x+800,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.(1)设该公司每月获得利润为w(元),求每月获得利润w(元)与销售单价x(元)之间的函数关系式,并确定自变量x的取值范围.(2)当销售单价定为多少元时,每月可获得最大利润?每月的最大利润是多少?【思路点拨】(1)由题意得,每月销售量与销售单价之间的关系可近似看作一次函数,利润=(定价﹣进价)×销售量,从而列出关系式;(2)首先确定二次函数的对称轴,然后根据其增减性确定最大利润即可;【答案与解析】解:(1)由题意,得:w=(x﹣15)•y=(x﹣15)•(﹣20x+800)=﹣20x2+1100x﹣12000,即w=﹣20x2+1100x﹣12000(15≤x≤24);(2)对于函数w=﹣20x2+1100x﹣12000(15≤x≤24)的图象的对称轴是直线x=27.5又∵a=﹣20<0,抛物线开口向下.∴当15≤x≤24时,W随着x的增大而增大,∴当x=24时,W=2880,答:当销售单价定为24元时,每月可获得最大利润,最大利润是2880元.变式训练1.某商场销售一批衬衫,平均每天可售出20件,每件盈利40元.为了扩大销售,增加盈利,商场采取了降价措施.假设在一定范围内,衬衫的单价每降1元,商场平均每天可多售出2件,设衬衫的单价降x元,每天获利y元.(1)如果商场里这批衬衫的库存只有44件,那么衬衫的单价应降多少元,才能使得这批衬衫一天内售完,且获利最大,最大利润是多少?(2)如果商场销售这批衬衫要保证每天盈利不少于1200元,那么衬衫的单价应降多少元?【思路点拨】(1)列出y=44(40﹣x)=﹣44x+1760,根据一次函数的性质求解;(2)根据题意列出y=(20+2x)(40﹣x)=﹣2(x﹣15)2+1250,结合二次函数的性质求解;【答案与解析】解:(1)y=44(40﹣x)=﹣44x+1760,∵20+2x≥44,∴x≥12,∵y随x的增大而减小,∴当x=12时,获利最大值1232;答:如果商场里这批衬衫的库存只有44件,那么衬衫的单价应12元,才能使得这批衬衫一天内售完,且获利最大1232元;(2)y=(20+2x)(40﹣x)=﹣2(x﹣15)2+1250,当y=1200时,1200=﹣2(x﹣15)2+1250,∴x=10或x=20,∵当x<15时,y随x的增大而增大,当x>15时,y随x的增大而减小,当10≤x≤20时,y≥1200,答:如果商场销售这批衬衫要保证每天盈利不少于1200元,那么衬衫的单价应降不少于10元且不超过20元.变式训练2.为建设美丽家园,某社区将辖区内的一块面积为1000m2的空地进行绿化,一部分种草,剩余部分栽花,设种草部分的面积为x(m2),种草所需费用y(元)与x(m2)的函1数关系图象如图所示,栽花所需费用y(元)与x(m2)的函数关系式为2xy=-0.01x2-20x+30000(0剟1000).2(1)求 y (元 ) 与 x(m 2) 的函数关系式;1(2)设这块1000m 2 空地的绿化总费用为W (元 ) ,请利用W 与 x 的函数关系式,求绿化总 费用 W 的最大值.【思路点拨】(1)根据函数图象利用待定系数法即可求得y 1(元)与 x (m 2)的函数关系式 (2)总费用为 W =y 1+y 2,列出函数关系式即可求解 【答案与解析】解:(1)依题意当 0≤x≤600 时,y 1=k 1x ,将点(600,18000)代入得 18000=600k 1,解得 k 1=30∴y 1=30x当 600<x≤1000 时,y 1=k 2x+b ,将点(600,18000),(1000,26000)代入得,解得∴y 1=20x+600综上,y 1(元)与 x (m 2)的函数关系式为:(2)总费用为:W =y 1+y 2∴W=整理得故绿化总费用 W 的最大值为 32500 元.变式训练 3.某公司生产的某种商品每件成本为 20 元,经过市场调研发现,这种商品在未来 40 天内的日销售量 m (件 ) 与时间 t (天 ) 的关系如下表:时间 t (天 ) 1 3 5 10 36日销售量 m94 90 86 76 24(件 )未来 40 天内,前 20 天每天的价格 y 1(元/件)与时间 t (天)的函数关系式为 y 1= t +25(1≤t ≤20 且 t 为整数),后20 天每天的价格 y 2(元/件)与时间 t (天)的函数关系式为y 2=﹣ t +40(21≤t ≤40 且 t 为整数).下面我们就来研究销售这种商品的有关问题:(1)认真分析上表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些数据的 m (件 ) 与 t (天 ) 之间的表达式;(2)请预测未来 40 天中哪一天的日销售利润最大,最大日销售利润是多少?【思路点拨】(1)从表格可看出每天比前一天少销售 2 件,所以判断为一次函数关系式;(2)日利润=日销售量×每件利润,据此分别表示前 20 天和后 20 天的日利润,根据函数性质求最大值后比较得结论.【答案与解析】解:(1)经分析知:m 与 t 成一次函数关系.设 m =kt+b (k≠0),将 t =1,m =94,t =3,m =90代入,解得,∴m=﹣2t+96;(2)前 20 天日销售利润为 P 1 元,后 20 天日销售利润为 P 2 元,则 P 1=(﹣2t+96)( t+25﹣20)=﹣ (t ﹣14)2+578,∴当 t =14 时,P 1 有最大值,为 578 元.P 2=(﹣2t+96)•( t+40﹣20)=﹣t 2+8t+1920=(t ﹣44)2﹣16,∵当 21≤t≤40 时,P 2 随 t 的增大而减小,∴t=21 时,P 2 有最大值,为 513 元. ∵513<578,∴第 14 天日销售利润最大,最大利润为 578 元.题型二 二次函数的应用—面积问题例 8.如图,用 30m 长的篱笆沿墙建造一边靠墙的矩形菜园,已知墙长18m ,设矩形的宽 AB为xm.(1)用含x的代数式表示矩形的长BC;(2)设矩形的面积为y,用含x的代数式表示矩形的面积y,并求出自变量的取值范围;(3)这个矩形菜园的长和宽各为多少时,菜园的面积y最大?最大面积是多少?【思路点拨】(1)设菜园的宽AB为xm,于是得到BC为(30﹣2x)m;(2)由面积公式写出y与x的函数关系式,进而求出x的取值范围;(3)利用二次函数求最值的知识可得出菜园的最大面积.【答案与解析】解:(1)∵AB=CD=xm,∴BC=(30﹣2x)m;(2)由题意得y=x(30﹣2x)=﹣2x2+30x(6≤x<15);(3)∵S=﹣2x2+30x=﹣2(x﹣7.5)2+112.5,∴当x=7.5时,S有最大值,S=112.5,最大此时这个矩形的长为15m、宽为7.5m.答:这个矩形的长、宽各为15m、7.5m时,菜园的面积最大,最大面积是112.5m2.变式训练1.为了节省材料,小浪底水库养殖户小李利用水库的岸堤(足够长)为一边,用总长为120米的网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为xm,矩形区域ABCD的面积为ym2.(1)求y与x之间的函数关系式,并注明自变量x的取值范围;(2)请你帮养殖户小李计算一下BC边多长时,养殖区ABCD面积最大,最大面积为多少?【思路点拨】(1)三个矩形的面值相等,可知2FG=2GE=BC,可知:2BC+8FC=120,即FC=,即可求解;(2)y=﹣x2+45x=﹣(x﹣30)2+675即可求解.【答案与解析】解:(1)∵三个矩形的面值相等,可知2FG=2GE=BC,∴BC×DF=BC×FC,∴2FC=DC,2BC+8FC=120,∴FC=,∴y与x之间的函数关系式为y=3FC×BC=x(120﹣2x),即y=﹣x2+45x,(0<x<60);(2)y=﹣x2+45x=﹣(x﹣30)2+675可知:当BC为30米是,养殖区ABCD面积最大,最大面积为675平方米.变式训练 2.如图,ABCD是一块边长为8米的正方形苗圃,园林部门拟将其改造为矩形AEFG的形状,其中点E在AB边上,点G在A的延长线上,DG2BE,设BE的长为x米,改造后苗圃AEFG的面积为y平方米.(1)求y与x之间的函数关系式(不需写自变量的取值范围);(2)若改造后的矩形苗圃AEFG的面积与原正方形苗圃ABCD的面积相等,此时BE的长为米.(3)当x为何值时改造后的矩形苗圃AEFG的最大面积?并求出最大面积.【思路点拨】(1)根据题意可得DG=2x,再表示出AE和AG,然后利用面积可得y与x之间的函数关系式;(2)根据题意可得正方形苗圃ABCD的面积为64,进而可得矩形苗圃AEFG的面积为64,进而可得:﹣2x2+8x+64=64再解方程即可;(3)根据二次函数的性质即可得到结论.【答案与解析】解:(1)y=(8﹣x)(8+2x)=﹣2x2+8x+64,故答案为:y=﹣2x2+8x+64;(2)根据题意可得:﹣2x2+8x+64=64,解得:x1=4,x2=0(不合题意,舍去),答:BE的长为4米;故答案为:y=﹣2x2+8x+64(0<x<8);(3)解析式变形为:y=﹣2(x﹣2)2+72,所以当x=2时,y有最大值,∴当x为2时改造后的矩形苗圃AEFG的最大面积,最大面积为72平方米.变式训练3.如图,一面利用墙(墙的最大可用长度为10m),用长为24m的篱笆围成中间隔有一道篱笆的矩形花圃,设花圃的一边AB的长为x(m),面积为y(m2).(1)若y与x之间的函数表达式及自变量x的取值范围;(2)若要围成的花圃的面积为45m2,则AB的长应为多少?【思路点拨】(1)根据题意可以得到y与x的函数关系式以及x的取值范围;(2)令y=45代入(1)中的函数解析式,即可求得x的值,注意x的取值范围.【答案与解析】解:(1)由题意可得,y=x(24﹣3x)=﹣3x2+24x,∵24﹣3x≤10,3x<24,解得,x≥∴且x<8,,即y与x之间的函数表达式是y=﹣3x2+24x((2)当y=45时,45=﹣3x2+24x,解得,x1=3(舍去),x2=5,答:AB的长应为5m.题型三二次函数的应用—抛物线问题);例9.如图,已知排球场的长度O D为18米,位于球场中线处球网的高度AB为2.4米,一队员站在点O处发球,排球从点O的正上方1.6米的C点向正前方飞出,当排球运行至离点O的水平距离OE为6米时,到达最高点G建立如图所示的平面直角坐标系.(1)当球上升的最大高度为3.4米时,对方距离球网0.4m的点F处有一队员,他起跳后的最大高度为3.1米,问这次她是否可以拦网成功?请通过计算说明.(2)若队员发球既要过球网,又不出边界,问排球飞行的最大高度h的取值范围是多少?(排球压线属于没出界)【思路点拨】(1)根据此时抛物线顶点坐标为(6,3.4),设解析式为y=a(x﹣6)2+3.4,再将点C坐标代入即可求得;由解析式求得x=9.4时y的值,与他起跳后的最大高度为3.1米比较即可得;(2)设抛物线解析式为y=a(x﹣6)2+h,将点C坐标代入得到用h表示a的式子,再根据球既要过球网,又不出边界即x=9时,y>2.4且x=18时,y≤0得出关于h的不等式组,解之即可得.【答案与解析】解:(1)根据题意知此时抛物线的顶点G的坐标为(6,3.4),设抛物线解析式为y=a(x﹣6)2+3.4,将点C(0,1.6)代入,得:36a+3.4=1.6,解得:a=﹣,∴排球飞行的高度y与水平距离x的函数关系式为y=﹣(x﹣6)2+;由题意当x=9.5时,y=﹣(9.4﹣6)2+≈2.8<3.1,故这次她可以拦网成功;(2)设抛物线解析式为y=a(x﹣6)2+h,将点C(0,1.6)代入,得:36a+h=1.6,即a=∴此时抛物线解析式为y=(x﹣6)2+h,,变式训练1.一位篮球运动员投篮,球沿抛物线y=-x2+运行,然后准确落入篮筐内,根据题意,得:,解得:h≥3.025,答:排球飞行的最大高度h的取值范围是h≥3.025.1752已知篮筐的中心距离底面的距离为3.05m.(1)求球在空中运行的最大高度为多少m?(2)如果该运动员跳投时,球出手离地面的高度为2.25m,要想投入篮筐,则问他距离蓝筐中心的水平距离是多少?【思路点拨】(1)由抛物线的顶点坐标即可得;(2)分别求出y=3.05和y=2.25时x的值即可得出答案.【答案与解析】解:(1)∵y=﹣x2+的顶点坐标为(0,),∴球在空中运行的最大高度为m;(2)当y=3.05时,﹣0.2x2+3.5=3.05,解得:x=±1.5,∵x>0,∴x=1.5;当y=2.25时,﹣0.2x2+3.5=2.25,解得:x=2.5或x=﹣2.5,由1.5+2.5=4(m),故他距离篮筐中心的水平距离是4米.变式训练2.甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式y=a(x-4)2+h,已知点O与球网的水平距离为5m,球网的高度为1.55m.(1)当a=-124时,①求h的值;②通过计算判断此球能否过网.(2)若甲发球过网后,羽毛球飞行到与点的O水平距离为7m,离地面的高度为处时,乙扣球成功,求a的值.125m的Q【思路点拨】(1)①将点P(0,1)代入y=﹣(x﹣4)2+h即可求得h;②求出x=5时,y的值,与1.55比较即可得出判断;(2)将(0,1)、(7,)代入y=a(x﹣4)2+h代入即可求得a、h.【答案与解析】解:(1)①当a=﹣时,y=﹣(x﹣4)2+h,将点P(0,1)代入,得:﹣解得:h=;×16+h=1,②把x=5代入y=﹣∵1.625>1.55,∴此球能过网;(x﹣4)2+,得:y=﹣×(5﹣4)2+=1.625,(2)把(0,1)、(7,,)代入y=a(x﹣4)2+h,得:解得:,∴a=﹣.变式训练3.小明跳起投篮,球出手时离地面20m,球出手后在空中沿抛物线路径运动,并9在距出手点水平距离4m处达到最高4m.已知篮筐中心距地面3m,与球出手时的水平距离为8m,建立如图所示的平面直角坐标系.(1)求此抛物线对应的函数关系式;(2)此次投篮,球能否直接命中篮筐中心?若能,请说明理由;若不能,在出手的角度和力度都不变的情况下,球出手时距离地面多少米可使球直接命中篮筐中心?(3)在篮球比赛中,当进攻方球员要投篮时,防守方球员常借身高优势及较强的弹跳封杀对方,这就是平常说的盖帽.(注:盖帽应在球达到最高点前进行,否则就是“干扰球”,属犯规.)若此时,防守方球员乙前来盖帽,已知乙的最大摸球高度为3.19m,则乙在进攻方球员前多远才能盖帽成功?【思路点拨】(1)根据顶点坐标(4,4),设抛物线的解析式为:y=a(x﹣4)2+4,由球出手时离地面m,可知抛物线与y轴交点为(0,),代入可求出a的值,写出解析式;(2)先计算当x=8时,y的值是否等于3,把x=8代入得:y=,所以要想球经过(8,3),则抛物线得向上平移3﹣=个单位,即球出手时距离地面3米可使球直接命中篮筐中心;(3)将由y=3.19代入函数的解析式求得x值,进而得出答案.【答案与解析】(1)设抛物线为y=a(x﹣4)2+4,将(0,)代入,得a(0﹣4)2+4=,解得a=﹣,∴所求的解析式为y=﹣(x﹣4)2+4;(2)令x=8,得y=﹣(8﹣4)2+4=∴抛物线不过点(8,3),故不能正中篮筐中心;≠3,=∵抛物线过点(8,),∴要使抛物线过点(8,3),可将其向上平移 7/9 个单位长度,故小明需向上多跳 m 再投篮(即球出手时距离地面 3 米)方可使球正中篮筐中心.(3)由(1)求得的函数解析式,当 y =3.19 时,3.19=﹣19(x ﹣4)2+4解得:x 1=6.7(不符合实际,要想盖帽,必须在篮球下降前盖帽,否则无效),x 2=1.3∴球员乙距离甲球员距离小于 1.3 米时,即可盖帽成功.题型四 二次函数与图形面积的综合例 10.如图,抛物线 y = a(x + 1)2的顶点为 A ,与 y 轴的负半轴交于点 B ,且 OB = OA .(1)求抛物线的解析式;(2)若点 C (-3,b ) 在该抛物线上,求 S∆ABC 的值.【思路点拨】(1)由抛物线解析式确定出顶点 A 坐标,根据 OA =OB 确定出 B 坐标,将 B坐标代入解析式求出 a 的值,即可确定出解析式;(2)将 C 坐标代入抛物线解析式求出 b 的值,确定出 C 坐标,过 C 作 CD 垂直于 x 轴,三角形 ABC 面积=梯形 OBCD 面积﹣三角形 ACD 面积﹣三角形 AOB 面积,求出即可.【答案与解析】解:(1)由题意得:A (﹣1,0),B (0,﹣1),将 x =0,y =﹣1 代入抛物线解析式得:a =﹣1,则抛物线解析式为 y =﹣(x+1)2=﹣x 2﹣2x ﹣1;(2)过 C 作 CD⊥x 轴,将 C (﹣3,b )代入抛物线解析式得:b =﹣4,即 C (﹣3,﹣4),则 △S ABC =S 梯形 OBCD △﹣S ACD △﹣S A OB ×3×(4+1)﹣ ×4×2﹣ ×1×1=3.变式训练1.如图,已知二次函数图象的顶点为(1,-3),并经过点C(2,0).(1)求该二次函数的解析式;(2)直线y=3x与该二次函数的图象交于点B(非原点),求点B的坐标和∆AOB的面积;【思路点拨】(1)设抛物线的解析式为y=a(x﹣1)2﹣3,由待定系数法就可以求出结论;(2)由抛物线的解析式与一次函数的解析式构成方程组,求出其解即可求出B的坐标,进而可以求出直线AB的解析式,就可以求出AB与x轴的交点坐标,就可以求出△AOB的面积;【答案与解析】解:(1)抛物线的解析式为y=a(x﹣1)2﹣3,由题意,得0=a(2﹣1)2﹣3,解得:a=3,∴二次函数的解析式为:y=3(x﹣1)2﹣3;(2)由题意,得,解得:.∵交点不是原点,∴B(3,9).如图2,设直线AB的解析式为y=kx+b,由题意,得,△+S,△+S△+S解得:,∴y=6x﹣9.当y=0时,y=1.5.∴E(1.5,0),∴OE=1.5,△∴SAOB=SA OE BOE=+,=9.答:B(3,9),△AOB的面积为9;变式训练2.如图,抛物线y=x2+x-2与x轴交于A、B两点,与y轴交于点C.(1)求点A,点B和点C的坐标;(2)在抛物线的对称轴上有一动点P,求PB+PC的值最小时的点P的坐标;(3)若点M是直线AC下方抛物线上一动点,求四边形ABCM面积的最大值.【思路点拨】(1)利用待定系数法即可解决问题.(2)连接AC与对称轴的交点即为点P.求出直线AC的解析式即可解决问题.(3)过点M作MN⊥x轴与点N,设点M(x,x2+x﹣2),则AN=x+2,0N=﹣x,0B=1,0C=2,MN=﹣(x2+x﹣2)=﹣x2﹣x+2,根据S四边形ABCM△=SAOM OCM BOC构建二次函数,利用二次函数的性质即可解决问题.【答案与解析】解:(1)由y=0,得x2+x﹣2=0解得x=﹣2x=l,∴A(﹣2,0),B(l,0),由x=0,得y=﹣2,∴C(0,﹣2).(2)连接AC与对称轴的交点即为点P.△+S + =设直线 AC 为 y =kx+b ,则﹣2k+b =0,b =﹣2:得 k =﹣l ,y =﹣x ﹣2.对称轴为 x =﹣ ,当 x =﹣ 时,y =_(﹣ )﹣2=﹣ ,∴P(﹣ ,﹣ ).(3)过点 M 作 MN⊥x 轴与点 N ,设点 M (x ,x 2+x ﹣2),则 AN =x+2,0N =﹣x ,0B =1,0C =2,MN =﹣(x 2+x ﹣2)=﹣x 2﹣x+2,S四边形 ABCM△=S AOM OCM △S BOC (x+2)(﹣x 2﹣x+2)+ (2﹣x 2﹣x+2)(﹣x )+ ×1× 2=﹣x 2﹣2x+3=﹣(x+1)2+4.∵﹣1<0,∴当 x =_l 时,S 四边形 ABCM 的最大值为 4.变式训练 3.如图,二次函数 y = ax 2 + b x 的图象经过点 A(2,4) 与 B(6,0) .(1)求 a , b 的值;(2)点 C 是该二次函数图象上 A , B 两点之间的一动点,横坐标为 x (2 < x < 6) ,写出四边形 OACB 的面积 S 关于点 C 的横坐标 x 的函数表达式,并求 S 的最大值.△=△=△=△+S△+S【思路点拨】(1)把A与B坐标代入二次函数解析式求出a与b的值即可;(2)如图,过A作x轴的垂直,垂足为D(2,0),连接CD,过C作CE⊥AD,CF⊥x轴,垂足分别为E,F,分别表示出三角形OAD,三角形ACD,以及三角形BCD的面积,之和即为S,确定出S关于x的函数解析式,并求出x的范围,利用二次函数性质即可确定出S的最大值,以及此时x的值.【答案与解析】解:(1)将A(2,4)与B(6,0)代入y=ax2+bx,得,解得:;(2)如图,过A作x轴的垂线,垂足为D(2,0),连接CD、CB,过C作CE⊥AD,CF⊥x 轴,垂足分别为E,F,SOADOD•AD=×2×4=4;SACDAD•CE=×4×(x﹣2)=2x﹣4;SBCDBD•CF=×4×(﹣x2+3x)=﹣x2+6x,则S=SOAD ACD BCD=4+2x﹣4﹣x2+6x=﹣x2+8x,∴S关于x的函数表达式为S=﹣x2+8x(2<x<6),∵S=﹣x2+8x=﹣(x﹣4)2+16,∴当x=4时,四边形OACB的面积S有最大值,最大值为16.。
苏科版数学中考复习专题练习— 二次函数及其应用(含答案)

二次函数及其应用一、学习目标1.掌握二次函数的定义;2.理解并掌握二次函数的图像以及性质;3.会利用二次函数的性质解决实际问题.二、典型例题题型一、二次函数的概念例题1.下列函数中,y关于x的二次函数是()A.y=ax2+bx+c B.y=1x2+1C.y=x(x+1) D.y=(x+2)2-x2【题小结】用二次函数的概念进行判断借题发挥:若y=(k-1)x k2+1是二次函数,则k=.题型二、二次函数的图像与性质例题2.关于抛物线y=3(x-1)2+2,下列说法错误的是()A.开口方向向上B.对称轴是直线x=1C.顶点坐标为(1,2)D.当x>1时,y随x的增大而减小例题3.已知二次函数y=2x2-8x+c的图象过点A(-2,y1),B(-1,y2),C(8,y3),则y1,y2,y3的大小关系是()A.y3>y1>y2B.y1>y2>y3C.y2>y3>y1D.y3>y2>y1【题小结】用二次函数的图像与性质解决借题发挥:1.当x≥2时,二次函数y=x2-2x-3有()A.最大值-3 B.最小值-3 C.最大值-4 D.最小值-42.二次函数y=ax2+bx+c的部分图象如图,图象过点A(3,0),对称轴为直线x=1,下列结论:①a -b+c=0;②2a+b=0;③4ac-b2>0;④a+b≥am2+bm(m为实数).其中正确的结论有()A.1个B.2个C.3个D.4个题型三、用待定系数法求二次函数例题5.如图,已知点A的坐标是(1,3),将线段OA绕点O逆时针旋转90°得到OB.(1)求经过A、O、B三点的抛物线的解析式;(2)若M是线段AB上的一个动点,过点M作MN⊥x轴交抛物线于点N,当线段MN的长度取最大值时,求点M的坐标.借题发挥:已知二次函数的图象如图所示:(1)求这个二次函数的表达式;(2)观察图象,当-3<x<0时,y的取值范围为;(3)将该二次函数图象沿x轴翻折后得到新图象,新图象的函数表达式为.题型四、二次函数与方程、不等式例题6.已知二次函数y=x2-6x-9k的图象与x轴有两个不同的交点,则k的取值范围为.例题7.如表是二次函数y=ax2+bx+c的几组对应值:()A.6<x<6.17 B.6.17<x<6.18 C.6.18<x<6.19 D.6.19<x<6.20例题8.如图,抛物线y=ax2+c与直线y=mx+n交于A(-2,-3),B(3,q)两点,则不等式ax2-mx+c<n的解集是.【题小结】二次函数的图像与x轴交点坐标,一元二次方程、不等式等问题的联系.。
江苏省徐州市2020年中考数学试题(Word版,含答案与解析)

江苏省徐州市2020年中考数学试卷一、选择题(本大题共有8小题,每小题3分,共24分.)(共8题;共24分)1.3的相反数是( ).A. -3B. 3C. −13D. 13【答案】 A【考点】相反数及有理数的相反数【解析】【解答】3的相反数是-3故答案为:A .【分析】相反数的定义:只有符号不同的两个数互为相反数,根据相反数的定义即可得.2.下列垃圾分类标识的图案既是轴对称图形,又是中心对称图形的是( ) A. B. C. D.【答案】 C【考点】轴对称图形,中心对称及中心对称图形【解析】【解答】A.不是轴对称图形,也不是中心对称图形,故此选项不符合题意;B.是轴对称图形,不是中心对称图形,故此选项不符合题意;C.是轴对称图形,是中心对称图形,故此选项符合题意;D.不是轴对称图形,也不是中心对称图形,故此选项不符合题意,故答案为:C.【分析】中心对称图形是图形绕某一点旋转180°后与原来的图形完全重合,轴对称图形是将一个图形沿某直线折叠后直线两旁的部分互相重合,再对各选项逐一判断。
3.三角形的两边长分别为 3cm 和 6cm ,则第三边长可能为( )A. 2cmB. 3cmC. 6cmD. 9cm【答案】 C【考点】三角形三边关系【解析】【解答】解:6-3=3<第三边长<6+3=9,只有6cm 满足题意,故答案为:C.【分析】根据三角形的两边之和大于第三边,且两边之差小于第三边即可列出不等式组,求解得出第三边的取值范围,进而即可一一判断得出答案.4.在一个不透明的袋子里装有红球、黄球共 20 个,这些球除颜色外都相同.小明通过多次实验发现,摸出红球的频率稳定在 0.25 左右,则袋子中红球的个数最有可能是( )A. 5B. 10C. 12D. 15【答案】 A【考点】概率的简单应用【解析】【解答】解:设袋子中红球有x个,=0.25,根据题意,得:x20解得x=5,答:袋子中红球有5个.故答案为:A.【分析】设袋子中红球有x个,根据摸出红球的频率稳定在0.25左右列出关于x的方程,求出x的值即可得答案.5.小红连续5天的体温数据如下(单位相°C):36.6,36.2,36.5,36.2,36.3.关于这组数据下列说法正确的是()A. 中位数是36.5°CB. 众数是36.2°CC. 平均数是36.2°CD. 极差是0.3°C【答案】B【考点】分析数据的集中趋势【解析】【解答】解:A.将这组数据从小到大的顺序排列:36.2,36.2,36.3,36.5,36.6,则中位数为36.3°C ,故此选项错误B.36.2出现了两次,故众数是36.2 °C,故此选项正确;(36.2+36.2+36.3+36.5+36.6)=36.36( °C ),故此选项错误;C.平均数为15D.极差为36.6-36.2=0.4( °C ),故此选项错误,故答案为:B.【分析】根据众数、中位数的概念求得众数和中位数,根据平均数和方差、极差公式计算平均数和极差即可得出答案.6.下列计算正确的是()A. a2+2a2=3a4B. a6÷a3=a2C. (a−b)2=a2−b2D. (ab)2=a2b2【答案】 D【考点】同底数幂的除法,完全平方公式及运用,合并同类项法则及应用,积的乘方【解析】【解答】解:A、a2+2a2=3a2,故A错误;B、a6÷a3=a3,故B错误;C、(a−b)2=a2−2ab+b2,故C错误;D、(ab)2=a2b2,故D正确;故答案为:D.【分析】由合并同类项、同底数幂除法,完全平方公式、积的乘方,分别进行判断,即可得到答案.7.如图,AB是⊙O的弦,点C在过点B的切线上,OC⊥OA,OC交AB于点P.若∠BPC=70°,则∠ABC的度数等于()A. 75°B. 70°C. 65°D. 60°【答案】B【考点】切线的性质【解析】【解答】解:∵∠BPC=70°,∴∠APO=70°,∵OC⊥OA,∴∠AOP=90°,∴∠A=20°,又∵OA=OB,∴∠ABO=20°,又∵点C在过点B的切线上,∴∠OBC=90°,∴∠ABC=∠OBC−∠ABO=90°−20°=70°,故答案为:B.【分析】根据题意可求出∠APO、∠A的度数,进一步可得∠ABO度数,从而推出答案.8.如图,在平面直角坐标系中,函数y=4x(x>0)与y=x−1的图像交于点P(a,b),则代数式1 a −1b的值为()A. −12B. 12C. −14D. 14【答案】C【考点】反比例函数与一次函数的交点问题【解析】【解答】解:∵函数y=4x(x>0)与y=x−1的图像交于点P( a,b),∴b=4a,b=a−1,即ab=4,b−a=−1,∴1a −1b=b−aab=−14.故答案为:C.【分析】把P( a,b)代入两解析式得出b−a和ab的值,整体代入1a −1b=b−aab即可求解C二、填空题(本大题共10小题,每小题3分,共30分.)(共10题;共30分)9.7的平方根是________.【答案】±√7【考点】平方根【解析】【解答】∵(±√7)2=7,∴7的平方根是±√7,故答案为±√7.【分析】根据平方根的定义,即可求解.10.分解因式:m2−4=________.【答案】(m+2)(m﹣2)【考点】因式分解﹣运用公式法【解析】【解答】解:m2−4=(m+2)(m﹣2).故答案为:(m+2)(m﹣2).【分析】直接利用平方差公式a2-b2=(a+b)(a-b)进行因式分解.11.式子√x−3在实数范围内有意义,则x 的取值范围是________ .【答案】x≥3【考点】二次根式有意义的条件【解析】【解答】由题意可得:x﹣3≥0,解得:x≥3,故答案为:x≥3.【分析】根据二次根式的被开方数不能为负数,列出不等式,求解即可。
(徐州专版)2020年中考数学复习第三单元函数及其图象第15课时二次函数的综合应用课件

| 考向精练 | 1. [2019·永州]如图15-8,已知抛物线经过两点A(-3,0),B(0,3),且其对称轴为直 线x=-1. (1)求此抛物线的解析式; (2)若点P是抛物线上点A与点B之间的 动点(不包括点A,点B),求△PAB面积的 最大值,并求出此时点P的坐标.
图15-8
(1)求A,C两点的坐标;
(2)求抛物线的表达式;
(3)若点P是直线AC下方的抛物线上的一个动点,作
PD⊥AC于点D,当PD的值最大时,求此时点P的坐标
及PD的最大值.
图15-7
解:(1)由题意知OA=OC=4OB=4, 故点A,C的坐标分别为(4,0),(0,-4).
例2 [2019·贺州]如图15-7,在平面直角坐标系中,已知点B的坐标为(-1,0),且 OA=OC=4OB,抛物线y=ax2+bx+c(a≠0)经过A,B,C三点. (2)求抛物线的表达式;
图15-4
(1)当1<x<2时,△BPQ的面积 不变 (填“变”或“不变”); (2)分别求出线段OM,曲线NK所对应的函数表达式; (3)当x为何值时,△BPQ的面积是5 cm2?
图15-4
例1 [2017·徐州26题]如图15-4①,菱形ABCD中,AB=5 cm,动点P从点B出发, 沿折线BC-CD-DA运动到点A停止,动点Q从点A出发,沿线段AB运动到点B停 止,它们运动的速度相同.设点P出发x s时,△BPQ的面积为y cm2.已知y与x之 间的函数关系如图②所示,其中OM,MN为线段,曲线NK为抛物线的一部分.请 根据图中的信息,解答下列问题: (2)分别求出线段OM,曲线 NK所对应的函数表达式;
图15-4
例1 [2017·徐州26题]如图15-4①,菱形ABCD中,AB=5 cm,动点P从点B出发, 沿折线BC-CD-DA运动到点A停止,动点Q从点A出发,沿线段AB运动到点B停 止,它们运动的速度相同.设点P出发x s时,△BPQ的面积为y cm2.已知y与x之 间的函数关系如图②所示,其中OM,MN为线段,曲线NK为抛物线的一部分.请 根据图中的信息,解答下列问题: (3)当x为何值时,△BPQ的面积是5 cm2?
2020年中考数学专题复习 一次函数及其应用(解析版)

2020中考数学专题复习一次函数及其应用(含答案)一、选择题(本大题共6道小题)1. 若点P在一次函数y=-x+4的图象上,则点P一定不在()A.第一象限B.第二象限C.第三象限D.第四象限2. 对于正比例函数y=-2x,当自变量x的值增加1时,函数y的值增加()A.-2B.2C.-D.3. 正比例函数y=kx(k≠0)的函数值y随着x的增大而减小,则一次函数y=x+k的图象大致是 ()4. 若一次函数y=kx+b(k,b为常数,且k≠0)的图象过点A(0,-1),B(1,1),则不等式kx+b>1的解集为()A.x<0B.x>0C.x<1D.x>15. 在同一平面直角坐标系中,直线y=4x+1与直线y=-x+b的交点不可能在()A.第一象限B.第二象限C.第三象限D.第四象限6. 一次函数y=kx-1的图象经过点P,且y的值随x值的增大而增大,则点P的坐标为()A.(-5,3)B.(1,-3)C.(2,2)D.(5,-1)二、填空题(本大题共6道小题)7. 直线y=2x-1与x轴的交点坐标为.8. 已知点A(x1,y1)、B(x2,y2)在直线y=kx+b上,且直线经过第一、二、四象限,当x1<x2时,y1与y2的大小关系为.9. 星期天,小明上午8:00从家里出发,骑车到图书馆去借书,再骑车回到家,他离家的距离y(千米)与时间t(分)的关系如图所示,则上午8:45小明离家的距离是千米.10. 如图所示,一次函数y=ax+b的图象与x轴相交于点(2,0),与y轴相交于点(0,4),结合图象可知,关于x的方程ax+b=0的解是x=.11. 如图,直线y=kx+b(k<0)经过点A(3,1),当kx+b<x时,x的取值范围为.12. 在平面直角坐标系中,点P(x0,y0)到直线Ax+By+C=0的距离公式为:d=,则点P(3,-3)到直线y=-x+的距离为.三、解答题(本大题共4道小题)13. 小王骑车从甲地到乙地,小李骑车从乙地到甲地,小王的速度小于小李的速度,两人同时出发,沿同一条公路匀速前进.图中的折线表示两人之间的距离y(km)与小王的行驶时间x(h)之间的函数关系.请你根据图象进行探究:(1)小王和小李的速度分别是多少?(2)求线段BC所表示的y与x之间的函数解析式,并写出自变量x的取值范围.14. 为了节能减排,我市某校准备购买某种品牌的节能灯,已知3只A型节能灯和5只B型节能灯共需50元,2只A型节能灯和3只B型节能灯共需31元.(1)求1只A型节能灯和1只B型节能灯的售价各是多少元?(2)学校准备购买这两种型号的节能灯共200只,要求A型节能灯的数量不超过B型节能灯的数量的3倍,请设计出最省钱的购买方案,并说明理由.15. 如图,在平面直角坐标系xOy中,过点A(-2,0)的直线交y轴正半轴于点B,将直线AB绕着点O顺时针旋转90°后,分别与x轴、y轴交于点D,C.(1)若OB=4,求直线AB的函数关系式;(2)连接BD,若△ABD的面积是5,求点B的运动路径长.16. 现代互联网技术的广泛应用,催生了快递行业的高速发展,小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元,设小明快递物品为x 千克.(1)根据题意,填写下表:快递物品质量0.5 1 3 4 …(千克)甲公司收费22 …(元)乙公司收费11 51 67 …(元)(2)设甲快递公司收费y1元,乙快递公司收费y2元,分别写出y1,y2关于x的函数关系式.(3)当x>3时,小明应选择哪家快递公司更省钱?请说明理由.2020中考数学一次函数及其应用-答案一、选择题(本大题共6道小题)1. 【答案】C[解析]∵-1<0,4>0,∴一次函数y=-x+4的图象经过第一、二、四象限,即不经过第三象限.∵点P在一次函数y=-x+4的图象上,∴点P一定不在第三象限.故选C.2. 【答案】A3. 【答案】A[解析]因为正比例函数y=kx(k≠0)的函数值y随着x的增大而减小,所以k<0,所以一次函数y=x+k的函数值y随着x增大而增大,图象与y轴交于负半轴,故选A.4. 【答案】D[解析]如图所示:不等式kx+b>1的解集为x>1.故选D.5. 【答案】D[解析]因为直线y=4x+1只经过第一、二、三象限,所以其与直线y=-x+b的交点不可能在第四象限.故选D.6. 【答案】C[解析]∵一次函数y=kx-1的图象经过点P,且y的值随x值的增大而增大,∴k>0.由y=kx-1得k=.分别将选项中坐标代入该式,只有当(2,2)时k==>0.二、填空题(本大题共6道小题)7. 【答案】,08. 【答案】y1>y2[解析]∵一次函数图象经过第二、四象限,∴k<0,y随x的增大而减小,∴当x1<x2时,y1>y2.9. 【答案】1.510. 【答案】2[解析]考查一元一次方程与一次函数的关系,即关于x的方程ax+b=0的解就是一次函数y=ax+b的图象与x轴交点(2,0)的横坐标2.11. 【答案】x>3[解析]当x=3时,x=×3=1,∴点A在一次函数y=x的图象上,且一次函数y=x的图象经过第一、三象限,∴当x>3时,一次函数y=x的图象在y=kx+b的图象上方,即kx+b<x.12. 【答案】[解析]∵y=-x+,∴2x+3y-5=0,∴点P(3,-3)到直线y=-x+的距离为:=.故答案为.三、解答题(本大题共4道小题)13. 【答案】解:(1)从线段AB得:两人从相距30 km的两地同时出发,1 h后相遇,则v小王+v小李=30 km/h,小王从甲地到乙地行驶了3 h,∴v小王=30÷3=10(km/h),∴v小李=20 km/h.(2)C点的意义是小李骑车从乙地到甲地用了30÷20=1.5(h),此时小王和小李的距离是1.5×10=15(km),∴C点坐标是(1.5,15).设直线BC的解析式为y=kx+b,将B(1,0),C(1.5,15)分别代入解析式,得解得:∴线段BC的解析式为y=30x-30(1≤x≤1.5).14. 【答案】解:(1)设1只A型节能灯的售价是x元,1只B型节能灯的售价是y元,根据题意,得解得答:1只A型节能灯的售价是5元,1只B型节能灯的售价是7元.(2)设购买A型节能灯a只,则购买B型节能灯(200-a)只,总费用为w元,w=5a+7(200-a)=-2a+1400,∵a≤3(200-a),∴a≤150,∵-2<0,w随a的增大而减小,∴当a=150时,w取得最小值,此时w=1100,200-a=50.答:最省钱的购买方案是:购买A型节能灯150只,B型节能灯50只.15. 【答案】解:(1)因为OB=4,且点B在y轴正半轴上,所以点B的坐标为(0,4).设直线AB的函数关系式为y=kx+b,将点A(-2,0),B(0,4)的坐标分别代入,得解得所以直线AB的函数关系式为y=2x+4.(2)设OB=m,因为△ABD的面积是5,所以AD·OB=5.所以(m+2)m=5,即m2+2m-10=0.解得m=-1+或-1-(舍去).因为∠BOD=90°,所以点B的运动路径长为×2π×(-1+)=π.16. 【答案】解:(1)11526719[解析]当x=0.5时,y甲=22×0.5=11.当x=3时,y甲=22+15×2=52;当x=4时,y甲=22+15×3=67;当x=1时,y乙=16×1+3=19.故答案为:11;52;67;19.(2)当0<x≤1时,y1=22x;当x>1时,y1=22+15(x-1)=15x+7.∴y1=y2=16x+3(x>0).(3)当x>3时,当y1>y2时,有15x+7>16x+3,解得x<4;当y2=y2时,有15x+7=16x+3,解得x=4;当y1<y2时,有15x+7<16x+3,解得x>4.∴当3<x<4时,小明选择乙公司省钱;当x=4时,两家公司费用一样;当x>4时,小明选择甲公司省钱.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
函数的实际应用题(10年7考)类型一行程问题(2019.27)1. (2019县区一模)如图①所示,在A,B两地间有一车站C,一辆汽车从A地出发经C站匀速驶往B地.如图①是汽车行驶时离C站的路程y(千米)与行驶时间x(小时)之间的函数关系的图象.(1)求a的值和AB两地的距离;(2)求线段PM、MN所表示的y与x之间的函数表达式;(3)求行驶时间x在什么范围时,汽车离车站C的路程不超过60千米?第1题图2. (2019吉林省卷)甲、乙两车分别从A、B两地同时出发,沿同一条公路相向行驶,相遇后,甲车继续以原速行驶到B地,乙车立即以原速原路返回到B地.甲、乙两车距B地的路程y(km)与各自行驶的时间x(h)之间的关系如图所示.(1)m=________,n=________;(2)求乙车距B地的路程y关于x的函数解析式,并写出自变量x的取值范围;(3)当甲车到达B地时,求乙车距B地的路程.第2题图3. (2018南京改编)小明从家出发,沿一条直道向东跑步,经过一段时间原路返回,刚好在第1.6 h回到家中.当小明返回时,妈妈步行从家出发,沿着直道向北直行,速度为4 km/h.设小明出发第t h 时的速度为v km/h ,离家的距离为s km ,v 与t 之间的函数关系如图所示(图中的空心圈表示不包含这一点).(1)求小明出发第0.2 h 时他离家的距离; (2)求s 与t 之间的函数表达式;(3)t 为何值时,小明在返程中与妈妈的距离最小.第3题图4. (2019市区二模)某班级同学从学校出发去某自然保护区研学旅行,一部分乘坐大客车先出发,余下的几人20分钟后乘坐小轿车沿同一路线出行,大客车中途停车等候,小轿车赶上来之后,大客车以出发时速度的107继续行驶,小轿车保持原速度不变,小轿车司机因路线不熟错过了景点入口,在驶过景点入口6km时,原路提速返回,恰好与大客车同时到达景点入口.两车距学校的路程s (km)和行驶时间t (min)之间的函数关系如图所示.请结合图象解决下面问题:(1)求学校到景点的路程以及a 的值;(2)在小轿车司机驶过景点入口时,大客车离景点入口还有多远?(3)小轿车司机到达景点入口时发现本路段限速80km/h ,请你帮助小轿车司机计算折返时是否超速? (4)若大客车一直以出发时的速度行驶,中途不再停车,那么小轿车折返后到达景点入口,需等待________分钟,大客车才能到达景点入口.第4题图类型二 阶梯收费问题(2015.27,2013.27,2012.25)1. (2019宜昌)《人民日报》点赞湖北宜昌“智慧停车平台”.作为“全国智慧城市”试点,我市通过“互联网+”、“大数据”等新科技,打造“智慧停车平台”,着力化解城市“停车难”问题,市内某智慧公共停车场的收费标准是:停车不超过30分钟,不收费;超过30分钟,不超过60分钟,计1小时,收费3元;超过1小时后,超过1小时的部分按每小时2元收费(不足1小时,按1小时计).(1)填空:若市民张先生某次在该停车场停车2小时10分钟,应交停车费________元.若李先生也在该停车场停车,支付停车费11元,则停车场按________小时(填整数)计时收费;(2)当x取整数且x≥1时,求该停车场停车费y(单位:元)关于停车计时x(单位:小时)的函数解析式.2. (2019泰州)小李经营一家水果店,某日到水果批发市场批发一种水果.经了解,一次性批发这种水果不得少于100 kg,超过300 kg时,所有这种水果的批发单价均为3元/kg.图中折线表示批发单价y(元/kg)与质量x(kg)的函数关系.(1)求图中线段AB所在直线的函数表达式;(2)小李用800元一次可以批发这种水果的质量是多少?第2题图3. 某市为节约电资源,制定了新的居民用电收费标准,实行阶梯式电价,新的收费价格如下表所示:(1)已知a>50,若甲用户某月用电为50千瓦时,则应缴费多少元?(2)若调价后每月支出的电费为y(元),每月的用电量为x(千瓦时),y与x之间的关系如图所示,求a的值及y与x之间的函数关系式;(3)在(2)的条件下,若乙用户某月用电350千瓦时,则该用户应缴费多少元?第3题图4. 某市水费采用阶梯收费制度,即:每月用水不超过15吨时,每吨需缴纳水费a元,每月用水量超过15吨时,超过15吨的部分按每吨提高为b元缴纳,小明家每月缴纳水费y(元)与用水量x(吨)之间的函数关系图象如图所示.(1)求a、b的值;(2)求每月缴纳水费y(元)与用水量x(吨)之间的函数关系式;(3)若小明家五月和六月的月缴水费相差24元,求这两月用水量差的最小值.第4题图类型三最大利润问题(2016.26,2014.26,2011.25)1. (2019成都)随着5G 技术的发展,人们对各类5G 产品的使用充满期待.某公司计划在某地区销售一款5G 产品,根据市场分析,该产品的销售价格将随销售周期的变化而变化,设该产品在第x (x 为正整数)个销售周期每台的销售价格为y 元,y 与x 之间满足如图所示的一次函数关系.(1)求y 与x 之间的关系式;(2)设该产品在第x 个销售周期的销售数量为p (万台),p 与x 的关系可以用p =12x +12来描述.根据以上信息,试问:哪个销售周期的销售收入最大?此时该产品每台的销售价格是多少元?第1题图2. (2019青岛)某商店购进一批成本为每件30元的商品,经调查发现,该商品每天的销售量y (件)与销售单价x (元)之间满足一次函数关系,其图象如图所示.(1)求该商品每天的销售量y 与销售单价x 之间的函数关系式;(2)若商店按单价不低于成本价,且不高于50元销售,则销售单价定为多少,才能使销售该商品每天获得的利润w(元)最大?最大利润是多少?(3)若商店要使销售该商品每天获得的利润不低于800元,则每天的销售量最少应为多少件?第2题图3. (2019武汉)某商店销售一种商品,经市场调查发现,该商品的周销售量y(件)是售价x(元/件)的一次函数,其售价、周销售量、周销售利润w(元)的三组对应值如下表:注:周销售利润=周销售量×(售价-进价)(1)①求y关于x的函数解析式(不要求写出自变量的取值范围);①该商品进价是______元/件;当售价是______元/件时,周销售利润最大,最大利润是______元.(2)由于某种原因,该商品进价提高了m元/件(m>0),物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求m的值.4. (2019盘锦)2018年非洲猪瘟疫情爆发后,专家预测,2019年我市猪肉售价将逐月上涨,每千克猪肉的售价y1(元)与月份x(1≤x≤12,且x为整数)之间满足一次函数关系,如下表所示;每千克猪肉的成本y2(元)与月份x(1≤x≤12,且x为整数)之间满足二次函数关系,且3月份每千克猪肉的成本全年最低为9元,如下图所示.(1)求y1与x之间的函数关系式;(2)求y2与x之间的函数关系式;(3)设销售每千克猪肉所获得的利润为w元,求w与x之间的函数关系式,哪个月份销售每千克猪肉所获得利润最大?最大利润是多少元?第4题图拓展类型1. (2020原创)如图,某住宅小区有一块矩形场地ABCD,AB=16 m,BC=12 m,开发商准备对这块地进行绿化,分别设计了①①①①①五块地,其中①①两块形状大小相同的正方形地用来种花,①①两块形状大小相同的矩形地用来种植草坪,①为矩形地用来养殖观赏鱼.(1)设矩形观赏鱼用地LJHF的面积为y m2,AG长为x m,求y与x之间的函数关系式;(2)求矩形观赏鱼用地LJHF面积的最大值.第1题图2. (2019绥化)甲、乙两台机器共同加工一批零件,一共用了6小时,在加工过程中乙机器因故障停止工作,排除故障后,乙机器提高了工作效率且保持不变,继续加工,甲机器在加工过程中工作效率保持不变,甲、乙两台机器加工零件的总数y(个)与甲加工时间x(h)之间的函数图象为折线OA-AB-BC,如图所示.(1)这批零件一共有________个,甲机器每小时加工________个零件,乙机器排除故障后每小时加工________个零件;(2)当3≤x≤6时,求y与x之间的函数解析式;(3)在整个加工过程中,甲加工多长时间时,甲与乙加工的零件个数相等?第2题图参考答案类型一 行程问题1. 解:(1)由题意和图象得, a =1502.5×4=240,A 、B 两地相距150+240=390 km ; (2)设线段PM 表达式为y 1=k 1x +150,点M (2.5,0)在该函数图象上,则2.5k 1+150=0, 解得k 1=-60,即线段PM 表达式为y 1=-60x +150(0≤x ≤2.5). 设线段MN 表达式为y =k 2x +b ,点M (2.5,0),N (6.5,240)在该函数图象上,则⎩⎪⎨⎪⎧2.5k 2+b =0,6.5k 2+b =240,解得⎩⎪⎨⎪⎧k 2=60,b =-150.即线段MN 表达式为y 2=60x -150(2.5<x ≤6.5); (3)在函数y 1=-60x +150中,令y 1=60, 则-60x +150=60,解得x =1.5, 在函数y 2=60x -150中,令y 2=60, 则60x -150=60,解得x =3.5, 结合题意得1.5≤x ≤3.5,即行驶时间在1.5小时至3.5小时之间时汽车离车站C 的路程不超过60千米. 2. 解:(1)4,120;(2)甲、乙两车相遇前,设y 关于x 的函数解析式为y =kx (0≤x ≤2). ①图象过(2,120), ①2k =120. 解得k =60.①甲、乙两车相遇前,y 关于x 的函数解析式为y =60x .甲、乙两车相遇后,设y 关于x 的函数解析式为y =k 1x +b (2<x ≤4). ①图象过(2,120),(4,0)两点,①⎩⎪⎨⎪⎧2k 1+b =120,4k 1+b =0.解得⎩⎪⎨⎪⎧k 1=-60,b =240.①甲、乙两车相遇后,y 关于x 的函数解析式为y =-60x +240. ①y 关于x 的解析式为y =⎩⎪⎨⎪⎧60x (0≤x ≤2)-60x +240(2<x ≤4); (3)当x =3.5时,y =-60×3.5+240=30.①当甲车到达B 地时,乙车距B 地的路程为30 km. 3. 解:(1)5×0.2=1 km ,故小明出发第0.2 h 时离家的距离为1 km ; (2)设小明返回之前所用时间为x h ,则由题意可得, 5×0.2+6×(0.5-0.2)+4×(x -0.5)=4×(1.6-x ) 解得x =0.7.由图象可得,当0≤t ≤0.2时,v =5,此时s =5t ;当0.2<t ≤0.5时,v =6,此时s =5×0.2+6×(t -0.2)=6t -0.2;当0.5<t ≤0.7时,v =4,此时s =5×0.2+6×(0.5-0.2)+4×(t -0.5)=4t +0.8; 当0.7<t ≤1.6时,v =4,此时s =4×(1.6-t )=6.4-4t ; ①s 关于t 的函数表达式为 ⎩⎪⎨⎪⎧5t (0≤t ≤0.2)6t -0.2 (0.2<t ≤0.5)4t +0.8 (0.5<t ≤0.7)6.4-4t (0.7<t ≤1.6); (3)由(2)可知,小明返程时,离家的距离为(6.4-4t )km , ①妈妈步行的速度为4 km/h , ①妈妈离家的距离为[4×(t -0.7)] km.设两者之间的距离为l ,则l 2=(6.4-4t )2+[4×(t -0.7)]2 =16×(1.6-t )2+16×(t -0.7)2=16(2.56+t 2-3.2t +t 2+0.49-1.4t ) =16×(2t 2-4.6t +3.05) ①-b2a =--4.62×2=1.15,①t 为1.15 h 时,小明在返程中与妈妈的距离最小. 4. 解:(1)由图象可得,学校到景点的路程为40km , 小轿车的速度为4060-20=1(km/min),a =(35-20)×1=15.①学校到景点的路程为40 km ,a 的值为15.(2)由(1)得a =15,①大客车的速度为1530=12(km/min). 小轿车赶上来之后,大客车又行驶了(60-35)×107×12=1257(km),40-1257-15=507(km). 答:在小轿车司机驶过景点入口时,大客车离景点入口还有507km ; (3)设直线CD 的表达式为s =kt +b ,将(20,0)和(60,40)代入得⎩⎪⎨⎪⎧20k +b =0,60k +b =40,解得⎩⎪⎨⎪⎧k =1,b =-20, ①直线CD 的表达式为s =t -20.当s =46km 时,46=t -20,解得t =66min.①小轿车赶上来之后,大客车又行驶的时间为40-1512×107=35(min), 则小轿车司机折返时的速度为6÷(35+35-66)=32(km/min)=90km/h>80km/h. 答:小轿车折返时已经超速;(4)大客车行驶的时间为4012=80(min),80-70=10(min). 故小轿车需等待10分钟,大轿车才能到达景点入口.类型二 阶梯收费问题1. 解:(1)7,5;【解法提示】①市民张先生某次在该停车场停车2小时10分钟,超过了1小时,①应交停车费为3+2×(3-1)=7(元);①11>3,①李先生在该停车场停车超过了1小时.设停车场按x (x 为整数)小时计时收费.根据题意得3+2(x -1)=11.解得x =5,即停车场按5小时计时收费.(2)根据题意,得y =3+2(x -1),即y =2x +1.①y 关于x 的函数解析式为y =2x +1(x ≥1).2. 解:(1)设线段AB 所在直线的函数表达式为y =kx +b (k ≠0),代入(100,5),(300,3),得⎩⎪⎨⎪⎧5=100k +b 3=300k +b ,解得⎩⎪⎨⎪⎧k =-0.01b =6, ①线段AB 所在直线的表达式为y =-0.01x +6;(2) ①300×3=900>800,100×5=500<800,①100<x <300,则水果的总价为w =x (-0.01x +6),令w =800,得-0.01x 2+6x =800,解得x 1=200,x 2=400(舍去).答:小李用800元一次可以批发这种水果的质量是200千克.3. 解:(1)①a >50,①用电为50千瓦时,单价为0.5元/千瓦时,即0.5×50=25元.①若甲用户某月用电为50千瓦时,应缴费用为25元;(2)由题意可知0.5a +0.6(2a -a )=110,即1.1a =110,a =100,则y =⎩⎪⎨⎪⎧0.5x 0.6(x -100)+500.8(x -200)+110,即y =⎩⎪⎨⎪⎧0.5x 0.6x -100.8x -50(0≤x ≤100)(100<x ≤200)(x >200); (3)①350>200,①y =0.8×350-50=230,故该用户应缴费230元.4. 解:(1)由题意得a =3913=3, 15×3+(18-15)b =60,解得b =5.①a 、b 的值分别为3、5;(2)由(1)得,y =⎩⎪⎨⎪⎧3x (0≤x ≤15)5x -30(x >15); (3)设六月份用水x 1吨,水费y 1元,五月份用水x 2吨,水费y 2元(x 1>x 2),①若x 1≤15,x 2≤15,则x 1-x 2=24÷3=8;①若x 1>15,x 2>15,则x 1-x 2=24÷5=4.8;①若x 2≤15<x 1时,y 1-y 2=5x 1-30-3x 2=24,①x 1-x 2=54-2x 25=-25x 2+545, ①x 2=15时,x 1-x 2有最小值4.8.综上所述,这两月用水量差的最小值为4.8吨.类型三 最大利润问题1. 解:(1)设y 关于x 的函数关系式为y =kx +b (k ≠0),由图象可知,将点(1,7000),(5,5000)代入得⎩⎪⎨⎪⎧k +b =70005k +b =5000,解得⎩⎪⎨⎪⎧k =-500b =7500, ①y 关于x 的函数关系式为y =-500x +7500;(2)设销售收入为W ,根据题意得W =yp =(-500x +7500)·(12x +12), 整理得W =-250(x -7)2+16000,①-250<0,①W 在x =7时取得最大值,最大值为16000元,此时该产品每台的销售价格为-500×7+7500=4000元.①第7个销售周期的销售收入最大,此时该产品每台的销售价格为4000元.2. 解:(1)设一次函数关系式为y =kx +b (k ≠0),①图象经过点(30,100)和(45,70),①⎩⎪⎨⎪⎧30k +b =10045k +b =70,解得⎩⎪⎨⎪⎧k =-2b =160, ①该商品每天的销售量y 与销售单价x 之间的函数关系式为y =-2x +160;(2)根据题意可得w =(x -30)(-2x +160)=-2x 2+220x -4800=-2(x -55)2+1250.①30≤x ≤50,①当x =50时,w 有最大值,w 最大=-2×(50-55)2+1250=1200.答:销售单价定为50元时,才能使销售该商品每天获得的利润w (元)最大,最大利润是1200元;(3)令w =-2(x -55)2+1250=800,解得x 1=40,x 2=70.①将x =40代入y =-2x +160,得y =80;将x =70代入y =-2x +160,得y =20.①每天的销售量最少应为20件.3. 解:(1)①y =-2x +200;【解法提示】设y =kx +b ,将x =50,y =100;x =60,y =80带入上式解得k =-2,b =200,故y =-2x +200.①40,70,1800;【解法提示】进价=50-1000÷100=40,利润w =(-2x +200)(x -40)=-2x 2+280x -8000,当x =-280-4=70时,最大利润w max =1800 元.(2)由题意可知w =(-2x +200)×(x -40-m )=-2x 2+(280+2m )x -8000-200m ,①对称轴为x =140+m 2, ①①当x =140+m 2>65时(舍);①当x =140+m 2≤65时,x =65时,w 取最大值1400,此时m =5. 答:若周销售最大利润是1400元,m 为5.4. 解:(1)设y 1关于x 的函数关系式为y 1=kx +b (k ≠0),将(3,12),(4,14)代入y 1得:⎩⎪⎨⎪⎧3k +b =12,4k +b =14, 解得⎩⎪⎨⎪⎧k =2,b =6. ①y 1关于x 的函数关系式为y 1=2x +6;(2)依题意得,y 2图象的顶点坐标为(3,9),设y 2=a (x -3)2+9,将(5,10)代入y 2,得a (5-3)2+9=10解得a =14, ①y 2关于x 的函数关系式为y 2=14(x -3)2+9=14x 2-32x +454; (3)w =y 1-y 2=2x +6-(14x 2-32x +454) =-14x 2+72x -214=-14(x -7)2+7 ①a =-14<0,抛物线开口向下, ①w 有最大值.①当x =7时,w 最大=7.答:7月份销售每千克猪肉所获得的利润最大,最大利润是7元.拓展类型1. 解:(1)在矩形ABCD 中,DC =AB =16,AD =BC =12,①正方形AEFG 和正方形JKCI 形状大小相同,矩形GHID 和矩形EBKL 形状大小相同,AG =x , ①DG =12-x ,FL =x -(12-x )=2x -12,BE =16-x ,LJ =(16-x )-x =16-2x .①S 矩形LJHF =FL ·LJ ,① y =(2x -12)(16-2x )=-4x 2+56x -192;(2)由(1)得y =-4x 2+56x -192=-4(x -7)2+4,①FL =2x -12>0,LJ =16-2x >0,①6<x <8.①a =-4<0,①当x =7时,y 最大为4.即矩形观赏鱼用地LJHF 面积的最大值为4 m 2.2. 解:(1)270,20,40;【解法提示】纵坐标最大值即加工总数为270;由AB 段可得甲机器效率为90-503-1=20;由BC 段可得排除故障后乙机器效率为270-906-3-20=40. (2)设当3≤x ≤6时,y 与x 之间的函数解析式为y =kx +b (k ≠0),把B (3,90),C (6,270)代入解析式,得⎩⎪⎨⎪⎧3k +b =90,6k +b =270, 解得⎩⎪⎨⎪⎧k =60,b =-90.①y 与x 之间的函数解析式为y =60x -90(3≤x ≤6);(3)设甲加工x 小时时,甲与乙加工的零件个数相等,由图象可得乙在排除故障之前共加工了50-20=30个.①20x =30,解得x =1.5;①20x =30+40(x -3),解得x =4.5.答:甲加工1.5 h 或4.5 h 时,甲与乙加工的零件个数相等.。
