Longitudinal polarization of $Lambda$ and $bar Lambda$ hyperons in deep-inelastic scatterin
光盘9-3 思考题和练习题题解(刘阅版)

第九章思考题和练习题解析1、简述下列科学家对原子结构理论的贡献:(1)玻尔(2)德布罗意(3)海森堡(4)薛定谔(5)洪特(6)泡利(7)徐光宪答:(1)玻尔将普朗克量子理论应用于原子结构,提出了原子能级不连续的概念,成功地解释了氢原子的不连续光谱;(2)德布罗意提出了电子的波动波粒二象性质;(3)海森堡提出不确定原理:不能同时准确地测定电子的位置和动量;(4)薛定谔提出了电子运动的波动方程,比玻尔模型能更好地阐明电子的行为; (5)洪特指出,电子在简并轨道上排布时,尽可能占据不同的轨道,且自旋方向相同; (6)泡利提出不相容原理,指出一个原子中不可能有2个电子的4个量子数完全一样; (7)徐光宪提出在多电子原子中填电子时能级高低可按照n + 0.7 l 来计算。
2、核外电子运动有什么特征?答:量子力学认为核外电子的运动具有如下特征:⑴ 电子具有波粒二象性,它既具有质量、能量等粒子特征,又具有波的波动特征。
电子波是概率波,只能采用统计的方法描述其运动状态;⑵ 微观粒子具有与宏观物体不同的运动特征,不能同时测准它的位置和动量,不存在玻尔理论中那样的运动轨道。
它在核外空间的出现体现为概率的大小,有的地方出现的概率小,有的地方出现的概率大;⑶ 电子的运动状态可用波函数ψ及其相应的能量来描述。
波函数ψ是薛定谔方程的合理解,|ψ|2表示概率密度。
⑷ 每一个ψ 对应一确定的能量值,称为“定态”。
电子的能量具有量子化的特征,是不连续的。
基态时原子能量最小,比基态能量高的是激发态。
3、如果电子的速度是7.00×105 m ·s -1,那么该电子束的de Broglie 波长应该是多少? 解:pm 1040m 10040.1)1Jsmkg 1(sm 107.00kg 109.11sJ 1063.69-221-531-34=⨯=⋅⋅⋅⨯⨯⨯⋅⨯==--υλm h4、设子弹质量为10 g ,速度为1000 m ·s -1,试根据de Broglie 式和测不准不确定关系式,用计算说明宏观物质主要表现为粒子性,它们的运动服从经典力学规律(设子弹速度的测量误差为△υx =10-3 m ·s -1)。
基本物理常数

Quantity量speed of light in vacuum光在真空中的速度magn. constant MAGN。
不变electric constant电热恒温characteristic impedance of vacuum特性阻抗的真空Newtonian constant of gravitation万有引力常数Newtonian constant of gravitation overh-bar c牛顿万有引力常数H-巴C Planck constant普朗克常数Planck constant in eV s普朗克常数EV小号Planck constant over 2 pi times c in MeV fm 普朗克常数超过2次c MeV的FM PIPlanck constant over 2 pi普朗克常数超过2 PIPlanck constant over 2 pi in eV s普朗克常数超过2π的EV小号Planck mass普朗克质量Planck temperature普朗克温度Planck length普朗克长度Planck time普朗克时间elementary charge基本电荷elementary charge over h基本电荷较Hmagn. flux quantum MAGN。
磁通量子conductance quantum电导量子inverse of conductance quantum逆的量子电导Josephson constant约瑟夫森常数von Klitzing constant冯Klitzing不变Bohr magneton玻尔磁子Bohr magneton in eV/T"EV / T单位下的玻尔磁子"Bohr magneton in Hz/T"Hz / T单位下的玻尔磁子"Bohr magneton in inverse meters pertesla玻尔磁子的逆米,每颗TeslaBohr magneton in K/T"K / T单位下的玻尔磁子"nuclear magneton核磁nuclear magneton in eV/T核磁EV / Tnuclear magneton in MHz/T核磁以MHz / Tnuclear magneton in inverse meters pertesla在逆米,每颗Tesla核磁nuclear magneton in K/T在K / T核磁fine-structure constant精细结构常数inverse fine-structure constant逆精细结构常数Rydberg constant里德伯常数Rydberg constant times c in Hz里德伯常数次c,单位为HzRydberg constant times hc in J里德伯常数次HC在JRydberg constant times hc in eV里德伯常数倍EV在HCBohr radius玻尔半径Hartree energy哈特里能源Hartree energy in eV哈特里能在EVquantum of circulation量子流通quantum of circulation times 2量子循环时间2Fermi coupling constant费米耦合常数Fundamental Physicalweak mixing angle弱混合角electron mass电子质量electron mass in u电子质量在uelectron mass energy equivalent电子质量的能量相当于electron mass energy equivalent in MeV电子质量在兆电子伏的能量相electron-muon mass ratio电子,μ介子的质量比electron-tau mass ratio电子tau蛋白的质量比electron-proton mass ratio电子,质子的质量比electron-neutron mass ratio电子,中子的质量比electron-deuteron mass ratio电子氘核的质量比electron to alpha particle mass ratioα粒子的质量比电子electron charge to mass quotient电子电荷量的商electron molar mass电子摩尔质量Compton wavelength康普顿波长Compton wavelength over 2 pi康普顿波长超过2 PI classical electron radius经典电子半径Thomson cross section汤姆森横截面electron magn. moment电子MAGN。
年硕士研究生入学考试及答案

目录1.05年北师大物理类各方向2.05年长光所3.05年东南大学4.05年中科大5.05年南京大学6.05年华中科大7.05年吉林大学(原子所)8.05年四川大学(原子与分子)9.05年北京理工10.05年河北理工11.05年长春理工北京师范大学2005年招收硕士研究生入学考试试题专业:物理类各专业科目代号:459研究方向:各方向考试科目:量子力学[注意]答案写在答题纸上,写在试题上无效。
1.(20分)一个电子被限制在一维谐振子势场中,活动范围求激发电子到第一激发态所需要的能量(用ev表示)(,,)提示:谐振子能量本征函数可以写成2.(30分)一个电子被限制在二维各向同性谐振子势场中(特征频率为)。
(1)写出其哈密顿量,利用一维谐振子能级公式找到此电子的能级公式和简并度。
(2)请推导电子的径向运动方程。
并讨论其在时的渐近解。
提示:极坐标下3.(50分)两个质量为的粒子,被禁闭在特征频率为的一维谐振子势场中,彼此无相互作用(此题中波函数无须写出具体形式):(1)如果两个粒子无自旋可分辨,写出系统的基态(两个都在自己的基态)和第一激发能级(即一个在基态,另一个在第一激发态)的波函数和能量(注意简并情形)。
(10分)(2)如果两个粒子是不可分辨的无自旋波色子,写出系统的基态和第一激发态的能量和波函数。
如果粒子间互作用势为,计算基态能级到一级微扰项。
(15分)(3分)如果两个粒子是不可分辨的自旋1/2粒子,写出基态能级和波函数(考虑自旋)。
如果粒子间互作用能为,计算基态能量。
(15分)(4)同(3),解除势阱,两个粒子以左一右飞出。
有两个探测器分别(同时)测量它们的y方向自旋角动量。
请问测量结果为两电子自旋反向的几率是多少?(10分)4.(30分)中心力场中电子自旋与轨道角动量存在耦合能。
总角动量,是的共同本征态。
现有一电子处于态,且。
(1)在一基近似下,可用代替,请问电子的能量与态差多少?(2)请计算该电子产生的平均磁矩,并由此计算在z方向均匀磁场B中电子的能量改变多少?(),当,,当,5.(20分)一个定域(空间位置不动)的电子(自旋1/2)处于z方向强磁场中。
BaVS3晶格动力学研究!-物理学报

究主 要 集 中 在 其 电 子 性 质 方 面
[), 1, .-, .2]
, 到目前为
止, 还未见对该材料的晶格动力学性质的研究报道 & 本文采用基于密度泛函理论的平面波赝势方 法, 研究了六角相的 !"#$% 材料的晶格动力学性质 & 声子谱中最为显著的的特征是 (. (> 模出现了虚频 & ( 模的振动方式对应于 # 原子沿 ) 轴或 * 轴的相
( (V
势
[(*]
& 在 局 域 密 度 近 似 下,采 用 AFHFD 参 数 化
-期
苗仁德等:0123’ 晶格动力学研究
’$!!
模 !! 由于它们的强度较弱, 实验上并没有 "# 和 ! !# ,
[!$] 观察 到 实验上测得其频率为 % 对 于 !" "# 模,
近 % 对于 !’ 实验上测得其频率为 ’./ () * ! ,本 "# 模, 文采 用 两 种 晶 格 常 数 下 计 算 得 到 的 频 率 分 别 是 理论结果与实验值差别较大 % 实验上 "$$,"&- () * ! , 观察到该模在低温时具有异常现象, 如随着温度的 降低, 这个模的强度显著增强, 谱线显示出非对称 性 % 我们初步分析认为 !’ "# 模可能具有较强的非谐 性, 而线性响应理论并没有考虑到非谐性, 导致了理 论和实验较大的差异 % 下文我们将用冻结声子方法 对该模进行详细研究 %
( & 计算方法
本文采用基于第一性原理计算的 ?!0@0A 程序 包, 计算了室温六角相的 !"#$% 材料的晶格动力学 性质 & 对 !", #, $ 参与计算的价电子分别为: 47 3B , % ( ( ) %C )B ,%B %7 ,赝势选用 AD6>EE9FDG/"DH9IB 模守恒赝
核子中奇异夸克分布不对称性与轻味夸克碎裂效应

29 10 2005 10HIGH ENERGY PHYSICS AND NUCLEAR PHYSICSVol.29,No.10Oct.,2005*( 100871)– , . , .D ..1, –[1—3]. ,. ,, –(DIS) (global analysis)[4,5], ,(intrinsic sea theory) ,µ CCFR NuTeV,[6,7]. ,. ,[4,8—12]NuTeVWeinberg [13,14],.. ,Fν2 F¯ν2,:Fν2−F¯ν2=2x[s(x)−¯s(x)]. ,,. c.CCFR NuTeV µ [6,15,16].νµs→µ−c νµd→µ−c,Cabibbo ,c ;, ¯c.CCFR NuTeV µµ+(µ−) c(¯c) ,c→H(c¯q)→µ+X. µ,µ ,. ,CCFR νµ(¯νµ) ,c(¯c) µ+(µ−) ¯B c(¯B¯c):¯Bc−¯B¯c0.1147∼0−20%[6]., ,µ . ,CCFR NuTeV µ,.( c ¯c10 965dξd y =G2s2|V cd|2].(1)s=2MEν ,r2≡(1+Q2/M2W)2.ξ . , c ,ξ Bjorken:ξ≈x(1+m2c /Q2). (1)f c≡1−m2c/2MEνξ c, [18]., ¯cd2σ¯νµN→µ+¯c Xπr2f c•ξ[¯s(ξ)|V cs|2+¯d(ξ)+¯u(ξ)dξd y−d2σ¯νµN→µ+¯c Xπr2f c•ξ (s(ξ)−¯s(ξ))|V cs|2+d v(ξ)+u v(ξ)2ξ[d v(ξ)+u v(ξ)] ,|V cs|2≃0.95 |V cd|2≃0.05[19] .12S−|V cs|2+Q V|V cd|2,(4)S−≡ ξ[s(ξ)−¯s(ξ)]dξ,Q V≡ ξ[d v(ξ)+u v(ξ)]dξ., NuTeV.[9—12],NuTeV ., (4) ,c ¯c P SA( 1).1 NuTeV c ¯c P SADing-Ma[9]Q2030%—80%0.007—0.01812%—26% Alwall-Ingelman[10]20GeV230%0.00915% Ding-Xu-Ma[11]Q2060%—100%0.014—0.02221%—29% Wakamatsu[12]16GeV270%—110%0.022—0.03530%—40%966 (HEP&NP) 29 2S+|V cs|2+(Q V+2Q S)|V cd|2.(5)S+≡ ξ[s(ξ)+¯s(ξ)]dξ,Q S≡ ξ[¯u(ξ)+¯d(ξ)]dξ.CTEQ5 Q2=16GeV2 S+,Q V,Q S, |V cs|2=0.95,|V cd|2=0.05,1 2S−/Q V 0.007(0.022), R 20%(25%). ,c ¯c, c¯c.3 µ, , c,( µ) ( ) . cH+d3σνµN→µ−H+Xdξd y D H+q(z),(6)D H+q(z) q H+ ,z H+ q . H+ c D+(c¯d) D0(c¯u) ,H− D−(¯c d) ¯D0(¯c u).c H+ H+ . , Lund , q¯qexp(−bm2q)[20], s¯s λ∼0.3[21,22], c¯c 10−5., . µ [17]. . , e+e− . , , c ¯c , D , c , , , c(¯c) , µ . , c ¯c D(c¯q) ¯D(¯c q). , , , :u→cu),d→D−(dξd y d z=G2s2|V cd|2]+δ dσνN→µ−µ+Xdξd y d z LQF=G2s2|V ud|2(1−y)2,(8)D q(z)≡D Dq(z)+D D∗q(z), D Dq(z)≡D¯D0u(z)=D D0¯u(z)=D D−d(z)=D D+¯d(z),D D∗q(z)≡D¯D∗0u(z)=D D∗0¯u(z)=D D∗−d(z)=D D∗+¯d(z). , D q(z) q , . (8) ,¯BD(∗)+=1dξd y d z=G2s2|V cd|2]+δ dσ¯νN→µ+µ−Xdξd y d z LQF=G2s2•|V ud|2(1−y)2.(10)10 967(σνN→µ−µ+X−σ¯νN→µ+µ−X)total≈−1Q V|V cd|2+2S−|V cs|2•D q¯BD(∗)+¯f c ¯Bc.D q¯BD(∗)+d x d y d z=G2s2|V ud|2D q(z)B¯D0,(12),B¯D0 ¯D0 µ− , ¯D∗0¯D0 , B¯D0 .,µ+µ+d3σ¯νN→µ+µ+Xπr2x¯u(x)+¯d(x)σµ−µ+≈Q ud|V ud|2¯fc¯Bc,(14)Q ud≡1¯fc¯Bc,D qσµ−µ+.(15)CDHSW[26] ( )µ µ σµ−µ−/σµ−µ+(σµ+µ+/σµ+µ−). 2E vis 100—200GeV ,3 .2 , , σµ−µ−/σµ−µ+σµ−µ−/σµ− ,, σµ−µ−/σµ−µ+, ,.2CDHSW 100<E vis<200GeV µ [26]pµ>6GeV(3.5±1.6)%(1.6±0.74)×10−4(4.5±2.0)%(2.2±1.0)×10−4 pµ>9GeV(2.9±1.2)%(1.05±0.43)×10−4(4.4±1.8)%(1.7±0.7)×10−4 pµ>15GeV(2.3±1.0)%(0.52±0.22)×10−4(4.1±2.3)%(0.8±0.45)×10−4968 (HEP&NP) 29dξd y d z −d3σ¯νµN→µ+H−Xπr2f cξ[(s(ξ)−¯s(ξ))|V cs|2+ d v(ξ)+u v(ξ)πr2xd v(x)+u v(x)πr2xd v(x)+u v(x)10 969(References)1Brodsky S J,MA B-Q.Phys.Lett.,1996,B381:3172Signal A I,Thomas A W.Phys.Lett.,1987,B191:2053Burkardt M,Warr B J.Phys.Rev.,1992,D45:9584Olness F et al.hep-ph/03123235Barone V et al.Eur.Phys.J.,2000,C12:2436Bazarko A O et al(CCFR Collaboration).Z.Phys.,1995, C65:1897Mason D(NuTeV Collaboration).hep-ex/04050378Kretzer S et al.Phys.Rev.Lett.,2004,93:0418029DING Y,MA B-Q.Phys.Lett.,2004,B590:216;DING Yong,L¨U Zhun,MA Bo-Qiang.HEP&NP,2004,28(9): 947(in Chinese)( , , . ,2004,28(9):947) 10Alwall J,Ingelman G.Phys.Rev.,2004,D70:111505.11DING Y,XU R-G,MA B-Q.Phys.Lett.,2005,B607:101 12Wakamatsu M.hep-ph/041120313Zeller G P et al.Phys.Rev.Lett.,2002,88:09180214Zeller G P et al.Phys.Rev.,2002,D65:11110315Rabinowitz S A et al.Phys.Rev.Lett.,1993,70:13416Goncharov M et al.Phys.Rev.,2001,D64:11200617Godbole R M,Roy D P.Z.Phys.,1984,C22:39;Z.Phys., 1989,C42:21918Astier P et al(NOMAD Collaboration).Phys.Lett.,2000, B486:3519Eidelman S et al(Particle Data Group).Phys.Lett.,2004, B592:120Andersson B et al.Nucl.Phys.,1981,B178:24221Lafferty G D.Phys.Lett.,1995,B353:54122Abe K et al(SLD Collaboration).Phys.Rev.Lett.,1997, 78:334123Smith J,Valenzuela G.Phys.Rev.,1983,D28:107124Aitala E M et al(Fermilab E791Collaboration).Phys.Lett.,1996,B371:15725Dias de Deus J,Dur˜a es F.Eur.Phys.J.,2000,C13:647 26Burkhardt H et al.Z.Phys.,1986,C31:3927Sandler P H et al.Z.Phys.,1993,C57:1,and References Therein.28Jonker M et al.Phys.Lett.,1981,B107:24129de Lellis G et al.Phys.Rep.,2004,399:22730Kayis-Topaksu A et al(CHORUS Collaboration).Phys.Lett.,2002,B549:4831¨Oneng¨u t G et al(CHORUS Collaboration).Phys.Lett., 2004,B604:145Nucleon Strange Asymmetry and the Light QuarkFragmentation Effect*GAO Pu-Ze MA Bo-Qiang(School of Physics,Peking University,Beijing100871,China)Abstract Nucleon strange asymmetry is an important non-perturbative effect in the study of nucleon structure,but it has not been checked by experiments yet.For effectively measuring the nucleon strange asymmetry,we investigate the light quark fragmentation effect that may affect the measurement of the strange asymmetry.We suggest an inclusive measurement of charged and neutral charmed hadrons by using an emulsion target in the neutrino and antineutrino in-duced charged current deep inelastic scattering,in which the strange asymmetry effect and the light quark fragmentation effect can be separated.Key words strange asymmetry,light quark fragmentation,charged current deep inelastic scattering。
反应堆物理题库
西安交通大学——核反应堆物理分析(共470题)从反应堆物理的角度看,良好的慢化剂材料应具有什么样的性能?答案:慢化剂是快中子与它的核发生碰撞后能减速成热中子的材料,这与它的三种中子物理性能有关:δ-平均对数能量缩减;Σs-宏观散射截面;Σa-宏观吸收截面。
综合评价应是δ和Σs都比较大而Σa又较小的材料才是较好的慢化材料,定量地用慢化能力δΣs和慢化比δ和Σs/Σa来比较。
试列出常用慢化剂的慢化能力和慢化比。
核力所具有的特点是什么?答案:基本特点是:核力是短程力,作用范围大约是1~2×10-13cm;核力是吸引力,中子与中子,质子与中子,质子与质子之间均是强吸引力。
核力与电荷无关。
核力具有饱和性,每一核子只与其邻近的数目有限的几个核子发生相互作用。
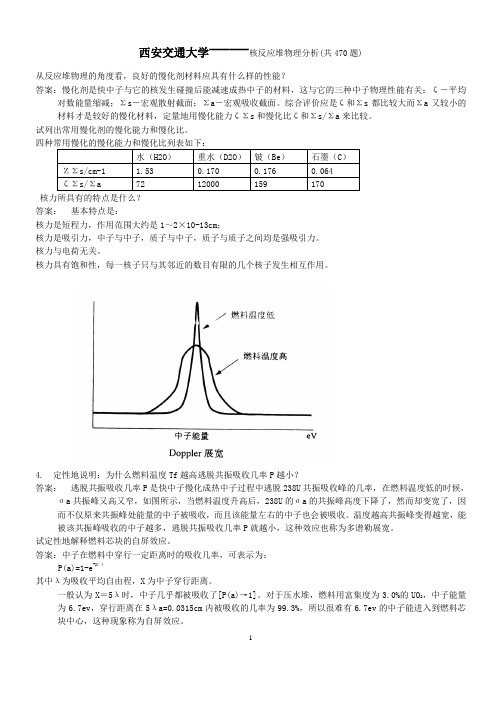
4. 定性地说明:为什么燃料温度Tf越高逃脱共振吸收几率P越小?答案:逃脱共振吸收几率P是快中子慢化成热中子过程中逃脱238U共振吸收峰的几率,在燃料温度低的时候,ζa共振峰又高又窄,如图所示,当燃料温度升高后,238U的ζa的共振峰高度下降了,然而却变宽了,因而不仅原来共振峰处能量的中子被吸收,而且该能量左右的中子也会被吸收。
温度越高共振峰变得越宽,能被该共振峰吸收的中子越多,逃脱共振吸收几率P就越小,这种效应也称为多谱勒展宽。
试定性地解释燃料芯块的自屏效应。
答案:中子在燃料中穿行一定距离时的吸收几率,可表示为:P(a)=1-e-X/λ其中λ为吸收平均自由程,X为中子穿行距离。
一般认为X=5λ时,中子几乎都被吸收了[P(a)→1]。
对于压水堆,燃料用富集度为3.0%的UO2,中子能量为6.7ev,穿行距离在5λa=0.0315cm内被吸收的几率为99.3%,所以很难有6.7ev的中子能进入到燃料芯块中心,这种现象称为自屏效应。
6. 什么是过渡周期?什么是渐近周期?答案:在零功率时,当阶跃输入-正反应性ρ0(ρ0<β)后,反应堆功率的上升速率(或周期)是随ρ0输入后的时间t而改变的(如图所示)。
原子与原子核物理学(张国营)习题答案
第一章1.1 若卢瑟福散射用的α粒子是放射性物质镭'C 放射的,其动能为67.6810⨯电子伏特。
散射物质是原子序数79Z =的金箔。
试问散射角150οθ=所对应的瞄准距离b 多大?解:根据卢瑟福散射公式:20222442K Mv ctgb b Ze Zeαθπεπε==得到:2192150152212619079(1.6010) 3.97104(48.8510)(7.681010)Ze ctg ctg b K οθαπεπ---⨯⨯===⨯⨯⨯⨯⨯⨯米式中212K Mvα=是α粒子的功能。
1.3 钋放射的一种α粒子的速度为71.59710⨯米/秒,正面垂直入射于厚度为710-米、密度为41.93210⨯3/公斤米的金箔。
试求所有散射在90οθ>的α粒子占全部入射粒子数的百分比。
已知金的原子量为197。
解:散射角在d θθθ+之间的α粒子数dn 与入射到箔上的总粒子数n 的比是:dnNtd nσ=其中单位体积中的金原子数:0//Au Au N m N A ρρ==而散射角大于090的粒子数为:2'dndn nNt d ππσ=⎰=⎰所以有:2'dn Nt d nππσ=⎰22218002903cos122()()4sin 2AuN Ze t d A Mu οοθρπθθπε=⋅⋅⎰ 等式右边的积分:180180909033cos sin 2221sin sin 22d I d οοοοθθθθθ=⎰=⎰=故'22202012()()4Au N dn Ze t n A Muρππε=⋅⋅ 648.5108.510--≈⨯=⨯即速度为71.59710/⨯米秒的α粒子在金箔上散射,散射角大于90ο以上的粒子数大约是4008.510-⨯。
1.4能量为3.5兆电子伏特的细α粒子束射到单位面积上质量为22/1005.1米公斤-⨯的银箔上,α粒子与银箔表面成ο60角。
在离L=0.12米处放一窗口面积为25100.6米-⨯的计数器。
Rb85能级图
1 Introduction
3
1 Introductiቤተ መጻሕፍቲ ባይዱn
In this reference we present many of the physical and optical properties of 85 Rb that are relevant to various quantum optics experiments. In particular, we give parameters that are useful in treating the mechanical effects of light on 85 Rb atoms. The measured numbers are given with their original references, and the calculated numbers are presented with an overview of their calculation along with references to more comprehensive discussions of their underlying theory. At present, this document is not a critical review of experimental data, nor is it even guaranteed to be correct; for any numbers critical to your research, you should consult the original references. We also present a detailed discussion of the calculation of fluorescence scattering rates, because this topic is often not treated clearly in the literature. More details and derivations regarding the theoretical formalism here may be found in Ref. [1]. The current version of this document is available at /alkalidata, along with “Cesium D Line Data,” “Sodium D Line Data,” and “Rubidium 87 D Line Data.” This is the only permanent URL for this document at present; please do not link to any others. Please send comments, corrections, and suggestions to dsteck@.
单晶结构解析加氢-绘图问题解答
1.通常,H原子的处理方法作者要给出(1)一般通过理论加H,其温度因子为固定值,可通过INS等文件查看(2) 水分子上H原子可通过Fourier syntheses得到(3)检查理论加上的H原子是否正确,主要看H原子的方向。
若不正确则删去再通过Fourier syntheses合成得到(4) 检查H原子的键长、键角、温度因子等参数是否正常。
通过检查分子间或分子内的H键是否合理最易看出H键的合理性(5) 技巧:有时通过Fourier syntheses得到的H原子是正确的,可一计算其温度因子等参就变得不正常,则可以固定其参数后再精修(如在INS中的该H原子前用afix 1,其后加afix 0)(6)各位来说说方法与心得?2.胡老师,下面的问题怎么解决啊?谢谢您。
220_ALERT_2_B Large Non-Solvent C Ueq(max)/Ueq(min) ... 3.70 Ratio222_ALERT_3_B Large Non-Solvent H Ueq(max)/Ueq(min) ... 4.97 Ratio342_ALERT_3_B Low Bond Precision on C-C bonds (x 1000) Ang (49)B 级提示当然得重视了。
建议你先把H撤消,精修到C的热椭球不太变形和键长趋正常。
如做不到就要看空间群?衍射点变量比太小?以至追查到原始数据的录取参数和处理等。
这些粗略意见仅供参考,如何?3.在XP中画图时,只有一部分,想长出另外的对称部分。
我是envi完了,然后sgen长出来的,可是和symm显示的对称信息不一样。
比如:我根据envi的结果用sgen O1 4555得到的是O1A而不是O1D,这跟文献中标注的不一样啊,怎么统一呢?很困扰,忘达人指教。
xp里是按顺序编号的,第一个sgen出的的统一为A,依次标号。
你如果想一开始就统一D 的话,重新name一下4.高氯酸根怎么精修呀?我用的SHETXL6.1版的,最好告诉我怎么用其中的XSHELL来做,我觉得他好用!Method 1DFIXDfix 1.42 0.02 Cl1 O1 Cl1 O2 Cl1 O3 Cl1 O4Dfix 1.42 0.02 O1 O2 O1 O3 O1 O4 O2 O3 O2 O4 O3 O4Method 2SADISadi 0.01 Cl1 O1 Cl1 O2 Cl1 O3 Cl1 O4Sadi 0.01 O1 O2 O1 O3 O1 O4 O2 O3 O2 O4 O3 O45. 晶体的无序是怎么造成的呀,是晶体培养的问题吗?如果无序太多,在解单晶的时候怎么办?我指的是很多的点,没有结构,他们的峰值都大于了0.5大于0.5没什么的,解完后都在1以下就可以了。
反应堆核物理基础习题集
选择题1)缓发中子的存在使中子倍增周期 A 。
A:变大B:变小C:不变2)在有源的次临界反应堆内,中子通量是C 的。
A:不断上升B:不断下降C:一定4)中子通量是:[C] 。
A 单位时间单位体积内的中子总数;B 单位时间内通过单位体积的中子总数;C 单位体积内的中子在单位时间内穿行距离的总和;D 单位时间内单方向通过单位面积的中子总数。
8)“功率亏损”的定义是:[A]A不反应堆功率上升时向堆芯引入的负反应性总值;B当慢化剂温度上升时向堆芯引入的负反应性总值;C当反应堆功率上升时向堆芯引入的正反应性总值;D当燃料温度降低时向堆芯引入的正反应性总值;21) 反应堆功率正比于 B 。
A:最大通量B:平均通量C:最小通量22) 处在临界状态下的反应堆的功率是 C 。
A:很高的B:一定的C:任意的25)反应堆在稳定功率运行时,假定所有其它条件不变,分别发生了如下的变化:1)功率上升;2)控制棒组下插。
则两种情况下的△I变化方向为:[D]。
A. 1)正;2)正。
B. 1)负;2)正。
C. 1)正;2)负。
D. 1)负;2)负。
解释所选答案的理由:1)由于△I=PT-PB,功率上升后,堆芯出口温度上升,导致堆芯下半部功率升高,△I减小;2)控制棒下插,堆芯上半部功率减小,堆芯轴向功率峰值将偏向堆芯下半部,△I减小。
26)反应堆在寿期中以75%FP运行,假定控制棒处在全提位置,那么在发生以下变化后,反应堆功率分布向堆芯顶部偏移最大的情形应当是:[A]。
A. 降低功率。
B. 降低冷却剂硼浓度。
C. 降低堆芯平均温度。
D. 降低反应堆冷却剂系统压力。
27)当反应堆以75%FP运行,一束中心控制棒下插到底与同一束控制棒下插50%,那么,比较这两种情形,正确的说法是:[B]。
A. 控制棒下插到底引起轴向功率分布的变化大。
B. 控制棒下插到底引起径向功率分布的变化大。
C. 控制棒下插到底引起停堆裕量的变化大。
D. 控制棒下插到底引起停堆裕量的变化小。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
arXiv:hep-ex/0502014v1 6 Feb 2005February7,20087:53ProceedingsTrimSize:9inx6indis04˙alexakhinLONGITUDINALPOLARIZATIONOFΛAND¯ΛHYPERONSINDEEP-INELASTICSCATTERINGATCOMPASS.
V.YU.ALEXAKHINONBEHALFOFTHECOMPASSCOLLABORATION.JointInstituteforNuclearResearchDubna141980,RussiaE-mail:Vadim.Alexakhine@cern.ch
ThestudyoflongitudinalpolarizationofΛ(¯Λ)hyperonsindeep-inelasticscat-teringisimportantbecauseitcanprovideaninformationonthefundamentalpropertiesofthenucleon,suchaspolarizationofthestrangequarksinthenu-cleonandtodeterminethemechanismofspintransferfrompolarizedquarktoapolarizedbaryon.TheproductionofΛand¯Λbypolarizedµ+of160GeV/conapolarized6LiDtargethasbeenstudiedusingtheCOMPASSspectrometer.AnimportantfeatureoftheCOMPASSexperimentaldatasampleisalargenumberof¯Λhyperons,whichiscomparablewithnumberofΛ.FirstpreliminaryresultsonthelongitudinalpolarizationofΛand¯Λhyperonsproducedinthedeep-inelasticscatteringwillbepresentedfor2002dataset.
MeasurementsofΛpolarizationintargetfragmentationregionprovideimportantinformationonthefundamentalpropertiesofthenucleonsuchastheroleofthe¯sspairsintheprotonwavefunction1.Thepolarizednucleonintrinsicstrangenessmodel2,3predictsnegativelongitudinalpolarizationofΛhyperonsproducedintargetfragmentationregion.ThemeasurementoftheΛpolarizationinthecurrentfragmentationregionallowstoinvestigateanotherphenomenon,namelythespintransferfrompolarizedquarktoapolarizedbaryon.RecenttheoreticalmodelsofΛpolarizationinDIScanbefoundinRefs.4–8.Anotherinterestingtopicisstudyofpossiblequark-antiquarkasymmetrieseitherinthequarktoΛfragmentationfunctionsand/orinthequarkandantiquarkdistributionsofthetargetnucleon.Cal-culationsfrommodel[8]showthatspintransfertoΛand¯Λshouldbethesameifstandardquarkdistributionss(x)=¯s(x)areused.Howevertherearedifficultiesintheinterpretationoftheresultsduetolargecontributionfromthediquarkfragmentation3andsignificantfractionofΛhyperons
1February7,20087:53ProceedingsTrimSize:9inx6indis04˙alexakhin2Table1.SummaryofexperimentalmeasurementsofΛhyperonpolarizationinDIS.Signofpolarizationisgivenwithrespecttovirtualphotonmomentum.
¯νµNe40xF<0403−0.63±0.13WA5912xF>066−0.11±0.45
νµN43.8xF<05608−0.21±0.042480.23±0.20NOMAD14xF>02479−0.09±0.06401−0.23±0.15
PBD=2500HERMES150.06±0.09
dcosθX
=NtotFebruary7,20087:53ProceedingsTrimSize:9inx6indis04˙alexakhin3whereNtotisthetotalnumberofevents,α=+(−)0.642±0.013isΛ(¯Λ)decayparameter,Pistheprojectionofthepolarizationvectoronthecor-respondingaxis,θXistheanglebetweenthedirectionofthedecayparticle(protonforΛ,antiprotonfor¯Λ)andX-axis.TheacceptancecorrectionwasdeterminedusingunpolarizedMonteCarlosimulation.TheDISeventsareproducedbyLEPTO6.5.1generator10andtheapparatusisdescribedbyafullGEANT3.2111model.Theanalysiswasperformedslicingeachangulardistributionin10binsandfittingtheinvariantmassdistributionofV0peaktoobtainthenum-berofeventsinthebin.Correctedangulardistributionswerefitusingequation(1).ResultsforlongitudinalpolarizationarePK0s=0.007±0.017(stat.),PΛ=0.03±0.04(stat.)±0.04(syst.)andP¯Λ=−0.11±0.06(stat.)±0.05(syst.).Allresultswereaveragedoveraccessiblekinematicalregion.SpintransfervariablefrombeamtoΛwascalculatedasS=PΛFebruary7,20087:53ProceedingsTrimSize:9inx6indis04˙alexakhin4
Fx-0.8-0.6-0.4-0.2-00.20.40.60.8Spin transfer
-0.500.511.5NOMADE665COMPASS 2002, PRELIMINARYΛ
Figure2.Spintransferfor¯Λhyperons.izationmeasurement.Datasamplescollectedin2003and2004willsignifi-cantlyincreasethestatistics.
References1.J.Ellisetal,Phys.Lett.,B353(1995)319;Nucl.Phys.,A673(2000)2562.J.Ellis,D.Kharzeev,A.M.Kotzinian,Z.PhysikC69(1996)4673.J.Ellis,A.M.KotzinianandD.V.Naumov,Eur.Phys.J.,C25(2002)6034.M.BurkardtandR.L.Jaffe,Phys.Rev.Lett.70(1993)25375.M.Anselmino,M.Boglione,U.D’Alesio,E.LeaderandF.Murgia,Phys.Lett.B509(2001)246,6.A.M.Kotzinian,A.BravarandD.vonHarrach,Eur.Phys.J.C2(1998)329,7.C.BorosandL.Zuo-Tang,Phys.Rev.D57(1998)4491.8.B.Q.Ma,I.Schmidt,J.SofferandJ.J.Yang,Phys.Lett.B488(2000)2549.A.Bressan,contributiontotheseproceedings.10.G.Ingelman,A.EdinandJ.RathsmanComp.Phys.Comm.101(1997)10811.GEANT,CERNProgramLibraryLongWriteupW501312.WillocqS.etal.[WA59Collaboration],Z.Phys.C53,(1992)20713.M.R.Adamsetal.[E665Collaboration],Eur.Phys.J.C17(2000)26314.P.Astieretal.,[NOMADCollaboration],Nucl.Phys.B588(2000)3;P.Astieretal.[NOMADCollaboration],Nucl.Phys.B605(2001)315.A.Airapetianetal.[HERMESCollaboration],Phys.Rev.B64(2001)112005S.Belostotski,talkatthisconference.
