一道平面几何题的十种证法
平面几何的证明方法

平面几何的证明方法平面几何是数学中的一个重要分支,主要研究平面内的点、线、面及其相互关系。
在解决平面几何问题时,证明是一个关键步骤。
本文将介绍一些常用的平面几何证明方法,并说明它们的应用场景。
一、直接证明法直接证明法是一种常用的证明方法,即通过逐步推导和陈述使命题成立。
这种方法依赖于已知条件和平面几何定理,逻辑严谨、思路清晰。
例如,当要证明某两条线段相等时,可以通过给出这两条线段的定义,然后根据它们的属性,逐步推导得出结论。
二、间接证明法间接证明法是通过否定反证法来证明结论。
假设原命题不成立,然后逐步推导,得出矛盾,从而推出原命题成立。
这种方法常用于证明无理数、无法被二分等问题。
例如,当要证明某条直线平分了一个角时,可以假设这条直线没有平分该角,然后通过逻辑推导得出矛盾,证明了该直线实际上是平分了这个角。
三、反证法反证法是通过假设结论不成立,然后推出矛盾,证明原结论的一个方法。
这种方法常用于证明唯一性问题。
例如,当要证明两个圆只有一个公共切点时,可以先假设它们有两个或更多个公共切点,然后通过推导得出矛盾,从而证明了原结论。
四、归纳法归纳法适用于一系列问题的证明。
首先证明基本情况成立,然后假设某个特定的情况成立,通过归纳法推导得出所有情况都成立。
这种方法常用于证明几何图形的性质。
例如,当要证明一个多边形的内角和公式时,可以通过归纳法证明三角形和四边形的情况,然后推广到所有多边形。
五、共线法共线法是通过证明多个点共线来证明结论的方法。
在平面几何中,当需要证明某些点共线时,可以利用已知条件中的共线关系,或者通过构造辅助线,从而达到共线的目的。
例如,当要证明一个四边形的对角线交于一点时,可以通过构造这两条对角线,然后利用平行线的性质证明它们的交点存在。
六、相似性法相似性法是通过画出几何图形的相似部分来证明结论的方法。
当需要证明两个三角形相似时,可以通过观察它们的角度和边长关系,利用相似三角形的性质得出结论。
平面几何的证明方法

平面几何的证明方法平面几何是数学中的一门重要学科,它研究了平面上的点、线、面以及它们之间的关系和性质。
为了证明平面几何中的命题和定理,我们需要运用一些特定的证明方法。
本文将介绍几种常见的平面几何证明方法,以帮助读者更好地理解和运用这些方法。
一、直角三角形的证明方法直角三角形是指其中一角为直角(即90度)的三角形。
证明一个三角形为直角三角形的常用方法有以下几种:1.边长关系法:利用勾股定理和勾股定理的逆定理(即若一个三角形的三边满足勾股定理,那么这个三角形一定是直角三角形)来证明。
例如,若已知三角形的两条边的平方之和等于第三条边的平方,那么可以得出这个三角形是直角三角形。
2.角度关系法:利用三角形内角和等于180度的性质,通过计算三角形的角度来判断是否为直角三角形。
例如,若一个三角形的某个角度等于90度,则可以得出这个三角形是直角三角形。
二、三角形相似的证明方法相似三角形是指具有相同形状但大小不同的三角形。
证明两个三角形相似的常用方法有以下几种:1.边长比较法:通过比较两个三角形的边长比例来判断它们是否相似。
若两个三角形的三条边对应成比例,即各边之比相等,则可以得出这两个三角形相似。
2.角度关系法:利用相似三角形的对应角相等的性质来证明。
例如,若两个三角形的某两个角度相等,则这两个三角形相似。
三、平行线的证明方法平行线是具有相同斜率且永不相交的直线。
证明两条直线平行的常用方法有以下几种:1.等距离法:通过证明两条直线上任意一对平行线段之间的距离相等来判断它们平行。
若两条直线上的任意一对平行线段之间的距离相等,则可以得出这两条直线平行。
2.平行线性质法:利用平行线的性质来证明。
例如,如果两条直线分别与第三条直线平行,并且这两条直线不重合,那么这两条直线也是平行的。
四、等腰三角形的证明方法等腰三角形是指具有两边长度相等的三角形。
证明一个三角形为等腰三角形的常用方法有以下几种:1.边长关系法:通过证明三角形的两边长度相等来判断它是等腰三角形。
平面几何100题及答案(前80题)
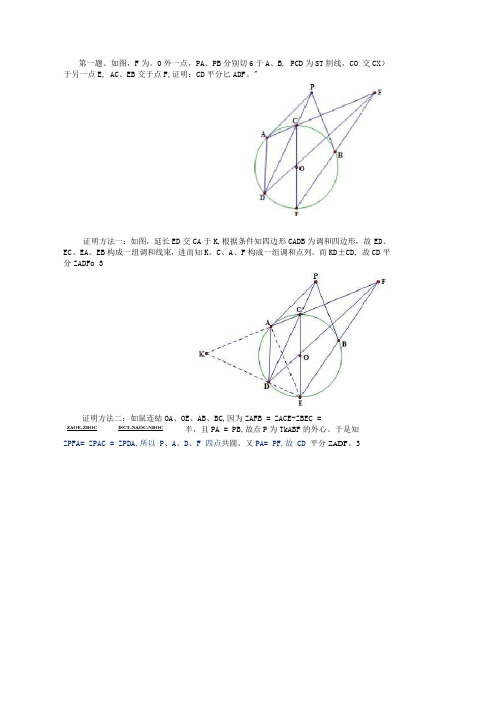
第一题、如图,F为。
0外一点,PA、PB分别切6于A、B, PCD为ST割线,CO 交CX)于另一点E, AC、EB交于点F,证明:CD平分匕ADF。
"证明方法一:如图,延长ED交CA于K,根据条件知四边形CADB为调和四边形,故ED、EC、EA、EB构成一组调和线束,进而知K、C、A、F构成一组调和点列。
而KD±CD, 故CD平分ZADFo 3证明方法二:如鼠连結OA、OE、AB、BC,因为ZAFB = ZACE-ZBEC =ZAOE-ZBOC ISCT-NAOC-NBOC 半,且PA = PB,故点P为TkABF的外心。
于是知ZPFA= ZPAC = ZPDA,所以P、A、D、F 四点共圆。
又PA= PF,故CD 平分Z A DF。
3第二题、如图,AB为©0直径,C、D为O。
上两点,且在AB同侧,。
在C、D两处的切城交于点E, BC、AD交于点F, EF交AB于证明:E、C、页、D四点共圆。
“证明:如图,延长白C、BD交于点K,则BC1AK, AD丄BK,从而知F^)AKAB的垂心。
又在圆内接六边形CCADDB中使用帕斯卡定理,知K、E、F三点共线,从而KM丄卽于価。
于是知匕CMF = ZCAF= ZCDE,所以E、C、页、D四点共圆。
K第三题、如图,AB为。
直径,C、D为伽上两点'且在AB同侧,O0在C. D两处的切线交于点E, BC、AD交于点F, EB交0。
于点G,证明;ZCEF = 2/AGF。
“证明:如图,根据条件知匕CF D =典牌=(脸-®;(i对-命)=Z CAB + / DBA = ZECF + ZEDF;且EC = ED;故点E 为△CED 外心。
于是知/EFC = ZECF = ZCAB = ZCGE,敌E、C、F、G四点共圆。
所以“ZCGF = ZCEF = 2(90° - ZECF)= 2(90° - ZCAB)= 2ZABC 二2ZAGC " 0lWZAGF = —=—,即得ZCEF = 2ZAGFo,2 2第四題、如图,AB为直径,P为AB延长线上一点,PC切于C,点C关于朋的对称点为点D, CE1AD于E, F为CE中点,AF交于K,求证:AP为ZXPCK外扬圆的切线。
平面几何证明题的解题方法

平面几何证明题的解题方法平面几何证明题是数学中的重要内容之一,通过证明题的解答,我们可以深入理解几何学的概念和性质。
然而,解答平面几何证明题并非易事,需要灵活运用多种证明方法和技巧。
本文将介绍几种常用的解题方法,帮助读者更好地应对平面几何证明题。
一、直接证明法直接证明法是解答平面几何证明题的基础方法之一。
它通过逻辑推理和已知条件与结论之间的关系,一步步地证明结论的正确性。
在使用直接证明法时,首先要仔细分析所给条件和待证明结论。
根据已知条件,可以运用各种几何定理和性质,逐步推导出结论,直至得到所要证明的结论。
例如,对于“证明三角形ABC的三条中线交于一点”的证明题,我们可以先通过已知条件得出三角形ABC的三条中线等长,再利用中位线的性质得出这三条中线交于一点的结论。
二、反证法反证法是解答平面几何证明题的另一种常用方法。
它通过假设所要证明的结论不成立,推导出一个与已知条件矛盾的结论,从而证明所要证明的结论成立。
在运用反证法时,我们需要首先假设所要证明的结论不成立,然后通过推理,得出一个矛盾的结论,以此证明原命题的正确性。
例如,对于“证明等腰三角形的底角相等”的证明题,我们可以先假设等腰三角形的底角不相等,然后推导出一个与已知条件矛盾的结论,例如底边不等长或者顶角不等于90度,从而证明等腰三角形的底角相等的结论成立。
三、合同法合同法是一种常用于证明线段或角相等的证明方法。
通过构造相等的辅助线段或角,以达到证明所要求的结论。
在使用合同法时,我们需要根据已知条件和待证明的结论,合理构造辅助线段或角,并利用几何定理和性质证明这些辅助线段或角相等,从而得出所要证明的结论。
例如,对于“证明两个三角形全等”的证明题,我们可以通过构造辅助线段或角,使得两个三角形的对应边或对应角相等,然后运用全等三角形的性质,推导出两个三角形全等的结论。
四、相似法相似法是一种常用于证明平行线、比例关系和相似三角形等性质的证明方法。
通过证明对象与已知对象之间的相似关系,来推导出所要求的结论。
数学平面几何证明

数学平面几何证明数学平面几何是数学中的一个重要分支,它研究平面内的图形和它们之间的关系。
而证明则是数学中非常重要的一部分,它能够推导出数学定理并加深我们对数学知识的理解。
在这篇文章中,我将介绍一些数学平面几何中的常见证明方法。
1. 旋转法证明平行线性质在平面几何中,平行线的性质是非常重要的。
一种常见的证明平行线性质的方法是使用旋转法。
具体步骤如下:(1) 根据给定的条件,作出一条直线和一条与之平行的直线。
(2) 以其中一条直线为轴,将另一条直线旋转一定角度。
(3) 观察旋转后的情况,如果旋转后的直线与原来的直线没有相交点或平行线组成的夹角为180度,则可以证明给定的两条直线平行。
2. 对称性证明线段垂直在平面几何中,线段垂直是一个重要的性质。
对称性则是我们常用的证明方法之一。
具体步骤如下:(1) 根据给定的条件,作出一个线段。
(2) 找到线段的中点,根据对称性将线段绕中点旋转180度。
(3) 观察旋转后的情况,如果旋转后的线段和原线段重合,并且两条线段的夹角为90度,则可以证明给定的线段垂直。
3. 数学归纳法证明等差数列性质等差数列常常出现在数学问题中,证明等差数列的性质可以使用数学归纳法。
具体步骤如下:(1) 先证明当n=1时,等差数列的性质成立。
(2) 假设当n=k时,等差数列的性质成立。
(3) 通过数学推导证明当n=k+1时,等差数列的性质也成立。
(4) 根据数学归纳法原理,可以得出等差数列的性质对于所有正整数n都成立。
4. 反证法证明平面几何定理反证法是一种常用的证明方法,它通过假设定理不成立,然后推导出矛盾,从而证明定理的正确性。
具体步骤如下:(1) 假设定理不成立,并且根据假设得出一个结论。
(2) 推导出的结论与已知的数学定理相矛盾。
(3) 由此可以推断原先假设的定理是正确的。
通过以上介绍的几种证明方法,我们可以看到数学平面几何中的证明过程是严谨而且逻辑性强的。
在实际应用中,我们可以根据问题的具体情况灵活运用这些方法来进行证明,从而加深对数学知识的理解和应用能力。
平面几何证明方法

平面几何证明方法
平面几何证明的方法主要有以下几种:
1. 充分必要条件证明方法:通过证明一个命题的充分条件和必要条件,来证明该命题的等价性。
通常先假设命题的充分条件成立,再证明必要条件成立;然后再假设命题的必要条件成立,再证明充分条件成立。
2. 反证法:先假设命题的反证成立,然后通过逻辑推理,推导出一个与已知条件或已经证明的命题矛盾的结论,从而推翻原命题的反证。
3. 数学归纳法:通过证明命题对某个起始值成立,并假设命题对于一个任意的自然数成立,推导出命题对于下一个自然数也成立,从而证明命题对于所有自然数都成立。
4. 对偶命题证明法:通过将一个命题中的部分语句取反或者替换为与之对偶的语句,从而将原命题转化为与之等价的命题,然后再根据已知条件和已经证明的命题推导出结论。
5. 直接证明法:通过逻辑推理,根据已知条件和已经证明的命题,推导出结论,从而证明命题的正确性。
6. 分类讨论法:根据问题的性质和已知条件,将问题分为几种情况进行讨论,
然后对每一种情况分别进行证明。
7. 形象化证明法:通过绘制示意图或者构造具体的示例,将命题转化为几何图形上的问题,然后通过观察或者计算,得出结论。
以上是平面几何证明中常用的一些方法,具体的证明方法根据不同的问题和命题可能会有所变化。
初中平面几何证法

思考:
1.如图,以ABC的边AB、AC向形外作正方形ABEF、 ACGH,求证FC=BH
2.已知等腰直角ABC中,∠BAC=90º,过点A作直线 l∥BC,在l上取一点F使BF=BC,BD与AC交于点E。求证: CE=CF
3.已知:如图,正方形ABCD的对角线交于O,点E在OA 上,CF⊥BE于F,交OB于G。求证:OE=OG
思考:若只交换条件“GF⊥BE”与 结论“OE=OG”,本题是否成立?
4.如图,在梯形ABCD中,AD∥BC, 点F在边AD上,EF∥AB交CD的延 长线于E,若AE∥BF, 求证:点D是EC的中点.
5.如图,MN∥BC,AD 是BC边上的中线,MN与 AD交于点P,求证:MP=NP
变式思考:
(1)P是ABC的中线AD上的一点, PE∥AB,PF∥AC,PE、PF分别交 BC于E、F,求证:ED=FD
根据三角形中位线定理,能证明MN∥PQ,且MN=PQ, 因而四边形PQMN是平行四边形,如果PM=NQ,则平行 四边形PQMN必定是矩形。得到启发:连结MN、NP、 PQ、QM,证明四边形PQMN是矩形。
例4:已知,直线DEF 与 ABC的边AB、 AC及
BC的延长线分别交于D、E、F,且
,
求证:AD=BD。
10.已知:如图,⊙O与⊙O1 交于A、B两点, O1点在⊙O上,AC是⊙O直径,AD是⊙O1的 直径,连结CD。求证:AC=CD
11.已知:如图,AB、AC、AD是⊙O的三 条弦,且AC 平分∠BAD,弦CE∥AB, 求证:CE=AD
12.如图,AB是⊙O的直径,C是⊙O上一点, CD⊥AB于D,以C为圆心,CD为半径作圆, 交⊙O于P、Q,PQ交CD于G。求证:CG=GD (提示:分别延长CD、DC交⊙O、⊙C于F、 E。)
平面几何常用证明方法

平面几何常见证明方法1,分析法分析法是从命题的结论入手,先承认它是正确的,执果索因,寻求结论正确的条件,这样一步一步逆而推之,直到与题设会合,于是就得出了由题设通往结论的思维过程。
分析法主要应用与的几何问题特点主要是:从证明推理的时候出现多个方向,不知道哪个方向能够成功推导到结论,也就是说从正向推导比较迷茫的时候,比较适合用分析法来解决这些问题。
例1 如图2.1.1,四边形ABCD 的一条对角线BD 平行于两对边之交点的连线EF ,求证:AC 平分BD 。
[1]证明:设AC 交BD 于M ,交EF 于N 则NFMD EN BM =,欲证MD BM = 作方向猜测,只需证NF EN =或1==NF EN MD BM 即可。
但我们意识到这不容易证明, (图2.1.1)再作方向猜测,欲证MD BM =,只需证明BM MD MD BM =即可。
而NFEN MD BM =,从而只需证NF EN BM MD =即可,又只需证NF BM EN MD =即可。
而NF BM CN MC EN MD ==,故得证。
2 综合法综合法则是由命题的题设条件入手,由因导果,通过一系列的正确推理,逐步靠近目标,最终获得结论。
再从已知条件着手,根据已知的定义、公式、定理,逐步推导出结论。
综合法和分析法有些不同的是分析法的思路从结论开始,综合法的思路从题设开始。
例2如图2.2.1设D 是ABC ∆底边BC 上任一点,则CD BD BC BD AC CD AB BC AD ⋅⋅-⋅+⋅=⋅222。
[1]证明:在ADB ∆和ABC ∆中 BDAD AB BD AD ADB ⋅-+=∠2cos 222 BDAD AC CD AD ADC ⋅-+=∠2cos 222 由ADC ADB ∠-=∠cos cos ,所以 (图2.2.1)BDAD AC CD AD BD AD AB BD AD ⋅-+-=⋅-+22222222有)()(222CD BD CD BD BD AC CD AB CD BD AD +⋅-⋅+⋅=+将BC CD BD =+代入上式则有CD BD BC BD AC CD AB BC AD ⋅⋅-⋅+⋅=⋅222,证毕。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一道平面几何题的十种证法
题目:如图1,△ABC中,D、F在AB上,AD=BF,过D作DE∥BC,交AC 于E,过F作FG∥BC交AC于G.
求证:BC=DE+FG.
分析:证明一条线段等于另外两条线段的和,常用的方法是将线段的位置平移:(1)延长较短线段与较长线段相等;
(2)在较长线段上截取与较短线段相等的线段;
(3)将线段适当移动位置后进行比较;
(4)采用其它比较方法,如解析法,三角法,面积法等.
一、延长较短线段与较长线段相等
解法1 如图2,延长FG到H,使FH等于BC,连结CH.(关键证GH=DE即可).
由作法知FH平行且等于BC FBCH是平行四边形CH=BF.
在△ADE和△CHG中,CH=BF=AD.
由CH∥AB∠A=∠2,又∠1=∠B,∠H=∠B,所以
∠1=∠H.∴△ADE≌△CHG,则DE=GH,
故BC=FG+GH=DE+FG.
证法2 如图3,仍延长FG到H,使GH=DE,连结CH.
(关键证BC=FH).
由DE∥BC∥FG∠1=∠2=∠3.
又AD=FB,所以AE=GC.
∴△ADE≌△CHG,(SAS)
∴∠A=∠GCH AB∥CH.
∴四边形FBCH是平行四边形,所以,BC=FH,
∴BC=DE+FG.
证法3 如图4,延长DE到H,使DH=BC,连结CH.
(关键证FG=EH).
由DBCH及DH=BC.
再△AFG≌△CHE,得FG=EH.
二、恰当地将线段平移
证法4 如图5
找EG的中点K,连接DK并延长DK交FG的延长线于H,可证得
△DEK≌△HGK DE=GH.
再证得△ADE≌△CHG,(或证△ADK≌△CHK)∠A=∠GCH
∴BC=GH+FG=DE+FG.
证法5 如图6.
过D作DH∥AC交BC于H,则DE=HC.不难证得△AFG≌△DBH,可得FG=BH,∴BC=BH+HC=DE+FG.
证法6 如图7
过F作FH∥AC交BC于H(或在BC上截取CH=FG).
三、在较长的线段上截取较短的线段
证法7 如图8
在BC上截取BH=DE.不难得出△ADE≌△FBH.则
∠1=∠2=∠3FH∥AC FG=HC.
(同理可在BC上截取BH=FG.再证HC=DE)
四、利用梯形或三角形的中位线定理
题中要证的结论系三角形的底边BC等于梯形DFGE两底之和,可猜想通过梯形DFGE的中位线沟通两者之间的关系.
证法8 如图9.
又AD=FB,由平行截割定理得MN也是△ABC的中位线,
五、利用相似三角形的性质和比例的性质
题中要证的边实质是相似三角形的对应边,因此,可从相似三角形的对应边成比例和比例的基本性质入手证明.
证法9 如图1.
又AD=BF,所以,AD+AF=AD+DB=AB.
即BC=DF+FG.
六、其它线段变换
证法10 如图10.
作AH⊥DE于H,作FP⊥BC于P,作GQ⊥BC于Q.易证
△ADH≌△FBP,
△AHE≌△GQC.
DH+HE=BP+QC,又FG=PQ.则BC=PQ+BP+QC=FG+DH+HE,即BC=DE +FG.。
