数学九年级上北师大版4.7相似三角形的性质同步训练B

合集下载

4.7 相似三角形的性质(数学北师大版九年级上册)

（1）对应角平分线之比等于
；
（2）对应高线之比等于
；
（3）对应中线之比等于
；
（4）周长之比等于
；
（5）面积之比等于
.
例 2 如图，在□ABCD中，AE:EB=1:2.
（1）求△AEF和△CDF的周长之比；
（2）如果
，求和 .
（3）连结BD交AC于点O，求AF:FO.
根据图形你能求出什么？
AE
A' A
B
DC
B'
△ABC∽△A' B' C'
D' C'
相似三角形的面积之比等于相似比的平方。
例 1 如图，在正方形方格图上有△ABC和△DEF.
（1）这两个三角形相似吗？如果相似，请给出证明；（2）这两个三角形的周长之比是多少？面积之比呢？
A
B
C
E
F
D
当堂练习
1.如果两个三角形相似，相似比为3:5，那么
B
F
O
D
C
F
AE
B
O
D
C
AE
B
F
D
C
A2 B O
D
4
C
例 3 如图所示，在△ABC和△EBD中，
.
（1）求证：∠ABD=∠CBE；
（2）若△ABC和△EBD的周长差为60cm，求这两个三角形的周长；
（3）若△ABC和△EBD的面积和为812cm2，求这两个三角形的面积。
A
D
C
B
E
当堂练习
1.如图，在△ABC中，AD:DB=1:2，DE∥BC，若△ABC的面积为9，求S四边形DBCE

新北师大版九年级数学上册第四章4.7相似三角形的性质第1课时相似三角形对应线段的比课时训练

4.7相似三角形的性质第1课时相似三角形对应线段的比对应练习：1.顺次连接三角形三边的中点，所构成的三角形与原三角形对应髙的比是（C）J.1：4 1：3C1：2 ・A1：√22.如果两个相似三角形对应角平分线之比为1：2,那么它们对应屮线之比为（A）J.1：2 1：3CI：4 1：83.已知△ABC^ΔA,B'C,,AD和A'D,是它们的对应角平分线，且AD=8皿，A'D z=3勿则OΔABC⅛∆A z B,C1对应高的比为4.已知△ABCSAA'Wc',AD,A f D Z是高，且AD=3c/w,A,D,=5c/n,AE,A z E z分别是BC和B'C,边上的中线，AE=6伽，则心E,=IO CZZA5.如图，AABC是一块锐角三角形,余料，其中BC=I5加，髙M）=IOCnb 现在要把它裁剪成一个矩形材料备用，使矩形的一边在BC±,其余两个顶点分别在AB、AC上，若矩形的一边PN=9,求矩形的另一边PQ的长是多少？解：设AD与PN交于点E.•・•四边形PQMN是矩形，ΛPN√BC,ΛZAPN=ZB,ZANP=ZC,AA PNAE PN・AD9×10ZXΛΔAPN^ΔABC,Λ-'∙AE=DC=—T厂=6S）,.IDE=AD-AE=10—6=4（⑵），由BCAD BC15题意可知：PQ=DE=4物.・・.矩形的另一边PQ的长是4cm.6.如图，在AABC是一张锐角三角形硬纸片，AD是边BC上的高，BC=40伽，AD=30伽，从这张勺更纸片上剪下一个长HG是宽HE的2倍的矩形E.FGH,使它的一边EF在BC±,顶点G,H分别在AC,AB上，AD 与HG的交点为M.(2)求矩形EFGH的周长.解：⑴易得AM丄HG,•・•四,边形EFGH为矩形，ΛEF/7GH,ΛZAHG=ZABC.又TZHAG=ZAMHG...z.Z-AMHG、”IBAC,ΛΔAHG^ΔABC,(2)由(1)得：—=—.设HE=XOT,则MD=HE=xc∕τz,VAD=30—X2x30tv/,ΛAM=(30-x)cw.VHG=2HE,ΛHG=2xc///,可得—环—=亦，解得，x=】2，2x=24,所以矩形EFGH的周长为：2X（12+24）=72（⑵）・。

九年级数学上册(北师大版)相似三角形的性质(同步课件)

【提问1】什么叫做相似三角形？
三角分别相等、三边成比例的两个三角形叫做相似三角形.
【提问2】相似三角形的判定方法有哪些？
三角形相似判定定理1：两角分别相等的两个三角形相似.
三角形相似判定定理2：两边成比例且夹角相等的两个三角形相似.
三角形相似判定定理3：三边成比例的两个三角形相似.
【提问3】你知道相似三角形的性质有哪些？
∵
AC
A′ C′
CD
= C′ D′ =
1
2
∴ CD = 2C ′ D′ = 3cm
4）由此你发现相似三角形还有哪些性质？
探索与思考
如图， △ ∽△ ′ ′ ′ ，相似比为，其中、 ′′分别是、 ′′边上的中线，问
AD 、 A′D′有什么关系呢？
解：∵ △ ∽△
【详解】解：∵AD经过△ ABC的重心，∴点D是BC中点，
∵BC=12，∴CD=BD=6，
∵GE∥BC，∴△AGE∽△ADC，
AE
AC
∵点E是AC中点，∴
解得：GE=3，故选D.
=
GE
CD
1
2
GE
6
= ，即
1
2
= ，
）
探索与思考
∴BD=
1
1
BC,B’D’= B’C’
3
3
∴
AB BD
=
A′ B′ B′ D′
∴
AB AD
=
=k
A′ B′ A′ D′
∴△ABE ∽△A' B' E' .
AB BC
=
A′ B′ B′ C′
=k
课堂小结
相似三角形的性质：
1）对应角相等，对应边成比例.

九年级数学第二十七章《相似三角形的性质》同步练习(含答案)

九年级数学第二十七章《相似三角形的性质》同步练习（含答案）一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的．1．如果△ABC ∽△DEF ，A 、B 分别对应D 、E ，且AB ：DE =1：2，那么下列等式一定成立的是 A ．BC ：DE =1：2B ．△ABC 的面积：△DEF 的面积=1：2 C ．∠A 的度数：∠D 的度数=1：2D ．△ABC 的周长：△DEF 的周长=1：2 【答案】D2．如图，AB 、CD 、EF 都与BD 垂直，且AB =1，CD =3，那么EF 的长是A ．13B ．23 C ．34D ．45【答案】C【解析】∵AB 、CD 、EF 都与BD 垂直，∴AB ∥CD ∥EF ， ∴△DEF ∽△DAB ，△BEF ∽△BCD ，∴EF DF AB DB =，EF BF CD BD =，∴EF EF DF BFAB CD DB BD+=+=1． ∵AB =1，CD =3，∴13EF EF +=1，∴EF =34．故选C ．3．已知：如图，在ABCD中，AE：EB=1：2，则FE：FC=A．1：2 B．2：3 C．3：4 D．3：2 【答案】B【解析】在ABCD中，AB=CD，AB∥CD，∵BE=2AE，∴BE=23AB=23CD，∵AB∥CD，∴EFFC=BEDC=23，故选B．4．已知：如图，E是ABCD的边AD上的一点，且32AEDE=，CE交BD于点F，BF=15cm，则DF的长为A．10cm B．5cmC．6cm D．9cm【答案】C【解析】∵四边形ABCD是平行四边形，点E在边AD上，∴DE∥BC，且AD=BC，∴∠DEF=∠BCF；∠EDF=∠CBF，∴△EDF∽△CBF，∴BC BF ED DF=，∵32AEDE=，∴设AE=3k，DE=2k，则AD=BC=5k，52BC BFED DF==，∵BF=15cm，∴DF=25BF═6cm．故选C．5．已知△ABC∽△DEF，△ABC的周长为3，△DEF的周长为1，则△DEF与△ABC的面积之比为A．9：1 B．1：9C．3：1 D．1：3【答案】B【解析】∵△ABC∽△DEF，△ABC的周长为3，△DEF的周长为1，∴△ABC与△DEF的相似比为3，∴△DEF与△ABC的相似比为1：3，∴△DEF与△ABC的面积之比为1：9，故选B．6．如图，△ABC∽△AB'C'，∠A=35°，∠B=72°，则∠AC'B'的度数为A．63°B．72°C．73°D．83°【答案】C【解析】∵∠A+∠B+∠C=180°，∠A=35°，∠B=72°，∴∠C=180°–35°–72°=73°，∵△ABC∽△AB'C'，∴∠AC′B′=∠C=73°，故选C．7．如图，△ABC中，E为AB中点，AB=6，AC=4.5，∠ADE=∠B，则CD=A．32B．1C．12D．23【答案】C【解析】∵E为AB中点，∴AE=12AB，∵∠ADE=∠B，∠A=∠A，∴△ADE∽△ABC，∴AE ADAC AB，∴12AB2=AD•AC，∴AD=4，∴CD=AC–AD=0.5，故选C．二、填空题：请将答案填在题中横线上．8．两个三角形相似，相似比是12，如果小三角形的面积是9，那么大三角形的面积是__________．【答案】36【解析】∵两个三角形相似，相似比是12，∴两个三角形的面积比是14，∵小三角形的面积是9，∴大三角形的面积是36，故答案为：36．9．矩形ABCD中，AB=6，BC=8．点P在矩形ABCD的内部，点E在边BC上，满足△PBE∽△DBC，若△APD是等腰三角形，则PE的长为__________．【答案】65或310．如图，在△ABC纸板中，AC=4，BC=2，AB=5，P是AC上一点，过点P沿直线剪下一个与△ABC相似的小三角形纸板，如果有4种不同的剪法，那么AP长的取值范围是__________．【答案】3≤AP<4【解析】如图所示，过P作PD∥AB交BC于D或PE∥BC交AB于E，则△PCD∽△ACB或△APE∽△ACB，此时0<AP<4；如图所示，过P作∠APF=∠B交AB于F，则△APF∽△ABC，此时0<AP≤4；如图所示，过P作∠CPG=∠CBA交BC于G，则△CPG∽△CBA，此时，△CPG∽△CBA，当点G与点B重合时，CB2=CP×CA，即22=CP×4，∴CP=1，AP=3，∴此时，3≤AP<4；综上所述，AP长的取值范围是3≤AP<4．故答案为：3≤AP<4．11．如图，点A、B、C、D的坐标分别是（1，7）、（1，1）、（4，1）、（6，1），且△CDE与△ABC相似，则点E的坐标是__________．【答案】（6，0），（6，5），（6，2），（4，2）、（4，5）、（4，0）．【解析】在△ABC中，∠ABC=90°，AB=6，BC=3，AB：BC=2．①当点E的坐标为（6，0）时，∠CDE=90°，CD=2，DE=1，则AB：BC=CD：DE，△CDE∽△ABC；②当点E的坐标为（6，5）时，∠CDE=90°，CD=2，DE=4，则AB：BC=DE：CD，△EDC∽△ABC；③当点E的坐标为（6，2）时，∠ECD=90°，CD=2，DE=1，则AB：BC=CD：DE，△CDE∽△ABC；同理，当点E的坐标为（4，2）、（4，5）、（4，0），故答案为：（6，0），（6，5），（6，2），（4，2）、（4，5）、（4，0）．三、解答题：解答应写出文字说明、证明过程或演算步骤．12．求证：相似三角形面积的比等于相似比的平方．（请根据题意画出图形，写出已知，求证并证明）【解析】已知：如图，已知△ABC ∽△A 1B 1C 1，顶点A 、B 、C 分别与A 1、B 1、C 1对应，△ABC 和△A 1B 1C 1的相似比为k ．求证：111ABC A B C S S △△=k 2；证明：作AD ⊥BC 于D ，A 1D 1⊥B 1C 1于D 1，∵△ABC ∽△A 1B 1C 1，顶点A 、B 、C 分别与A 1、B 1、C 1对应， ∴∠B =∠B 1，∵AD 、A 1D 1分别是△ABC ，△A 1B 1C 1的高线， ∴∠BDA =∠B 1D 1A 1，∴△ABD ∽△A 1B 1D 1，∴11AD A D =11ABA B =k ， ∴111ABC A B C S S △△=11111212BC AD B C A D ⋅⋅⋅⋅=k 2．13．如图所示，Rt △ABC ∽Rt △DFE ，CM 、EN 分别是斜边AB 、DF 上的中线，已知AC =9cm ，CB =12cm ，DE =3cm ．（1）求CM 和EN 的长；（2）你发现CMEN的值与相似比有什么关系？得到什么结论？【解析】（1）在Rt △ABC 中，AB =22AC CB +=22912+=15，∵CM 是斜边AB 的中线， ∴CM =12AB=7.5， ∵Rt △ABC ∽Rt △DFE ， ∴DE DF AC AB =，即319315DF==， ∴DF =5，∵EN 为斜边DF 上的中线，∴EN =12DF =2.5；（2）∵7.532.51CM EN ==，相似比为9331AC DE ==，∴相似三角形对应中线的比等于相似比．14．如图，点C 、D 在线段AB 上，△PCD 是等边三角形，且△ACP ∽△PDB ．（1）求∠APB 的大小．（2）说明线段AC 、CD 、BD 之间的数量关系．15．从三角形（不是等腰三角形）一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原三角形相似，我们把这条线段叫做这个三角形的完美分割线．（1）如图1，在△ABC 中，∠A =48°，CD 是△ABC 的完美分割线，且AD =CD ，则∠ACB =__________°．（2）如图2，在△ABC 中，AC =2，BC 2，CD 是△ABC 的完美分割线，且△ACD 是以CD 为底边的等腰三角形，求完美分割线CD的长．【解析】（1）当AD=CD时，如图，∠ACD=∠A=48°，∵△BDC∽△BCA，∴∠BCD=∠A=48°，∴∠ACB=∠ACD+∠BCD=96°．（2）由已知得AC=AD=2，∵△BCD∽△BAC，∴BCBA=BDBC，设BD=x2）2=x（x+2），∵x＞0，∴x3–1，∵△BCD∽△BAC，∴CD BDAC BC=32，∴CD 312-×62．故答案为：96．。

九年级数学(2019秋北师大版)上册校本作业：4.7相似三角形的性质(1)

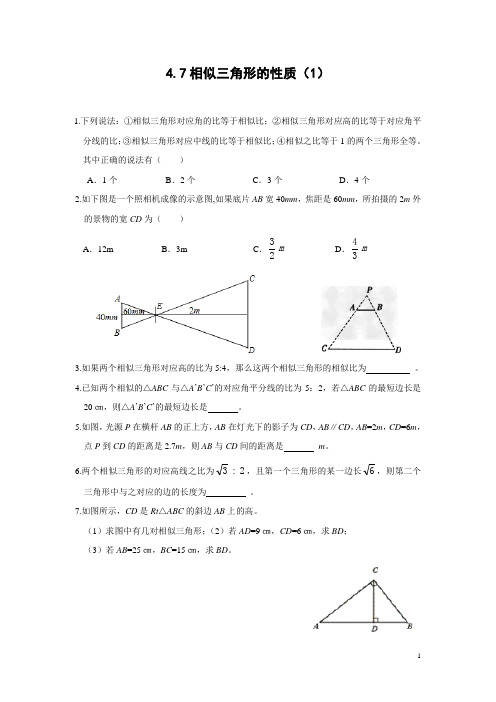
4.7相似三角形的性质（1）1.下列说法：①相似三角形对应角的比等于相似比；②相似三角形对应高的比等于对应角平分线的比；③相似三角形对应中线的比等于相似比；④相似之比等于1的两个三角形全等。

其中正确的说法有（）A ．1个B ．2个C ．3个D ．4个2.如下图是一个照相机成像的示意图,如果底片AB 宽40mm ，焦距是60mm ，所拍摄的2m 外的景物的宽CD 为（）A ．12mB ．3mC ．m 23D ．m 343.如果两个相似三角形对应高的比为5:4，那么这两个相似三角形的相似比为。

4.已知两个相似的△ABC 与△A ’B ’C ’的对应角平分线的比为5：2，若△ABC 的最短边长是20㎝，则△A ’B ’C ’的最短边长是。

5.如图，光源P 在横杆AB 的正上方，AB 在灯光下的影子为CD ，AB ∥CD ，AB =2m ，CD =6m ，点P 到CD 的距离是2.7m ，则AB 与CD 间的距离是 m 。

6.两个相似三角形的对应高线之比为2:3，且第一个三角形的某一边长6，则第二个三角形中与之对应的边的长度为。

7.如图所示，CD 是Rt △ABC 的斜边AB 上的高。

（1）求图中有几对相似三角形；（2）若AD =9㎝，CD =6㎝，求BD ；（3）若AB =25㎝，BC =15㎝，求BD 。

8.如图所示，有一侦察员在距敌方200m的地方A处发现敌人的一座建筑物DE，但不知其高度，又不能靠近建筑物测量，机灵的侦察员食指竖直举在右眼前，闭上左眼，并将食指前后移动，使食指恰好将该建筑物遮住。

若此时眼睛到食指的距离约为40cm，食指的长约为8cm,你能根据上述条件计算出敌方建筑物的高度吗？请写出你的推理过程。

相似三角形的性质与判定(原卷版)-九年级数学(北师大版)

第22讲相似三角形的性质与判定1、探索相似三角形的性质，能运用性质进行有关计算；2、通过典型实例认识现实生活中物体的相似，能运用图形相似的知识解决一些简单的实际问题（如何把实际问题抽象为数学问题）.一、相似三角形的性质1．相似三角形的对应角相等，对应边的比相等.2.相似三角形中的重要线段的比等于相似比.相似三角形对应高，对应中线，对应角平分线的比都等于相似比.要点：要特别注意“对应”两个字，在应用时，要注意找准对应线段.3.相似三角形周长的比等于相似比.∽，则由比例性质可得：4.相似三角形面积的比等于相似比的平方.∽，则分别作出与的高和，则21122=1122ABCA B C BC AD k B C k A D S k S B C A D B C A D '''''''⋅⋅⋅⋅=='''''''''⋅⋅△△要点：相似三角形的性质是通过比例线段的性质推证出来的.二、相似三角形的应用1.测量高度测量不能到达顶部的物体的高度，通常使用“在同一时刻物高与影长的比例相等”的原理解决.要点：测量旗杆的高度的几种方法：平面镜测量法影子测量法手臂测量法标杆测量法2.测量距离测量不能直接到达的两点间的距离，常构造如下两种相似三角形求解。

1．如甲图所示，通常可先测量图中的线段DC、BD、CE的距离（长度），根据相似三角形的性质，求出AB的长.2．如乙图所示，可先测AC、DC及DE的长，再根据相似三角形的性质计算AB的长.要点：1．比例尺：表示图上距离比实地距离缩小的程度，比例尺=图上距离/实际距离;2．太阳离我们非常遥远，因此可以把太阳光近似看成平行光线．在同一时刻，两物体影子之比等于其对应高的比;3．视点：观察事物的着眼点（一般指观察者眼睛的位置）;4.仰（俯）角：观察者向上（下）看时，视线与水平方向的夹角．例A．1:C．1:2例例例短边为_________例A ．1：2B ．1：3C ．1：4D ．1：16考点2：相似三角形的应用（利用相似三角形测高）例6．如图，身高为1.6m 的小明想测量一下操场边大树的高度，他沿着树影BA 由B 到A 走去，当走到C 点时，他的影子顶端正好与树的影子顶端重合，测得 1.4m BC =，.7m 0CA =，于是得出树的高度为（）A ．3.2mB ．4.8mC ．6.4mD ．8m例7．如图，放映幻灯片时，通过光源，把幻灯片上的图形放大到屏幕上．若光源到幻灯片的距离为20cm 光源，到屏幕的距离为40cm ，且幻灯片中图形的高度为8cm ，则屏幕上图形的高度为（）A ．8cmB ．12cmC ．16cmD ．24cm例8．中国教育家孔子周游列国14年，其中10年居卫(卫国即现在的濮阳)，龙湖论语广场有一尊孔子雕像，数学兴趣小组的同学为了测量雕像的高度(AB 顶端A 到水平地面BE 的距离)，在雕像旁边的水平地面上C 处放了一面镜子(平面镜的厚度忽略不计)，组长小丽沿直线BC 后退到点E 处，这时恰好在镜子里看到雕像的顶端A ，此时测得7BC =米，2EC =米，小丽的眼睛距地面的高度 1.6DE =米，则雕像的高度AB =______米．考点3：利用相似三角形的性质求解平行问题例9．如图，12l l ∥，AF ：BF ＝2：5，BC ：CD ＝4：1，则AE ：EC 的值为（）A ．5：2B ．1：4C ．2：1D ．3：2例S S：A．3：5B．3：25C．例11．如图，在长线于点D．若ECD的面积等于例12．如图，在＝12；③ADAB＝OEOB；④ADE A．1个B．2个考点4：网格问题例13．如图，在33⨯的正方形网格中，考点5：分类讨论问题例点的三角形与考点6：最值问题例15．如图，在矩形ABCD 且分别交对角线AC ，直线BC 于点A ．25552-B ．2552+考点7：相似三角形的性质与判定综合问题例16．ABC 的边上有D 7BE =，4EF =，5FC =，则四边形A ．1:3B ．1:4C ．2:5D ．3:8例17．如图，ABC 为等边三角形，相交于点O ，现有如下两个结论：①AP A ．①对，②对B ．①对，②错例EF 折叠得A ．2个B 考点8：相似三角形的性质与判定解答证明题例19．如图，在梯形(1)求证：DE AF=(2)若ABC CDE ∠=∠，求证：2AF BF CE=⋅例20．如图，在ABC 中，AB AC =，(1)求证：BAE CAE ≌；(2)在如图1中，若AE AD =，其它条件不变得到图2，在图点，过点H 作HG AB 交FD 于G ，交DE 于M ．求证：①AF MH AM AE ⋅=⋅；②GF GD =．一、单选题1．（2023·重庆·统考中考真题）若两个相似三角形周长的比为1:4，则这两个三角形对应边的比是（）A ．1:2B ．1:4C ．1:8D ．1:162．（2023·四川巴中·统考中考真题）如图，在Rt ABC △中，6cm 8cm AB BC ==，，D 、E 分别为AC BC 、中点，连接AE BD 、相交于点F ，点G 在CD 上，且12DG GC =::，则四边形DFEG 的面积为（）A ．22cmB ．24cmC ．26cmD ．28cm 3．（2023·山东东营·统考中考真题）如图，ABC 为等边三角形，点D ，E 分别在边BC ，AB 上，60ADE ∠=︒，若4BD DC =， 2.4DE =，则AD 的长为（）A ．1.8B ．2.4C ．3D ．3.24．（2023·安徽·统考中考真题）如图，点E 在正方形ABCD 的对角线AC 上，EF AB ⊥于点F ，连接DE 并延长，交边BC 于点M ，交边AB 的延长线于点G ．若2AF =，1FB =，则MG =（）A ．23B ．352C ．51+D ．105．（2023·黑龙江·统考中考真题）如图，在平面直角坐标中，矩形ABCD 的边5,:1:4AD OA OD ==，将矩形ABCD 沿直线OE 折叠到如图所示的位置，线段1OD 恰好经过点B ，点C 落在y 轴的点1C 位置，点E 的坐标是（）A ．()1,2B ．(-二、填空题6．（2022·辽宁阜新·统考中考真题）如图，在矩形ABCD 中，E 是AD 边上一点，且2AE DE =，BD 与CE 相交于点F ，若DEF 的面积是3，则BCF △的面积是______．7．（2022·山东东营·统考中考真题）如图，在ABC 中，点F 、G 在BC 上，点E 、H 分别在AB 、AC 上，四边形EFGH 是矩形，2,EH EF AD =是ABC 的高．8,6BC AD ==，那么EH 的长为____________．三、解答题8．（2018·陕西·统考中考真题）周末，小华和小亮想用所学的数学知识测量家门前小河的宽．测量时，他们选择了河对岸边的一棵大树，将其底部作为点A ，在他们所在的岸边选择了点B ，使得AB 与河岸垂直，并在B 点竖起标杆BC ，再在AB 的延长线上选择点D 竖起标杆DE ，使得点E 与点C 、A 共线．已知：CB ⊥AD ，ED ⊥AD ，测得BC ＝1m ，DE ＝1.5m ，BD ＝8.5m ．测量示意图如图所示．请根据相关测量信息，求河宽AB ．9．（2023·福建·统考中考真题）如图1，在ABC 中，90,,BAC AB AC D ∠=︒=是AB 边上不与,A B 重合的一个定点．AO BC ⊥于点O ，交CD 于点E ．DF 是由线段DC 绕点D 顺时针旋转90︒得到的，,FD CA 的延长线相交于点M ．(1)求证：ADE FMC △∽△；(2)求ABF ∠的度数；(3)若N 是AF 的中点，如图2．求证：ND NO =．一、单选题A．6B．8 5．如图，已知在ABC中，DE∥①DE AEBC EC=②ADABB CEC=③CECF A．1个6．如图，BD、CE是A．ADEV∽ABCC．BOE△∽COD△7．如图，已知ABC的面积是DEFG1212A．17B．217∠9．如图，直角三角形ABC中，ACB 个．①图中有4个三角形与ACB△相似；②16AE AD二、填空题14．如图，EF分别为矩形ABCD15．如图，点E是平行四边形BF=17．如图，△ABC中，AB＝8cm，AC 以A、P、Q为顶点的三角形与△18．如图，边长为6的正方形ABCD三、解答题20．如图，在ABC 和DEF 中，G ，H 分别是边22．如图，为了估计河的宽度，在河的对岸选定一个目标点23．如图，在ABC 中，点D 24．如图，已知cm,cm,2AD a AC b BC ===（1）试证BFG FEG△△∽（2）求:AP PC．27．如图所示，在等腰三角形ABC中，AE²=AQ·AB求证：(1)∠CAE=∠BAF；(2)CF·FQ=AF·BQ，以B为直角顶点向右作等腰直角28．如图1，已知等边ABC(1)若62AC=，求点D到AB边的距离；=+；(2)如图2，过点B作AD的垂线，分别交AD，CD于点E，F，求证：EF CF BE=，连接CM，CN，若AC (3)如图3，点M，N分别为线段AD，BD上一点，AM BN△的面积．取得最小值时，直接写出ACM。

北师大版九年级上册4.7相似三角形性质(包含答案)

北师大版九年级上册相似三角形的性质〔1〕〔包含答案〕相似三角形的性质〔1〕〔含答案〕一、选择题：1、两个相似三角形的对应高之比为 1：2，那么它们的对应中线之比是〔〕：2 ：3 ：4 ：82、等腰△ABC和△DEF相似，相似比为3：4，那么它们底边上对应高线的比为〔〕A.3：4B.4：3C.1：2 ：13、假设两个相似三角形的对应高的比是 9:16，那么它们对应的对角线的比为〔〕A.9:16B.16:9C.3:4D.4:34、如图，△ABC∽△A'B'C'，AD、BE分别是△ABC的高线和中线，A'D'、B'E'分别是△A'B'C'的高线和中线，且 AD=4，A'D'=3，BE=6，那么B'E'=〔〕3579A. B. C. D.2222第4题图第5题图5、如图，D、E分别是△ABC的边AB、AC上的点，DE//BC，且AD:BD=4:5，那么△ADE与△ABC的对应高的比是〔〕A.1:4B.1:3C.4:5D.4:96、两个相似三角形的相似比是2:7，它们的对应中线的差是25，那么较大的三角形的中线长为〔〕7、如图，四边形DEFG是△ABC的内接矩形，如果△ABC的高线AH长8cm，底边BC的长为10cm，设DG=xcm，DE=ycm，那么y关于x的函数关系式为〔〕1/6北师大版九年级上册相似三角形的性质〔1〕〔包含答案〕A.y4xB.y5xC.y 4x8 D.y5x85454第7题图第8题图8、如图，点光源P在在横杆AB的正上方，AB在灯光下的影子为CD，AB//CD，AB=2m，CD=6m，点P到CD的距离是，那么AB与CD的距离是〔〕A.二、填空题：9、如果两个相似三角形的相似比是1：4，那么这两个三角形的对应高之比是______，对应角平分线之比是_______；10、△ABC∽△A'B'C'，AB1，AB边上的中线CD=4cm，那么A'B'边上的中线AB2C'D'=_____；11、两个相似三角形的对应中线之比是1：3，且较大的三角形最长边是18cm，那么较小三角形的最长边为_____cm；12、顺次连接三角形三边的中点，所形成的三角形与原三角形的对应中线的比是_______；三、解答题：13、如下列图，Rt△ABC∽Rt△DFE，CM，EN分别是边AB，DF上的中线，AC=9cm，CB=12cm，DE=3cm；（1〕求CM，DN的长；2〕CM的值与相似比有什么关系？可得到什么结论？EN2/6北师大版九年级上册相似三角形的性质〔1〕〔包含答案〕14、如图，AF是△ABC的高，点D，E分别在AB，AC上，且DE//BC，DE交AF于点G；AD=10，AB=30，AC=24，GF=12；1〕求AE的长；（2〕求点A到DE的距离；3/6北师大版九年级上册相似三角形的性质〔1〕〔包含答案〕15、如图，在△ABC 中，AB=8，BC=7，AC=6，点D ，E 分别在AB ，AC 上；如果以A ，D ，E 为顶点的三角形和△ABC 相似，且对应角平分线的比是1，试求AD ，AE 的长；416、有一批形状、大小相同的直角三角形不锈钢钢片，如下列图①；在△ABC 中，∠C=90°，BC=3cm ，AC=4cm ；分别采取如图②③所示的两种方法截取一个正方形不锈钢钢片，且使正方形的面积较大；试判断哪种方法更好些，并说明理由；4/6北师大版九年级上册相似三角形的性质〔1〕〔包含答案〕参考答案：1~8 AAADD CDB9、1：4，1：4；10、8cm；11、6；12、1：2；12、〔1〕，；〔2〕CM的值等于相似比；结论：相似三角形对应中线的比等于相似比；EN14、〔1〕AE=8；〔2〕点A到DE的距离是6；15、，AE=2；16、图②的截法更好些；5/6北师大版九年级上册相似三角形的性质〔1〕〔包含答案〕6/6。

北师大版九年级上册数学《相似三角形的性质》图形的相似说课教学复习课件

∴
即
=
=
( 相似三角形的面积比等于相似比的平方 )，
.
∴EC2 = 2，∴EC =
( 负值舍去 ).
∴BE = BC – EC = 2 –
即 △ABC 平移的距离为 2 –
，
.
C
F
4.7.2 相似三角形的周长比、面积比的性质
温馨提示
相似多边形周长的比等于相似比，面积比等于相似比的平方.
4.7.2 相似三角形的周长比、面积比的性质
△A′B′C′，CD 和 C′D′ 分别是它们的立柱.
(2) 如果 CD = 1.5 cm，那么模型房的房梁立柱有多高？
解：(2) 由 CD:C′D′ = 1:2，得 C′D′ = 2CD = 3 cm，即模型房的房梁立柱
高 3 cm.
4.7.1 相似三角形中对应线段的性质
如图，已知△ABC∽△A′B′C′， △ABC 与△A′B′C′ 相似比为 k ( k > 0 )，
∴AD : A′D′ = k.
∴AF : A′F′ = k.
A
符号语言：
∵△ABC∽△A′B′C′，
且∠BAE =∠EAC，∠B′A′E′ =∠E′A′C′，
∴AE : A′E′ = k.
B
A′
D
B′ D′ E′ F′
E F
C′
C
4.7.1 相似三角形中对应线段的性质
温馨提示
这些结论以后在解决问题过程中能作为定理直接用.
如果是四边形呢？
你能通过类比得出
四边形的结论吗？
4.7.2 相似三角形的周长比、面积比的性质
例2
如图，四边形 ABCD ∽四边形 A′B′C′D′，相似比为 k ( k > 0 ).

4-7-2 相似三角形周长和面积的性质-北师大版数学九年级上册

解：根据题意，可知EG∥AB. ∴∠GEC=∠B，∠EGC=∠A. ∴△GEC∽△ABC（两角分别相等的两个三角形相似）.
SGEC S ABC
EC BC
2
EC 2
（相似三角形的面积比等于相似的平方比）
BC 2
即
1 2
=
EC 2 22
∴EC2=2.∴EC=
2 .∴BE=BC－EC= 2
2，
即△ACB平移的距离为 2 2 .
C
∴ AB AC BC =k
AB AC BC
∴AB kAB，AC kAC，BC=kBC A
B
C′
∴C△ABC=AB+AC+BC=k(A′B′+A′C′+B′C′)
C△A′B′C′= A′B′+A′C′+B′C′
A′
B′
∴ C△ABC =k C△A B C
相似三角形的周长比等于相似比
C C′
A D
B
A′
B′
D′
分别作BC，BC边上的高A′D，AD，则 AD = k
因此， S△ABC
S△A B C
=
1 BC AD 2 1 BC AD
BC BC
AD AD
AD
k k=k 2
2
相似三角形的面积比等于相似比的平方
相似三角形的性质(2)
C C′
A
B
A′
B′
相似三角形的周长的比等于相似比，面积比等于相似比的平方.
4
相似三角形周长和面积的性质
北师版九年级上册
情境导入
(1)如图，△ABC∽△A'B'C' ，相似比为2，△ABC与

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

相似三角形的性质定理（B ）
一、选择题
1．已知△ABC∽△DEF，若△ABC 与△DEF 的相似比为3∶4，则△ABC 与△DEF 的周长之比为( )
A ．4∶3
B ．3∶4
C ．16∶9
D ．9∶16
2．已知△ABC∽△A′B′C′且AB A′B′＝1
2，则S △ABC ∶S △A ′B ′C ′为( )
A ．1∶2
B ．2∶1
C ．1∶4
D ．4∶1 3．下列命题中错误的是( )
A ．相似三角形的周长比等于对应中线的比
B ．相似三角形对应高的比等于相似比
C ．相似三角形的面积比等于相似比
D ．相似三角形对应角平分线的比等于相似比
4．已知两个三角形相似，对应中线之比为1∶4，那么对应周长之比为( ) A ．1∶2 B ．1∶16 C ．1∶4 D ．无法确定
5．三角尺在灯泡O 的照射下在墙上形成的影子如图所示．若OA ＝20 cm ，OA ′＝50 cm ，则这个三角尺的周长与它在墙上形成的影子的周长的比是( )
A ．5∶2
B ．2∶5
C ．4∶25
D ．25∶4
6.△ABC∽△A1B1C1，且相似比为，△A1B1C1∽△A2B2C2，且相似比为，则△ABC 与△A2B2C2的相似比为( )
A. B. C.或 D.
7.如图，△ABC ， AB=12，AC=15，D为AB上一点，且AD= AB ，在AC上取一点E，使以A、D、E为顶点的三角形与ABC相似，则AE等于( )
A. B.10 C.或10 D.以上答案都不对
8.如图，△ADE∽△ABC，若AD=1，BD=2，则△ADE与△ABC的相似比是( )
A.1：2
B.1：3
C.2：3
D.3：2
二、填空题
9．已知△ABC与△DEF相似且周长比为2∶5，则△ABC与△DEF的相似比为________．
10．如图，D，E分别是△ABC的边AB，AC上的中点，则S△ADE∶S△ABC＝________.
11．某小区广场有两块相似三角形的草坪，相似比为2∶3，面积差是30 m 2，则小区广场两块相似三角形的面积分别是____________．
12.两个三角形相似，其中一个三角形的两个内角是40°、60°．那么另一个三角形的最大角是________度，最小角是________度．三、解答题
13．已知△ABC∽△A′B′C′，AB A′B′＝12，AB 边上的中线CD ＝4 cm ，△ABC 的周长
为20 cm ，△A ′B ′C ′的面积是64 cm 2，求： (1)A′B′边上的中线C′D′的长； (2)△A′B′C′的周长； (3)△ABC 的面积．
14．某施工地在道路拓宽施工时，遇到这样一个问题，马路旁边原有一个面积为100平方米，周长为80米的三角形绿化地，由于马路拓宽绿地被消去了一个角△ADE，变成了一个梯形BCED ，原绿化地一边AB 的长由原来的30米缩短成BD 长18米，现在的问题是：被消去的部分面积有多大？它的周长是多少？
15．(乐山中考)如图，在□ABCD中，对角线AC，BD交于点O.M为AD中点，连接CM 交BD于点N，且ON＝1.
(1)求BD的长；
(2)若△DCN的面积为2，求四边形ABCM的面积．
16．(绍兴中考改编)课本中有一道作业题：有一块三角形余料ABC，它的边BC＝120 mm，高AD＝80 mm.要把它加工成正方形零件，使正方形的一边在BC上，其余两个顶点分别在AB，AC上．问加工成的正方形零件的边长是多少mm？小颖解得此题的答案为48 mm，小颖善于反思，她又提出了如下的问题．如果原题中要加工的零件是一个矩形，且此矩形是由两个并排放置的正方形所组成，如图，此时，这个矩形零件的两条边长又分别为多少mm？请你计算．
参考答案
一、选择题
1．B 2.C 3.C 4.C 5.B 6.A 7.C 8.B 二、填空题
9.2∶5 10.1∶4 11.24 m 2、54 m 2 12.80，40．三、解答题
13.(1)∵△ABC∽△A′B′C′，AB A′B′＝12，AB 边上的中线CD ＝4 cm ，∴CD C′D′＝1
2.
∴C ′D ′＝2CD ＝4×2＝8(cm)．∴A ′B ′边上的中线C′D′的长为8 cm.(2)∵△ABC∽△A′B′C′，AB A′B′＝12，△ABC 的周长为20 cm ，∴C △ABC C △A ′B ′C ′＝1
2，
即
20
C △A ′B ′C ′＝1
2.∴C △A ′B ′C ′＝20×2＝40(cm)．∴△A ′B ′C ′的周长为40
cm.(3)∵△ABC∽△A′B′C′，AB A′B′＝12，△A ′B ′C ′的面积是64 cm 2
，∴
S △ABC S △A ′B ′C ′＝(12)2＝14.∴S △ABC 64＝1
4.∴S △ABC ＝64÷4＝16(cm 2)．∴△ABC 的面积是16 cm 2. 14.由题意可得DE∥BC，则△ADE∽△ABC.故AD AB ＝DE BC ＝AE AC ＝C △ADE
C △ABC .∵AB 的长由原来的
30米缩短成BD 长18米，∴AD ＝12 m ．∴1230＝C △ADE C △ABC ＝C △ADE 80.解得C △ADE ＝32 m.S △ADE S △ABC ＝(25)
2
＝425＝S △ADE
100.解得S △ADE ＝16 m 2.∴绿化地被消去的面积为16 m 2，周长为32 m ． 15.(1)∵四边形ABCD 是平行四边形，∴AD ∥BC ，AD ＝BC ，OB ＝OD.∴∠DMN＝∠BCN，∠MDN ＝∠NBC.∴△MND∽△CNB.∴MD BC ＝DN BN .∵M 为AD 中点，∴MD ＝12AD ＝12BC ，即MD
BC
＝
12.∴DN BN ＝12
，即BN ＝2DN.设OB ＝OD ＝x ，则有BD ＝2x ，BN ＝OB ＋ON ＝x ＋1，DN ＝x －1，∴x ＋1＝2(x －1)．解得x ＝3，∴BD ＝2x ＝6.(2)∵△MND∽△CNB，且相似比为1∶2，∴MN ∶CN ＝1∶2.∴S △MND ∶S △CND ＝1∶2，∵△DCN 的面积为2，∴△MND 的面积为1.∴△MCD 的面积为3.∵S ABCD ＝AD·h，S △MCD ＝12MD ·h ＝1
4
AD ·h ，∴S □ABCD ＝4S △MCD ＝12.∴S
□ABCM
＝S □ABCD －S △MCD ＝12－3＝9.
16.设矩形的边长PN ＝2y mm ，则PQ ＝y mm ，由条件可得△APN∽△ABC，∴PN BC ＝AE
AD ，
即2y 120＝80－y 80.解得y ＝2407.∴PN ＝2407×2＝4807(mm)．答：这个矩形零件的两条边长分别为2407 mm ，480
7
mm.。