XU8--2010高三一轮复习达标测试卷选修八
吉林省实验中学2010高三数学第八次高考模拟考试 理 新人教版

吉林省实验中学2010年高三年级第九次模拟考试数学试题(理科)一、选择题(每小题5分,共60分)1.已知全集U Z =,2{1,0,1,2},{|}A B x x x =-==,则U A C B 为( )A .{1,2}-B .{1,0}-C .{0,1}D .{1,2}2.已知复数z 的实部为1-,虚部为2,则5i z=( )A .2i -B .2i +C .2i --D .2i -+ 3.直线1y x =+与圆221x y +=的位置关系为( )A .相切B .相交但直线不过圆心C .直线过圆心D .相离4.已知两条直线,m n ,两个平面,αβ,给出下面四个命题: ①//,m n m n αα⊥⇒⊥ ②//,,//m n m n αβαβ⊂⊂⇒ ③//,////m n m n αα⇒ ④//,//,m n m n αβαβ⊥⇒⊥ 其中正确命题的序号是( )A .①③B .②④C .①④D .②③ 5.已知命题:p x ∀∈R ,sin 1x ≤,则( )A .:p x ⌝∃∈R ,sin 1x ≥B .:p x ⌝∀∈R ,sin 1x ≥C .:p x ⌝∃∈R ,sin 1x >D .:p x ⌝∀∈R ,sin 1x >6.锅中煮有芝麻馅汤圆6个,花生馅汤圆5个,豆沙馅汤圆4个,这三种汤圆的外部特征完全相同。
从中任意舀取4个汤圆,则每种汤圆都至少取到1个的概率为 ( )A .891B .2591C .4891D .60917.在平面直角坐标系xOy 中,双曲线中心在原点,焦点在y 轴上,一条渐近线方程为20x y -=,则它的离心率为( )A B .2C D .28.若对于任意实数x ,有3230123(2)(2)(2)x a a x a x a x =+-+-+-,则2a 的值为( )S =0,T =0,n =0T >S ?S = S +4输出T结 束n = n +2T =T + n是否A .3B .6C .9D .129.执行如图所示的程序框图,输出的T 等于 ( ) A .10 B .15 C .20 D .3010.右图是一个几何的三视图,根据图中的数据, 计算该几何体的表面积为 ( ) A .15π B .18π C .22π D .33π11.已知二次函数2()f x ax bx c =++的导数为'()f x ,'(0)0f >,对于任意实数x 都有()0f x ≥,则(1)'(0)f f 的最小值为 ( )A .3B .52C .2D .3212.在平面直角坐标系xOy ,已知平面区域{(,)|1,A x y x y =+≤且0,0}x y ≥≥,则平面区域{(,)|(,)}B x y x y x y A =+-∈的面积为( )A .2B .1C .12D .14二、填空题(每小题解5分,共20分)13.已知向量(0,1,1)a =-,(4,1,0)b =,||29a b λ+=且0λ>,则λ= .14.某校准备召开高中毕业生代表会,把6个代表名额分配给高三年级的3个班,每班至少一个名额,不同的分配方案共有 种. 15.已知正四棱柱ABCD —A 1B 1C 1D 1的底面ABCD 边长为1,高AA 1=2,它的八个顶点都在同一球面上,那么球的半径是 . 16.定义一种运算“*”,它对正整数n 满足以下运算: (1)2*1001=1;侧视图 4 35俯视图·(2)]1001)2[(31001)22(*⋅=*+n n ,则2008*1001的值是 .三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤) 17.(本小题满分12分)已知向量m ),cos ,(sin A A = n )sin ,(cos B B =, m .n C B A C ,,,且2sin =分别为△ABC 的三边a ,b ,c 所对的角. (Ⅰ)求角C 的大小;(Ⅱ)若sin A , sin C , sin B 成等比数列, 且18)(=-⋅AC AB CA , 求c 的值. 18.(本小题满分12分)“ 五·一”黄金周某旅游公司为3个旅游团提供4条旅游线路,每个旅游团任选其中一条旅游线路.(Ⅰ)求3个旅游团选择3条不同的线路的概率; (Ⅱ)求恰有2条线路被选择的概率; (Ⅲ)求选择甲线路的旅游团个数的期望. 19.(本小题满分12分)如图,在底面为直角梯形的四棱锥,//,BC AD ABCD P 中-,90︒=∠ABC平面⊥PA ABCD ,32,2,3===AB AD PA ,6=BC(Ⅰ)求证:;PAC BD 平面⊥(Ⅱ)求二面角A BD P --的大小.N20.(本小题满分12分)已知向量OA → =(2 2 ,0),O 是坐标原点,动点 M 满足:| OM → + OA → |+| OM →-OA →| = 6。
《高考调研》高三数学第一轮复习 第八章《直线和圆的方程》课件8-3

121 +8)= . 4
• 探究1 (1)确定Ax+By+C≥0表示的区域有两种方法.① 试点法,一般代入原点,②化为y≥kx+b(y≤kx+b)的形式 .不等式y≥kx+b表示的区域为直线y=kx+b的上方,不 等式y≤kx+b表示的区域为直线y=kx+b的下方. • (2)在封闭区域内找整点数目时,若数目较小时,可画网 格逐一数出;若数目较大,则可分x=m逐条分段统计.
• 1.(08·全国卷Ⅰ)点A(1,1),B(-1,b)位于 直线2x-3y+4=0的同侧,则实数b的取值 范围是________.
2 答案 b< . 3
2 . 已 知 函 数 f(x) = x2 - 5x + 4 , 则 不 等 式 组
fx-fy≥0, 1≤x≤4
对应的平面区域为(
• 1.二元一次不等式表示平面区域 • (1)一般地,二元一次不等式Ax+By+C>0在平面直角坐标 系中表示直线Ax+By+C=0某一侧所有点组成的 . • (2)由于对在直线Ax+By+C=0同一侧的所有点(x,y),把 它的坐标(x,y)代入Ax+By+C,所得到实数的符号都 ,所以只需在此直线的某一侧取一个特殊点(x0,y0), 从 集合 Ax0+By0+C的 即可判断Ax+By+C>0表示直线哪一 侧的平面区域. 相同符号
3 【答案】 ;(-∞,-2]∪[1,+∞) 2
பைடு நூலகம்
• 题型三 线性规划实际应用 • 例3 (2010·广东卷,理)某营养师要为某个儿童预订午餐 和晚餐.已知一个单位的午餐含12个单位的碳水化合物 ,6个单位的蛋白质和6个单位的维生素C;一个单位的晚 餐含8个单位的碳水化合物,6个单位的蛋白质和10个单 位的维生素C.另外,该儿童这两餐需要的营养中至少含64 个单位的碳水化合物,42个单位的蛋白质和54个单位的 维生素C. • 如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那 么要满足上述的营养要求,并且花费最少,应当为该儿 童分别预订多少个单位的午餐和晚餐?
浙江省平湖市乍浦中学2010届高三数学高考模拟周练试题八新人教版
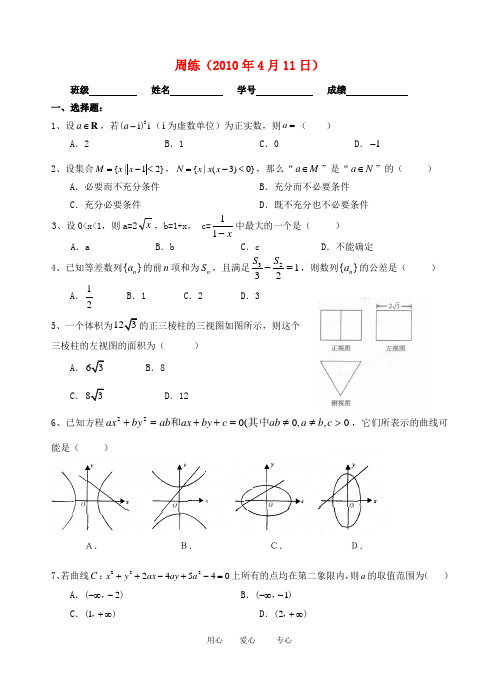
用心 爱心 专心 周练(2010年4月11日) 班级 姓名 学号 成绩 一、选择题: 1、设aR,若2iia()(i为虚数单位)为正实数,则a( ) A.2 B.1 C.0 D.1
2、设集合{|12}Mxx,{|(3)0}Nxxx,那么“aM”是“aN”的( ) A.必要而不充分条件 B.充分而不必要条件 C.充分必要条件 D.既不充分也不必要条件 3、设0A.a B.b C.c D.不能确定 4、已知等差数列{}na的前n项和为nS,且满足32132SS,则数列{}na的公差是( )
A.12 B.1 C.2 D.3 5、一个体积为123的正三棱柱的三视图如图所示,则这个 三棱柱的左视图的面积为( ) A.63 B.8
C.83 D.12 6、已知方程0,,0(022cbaabcbyaxabbyax其中和,它们所表示的曲线可能是( )
A. B. C. D. 7、若曲线C:22224540xyaxaya上所有的点均在第二象限内,则a的取值范围为( ) A.2(,) B.1(,) C.1(,) D.2(,) 用心 爱心 专心
8、已知函数2xfxx(),lngxxx(),1hxxx()的零点分别为123xxx,,,则123xxx,,
的大小关系是( ) A.123xxx B.213xxx C.132xxx D.321xxx
9、在棱长为1的正四面体ABCD中,E是BC的中点,则AECD( ) A.0 B.12 C.12 D.14
10、设1a,2a,…,na是1,2,…,n的一个排列,把排在ia的左边..且比ia小.的数的个数称为ia
的顺序数(12in,,,).如在排列6,4,5,3,2,1中,5的顺序数为1,3的顺序数为0.则在1至8这八个数字构成的全排列中,同时满足8的顺序数为2,7的顺序数为3,5的顺序数为3的不同排列的种数为( ) A.48 B.96 C.144 D.192 二、填空题:
2010年新课标省市高三数学模拟题分类:第八节__优化重组综合测试卷

2010年新课标省市高三数学模拟题分类第八节优化重组综合测试卷本试卷分第I卷(选择题)和第II卷(非选择题)两部分,其中第II卷第(22)题~第(24)题为选考题,其它题为必考题.考生作答时,将答案答在答题卡上,在本试卷上答题无效.考试结束后,将本试卷和答题卡一并交回.参考公式:锥体体积公式其中为底面积,为高球的表面积公式、体积公式、其中为球的半径样本数据x1,x2, …,x n的标准差柱体体积公式其中为底面积,为高第I卷一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的,请用2B铅笔把答题卡上对应题目的答案标号涂黑.(1)(2010哈尔滨六中二模)若集合,则等于(A)(B)(C)(D){1}(2)(2010辽宁沈阳一模)在等差数列中,为前项和,且<0,,则中最小的是(A)(B)(C)或(D)(3)(2010宁夏银川一中二模)设m、n是两条不同的直线,、β是两个不同的平面,则下列命题中正确的是(A)若m∥n,m∥,则n∥(B)若⊥β,m∥,则m⊥β(C)若⊥β,m⊥β,则m∥(D)若m⊥n,m⊥,n⊥β,则⊥β(4)(2010辽宁丹东一模)直线被圆所截得的弦长为科网(A)1 (B)2 (C)(D)(5)(2010辽宁大连二模)函数的图象恒过定点A,且点A在直线上,则的最小值为(A)12 (B)10 (C)8 (D)14(6)(2010辽宁丹东一模)在等差数列中,,,则的展开式中含项的系数是该数列的(A)第13项(B)第9项(C)第7项(D)第6项(7)(2010浙江菱湖中学二模)把函数的图像适当迹换就可以得到的图像,这种变换可以是(A)沿x轴方向向右平移个单位(B)沿x轴方向向左平移个单位(C)沿x轴方向向右平移个单位(D)沿x轴方向向左平移个单位(8)(2010山东聊城三中二模)已知抛物线的焦点与双曲线的右焦点重合,抛物线的准线与轴的交点为,点在抛物线上且,则的面积为(A)4 (B)8 (C)16 (D)32(9)(2010北京宣武区一模)设函数的定义域为,若对于给定的正数,定义函数,则当函数时,定积分的值为(A)(B)(C)(D)(10)(2010辽宁丹东二模)有编号为1,2,…,1000的产品,现需从中抽取所有编号能被3整除的产品作为样品进行检验,下面是四位同学设计的输出样品编号的程序框图:其中正确程序框图的个数是(A)0 (B)1 (C)2 (D)3(11)(2010辽宁沈阳三模)设奇函数在上是减函数,且,若存在使不等式成立,则实数的取值范围是(A)(B)(C)(D)(12)(2010北京英才苑模拟)已知、都是定义在R上的函数,,,,,在有穷数列(=1,2,…,10)中,任意取前项相加,则前项和大于的概率是(A)(B)(C)(D)第II卷本卷包括必考题和选考题两部分,第(13)题~第(21)题为必考题,每个试题考生都必须做答.第(22)题~第(24)题为选考题,考生根据要求做答.二、填空题:本大题共4小题,每小题5分,共20分.请把答案填在答题卡相应的位置上.(13)(2010辽宁大连一模)已知复数和复数,则复数= ;(14)(2010东北育才、大连育明三模)如图为一三角形数阵,它满足:①第行首尾两数均为;②表中的递推关系类似杨辉三角(三角形数阵中的数为其肩上两数之和),则第行(第2个数是;12 23 4 34 7 7 45 11 14 11 56 16 25 25 16 6… … … … … … …(15)(2010辽宁丹东一模)下图是一个空间几何体的三视图,则该几何体的体积是;(16)(2010哈尔滨九中四模)将5名上海世博会的志愿者分配到中国馆、美国馆、英国馆工作,要求每个国家馆至少分配一名志愿者且其中甲、乙两名志愿者不同时在同一个国家馆工作,则不同的分配方案有种。
江西八校高三下学期联考试卷数学文

抚州一中 赣州一中1. 2. 3. 吉安一■中2010年江西省 萍乡中学宜春中学高三数学试卷(文)命题人:赣州一中徐义华 、选择题(本大题共 12小题,每小题 已知集合M A. B. “ ab 4 ” 5分,共 2 2 x y_ 16 9 (4,0),(0,3) 是“直线2x A.充分不必要条件 B.C.充要条件D. 已知数列{a n }为等差数列,且 A. ,3 B. ,3 C. ay a 1 ,N C. 新余-中联合考试 上饶县中(2010.4 )九江一中刘建华杨相春 60分. 4,3 D. 每小题只有一个选项符合题目要求)0与直线bx 2y 必要不充分条件既不充分也不必要条件 4,4 2 0平行” 的() a 7 a 13 4 ,贝U tan (a ? &2).3 D. 为了了解某次考试中 1000名学生的成绩,运用简单随机抽样的方法从中抽出一个容量为 100的样本,则该次考试中的学生甲被第 是( ) A.二 1000 4. 100次抽到的概率及在整个过程中被抽到的概率分别 C.丄丄100010 5.若在(3x 2丄 B.丄丄 100 10'10 1 3)n的展开式中含有常数项,则正整数 2x 3 D. --------- -------- --- 10001000 n 取得最小值时常数项为(135 A. B. 2 135 C. 1352 D. 135 6•设定义在R 上的函数y f (x)满足 f(x) f(x 2) 12,且 f (2010) 2,则 f (0)(A. 12B.6C.3D.2 7 •平面的斜线AB 交 于点B,过定点A 的动直线l 与AB 垂直,且交 于点C,则动点轨迹是( ) A. 一条直线 B. 2 2 8 .已知双曲线乞y_ 2 .2a b的右支有且只有一个交点, C. 椭圆 D.双曲线的一支 1(a o,b 0)的右焦点为F ,若过点F 且倾斜角为则此双曲线离心率的取值范围是( A. (1,2] B. (1,2) C. (2, ) D. [2,) 600的直线与双曲线uuu uuu uuur9. O 为 ABC 内的一点, AOB = 150o , AOC =120o ,向量 OA,OB,OC 的模分别为 2、 uur uuu uuu 1、3,若OC mOA nOB ,则实数m,n 的值为( )A. m 3,n 3.3B. C. m3.3, n 3D.二、填空题(本大题共 4小题,每小题4分,共16分•请将正确答案填写在答题卡相应横 线上)13•已知 tan( ) — ,tan() —,贝U ~OS Si 的值为 ____________ .54 4 cos sinx y 014. _________________________________________________________________________ 若不等式组 x 2y 3表示的平面区域是三角形,则实数 a 的取值范围是 ________________________ .y a(x 3)15. 从0、1、2、3、4、5这6个数中任取3个数字组成一个没有重复数字的三位数,且这个 三位数能被4整除,则这样的三位数的个数为 __________ . 16. 已知函数f x ,如果对任意一个三角形,只要它的三边长 a,b,c 都在f x 的定义域内,就有f a , f b ,f c 也是某个三角形的三边长,则称 f x 为“保三角形函数”.在函数①f 1 x '、x ,②f 2 x x ,③f 3 x x 2中,其中 ________ 是“保三角形函数”(填上正确的函数序号)m 3,n 3、、3 m 6, n 3 . 3cos —x,x 02 的图像中存在关于原点对称的点的组数为A. 1 Iog 4(xB. 2C. 31),x 0D. 411 对任意x1,2 及 y2,3 ,不等式xy( )A. a1 B. a3 C. a 1812 已知函数 f(x)(x R)满足f (1)1,且 集为()A. x1 x 1B.x x 12 _ 2ax 2y 恒成立,贝y 实数a 的取值范围是D.3 a 1f(x) 的导函数f (x)1-,则 f(x)x 1--的解2 2 2C.x x1或x 1 D.x x 1io .函数 f (x)三、解答题(本大题共6小题,共计74分,解答应写出文字说明,证明过程或演算步骤)17•已知锐角ABC中内角A,B,C的对边分别为a,b,c,向量m (2sin B, 3),r2B LT rn (2cos 1,cos2B),且m n .(1)求B的大小;(2)若sinA,sinB,sinC成等差数列,且BA (AC AB) 18,求b的值•18. 某中学数学组办公室有5名教师,只有3台电脑供他们使用,教师是否使用电脑是相互独立的•1 2 2①某上午某一时间段该办公室中的甲、乙、丙三位教师需要使用电脑的概率分别是-4 35 求这一时间段甲、乙、丙三位教师中恰有两位教师使用电脑的概率;1②某下午某一时间段每位教师需要使用电脑的概率都是-,求这一时间段该办公室电脑无法3满足需求的概率•19. 如图,正三棱柱ABO A1B1C的所有棱长都为2, D为CC中点•(I)求证:AB丄面A1BDA (H)求二面角A- AD— B的大小;(川)求点C到平面ABD的距离•20.已知S n 为数列{a n }的前n 项和,且S n 2% n 2 3n 2(n N*). ① 求证:数列{a n 2n }为等比数列;② 设b n a n cosn (n N*),求数列{g }的前n 项和T n .21 •已知函数 f(x) x 3 3ax 2(a R).这样的X 。
2010年江西省高三八校联考语文试卷

命题人:九江一中权小平萍乡中学刘忠萍第1卷(选择题共36分)本卷共12小题,每小题3分,共36分。
在每小题给出的四个选项中,只有一项符合题目要求。
一、(15分,每小题3分)1.下列加点字读音全都正确的一组是( )2.下列各组词语中有两个错别字的一项是( )A.簿册狼藉绿草如荫以点带面B.宏图融资漫不经心真知卓见C.眉稍咆啸前仆后继坐无虚席D.藩衍调和书声琅琅忧柔寡断3.下列各句中,加点的词语使用恰当的一句是( )A.这位代表说的虽不是什么崇论宏议....,但他的话发自肺腑,句句实在,没有套话和假话,因此我们更加重视。
B.改革开放的成果越来越令人瞩目,许多来中国的人都有感于二十几年来中国发生的石破天...惊.的变化。
C.旧中国,洋人凭借为所欲为的“领事裁判权”,画地为牢....,各自为政,在租界里盖洋房,开银行,走私鸦片,贩卖军火。
D.此次国际金融危机对我国经济的发展既是挑战,又是机遇,只要顺水推舟....,及时调整,应对得当,就能化不利为有利。
4.下列句子中没有语病的一项是( )A.普希金一生历尽磨难,他追求真善美的自由天性,他所处的沙皇统治下的黑暗现实和他产生了不可调和的矛盾。
B.作者为了使作品情节曲折、生动,牵肠挂肚,常常在戏剧、电影或其他文学作品中设置一系列悬念。
C.以生漆为底层的彩陶的保护是世界性难题,如何将秦俑艳丽的彩绘保存下来,目前己成为文物工作的当务之急。
D.再创造活动在诗的欣赏活动中不仅是允许的,而且是受到鼓励的。
这种想象活动可以使欣赏者在想象中创造出与自己有关的动人的画面来。
5.在下列横线上填上相关语句,最为连贯的一项是( )有人说, _____________;有人说,_____________;有人说,_____________有人说……他,就是钱学森,一个充满传奇、更孕育感动的中国人!①他有毅力,在功成名就颐享天伦之乐时,他孜孜不倦。
②他有大爱,在诬陷迫害与艰难险阻中,他痴心不改。
2020人教版《导与练》高考英语一轮复习课件选修8 Unit 1 A land of diversity 单元知识检测
you want.
答案:1.by means of 2.The majority of 3.team up with
4.I’m
(申请) a part-time job at a foreign company
in my city during the summer vacation.
5.Gazing up into his eyes,she seemed to
(thank) for all
of the good in your life.
答案:8.majority 9.by 10.thankful
Ⅱ.单句语法改错 1.The gold medal will be awarded to whatever wins the first place in
the bicycle race.(2018天津卷) 2.We express our thoughts in means of words and body language. 3.The possibility never occurred me that I would win the first in
8.A great many of houses were knocked down by the earthquake. 9.Having punished by his boss,he was in a very bad mood. 10.To team up the big company is the only means of solving the
exams. 4.It’s apparently to all of us that the boy is very clever.
数学-高三-2010年全国高中数学联合竞赛一试试题参考答案及评分标准(B卷)2010.10
2010年全国高中数学联合竞赛一试 试题参考答案及评分标准(B 卷)说明:1. 评阅试卷时,请依据本评分标准. 填空题只设8分和0分两档;其他各题的评阅,请严格按照本评分标准的评分档次给分,不要增加其他中间档次.2. 如果考生的解答方法和本解答不同,只要思路合理、步骤正确,在评卷时可参考本评分标准适当划分档次评分,解答题中第9小题4分为一个档次,第10、11小题5分为一个档次,不要增加其他中间档次。
一、填空题(本题满分64分,每小题8分) 函数x x x f 3245)(---=的值域是 ]3,3[-.解:易知)(x f 的定义域是[]8,5,且)(x f 在[]8,5上是增函数,从而可知)(x f 的值域为]3,3[-.已知函数x x a y sin )3cos (2-=的最小值为3-,则实数a 的取值范围是 1223≤≤-a .解:令t x =sin ,则原函数化为t a at t g )3()(2-+-=,即 t a at t g )3()(3-+-=.由3)3(3-≥-+-t a at ,0)1(3)1(2≥----t t at , 0)3)1()(1(≥-+--t at t 及01≤-t 知03)1(≤-+-t at 即3)(2-≥+t t a (1) 当1,0-=t 时(1)总成立;对20,102≤+<≤<t t t ; 对041,012<+≤-<<-t t t . 从而可知1223≤≤-a .双曲线122=-y x 的右半支与直线100=x 围成的区域内部(不含边界)整点(纵横坐标均为整数的点)的个数是 9800 .解:由对称性知,只要先考虑x 轴上方的情况,设)99,,2,1( ==k k y 与双曲线右半支于k A ,交直线100=x 于kB ,则线段kk B A 内部的整点的个数为99k -,从而在x 轴上方区域内部整点的个数为991(99)99494851k k =-=⨯=∑.又x 轴上有98个整点,所以所求整点的个数为 98009848512=+⨯. 已知}{n a 是公差不为0的等差数列,}{n b 是等比数列,其中3522113,,1,3b a b a b a ====,且存在常数βα,使得对每一个正整数n 都有βα+=n n b a log ,则=+βα3.解:设}{n a 的公差为}{,n b d 的公比为q ,则,3q d =+ (1)2)43(3q d =+, (2)(1)代入(2)得961292++=+d d d ,求得9,6==q d .从而有 βα+=-+-19log )1(63n n 对一切正整数n 都成立,即βα+-=-9log )1(36n n 对一切正整数n 都成立.从而βαα+-=-=9log 3,69log ,求得 3,33==βα,333+=+βα.函数)1,0(23)(2≠>-+=a a a a x f xx 在区间]1,1[-∈x 上的最大值为8,则它在这个区间上的最小值是41-.解:令,y a x=则原函数化为23)(2-+=y y y g ,)(y g 在3(,+)2-∞上是递增的.当10<<a 时,],[1-∈a a y , 211max 1()32822g y a a a a ---=+-=⇒=⇒=,所以412213)21()(2min -=-⨯+=y g ; 当1>a 时,],[1a a y -∈, 2823)(2max =⇒=-+=a a a y g ,所以412232)(12min -=-⨯+=--y g .综上)(x f 在]1,1[-∈x 上的最小值为41-.两人轮流投掷骰子,每人每次投掷两颗,第一个使两颗骰子点数和大于6者为胜,否则轮由另一人投掷.先投掷人的获胜概率是 1217.解:同时投掷两颗骰子点数和大于6的概率为1273621=,从而先投掷人的获胜概率为+⨯+⨯+127)125(127)125(1274217121442511127=-⨯=.正三棱柱111C B A ABC -的9条棱长都相等,P 是1CC 的中点,二面角α=--11B P A B ,则=αsin4 .解一:如图,以AB 所在直线为x 轴,线段AB 中点O 为原点,OC 所在直线为y 轴,建立空间直角坐标系.设正三棱柱的棱长为2,则)1,3,0(),2,0,1(),2,0,1(),0,0,1(11P A B B -,从而,)1,3,1(),0,0,2(),1,3,1(),2,0,2(1111--=-=-=-=B A B .设分别与平面P BA 1、平面P A B 11垂直的向量是),,(111z y x m =、),,(222z y x n =,则⎪⎩⎪⎨⎧=++-=⋅=+-=⋅,03,022111111z y x BP m z x BA ⎪⎩⎪⎨⎧=-+-=⋅=-=⋅,03,022221211z y x P B n x A B由此可设 )3,1,0(),1,0,1(==, 所以cos m n m n α⋅=⋅,2cos cos 4αα=⇒=.所以410sin =α.解二:如图,PB PA PC PC ==11, . 设B A 1与1AB 交于点,O 则1111,,OA OB OA OB A B AB ==⊥ . 11,,PA PB PO AB =⊥因为 所以从而⊥1AB 平面B PA 1 .过O 在平面B PA 1上作P A OE 1⊥,垂足为E . 连结E B 1,则EO B 1∠为二面角11B P A B --的平面角. 设21=AA ,则易求得3,2,5111=====PO O B O A PA PB .在直角O PA 1∆中,OE P A PO O A ⋅=⋅11,即56,532=∴⋅=⋅OE OE.OEPC 1B 1A 1CBA又554562,222111=+=+=∴=OE O B E B O B .4105542sin sin 111===∠=E B O B EO B α.方程2010=++z y x 满足z y x ≤≤的正整数解(x,y,z )的个数是 336675 .解:首先易知2010=++z y x 的正整数解的个数为 1004200922009⨯=C .把2010=++z y x 满足z y x ≤≤的正整数解分为三类: (1)z y x ,,均相等的正整数解的个数显然为1;(2)z y x ,,中有且仅有2个相等的正整数解的个数,易知为1003; (3)设z y x ,,两两均不相等的正整数解为k . 易知 100420096100331⨯=+⨯+k , 110033*********-⨯-⨯=k200410052006123200910052006-⨯=-⨯+-⨯=, 3356713343351003=-⨯=k . 从而满足z y x ≤≤的正整数解的个数为 33667533567110031=++. 二、解答题(本题满分56分)9.(本小题满分16分)已知函数)0()(23≠+++=a d cx bx ax x f ,当10≤≤x 时,1)(≤'x f ,试求a 的最大值.解一: ,23)(2c bx ax x f ++='由 ⎪⎪⎩⎪⎪⎨⎧++='++='='cb a fc b a f c f 23)1(,43)21(,)0( 得 (4分))21(4)1(2)0(23f f f a '-'+'=. (8分)所以)21(4)1(2)0(23f f f a '-'+'=)21(4)1(2)0(2f f f '+'+'≤ 8≤,38≤a . (12分)又易知当m x x x x f ++-=23438)((m 为常数)满足题设条件,所以a 最大值为38.(16分)解二:c bx ax x f ++='23)(2. 设1)()(+'=x f x g ,则当10≤≤x 时,2)(0≤≤x g .设 12-=x z ,则11,21≤≤-+=z z x .14322343)21()(2++++++=+=c b az b a z a z g z h . (4分)容易知道当11≤≤-z 时,2)(0,2)(0≤-≤≤≤z h z h . (8分)从而当11≤≤-z 时,22)()(0≤-+≤z h z h ,即21434302≤++++≤c b az a ,从而 0143≥+++c b a ,2432≤z a ,由 102≤≤z 知38≤a . (12分)又易知当m x x x x f ++-=23438)((m 为常数)满足题设条件,所以a 最大值为38.(16分)10.(本小题满分20分)已知抛物线x y 62=上的两个动点1122(,)(,)A x y B x y 和,其中21x x ≠且421=+x x .线段AB 的垂直平分线与x 轴交于点C ,求ABC ∆面积的最大值.解一:设线段AB 的中点为),(00y x M ,则2,22210210y y y x x x +==+=,01221221212123666y y y y y y y x x y y k AB =+=--=--=.线段AB 的垂直平分线的方程是)2(300--=-x y y y . (1)易知0,5==y x 是(1)的一个解,所以线段AB 的垂直平分线与x 轴的交点C 为定点,且点C 坐标为)0,5(. (5分) 由(1)知直线AB 的方程为)2(300-=-x y y y ,即 2)(300+-=y y y x . (2)(2)代入x y 62=得12)(2002+-=y y y y ,即12222002=-+-y y y y .(3)依题意,21,y y 是方程(3)的两个实根,且21y y ≠,所以 22200044(212)4480y y y ∆=--=-+>,32320<<-y .221221)()(y y x x AB -+-=22120))()3(1(y y y -+=]4))[(91(2122120y y y y y-++=))122(44)(91(202020--+=y y y)12)(9(322020y y -+=.定点)0,5(C 到线段AB 的距离202029)0()25(y y CM h +=-+-==.(10分)2020209)12)(9(3121y y y h AB S ABC +⋅-+=⋅=∆)9)(224)(9(2131202020y y y +-+=3202020)392249(2131y y y ++-++≤7314=. (15分) 当且仅当2022249yy -=+,即0y =,66((33A B或A B -时等号成立.所以ABC ∆面积的最大值为7314. (20分)解二:同解一,线段AB 的垂直平分线与x 轴的交点C 为定点,且点C 坐标为)0,5(.(5分)设4,,,222121222211=+>==t t t t t x t x ,则161610521222121t t t t S ABC =∆的绝对值, (10分)2222122112))656665(21(t t t t t t S ABC--+=∆ 221221)5()(23+-=t t t t)5)(5)(24(23212121++-=t t t t t t3)314(23≤,7314≤∆ABC S , (15分)当且仅当5)(21221+=-t t t t 且42221=+t t , 即,6571-=t6572+-=t,66((33A B +或A B -时等号成立.所以ABC ∆面积的最大值是7314. (20分)11.(本小题满分20分)数列{}n a 满足),2,1(1,312211 =+-==+n a a a a a n n n n .求证: nn n a a a 2212312131211-<+++<-- . (1) 证明:由1221+-=+n n n n a a a a 知 111121+-=+nn n a a a ,)11(1111-=-+nn n a a a . (2)所以 211,111n n n n n n na a aa a a a ++==----即 1111n n n n n a aa a a ++=---. (5分)从而na a a +++ 211133222*********++---++---+---=n n n n a a a a a a a aa a a a11111112111++++--=---=n n n n a a a a a a .所以(1)等价于n n n n a a 2112312112131211-<--<-++-,即n n n n a a 21123131<-<++- . (3) (10分)由311=a 及 1221+-=+n n n n a a a a 知 712=a . 当1n =时 ,2216a a -=,11122363<<- ,即1n =时,(3)成立.设)1(≥=k k n 时,(3)成立,即 k k k k a a 21123131<-<++-.当1+=k n 时,由(2)知kk k k k k k k a a a a a a a 2211111223)1()1(11>->-=-+++++++; (15分)又由(2)及311=a 知 )1(1≥-n a a n n均为整数,从而由 k k k a a 21131<-++ 有131211-≤-++k k k a a 即kk a 2131≤+ ,所以122211122333111+<⋅<-⋅=-+++++k k k k k k k k a a a a a ,即(3)对1+=k n 也成立.所以(3)对1≥n 的正整数都成立,即(1)对1≥n 的正整数都成立. (20分)。
2010届温州第一学期高三年级八校联考理
2010届浙江省温州市第一学期高三年级八校联考数学试卷(理科)本试卷共22小题,满分150分,考试时间120分钟第I 卷(共50分)一、选择题:本大题共10题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知R U =,[0,2]A =,{|2,0}x B y y x ==>,则U AC B =( ) A .[0,1](2,)+∞ B .[0,1)(2,)+∞ C .[0,1]D .[0,2] 2.已知b a ,是实数,则“11>>b a 且”是“12>>+ab b a 且”的( )A .充要条件B .充分不必要条件C .必要不充分条件D .既不充分也不必要条件3.已知复数z 满足z i 为虚数单位),则z 的虚部为( ) A .43 B .i 43- C .43 D .i 43 4.23sin 602cos 15--=( )A .12B C .2 D .32 5.在52)1)(21(x x x +-+的展开式中,含3x 的项的系数是( )A .20B .10C .5D .76.阅读如图的程序框图.若输入m=4,n=6,则输出的a ,i 分别等于( )A .12,2B .12,3C .12,4D .24,47.ABC ∆中,BC 上有一点D ,已知AC AB AD 3132+=,则有( ) A .CAD BAD ∠<∠B .CAD BAD ∠>∠C >D <8.已知a 、b 、c 是不重合的直线,δγβα,,,是不重合的平面. 则下列命题中正确的是( )A ..//,//,//,,b a b a 则若δβγαδγβα=⋂=⋂B .αβα在若c b a ,,=⋂内的射影相互平行,则在β内的射影也相互平行.C .c b c a ⊥⊥,,则b a ∥.D ..//,,βαγβγα则⊥⊥9.数列{}n a 的各项均为正数,n S 为其前n 项和,对于任意*N n ∈,总有2,,n n n a S a 成等差数列,则=2009a ( )A .1B .4018C .2010D .200910.已知双曲线)0(12222>>=-b a by a x ,N M ,是双曲线上关于原点对称的两点,P 是双曲线上的动点,且直线PN PM ,的斜率分别为21,k k ,021≠k k ,若21k k +的最小值为1,则双曲线的离心率为( )A .2B . 25C . 23D .23 第II 卷(共100分)二、填空题:本大题共7小题,每小题4分,共28分。
2024-2025学年高三一轮复习联考(三)_全国卷文数(含答案)
2024届高三一轮复习联考(三)全国卷文科数学试题注意事项:1.答卷前,考生务必将自己的姓名、考场号、座位号、准考证号填写在答题卡上.2.回答选择题时,选出每小题答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号,回答非选择题时,将答案写在答题卡上,写在本试卷上无效.3.考试结束后,将本试卷和答题卡一并交回,考试时间为120分钟,满分150分一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}{}212,1A xx B x x =<<=∣∣,则A B ⋃=()A.[)1,2-B.(),2∞-C.[)1,3- D.[]1,2-2.命题2:,220p x R x x ∀∈+-<的否定p ⌝为()A.2000,220x R x x ∃∈+->B.2,220x R x x ∀∈+-C.2,220x R x x ∀∈+->D.2000,220x R x x ∃∈+-3.3.已知复数2(1i)z =+(i 为虚数单位),则复数z 的虚部为()A.2B.2- C.2iD.2i-4.若函数()222,0,log ,0,x x x f x x x ⎧-=⎨>⎩则()2f f ⎡⎤-=⎣⎦()A.2- B.2 C.3- D.35.已知1sin 62πα⎛⎫-= ⎪⎝⎭,则2cos 23πα⎛⎫+= ⎪⎝⎭()A.14-B.14C.12-D.126.函数()21x xe ef x x --=+在[]3,3-上的大致图象为()A.B.C. D.7.函数2sin cos21y x x=-+的最小值是()A.3-B.1-C.32- D.12-8.已知数列{}n a的前n项和22nS n n m=-++,且对任意*1,0n nn N a a+∈-<,则实数m 的取值范为是()A.()2,∞-+ B.(),2∞--C.()2,∞+ D.(),2∞-9.已知等比数列()*a满足4221,m nq a a a≠=,(其中,*m n N∈),则91m n+的最小值为()A.6 B.16 C.32 D.210.已知函数()cos3f x xπ⎛⎫=+⎪⎝⎭,若()f x在[]0,a上的值域为11,2⎡⎤-⎢⎥⎣⎦,则实数a的取值范为()A.40,3π⎛⎤⎥⎝⎦B.24,33ππ⎡⎤⎢⎥⎣⎦C.2,3π∞⎡⎫+⎪⎢⎣⎭ D.25,33ππ⎡⎤⎢⎥⎣⎦11.设4sin1,3sin2,2sin3a b c===,则()A.a b c<< B.c b a<<C.c a b<< D.a c b<<12.已矨,,A B C均在球O的球面上运动,且满足3AOBπ∠=,若三棱锥O ABC-体积的最大值为6,则球O的体积为()A.12πB.48πC.D.二、填空题:本题共4小题,每小题5分,共20分.13.已知()(1,,a k b==,若a b⊥,则k=__________.14.已知{}n a是各项不全为零的等差数列,前n项和是n S,且2024S S=,若()2626nS S m=≠,则正整数m=__________.15.设,m n为不重合的直线,,,αβγ为不重合的平面,下列是αβ∥成立的充分条件的有()(只填序号).①,m a m β⊂∥②,,m n n m αβ⊂⊥⊥③,αγβγ⊥⊥④,m m αβ⊥⊥16.已知函数()14sin ,01,2,1,x x x f x x x π-<⎧=⎨+>⎩若关于x 的方程()()()2[]210f x m f x m --+-=恰有5个不同的实数解,则实数m 的取值集合为__________.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17-21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:60分.17.(12分)已知数列{}n a 满足12122,log log 1n n a a a +==+,(1)求数列{}n a 的通项公式;(2)求(){}32nn a -的前n 项和nS.18.(12分)已知ABC 中,三个内角,,A B C 的对边分别为,,,,cos cos 2cos 4a b c C a A c C b B π=+=.(1)求tan A ;(2)若c =,求ABC 的面积.19.(12分)如图,在四棱锥P ABCD -中,底面ABCD 是矩形,O 是BC 的中点,PB PC ==,22PD BC AB ===.(1)求证:平而PBC ⊥平面ABCD ;(2)求点A 到平面PCD 的距离.20.(12分)已知数列()n a 满足()21112122222326n n n n n a a a a n -+-++++=-⋅+ .(1)求{}n a 的通项公式;(2)若2n an n b a =+,求数列n b 的前n 项和T .21.(12分)已知函数()ln x af x ex x -=-+.(1)当1a =时,求曲线()f x 在点()()1,1f 处的切线方程,(2)当0a 时,证明,()2f x x >+.(二)选考题:共10分.请考生在第22,23题中任选一题作答.如果多做,则按所做的第一题计分.22.[选修4-4:坐标系与参数方程](10分)在平面直角坐标系,xOy 中,直线l的参数方程为2,21,2x a y t ⎧=+⎪⎪⎨⎪=⎪⎩(t 为参数),以O 为极点,x 轴的非负半轴为极轴建立极坐标系,曲线C 的极坐标方程为22413sin ρθ=+.(1)求直线l 和曲线C 的直角坐标方程;(2)若曲线C 经过伸缩变换,2,x x y y ⎧=⎪⎨⎪='⎩'得到曲线C ',若直线l 与曲线C '有公共点,试求a 的取值范围.23.[选修4-5:不等式选讲](10分)已知函数()22(0)f x x x t t =++->,若函数()f x 的最小值为5.(1)求t 的值;(2)若,,a b c 均为正实数,且2a b c t ++=,求1412a b c++的最小值.2024届高三一轮复习联考(三)全国卷文科数学参考答案及评分意见1.A【解析】由21x ,即()()110x x -+,解得11x -,所以{}11B xx =-∣,所以{12}A B xx ⋃=-<∣.故选A .2.D 【解析】2,220x x x ∀∈+-<R 的否定为:2000,220x x x ∃∈+-R ,故选D.3.A 【解析】2(1i)2i z =+=,即复数z 的虚部为2,故选A .4.D【解析】()()()222(2)228,8log 83f f -=--⨯-===,故选D.5.C 【解析】因为1sin 62πα⎛⎫-= ⎪⎝⎭,所以2211cos 2cos 2cos 22sin 11366622ππππααπαα⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫+=-+=--=--=-=- ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦.故选C.6.A 【解析】()()2e e 1x xf x f x x ---==-+,所以函数()y f x =是奇函数,排除B 选项,又()22e e 215f --=>,排除C ,D 选项,故选A.7.D 【解析】由题意,函数22sin cos212sin 2sin y x x x x =-+=+,令[]sin 1,1t x =∈-,可得221122222y t t t ⎛⎫=+=+- ⎪⎝⎭,当12t =-,即1sin 2x =-时,函数取得最小值,最小值为12-.故选D.8.A【解析】因为10n n a a +-<,所以数列{}n a 为递减数列,当2n 时,()2212(1)2123n n n a S S n n m n n m n -⎡⎤=-=-++---+-+=-+⎣⎦,故可知当2n 时,{}n a 单调递减,故{}n a 为递减数列,只需满足21a a <,即112m m-+⇒-.故选A .9.D【解析】由等比数列的性质,可得()911911918,10102888m n m n m n m n m n n m ⎛⎛⎫⎛⎫+=+=++=+++= ⎪ ⎪ ⎝⎭⎝⎭⎝,当且仅当6,2m n ==时,等号成立,因此,91m n +的最小值为2.故选D.10.B 【解析】()cos 3f x x π⎛⎫=+⎪⎝⎭,结合图象,()f x 的值域是11,,0,2333x a x a πππ⎡⎤-++⎢⎣⎦,于是533a πππ+,解得2433aππ,所以实数a 的取值范围为24,33ππ⎡⎤⎢⎥⎣⎦.故选B.11.B 【解析】设()()2sin cos sin ,x x x xf x f x x x -==',令()()cos sin ,sing x x x x g x x x =-'=-,当()0,x π∈时,()0g x '<,故()g x 在()0,π上递减,()()()00,0g x g f x <=∴<',故()sin xf x x=在()0,π上递减,023π<<< .()()sin3sin232,,2sin33sin232f f ∴<<<,故c b <,()()()sin 2012,sin1,sin22sin1,3sin232sin14sin12ππππππ-<<-<<<-<-<-,故b a <,故c b a <<,故选B.12.C 【解析】如图所示,当点C 位于垂直于面AOB 的直径端点时,三棱锥O ABC -的体积最大,设球O 的半径为R ,此时231133632212O ABC C AOB V V R R --==⨯⨯⨯==,故3R =O 的体积为343R V π==,故选C.13.3-【解析】0a b a b ⊥⇔⋅=,所以()(1,10,3k k ⋅=+==-.14.18【解析】设等差数列{}n a 的首项和公差分别为1,a d ,则2122n d d S n a n ⎛⎫=+- ⎪⎝⎭,所以n S 可看成关于n 的二次函数,由二次函数的对称性及202426,m S S S S ==,可得20242622m++=,解得18m =.15.④【解析】根据线面的位置关系易知,①②③中面α和面β可能相交也可能平行,④:若m α⊥且m β⊥,根据面面平行的判定可知垂直于同一直线的两平面互相平行,故④正确.16.()3,1--【解析】作出函数()f x 的大致图象,如图所示,令()t f x =,则()()()2[]210f x m f x m --+-=可化为()()()221110t m t m t m t --+-=-+-=,则11t =或21t m =-,则关于x 的方程()()()2[]210f x m f x m --+-=恰有5个不同的实数解等价于()t f x =的图象与直线12,t t t t ==的交点个数之和为5个,由图可得函数()t f x =的图象与直线1t t =的交点个数为2,所以()t f x =的图象与直线2t t =的交点个数为3个,即此时214m <-<,解得31m -<<-.17.【解析】(1)在数列{}n a 中,已知12122log log log 1n n n na a a a ++-==,所以12n na a +=,.即{}n a 是首项为12a =,公比为2的等比数列,所以()1*222n n n a n -=⨯=∈N .(2)由()()32322nn n a n -=-⨯,故()()231124272352322n n n S n n -=⨯+⨯+⨯++-⨯+-⨯ ,所以()()23412124272352322nn n S n n +=⨯+⨯+⨯++-⨯+-⨯ ,则()23123222322n n n S n +⎡⎤-=+⨯+++--⨯⎣⎦,()()()11212433221053212n n n n n ++-=-+⨯--⨯=-+-⋅-,故()110352n n S n +=+-⋅.18.【解析】(1)解法一:由题,cos cos 2cos a A c C b B +=,由正弦定理得,sin2sin cos sin cos B A A C C =+,.3,,sin2sin 2sin 2cos2422C A B C B A A A ππππ⎛⎫⎛⎫=++==-=-=- ⎪ ⎪⎝⎭⎝⎭,所以1cos2sin cos 2A A A -=+,221sin cos sin cos 2A A A A --=22tan 1tan 1tan 12A A A --=+,化简得2tan 2tan 30A A --=,解得tan 3A =或tan 1A =-(舍去).解法二:由题,cos cos 2cos a A c C b B +=,由正弦定理得,2sin2sin2sin2B A C =+,即()()()()2sin2sin sin B A C A C A C A C ⎡⎤⎡⎤=++-++--⎣⎦⎣⎦,即()()sin2sin cos B A C A C =+-,又A B C π++=,故()sin sin A C B +=,所以()2sin cos sin cos B B B A C =-,又0B π<<,故sin 0B ≠,所以()2cos cos B A C =-,又A B C π++=,故()cos cos B A C =-+,化简得sin sin 3cos cos A C A C =,因此tan tan 3A C =且tan 1C =,所以tan 3A =.(2)由(1)知tan 3A =,因此()tan tan tan tan 21tan tan A CB AC A C+=-+=-=-,.所以sin 10A =,sin 5B =2sin 2C =,因为,6sin sin a c a A C==,.所以1125sin 612225ABC S ac B ==⨯⨯= .19.【解析】(1)因为,PB PC O =是BC 的中点,所以PO BC ⊥,在直角POC 中,1PC OC ==,所以PO =,在矩形ABCD 中,1,2AB BC ==,所以DO =,又因为2PD =,所以在POD 中,222PD PO OD =+,即PO OD ⊥.而,,BC OD O BC OD ⋂=⊂平面ABCD ,所以PO ⊥平面ABCD ,而PO ⊂平面PBC ,所以平面PBC ⊥平面ABCD .'(2)由(1)平面PBC ⊥平面ABCD ,且DC BC ⊥,所以DC ⊥平面PBC ,所以DC PC ⊥,即PCD 是直角三角形,因为1PC CD ==,所以13122PDC S =⨯=,又知11212ACD S =⨯⨯= ,PO ⊥平面ABCD ,设点A 到平面PCD 的距离为d ,则A PCD P ACD V V --=,即1133PCD ACD S d S PO ⨯⨯=⨯⨯ ,即1311323d ⨯⨯=⨯⨯所以263d =,所以点A 到平面PCD 的距离为3..20.【解析】(1)由题当1n =时,()111223262a +=-⋅+=,即11a =.()21112122222326n n n n n a a a a n -+-++++=-⋅+ ①当2n 时,()211212222526n n n a a a n --+++=-⋅+ ②.①-②得()()()1223262526212nn n n n a n n n +=-⋅+--⋅-=-⋅,所以21n a n =-..(2)由(1)知,212221n an n n b a n -=+=+-,则()()()()3521212325221n n T n -=++++++++- ()()3521222213521n n -=+++++++++-⋅()()212214121232..1423nn n n n +⨯-+-+-=+=-21.【解析】(1)当1a =时,()()111e ln ,e 1x xf x x x f x x--=-+=-+',所以()()12,11f f '==,.则切线方程为()211y x -=⨯-,.即10x y -+=曲线()f x 在点()()1,1f 处的切线方程为10x y -+=.(2)证明:要证()2f x x >+,即证e ln 2x a x -->,设()eln ,0x aF x x x -=->,即证()2F x >,当0a 时,()()1e 1e ln ,ex a x ax ax F x x F x x x----=-=-='在()0,∞+上为增函数,且()e1x ah x x -=-中,()()0100e 110,1e 1e 10a a h h --=⨯-=-=-->.故()0F x '=在()0,∞+上有唯一实数根0x ,且()00,1x ∈..当()00,x x ∈时,()0F x '<,当()0,x x ∞∈+时,()0F x '>,从而当0x x =时,()F x 取得最小值.由()00F x '=,得001ex ax -=,故()()000001eln 2x aF x F x x x a a x -=-=+->.综上,当0a 时,()2F x >即()2f x x >+.22.【解析】(1)由题2,21,2x a t y t ⎧=+⎪⎪⎨⎪=⎪⎩(t 为参数),消去参数t得直线:20l x a -=,.22413sin ρθ=+,即2224cos 4sin ρθθ=+,即曲线C 的直角坐标方程为2214x y +=.(2)由,2,x x y y ⎧=⎪⎨⎪='⎩'得2,,x x y y =⎧⎨=''⎩又2214x y +=,所以()()22214x y +'=',即'2'21x y +=,所以曲线C '的方程是221x y +=,.由1d =得11a -.所以a 的取值范围是[]1,1-.23.【解析】(1)()222f x x x t x x t x t =++-=++-+-,()2222y x x tx x t t t =++-+--=+=+,当2x t -时等号成立,.⋅又知当x t =时,x t -取得最小值,所以当x t =时,()f x 有最小值,此时()min ()25f x f t t ==+=,所以3t =..(2)由(1)知,23a b c ++=,()22141114111162(121)232333a b c a b c a b c ⎛⎫++=++++=++= ⎪⎝⎭,当且仅当333,,824a b c ===时取等号,所以1412a b c ++的最小值为163.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
- 1 - 2010届高三英语一轮复习达标测试卷选修八 (课标版) 时量: 120分钟 总分: 150分 第I 卷 (共115分)
第一部分:听力(共三节, 满分30分) 第一节(共5小题;每小题1.5分,满分7.5分) 听下面5段对话,每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题,每段对话仅读一遍。 1 Where does the conversation most probably take place? A. At home B. At a restaurant C. In an Internet café 2. Why won’t the woman go to the concert? A. Because she will go to see her friend. B. Because she will take care of her friend’s baby C. Because she will help her friend with her lessons. 3. What’s wrong with the woman? A. She lost her daughter B. she lost her luggage C. Her daughter was taken somewhere illegally 4. What will the woman probably do? A. She will do eye exercises and protect her eye-sight B. She will have her eyes examined and get a pair of glasses C. She will have her eyes examined and change a pair of glasses. 5. When does this conversation take place? A. At about 8:15 pm B. At about 8:45 pm. C. At about 9:15 pm. 第二节(共12小题,每小题1.5分,满分18分) 听下面4段对话,每段对话后有几个小题,从题中所给的A、B、c三个选项中选出最佳选项,并标在试卷的相应位置。听完每段对话后,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟的作答时问,每段对话读两遍。 听下面一段对话,回答第6至第7两个小题 - 2 -
6. What can we learn about the garden? A. It’s tidy B. It’s big C. It’s just OK. 7. What does the man think of that place? A. It is the best place he has ever known B. It’s very quiet and good for his life C. It’s very convenient with so many life facilities. 请听下面一段对话,回答第8至第10三个小题。 8. Where does this conversation most probably take place? A. At a hotel. B. On an island C. In a travel agency 9. Which pages contain the information of the Island of Pearl? A. Pages 45 to 48 B. Pages 54 to 58 C. Pages 45 to 58 10. What is the man doing? A. Planning a tour B. Looking for a hotel C. Trying to find a book 请听下面一段对话,回答第11至第13三个小题。 11. What causes the conversation? A. An advertisement B. A TV program C. An article 12. Who will shop quickly? A. Those who know what they want to buy. B. Those who have little money to spend. C. Those who shop at the cheapest stores. 13. What can we conclude from the conversation? A. People spend more time looking than shopping. B. People enjoy shopping when they are free. C. People buy things easily if time is limited 请听下面一段对话,回答第14至第17四个小题。 14. Why does the man make a call to Marketing Department? A. Because she wants to know something about the department. B. Because she is interested in marketing research. C. Because she wants to get a job in the department. 15. How did the man know the telephone number of the department? A. By watching an ad on TV. B. By reading an ad in the newspaper. - 3 -
C. By reading an ad on the Internet 16. How many courses did the man study at college except his major? A. 15 B. 13 C. 11 17. When does the manager promise to give an interview to the man? A. At 2:45 on Thursday B. At 2:50 on Wednesday C. At 2:15 on Wednesday 第三节(共3小题;每小题1.5分,满分4.5分) 听下面一段材料,将第18至第20三个小题的信息补充完整。每小题不超过三个单 词。听材料前,你将有时间阅读各个小题,每小题5秒钟,听完后,各小题将给出15秒钟的作答时间,本段材料读两遍。 Market Goods Sold Open Time How to arrive
East Street SE17 18_____________ and hardware 8:00 am--- 5:00 pm Take the 19___________ and get off at the Castle Petticoat Lane E1 Clothes, shoes and household goods 20_____________ (Sunday mornings) Get off at Aldgate Station
第二部分:英语知识运用(共两节,满分45分) 第一节:单项填空(共15小题;每小题1分,满分15分) 从A、B、c、D四个选项中,选出可以填入空白处的最佳选项,并在答题卡上将该项涂黑。 21.This problem may lead to more serious ones if _____ unsolved. A. left B. keeping C. remained D. making 22._____ that they had to stay at home all day. A. So the weather was terrible B. The weather so terrible was C. So terrible was the weather D. So was the terrible weather 23.He was admitted ______the Party last week due to outstanding contributions. A. on B. into C. in D. for 24.These children have a strong desire ______some presents at Christmas. A. getting B. get C. got D. to get 25.It is _____ Tom often surfs the Internet playing games ______ makes his parents very angry. A.不填; that B. what; that C. that; that D. that; what - 4 -
26._____ in teaching in a small village, he felt very happy. A. Anchor B. Anchored C. Anchoring D. To anchor 27._____ can tell you how to get to the station. Some people don’t know the way. A. Anyone B. Everyone C. Not everyone D. No one 28.It is very important for us to ______ between right and wrong. A. reject B. realize C. range D. distinguish 29.The government has made many laws ______ the people’s interests. A. in favor of B. in celebration of C. in defence of D. in front of 30.They felt very disappointed because the result was contrary _______ expectation. A. on B. to C. from D. with 31.No matter how difficult it is, we are determined to _____ at this idea. A. have a try B. try C. have a go D. work 32.Rather than ______ that film, I would rather ______ at home. A. to see; to stay B. seeing; staying C. to see; stay D. see; stay 33.I had hardly got on the train ______ it began to move. A. than B. while C. when D. as 34.______ wind or rain, we always go to school on time. A. Whether B. If C. No matter D. Regardless of 35.It is hard to imagine his ______ the decision without any consideration. A. accept B. accepting C. accepted D. to accept 第二节:完形填空(共20小题;每小题l 5分,满分30分) 阅读下面短文,掌握其大意,然后从36—55各题所给的四个选项(A、B、C和D)中,选出最佳选项,并在答题卡上将该项涂黑。 Soon it would be the holidays, but before that, there were year exams. All the 36 had been working hard for some time, reviewing their lessons for the exams. If they didn’t 37 they would have to retake them in September. There were usually a few who 38, but Jane didn’t want to be one of them. She had worked hard all year, 39 just before the exams she was working so hard that her sister Barbara was 40 about her. She went to bed too 41. The night before the first exam, Barbara 42_
