2020届中考数学反比例函数真题汇编(含答案)

合集下载

2023中考数学真题汇编11 反比例函数及其应用(含答案与解析)

2023中考数学真题汇编·11反比例函数及其应用一、单选题1.（2023·云南）若点 1,3A 是反比例函数(0)ky k x图象上一点，则常数k 的值为（）A ．3B ．3C ．32D ．322.（2023·湖南永州）已知点 2,M a 在反比例函数ky x的图象上，其中a ，k 为常数，且0k ﹐则点M 一定在（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限3.（2023·湖北随州）已知蓄电池的电压为定值，使用某蓄电池时，电流I (单位：A)与电阻R (单位： )是反比例函数关系，它的图象如图所示，则当电阻为6 时，电流为()A ．3AB ．4AC ．6AD ．8A4.（2023·湖南）如图，矩形OABC 的顶点B 和正方形ADEF 的顶点E 都在反比例函数 0ky k x的图像上，点B 的坐标为 2,4，则点E 的坐标为（）A ． 4,4B ． 2,2C ． 2,4D ．4,25.（2023·浙江）如果100N 的压力F 作用于物体上，产生的压强P 要大于1000Pa ，则下列关于物体受力面积 2S m 的说法正确的是（）A ．S 小于20.1mB ．S 大于20.1m C ．S 小于210m D ．S 大于210m 6.（2023·浙江嘉兴）已知点 1232,,1,,1,A y B y C y 均在反比例函数3y x的图象上，则123,,y y y 的大小关系是（）A ．123y y y B ．213y y y C ．312y y y D ．321y y y 7.（2023·天津）若点 123,2,,1,)2(,A x B x C x 都在反比例函数2y x的图象上，则123,,x x x 的大小关系是（）A ．321x x x B ．213x x x C ．132x x x D ．231x x x 8.（2023·山西）已知(2,),(1,),(3,)A a B b C c 都在反比例函数4y x的图象上，则a 、b 、c 的关系是（）A ．a b cB ．b a cC ．c b aD ．c a b9.（2023·湖北宜昌）某反比例函数图象上四个点的坐标分别为 1233,,2,3,1,,2,y y y ，则，123,,y y y 的大小关系为（）A ．213y y y B ．321y y y C ．231y y y D ．132y y y 10.（2023·内蒙古通辽）已知点 1122,,,A x y B x y 在反比例函数2y x的图像上，且120x x ，则下列结论一定正确的是（）A ．120y y B ．120y y C ．120y y D ．120y y 11.（2023·湖北）在反比例函数4ky x的图象上有两点 1122,,,A x y B x y ，当120x x 时，有12y y ，则k 的取值范围是（）A ．0k B ．0k C ．4k D ．4k 12.（2023·吉林长春）如图，在平面直角坐标系中，点A 、B 在函数(0,0)k y k x x的图象上，分别以A 、B 为圆心，1为半径作圆，当A 与x 轴相切、B 与y 轴相切时，连结AB ，32AB ，则k 的值为（）A ．3B ．32C ．4D ．613.（2023·湖南）如图，平面直角坐标系中，O 是坐标原点，点A 是反比例函数 0ky k x图像上的一点，过点A 分别作AM x 轴于点M ，AN y 轴于直N ，若四边形AMON 的面积为2．则k 的值是（）A ．2B ．2C ．1D ．114.（2023·黑龙江绥化）在平面直角坐标系中，点A 在y 轴的正半轴上，AC 平行于x 轴，点B ，C 的横坐标都是3，2BC ，点D 在AC 上，且其横坐标为1，若反比例函数ky x（0x ）的图像经过点B ，D ，则k 的值是（）A ．1B ．2C ．3D ．3215.（2023·湖南张家界）如图，矩形OABC 的顶点A ，C 分别在y 轴、x 轴的正半轴上，点D 在AB 上，且14AD AB，反比例函数 0ky k x的图象经过点D 及矩形OABC 的对称中心M ，连接,,OD OM DM ．若ODM △的面积为3，则k 的值为（）A ．2B ．3C ．4D ．516.（2023·内蒙古）如图，在平面直角坐标系中，OAB 三个顶点的坐标分别为(0,0),(23,0),(3,1),O A B OAB △与OAB 关于直线OB 对称，反比例函数(0,0)ky k x x的图象与A B 交于点C ．若A C BC ，则k 的值为（）A ．23B ．332C ．3D ．3217.（2023·湖南怀化）如图，反比例函数(0)ky k x的图象与过点(1,0) 的直线AB 相交于A 、B 两点．已知点A 的坐标为(1,3)，点C 为x 轴上任意一点．如果9ABC S ，那么点C 的坐标为（）A ．(3,0)B ．(5,0)C ．(3,0) 或(5,0)D ．(3,0)或(5,0)18.（2023·福建）如图，正方形四个顶点分别位于两个反比例函数3y x和ny x的图象的四个分支上，则实数n 的值为（）A ．3B ．13C ．13D ．319.（2023·广西）如图，过(0)ky x x 的图象上点A ，分别作x 轴，y 轴的平行线交1y x的图象于B ，D两点，以AB ，AD 为邻边的矩形ABCD 被坐标轴分割成四个小矩形，面积分别记为1S ，2S ，3S ，4S ，若23452S S S ，则k 的值为（）A ．4B ．3C ．2D ．120.（2023·黑龙江）如图，ABC 是等腰三角形，AB 过原点O ，底边BC x ∥轴，双曲线ky x过,A B 两点，过点C 作CD y ∥轴交双曲线于点D ，若12BCD S ，则k 的值是（）A ．6B ．12C ．92D ．921.（2023·四川宜宾）如图，在平面直角坐标系xOy 中，点A 、B 分别在y ，x轴上，BC x 轴．点M 、N 分别在线段BC 、AC 上，BM CM ，2NC AN ，反比例函数 0ky x x的图象经过M 、N 两点，P 为x 正半轴上一点，且:1:4OP BP ，APN 的面积为3，则k 的值为（）A ．454B ．458C ．14425D ．7225二、填空题22.（2023·广东）某蓄电池的电压为48V ，使用此蓄电池时，电流I (单位：A )与电阻R (单位： )的函数表达式为48I R，当12R 时，I 的值为_______A ．23．（2023·四川成都）若点 123,y ,1,A B y 都在反比例函数6y x的图象上，则1y _______2y （填“ ”或“ ”）．23.（2023·浙江温州）在温度不变的条件下，通过一次又一次地对汽缸顶部的活塞加压，加压后气体对汽缸壁所产生的压强P （kPa ）与汽缸内气体的体积V （mL ）成反比例，P 关于V 的函数图象如图所示．若压强由75kPa 加压到100kPa ，则气体体积压缩了___________mL ．24.（2023·河北）如图，已知点(3,3),(3,1)A B ，反比例函数(0)ky k x图像的一支与线段AB 有交点，写出一个符合条件的k 的数值：_________．25.（2023·黑龙江齐齐哈尔）如图，点A 在反比例函数 0ky k x图像的一支上，点B 在反比例函数2ky x图像的一支上，点C ，D 在x 轴上，若四边形ABCD 是面积为9的正方形，则实数k 的值为______．26.（2023·广东深圳）如图，Rt OAB 与Rt OBC △位于平面直角坐标系中，30AOB BOC ，BA OA ，CB OB ，若AB 0ky kx恰好经过点C ，则k ______．27.（2023·江苏连云港）如图，矩形OABC 的顶点A 在反比例函数(0)ky x x的图像上，顶点B C 、在第一象限，对角线AC x ∥轴，交y 轴于点D ．若矩形OABC 的面积是6，2cos 3OAC ，则k __________．28.（2023·新疆）如图，在平面直角坐标系中，OAB 为直角三角形，90A ，30AOB ，4OB ．若反比例函数 0ky k x的图象经过OA 的中点C ，交AB 于点D ，则k ______．29.（2023·山东烟台）如图，在直角坐标系中，A 与x 轴相切于点,B CB 为A 的直径，点C 在函数(0,0)ky k x x的图象上，D 为y 轴上一点，ACD 的面积为6，则k 的值为________．26．（2023·湖北鄂州）如图，在平面直角坐标系中，直线11y k x b 与双曲线22k y x（其中120k k ）相交于 2,3A ， ,2B m 两点，过点B 作BP x ∥轴，交y 轴于点P ，则ABP 的面积是___________．30.（2023·浙江绍兴）如图，在平面直角坐标系xOy 中，函数ky x（k 为大于0的常数，0x ）图象上的两点 1122,,,A x y B x y ，满足212x x ．ABC 的边AC x ∥轴，边∥BC y 轴，若OAB 的面积为6，则ABC 的面积是________．31.（2023·四川内江）如图，在平面直角坐标系中，O 为坐标原点，MN 垂直于x 轴，以MN 为对称轴作ODE 的轴对称图形，对称轴MN 与线段DE 相交于点F ，点D 的对应点B 恰好落在反比例函数(0)ky x x的图象上，点O 、E 的对应点分别是点C 、A ．若点A 为OE 的中点，且14EAF S △，则k 的值为___________．32.（2023·浙江宁波）如图，点A ，B 分别在函数(0)ay a x图象的两支上（A 在第一象限），连接AB 交x 轴于点C ．点D ，E 在函数(0,0)by b x x图象上，AE x 轴，BD y ∥轴，连接,DE BE ．若2AC BC ，ABE 的面积为9，四边形ABDE 的面积为14，则a b 的值为__________，a 的值为__________．33.（2023·湖北荆州）如图，点 2,2A 在双曲线(0)k y x x上，将直线OA 向上平移若干个单位长度交y 轴于点B ，交双曲线于点C ．若2BC ，则点C 的坐标是___________．34.（2023·山东枣庄）如图，在反比例函数8(0)y x x的图象上有1232024,,,P P P P 等点，它们的横坐标依次为1，2，3，…，2024，分别过这些点作x 轴与y 轴的垂线，图中所构成的阴影部分的面积从左到右依次为1232023,,,,S S S S ，则1232023S S S S ___________．35.（2023·湖北十堰）函数ky x a的图象可以由函数k y x的图象左右平移得到．（1）将函数1y x的图象向右平移4个单位得到函数1y x a的图象，则 a ____；（2）下列关于函数1y x a的性质：①图象关于点 ,0a 对称；②y 随x 的增大而减小；③图象关于直线y x a 对称；④y 的取值范围为0y ．其中说法正确的是________（填写序号）；（3）根据（1）中a 的值，写出不等式11x a x的解集：_________．三、解答题36.（2023·湖南常德）如图所示，一次函数1y x m 与反比例函数2ky x相交于点A 和点 3,1B ．（1）求m 的值和反比例函数解析式；（2）当12y y 时，求x 的取值范围．37.（2023·湖南）如图，点A 的坐标是 3,0 ，点B 的坐标是(0,4)，点C 为OB中点，将ABC 绕着点B 逆时针旋转90 得到A BC △．（1）反比例函数ky x的图像经过点C ，求该反比例函数的表达式；（2）一次函数图像经过A 、A 两点，求该一次函数的表达式．38.（2023·四川广安）如图，一次函数94y kx（k 为常数，0k ）的图象与反比例函数(my m x为常数，0)m 的图象在第一象限交于点 1,A n ，与x 轴交于点 3,0B ．（1）求一次函数和反比例函数的解析式．（2）点P 在x 轴上，ABP 是以AB 为腰的等腰三角形，请直接写出点P 的坐标．39.（2023·山东）如图，已知坐标轴上两点 0,4,2,0A B ，连接AB ，过点B 作BC AB ，交反比例函数ky x在第一象限的图象于点(,1)C a ．（1）求反比例函数ky x和直线OC 的表达式；（2）将直线OC 向上平移32个单位，得到直线l ，求直线l 与反比例函数图象的交点坐标．40.（2023·浙江杭州）在直角坐标系中，已知120k k ，设函数11k y x与函数 2225y k x 的图象交于点A 和点B ．已知点A 的横坐标是2，点B 的纵坐标是4 ．（1）求12,k k 的值．（2）过点A 作y 轴的垂线，过点B 作x 轴的垂线，在第二象限交于点C ；过点A 作x 轴的垂线，过点B 作y 轴的垂线，在第四象限交于点D ．求证：直线CD 经过原点．41.（2023·四川自贡）如图，点 24A ，在反比例函数1my x图象上．一次函数2y kx b 的图象经过点A ，分别交x 轴，y 轴于点B ，C ，且OAC △与OBC △的面积比为2:1．（1）求反比例函数和一次函数的解析式；（2）请直接写出12y y 时，x 的取值范围．42.（2023·四川泸州）如图，在平面直角坐标系xOy 中，直线:2l y kx 与x ，y 轴分别相交于点A ，B ，与反比例函数 0my x x的图象相交于点C ，已知1OA ，点C 的横坐标为2．（1）求k ，m 的值；（2）平行于y 轴的动直线与l 和反比例函数的图象分别交于点D ，E ，若以B ，D ，E ，O 为顶点的四边形为平行四边形，求点D 的坐标．43.（2023·四川南充）如图，一次函数图象与反比例函数图象交于点 16A ，3,3B a a，与x 轴交于点C ，与y 轴交于点D ．（1）求反比例函数与一次函数的解析式；（2）点M 在x 轴上，若OAM OAB S S △△，求点M 的坐标．44.（2023·四川宜宾）如图，在平面直角坐标系xOy 中，等腰直角三角形ABC 的直角顶点 30C ，，顶点A 、 6B m ，恰好落在反比例函数ky x第一象限的图象上．（1）分别求反比例函数的表达式和直线AB 所对应的一次函数的表达式；（2）在x 轴上是否存在一点P ，使ABP 周长的值最小．若存在，求出最小值；若不存在，请说明理由．45.（2023·四川遂宁）如图，一次函数1y k x b 的图像与反比例函数2k y x的图像交于 41A ，， 4B m ，两点．（1k ，2k ，b 为常数）（1）求一次函数和反比例函数的解析式；（2）根据图像直接写出不等式21k k x b x的解集；（3）P 为y 轴上一点，若PAB 的面积为3，求P 点的坐标．46.（2023·四川眉山）如图，在平面直角坐标系xOy 中，直线y kx b与x 轴交于点 4,0A ，与y 轴交于点 0,2B ，与反比例函数m y x在第四象限内的图象交于点 6,C a ．（1）求反比例函数的表达式：（2）当mkx b x时，直接写出x 的取值范围；（3）在双曲线my x上是否存在点P ，使ABP 是以点A 为直角顶点的直角三角形？若存在，求出点P 的坐标；若不存在，请说明理由．47.（2023·江西）如图，已知直线y x b 与反比例函数(0)k y x x的图象交于点(2,3)A ，与y 轴交于点B ，过点B 作x 轴的平行线交反比例函数(0)k y x x的图象于点C ．（1）求直线AB 和反比例函数图象的表达式；（2）求ABC 的面积．48.（2023·四川乐山）如图，一次函数y kx b 的图象与反比例函数4y x的图象交于点 ,4A m ，与x 轴交于点B ，与y 轴交于点 0,3C ．（1）求m 的值和一次函数的表达式；（2）已知P 为反比例函数4y x图象上的一点，2OBP OAC S S △△，求点P 的坐标．49.（2023·湖南岳阳）如图，反比例函数kyx（k 为常数，0k ）与正比例函数y mx （m 为常数，0m ）的图像交于 1,2,A B 两点．（1）求反比例函数和正比例函数的表达式；（2）若y 轴上有一点 0,,C n ABC △的面积为4，求点C 的坐标．50.（2023·湖南）如图，正比例函数43y x的图象与反比例函数12(0)y x x的图象相交于点A ．（1）求点A 的坐标．（2）分别以点O 、A 为圆心，大于OA 一半的长为半径作圆弧，两弧相交于点B 和点C ，作直线BC ，交x 轴于点D ．求线段OD 的长．51.（2023·江苏苏州）如图，一次函数2y x 的图象与反比例函数(0)ky x x的图象交于点 4,A n ．将点A 沿x 轴正方向平移m 个单位长度得到点,B D 为x 轴正半轴上的点，点B 的横坐标大于点D 的横坐标，连接,BD BD 的中点C 在反比例函数(0)k y x x的图象上．（1）求,n k 的值；（2）当m 为何值时，AB OD 的值最大?最大值是多少?52.（2023·山东东营）如图，在平面直角坐标系中，一次函数 0y ax b a与反比例函数 0ky k x交于 ,3A m m ， 4,3B 两点，与y 轴交于点C ，连接OA ，OB ．（1）求反比例函数和一次函数的表达式；（2）求AOB 的面积；（3）请根据图象直接写出不等式kax b x的解集．53.（2023·山东枣庄）如图，一次函数(0)y kx b k 的图象与反比例函数4y x的图象交于(,1),(2,)A m B n 两点．（1）求一次函数的表达式，并在所给的平面直角坐标系中画出这个一次函数的图象；（2）观察图象，直接写出不等式4kx b x的解集；（3）设直线AB 与x 轴交于点C ，若(0,)P a 为y 轴上的一动点，连接,AP CP ，当APC △的面积为52时，求点P 的坐标．54.（2023·山东滨州）如图，直线(,y kx b k b 为常数)与双曲线my x（m 为常数）相交于 2,A a ， 1,2B 两点．（1）求直线y kx b 的解析式；（2）在双曲线my x上任取两点 11,M x y 和 22,N x y ，若12x x ，试确定1y 和2y 的大小关系，并写出判断过程；（3）请直接写出关于x 的不等式mkx b x的解集．55.（2023·甘肃兰州）如图，反比例函数 0ky x x与一次函数2y x m的图象交于点 1,4A ，BC y 轴于点D ，分别交反比例函数与一次函数的图象于点B ，C ．（1）求反比例函数ky x与一次函数2y x m 的表达式；（2）当1OD 时，求线段BC 的长．56.（2023·湖北黄冈）如图，一次函数1(0)y kx b k 与函数为2(0)my x x的图象交于1(4,1),,2A B a两点．（1）求这两个函数的解析式；（2）根据图象，直接写出满足120y y 时x 的取值范围；（3）点P 在线段AB 上，过点P 作x 轴的垂线，垂足为M ，交函数2y 的图象于点Q ，若POQ △面积为3，求点P 的坐标．57.（2023·四川）如图，已知一次函数6y kx 的图象与反比例函数 0my m x的图象交于 34A ，，B 两点，与x 轴交于点C ，将直线AB 沿y 轴向上平移3个单位长度后与反比例函数图象交于点D ，E ．（1）求k ，m 的值及C 点坐标；（2）连接AD ，CD ，求ACD 的面积．58.（2023·山东）如图，正比例函数112y x和反比例函数2(0)ky x x的图像交于点 ,2A m ．（1）求反比例函数的解析式；（2）将直线OA 向上平移3个单位后，与y 轴交于点B ，与2(0)ky x x的图像交于点C ，连接AB AC ，，求ABC 的面积．59.（2023·四川内江）如图，在平面直角坐标系中，一次函数y mx n 与反比例函数ky x的图象在第一象限内交于 ,4A a 和 4,2B 两点，直线AB 与x 轴相交于点C ，连接OA ．（1）求一次函数与反比例函数的表达式；（2）当0x 时，请结合函数图象，直接写出关于x 的不等式kmx n x≥的解集；（3）过点B 作BD 平行于x 轴，交OA 于点D ，求梯形OCBD 的面积．60.（2023·山东聊城）如图，一次函数y kx b 的图像与反比例函数m y x的图像相交于 1,4A ， ,1B a 两点．（1）求反比例函数和一次函数的表达式；（2）点 ,0P n 在x 轴负半轴上，连接AP ，过点B 作BQ AP ∥，交my x的图像于点Q ，连接PQ ．当BQ AP 时，若四边形APQB 的面积为36，求n 的值．61.（2023·河南）小军借助反比例函数图象设计“鱼形”图案，如图，在平面直角坐标系中，以反比例函数ky x图象上的点A 和点B 为顶点，分别作菱形AOCD 和菱形OBEF ，点D ，E 在x 轴上，以点O 为圆心，OA 长为半径作 AC ，连接BF ．（1）求k 的值；（2）求扇形AOC 的半径及圆心角的度数；（3）请直接写出图中阴影部分面积之和．62.（2023·四川成都）如图，在平面直角坐标系xOy 中，直线5y x 与y 轴交于点A ，与反比例函数ky x的图象的一个交点为(,4)B a ，过点B 作AB 的垂线l ．（1）求点A 的坐标及反比例函数的表达式；（2）若点C 在直线l 上，且ABC 的面积为5，求点C 的坐标；（3）P 是直线l 上一点，连接PA ，以P 为位似中心画PDE △，使它与PAB 位似，相似比为m ．若点D ，E 恰好都落在反比例函数图象上，求点P 的坐标及m 的值．【参考答案与解析】1.【答案】A【解析】解：∵点 1,3A 是反比例函数(0)ky k x图象上一点，∴133k ，故选：A ．2.【答案】A【解析】解：0k ∵，反比例函数ky x的图象经过第一、三象限，故点M 可能在第一象限或者第三象限，2,M a ∵的横坐标大于0， 2,M a 一定在第一象限，故选：A ．3.【答案】B【解析】解：设该反比函数解析式为 0kI k R，由题意可知，当8R 时，3I ，38k，解得：24k ，设该反比函数解析式为24I R，当6R 时，2446I，即电流为4A ，故选：B ．4.【答案】D【解析】∵ 0k y k x经过 2,4，∴解析式为8y x，设正方形的边长为x ，则点 2,E x x ，∴ 28x x ，解得122,4x x （舍去），故点 4,2E ，故选：D ．5.【答案】A【解析】解：假设P 为1000Pa ，∵F 为100N ，2F 100S =0.1m P 1000.P 1000Pa Q ，2S 0.1m .故选：A.6.【答案】B【解析】解：∵30k ，∴图象在一三象限，且在每个象限内y 随x 的增大而减小，∵2101 ，∴2130y y y ．故选：B ．7.【答案】D【解析】解：2y x，20 ，∴双曲线在二，四象限，在每一象限，y 随x 的增大而增大；∵ 123,2,,1,)2(,A x B x C x ，∴1230,0x x x ，∴231x x x ；故选：D ．8.【答案】B【解析】解：∵反比例函数4y x中0k ，∴函数图象的两个分支分别位于一、三象限，且在每一象限内y 随x 的增大而减小．∵20,10, ∴(2,),(1,)A a B b 位于第三象限，∴0,0,a b ∵210, ∴0.a b ∵30,∴点(3,)C c 位于第一象限，∴0,c ∴.b a c 故选：B ．9.【答案】C【解析】解：设反比例函数的解析式为k y x，将点 2,3 代入得：236k ，则反比例函数的解析式为6y x，所以这个函数的图象位于第二、四象限，且在每一象限内，y 随x 的增大而增大，又∵点 1233,,1,,2,y y y 在函数6y x 的图象上，且3012 ，1320y y y ，即231y y y ，故选：C ．10.【答案】D【解析】解：∵点 11,A x y ， 22,B x y ）是反比例函数2y x的图像上的两点，∴11222x y x y ，∵120x x ，∴210y y ，即120y y ，故D 正确．故选：D ．11.【答案】C【解析】解：∵当120x x 时，有12y y ，∴反比例函数4ky x的图象在一三象限，∴40k 解得：4k ，故选：C ．12.【答案】C【解析】解：如图所示，过点A B ，分别作y x ，轴的垂线，垂足分别为E D ，，AE BD ，交于点C ，依题意，B 的横坐标为1，A 的纵坐标为1，设 ,1A k ， 1,B k ∴ 1,1C ，则1,1AC k BC k ，又∵90ACB ，AB ∴ 22211k k ，∴3BC AC ，∴13k 解得：4k ，故选：C ．13.【答案】A【解析】解：AM x ∵轴于点M ，AN y 轴于直N ，90MON ，四边形AMON 是矩形，∵四边形AMON 的面积为2，2k ，∵反比例函数在第一、三象限，2k ，故选：A ．14.【答案】C 【解析】设 3,B m ，∵点B ，C 的横坐标都是3，2BC ，AC 平行于x 轴，点D 在AC 上，且其横坐标为1，∴ 3,2,1,2C m D m ，∴32m m ，解得1m ，∴ 3,1B ，∴313k ，故选：C ．15.【答案】C【解析】解：∵四边形OCBA 是矩形，∴AB OC ，OA BC ，设B 点的坐标为(,)a b ，∵矩形OABC 的对称中心M ，∴延长OM 恰好经过点B ，(,)22a bM ，∵点D 在AB 上，且14AD AB ，∴1(,)4D a b ，∴34BD a ，∴1133()224216BDM b S BD h a b ab∵D 在反比例函数的图象上，∴14ab k ，∵11332216ODM AOB AOD BDM ab S S S S ab k ，∴11332816ab ab ab ，解得：16ab ，∴144k ab，故选：C ．16.【答案】A【解析】解：如图所示，过点B 作BD x 轴，∵(0,0),(23,0),(3,1)O A B ，∴1,3BD OD ∴3AD OD ，3tan BD BOA OD∴222OB AB OD BD ，30BOA BAO ，∴60OBD ABD ，120OBA ，∵OA B 与OAB 关于直线OB 对称，∴120OBA ，∴180OBA OBD ，∴A ，B ，O 三点共线，∴2A B AB ，∵A C BC ，∴1BC ，∴2CD ，∴3,2C ，将其代入(0,0)ky k x x得：23k ，故选：A ．17.【答案】D【解析】解：∵反比例函数(0)k y k x的图象过点(1,3)，∴133k ∴3y x设直线AB 的解析式为y mx n ，∴30m n m n ，解得：3232m n,∴直线AB 的解析式为3322y x，联立33223y x y x，解得：13x y 或232x y ，∴32,2B ，设 ,0C c ，∵1313922ABC S c，解得：3c 或5c ，∴C 的坐标为(3,0)或(5,0) ，故选：D ．18.【答案】A【解析】解：如图所示，连接正方形的对角线，过点,A B 分别作x 轴的垂线，垂足分别为,C D ，点B 在3y x上，∵OB OA ，90AOB BDO ACO ，∴90CAO AOC BOD ．∴AOC OBD ≌．∴32AOC OBD S S2n ．∵A 点在第二象限，∴3n ．故选：A ．19.【答案】C【解析】设 ,A a b ，则1,B b b ，1,D a a，11,C b a∵点A 在(0)ky x x的图象上，则1S ab k ，同理∵B ，D 两点在1y x 的图象上，则241S S ，故3511122S ，又∵31211S b a，即112ab ，故2ab ，∴2k ，故选：C ．20.【答案】C【解析】解：由题意，设,k B b b，∵AB 过原点O ，∴,k A b b，过点A 作AE BC 于E ，∵ABC 是等腰三角形，∴ 2CE BE b b b ，∴4BC b ，点D 的横坐标为3b ，∵底边BC x ∥轴，CD y ∥轴，∴1141222BCD S BC CD b CD，∴6CD b，∴点D 的纵坐标为66k k b b b ，∴63,k D b b，∴ 6336k k b k b ，解得：92k ，故选：C．21.【答案】B【解析】解：如图，过点N 作NQ x 轴于点Q，设点A 的坐标为 0,0A a a ，点M 的坐标为 5,0,0M b c b c ，点N 的坐标为 ,0,0N m n m n ，则 5,2C b c ，OA a ，5OB b ，:1:4OP BP ∵，,4OP b BP b ，2NC AN ∵， 5202223b m m n c a c，解得53223b m a c n，522,33b a c N ，522,33b a cOQ NQ，23bPQ OQ OP，APN ∵ 的面积为3，3AOP NPQ OANQ S S S 梯形，即15221122232332233a c b a c b a ab ，整理得：29ab bc ，将点 5225,,,33b a c M b c N代入k y x 得：522533b a c k bc ，整理得：27a c ，将27a c 代入29ab bc 得：79bc bc ，解得98bc ，则4558k bc，故选：B ．二、填空题22.【答案】4【解析】解：∵12R ，∴4848412I R A 故答案为：4．23．【答案】【解析】解：∵点 123,y ,1,A B y 都在反比例函数6y x的图象上，∴1623y，2661y ，∵26 ，∴1y 2y ，故答案为：．23.【答案】20【解析】解：设P 关于V 的函数解析式为kP V，由图象可把点 100,60代入得：6000k ，∴P 关于V 的函数解析式为6000P V，∴当75kPa P 时，则60008075V，∴压强由75kPa 加压到100kPa ，则气体体积压缩了1008020mL ；故答案为：20．24.【答案】4（答案不唯一，满足39k 均可）【解析】解：当反比例函数(0)ky k x图像过(3,3)A 时，339k ；当反比例函数(0)ky k x图像过(3,1)B 时，313k ；∴k 的取值范围为39k ，∴k 可以取4．故答案为：4（答案不唯一，满足39k 均可）．25.【答案】6 【解析】解：如图：∵点A 在反比例函数 0k y k x 图像的一支上，点B 在反比例函数2ky x 图像的一支上，∴,22ODAE OCBE k k S k k S∵四边形ABCD 是面积为9的正方形，∴9ODAE OCBE S S ，即92kk ，解得：6k ．故答案为：6 ．26.【答案】3【解析】解：过点C 作CD x 轴于点D ，如图所示：∵30AOB BOC ，BA OA ，CB OB ，∴11,22AB OB BC OC ，∵90AOD ，∴30COD ，∵3AB ∴23OB AB 在Rt OBC △中，2233OB OC BC BC ，∴2BC ，4OC ，∵30COD ，90CDO ，∴122CD OC ，∴323OD CD ，∴点23,2C ，∴43k ，故答案为：4327.【答案】83【解析】解：方法一：∵2cos 3OAC ，∴2cos 3AD AO OAC AO AC设2AD a ，则3AO a ，∴92AC a∵矩形OABC 的面积是6，AC 是对角线，∴AOC 的面积为3，即132AO OC ∴623OC a a在Rt AOC 中，222AC AO OC 即 2229232a a a即22813644a a解得：2a 在Rt ADC中，DO∵对角线AC x ∥轴，则AD OD ，∴2458222153AOD k S a ,∵反比例函数图象在第二象限，∴83k ，方法二：∵2cos 3OAC ，∴2cos 3AD AO OAC AO AC设2AD a ，则3AO a ，∴92AC a，∴24992AD a AC a，488226993AOD AOC S S，∵0k ，∴83k ，故答案为：83．28.【答案】334【解析】解：如图，作CE OB 交OB 于点E ，，∵90A ，30AOB ，4OB ，3cos3043OA OB∵点C 为OA 的中点，113322OC OA∵CE OB ，90OEC ，30COE ∵，113333cos303222CE OC OE OC ，332C，，∵点C 在反比例函数图象上，333224k，3329.【答案】24【解析】解：设,k C a a，∵A 与x 轴相切于点B ，∴BC x 轴，∴,kOB a AC a，则点D 到BC 的距离为a ，∵CB 为A 的直径，∴122k AC BC a ，∴16224ACDk k S a a ，解得：24k ，故答案为：24．26．【答案】152【解析】∵直线11y k x b 与双曲线22k y x（其中120k k ）相交于 2,3A ， ,2B m 两点，∴2232k m ∴263k m ，，∴双曲线的表达式为：26y x， 3,2B ，∵过点B 作BP x ∥轴，交y 轴于点P ，∴3BP ，∴1153(32)22ABP S，故答案为：152．30.【答案】2【解析】解：如图，过点A B 、作AF y 轴于点F ，AD x 轴于点D ，BE x ⊥于点E，6AFO ABO BOE FABEO S S S S k ∵五边形AFOD FABEO ADEB ADEB S S S k S 矩形五边形梯形梯形6ADEB S 梯形2121()()62y y x x∵212x x 2112y y11112121111()(2)()()32==6224y y x x y y x x y x 11=8x y 8k21121111111111()()82222244ABC S AC BC x x y y x y x y =×=-×-=×==´=故答案为：2．31.【答案】6 【解析】解：连接BO，设对称轴MN 与x 轴交于点G ，∵ODE 与CBA △关于对称轴MN ，∴AG EG ，AC EO ，EC AO ，∵点A 为OE 的中点，设AG EG a ，则2EC AO AE a ，∴4AC EO a ，∵14EAF S △，∴8112EGF EAF S S△△，∵GF OD ，∴EFG EDO ∽△△，∴2EGF EOD S EG S EO △△，即2184EOD a S a △，∴11628EOD S △，∴2ACB S △，∵4AC a ，2AO a ，∴213OCB ACB AOB S S S △△△，∴132k ，∵0k ，∴6k ，故答案为：6 ．32.【答案】12；9【解析】解：如图，延长BD ，AE 交于点Q ，BD 与x 轴交于点K ，而AE x 轴，BD y ∥轴，∴90Q ，∵ABE 的面积为9，四边形ABDE 的面积为14，∴BDE △的面积是5，设,a A m m ，,a B n n，∴,a Q n m ，,b D n n ，,bm a E a m∴b a BD n n ，bm EQ n a ，bm AE m a，a a BQ m n ，∴152b a bm n n n a ，192bm a a m a m n ，整理得： 10b a bm an na ①， 18n m a b n ②，∵OK AQ ∥，2AC BC ，∴12BK BC QK AC ，∴2QK BK ，∴2a a m n，则2n m ③，把③代入②得： 3182m a b m ，∴12a b ，即12b a ④，把③代入①得： 220b a b a a ⑤，把④代入⑤得：9a ；故答案为：12；9.33.【答案】【解析】解：把 2,2A 代入(0)ky x x ，可得22k ，解得4k ，反比例函数解析式4(0)y x x，如图，过点A 作x 轴的垂线段交x 轴于点E ，过点C 作y 轴的垂线段交y 轴于点D ，2,2A ∵，AE OE ，45AOE ，9045AOD AOE ，∵将直线OA 向上平移若干个单位长度交y 轴于点B ，45CBD ,在Rt CBD △中，sin 45CD CB 22CD即点C把x 4(0)y x x，可得yC ，故答案为：．34.【答案】2023253【解析】当1x 时，1P 的纵坐标为8，当2x 时，2P 的纵坐标为4，当3x 时，3P 的纵坐标为83，当4x 时，4P 的纵坐标为2，当5x 时，5P 的纵坐标为85，…则11(84)84S ；2881(4)433S ；3881(2)233S ；481(22558S ；…881n S n n ；1238888888844228335111n n S S S S n n n n ，∴12320238202320242532023S S S S．故答案为：2023253．35.【答案】（1）4 ；（2）①④．（3）0x 或4x ．【解析】（1）根据“左加右减”的规律即可求解；∵函数1y x 的图象向右平移4个单位得到函数14y x 的图象，∴4a ；（2）根据平移的性质得出①正确；类比反比例函数图象的性质即可判断②④，根据平移的性质将y x 向左平移a 个单位，得出y x a ，即可判断③；∵1y x a可以看作是由1y x 向左平移a 0a 个单位得到的，∵函数1y x 图象的对称中心为 00，，将其对称中心向左平移a 个单位，则对称中心为 ,0a ，故①正确，②类比反比例函数图象，可得x a ¹-，故函数图象不是连续的，在直线x a 两侧，y 随x 的增大而减小；故②错误；③∵1y x关于y x 对称，同①可得，y x 向左平移a 个单位得到： y x a x a ，∴图象关于直线y x a 对称；故③不正确；④∵平移后的对称中心为 ,0a ，左右平移图象后，1y x a与y 轴没有交点，∴y 的取值范围为0y ．故④正确，（3）根据题意，画出两个函数图象，结合图象即可求解．∵4a ，∴不等式114x x如图所示，在第三象限内和第一象限内，114x x ，∴0x 或4x ，36.【答案】（1）2m ，3y x；（2）1x 或03x 【解析】（1）将点 3,1B 代入1y x m 得：31m 解得：2m 将 3,1B 代入2k y x得： 313k ∴23y x（2）由12y y 得：32x x，解得121,3x x 所以,A B 的坐标分别为1,3,3,1A B 由图形可得：当1x 或03x 时，12y y 37.【答案】（1）解：∵点B 的坐标是(0,4)，点C 为OB 中点，∴ 0,2C ，2OC BC ，由旋转可得：2BC BC ，90CBC ，∴ 2,4C ，∴248k ，∴反比例函数的表达式为8y x；（2）如图，过A 作A H BC 于H ，则90AOB A HB ，而90ABA ，AB A B，∴90ABO BAO ABO A BO ，∴BAO A BH ¢Ð=Ð，∴ABO BA H ≌，∴3AO BH ，4OB A H ，∴431OH ，∴ 4,1A ，设直线AA 为y mx n ，∴3041m n m n ，解得：1737m n，∴直线AA 为1377y x ．【解析】（1）由点B 的坐标是(0,4)，点C 为OB 中点，可得 0,2C ，2OC BC ，由旋转可得：2BC BC ，90CBC ，可得 2,4C ，可得248k ，从而可得答案；（2）如图，过A 作A H BC 于H ，则90AOB A HB ，而90ABA ，AB A B ，证明ABO BA H ≌，可得3AO BH ，4OB A H ， 4,1A ，设直线AA 为y mx n ，再建立方程组求解即可．38.【答案】（1）解：把点 3,0B 代入一次函数94y kx 得，930,4k 解得：34k ，故一次函数的解析式为3944y x，把点 1,A n 代入3944y x ，得39344n ，(1,3)A ，把点(1,3)A 代入m y x，得3m ，故反比例函数的解析式为3y x；（2）解： 3,0B ，(1,3)A ，5AB ，当5AB PB 时，(8,0)P 或(2,0)，当PA AB 时，点,P B 关于直线1x 对称，(5,0)P ，综上所述：点P 的坐标为(8,0) 或(2,0)或(5,0)．【解析】（1）根据待定系数法，把已知点代入再解方程即可得出答案；（2）首先利用勾股定理求出得AB 的长，再分两种情形讨论即可．39.【答案】（1）如图，过点C 作CD x 轴于点D ，则1CD ，90CDB ，∵BC AB ，∴90ABC ，∴90ABO CBD ，∵90CDB ，∴90BCD CBD ，∴BCD ABO ，∴ABO BCD ∽ ，∴OA BD OB CD，∵ 0,4,2,0A B ，∴4OA ，2OB ，∴421BD ，∴2BD ，∴224OD ，∴点 4,1C ，将点C 代入k y x 中，可得4k ，∴4y x，设OC 的表达式为y mx ，将点 4,1C 代入可得14m ，解得：14m，∴OC 的表达式为14y x ；（2）直线l 的解析式为1342y x，当两函数相交时，可得13442x x ，解得12x ,8x ,代入反比例函数解析式，得1122x y ，22812x y∴直线l 与反比例函数图象的交点坐标为 2,2或18,2【解析】（1）如图，过点C 作CD x 轴于点D ，证明ABO BCD ∽ ，利用相似三角形的性质得到2BD ，求出点C 的坐标，代入k y x可得反比例函数解析式，设OC 的表达式为y mx ，将点 4,1C 代入即可得到直线OC 的表达式；（2）先求得直线l 的解析式，联立反比例函数的解析式即可求得交点坐标．40.【答案】（1）∵点A 的横坐标是2，∴将2x 代入 22255y k x ，∴ 2,5A ，∴将 2,5A 代入11k y x得，110k ，∴110y x ，∵点B 的纵坐标是4 ，∴将4y 代入110y x 得，52x ，∴5,42B ，∴将5,42B 代入 2225y k x 得，254252k，∴解得22k ，∴ 222521y x x ；（2）如图所示，由题意可得，5,52C， 2,4D ，∴设CD 所在直线的表达式为y kx b ，∴55224k b k b ，解得20k b ，∴2y x ，∴当0x 时，0y ，∴直线CD 经过原点．【解析】（1）首先将点A 的横坐标代入 2225y k x 求出点A 的坐标，然后代入11k y x 求出110k ，然后将点B 的纵坐标代入110y x 求出5,42B，然后代入 2225y k x 即可求出22k ；（2）首先根据题意画出图形，然后求出点C 和点D 的坐标，然后利用待定系数法求出CD 所在直线的表达式，进而求解即可．41.【答案】（1）解：将 24A ，代入1m y x 得，42m ，解得8m ，∴反比例函数解析式为18y x；当0x ，2y b ，则 0C b ，，OC b ，当20y ，b x k，则0b B k ，b OB k ，∵OAC 与OBC △的面积比为2:1，∴2212A OC x OC OB ，整理得2A x OB ，即22b k ，解得b k 或b k ，当b k 时，将 24A ，代入2y kx b 得，42k k ，解得43k ，则24433y x ；当b k 时，将 24A ，代入2y kx b 得，42k k ，解得4k ，则244y x ；综上，一次函数解析式为24433y x 或244y x ；∴反比例函数解析式为18y x ，一次函数解析式为24433y x 或244y x ；（2）解：由题意知，由一次函数解析式不同分两种情况求解：①当一次函数解析式为24433y x 时，如图1，联立1284433y x y x ，解得383x y 或24x y ，由函数图象可知，12y y 时，x 的取值范围为3x 或02x ；②当一次函数解析式为244y x 时，如图2，联立12844y x y x ，解得18x y 或24x y ，由函数图象可知，12y y 时，x 的取值范围为1x 或02x ；综上，当一次函数解析式为24433y x 时，x 的取值范围为3x 或02x ；当一次函数解析式为244y x 时x 的取值范围为1x 或02x ．【解析】（1）将 24A ，代入1m y x 得，42m ，解得8m ，可得反比例函数解析式为18y x ；当0x ，2y b ，则 0C b ，，OC b ，当20y ，b x k，则0b B k ，，b OB k ，由OAC 与OBC △的面积比为2:1，可得2212A OC x OC OB ，整理得2A x OB ，即22b k ，解得b k 或b k ，当b k 时，将 24A ，代入2y kx b 得，42k k ，解得43k ，则24433y x ；当b k 时，将 24A ，代入2y kx b 得，42k k ，解得4k ，则244y x ；（2）由一次函数解析式不同分两种情况求解：①当一次函数解析式为24433y x 时，如图1，联立1284433y x y x ，解得383x y 或24x y ，根据函数图象判断x 的取值范围即可；②当一次函数解析式为244y x 时，如图2，联立12844y x y x ，解得18x y 或24x y ，根据函数图象判断x 的取值范围即可．42.【答案】（1）解：∵1OA ，∴ 10A ，，∵直线2y kx 经过点 10A ，，∴02k ，解得，2k ，∴直线的解析式为22y x ，∵点C 的横坐标为2，∴2226y ，∴ 26C ，，∵反比例函数 0m y x x的图象经过点C ，∴2612m ；（2）解：由（1）得反比例函数的解析式为12y x ，令0x ，则2022y ，∴点 02B ，，设点 22D a a ，，则点12E a a，，∵以B ，D ，E ，O 为顶点的四边形为平行四边形，∴2DE OB ，∴12222a a，整理得12222a a 或12222a a ，由12222a a得222122a a a ，整理得26a ，解得a ∵0a ，∴a∴点 2D ；由12222a a得222122a a a ，整理得2260a a ，解得1a ，∵0a ，∴1a ，∴点1D ；综上，点D 的坐标为 2或1．【解析】（1）求得 10A ，，利用待定系数法即可求得直线的式，再求得 26C ，，据此即可求解；（2）设点 22D a a ，，则点12E a a，，利用平行四边形的性质得到12222a a ，解方程即可求解．43.【答案】（1）解：设反比例函数解析式为1k y x ，将 16A ，代入1k y x ，可得161k ，解得16k ，反比例函数的解析式为6y x ，把3,3B a a 代入6y x ，可得336a a ，解得1a ，经检验，1a 是方程的解，3,2B ，设一次函数的解析式为2y k x b ，将 16A ，， 3,2B 代入2y k x b ，可得623x bx b ，解得224k b ，一次函数的解析式为24y x ；（2）解：当0y 时，可得024x ，解得2x ，2,0C ，2OC ，112622822OAC OBC OAB S S S △△△，。

2020全国各地中考数学模拟试卷专项解析：反比例函数

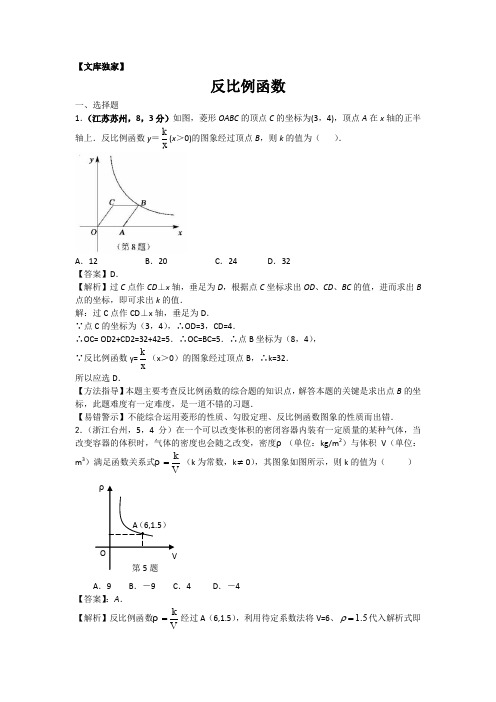
【文库独家】反比例函数一、选择题 1．（江苏苏州，8，3分）如图，菱形OABC 的顶点C 的坐标为(3，4)，顶点A 在x 轴的正半轴上．反比例函数y ＝kx(x ＞0)的图象经过顶点B ，则k 的值为（）．A ．12B ．20C ．24D ．32 【答案】D ．【解析】过C 点作CD ⊥x 轴，垂足为D ，根据点C 坐标求出OD 、CD 、BC 的值，进而求出B 点的坐标，即可求出k 的值．解：过C 点作CD ⊥x 轴，垂足为D ． ∵点C 的坐标为（3，4），∴OD=3，CD=4．∴OC= OD2+CD2=32+42=5．∴OC=BC=5．∴点B 坐标为（8，4）， ∵反比例函数y=kx（x ＞0）的图象经过顶点B ，∴k=32．所以应选D ．【方法指导】本题主要考查反比例函数的综合题的知识点，解答本题的关键是求出点B 的坐标，此题难度有一定难度，是一道不错的习题．【易错警示】不能综合运用菱形的性质、勾股定理、反比例函数图象的性质而出错． 2．（浙江台州，5，4分）在一个可以改变体积的密闭容器内装有一定质量的某种气体，当改变容器的体积时，气体的密度也会随之改变，密度ρ（单位：kg/m 2）与体积V （单位：m 3）满足函数关系式Vk=ρ（k 为常数，k ≠0），其图象如图所示，则k 的值为（）A ．9B ．－9C ．4D ．－4 【答案】：A ．【解析】反比例函数Vk=ρ经过A （6,1.5），利用待定系数法将V=6、 1.5ρ=代入解析式即可求出解析式。

【方法指导】本题考查待定系数法求反比例函数解析式。

先设出函数解析式，再根据条件确定解析式中未知数的系数，从而具体写出这个式子的方法，叫做待定系数法。

3.（贵州安顺，7，3分）若22)1(-+=ax a y 是反比例函数，则a 的取值为（）A ．1B ．－1C ．±1D ．任意实数【答案】：A ．【解析】∵此函数是反比例函数， ∴，解得a=1．【方法指导】本题考查的是反比例函数的定义，先根据反比例函数的定义列出关于a 的不等式组，求出a 的值即可．【易错警示】解答时易把系数a+1≠0漏掉而错得a=±1． 4．（山东临沂，13，3分）如图，等边三角形OAB 的一边OA 在x 轴上，双曲线y在第一象限内的图象经过OB 边的中点C ，则点B 的坐标是（）A ．（1B ．1）C ．（2，D ．（2）【答案】：C ．【方法指导】【易错警示】5．（山东滨州，6，3分）若点A(1，y 1)、B(2，y 2)都在反比例函数y=kx(k ＞0)的图象上，则y 1、y 2的大小关系为（）A ．y 1＜y 2B ．y 1≤y 2C ．y 1＞y 2D ．y 1≥y 2 【答案】：C ．【解析】根据反比例函数的图象.由 k ＞0可知图象在第一象限内y 随x 的增大而减小；因为1＜2，所以y 1＞y 2．【方法指导】本题考查反比例函数的图象及性质. 当k>0时，反比例函数图象的两个分支分别在第一、三象限内，且在每个象限内，y 随x 的增大而减小；当k<0时，图象的两个分支分别在第二、四象限内，且在每个象限内，y 随x 的增大而增大．注意：不能说成“当k ＞0时，反比例函数y 随x 的增大而减小，当k ＜0时，反比例函数y 随x 的增大而增大.”因为，当x 由负数经过0变为正数时，上述说法不成立.6. 广东省，10，3分）已知210k k <<，则函数11-=x k y 和xk y 2=的图象大致是【答案】 A .【解析】因为01<k ，所以直线11-=x k y 经过一、三、四象限，由此，可以排除选项B 和D ；又因为02>k ，双曲线xk y 2=的两个分支分别在第一、三象限，只有选项A 符合．由此确定答案只能选A ．【方法指导】在同一坐标系中综合考查几种函数图象的问题比较常见，因为这类题通常涉及到地待定系数比较多，而且范围不定，如果把步骤规划好，不理清思路，就会弄糊涂． 7. (湖南邵阳,7,3分)下列四个点中，在反比例函数y = －6x 的图象上的是( ） A ．(3，－2) B ．(3，2) C ．(2，3) D ．(－2，－3) 【答案】：A ．【解析】：A 、∵3×（﹣2）=﹣6，∴此点在反比例函数的图象上，故本选项正确； B 、∵3×2=6≠﹣6，∴此点不在反比例函数的图象上，故本选项错误； C 、∵2×3=6≠﹣6，∴此点不在反比例函数的图象上，故本选项错误； D 、∵（﹣2）×（﹣3）=6≠﹣6，∴此点不在反比例函数的图象上，故本选项错误．故选A ．【方法指导】：本题考查的是反比例函数图象上点的坐标特点，熟知反比例函数xky =中，xy k =为定值是解答此题的关键.8. (湖南株洲,7,3分)已知点A （1，1y ）、B （2，2y ）、C （－3，3y ）都在反比例函数xy 6=的图象上，则的大小关系是（）A. 213y y y <<B. 321y y y <<C. 312y y y <<D. 123y y y << 【答案】：D【解析】：将A （1，1y ）、B （2，2y ）、C （－3，3y ）代入xy 6=得到1y =6,2y =3,3y =－2,则大小关系是123y y y .【方法指导】本题考查了反比例函数的图像，将值代入求出即可.9．（山东德州，8，3分）下列函数中，当x>0时，y 随x 的增大而增大的是（）A 、y=－x+1B 、y=x 2－1C 、y=x1D 、y=－x 2+1【答案】B【解析】A 、函数y=－x+1 ，当x>0时，y 随x 的增大而减小；B 、函数y=x 2－1 ，当x>0（对称轴y 轴右侧）时，y 随x 的增大而增大；C 、函数y=x1，当x>0（第－象限）时，双曲线一分支y 随x 的增大而减小； D 、抛物线y=－x 2+1，当x>0（对称轴y 轴右侧）时，y 随x 的增大而减小.【方法指导】本题考查一次函数、反比例函数、二次函数图象与性质.解答本题需要了解各函数图象的增减性特点，解题时不妨画个示意图进行直观判断. 10．（四川凉山州，12，4分）如图，正比例函数1y 与反比例函数2y 相交于点E （1-，2），若120y y >>，则x 的取值【答案】A.【解析】先利用函数的图象可知,当120y y >>时, x 的取值范围是x ＜－1,所以其在数轴上表示为A.【方法指导】本题考查利用函数图象比较大小及在数轴上如何表示不等式的解集的问题.利用图象比较大小时,图象在上方的函图值大,函数图象的交点即为函数值相等,函数图象在下方的函数值小.在数轴上表示不等式的解集是,一般有等号时有实数点表示,没有等号是圆表示.11．（江西，4，3分）如图，直线y =x +a －2与双曲线y=x4交于A ，B 两点，则当线段AB 的长度取最小值时，a 的值为（）． A ．0 B ．1 C ．2D ．5【答案】CD ．C ．B ．A ．【解析】把原点（0，0）代入2y x a =+-中，得2a =.选C..【方法指导】要求a 的值，必须知道x 、y 的值（即一点的坐标）由图形的对称性可直观判断出直线AB 过原点（0，0）时，线段AB 才最小，把原点的坐标代入解析式中即可求出a 的值.12．（兰州，5，3分）当x ＞0时，函数的图象在（）A ．第四象限B ．第三象限C ．第二象限D ．第一象限考点：反比例函数的性质．分析：先根据反比例函数的性质判断出反比例函数的图象所在的象限，再求出x ＞0时，函数的图象所在的象限即可．解答：解：∵反比例函数中，k =﹣5＜0，∴此函数的图象位于二、四象限， ∵x ＞0，∴当x ＞0时函数的图象位于第四象限．故选A点评：本题考查的是反比例函数的性质，即反比例函数y =（k ≠0）的图象是双曲线；当k ＜0时，双曲线的两支分别位于第二、第四象限．13．（兰州，11，3分）已知A （﹣1，y 1），B （2，y 2）两点在双曲线y =上，且 y 1＞y 2，则m 的取值范围是（） A ．m ＜0B ．m ＞0C ．m ＞﹣D ．m ＜﹣考点：反比例函数图象上点的坐标特征．专题：计算题．分析：将A （﹣1，y 1），B （2，y 2）两点分别代入双曲线y =，求出 y 1与y 2的表达式，再根据 y 1＞y 2则列不等式即可解答．解答：解：将A （﹣1，y 1），B （2，y 2）两点分别代入双曲线y =得，y 1=﹣2m ﹣3， y 2=，∵y 1＞y 2， ∴﹣2m ﹣3＞，解得m＜﹣，故选D．点评：本题考查了反比例函数图象上点的坐标特征，要知道，反比例函数图象上的点符合函数解析式．14．（贵州安顺，7，3分）若是反比例函数，则a的取值为（）A．1 B．﹣l C．±l D．任意实数考点：反比例函数的定义．专题：探究型．分析：先根据反比例函数的定义列出关于a的不等式组，求出a的值即可．解答：解：∵此函数是反比例函数，∴，解得a=1．故选A．点评：本题考查的是反比例函数的定义，即形如y=（k为常数，k≠0）的函数称为反比例函数．15．（贵州毕节，13，3分）一次函数y=kx+b（k≠0）与反比例函数的图象在同一直角坐标系下的大致图象如图所示，则k、b的取值范围是（）又∵反比例函数16．（湖北孝感，11，3分）如图，函数y=﹣x与函数的图象相交于A，B两点，过A，B两点分别作y轴的垂线，垂足分别为点C，D．则四边形ACBD的面积为（）的图象上过点B分别向x轴，y轴作垂线，垂足分别为A，C，则矩形OABC的面积为（）18. .[湖南邵阳，7，3分]下列四个点中，在反比例函数y = -6x 的图象上的是( ） A ．(3，-2) B ．(3，2) C ．(2，3) D ．(-2，-3)知识考点：反比例函数图象上的点的坐标.审题要津：此题可将y = -6x 转换为6= -xy 即可解答.满分解答：解：A.∵3×（-2）=-6，∴此点在反比例函数图象上；B .∵3×2=6，∴此点不在反比例函数图象上；C .∵2×3=6，∴此点不在反比例函数图象上；D .∵（-2）×（-3）=6，∴此点不在反比例函数图象上.故选A .名师点评：解决此题还应熟练掌握反比函数解析式的三种形式的转换：y =xk⇔y =kx ⇔k =xy (k ≠0，k 为常数). 19. ．（湖南张家界，13，3分）如图，直线x=2与反比例函数和的图象分别交于A 、B 两点，若点P 是y 轴上任意一点，则△PAB 的面积是．分别代入、，得1数y =k 2x 的图像没有公共点，则(A) k 1+k 2<0 (B) k 1+k 2>0 (C) k 1k 2<0 (D) k 1k 2>0 答案：C解析：当k 1>0，k2<0时，正比函数经过一、三象限，反比函数在二、四象限，没有交点；当k 1＜0，k2＞0时，正比函数经过二、四象限，反比函数在一、三象限，没有交点；所以，选C 。

中考数学复习----《反比例函数之综合应用》知识点总结与练习题(含答案解析)

中考数学复习----《反比例函数之综合应用》知识点总结与练习题（含答案解析）知识点总结1. 反比例函数k 的集合意义：①过反比例函数图像上任意一点作坐标轴的垂线，两垂线与坐标轴构成一个矩形，矩形的面积等于k 。

②过反比例函数图像上任意一点作其中一条坐标轴的垂线，并连接这个点与原点，则构成一个三角形。

这个三角形的面积等于2k 。

2. 待定系数法求反比例函数解析式：在反比例函数中只有一个系数k ，所以只需要在图像上找一个对应的点即可求出k 的值，从而求出反比例函数解析式。

3. 反比例函数与一次函数的不等式问题：若反比例函数()0≠=k x ky 与一次函数()0≠+=k b kx y 有交点，则不等式b kx xk +＞的解集取反比例函数图像在一次函数图像上方的部分所对应的自变量取值范围；等式b kx xk+＜的解集取反比例函数图像在一次函数图像下方的部分所对应的自变量取值范围。

反比例函数与一次函数的交点把自变量分成三部分。

练习题1、（2022•日照）如图，矩形OABC 与反比例函数y 1＝xk1（k 1是非零常数，x ＞0）的图像交于点M ，N ，与反比例函数y 2＝xk2（k 2是非零常数，x ＞0）的图像交于点B ，连接OM ，ON ．若四边形OMBN 的面积为3，则k 1﹣k 2＝（）A ．3B ．﹣3C ．23 D ．﹣23【分析】根据矩形的性质以及反比例函数系数k 的几何意义即可得出结论．【解答】解：∵y 1、y 2的图像均在第一象限， ∴k 1＞0，k 2＞0，∵点M 、N 均在反比例函数y 1＝（k 1是非零常数，x ＞0）的图像上，∴S △OAM ＝S △OCN ＝k 1，∵矩形OABC 的顶点B 在反比例函数y 2＝（k 2是非零常数，x ＞0）的图像上，∴S 矩形OABC ＝k 2，∴S 四边形OMBN ＝S 矩形OABC ﹣S △OAM ﹣S △OCN ＝3， ∴k 2﹣k 1＝3， ∴k 1﹣k 2＝﹣3，故选：B ．2、（2022•牡丹江）如图，等边三角形OAB ，点B 在x 轴正半轴上，S △OAB ＝43，若反比例函数y ＝xk（k ≠0）图像的一支经过点A ，则k 的值是（）A ．233 B ．23C ．433 D ．43【分析】根据正三角形的性质以及反比例函数系数k 的几何意义，得出S △AOC ＝S △AOB ＝2＝|k |，即可求出k 的值．【解答】解：如图，过点A 作AC ⊥OB 于点C ， ∵△OAB 是正三角形， ∴OC ＝BC ，∴S △AOC ＝S △AOB ＝2＝|k |，又∵k ＞0， ∴k ＝4，故选：D ．3、（2022•郴州）如图，在函数y ＝x2（x ＞0）的图像上任取一点A ，过点A 作y 轴的垂线交函数y ＝﹣x8（x ＜0）的图像于点B ，连接OA ，OB ，则△AOB 的面积是（）A ．3B ．5C ．6D ．10【分析】根据反比例函数系数k 的几何意义进行计算即可．【解答】解：∵点A 在函数y ＝（x ＞0）的图像上， ∴S △AOC ＝×2＝1，又∵点B 在反比例函数y ＝﹣（x ＜0）的图像上， ∴S △BOC ＝×8＝4， ∴S △AOB ＝S △AOC +S △BOC ＝1+4 ＝5，故选：B ．4、（2022•黑龙江）如图，在平面直角坐标系中，点O 为坐标原点，平行四边形OBAD 的顶点B 在反比例函数y ＝x 3的图像上，顶点A 在反比例函数y ＝xk的图像上，顶点D 在x 轴的负半轴上．若平行四边形OBAD 的面积是5，则k 的值是（）A ．2B ．1C ．﹣1D ．﹣2【分析】设B （a ，），根据四边形OBAD 是平行四边形，推出AB ∥DO ，表示出A 点的坐标，求出AB ＝a ﹣，再根据平行四边形面积公式列方程，解出即可．【解答】解：设B （a ，）， ∵四边形OBAD 是平行四边形， ∴AB ∥DO ， ∴A （，），∴AB ＝a ﹣，∵平行四边形OBAD 的面积是5， ∴（a ﹣）＝5，解得k ＝﹣2，故选：D ．5、（2022•十堰）如图，正方形ABCD 的顶点分别在反比例函数y ＝xk 1（k 1＞0）和y ＝xk 2（k 2＞0）的图像上．若BD ∥y 轴，点D 的横坐标为3，则k 1+k 2＝（）A ．36B ．18C ．12D ．9【分析】连接AC交BD于E，延长BD交x轴于F，连接OD、OB，设AE＝BE＝CE＝DE ＝m，D（3，a），根据BD∥y轴，可得B（3，a+2m），A（3+m，a+m），即知k1＝3（a+2m）＝（3+m）（a+m），从而m＝3﹣a，B（3，6﹣a），由B（3，6﹣a）在反比例函数y＝（k1＞0）的图像上，D（3，a）在y＝（k2＞0）的图像上，得k1＝3（6﹣a）＝18﹣3a，k2＝3a，即得k1+k2＝18﹣3a+3a＝18．【解答】解：连接AC交BD于E，延长BD交x轴于F，连接OD、OB，如图：∵四边形ABCD是正方形，∴AE＝BE＝CE＝DE，设AE＝BE＝CE＝DE＝m，D（3，a），∵BD∥y轴，∴B（3，a+2m），A（3+m，a+m），∵A，B都在反比例函数y＝（k1＞0）的图像上，∴k1＝3（a+2m）＝（3+m）（a+m），∵m≠0，∴m＝3﹣a，∴B（3，6﹣a），∵B（3，6﹣a）在反比例函数y＝（k1＞0）的图像上，D（3，a）在y＝（k2＞0）的图像上，∴k1＝3（6﹣a）＝18﹣3a，k2＝3a，∴k1+k2＝18﹣3a+3a＝18；故选：B ．6、（2022•邵阳）如图是反比例函数y ＝x1的图像，点A （x ，y ）是反比例函数图像上任意一点，过点A 作AB ⊥x 轴于点B ，连接OA ，则△AOB 的面积是（）A ．1B ．C ．2D ．【分析】由反比例函数的几何意义可知，k ＝1，也就是△AOB 的面积的2倍是1，求出△AOB 的面积是．【解答】解：∵A （x ，y ）， ∴OB ＝x ，AB ＝y ，∵A 为反比例函数y ＝图像上一点， ∴xy ＝1，∴S △ABO ＝AB •OB ＝xy ＝1＝，故选：B ．7、（2022•内江）如图，在平面直角坐标系中，点M 为x 轴正半轴上一点，过点M 的直线l ∥y 轴，且直线l 分别与反比例函数y ＝x 8和y ＝xk的图像交于P 、Q 两点．若S △POQ ＝15，则k 的值为（）A ．38B ．22C ．﹣7D ．﹣22【分析】利用k 的几何意义解题即可．【解答】解：∵直线l ∥y 轴， ∴∠OMP ＝∠OMQ ＝90°，∴S △OMP ＝×8＝4，S △OMQ ＝﹣k ．又S △POQ ＝15， ∴4﹣k ＝15，即k ＝11，∴k ＝﹣22．故选：D ．8、（2022•东营）如图，△OAB 是等腰直角三角形，直角顶点与坐标原点重合，若点B 在反比例函数y ＝x1（x ＞0）的图像上，则经过点A 的函数图像表达式为．【分析】作AD ⊥x 轴于D ，BC ⊥x 轴于C ，根据△OAB 是等腰直角三角形，可证明△BOC ≌△OAD ，利用反比例函数k 的几何意义得到S △OBC ＝，则S △OAD ＝，所以|k |＝，然后求出k 得到经过点A 的反比例函数解析式．【解答】解：如图，作AD ⊥x 轴于D ，BC ⊥x 轴于C ， ∴∠ADO ＝∠BCO ＝90°，∵∠AOB ＝90°， ∴∠AOD +∠BOC ＝90°， ∴∠AOD +∠DAO ＝90°， ∴∠BOC ＝∠DAO ， ∵OB ＝OA ，∴△BOC ≌△OAD （AAS ），∵点B 在反比例函数y ＝（x ＞0）的图像上， ∴S △OBC ＝， ∴S △OAD ＝， ∴k ＝﹣1，∴经过点A 的反比例函数解析式为y ＝﹣．故答案为：y ＝﹣．9、（2022•盐城）已知反比例函数的图像经过点（2，3），则该函数表达式为．【分析】利用反比例函数的定义列函数的解析式，运用待定系数法求出函数的解析式即可．【解答】解：令反比例函数为y ＝（k ≠0）， ∵反比例函数的图像经过点（2，3）， ∴3＝， k ＝6，∴反比例函数的解析式为y ＝．故答案为：y ＝．10、（2022•湖北）在反比例函数y ＝xk 1−的图像的每一支上，y 都随x 的增大而减小，且整式x 2﹣kx +4是一个完全平方式，则该反比例函数的解析式为．【分析】由整式x 2﹣kx +4是一个完全平方式，可得k ＝±4，由反比例函y ＝的图像的每一支上，y 都随x 的增大而减小，可得k ﹣1＞0，解得k ＞1，则k ＝4，即可得反比例函数的解析式．【解答】解：∵整式x 2﹣kx +4是一个完全平方式，∴k ＝±4， ∵反比例函数y ＝的图像的每一支上，y 都随x 的增大而减小，∴k ﹣1＞0，解得k ＞1， ∴k ＝4，∴反比例函数的解析式为y ＝．故答案为：y ＝．35．（2022•陕西）已知点A （﹣2，m ）在一个反比例函数的图像上，点A '与点A 关于y 轴对称．若点A '在正比例函数y ＝21x 的图像上，则这个反比例函数的表达式为．【分析】根据轴对称的性质得出点A '（2，m ），代入y ＝x 求得m ＝1，由点A （﹣2，1）在一个反比例函数的图像上，从而求得反比例函数的解析式．【解答】解：∵点A '与点A 关于y 轴对称，点A （﹣2，m ）， ∴点A '（2，m ），∵点A '在正比例函数y ＝x 的图像上， ∴m ＝＝1，∴A （﹣2，1），∵点A （﹣2，1）在一个反比例函数的图像上， ∴反比例函数的表达式为y ＝﹣，故答案为：y ＝﹣．11、（2022•攀枝花）如图，正比例函数y ＝k 1x 与反比例函数y ＝xk 2的图像交于A （1，m ）、B 两点，当k 1x ≤xk2时，x 的取值范围是（）A ．﹣1≤x ＜0或x ≥1B ．x ≤﹣1或0＜x ≤1C ．x ≤﹣1或x ≥1D ．﹣1≤x ＜0或0＜x ≤1【分析】根据反比例函数的对称性求得B 点的坐标，然后根据图像即可求得．【解答】解：∵正比例函数y ＝k 1x 与反比例函数y ＝的图像交于A （1，m ）、B 两点，∴B （﹣1，﹣m ），由图像可知，当k 1x ≤时，x 的取值范围是﹣1≤x ＜0或x ≥1，故选：A ．37．（2022•东营）如图，一次函数y 1＝k 1x +b 与反比例函数y 2＝xk 2的图像相交于A ，B 两点，点A 的横坐标为2，点B 的横坐标为﹣1，则不等式k 1x +b ＜xk2的解集是（）A ．﹣1＜x ＜0或x ＞2B ．x ＜﹣1或0＜x ＜2C ．x ＜﹣1或x ＞2D ．﹣1＜x ＜2【分析】根据两函数图像的上下位置关系结合交点横坐标，即可得出不等式k 1x +b ＜的解集，此题得解．【解答】解：观察函数图像可知，当﹣1＜x ＜0或x ＞2时，一次函数y 1＝k 1x +b 的图像在反比例函数y 2＝的图像的下方，∴不等式k 1x +b ＜的解集为：﹣1＜x ＜0或x ＞2，故选：A ．12、（2022•朝阳）如图，正比例函数y ＝ax （a 为常数，且a ≠0）和反比例函数y ＝xk（k 为常数，且k ≠0）的图像相交于A （﹣2，m ）和B 两点，则不等式ax ＞xk的解集为（）A ．x ＜﹣2或x ＞2B ．﹣2＜x ＜2C ．﹣2＜x ＜0或x ＞2D ．x ＜﹣2或0＜x ＜2【分析】根据关于原点对称的点的坐标特征求得B （2，﹣m ），然后根据函数的图像的交点坐标即可得到结论．【解答】解：∵正比例函数y ＝ax （a 为常数，且a ≠0）和反比例函数y ＝（k 为常数，且k ≠0）的图像相交于A （﹣2，m ）和B 两点， ∴B （2，﹣m ），∴不等式ax ＞的解集为x ＜﹣2或0＜x ＜2，故选：D ．13、（2022•无锡）一次函数y ＝mx +n 的图像与反比例函数y ＝xm的图像交于点A 、B ，其中点A 、B 的坐标为A （﹣m1，﹣2m ）、B （m ，1），则△OAB 的面积是（） A ．3B ．413C ．27D ．415【分析】根据反比例函数图像上点的坐标特征求出m ，进而求出点A 、B 的坐标，根据三角形的面积公式计算即可．【解答】解：∵点A （﹣，﹣2m ）在反比例函数y ＝上， ∴﹣2m ＝，解得：m ＝2，∴点A 的坐标为：（﹣，﹣4），点B 的坐标为（2，1）， ∴S △OAB ＝××5﹣××4﹣×2×1﹣×1＝，故选：D ．14、（2022•荆州）如图是同一直角坐标系中函数y 1＝2x 和y 2＝x2的图像．观察图像可得不等式2x ＞x2的解集为（）A ．﹣1＜x ＜1B ．x ＜﹣1或x ＞1C ．x ＜﹣1或0＜x ＜1D ．﹣1＜x ＜0或x ＞1【分析】结合图像，数形结合分析判断．【解答】解：由图像，函数y 1＝2x 和y 2＝的交点横坐标为﹣1，1， ∴当﹣1＜x ＜0或x ＞1时，y 1＞y 2，即2x ＞，故选：D ．15、（2022•怀化）如图，直线AB 交x 轴于点C ，交反比例函数y ＝xa 1−（a ＞1）的图像于A 、B 两点，过点B 作BD ⊥y 轴，垂足为点D ，若S △BCD ＝5，则a 的值为（）A．8B．9C．10D．11【分析】设点B的坐标为（m，），然后根据三角形面积公式列方程求解．【解答】解：设点B的坐标为（m，），∵S△BCD＝5，且a＞1，∴×m×＝5，解得：a＝11，故选：D．16、（2022•宁夏）在显示汽车油箱内油量的装置模拟示意图中，电压U一定时，油箱中浮子随油面下降而落下，带动滑杆使滑动变阻器滑片向上移动，从而改变电路中的电流，电流表的示数对应油量体积，把电流表刻度改为相应油量体积数，由此知道油箱里剩余油量．在不考虑其他因素的条件下，油箱中油的体积V与电路中总电阻R总（R总＝R+R0）是反比例关系，电流I与R总也是反比例关系，则I与V的函数关系是（）A．反比例函数B．正比例函数C．二次函数D．以上答案都不对【分析】由油箱中油的体积V与电路中总电阻R总是反比例关系，电流I与R总是反比例关系，可得V＝I（为常数），即可得到答案．【解答】解：由油箱中油的体积V与电路中总电阻R总是反比例关系，设V•R总＝k（k为常数），由电流I与R总是反比例关系，设I•R总＝k'（k为常数），∴＝，∴V＝I（为常数），∴I与V的函数关系是正比例函数，故选：B．17、（2022•宜昌）已知经过闭合电路的电流I（单位：A）与电路的电阻R（单位：Ω）是反比例函数关系．根据下表判断a和b的大小关系为（）A．a＞b B．a≥b C．a＜b D．a≤b【分析】根据等量关系“电流＝”，即可求解．【解答】解：∵闭合电路的电流I（单位：A）与电路的电阻R（单位：Ω）是反比例函数关系，∴40a＝80b，∴a＝2b，∴a＞b，故选：A．18、（2022•丽水）已知电灯电路两端的电压U为220V，通过灯泡的电流强度I（A）的最大限度不得超过0.11A．设选用灯泡的电阻为R（Ω），下列说法正确的是（）A．R至少2000ΩB．R至多2000ΩC．R至少24.2ΩD．R至多24.2Ω【分析】利用已知条件列出不等式，解不等式即可得出结论．【解答】解：∵电压U一定时，电流强度I（A）与灯泡的电阻为R（Ω）成反比例，∴I＝．∵已知电灯电路两端的电压U为220V，∴I＝．∵通过灯泡的电流强度I（A）的最大限度不得超过0.11A，∴≤0.11，∴R≥2000．故选：A．19、（2022•郴州）科技小组为了验证某电路的电压U（V）、电流I（A）、电阻R（Ω）三者之间的关系：I＝U，测得数据如下：那么，当电阻R＝55Ω时，电流I＝A．【分析】由表格数据求出反比例函数的解析式，再将R＝55Ω代入即可求出答案．【解答】解：把R＝220，I＝1代入I＝得：1＝，解得U＝220，∴I＝，把R＝55代入I＝得：I＝＝4，故答案为：4．20、（2022•山西）根据物理学知识，在压力不变的情况下，某物体承受的压强p（Pa）是它的受力面积S（m2）的反比例函数，其函数图像如图所示．当S＝0.25m2时，该物体承受的压强p的值为Pa．【分析】设p＝，把（0.1，1000）代入得到反比例函数的解析式，再把S＝0.25代入解析式即可解决问题．【解答】解：设p＝，∵函数图像经过（0.1，1000），∴k＝100，∴p＝，当S＝0.25m2时，物体所受的压强p＝＝400（Pa），故答案为：400．。

中考数学总复习《待定系数法求反比例函数解析式》练习题(含答案)

待定系数法求反比例函数解析式一、填空题（本大题共2小题）1.已知：如图，在平面直角坐标系xOy 中，Rt OCD ∆的一边OC 在x 轴上，90C ∠=︒，点D 在第一象限，3OC =，4DC =，反比例函数的图象经过OD 的中点A ． ⑴求该反比例函数的解析式；⑵若该反比例函数的图象与Rt OCD ∆的另一边交于点B ，求过A 、B 两点的直线的解析式．2.已知关于x 的一次函数2y x m =-+和反比例函数xn y 1+=的图象都经过点(2,1)A -，则____m =，____n =．二、解答题（本大题共5小题）3.已知：如图，在平面直角坐标系xOy 中，Rt OCD ∆的一边OC 在x 轴上，90C ∠=︒，点D 在第一象限，3OC =，4DC =，反比例函数的图象经过OD 的中点A ． ⑴求该反比例函数的解析式；⑵若该反比例函数的图象与Rt OCD ∆的另一边交于点B ，求过A 、B 两点的直线的解析式．4.已知反比例函数k y x=的图象经过点(A⑴试确定此反比例函数的解析式；⑵点O 是坐标原点，将线段OA 绕O 点顺时针旋转30︒得到线段OB ，判断点B是否在此反比例函数的图象上，并说明理由5.已知点(,2)A m 、(2,)B n 都在反比例函数xm y 3+=的图象上． (1)求m 、n 的值；(2)若直线y mx n =-与x 轴交于点C ，求C 关于y 轴对称点'C 的坐标．6.如图，反比例函数x k y =的图象与直线2y x =-交于点A ，且A 点纵坐标为1，求该反比例函数的解析式．7.已知函数12y y y =-，且1y 为x 的反比例函数，2y 为x 的正比例函数，且23-=x 和1x =时，y 的值都是1．求y 关于x 的函数关系式．待定系数法求反比例函数解析式答案解析一、填空题1.⑴)0(3>=x x y ；⑵.332+-=x y 2.－3；－3二、解答题3.⑴)0(3>=x x y ；⑵.332+-=x y 4.注意“30︒角所对直角边等于斜边一半”⑴y =；⑵B 点坐标为(-，因此点B 在反比例函数的图象上 5.(1)3m n ==；(2)'(1,0)C - 6.xy 3=． 7..23x x y -=。

2020年中考数学高频重点《反比例函数与一次函数的综合》专题突破精练精解(含答案)

【中考数学】专题07 反比例函数与一次函数的综合【达标要求】1.认识反比例函数是描述具有反比例变化规律的数学模型.2.结合具体情境体会反比例函数的意义，能根据已知条件确定反比例函数的解析式.3.能画出反比例函数ky x=(k 为常数，0k ≠)的图象，根据图象和解析式探索并理解0k > 和0k <时图象的变化情况.4.能用反比例函数解决简单的实际问题.【知识梳理】知识点1 反比例函数的概念形如 (k 为常数，0k ≠)的函数，叫做反比例函数，其中x 叫自变量，y 是x 的函数.变式:1y kx -=或xy k =(k 为常数，0k ≠). 知识点2 反比例函数的图像和性质知识点3 k的集合意义在反比例函数kyx=(k为常数，0k≠)的图象上任取一点，过这个点分别作x轴、y轴的平行线，两平行线与坐标轴围成的矩形的面积的于知识点4 用待定系数法求反比例函数的解析式先设函数解析式为kyx=(k为常数，0k≠)，在根据条件求出未知系数k的值，从而写出这个函数解析式.【精练精解】1.在同一平面直角坐标系中，函数y=﹣x+k与y=（k为常数，且k≠0）的图象大致是（）A．B．C．D．2.若反比例函数的图象上有两个不同的点关于y轴对称点都在一次函数y=–x+m的图象上，则m的取值范围是（）A．m>B．m<-C．m m><-．m-<<kxxy2-=3.如图，一次函数y=－x+3的图象与反比例函数y=kx（k≠0）在第一象限的图象交于A（1，a）和B两点，与x轴交于点C．（1）求反比例函数的解析式；（2）若点P在x轴上，且△APC的面积为5，求点P的坐标．4.如图，已知反比例函数y=kx（k≠0）的图象与一次函数y=﹣x+b的图象在第一象限交于A（1，3），B（3，1）两点．（1）求反比例函数和一次函数的表达式；（2）已知点P（a，0）（a>0），过点P作平行于y轴的直线，在第一象限内交一次函数y=﹣x+b的图象于点M，交反比例函数y=kx上的图象于点N．若PM>PN，结合函数图象直接写出a的取值范围．5.已知一次函数y =kx +b 的图象与反比例函数y =mx的图象交于点A ，与x 轴交于点B （5，0），若OB =AB ，且S △OAB =152．（1）求反比例函数与一次函数的表达式；（2）若点P 为x 轴上一点，△ABP 是等腰三角形，求点P 的坐标．6.如图，一次函数y =k 1x +b 的图象与反比例函数y =2k x的图象相交于A 、B 两点，其中点A 的坐标为（–1，4），点B 的坐标为（4，n ）．（1）根据图象，直接写出满足k 1x +b ＞2k x的x 的取值范围；（2）求这两个函数的表达式；（3）点P 在线段AB 上，且S △AOP ：S △BOP =1：2，求点P 的坐标．7.如图，一次函数y=kx+b的图象与反比例函数y=mx的图象相交于A（–1，n）、B（2，–1）两点，与y轴相交于点C．（1）求一次函数与反比例函数的解析式；（2）若点D与点C关于x轴对称，求△ABD的面积；（3）若M（x1，y1）、N（x2，y2）是反比例函数y=mx上的两点，当x1<x2<0时，比较y2与y1的大小关系．8.如图，四边形ABCD 是平行四边形，点A(1，0)，B(3，1)，C(3，3)．反比例函数y ＝mx (x ＞0)的图象经过点D ，点P 是一次函数y ＝kx ＋3－3k(k ≠0)的图象与该反比例函数图象的一个公共点． (1)求反比例函数的解析式；(2)通过计算，说明一次函数y ＝kx ＋3－3k(k ≠0)的图象一定经过点C ；(3)对于一次函数y ＝kx ＋3－3k(k ≠0)，当y 随x 的增大而增大时，确定点P 横坐标的取值范围．(不必写出过程)9.某蔬菜生产基地的气温较低时，用装有恒温系统的大棚栽培一种新品种蔬菜．如图是试验阶段的某天恒温系统从开启到关闭后，大棚内的温度y(℃)与时间x(h)之间的函数关系，其中线段AB ，BC 表示恒温系统开启阶段，双曲线的一部分CD 表示恒温系统关闭阶段．请根据图中信息解答下列问题：(1)求这天的温度y 与时间x(0≤x ≤24)的函数关系式；(2)求恒温系统设定的恒定温度；(3)若大棚内的温度低于10 ℃时，蔬菜会受到伤害．问这天内，恒温系统最多可以关闭多少小时，才能使蔬菜避免受到伤害？10.如图，已知点D在反比例函数y=的图象上，过点D作DB⊥y轴，垂足为B（0，3），直线y=kx+b经过点A（5，0），与y轴交于点C，且BD=OC，OC：OA=2：5．（1）求反比例函数y=和一次函数y=kx+b的表达式；（2）直接写出关于x的不等式＞kx+b的解集．11.如图，矩形ABCD 的两边AD ，AB 的长分别为3，8，E 是DC 的中点，反比例函数y ＝mx 的图象经过点E ，与AB 交于点F.(1)若点B 坐标为(－6，0)，求m 的值及图象经过A ，E 两点的一次函数的解析式； (2)若AF －AE ＝2，求反比例函数的解析式．12.如图，直线AB 与x 轴交于点A （1，0），与y 轴交于点B （0，2），将线段AB 绕点A 顺时针旋转90°得到线段AC ，反比例函数y ＝（k ≠0，x ＞0）的图象经过点C ．（1）求直线AB 和反比例函数y ＝（k ≠0，x ＞0）的解析式；（2）已知点P 是反比例函数y ＝（k ≠0，x ＞0）图象上的一个动点，求点P 到直线AB 距离最短时的坐标．13.如图，已知点A在反比例函数(x>0)的图象上，过点A作AC⊥x轴，垂足是C，AC=OC．一次函数y=kx+b 的图象经过点A，与y轴的正半轴交于点B．（1）求点A的坐标；（2）若四边形ABOC的面积是3，求一次函数y=kx+b的表达式．14.如图，直线y=kx+b（k≠0）与双曲线y=（m≠0）交于点A（﹣，2），B（n，﹣1）．（1）求直线与双曲线的解析式．（2）点P在x轴上，如果S△ABP=3，求点P的坐标．15.一次函数y=kx+b的图象经过点A(-2,12)，B(8,-3)．（1）求该一次函数的解析式；（2）如图，该一次函数的图象与反比例函数的图象相交于点C(x1，y1)，D(x2,y2)，与轴交于点E，且CD=CE，求m的值．16.如图，某反比例函数图象的一支经过点A（2，3）和点B（点B在点A的右侧），作BC⊥y轴，垂足为点C，连结AB，AC．（1）求该反比例函数的解析式；（2）若△ABC的面积为6，求直线AB的表达式．专题07 反比例函数与一次函数的综合【达标要求】1.认识反比例函数是描述具有反比例变化规律的数学模型.2.结合具体情境体会反比例函数的意义，能根据已知条件确定反比例函数的解析式.3.能画出反比例函数ky x=(k 为常数，0k ≠)的图象，根据图象和解析式探索并理解0k > 和0k <时图象的变化情况.4.能用反比例函数解决简单的实际问题.【知识梳理】知识点1 反比例函数的概念形如ky x=(k 为常数，0k ≠)的函数，叫做反比例函数，其中x 叫自变量，y 是x 的函数. 变式:1y kx -=或xy k =(k 为常数，0k ≠). 知识点2 反比例函数的图像和性质知识点3 k 的集合意义在反比例函数ky x=(k 为常数，0k ≠)的图象上任取一点，过这个点分别作x 轴、y 轴的平行线，两平行线与坐标轴围成的矩形的面积的于k ｜｜ .知识点4 用待定系数法求反比例函数的解析式先设函数解析式为kyx=(k为常数，0k≠)，在根据条件求出未知系数k的值，从而写出这个函数解析式.【精练精解】1.在同一平面直角坐标系中，函数y=﹣x+k与y=（k为常数，且k≠0）的图象大致是（）A．B．C．D．【答案】C【解析】∵函数y=﹣x+k与y=（k为常数，且k≠0），∴当k>0时，y=﹣x+k经过第一、二、四象限，y=经过第一、三象限，故选项D错误，当k<0时，y=﹣x+k经过第二、三、四象限，y=经过第二、四象限，故选项C正确，选项A、B错误，故选C．【点评】本题考查反比例函数的图象、一次函数的图象，解答本题的关键是明确题意，利用一次函数和反比例函数的性质解答．2.若反比例函数的图象上有两个不同的点关于y轴对称点都在一次函数y=–x+m的图象上，则m的取值范围是（）A．m>B．m<-C．m m><-．m-<<kxkxk xkx xy2-=【答案】C【解析】∵反比例函数2y x=-上两个不同的点关于y 轴对称的点，在一次函数y =–x +m 图象上，∴反比例函数2y x=-与一次函数y =–x +m 有两个不同的交点，联立两个函数解方程22220y x m x mx x x y x m⎧=⎪⇒=-+⇒-+=⎨⎪=-+⎩，∵有两个不同的交点，∴有两个不等的根，∴Δ=m 2–8>0，∴m或m <–，故选C ．3.如图，一次函数y =－x +3的图象与反比例函数y =kx（k ≠0）在第一象限的图象交于A （1，a ）和B 两点，与x 轴交于点C ．（1）求反比例函数的解析式；（2）若点P 在x 轴上，且△APC 的面积为5，求点P 的坐标．【解析】（1）把点A （1，a ）代入y =－x +3，得a =2，∴A （1，2），把A （1，2）代入反比例函数y =kx，∴k =1×2=2； ∴反比例函数的表达式为y =2x；（2）∵一次函数y =－x +3的图象与x 轴交于点C ，∴C （3，0），设P （x ，0），∴PC =|3－x |，∴S △APC =12|3－x |×2=5，∴x =－2或x =8， 022=+-mxx∴P 的坐标为（－2，0）或（8，0）．【点评】本题考查了反比例函数与一次函数的交点问题，用待定系数法求出反比例函数的解析式等知识点，能用待定系数法求出反比例函数的解析式是解此题的关键．4.如图，已知反比例函数y =kx（k ≠0）的图象与一次函数y =﹣x +b 的图象在第一象限交于A （1，3），B （3，1）两点．（1）求反比例函数和一次函数的表达式；（2）已知点P （a ，0）（a >0），过点P 作平行于y 轴的直线，在第一象限内交一次函数y =﹣x +b 的图象于点M ，交反比例函数y =kx上的图象于点N ．若PM >PN ，结合函数图象直接写出a 的取值范围．【解析】（1）∵反比例函数y =kx（k ≠0）的图象与一次函数y =﹣x +b 的图象在第一象限交于A （1，3），B （3，1）两点，∴3=1k，3=﹣1+b ，∴k =3，b =4， ∴反比例函数和一次函数的表达式分别为y =3x，y =﹣x +4；（2）由图象可得：当1<a <3时，PM >PN ．【点评】本题考查了一次函数与反比例函数的交点问题，待定系数法求解析式，利用函数图象性质解决问题是本题的关键．5.已知一次函数y=kx+b的图象与反比例函数y=mx的图象交于点A，与x轴交于点B（5，0），若OB=AB，且S△OAB=152．（1）求反比例函数与一次函数的表达式；（2）若点P为x轴上一点，△ABP是等腰三角形，求点P的坐标．【解析】（1）如图1，过点A作AD⊥x轴于D，∵B（5，0），∴OB=5，∵S△OAB=152，∴12×5×AD=152，∴AD=3，∵OB=AB，∴AB=5，在Rt△ADB中，BD，∴OD=OB+BD=9，∴A（9，3），将点A坐标代入反比例函数y=mx中得，m=9×3=27，∴反比例函数的解析式为y=27x，将点A（9，3），B（5，0）代入直线y=kx+b中，9350k bk b+=⎧⎨+=⎩，∴3434kb⎧=⎪⎪⎨⎪=-⎪⎩，∴直线AB的解析式为y=34x﹣34；（2）由（1）知，AB=5，∵△ABP是等腰三角形，∴①当AB=PB时，∴PB=5，∴P（0，0）或（10，0），②当AB=AP时，如图2，由（1）知，BD=4，易知，点P与点B关于AD对称，∴DP=BD=4，∴OP=5+4+4=13，∴P（13，0），③当PB =AP 时，设P （a ，0）， ∵A （9，3），B （5，0），∴AP 2=（9﹣a ）2+9，BP 2=（5﹣a ）2， ∴（9﹣a ）2+9=（5﹣a ）2，∴a =658， ∴P （658，0），即：满足条件的点P 的坐标为（0，0）或（10，0）或（13，0）或（658，0）．【点评】此题是反比例函数综合题，主要考查了待定系数法，勾股定理，三角形的面积，等腰三角形的性质，用分类讨论的思想解决问题是解本题的关键．6.如图，一次函数y =k 1x +b 的图象与反比例函数y =2k x的图象相交于A 、B 两点，其中点A 的坐标为（–1，4），点B 的坐标为（4，n ）．（1）根据图象，直接写出满足k 1x +b ＞2k x的x 的取值范围；（2）求这两个函数的表达式；（3）点P 在线段AB 上，且S △AOP ：S △BOP =1：2，求点P 的坐标．【答案】（1）由图象可得：k 1x +b ＞2k x的x 的取值范围是x <–1或0<x <4；（2）直线解析式y =–x +3，反比例函数的解析式为y =–4x；（3）P （23，73）．【解析】（1）∵点A 的坐标为（–1，4），点B 的坐标为（4，n ）．由图象可得：k 1x +b ＞2k x的x 的取值范围是x <–1或0<x <4；（2）∵反比例函数y =2k x的图象过点A （–1，4），B （4，n ）， ∴k 2=–1×4=–4，k 2=4n ，∴n =–1，∴B （4，–1）， ∵一次函数y =k 1x +b 的图象过点A ，点B ，∴11441k b k b -+=+=-⎧⎨⎩，解得k =–1，b =3，∴直线解析式y =–x +3，反比例函数的解析式为y =–4x；（3）设直线AB 与y 轴的交点为C ，∴C （0，3），∵S △AOC =12×3×1=32， ∴S △AOB =S △AOC +S △BOC =12×3×1+12×3×4=152， ∵S △AOP ：S △BOP =1：2，∴S △AOP =152×13=52， ∴S △COP =52–32=1，∴12×3x P =1，∴x P =23， ∵点P 在线段AB 上，∴y =–23+3=73，∴P （23，73）．【点评】本题考查了反比例函数图象与一次函数图象的交点问题，熟练运用图象上的点的坐标满足图象的解析式是本题的关键．7.如图，一次函数y=kx+b的图象与反比例函数y=mx的图象相交于A（–1，n）、B（2，–1）两点，与y轴相交于点C．（1）求一次函数与反比例函数的解析式；（2）若点D与点C关于x轴对称，求△ABD的面积；（3）若M（x1，y1）、N（x2，y2）是反比例函数y=mx上的两点，当x1<x2<0时，比较y2与y1的大小关系．【答案】（1）一次函数的解析式为y=–x+1，反比例函数的解析式为y=–2x．（2）S△ABD=3．（3）y1<y2．【解析】（1）∵反比例函数y=mx经过点B（2，–1），∴m=–2，∵点A（–1，n）在y=2x-上，∴n=2，∴A（–1，2），把A，B坐标代入y=kx+b，则有221k bk b-+=+=-⎧⎨⎩，解得11kb=-=⎧⎨⎩，∴一次函数的解析式为y=–x+1，反比例函数的解析式为y=–2x．（2）∵直线y=–x+1交y轴于C，∴C（0，1），∵D，C关于x轴对称，∴D（0，–1），∵B（2，–1），∴BD∥x轴，∴S △ABD =12×2×3=3．（3）∵M （x 1，y 1）、N （x 2，y 2）是反比例函数y =–2x 上的两点，且x 1<x 2<0，s ∴y 1<y 2．【点评】本题考查反比例函数与一次函数的交点问题，解题的关键是熟练掌握待定系数法解决问题，学会利用函数的增减性，比较函数值的大小．8.如图，四边形ABCD 是平行四边形，点A(1，0)，B(3，1)，C(3，3)．反比例函数y ＝m x(x ＞0)的图象经过点D ，点P 是一次函数y ＝kx ＋3－3k(k ≠0)的图象与该反比例函数图象的一个公共点．(1)求反比例函数的解析式；(2)通过计算，说明一次函数y ＝kx ＋3－3k(k ≠0)的图象一定经过点C ；(3)对于一次函数y ＝kx ＋3－3k(k ≠0)，当y 随x 的增大而增大时，确定点P 横坐标的取值范围．(不必写出过程)【解析】：(1)∵B(3，1)，C(3，3)，四边形ABCD 是平行四边形，∴AD ＝BC ＝2，BC ⊥x 轴．∴AD ⊥x 轴．又∵A(1，0)，∴D(1，2)．∵D 在反比例函数y ＝m x的图象上， ∴m ＝1×2＝2.∴反比例函数的解析式为y ＝2x. (2)当x ＝3时，y ＝kx ＋3－3k ＝3，∴一次函数y ＝kx ＋3－3k(k ≠0)的图象一定过点C.(3)设点P 的横坐标为a ，则23＜a ＜3. 归纳：反比例函数中，y 随x 的大小变化的情况，应分x ＞0与x ＜0两种情况讨论，而不能笼统地说成“k ＜0时，y 随x 的增大而增大”．双曲线上的点在每个象限内，y 随x 的变化是一致的．运用反比例函数的性质时，要注意在每一个象限内的要求．9.某蔬菜生产基地的气温较低时，用装有恒温系统的大棚栽培一种新品种蔬菜．如图是试验阶段的某天恒温系统从开启到关闭后，大棚内的温度y(℃)与时间x(h)之间的函数关系，其中线段AB ，BC 表示恒温系统开启阶段，双曲线的一部分CD 表示恒温系统关闭阶段．请根据图中信息解答下列问题：(1)求这天的温度y 与时间x(0≤x ≤24)的函数关系式；(2)求恒温系统设定的恒定温度；(3)若大棚内的温度低于10 ℃时，蔬菜会受到伤害．问这天内，恒温系统最多可以关闭多少小时，才能使蔬菜避免受到伤害？【点拨】 (1)用待定系数法分段求函数解析式；(2)观察图象可得；(3)代入临界值y ＝10即可．【解答】解：(1)设线段AB 解析式为y ＝k 1x ＋b(k ≠0)，∵线段AB 过点(0，10)，(2，14)，代入，得⎩⎪⎨⎪⎧b ＝10，2k 1＋b ＝14，解得⎩⎪⎨⎪⎧k 1＝2，b ＝10. ∴AB 解析式为y ＝2x ＋10(0≤x ＜5)．∵B 在线段AB 上，当x ＝5时，y ＝20.∴B 坐标为(5，20)．∴线段BC 的解析式为y ＝20(5≤x ＜10)．设双曲线CD 的解析式为y ＝k 2x(k 2≠0)． ∵C(10，20)，∴k 2＝200.∴双曲线CD 解析式为y ＝200x(10≤x ≤24)． ∴y 关于x 的函数解析式为y ＝⎩⎪⎨⎪⎧2x ＋10（0≤x<5），20（5≤x<10），200x （10≤x ≤24）.(2)由(1)可知，恒温系统设定恒定温度为20 ℃.(3)把y ＝10代入y ＝200x中，解得x ＝20. ∴20－10＝10.答：恒温系统最多关闭10小时，蔬菜才能避免受到伤害．归纳：反比例函数实际应用题是近年中考常见的题型，解题时首先要仔细审读题目(或图象)中给予的信息，挖掘题目(或图象)中隐含的条件，提取有用信息，综合运用所学知识解决问题． 10.如图，已知点D 在反比例函数y=的图象上，过点D 作DB ⊥y 轴，垂足为B （0，3），直线y=kx+b 经过点A （5，0），与y 轴交于点C ，且BD=OC ，OC ：OA=2：5．（1）求反比例函数y=和一次函数y=kx+b 的表达式；（2）直接写出关于x 的不等式＞kx+b 的解集．【分析】（1）由OC、OA、BD之间的关系结合点A、B的坐标可得出点C、D的坐标，由点D的坐标利用反比例函数图象上点的坐标特征可求出a值，进而可得出反比例函数的表达式，再由点A、C的坐标利用待定系数法，即可求出一次函数的表达式；（2）将一次函数表达式代入反比例函数表达式中，利用根的判别式△＜0可得出两函数图象无交点，再观察图形，利用两函数图象的上下位置关系即可找出不等式＞kx+b的解集．解：（1）∵BD=OC，OC：OA=2：5，点A（5，0），点B（0，3），∴OA=5，OC=BD=2，OB=3，又∵点C在y轴负半轴，点D在第二象限，∴点C的坐标为（0，﹣2），点D的坐标为（﹣2，3）．∵点D（﹣2，3）在反比例函数y=的图象上，∴a=﹣2×3=﹣6，∴反比例函数的表达式为y=﹣．将A（5，0）、B（0，﹣2）代入y=kx+b，，解得：，∴一次函数的表达式为y=x﹣2．（2）将y=x ﹣2代入y=﹣，整理得： x 2﹣2x+6=0， ∵△=（﹣2）2﹣4××6=﹣＜0，∴一次函数图象与反比例函数图象无交点．观察图形，可知：当x ＜0时，反比例函数图象在一次函数图象上方，∴不等式＞kx+b 的解集为x ＜0．11.如图，矩形ABCD 的两边AD ，AB 的长分别为3，8，E 是DC 的中点，反比例函数y ＝m x的图象经过点E ，与AB 交于点F.(1)若点B 坐标为(－6，0)，求m 的值及图象经过A ，E 两点的一次函数的解析式；(2)若AF －AE ＝2，求反比例函数的解析式．【解析】：(1)点B 坐标为(－6，0)，AD ＝3，AB ＝8，E 为CD 的中点，∴点A(－6，8)，E(－3，4)．∵函数图象经过点E ，∴m ＝－3×4＝－12.设AE 的解析式为y ＝kx ＋b ，将点A ，E 坐标代入，得⎩⎪⎨⎪⎧－6k ＋b ＝8，－3k ＋b ＝4，解得⎩⎪⎨⎪⎧k ＝－43，b ＝0.∴一次函数的解析式为y ＝－43x. (2)AD ＝3，DE ＝4，∴AE ＝AD 2＋DE 2＝5.∵AF －AE ＝2，∴AF ＝7，BF ＝1.设点E 坐标为(a ，4)，则点F 坐标为(a －3，1)，∵E ，F 两点在函数y ＝m x图象上， ∴4a ＝a －3，解得a ＝－1.∴E(－1，4)．∴m ＝－1×4＝－4.∴反比例函数的解析式为y ＝－4x. 12.如图，直线AB 与x 轴交于点A （1，0），与y 轴交于点B （0，2），将线段AB 绕点A 顺时针旋转90°得到线段AC ，反比例函数y ＝（k ≠0，x ＞0）的图象经过点C ．（1）求直线AB 和反比例函数y ＝（k ≠0，x ＞0）的解析式；（2）已知点P 是反比例函数y ＝（k ≠0，x ＞0）图象上的一个动点，求点P 到直线AB 距离最短时的坐标．【答案】见解析。

中考数学综合题专题复习【反比例函数】专题解析附答案

一、反比例函数真题与模拟题分类汇编（难题易错题）1．如图．一次函数y=x+b的图象经过点B（﹣1，0），且与反比例函数（k为不等于0的常数）的图象在第一象限交于点A（1，n）．求：（1）一次函数和反比例函数的解析式；（2）当1≤x≤6时，反比例函数y的取值范围．【答案】（1）解：把点B（﹣1，0）代入一次函数y=x+b得： 0=﹣1+b，∴b=1，∴一次函数解析式为：y=x+1，∵点A（1，n）在一次函数y=x+b的图象上，∴n=1+1，∴n=2，∴点A的坐标是（1，2）．∵反比例函数的图象过点A（1，2）．∴k=1×2=2，∴反比例函数关系式是：y=（2）解：反比例函数y= ，当x＞0时，y随x的增大而减少，而当x=1时，y=2，当x=6时，y= ，∴当1≤x≤6时，反比例函数y的值：≤y≤2【解析】【分析】（1）根据题意首先把点B（﹣1，0）代入一次函数y=x+b求出一次函数解析式，又点A（1，n）在一次函数y=x+b的图象上，再利用一次函数解析式求出点A的坐标，然后利用代入系数法求出反比例函数解析式，（2）根据反比例函数的性质分别求出当x=1，x=6时的y值，即可得到答案．2．心理学家研究发现，一般情况下，一节课40分钟中，学生的注意力随教师讲课的变化而变化．开始上课时，学生的注意力逐步增强，中间有一段时间学生的注意力保持较为理想的稳定状态，随后学生的注意力开始分散．经过实验分析可知，学生的注意力指标数y 随时间x（分钟）的变化规律如下图所示（其中AB、BC分别为线段，CD为双曲线的一部分）：（1）开始上课后第五分钟时与第三十分钟时相比较，何时学生的注意力更集中？（2）一道数学竞赛题，需要讲19分钟，为了效果较好，要求学生的注意力指标数最低达到36，那么经过适当安排，老师能否在学生注意力达到所需的状态下讲解完这道题目？【答案】（1）解：设线段AB所在的直线的解析式为y1=k1x+20，把B（10，40）代入得，k1=2，∴y1=2x+20．设C、D所在双曲线的解析式为y2= ，把C（25，40）代入得，k2=1000，∴当x1=5时，y1=2×5+20=30，当，∴y1＜y2∴第30分钟注意力更集中．（2）解：令y1=36，∴36=2x+20，∴x1=8令y2=36，∴，∴∵27.8﹣8=19.8＞19，∴经过适当安排，老师能在学生注意力达到所需的状态下讲解完这道题目．【解析】【分析】（1）根据一次函数和反比例函数的应用，用待定系数法求出线段AB所在的直线的解析式，和C、D所在双曲线的解析式；把x1=5时和进行比较得到y1＜y2，得出第30分钟注意力更集中；（2）当y1=36时，得到x1=8，当y2=36，得到，由27.8﹣8=19.8＞19，所以经过适当安排，老师能在学生注意力达到所需的状态下讲解完这道题目.3．抛物线y= +x+m的顶点在直线y=x+3上，过点F（﹣2，2）的直线交该抛物线于点M、N两点（点M在点N的左边），MA⊥x轴于点A，NB⊥x轴于点B．（1）先通过配方求抛物线的顶点坐标（坐标可用含m的代数式表示），再求m的值；（2）设点N的横坐标为a，试用含a的代数式表示点N的纵坐标，并说明NF=NB；（3）若射线NM交x轴于点P，且PA•PB= ，求点M的坐标．【答案】（1）解：y= x2+x+m= （x+2）2+（m﹣1）∴顶点坐标为（﹣2，m﹣1）∵顶点在直线y=x+3上，∴﹣2+3=m﹣1，得m=2；（2）解：过点F作FC⊥NB于点C，∵点N在抛物线上，∴点N的纵坐标为： a2+a+2，即点N（a， a2+a+2）在Rt△FCN中，FC=a+2，NC=NB﹣CB= a2+a，∴NF2=NC2+FC2=（ a2+a）2+（a+2）2，=（ a2+a）2+（a2+4a）+4，而NB2=（ a2+a+2）2，=（ a2+a）2+（a2+4a）+4∴NF2=NB2，NF=NB（3）解：连接AF、BF，由NF=NB，得∠NFB=∠NBF，由（2）的思路知，MF=MA，∴∠MAF=∠MFA，∵MA⊥x轴，NB⊥x轴，∴MA∥NB，∴∠AMF+∠BNF=180°∵△MAF和△NFB的内角总和为360°，∴2∠MAF+2∠NBF=180°，∠MAF+∠NBF=90°，∵∠MAB+∠NBA=180°，∴∠FBA+∠FAB=90°，又∵∠FAB+∠MAF=90°，∴∠FBA=∠MAF=∠MFA，又∵∠FPA=∠BPF，∴△PFA∽△PBF，∴ = ，PF2=PA×PB= ，过点F作FG⊥x轴于点G，在Rt△PFG中，PG= = ，∴PO=PG+GO= ，∴P（﹣，0）设直线PF：y=kx+b，把点F（﹣2，2）、点P（﹣，0）代入y=kx+b，解得k= ，b= ，∴直线PF：y= x+ ，解方程 x2+x+2= x+ ，得x=﹣3或x=2（不合题意，舍去），当x=﹣3时，y= ，∴M（﹣3，）．【解析】【分析】（1）利用配方法将二次函数化成顶点式，写出顶点坐标，由顶点再直线y=x+3上，建立方程求出m的值。

第11章反比例函数-2020年中考数学学霸专题训练营(解析版)

第12章反比例函数一、选择题1. 已知反比例函数k yx=的图象经过（1，－2）．则k=．【答案】－22．已知点（1,1）在反比例函数kyx=（k为常数，k≠0）的图象上，则这个反比例函数的大致图象是（）【答案】C提示：反比例函数过第一象限（也可由点（1,1）求得k=1），故选C。

3.关于反比例函数4yx=的图象，下列说法正确的是（）A．必经过点（1，1）B．两个分支分布在第二、四象限C．两个分支关于x轴成轴对称D．两个分支关于原点成中心对称【答案】D4. 如图，矩形ABCD的对角线BD经过坐标原点，矩形的边分别平行于坐标轴，点C在反比例函数221k kyx++=的图象上。

若点A的坐标为（－2，－2），则k的值为A．1 B．－3 C．4 D．1或－3【答案】DxyOABCD5. 函数2y x =与函数1y x-=在同一坐标系中的大致图象是【答案】D6. 如图，反比例函数ky x=的图象经过点A (-1,-2).则当x ＞1时，函数值y 的取值范围是（）A.y ＞1B.0＜y ＜1C. y ＞2D.0＜ y ＜2【答案】D7. 如图（6），直线 6y x =- 交x 轴、y 轴于A 、B 两点，P 是反比例函数4(0)y x x=>图象上位于直线下方的一点，过点P 作x 轴的垂线，垂足为点M ，交AB 于点E ，过点P 作y 轴的垂线，垂足为点N ，交AB 于点F 。

则AF BE ⋅= A ．8 B ．6 C ．4 D ．2 【答案】A8. 若双曲线y=x k 12-的图象经过第二、四象限，则k 的取值范围是A.k ＞21 B. k ＜21 C. k =21D. 不存在【答案】B9. 已知点（1,1）在反比例函数ky x=（k 为常数，k≠0）的图象上，则这个反比例函数的大致图象是（）【答案】C10. 如图，反比例函数y 1=k 1x 和正比例函数y 2=k 2x 的图象交于A （-1，-3）、B （1，3）两点，若k 1x＞k 2x ，则x 的取值范围是（第10题图）（A ）-1＜x ＜0 （B ）-1＜x ＜1（C ）x ＜-1或0＜x ＜1 （D ）-1＜x ＜0或x ＞1 【答案】C 11. 若函数xm y 2+=的图象在其象限内y 的值随x 值的增大而增大，则m 的取值范围是 A ．2->m B ．2-<mC ．2>mD ．2<m【答案】B12．对于反比例函数y = 1x，下列说法正确的是A ．图象经过点（1，-1）B ．图象位于第二、四象限C ．图象是中心对称图形D ．当x ＜0时，y 随x 的增大而增大y xOy x OyxOy xO 【答案】C13. 如图,直线l 和双曲线(0)ky k x=>交于A 、B 亮点,P 是线段AB 上的点（不与A 、B 重合）,过点A 、B 、P 分别向x 轴作垂线,垂足分别是C 、D 、E,连接OA 、OB 、OP,设△AOC 面积是S 1、△B OD 面积是S 2、△P OE 面积是S 3、则（）A. S 1＜S 2＜S 3B. S 1>S 2>S 3C. S 1=S 2>S 3D. S 1=S 2<S 3 【答案】D14. 图1是我们学过的反比例函数图象,它的函数解析式可能是（） A ．2y x =B ．4y x =C ．3y x =-D ．12y x =【答案】 B15. 某反比例函数的图象经过点（-1,6），则下列各点中，此函数图象也经过的点是（） A. （-3,2） B. （3,2） C. （2，3） D. （6,1）【答案】A16. ）下列各点中，在函数6y x=-图象上的是（） A ．（－2，－4） B ．（2，3）C ．（－1，6）D ．1(,3)2-【答案】C17. 小明乘车从南充到成都，行车的平均速度y (km/h)和行车时间x (h)之间的函数图象是（）O xy图1A B C D 【答案】B.18. 如图，函数11y x =-和函数22y x=的图象相交于点M (2，m )，N (-1，n )，若12y y >，则x 的取值范围是（）A ．102x x <-<<或B ．12x x <->或C ．1002x x -<<<<或D ．102x x -<<>或【答案】D19. 如图，反比例函数xmy =的图象与一次函数b kx y -=的图象交于点M ，N ，已点M 的坐标为（1，3），点N 的纵坐标为－1，根据图象信息可得关于x 的方程xm=b kx -的解为（）A. －3,1B. －3,3C. －1,1D.3，-1【答案】A20. 已知点P (-l ，4)在反比例函数(0)ky k x=≠的图象上，则k 的值是( ) A ．14-B ．14C ．4D ．－4【答案】D21. 如图，某反比例函数的图象过点（－2，1），则此反比例函数表达式为 A ．2y x=B ．2y x=-C ．12y x=D ．12y x=-【答案】B22. 在同一直角坐标系中，正比例函数y x =与反比例函数2y x=的图象大致是A B C D 【答案】B23. 根据图5—1所示的程序，得到了y 与x 的函数图象，过点M 作PQ ∥x 轴交图象于点P,Q ，连接OP,OQ.则以下结论 ①x ＜0时，x2y =， ②△OPQ 的面积为定值， ③x ＞0时，y 随x 的增大而增大 ④MQ=2PM⑤∠POQ 可以等于90°图5—2图5—1输出y 取相反数42取倒数取倒数输入非零数xPQMxy-21O其中正确的结论是（） A ．①②④B ．②④⑤C ．③④⑤D ．②③⑤【答案】B24. 已知反比例函数xy 1=，下列结论中不正确的是（） A.图象经过点（－1，－1） B.图象在第一、三象限C.当1>x 时，10<<yD.当0<x 时，y 随着x 的增大而增大【答案】D25. 已知如图,A 是反比例函数xky =的图象上的一点,AB ⊥x 轴于点B,且△ABO 的面积是3,则k 的值是( )A.3B.-3C.6D.-6·【答案】C·26.如图，直线y=x +2与双曲线y=xm 3-在第二象限有两个交点，那么m 的取值范围在数轴上表示为（）（第15题图）【答案】B 二、填空题1. 如图，将一块直角三角板OAB 放在平面直角坐标系中，B （2，0），∠AOC ＝60°，点A 在第一象限，过点A 的双曲线为y = kx，在x 轴上取一点P ，过点P 作直线OA 的垂线l ，yoA Bx以直线l 为对称轴，线段OB 经轴对称变换后的像是O ′B ′. （1）当点O ′与点A 重合时，点P 的坐标是.（2）设P （t ，0）当O ′B ′与双曲线有交点时，t 的取值范围是 .【答案】（1）（4，0）；（2）4≤t ≤25或－25≤t ≤－4 2. 已知反比例函数ky x=的图象经过（1，－2）．则k = ．【答案】－23. 若点A(m ，－2)在反比例函数4y x=的图象上，则当函数值y≥－2时，自变量x 的取值范围是___________. 【答案】x≤-2或x>0 4. 过反比例函数y=xk(k≠0)图象上一点A ，分别作x 轴，y 轴的垂线，垂足分别为B,C ，如果⊿ABC 的面积为3.则k 的值为 . 【答案】6或﹣6.5. 如图，正方形A 1B 1P 1P 2的顶点P 1、P 2在反比例函数y ＝2x （x ＞0）的图象上，顶点A 1、B 1分别在x 轴和y 轴的正半轴上，再在其右侧作正方形P 2P 3A 2B 2，顶点P 3在反比例函数y ＝2x（x ＞0）的图象上，顶点A 3在x 轴的正半轴上，则点P 3的坐标为【答案】（3＋1，3－1）6. 在直角坐标系中，有如图所示的t ,R ABO AB x ∆⊥轴于点B ，斜边35=,(0)kxx=>的图象经过AO的中点C，且与AB 的坐标为.【答案】382（，）7. 若点12(1,),(2,)A yB y是双曲线3yx=上的点，则1y2y（填“>”,“<”“=”）. 【答案】>8. 如图，将一块直角三角板OAB放在平面直角坐标系中，B(2，0)，∠AOC＝60°，点A在第一象限，过点A的双曲线为y=kx，在x轴上取一点P，过点P作直线OA的垂线l，以直线l为对称轴，线段OB经轴对称变换后的像是O′B′.（1）当点O′与点A重合时，点P的坐标是.（2）设P(t，0)当O′B′与双曲线有交点时，t的取值范围是.【答案】（1）(4，0)；（2）4≤t≤25或－25≤t≤－49. 如图1所示的曲线是一个反比例函数图象的一支，点A在此曲线上，则该反比例函数的解析式为_______________.y1OAx3图1xyCDBOI【答案】3y x=10．如图，已知点A 的坐标为（3，3），AB ⊥x 轴，垂足为B ，连接OA ，反比例函数y=xk （k>0）的图象与线段OA 、AB 分别交于点C 、D.若AB=3BD ，以点C 为圆心，CA 的45倍的长为半径作圆，则该圆与x 轴的位置关系是___________（填“相离”、“相切”或“相交”）【答案】相交 11. 反比例函数1m y x-=的图象在第一、三象限，则m 的取值范围是．【答案】x ＞112. 在平面直角坐标系xOy 中，已知反比例函数2(0)ky k x=≠满足：当0x <时，y 随x 的增大而减小．若该反比例函数的图象与直线3y x k =-+都经过点P ，且7OP =，则实数k=_________. 【答案】37. 13. 如图，在平面直角坐标系中有一正方形AOBC ，反比例函数ky x=经过正方形AOBC 对角线的交点，半径为（422-）的圆内切于△ABC ，则k 的值为．【答案】414. 已知反比例函数kyx=的图象经过（1，－2）．则k=．【答案】－215. 设函数2yx=与1y x=-的图象的交战坐标为（a，b），则11a b-的值为__________．【答案】12-16.如果反比例函数kyx=（k是常数，k≠0）的图象经过点(－1，2)，那么这个函数的解析式是__________．【答案】2yx=-17. 如图，□ABCD的顶点A，B的坐标分别是A（－1，0），B（0，－2），顶点C，D在双曲线y=xk上，边AD交y轴于点E，且四边形BCDE的面积是△ABE面积的5倍，则k=_____．【答案】1218. 如图：点A在双曲线kyx=上，AB⊥x轴于B，且△AOB的面积S△AOB=2，则k=______．【答案】－419. 若一次函数y=kx+1的图象与反比例函数y=x1的图象没有公共点，则实数k的取值范围是。

2024年中考数学真题汇编专题13 反比例函数及其应用+答案详解

2024年中考数学真题汇编专题13 反比例函数及其应用+答案详解（试题部分）一、单选题1．（2024·安徽·中考真题）已知反比例函数()0ky k x=≠与一次函数2y x =−的图象的一个交点的横坐标为3，则k 的值为（） A ．3−B ．1−C ．1D ．32．（2024·重庆·中考真题）反比例函数10y x=−的图象一定经过的点是（） A ．()1,10B ．()2,5−C ．()2,5D ．()2,83．（2024·天津·中考真题）若点()()()123,1,,1,,5A x B x C x −都在反比例函数5y x=的图象上，则123,,x x x 的大小关系是（） A ．123x x x << B ．132x x x << C ．321x x x <<D ．213x x x <<4．（2024·广西·中考真题）已知点()11,M x y ，()22,N x y 在反比例函数2y x=的图象上，若120x x <<，则有（）A ．120y y <<B ．210y y <<C ．120y y <<D ．120y y <<5．（2024·浙江·中考真题）反比例函数4y x=的图象上有()1,P t y ，()24,Q t y +两点．下列正确的选项是（）A ．当4t <−时，210y y <<B ．当40t −<<时，210y y <<C ．当40t −<<时，120y y <<D ．当0t >时，120y y <<6．（2024·河北·中考真题）节能环保已成为人们的共识．淇淇家计划购买500度电，若平均每天用电x 度，则能使用y 天．下列说法错误的是（） A ．若5x =，则100y = B ．若125y =，则4x =C ．若x 减小，则y 也减小D ．若x 减小一半，则y 增大一倍7．（2024·四川泸州·中考真题）已知关于x 的一元二次方程2210x x k ++−=无实数根，则函数y kx =与函数2y x=的图象交点个数为（） A ．0 B ．1 C ．2 D ．38．（2024·重庆·中考真题）已知点()3,2−在反比例函数()0ky k x=≠的图象上，则k 的值为（） A ．3−B ．3C ． 6−D ．69．（2024·黑龙江牡丹江·中考真题）矩形OBAC 在平面直角坐标系中的位置如图所示，反比例函数k y x=的图象与AB 边交于点D ，与AC 边交于点F ，与OA 交于点E ，2OE AE =，若四边形ODAF 的面积为2，则k 的值是（）A ．25B ．35C ．45D ．8510．（2024·黑龙江大兴安岭地·中考真题）如图，双曲线()120y x x=>经过A 、B 两点，连接OA 、AB ，过点B 作BD y ⊥轴，垂足为D ，BD 交OA 于点E ，且E 为AO 的中点，则AEB △的面积是（）A ．4.5B ．3.5C ．3D ．2.511．（2024·江苏扬州·中考真题）在平面直角坐标系中，函数42=+y x 的图像与坐标轴的交点个数是（）A ．0B ．1C ．2D ．412．（2024·吉林长春·中考真题）如图，在平面直角坐标系中，点O 是坐标原点，点()4,2A 在函数()0,0ky k x x=>>的图象上．将直线OA 沿y 轴向上平移，平移后的直线与y 轴交于点B ，与函数()0,0ky k x x=>>的图象交于点C ．若BC B 的坐标是（）A ．(B ．()0,3C ．()0,4D ．(0,13．（2024·四川宜宾·中考真题）如图，等腰三角形ABC 中，AB AC =，反比例函数()0ky k x=≠的图象经过点A 、B 及AC 的中点M ，BC x ∥轴，AB 与y 轴交于点N ．则ANAB的值为（）A ．13B ．14C ．15D ．25二、填空题14．（2024·北京·中考真题）在平面直角坐标系xOy 中，若函数()0ky k x=≠的图象经过点()13,y 和()23,y −，则12y y +的值是 .15．（2024·云南·中考真题）已知点()2,P n 在反比例函数10y x=的图象上，则n = ． 16．（2024·山东威海·中考真题）如图，在平面直角坐标系中，直线()10y ax b a =+≠与双曲线()20ky k x=≠交于点()1,A m −，()2,1B −．则满足12y y ≤的x 的取值范围．17．（2024·湖南·中考真题）在一定条件下，乐器中弦振动的频率f 与弦长l 成反比例关系，即kf l=（k 为常数．0k ≠），若某乐器的弦长l 为0.9米，振动频率f 为200赫兹，则k 的值为．18．（2024·陕西·中考真题）已知点()12,A y −和点()2,B m y 均在反比例函数5y x=−的图象上，若01m <<，则12y y + 0．19．（2024·湖北武汉·中考真题）某反比例函数ky x=具有下列性质：当0x >时，y 随x 的增大而减小，写出一个满足条件的k 的值是．20．（2024·黑龙江齐齐哈尔·中考真题）如图，反比例函数(0)ky x x=<的图象经过平行四边形ABCO 的顶点A ，OC 在x 轴上，若点()1,3B −，3ABCOS=，则实数k 的值为．21．（2024·内蒙古包头·中考真题）若反比例函数12y x =，23y x=−，当13x ≤≤时，函数1y 的最大值是a ，函数2y 的最大值是b ，则b a = ． 22．（2024·四川遂宁·中考真题）反比例函数1k y x−=的图象在第一、三象限，则点()3k −,在第象限． 23．（2024·江苏扬州·中考真题）如图，在平面直角坐标系中，点A 的坐标为(1,0)，点B 在反比例函数(0)ky x x=>的图像上，BC x ⊥轴于点C ，30BAC ∠=︒，将ABC 沿AB 翻折，若点C 的对应点D 落在该反比例函数的图像上，则k 的值为．24．（2024·内蒙古呼伦贝尔·中考真题）如图，在平面直角坐标系中，点A ，B 的坐标分别为()5,0，()2,6，过点B 作BC x ∥轴交y 轴于点C ，点D 为线段AB 上的一点，且2BD AD =．反比例函数(0)ky x x=>的图象经过点D 交线段BC 于点E ，则四边形ODBE 的面积是．25．（2024·四川广元·中考真题）已知y =与()0ky x x=>的图象交于点()2,A m ，点B 为y 轴上一点，将OAB 沿OA 翻折，使点B 恰好落在()0ky x x=>上点C 处，则B 点坐标为．26．（2024·广东深圳·中考真题）如图，在平面直角坐标系中，四边形AOCB 为菱形，4tan 3AOC ∠=，且点A 落在反比例函数3y x=上，点B 落在反比例函数()0ky k x=≠上，则k = ．27．（2024·广东广州·中考真题）如图，平面直角坐标系xOy 中，矩形OABC 的顶点B 在函数(0)k y x x=>的图象上，(1,0)A ，(0,2)C ．将线段AB 沿x 轴正方向平移得线段A B ''（点A 平移后的对应点为A '），A B ''交函数(0)ky x x=>的图象于点D ，过点D 作DE y ⊥轴于点E ，则下列结论：①2k =；②OBD 的面积等于四边形ABDA '的面积；③A E ' ④B BD BB O ''∠=∠．其中正确的结论有．（填写所有正确结论的序号）28．（2024·四川乐山·中考真题）定义：函数图象上到两坐标轴的距离都小于或等于1的点叫做这个函数图象的“近轴点”．例如，点()0,1是函数1y x =+图象的“近轴点”．（1）下列三个函数的图象上存在“近轴点”的是（填序号）； ①3y x =−+；②2y x=；③221y x x =−+−．（2）若一次函数3y mx m =−图象上存在“近轴点”，则m 的取值范围为．三、解答题29．（2024·甘肃·中考真题）如图，在平面直角坐标系中，将函数y ax =的图象向上平移3个单位长度，得到一次函数y ax b =+的图象，与反比例函数()0ky x x=>的图象交于点()24A ，．过点()02B ，作x 轴的平行线分别交y ax b =+与()0ky x x=>的图象于C ，D 两点．(1)求一次函数y ax b =+和反比例函数ky x=的表达式； (2)连接AD ，求ACD 的面积．30．（2024·青海·中考真题）如图，在同一直角坐标系中，一次函数y x b =−+和反比例函数9y x=的图象相交于点()1,A m ，(),1B n ．(1)求点A ，点B 的坐标及一次函数的解析式； (2)根据图象，直接写出不等式9x b x−+>的解集． 31．（2024·吉林·中考真题）已知蓄电池的电压为定值，使用蓄电池时，电流I （单位：A ）与电阻R （单位：Ω）是反比例函数关系，它的图象如图所示．(1)求这个反比例函数的解析式（不要求写出自变量R 的取值范围）． (2)当电阻R 为3Ω时，求此时的电流I ．32．（2024·山东·中考真题）列表法、表达式法、图像法是三种表示函数的方法，它们从不同角度反映了自变量与函数值之间的对应关系．下表是函数2y x b =+与ky x=部分自变量与函数值的对应关系：(1)求a 、b 的值，并补全表格； (2)结合表格，当2y x b =+的图像在ky x=的图像上方时，直接写出x 的取值范围． 33．（2024·湖北·中考真题）一次函数y x m =+经过点()3,0A −，交反比例函数ky x=于点(),4B n ．(1)求m n k ，，； (2)点C 在反比例函数ky x=第一象限的图象上，若AO OB C A S S <△△，直接写出C 的横坐标a 的取值范围． 34．（2024·四川凉山·中考真题）如图，正比例函数112y x =与反比例函数()20ky x x=>的图象交于点()2A m ，．(1)求反比例函数的解析式； (2)把直线112y x =向上平移3个单位长度与()20ky x x=>的图象交于点B ，连接,AB OB ，求AOB 的面积． 35．（2024·贵州·中考真题）已知点()1,3在反比例函数ky x=的图象上． (1)求反比例函数的表达式；(2)点()3,a −，()1,b ，()3,c 都在反比例函数的图象上，比较a ，b ，c 的大小，并说明理由．36．（2024·河南·中考真题）如图，矩形ABCD 的四个顶点都在格点（网格线的交点）上，对角线AC ，BD 相交于点E ，反比例函数()0ky x x=>的图象经过点A ．(1)求这个反比例函数的表达式．(2)请先描出这个反比例函数图象上不同于点A 的三个格点，再画出反比例函数的图象． (3)将矩形ABCD 向左平移，当点E 落在这个反比例函数的图象上时，平移的距离为________． 37．（2024·四川乐山·中考真题）如图，已知点()1,A m 、(),1B n 在反比例函数()30y x x=>的图象上，过点A 的一次函数y kx b =+的图象与y 轴交于点()0,1C ．(1)求m 、n 的值和一次函数的表达式；(2)连接AB ，求点C 到线段AB 的距离．38．（2024·四川眉山·中考真题）如图，在平面直角坐标系xOy 中，一次函数y kx b =+与反比例函数()0my x x=>的图象交于点()1,6A ，(),2B n ，与x 轴，y 轴分别交于C ，D 两点．(1)求一次函数和反比例函数的表达式；(2)若点P 在y 轴上，当PAB 的周长最小时，请直接写出点P 的坐标；(3)将直线AB 向下平移a 个单位长度后与x 轴，y 轴分别交于E ，F 两点，当12EF AB =时，求a 的值． 39．（2024·甘肃临夏·中考真题）如图，直线y kx =与双曲线4y x=−交于A ，B 两点，已知A 点坐标为(),2a ．(1)求a ，k 的值；(2)将直线y kx =向上平移()0m m >个单位长度，与双曲线4y x=−在第二象限的图象交于点C ，与x 轴交于点E ，与y 轴交于点P ，若PE PC =，求m 的值． 40．（2024·四川广元·中考真题）如图，已知反比例函数1ky x=和一次函数2y mx n =+的图象相交于点()3,A a −，3,22B a ⎛⎫+− ⎪⎝⎭两点，O 为坐标原点，连接OA ，OB ．(1)求1ky x=与2y mx n =+的解析式；(2)当12y y >时，请结合图象直接写出自变量x 的取值范围； (3)求AOB 的面积．41．（2024·内蒙古赤峰·中考真题）在平面直角坐标系中，对于点()11,M x y ，给出如下定义：当点()22,N x y ，满足1212x x y y +=+时，称点N 是点M 的等和点．(1)已知点()1,3M ，在()14,2N ，()23,1N −，()30,2N −中，是点M 等和点的有_____； (2)若点()3,2M −的等和点N 在直线y x b =+上，求b 的值； (3)已知，双曲线1ky x=和直线22y x =−，满足12y y <的x 取值范围是4x >或20x −<<．若点P 在双曲线1ky x=上，点P 的等和点Q 在直线22y x =−上，求点P 的坐标．2024年中考数学真题汇编专题13 反比例函数及其应用+答案详解（答案详解）一、单选题1．（2024·安徽·中考真题）已知反比例函数()0ky k x=≠与一次函数2y x =−的图象的一个交点的横坐标为3，则k 的值为（） A ．3− B ．1− C ．1 D ．32．（2024·重庆·中考真题）反比例函数10y x=−的图象一定经过的点是（） A ．()1,10 B ．()2,5− C ．()2,5 D ．()2,83．（2024·天津·中考真题）若点()()()123,1,,1,,5A x B x C x −都在反比例函数5y x=的图象上，则123,,x x x 的大小关系是（）A ．123x x x <<B ．132x x x <<C ．321x x x <<D ．213x x x <<【详解】解：50k =>5y x=的图象分布在第一、三象限，在每一象限点()3,5C x ，都在反比例函数(),1x −在反比例函数4．（2024·广西·中考真题）已知点()11,M x y ，()22,N x y 在反比例函数2y x=的图象上，若120x x <<，则有（）A ．120y y <<B ．210y y <<C ．120y y <<D ．120y y <<【详解】解： 5．（2024·浙江·中考真题）反比例函数4y x=的图象上有()1,P t y ，()24,Q t y +两点．下列正确的选项是（）A ．当4t <−时，210y y <<B ．当40t −<<时，210y y <<C ．当40t −<<时，120y y <<D ．当0t >时，120y y <<6．（2024·河北·中考真题）节能环保已成为人们的共识．淇淇家计划购买500度电，若平均每天用电x 度，则能使用y 天．下列说法错误的是（） A ．若5x =，则100y = B ．若125y =，则4x =C ．若x 减小，则y 也减小D ．若x 减小一半，则y 增大一倍7．（2024·四川泸州·中考真题）已知关于x 的一元二次方程2210x x k ++−=无实数根，则函数y kx =与函数2y x=的图象交点个数为（） A ．0 B ．1 C ．2 D ．38．（2024·重庆·中考真题）已知点()3,2−在反比例函数()0ky k x=≠的图象上，则k 的值为（） A ．3− B ．3C ． 6−D ．69．（2024·黑龙江牡丹江·中考真题）矩形OBAC 在平面直角坐标系中的位置如图所示，反比例函数ky x=的图象与AB 边交于点D ，与AC 边交于点F ，与OA 交于点E ，2OE AE =，若四边形ODAF 的面积为2，则k 的值是（）A ．25B ．35C ．45D ．85EM AC ，设，由OME OCA ∽，可得O O F OBDCFA D SSS ++四边形，列方程，即可得出k 的值．【详解】过点E 作EM OC ⊥，则EM AC ，∴OME OCA ∽， ∴OM EM OEOC AC OA== 设k E a a ⎛⎫ ⎪⎝⎭，，∵2OE AE = 2OM EM ==， OBDOCFS SS ++四边形3322k a a⋅⋅，解得：10．（2024·黑龙江大兴安岭地·中考真题）如图，双曲线()120y x x=>经过A 、B 两点，连接OA 、AB ，过点B 作BD y ⊥轴，垂足为D ，BD 交OA 于点E ，且E 为AO 的中点，则AEB △的面积是（）A ．4.5B ．3.5C ．3D ．2.5，证明AFE ODE ∽，有OD 1122DF a ==，AF =【详解】如图，过点A 作AF BD ⊥设12,A a a ⎛⎫⎪⎝⎭，0a >，∵BD y ⊥轴，AF BD ⊥∴AF y ∥轴，DF =∴AFE ODE ∽， AF AE EFOD OE DE==， E 为AO 的中点， AE OE =， 1AF AE EFOD OE DE===ABES=故选：A ．11．（2024·江苏扬州·中考真题）在平面直角坐标系中，函数42=+y x 的图像与坐标轴的交点个数是（）A ．0B ．1C ．2D ．412．（2024·吉林长春·中考真题）如图，在平面直角坐标系中，点O 是坐标原点，点()4,2A 在函数()0,0ky k x x=>>的图象上．将直线OA 沿y 轴向上平移，平移后的直线与y 轴交于点B ，与函数()0,0ky k x x=>>的图象交于点C ．若BC B 的坐标是（）A ．(B ．()0,3C ．()0,4D ．(0,∵()4,2A ，∴4OE =，222425OA =+=∴42sin 525OE OAE OA ∠===∵()4,2A 在反比例函数的图象上，13．（2024·四川宜宾·中考真题）如图，等腰三角形ABC 中，AB AC =，反比例函数()0ky k x=≠的图象经过点A 、B 及AC 的中点M ，BC x ∥轴，AB 与y 轴交于点N ．则ANAB的值为（）A ．13B ．14C ．15D ．25【答案】B【分析】本题考查反比例函数的性质，平行线分线段成比例定理，等腰三角形的性质等知识，找到坐标之间的关系是解题的关键．作辅助线如图，利用函数表达式设出A 、B 两点的坐标，利用D ，M 是中点，找到坐标之间的关系，利用平行线分线段成比例定理即可求得结果．【详解】解：作过A 作BC 的垂线垂足为D ，BC 与y 轴交于E 点，如图，二、填空题14．（2024·北京·中考真题）在平面直角坐标系xOy 中，若函数()0ky k x=≠的图象经过点()13,y 和()23,y −，则12y y +的值是 . 【答案】0【分析】本题考查了反比例函数图象上点的坐标特征，已知自变量求函数值，熟练掌握反比例函数的性质是解题的关键．15．（2024·云南·中考真题）已知点()2,P n 在反比例函数10y x=的图象上，则n = ．【详解】解：点16．（2024·山东威海·中考真题）如图，在平面直角坐标系中，直线()10y ax b a =+≠与双曲线()20ky k x=≠交于点()1,A m −，()2,1B −．则满足12y y ≤的x 的取值范围．【答案】10x −≤<或2x ≥【分析】本题考查了一次函数与反比例函数的交点问题，根据图象解答即可求解，利用数形结合思想解答是解题的关键．【详解】解：由图象可得，当10x −≤<或2x ≥时，12y y ≤， ∴满足12y y ≤的x 的取值范围为10x −≤<或2x ≥，故答案为：10x −≤<或2x ≥．17．（2024·湖南·中考真题）在一定条件下，乐器中弦振动的频率f 与弦长l 成反比例关系，即kf l=（k 为常数．0k ≠），若某乐器的弦长l 为0.9米，振动频率f 为200赫兹，则k 的值为．【答案】18018．（2024·陕西·中考真题）已知点()12,A y −和点()2,B m y 均在反比例函数5y x=−的图象上，若01m <<，则12y y + 0．19．（2024·湖北武汉·中考真题）某反比例函数ky x=具有下列性质：当0x >时，y 随x 的增大而减小，写出一个满足条件的k 的值是．【答案】1（答案不唯一）【分析】本题考查的是反比例函数的性质，反比例函数的图象是双曲线，当0k >，双曲线的两支分别位于第一、第三象限，在每一象限内y 随x 的增大而减小，当0k <，双曲线的两支分别位于第二、第四象限，在每一象限内y 随x 的增大而增大．直接根据反比例函数的性质写出符合条件的的值即可．【详解】解：∵当0x >时，y 随x 的增大而减小， ∴0k >故答案为：1（答案不唯一）．20．（2024·黑龙江齐齐哈尔·中考真题）如图，反比例函数(0)ky x x=<的图象经过平行四边形ABCO 的顶点A ，OC 在x 轴上，若点()1,3B −，3ABCOS=，则实数k 的值为．ABCOS =【详解】ABCO 是平行四边形纵坐标相同()1,3B − A ∴的纵坐标是3 A 在反比例函数图象上∴将3y =,33k A ⎛⎫∴ ⎪⎝⎭AB ∴=−ABCOS=3AB ∴⨯即：1⎛−− ⎝解得：k =故答案为：21．（2024·内蒙古包头·中考真题）若反比例函数12y x =，23y x=−，当13x ≤≤时，函数1y 的最大值是a ，函数2y 的最大值是b ，则b a = ．【详解】解：函数23y x =−12b a −∴=故答案为：22．（2024·四川遂宁·中考真题）反比例函数1k y x−=的图象在第一、三象限，则点()3k −,在第象限．23．（2024·江苏扬州·中考真题）如图，在平面直角坐标系中，点A 的坐标为(1,0)，点B 在反比例函数(0)ky x x=>的图像上，BC x ⊥轴于点C ，30BAC ∠=︒，将ABC 沿AB 翻折，若点C 的对应点D 落在该反比例函数的图像上，则k 的值为．24．（2024·内蒙古呼伦贝尔·中考真题）如图，在平面直角坐标系中，点A ，B 的坐标分别为()5,0，()2,6，过点B 作BC x ∥轴交y 轴于点C ，点D 为线段AB 上的一点，且2BD AD =．反比例函数(0)ky x x=>的图象经过点D 交线段BC 于点E ，则四边形ODBE 的面积是．OCEOADSS−即可求解，熟练掌握知识点的应用是解题的关键．x ⊥轴于M ，作12OCEOADS S−=⨯25．（2024·四川广元·中考真题）已知y =与()0ky x x=>的图象交于点()2,A m ，点B 为y 轴上一点，将OAB 沿OA 翻折，使点B 恰好落在()0ky x x=>上点C 处，则B 点坐标为．Rt tan AHO ，130=︒，B 为y 轴上一点，将OAB 沿OA 2130=∠=OB ， 390=︒−∠︒， 3m m，26．（2024·广东深圳·中考真题）如图，在平面直角坐标系中，四边形AOCB 为菱形，4tan 3AOC ∠=，且点A 落在反比例函数3y x=上，点B 落在反比例函数()0ky k x=≠上，则k = ．27．（2024·广东广州·中考真题）如图，平面直角坐标系xOy 中，矩形OABC 的顶点B 在函数(0)k y x x=>的图象上，(1,0)A ，(0,2)C ．将线段AB 沿x 轴正方向平移得线段A B ''（点A 平移后的对应点为A '），A B ''交函数(0)k y x x=>的图象于点D ，过点D 作DE y ⊥轴于点E ，则下列结论：①2k =；②OBD 的面积等于四边形ABDA '的面积；③A E ' ④B BD BB O ''∠=∠．其中正确的结论有．（填写所有正确结论的序号）的几何意义可得OBD 的面积等于四边形为矩形，可得当OD 合题意；如图，设平移距离为n ，可得，证明B BD A OB '''∽，可得，(0,2)C ，四边形∵1212AOBA ODS S'==⨯=， ∴BOKAKDA SS '=四边形，BOK BKD BKD AKDA S S S S '+=+四边形，∴OBD 的面积等于四边形ABDA '的面积；故②符合题意；如图，连接A E '，∵DE y ⊥轴，DA O EOA '∠=∠∴四边形A DEO '为矩形，∴A E OD '=，∴当OD 最小，则A E '最小，设()2,0D x x x ⎛⎫> ⎪⎝⎭，∴B BD A OB '''∽，∴B BD B OA '''∠=∠，∵B C A O ''∥，∴CB O A OB '''∠=∠，∴B BD BB O ''∠=∠，故④符合题意；故答案为：①②④【点睛】本题考查的是反比例函数的图象与性质，平移的性质，矩形的判定与性质，相似三角形的判定与性质，勾股定理的应用，作出合适的辅助线是解本题的关键．28．（2024·四川乐山·中考真题）定义：函数图象上到两坐标轴的距离都小于或等于1的点叫做这个函数图象的“近轴点”．例如，点()0,1是函数1y x =+图象的“近轴点”．（1）下列三个函数的图象上存在“近轴点”的是（填序号）；①3y x =−+；②2y x=；③221y x x =−+−．（2）若一次函数3y mx m =−图象上存在“近轴点”，则m 的取值范围为．三、解答题29．（2024·甘肃·中考真题）如图，在平面直角坐标系中，将函数y ax =的图象向上平移3个单位长度，得到一次函数y ax b =+的图象，与反比例函数()0k y x x =>的图象交于点()24A ，．过点()02B ，作x 轴的平行线分别交y ax b =+与()0k y x x=>的图象于C ，D 两点．(1)求一次函数y ax b =+和反比例函数k y x=的表达式； (2)连接AD ，求ACD 的面积．30．（2024·青海·中考真题）如图，在同一直角坐标系中，一次函数y x b =−+和反比例函数9y x=的图象相交于点()1,A m ，(),1B n ．(1)求点A ，点B 的坐标及一次函数的解析式；(2)根据图象，直接写出不等式9x b x−+>的解集．31．（2024·吉林·中考真题）已知蓄电池的电压为定值，使用蓄电池时，电流I（单位：A）与电阻R（单位：Ω）是反比例函数关系，它的图象如图所示．(1)求这个反比例函数的解析式（不要求写出自变量R的取值范围）．(2)当电阻R为3Ω时，求此时的电流I．32．（2024·山东·中考真题）列表法、表达式法、图像法是三种表示函数的方法，它们从不同角度反映了自变量与函数值之间的对应关系．下表是函数2y x b =+与k y x=部分自变量与函数值的对应关系：(1)求a 、b 的值，并补全表格；(2)结合表格，当2y x b =+的图像在k y x=的图像上方时，直接写出x 的取值范围．∴当2y x b =+的图像在k y x =的图像上方时，33．（2024·湖北·中考真题）一次函数y x m =+经过点()3,0A −，交反比例函数k y x =于点(),4B n ．(1)求m n k ，，；(2)点C 在反比例函数k y x=第一象限的图象上，若AO OB C A S S <△△，直接写出C 的横坐标a 的取值范围．【答案】(1)3m =，1n =，4k =；(2)1a >．34．（2024·四川凉山·中考真题）如图，正比例函数112y x =与反比例函数()20k y x x=>的图象交于点()2A m ，．(1)求反比例函数的解析式；(2)把直线112y x =向上平移3个单位长度与()20k y x x=>的图象交于点B ，连接,AB OB ，求AOB 的面积． AOB ADO SS =，代入）解：点(4,2)A 在反比例函数图象上，8k ∴=，∴反比例函数解析式为（2）解：把直线35．（2024·贵州·中考真题）已知点()1,3在反比例函数ky x=的图象上． (1)求反比例函数的表达式；(2)点()3,a −，()1,b ，()3,c 都在反比例函数的图象上，比较a ，b ，c 的大小，并说明理由．36．（2024·河南·中考真题）如图，矩形ABCD 的四个顶点都在格点（网格线的交点）上，对角线AC ，BD 相交于点E ，反比例函数()0ky x x=>的图象经过点A ．(1)求这个反比例函数的表达式．(2)请先描出这个反比例函数图象上不同于点A的三个格点，再画出反比例函数的图象．(3)将矩形ABCD向左平移，当点E落在这个反比例函数的图象上时，平移的距离为________．37．（2024·四川乐山·中考真题）如图，已知点()1,A m 、(),1B n 在反比例函数()30y x x=>的图象上，过点A 的一次函数y kx b =+的图象与y 轴交于点()0,1C ．(1)求m 、n 的值和一次函数的表达式； (2)连接AB ，求点C 到线段AB 的距离．ABCS=）点又一次函数C 点Rt ADB 中，又12ABCSBC =1322⨯⨯=⨯322CE =，即点38．（2024·四川眉山·中考真题）如图，在平面直角坐标系xOy 中，一次函数y kx b =+与反比例函数()0my x x=>的图象交于点()1,6A ，(),2B n ，与x 轴，y 轴分别交于C ，D 两点．(1)求一次函数和反比例函数的表达式；(2)若点P在y轴上，当PAB的周长最小时，请直接写出点P的坐标；(3)将直线AB向下平移a个单位长度后与x轴，y轴分别交于E，F两点，当12EF AB=时，求a的值．，则此时，PAB的周长最小，根据轴对称5，于是得到点8a+−，得到）解：一次函数(此时，PAB 的周长最小，点()1,6A ，()1,6E ∴−，BE 的解析式为12EF AB =39．（2024·甘肃临夏·中考真题）如图，直线y kx =与双曲线4y x=−交于A ，B 两点，已知A 点坐标为(),2a ．(1)求a ，k 的值；(2)将直线y kx =向上平移()0m m >个单位长度，与双曲线4y x=−在第二象限的图象交于点C ，与x 轴交于点E ，与y 轴交于点P ，若PE PC =，求m 的值． ∴FCP OEP ∴∠=∠，CFP ∠PE PC =，(AAS CFP EOP ∴≌CF OE =，OP PF =∵直线y x =−向上平移令0x =，得y m =，令(),0E m ∴，()0,P m ，双曲线40．（2024·四川广元·中考真题）如图，已知反比例函数1ky x=和一次函数2y mx n =+的图象相交于点()3,A a −，3,22B a ⎛⎫+− ⎪⎝⎭两点，O 为坐标原点，连接OA ，OB ．(1)求1ky x=与2y mx n =+的解析式； (2)当12y y >时，请结合图象直接写出自变量x 的取值范围； (3)求AOB 的面积．12AOBAOCBOCS SSOC =+=12AOBAOCBOCSSSOC =+=41．（2024·内蒙古赤峰·中考真题）在平面直角坐标系中，对于点()11,M x y ，给出如下定义：当点()22,N x y ，满足1212x x y y +=+时，称点N 是点M 的等和点．(1)已知点()1,3M ，在()14,2N ，()23,1N −，()30,2N −中，是点M 等和点的有_____； (2)若点()3,2M −的等和点N 在直线y x b =+上，求b 的值； (3)已知，双曲线1ky x=和直线22y x =−，满足12y y <的x 取值范围是4x >或20x −<<．若点P 在双曲线1ky x=上，点P 的等和点Q 在直线22y x =−上，求点P 的坐标．。

2020年中考数学一轮复习基础考点题型练：《反比例函数》(含答案)

2020年中考数学一轮复习基础考点题型练：《反比例函数》一．选择题1．下列函数中，其图象经过原点的是（）A ．y ＝2x ﹣3B ．y ＝C ．y ＝x 2﹣1D ．y ＝2．已知函数y ＝的图象过点（2，﹣3），则该函数的图象必在（）A ．第二、三象限B ．第二、四象限C ．第一、三象限D ．第三、四象限 3．若点A （x 1，y 1），B （x 2，y 2），C （x 3，y 3）在反比例函数y ＝（k ＜0）的图象上，且y 1＞0＞y 2＞y 3，则下列各式正确的是（）A ．x 1＜x 2＜x 3B ．x 2＜x 1＜x 3C ．x 1＜x 3＜x 2D ．x 3＜x 2＜x 14．如图，矩形AOBC 的面积为4，反比例函数y ＝的图象的一支经过矩形对角线的交点P ，则k 的值是（）A ．1B ．﹣2C ．﹣1D ．﹣5．如图，已知直线y ＝x 与双曲线y ＝（k ＞0）交于A 、B 两点，A 点的横坐标为3，则下列结论：①k ＝6；②A 点与B 点关于原点O 中心对称；③关于x 的不等式＜0的解集为x ＜﹣3或0＜x ＜3；④若双曲线y ＝（k ＞0）上有一点C 的纵坐标为6，则△AOC 的面积为8，其中正确结论的个数（）A ．4个B ．3个C ．2个D ．1个6．如图，在平面直角坐标系中，直线y＝﹣2x+2与x轴、y轴分别交于A、B两点，以AB 为边在第一象限作正方形ABC D沿x轴负方向平移a个单位长度后，点C恰好落在双曲线上则a的值是（）A．1 B．2 C．3 D．47．如图，已知二次函数y＝ax2+bx+c的图象分别与x轴的正半轴和负半轴交于A、B两点，且OA＜OB，则一次函数y＝ax+b和反比例函数y＝的图象可能是（）A．B．C．D．8．如图，四边形ABCO是平行四边形，OA＝2，AB＝6，点C在x轴的负半轴上，将平行四边形ABCO绕点A逆时针旋转得到平行四边形ADEF，AD经过点O，点F恰好落在x轴的正半轴上．若点D在反比例函数y＝（x＜0）的图象上，则k的值为（）A．4B．12 C．8D．69．如图，A 、B 两点在双曲线y ＝上，分别经过点A 、B 两点向x 、y 轴作垂线段，已知S 阴影＝2，则S 1+S 2＝（）A ．3B ．4C ．5D ．610．如图所示，是反比例函数y ＝与y ＝在x 轴上方的图象，点C 是y 轴正半轴上的一点，过点C 作AB ∥x 轴分别交这两个图象于A 点和B 点，若点P 在x 轴上运动，则△ABP 的面积等于（）A ．5B ．4C ．10D ．2011．已知反比例函数的图象经过点P （4，﹣1），则该反比例函数的图象所在的象限是（）A ．第一、二象限B ．第一、三象限C ．第二、三象限D ．第二、四象限 12．如图，过点O 作直线与双曲线y ＝（k ≠0）交于A 、B 两点，过点B 作BC ⊥x 轴于点C ，作BD ⊥y 轴于点D ．在x 轴，y 轴上分别取点E 、F ，使点A 、E 、F 在同一条直线上，且AE ＝AF ．设图中矩形ODBC 的面积为S 1，△EOF 的面积为S 2，则S 1、S 2的数量关系是（）A ．S 1＝S 2B ．2S 1＝S 2C ．3S 1＝S 2D ．4S 1＝S 213．已知正比例函数y ＝mx 图象与反比例函数y ＝图象的一个交点是A （3，1），则不等式mx ＜的解集是．14．如图，过双曲线y ＝上的A 、B 两点分别向x 轴、y 轴作垂线，垂足分别为C 、E 、D 、F ，AC 、BF 相交于点G ，矩形ADFG 和矩形BECG 的面积分别为S 1、S 2，若S 阴影＝1，则S 1+S 2＝．15．如图，平行四边形ABOC 的顶点A 、C 分别在y 轴和x 轴上，顶点B 在反比例函数的图象上，则平行四边形ABOC 的面积是．16．在以O 为原点的直角坐标系中，矩形OABC 的两边OC 、OA 分别在x 轴、y 轴的正半轴上，反比例函数y ＝（x ＞0）的图象与AB 相交于点D ，与BC 相交于点E ，若BD ＝3AD ，且△ODE 的面积为15，则k 的值是．17．如图，在平面直角坐标系中，直线y ＝﹣4x +4与x 轴、y 轴分别交于A 、B 两点，以AB 为边在第一象限作正方形ABCD ，点D 在双曲线y ＝上；将正方形ABCD 沿x 轴负方向平移a 个单位长度后，点C 恰好落在双曲线在第一象限的分支上，则a 的值是．18．如图，在平面直角坐标系中，直线AB与x轴交于点B，与y轴交于点A，直线AB与反比例函数y＝（m＞0）在第一象限的图象交于点C、点D，其中点C的坐标为（1，8），点D的坐标为（4，n）．（1）分别求m、n的值；（2）连接OD，求△ADO的面积．19．已知在平面直角坐标中，点A（m，n）在第一象限内，AB⊥OA且AB＝OA，反比例函数y ＝的图象经过点A，（1）当点B的坐标为（4，0）时（如图），求这个反比例函数的解析式；（2）当点B在反比例函数y＝的图象上，且在点A的右侧时（如图2），用含字母m，n 的代数式表示点B的坐标；（3）在第（2）小题的条件下，求的值．20．如图，已知直线y ＝ax +b 与双曲线y ＝（x ＞0）交于A （x 1，y 1），B （x 2，y 2）两点，点A 与点B 不重合，直线AB 与x 轴交于点P （x 0，0），与y 轴交于点C（1）若A 、B 两点坐标分别为（1，4），（4，y 2），求点P 的坐标；（2）若b ＝y 1+1，x 0＝6，且y 1＝2y 2，求A ，B 两点的坐标；（3）若将（1）中的点A ，B 绕原点O 顺时针旋转90°，A 点对应的点为A ′，B 点的对应点为B ′点，连接AB ′，A ′B ′，动点M 从A 点出发沿线段AB ′以每秒1个单位长度的速度向终点B ′运动；动点N 同时从B ′点出发沿线段B ′A ′以每秒1个单位长度的速度向终点A ′运动，当其中一个点停止运动时另一个点也随之停止运动．设运动的时间为t 秒，试探究：是否存在使△MNB ′为等腰直角三角形的t 值，若存在，求出t 的值；若不存在，说明理由．21．如图，反比例函数的图象经过点C ，过点C 作y 轴、x 轴的垂线，垂足分别为点A 、B ，过点P （0，4）的直线交直线AC 于点D 、交直线OB 于点E ．（1）若PD ＝DE ，直线PD 平分矩形AOBC 的面积直接写出：S 矩形AOBC ＝，直线PD 的解析式：；（2）在（1）的条件下，将过点P 的直线绕点P 旋转，连接DO ，若DO 平分∠ADE ，求旋转后直线的解析式：．（3）在（1）的条件下，将过点P 的直线沿y 轴平移，再将矩形ABCD 沿过点P 的直线翻折，使点O 落在反比例函数图象上M 点处，求M 点的坐标．参考答案一．选择题1．解：A 、当x ＝0时，y ＝﹣3，（0，0）不在y ＝2x ﹣3上；B 、反比例函数一定不过原点；C 、当x ＝0时，y ＝﹣1，（0，0）不在y ＝x 2﹣1上．D ．x ＝0时，y ＝0，综上可得：只有D 正确．故选：D ．2．解：∵函数y ＝的图象过点（2，﹣3），∴k ＝2×（﹣3）＝﹣6＜0，∴函数的图象在二、四象限，故选：B ．3．解：∵反比例函数为y ＝（k ＜0），∴函数图象在第二、四象限，在每个象限内，y 随着x 的增大而增大，又∵y 1＞0＞y 2＞y 3，∴x 1＜0，x 2＞x 3＞0，∴x 1＜x 3＜x 2，故选：C ．4．解：作PE ⊥x 轴于E ，PF ⊥y 轴于F ，如图，∵点P 为矩形AOBC 对角线的交点，∴矩形OEPF 的面积＝矩形AOBC 的面积＝×4＝1，∴|k |＝1，而k ＜0，∴k＝﹣1，故选：C．5．解：①∵直线y＝x与双曲线y＝（k＞0）交于A、B两点，A点的横坐标为3，∴点A的纵坐标为：y＝×3＝2，∴点A（3，2），∴k＝3×2＝6，故①正确；②∵直线y＝x与双曲线y＝（k＞0）是中心对称图形，∴A点与B点关于原点O中心对称，故②正确；③∵直线y＝x与双曲线y＝（k＞0）交于A、B两点，∴B（﹣3，﹣2），∴关于x的不等式＜0的解集为：x＜﹣3或0＜x＜3，故③正确；④过点C作CD⊥x轴于点D，过点A作AE⊥x轴于点E，∵点C的纵坐标为6，∴把y＝6代入y＝得：x＝1，∴点C（1，6），∴S△AOC ＝S△OCD+S梯形AEDC﹣S△AOE＝S梯形AEDC＝×（2+6）×（3﹣1）＝8，故④正确；故选：A．6．解：（1）作DF⊥x轴于点F．在y＝﹣3x+3中，令x＝0，则y＝3，即B（0，2），令y＝0，则x＝1，即A（1，0），则OB＝2，OA＝1，∵∠BAD＝90°，∴∠BAO+∠DAF＝90°，∵Rt△ABO中，∠BAO+∠DAF＝90°，∴∠DAF＝∠OBA，在△OAB与△FDA中，，∴△OAB≌△FDA（AAS），∴AF＝OB＝2，DF＝OA＝1，∴OF＝3，∴D（3，1），∵点D在反比例函数y＝（k≠0）的图象上，∴1＝，解得k＝3；作CE⊥y轴，交反比例函数的图象于点G，∵同（1）可得△OAB≌△EBC，∴OB＝EC＝2，OA＝BE＝1，∴OE＝3，C（2，3），∵点C的纵坐标是3，∴G（1，3），∴CG＝1，即m＝1．故选：A．7．解：∵二次函数y＝ax2+bx+c的图象分别与x轴的正半轴和负半轴交于A、B两点，且OA ＜OB，∴a＜0，b＜0，c＞0，∴一次函数y＝ax+b的图象在第二、三、四象限，反比例函数y ＝的图象在第二、四象限，故选：D ．8．解：由题意可得，OA ＝2，AF ＝2，∴∠AFO ＝∠AOF ，∵AB ∥OF ，∠BAO ＝∠OAF ，∴∠BAO ＝∠AOF ，∠BAF +∠AFO ＝180°，解得，∠BAO ＝60°，∴∠DOC ＝60°，∵AO ＝2，AD ＝6，∴OD ＝4，∴点D 的横坐标是：﹣4×cos60°＝﹣2，纵坐标为：﹣4×sin60°＝﹣2， ∴点D 的坐标为（﹣2，﹣2），∵D 在反比例函数y ＝（x ＜0）的图象上， ∴﹣2＝，得k ＝4，故选：A ．9．解：根据题意得S 1+S 阴影＝S 2+S 阴影＝4，而S 阴影＝2，所以S 1＝S 2＝2，所以S 1+S 2＝4．故选：B ．10．解：设点A （a ，）∵AB ∥x 轴∴点B 纵坐标为，且点B 在反比例函数y ＝图象上， ∴点B 坐标（﹣，） ∴S △ABP ＝（a +）×＝5 故选：A ．11．解：设反比例函数的解析式为y ＝，∵反比例函数的图象经过点P （4，﹣1），可得k ＝﹣4＜0，则它的图象在第二、四象限．故选：D ．12．解：设A 点坐标为（m ，﹣n ），过点O 的直线与双曲线y ＝交于A 、B 两点，则A 、B 两点关与原点对称，则B 的坐标为（﹣m ，n ）；矩形OCBD 中，易得OD ＝n ，OC ＝m ；则S 1＝mn ；在Rt △EOF 中，AE ＝AF ，故A 为EF 中点，由中位线的性质可得OF ＝2n ，OE ＝2m ；则S 2＝OF ×OE ＝2mn ；故2S 1＝S 2．故选：B ．二．填空题（共5小题）13．解：∵正比例函数y ＝mx 图象与反比例函数y ＝图象的一个交点是A （3，1）， ∴另一交点B 为（﹣3，﹣1）．观察函数图象，发现：当x ＜﹣3或0＜x ＜3时，正比例函数图象在反比例函数图象的下方，∴mx ＜的解集是0＜x ＜3或x ＜﹣3故答案为0＜x ＜3或x ＜﹣3．14．解：∵过双曲线y＝上的A、B两点分别向x轴、y轴作垂线，垂足分别为C、E，∴S1+S阴影＝S2+S阴影＝3，∵S阴影＝1，∴S1＝S2＝2，∴S1+S2＝4，故答案为4．15．解：作BD⊥x轴于D，∴四边形AODB是矩形，∵顶点B在反比例函数的图象上，∴四边形AODB的面积为3，∵平行四边形ABOC的面积＝矩形AODB的面积，∴平行四边形ABOC的面积为3，故答案为3．16．解：∵四边形OCBA是矩形，∴AB＝OC，OA＝BC，设B点的坐标为（a，b），∵BD＝3AD，∴D（，b）∵D、E在反比例函数的图象上，∴＝k，设E的坐标为（a，y），∴ay＝k∴E（a，），∵S△ODE ＝S矩形OCBA﹣S△AOD﹣S△OCE﹣S△BDE＝ab﹣k﹣k﹣••（b﹣）＝15，∴4k﹣k﹣+＝15，解得：k＝8，故答案为：8．17．解：当x＝0时，y＝4，∴B（0，4），当y＝0时，x＝1，∴A（1，0），∴OA＝1，OB＝4，∵ABCD是正方形，∴AB＝BC＝CD＝DA，∠ABC＝∠BCD＝∠CDA＝∠DAB＝90°，过点D、C作DM⊥x轴，CN⊥y轴，垂足为M、N，∴∠ABO＝∠BCN＝∠DAM，∵∠AOB＝∠BNC＝∠AMD＝90°，∴△AOB≌△BNC≌△DMA（AAS），∴OA＝DM＝BN＝1，AM＝OB＝CN＝4∴OM＝1+4＝5，ON＝4+1＝5，∴C（4，5），D（5，1），把D（5，1）代入y＝得：k＝5，∴y＝，当y＝5时，x＝1，∴E（1，5），点C向左平移到E时，平移距离为4﹣1＝3，即：a＝3，故答案为：3．三．解答题（共4小题）18．解：（1）∵反比例函数y＝（m＞0）在第一象限的图象交于点C（1，8），∴8＝，∴m＝8，∴函数解析式为y＝，将D（4，n）代入y＝得，n＝＝2．（2）设直线AB的解析式为y＝kx+b，由题意得，解得，∴直线AB的函数解析式为y＝﹣2x+10，令x＝0，则y＝10，∴A（0，10），∴△ADO的面积＝＝20．19．解：（1）过A作AC⊥OB，交x轴于点C，∵OA＝AB，∠OAB＝90°，∴△AOB为等腰直角三角形，∴AC＝OC＝BC＝OB＝2，∴A（2，2），将x＝2，y＝2代入反比例解析式得：2＝，即k＝4，则反比例解析式为y＝；（2）过A作AE⊥x轴，过B作BD⊥AE，∵∠OAB＝90°，∴∠OAE+∠BAD＝90°，∵∠AOE+∠OAE＝90°，∴∠BAD＝∠AOE，在△AOE和△BAD中，，∴△AOE≌△BAD（AAS），∴AE＝BD＝n，OE＝A D＝m，∴DE＝AE﹣AD＝n﹣m，OE+BD＝m+n，则B（m+n，n﹣m）；（3）由A与B都在反比例图象上，得到mn＝（m+n）（n﹣m），整理得：n2﹣m2＝mn，即（）2+﹣1＝0，这里a＝1，b＝1，c＝﹣1，∵△＝1+4＝5，∴＝，∵A（m，n）在第一象限，∴m＞0，n＞0，则＝．20．解：（1）∵直线y＝ax+b与双曲线y＝（x＞0）交于A（1，4）∴k＝1×4＝4，∴y＝，∵B （4，y 2）在反比例函数的图象上，∴y 2＝＝1，∴B （4，1），∵直线y ＝ax +b 经过A 、B 两点， ∴，解得，∴直线为y ＝﹣x +5，令y ＝0，则x ＝5，∴P （5，0）；（2）如图，作AD ⊥y 轴于D ，AE ⊥x 轴于E ，BF ⊥x 轴于F ，BG ⊥y 轴于G ，AE 、BG 交于H ，则AD ∥BG ∥x 轴，AE ∥BF ∥y 轴， ∴＝，＝＝，∵b ＝y 1+1，y 1＝2y 2， ∴＝，＝＝，∴B （， y 1），∵A ，B 两点都是反比例函数图象上的点， ∴x 1•y 1＝•y 1，解得x 1＝2，代入＝，解得y 1＝2，∴A （2，2），B （4，1）；（3）存在，如图2，∵A 、B 两点坐标分别为（1，4），（4，1），将B 绕原点O 顺时针旋转90°， ∴B ′（1，﹣4），∴AB ′＝8，由题意得：AM ＝BN ＝t ，∴B ′M ＝8﹣t ，∵△MNB ′为等腰直角三角形，∴①当∠B ′N 1M 1＝90°，即B ′M 1＝B ′N 1， ∴8﹣t ＝t ，解得：t ＝8﹣8；②当∠B ′M 2N 2＝90°，即B ′N 2＝B ′M 2， ∴t ＝（8﹣t ），解得：t ＝16﹣8；综上所述，t 的值为8﹣8或16﹣8．21．解：（1）∵AD ∥OE ，PD ＝DE ，OP ＝4，∴PA ＝AO ＝2，∴C （4，2），∴S 矩形ACBO ＝2×4＝8，∵PD 平分矩形ACBO 的面积，∴直线PE 经过OC 的中点（2，1）设直线PD 的解析式为y ＝kx +b ，则有，∴直线PD 的解析式为y ＝﹣x +4．故答案为8，y＝﹣x+4（2）如图，连接OD．∵OD平分∠ADE，∴∠ADO＝∠ODE，∵AD∥OE，∴∠ADO＝∠DOE，∴∠DOE＝∠EDO，∴OE＝DE＝PD，∴PE＝2OE，∴∠OPE＝30°，∴OE＝OP•tan30°＝，∴E（，0），∴直线PE的解析式为y＝﹣x+4，根据对称性可知：直线y＝x+4也满足条件，故答案为y＝±x﹣4（3）如图，作OM⊥PE交反比例函数的图象于M，点M即为所求．∵OM⊥PE，∴直线OM的解析式为y＝x，由，解得或（舍弃），∴M（2，）．。

反比例函数及其应用(26题)(解析版)—2024年中考数学真题分类汇编(全国通用)

反比例函数及其应用（26题）一、单选题1．（2024·黑龙江大庆·中考真题）在同一平面直角坐标系中，函数()0y kx k k =-¹与ky x=的大致图象为（）A ．B ．C ．D ．2．（2024·山东济宁·中考真题）已知点()()()1232,,1,,3,A y B y C y --在反比例函数(0)ky k x=<的图象上，则123,,y y y 的大小关系是（）A ．123y y y <<B ．213y y y <<C ．312y y y <<D ．321y y y <<3．（2024·内蒙古通辽·中考真题）如图，平面直角坐标系中，原点O 为正六边形ABCDEF 的中心，EF x ∥轴，点E 在双曲线(ky k x=为常数，0)k >上，将正六边形ABCDEF D 恰好落在双曲线上，则k 的值为（）A ．B ．C ．D ．3二、填空题4．（2024·江苏无锡·中考真题）某个函数的图象关于原点对称，且当0x >时，y 随x 的增大而增大．请写出一个符合上述条件的函数表达式：．5．（2024·江苏连云港·中考真题）杠杆平衡时，“阻力´阻力臂=动力´动力臂”．已知阻力和阻力臂分别为1600N 和0.5m ，动力为(N)F ，动力臂为(m)l ．则动力F 关于动力臂l 的函数表达式为．6．（2024·江苏无锡·中考真题）在探究“反比例函数的图象与性质”时，小明先将直角边长为5个单位长度的等腰直角三角板ABC摆放在平面直角坐标系中，使其两条直角边AC BC，分别落在x轴负半轴、y轴正半轴上（如图所示），然后将三角板向右平移a个单位长度，再向下平移a个单位长度后，小明发现A B，两点恰好都落在函数6yx=的图象上，则a的值为．故答案为：2或3．7．（2024·福建·中考真题）如图，在平面直角坐标系xOy 中，反比例函数ky x=的图象与O e 交于,A B 两点，且点,A B 都在第一象限．若()1,2A ，则点B 的坐标为．∵反比例函数ky x=的图象与∴221kk ==，设()B n m ，，则2nm k ==∵22215OB OA ==+=三、解答题8．（2024·江苏常州·中考真题）如图，在平面直角坐标系xOy 中，一次函数y kx b =+的图像与反比例函数my x=的图像相交于点()1,A n -、()2,1B ．(1)求一次函数、反比例函数的表达式；(2)连接OA OB 、，求OAB V 的面积．∵1y x =-，∴当0x =时，1y =-，∴()0,1C -，∴OAB V 的面积12OC x =×9．（2024·四川内江·中考真题）如图，一次函数y ax b =+的图象与反比例函数ky x=的图象相交于A 、B 两点，其中点A 的坐标为()2,3-，点B 的坐标为()3,n(1)求这两个函数的表达式；(2)根据图象，直接写出关于x 的不等式kax b x+<的解集10．（2024·四川资阳·中考真题）如图，已知平面直角坐标系中，O 为坐标原点，一次函数y kx b =+（0k ¹）的图象与反比例函数4y x=的图象相交于(),4A m ，()4,B n 两点．(1)求一次函数的解析式；C t t在一次函数的图象上，直线CO与反比例函数的图象在第三象限内交于点D，求点D的坐标，(2)若点(),并写出直线CD在图中的一个特征．11．（2024·黑龙江大庆·中考真题）如图1，在平面直角坐标系中，O 为坐标原点，点A 在x 轴的正半轴上，点B ，C 在第一象限，四边形OABC 是平行四边形，点C 在反比例函数ky x=的图象上，点C 的横坐标为2，点B 的纵坐标为3．提示：在平面直角坐标系中，若两点分别为()111,P x y ，()222,P x y ，则12PP 中点坐标为1212,22x x y y ++⎛⎫⎪⎝⎭．(1)求反比例函数的表达式；(2)如图2，点D 是AB 边的中点，且在反比例函数ky x=图象上，求平行四边形OABC 的面积；(3)如图3，将直线13:4l y x =-向上平移6个单位得到直线2l ，直线2l 与函数()0ky x x =>图象交于1M ，2M 两点，点P 为12M M 的中点，过点1M 作11M N l ⊥于点N ．请直接写出P 点坐标和1M NOP的值．【点睛】本题考查平行四边形的性质、中点坐标公式、一次函数的平移规律、一次函数与反比例函数的交点问题、锐角三角函数、平行线定理、一次函数与坐标轴的交点问题、勾股定理、一元二次方程的根与系数的关系、用待定系数法求反比例函数解析式，熟练掌握相关知识是解题的关键．12．（2024·四川巴中·中考真题）如图，在平面直角坐标系中，直线2y x =+与反比例函数()0ky k x=¹的图象交于AB 、两点，点A 的横坐标为1．(1)求k 的值及点B 的坐标．(2)点P 是线段AB 上一点，点M 在直线OB 上运动，当12BPO ABO S S =△△时，求PM 的最小值．∴222210510BP OP PM OB ×´===【点睛】本题考查的是一次函数与反比例函数的综合，求解函数解析式，一元二次方程的解法，勾股定理的应用，等腰三角形的性质，理解题意是解本题的关键13．（2024·四川·中考真题）如图，在平面直角坐标系xOy 中，已知()()2,3,,2A B m -两点在反比例函数ky x=的图象上．(1)求k 与m 的值；(2)连接BO ，并延长交反比例函数ky x=的图象于点C ．若一次函数的图象经过A ，C 两点，求这个一次函数的解析式．14．（2024·江西·中考真题）如图，AOB V 是等腰直角三角形，90Ð=°ABO ，双曲线()0,0ky k x x=>>经过点B ，过点()4,0A 作x 轴的垂线交双曲线于点C ，连接BC ．(1)点B 的坐标为______；(2)求BC 所在直线的解析式．∵AOB V 是等腰直角三角形，90Ð=ABO ∴4OA =，∴2BD OD AD ===，∴()2,2B ，15．（2024·山东泰安·中考真题）直线()10y kx b k =+¹与反比例函数28y x=-的图象相交于点()2,A m -，(),1B n -，与y 轴交于点C ．(1)求直线1y 的表达式；(2)若12y y >，请直接写出满足条件的x 的取值范围；(3)过C 点作x 轴的平行线交反比例函数的图象于点D ，求ACD V 的面积．16．（2024·四川泸州·中考真题）如图，在平面直角坐标系xOy 中，一次函数y kx b =+与x 轴相交于点()2,0A -，与反比例函数ay x=的图象相交于点()2,3B ．(1)求一次函数和反比例函数的解析式；(2)直线()2x m m =>与反比例函数()0a y x x =>和()20y x x=->的图象分别交于点C ，D ，且2OBC OCD S S =△△，求点C 的坐标．【分析】本题主要考查了一次函数与反比例函数综合，反比例函数与几何综合：17．（2024·四川广安·中考真题）如图，一次函数y ax b =+（a ，b 为常数，0a ¹）的图象与反比例函数ky x=（k 为常数，0k ¹）的图象交于(2,4)A ，(,2)B n -两点．(1)求一次函数和反比例函数的解析式．(2)直线AB 与x 轴交于点C ，点(,0)P m 是x 轴上的点，若PAC △的面积大于12，请直接写出m 的取值范围．对于2y x =+，当20y x =+=，解得∴()2,0C -，∵(,0)P m ，∴2CP m =+，18．（2024·江苏连云港·中考真题）如图1，在平面直角坐标系xOy 中，一次函数1(0)y kx k =+¹的图像与反比例函数6y x=的图像交于点A 、B ，与y 轴交于点C ，点A 的横坐标为2．(1)求k 的值；(2)利用图像直接写出61kx x+<时x 的取值范围；(3)如图2，将直线AB 沿y 轴向下平移4个单位，与函数6(0)y x x =>的图像交于点D ，与y 轴交于点E ，再将函数6(0)y x x=>的图像沿AB 平移，使点A 、D 分别平移到点C 、F 处，求图中阴影部分的面积．19．（2024·上海·中考真题）在平面直角坐标系xOy 中，反比例函数k y x=（k 为常数且0k ¹）上有一点()3,A m -，且与直线24y x =-+交于另一点(),6B n ．(1)求k 与m 的值；(2)过点A 作直线l x ∥轴与直线24y x =+交于点C ，求sin OCA Ð的值．∵l x ∥轴，x 轴y ⊥轴，∴A 、C 、D 的纵坐标相同，均为把2y =代入24y x =-+解得1x =，∴()1,2C ，20．（2024·江苏盐城·中考真题）小明在草稿纸上画了某反比例函数在第二象限内的图像，并把矩形直尺放在上面，如图．请根据图中信息，求：(1)反比例函数表达式；(2)点C 坐标．由图可得3AD =，2OD =，设点C 的坐标为6,m m ⎛⎫- ⎪⎝⎭，则CE \63BE OE OB m=-=--，Q 矩形直尺对边平行，21．（2024·四川达州·中考真题）如图，一次函数y kx b =+（k 、b 为常数，0k ¹）的图象与反比例函数m y x=（m 为常数，0m ¹）的图象交于点()2,3A ，(),2B a -．(1)求反比例函数和一次函数的解析式；(2)若点C 是x 轴正半轴上的一点．且90BCA Ð=°．求点C 的坐标．90BCA Ð=°Q NCB ACM \Ð+Ð=MAC ACM Ð+Ð=Q NCB MAC\Ð=Ðtan tan NCB MAC\Ð=Ð即NB MC NC AM=22．（2024·四川遂宁·中考真题）如图，一次函数()10y kx b k =+¹的图象与反比例函数()20m y m x=¹的图象相交于()()1,3,1A B n -，两点．(1)求一次函数和反比例函数的表达式；(2)根据图象直接写出12y y >时，x 的取值范围；V的面积．(3)过点B作直线OB，交反比例函数图象于点C，连结AC，求ABC∵点B C 、关于原点对称，∴()3,1C ，∴312MN =-=，1CN =，ON ∴ABC BOD ADOM S S S S =++V V 梯形梯形()(11123．（2024·四川宜宾·中考真题）如图，一次函数．()0y ax b a =+¹的图象与反比例函数()0k y k x=¹的图象交于点()()1,4,1A B n -、．(1)求反比例函数和一次函数的表达式；(2)利用图象，直接写出不等式k ax b x+<的解集；(3)已知点D 在x 轴上，点C 在反比例函数图象上．若以A 、B 、C 、D 为顶点的四边形是平行四边形，求点C 的坐标．24．（2024·四川德阳·中考真题）如图，一次函数22y x =-+与反比例函数(0)k y x x=<的图象交于点()1,A m -．(1)求m 的值和反比例函数k y x=的解析式；(2)将直线22y x =-+向下平移h 个单位长度(0)h >后得直线y ax b =+，若直线y ax b =+与反比例函数(0)k y x x =<的图象的交点为(),2B n ，求h 的值，并结合图象求不等式k ax b x<+的解集．25．（2024·山东潍坊·中考真题）如图，正比例函数y =的图象与反比例函数k y x =的图象的一个交点是(A m ．点()P n 在直线y =上，过点P 作y 轴的平行线，交k y x =的图象于点Q ．(1)求这个反比例函数的表达式；(2)求OPQ △的面积．26．（2024·四川雅安·中考真题）如图，在平面直角坐标系中，一次函数的图象l 与反比例函数k y x =的图象交于1,42M ⎛⎫ ⎪⎝⎭，(),1N n 两点．(1)求反比例函数及一次函数的表达式；(2)求OMN V 的面积；(3)若点P 是y 轴上一动点，连接PM PN ，．当PM PN +的值最小时，求点P 的坐标．又直线l 为25y x =-+，∴5,02A ⎛⎫ ⎪⎝⎭，()0,5B ．∴52OA =，5OB =，∴12OMN AOB AON BOM S S S S =--=´△△△△轴于点∵1,42M ⎛⎫ ⎪⎝⎭与M ¢关于y 轴对称，∴M ¢为1,42⎛⎫- ⎪⎝⎭．又()2,1N ，设M N ¢的解析式为则14221c d c d ì-+=ïíï+=î，解得65175c d ì=-ïïíï=ïî。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1 2018年辽宁省鞍山市中考英语试卷 (时间100分钟满分120分) 第1卷(选择题)(共50分) I.单项选择(共10小题;每小题1分，满分10分) 从各题所给的四个选项中，选出可以填人空白处的最佳选项 1.--Do you enjoy the_____? -- Yes, it is wonderful, I like that nice actress in it. A. party b.movie C. trip D. book 解析:考査名词词义辨析。party意为”聚会＂，movie意为”电影＂，trip意为“旅行＂，book为“书＂。根据答句中的 that nice actress可知问句意为”你喜欢那个电影吗”，因此答案应为B。 2. -What's the matter with Tom? -He hit_____on the knee by mistake yesterday. A. his B.him C. himself D, her 解析:考查代词的用法。hit sb. on/in+身体部位，固定用法，意为”击打......(身体部位)”。答句句意:昨天由于疏忽，他伤到了膝盖。主语是He，故空处应用反身代词 himself，因此答案应为C。 3. Susan went to_____supermarket to buy______orange scarf for her sister yesterday. A.a; a B. a: an C. a: the D, the: / 解析:考查冠词的用法。句意:昨天 Susan去了一家超市给她的妹妹买了一条橙色围巾。本题中的两个空都表示泛指，故填不定冠词。 supermarket是以辅音音素开头的单词， orange是以元音音素开头的单词，因此答案应为B 4. -Thirty dollars for such a T-shirt! You_____be joking! -I’m serious. It's made of cotton A, must B, need C. may D. can 解析:考查情态动词的用法。句意:这么一件T恤衫要三干美元!你一定是在开玩笑吧!＂ “You must be joking!＂是固定用法，因此答案应为A。 5. -When is your birthday? --It's on May 1st. It's my______birthday this year. A. fifteen B, fifteenth C. the fifteen D. the fifteenth 解析:考查数词的用法。表达“第十五个”应该用序数词，另外，序数词前面有物主代词时，无须定冠词the，因此答案应为B 6. -I love the beach in summer. -Yes, it_____good to swim in the cool water. A. tastes B. looks C. smells D. feels 解析:考查感官动词词义辨析。根据句意“是的，在凉爽的水里游泳的感觉很好”可知答案应为D 7. -It is said that thousands of trees______every year. -It's great. A. plant B is planted C. are planted D. were planted 【解析】考查动词的时态和语态。句意:据说每年有数以千计的树被栽种。主语trees和动词plant构成被动关系，故用被动语态，另外根据 every year以及主语是名词复数可知答案应为C 8.______bad weather is! You’d better stay at home. A. What B. How C. What a D. How a 【解析】考査感叹句的用法。感叹句的常用句型:(1)what+名词+主语+谓语;(2)How+形容词/副词+主语+谓语。题干中有核心词名词 bad weather，是不可数名词，因此答案应为A 9. -Could you tell me______? --Yes. She____to America A. where is Jane: has been B. where Jane is; has been 2

C. where is Jane; has gone D. where Jane is; has gone 解析:考查宾语从句及 have been to与 have gone to的区别。宾语从句三要素:引导词、陈述句语序和时态。通过语序可排除A、C选项;have/ has been to表示去过某地(已经回来);have/ has gone to表示去了某地(还没回来)。根据句意“你能告诉我Jane在哪里吗”可知， Jane并不在说话者身边，所以应该用have/ has gone to，因此答案应为D。 10. -Would you like to join me in playing basketball tomorrow? --_________ A. It doesn't matter B. You're welcome C. I don’t D. I’d love to 【解析】考个交际用语。根据问句“ Would you like to..?”可知这是建议句型，其肯定回答应该用＂ I’d love to.＂来回答，因此答案应为D

Ⅱ.情景交际(共5小题;每小题1分，满分5分) 根据对话内容，从所给的七个选项中选出可以填入空白处的最佳选项，使对话内容完整。 A: Hi, Bob! How was your weekend? B: Pretty good. 11. ___________ A: What did you do last weekend? B: I played basketball A:12._______ B. Twice a week. I like it very much. 13. _______ A: I went to the mountains last weekend B: 14. ______ Do you often go to the mountains? A. Yes. Once a week. Will you go there with us this weekend? B:15._______Maybe next week is OK. A. I’m afraid I can't B. How often do you play basketball? C. How did you spend your last weekend? D. I really had a good time. E. Do you have any plans for it? F. We'll enjoy it G. Sounds interesting. 11.D「解析】根据前一句＂ Pretty good.＂可知此处应该表达玩得高兴，因此答案应为D。 12.B【解析】根据答句＂ Twice a week，＂可知空处是询问打篮球的频率，因此答案应为B。 13.C【解析】根据答句“ I went to the mountains last weekend.＂可知空处是询问对方上个周末是怎么度过的，因此答案应为C 14.G【解析】根据一句”I went to the mountains last weekend.”可知，这里应该对此做出回应，因此答案应为G 15.A【解析】根据上一句“＂ Will you go there with us this weekend?＂和下一句”Maybe next week is OK”可知这里应委婉地拒绝对方的邀请，因此答案应为A。

Ⅲ.完形填空(共10小题;每小题1分，满分10分) 根据短文内容，从A、B、C、D四个选项中选择一个最佳答案。 It was Monday. A boy named Ted 16______ from school.17_______ he got home, his mom was sweeping the floor. His mom looked at 18______ and said, “It's six o'clock.Your school finishes 19_______ four. What did you do?” "Oh. Mom. "said Ted. "After school I went to the library 20_____ a book. Can we have our 3

dinner now? I’m 21_______."Then they had a quick dinner. After dinner,Ted stayed in his room alone. "What a shame it is that you tried to cheat your mother!"said a voice in Ted's heart. "You didn’t tell your mother 22________ .You didn’t go to the library. You made a terrible mess in your classroom.” “I don't want to cheat my mom, "thought Ted. "I don,t want my mom to 23______me. I don’t want her to get angry.” The voice got louder suddenly, "24______ your mom knows the truth, she will be 25_____ angrier. Ted realized he was wrong. He got up, opened the door and went into his mom’s room. 16. A. came B. returned C. got D. brought 17. A. Although B. Before C. After D. When 18. A. the alarm B. the blackboard C.the sky D. the book 19. A. in B.on C. at D. about 20. A. to buy B.to borrow C. to sell D. to lend 21. A. tired B. thirsty C. hungry D. bored 22. A. the truth B. the lie C. the news D. the report 23. A. wait for B. care about C. care for D. worry about 24. A. Since B. Though C. Unless D. Because 25. A. very B. much C. too D. so 【主旨大意】本文讲述了一个男孩在对妈妈说谎后的心理斗争，最终他战胜自己去向妈妈承认错误。 16.B【解析】根据空后的 from school 可知Ted是从学校回来，因此答案应为B come from意为“来自”，不符合句意。 17.D【解析】根据句意“当他到家时，他的妈妈正在擦地”可知这是一个由when引导的时间状语从句，表示当一个动作发生时，另一个动作正在进行，因此答案应为D。 18.A【解析：句意:妈妈看了看钟表，说:“現在六点钟了......＂由此可知答案应为A 9.C【解析】表示在某个具体时刻要用介词at，因此答案应为C。 20.B【解析】根据 the library可知，Ted撒谎说去图书馆借书。 borrow意为“从.....借＂;lend意为“借出”。因此答案应为B 21.C【解析】根据前一句“ Can we have our dinner now?＂可知后一句的意思是“我饿了”，因此答案应为C。 22.A【解析】 tell sb. the truth意为“告诉某人真相”，是固定搭配，因此答案应为A。 23.D【解析]根据句意“我不想让妈妈担心我”可知答案应为D。 24.C【解析:根据句意“除非你的妈妈知道真相，否则她会更生气”可知答案为C 25.B【解析】空处应填可修饰形容词比较级 angrier的词，故填much