力的动态平衡问题PPT课件

人教版(2019)高一物理必修一第三章专题三共点力平衡的应用课件(共41张PPT)

核心模型考点对点练核心能力提升练
核心模型考点对点练
提升训练
对点训练
典型考点一静态平衡问题 1．(多选)如图所示，质量为 m 的木块 A 放在质量为 M 的三角形斜面体 B 上，现用大小不相等、方向相反的水平力 F1、F2 分别推 A 和 B，它们均静止不动，且 F1<F2，重力加速度为 g，则( )
解析
2. 如图所示，光滑斜面的倾角为 30°，轻绳通过两个滑轮与 A 相连，轻绳的另一端固定于天花板上，不计轻绳与滑轮的摩擦。物块 A 的质量为 m，不计滑轮的质量，挂上物块 B 后，当动滑轮两边轻绳的夹角为 90°时，A、 B 恰能保持静止，则物块 B 的质量为( )
2 A. 2 m
B. 2m
核心概念规律再现
核心模型考点对点练核心能力提升练
解析
6．如图所示，硬杆 OA 可绕过 A 点且垂直于纸面的轴进行转动，不计钢索 OB 和硬杆 OA 的重力，∠AOB 等于 30°，如果钢索 OB 的最大承受拉力为 2.0×104 N，求：
(1)O 点悬挂物的最大重力； (2)杆 OA 对 O 点的最大支持力。答案 (1)1.0×104 N (2)1.7×104 N
核心概念规律再现
核心模型考点对点练核心能力提升练
A．A 受到四个力的作用 B．B 对 A 的摩擦力方向一定沿斜面向下 C．地面对 B 的摩擦力方向水平向右，大小为 F2－F1 D．地面对 B 的支持力大小一定等于(M＋m)g
答案 CD
核心概念规律再现
核心模型考点对点练核心能力提升练
答案
A．FOA 逐渐增大
C．FOB 逐渐增大答案 B
B．FOA 逐渐减小 D．FOB 逐渐减小

共点力的平衡-PPT课件

提示：选 B. 法一：解析法如图所示，由平衡条件得 FN1＝tamngθ FN2＝smingθ，θ 逐渐增大到 90°，tan θ、sin θ 都增大， FN1、FN2 都逐渐减小，所以选项 B 正确．
法二：图解法对球受力分析，球受 3 个力，分别为重力 G、墙对球的弹力 FN1 和板对球的弹力 FN2. 当板逐渐放至水平的过程中，球始终处于平衡状态，即 FN1 与 FN2 的合力 F 始终竖直向上，大小等于球的重力 G，如图所示，由图可知 FN1 的方向不变，大小逐渐减小，FN2 的方向发生变化，大小也逐渐减小，故选项 B 正确．
(2)如图，一小球放置在木板与竖直墙面之间．设墙面对球的弹力大小为 FN1，木板对球的弹力大小为 FN2.以木板与墙连接点所形成的水平直线为轴，将木板从图示位置开始缓慢地转到水平位置．不计摩擦，在此过程中( ) A．FN1 始终减小，FN2 始终增大 B．FN1 始终减小，FN2 始终减小 C．FN1 先增大后减小，FN2 始终减小 D．FN1 先增大后减小，FN2 先减小后增大
[思路点拨] 本题可按以下思路进行求解：
[解析] 选取金属球为研究对象，它受到三个力的作用，如图甲所示．金属球处于平衡状态，这三个力的合力为零．可用以下四种方法求解．
法一：力的合成法如图乙所示，风力 F 和拉力 FT 的合力与重力等大反向，由平行四边形定则可得 F＝mgtan θ. 法二：效果分解法重力有两个作用效果：使金属球抵抗风的吹力和使金属丝拉紧，所以可以将重力沿水平方向和金属丝的方向进行分解，如图丙所示，由几何关系可得 F＝F′＝mgtan θ.
【核心深化】
物体受共点力作用，下列说法正确的是( ) A．物体的速度等于零，物体就一定处于平衡状态 B．物体相对另一物体保持静止时，物体一定处于平衡状态 C．物体所受合力为零时，就一定处于平衡状态 D．物体做匀加速运动时，物体处于平衡状态

2024届高考物理一轮复习课件：共点力平衡的十一种解题方法(共22张PPT)

2024届高考物理一轮复习课件：共点力平衡的十一种解题方法(共22张PPT)(共22张PPT)求解共点力平衡问题的十一种方法一、平衡状态一个物体在共点力的作用下，保持静止或做匀速直线运动的状态。

两种情形①静止②匀速直线运动注意：“缓慢移动” “慢慢地”也可看做处于平衡状态。

复习二、平衡条件在共点力作用下物体的平衡条件是合力为零。

F合=0Fx合=0Fy合=0或①物体在两个力作用下处于平衡状态，则这两个力必定等大反向，是一对平衡力．②物体在三个共点力作用下处于平衡状态时，任意两个力的合力与第三个力等大反向．③物体受N个共点力作用处于平衡状态时，其中任意一个力与剩余(N－1)个力的合力一定等大反向．几个有用推论求解共点力平衡问题的十一种方法一、力的合成法二、力的分解法三、正交分解法五、整体法与隔离法六、用图解法处理动态平衡问题七、解析法处理动态平衡问题四、三力交汇原理八、相似三角形法九、正弦定理法十、对称法十一．矢量三角形法一、力的合成法。

物体在三个共点力作用下处于平衡状态，则任意两个力的合力一定与第三个力等大，反向、共线。

37°F合=G37°FABF合mg例：已知物重和角，求其它力。

二、力的分解法。

在实际问题中，一般根据力产生的实际作用效果进行分解。

ABαFF1F2αF三、正交分解法。

解多个共点力作用下物体平衡问题的方法物体受到三个或三个以上力的作用时，常用正交分解法列平衡方程求解:Fx合=0，Fy合=0 。

为方便计算，建立坐标系时以尽可能多的力落在坐标轴上为原则。

37°FNGFxy解：由于物体做匀速运动，由平衡条件，得：水平方向：Fcos370 =Ff ①竖直方向：FN+Fsin370 =G ②又Ff= μFN ③由①②③得：例：物体做匀速运动，已知F=10N、G=30N,求物体与地面间的动摩擦因数。

四、三力交汇原理。

物体受三个共面非平行力作用而平衡时，这三个力必为共点力.mgF2F1F合=mgmgN2N1α五、整体法与隔离法求系统受到的外力，用整体法；求系统内各物体（各部分）间相互作用力时，用隔离法。

高中物理必修一动态平衡

详细描述
当带电物体在电场中受到电场力作用时，电荷将发生移动以重新分布，直到物体内部电荷产生的电场与外界电场相平衡，此时物体达到动态平衡状态。
Hale Waihona Puke 物体在磁场作用下的动态平衡
总结词
物体在磁场中由于磁力作用而达到平衡状态的过程。
VS
详细描述
当带电物体或磁体在磁场中受到磁力作用时，磁力将使物体发生移动以重新分布，直到物体内部磁力与外界磁力相平衡，此时物体达到动态平衡状态。
03
动态平衡的应用
物体在重力作用下的动态平衡
总结词
物体在重力作用下保持平衡状态的过程。
详细描述
当物体在重力作用下处于平衡状态时，其受到的重力与支持力等大反向，同时物体可能还受到其他外力的作用，这些外力与重力等大反向，使物体保持静止或匀速直线运动状
态。
物体在电场作用下的动态平衡
总结词
物体在电场中由于电荷分布变化而达到平衡状态的过程。
中等难度习题解析
总结词
运用物理规律
详细描述
中等难度的习题解析要求学生在掌握动态平衡概念的基础上，能够运用物理规律解决实际问题。这类题目通常涉及多个力的平衡问题，需要学生正确分析受力情况，并运用平衡条件求解未知量。
高难度习题解析
总结词
综合运用能力
详细描述
高难度习题解析要求学生具备综合运用物理知识和方法的能力。这类题目通常涉及复杂的受力分析和运动过程，需要学生灵活运用动态平衡的原理，结合运动学、动力学等知识进行分析和求解。同时，这类题目还可能涉及到多种物理情景和实际应用，要求学生
详细描述
力的平衡原理指出，如果物体受到两个或更多力的作用，且这些力大小相等、方向相反，则物体将保持静止或匀速直线运动状态。这种平衡状态可以通过平行四边形法则或三角形法则进行求解。

物理课件：第4章--43共点力的平衡及其应用

(5)利用方程组求解，必要时需对解进行讨论．注意：建立直角坐标系时，一般尽量使更多的力落在坐标轴上，以减少分解力的个数，从而达到简化计算的目的．
如图4－3－3所示，一个半球形的碗放在桌面
Байду номын сангаас
上，碗口水平，O点为其球心，碗的内表面及碗口是光滑
的．一根细线跨在碗口上，线的两端分别系有质量为m1和 m2的小球，当它们处于平衡状态时，质量为m1的小球与O
可以认为球始终处于平衡状态，那么，重力的两个分力随之而变．N2 始终和挡板垂直，N1 方向不变，所以左边 N1 的平行线也不变，那么 N2 的变化如图所示，可得其先减小后增大．N1 逐渐减小．
【答案】 N1 逐渐减小；N2 先减小后增大
如图4－3－7所示，一个表面光滑的半球固定在水平面上，其球心的正上方一定高度处固定一小滑轮，
点的连线和水平线的夹角为α＝60°.两小球的质量比
m2 m1
为多
少？
【解析】 (方法一)正交分解法．
小球m2受重力和细线的拉力处于平衡状态，则由二力平衡条件得FT＝m2g.
以小球m1为研究对象，受力分析如图所示，以FN的方向为y轴，以垂直于 FN的方向为x轴建立坐标系．FN与FT的夹角为60°，m1g与y 轴成30°角．
设光滑半球的半径为R，滑轮中心到半球顶端的距离为
h，OA间的距离为L，由相似三角形
列等式
FN R
＝
FT L
＝
F′ R＋h
，因
F′ R＋h
不
变，半径R一定，所以FN大小不变，
而绳长L逐渐减小，所以FT逐渐减
小．故正确选项为C 【答案】 C
在利用矢量三角形解决力学问题时，应找出一个“几何三角形”和“力的矢量三角形”，在这两个三角形相似的基础上，根据有向线段的长度表示力的大小，从而得两三角形对应边的大小的比值相等，这样就可以求某一个力的大小或各个力之间的关系．

3.8力的动态分析_平衡三角形法

利用“平衡三角形”处理力的动态分析问题的步骤 1. 受力分析 2. 平移成首尾相接的三角形——“平衡三角形” 3. 明确每个力的特点——大小、方向是否改变 4. 旋转方向改变的力 5. 判断每个力的大小变化
课后作业
1.课件上的题作本上
下课了啦！
继续努力！
下次课见！
温故而知新
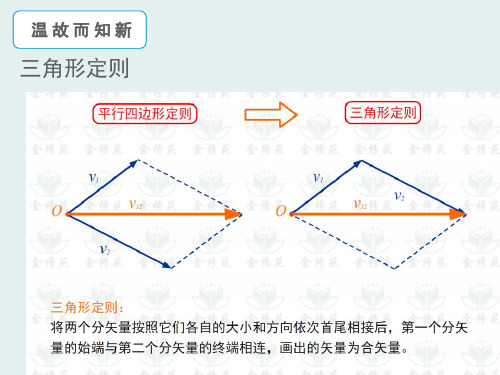
三角形定则
温故而知新
三角形定则的应用
▐
如图所示，大小分别为F1、F2、F3的三个力恰好围成一个闭合的三角形，且三个力的大小关系是F1＜F2＜F3，则下列四个图中，这三个力的合力最大的是（）
力的动态分析之平衡三角形法
刘雨雷老师
知识点/例题/课堂练习/
要点一了解平衡三角形
要点二利用“平衡三角形”处理力的动态分析问题的步骤
知识点/例题/课堂练习/
练习2 如图所示，电灯悬挂于两墙壁之间，更换水平绳OA，使连接点A向上移动而保持O点的位置和OB绳的位置不变，则在A 点向上移动的过程中( ) A．绳OB的拉力逐渐增大 B．绳OB的拉力逐渐减小 C．绳OA的拉力先增大后减小 D．绳OA的拉力先减小后增大
课堂小结
平衡三角形受到三个力而平衡的物体，把它受到的三个力经过平移，一定能组成首尾相接的三角形另外，受到多个力而平衡的物体则能组成首尾相接的多边形
知识点/例题/课堂练习/
平衡三角形
• 受到三个力而平衡的物体，把它受到的三个力经过平移，一定能组成首尾相接的三角形 • 另外，受到多个力而平衡的物体则能组成首尾相接的多边形
知识点/例题/课堂练习/
1
3 O F 2 F3 2
F1
F1
1 O F2 2
3 F3
知识点/例题/课堂练习/

共点力平衡专题ppt课件

矢
量
三角
闭合
FT
矢量三角形
形
G
FN 编辑版pppt
FT
G
FN
23
例3.光滑半球面上的小球被一通过定滑轮的力F由底端缓拉到顶端的过程中，试分析绳的拉力F及半球面对小球的支持力FN的变化情况
F1与F2的方向均变化，此时力的平行四边形的形状
变化规律不直观，力随角度变化的关系也难建立
C
力的矢量三角形与题目中长度L 关β系构成的三角形相似
编辑版pppt
18
→墙面挂绳变化
编辑版pppt
θ FT
G1
FN
G G2
19
2.共点力的作用下动态平衡常见问题 →小结：解析法
步解 1. 选某一状态对物体进行受力分析 2. 将物体受的力按实际效果分解或正交分解
骤析 3. 列平衡方程求出未知量与已知量的关系表达式 4. 根据已知量的变化情况来确定未知量的变化情况
解：箱子受四个力：mg、FN、f、F 作用，如图乙所示．建
立直角坐标系，将拉力 F 分解为：
Fx＝Fcos θ，Fy＝Fsin θ.根据共点平衡条件得：
x 轴上：Fcos θ＝f
①
y 轴上：Fsin θ＋FN＝mg
②
又：f＝μFN
③
由①②③得：F＝cos
μmg θ＋μsin
θ.
编辑版pppt
12
练一练：
合成法
分解法
正交分解法
处理方法
将三个力中的任意两个力合成，则其合力必与第三个力平衡，即三力平衡问题转化为二力平衡问题
将其中一个力沿其他两个力的反方向分解，即三力平衡问题转化为两个方向上的二力平衡问题

人教版高中物理《共点力的平衡》优秀PPT课件

共点力的平衡解题方法小结 1.正确选取研究对象 2.隔离物体，分析物体的受力，画出受力图 3.根据平衡条件，确定解题方法：
几何法（建议使用合成法）正交分解法 4、几何法：根据几何特点，列方程求解；正交分解法：建立两个轴的合力为零的方程，
组成方程组求解。
正交分解法
例题：物体重力为100N，放在倾角为30°的斜面上，始终静止。求：若沿斜面施加向上拉力F1=20N，物体的摩擦力和支持力是多大？
正交分解法
例题：物体重力为100N，放在倾角为30°的斜面上，物体与斜面之间最大静摩擦力为40N。求：1）为保持物体静止在斜面上，沿斜面向上
的拉力最小值是多少？ 2）为保持物体静止在斜面上，沿斜面向上
的拉力的最大值不能超过多大？
二、正交分解法练习例题8：质量为m的物体放在倾角为θ的粗糙斜面上，动摩擦因数为μ，在水平恒定推力的作用下，物体沿斜面匀速向下运动。求：水平推力的大小_____________ 斜面对物体支持力的大小__________
B．FT = mg，FN = 2mg
C．FT = mg，FN = 3 mg
D．FT =
23 3
m，g
FN
2
=3
mg
动态平衡问题
几何法和正交分解法的应用
动态平衡问题
• 讨论物体静止时，受力的大小及方向的变化的一类问题
• 解决问题的方法几何法-----画平行四边形或三角形正交分解法----建立方程组讨论
F α
FN α
G F合
解法一：合成法
如图，物体静止，合力为零。几何知识可得：
F=F合=G/cosα FN=Gtanα
例1：如图所示，一个重为G的圆球，被一段细绳挂在