捷联惯性导航系统的解算方法ppt课件
合集下载
捷联惯性导航系统的解算方法ppt课件

的 分量构成的矩阵,则
r rnT n r nT Cnb n rnT r nT Cbn
由于坐标系不动而是矢量转动,它 相应于矢量固定时坐标系方向转动
rn
n
C
n b
r
2010-03-19
方向余弦矩阵微分方程
由矢量相对导数和绝对导数的关系式
dr dt
n
dr dt
b
ω nb r
假定地理坐标系为参考坐标系,作为参考 坐标系认为它在空间是不动的,即
如把OXbYbZb作为动坐标系, ENU作为参考坐标系,则航向 角H,纵摇角(俯仰角)P和横 摇角(横滚角、倾斜角)R。就 是一组欧拉角。
Zb Zb'' U Zb' P
欧拉角没有严格的定义,根 据
需要,可以选用不同的欧拉 角
组。第一次转动,可以绕三 个
轴中的任一个转动,故有3种 可
能,第二次有2种可能,第三 次
启动
自检 测
初始 化
返回9
姿态
迭 数
代
次阵计 算
N O
YES
导 航 计 控 制 信 息算提 取
3.2 姿态矩阵的计算
捷联式惯导中,载体地理位置就是地理坐标系相对 地球坐标系的方位。而载体的姿态和航向则是载体 坐标系相对于地理坐标系的方位关系。确定两个坐 标系的方位关系问题,是力学中的刚体定点转到理 论。在刚体定点转动理论中,描述动坐标系相对参 考坐标系方位关系的方法有多种。
求解方程可以直接得到航向和姿态信息,
欧 拉角法得到的姿态阵永远是正交阵,用这
个矩 阵将比力fb→fn信息的坐标变换时,变换后的信 息
中不存在非正交误差。因此,用欧拉角法得 到的姿态矩阵无
第五章惯性导航系统(PPT-70)

导航是引导飞机到达目的地的过程。飞机的导航系统有两种工 作状态:提供导航信息,驾驶员根据提供的信息引导飞机沿规定 的航线到达目的地;提供导航信息输入飞机飞行自动控制系统, 使飞机自动地沿规定航线飞行,后者构成了制导系统。
第五章 惯性导航系统
一、概 述
用一种叫加速度计的仪表测量到飞机(物体)的运动加速度后,飞
第五章 惯性导航系统
所谓导航,是指在某参考系内将运动物体以一点引导到 另一点的过程。
惯性导航所要解决的基本问题是不断确定载体的姿态、 速度和位置。
任何物质的运动和变化,都是在空间和时间中进行的。物 体的运动或静止及其在空间的位置,是指它相对另一物体而 言。这就是说,在描述物体的运动时,必须选定一个或几个 物体作为参考系。当物体对于参考系的位置有了变化时,就 说明该物体发生了运动。
速度分解为沿地理北向和地理东向两
个分量
vN v cos
vE v sin
飞行速度北向分量vN引起地理坐标系绕 平行于地理东西方向的地心轴转动,其
转动角速度为
vN v cos Rh Rh
飞行速度引起地理坐标系转动
第五章 惯性导航系统
二、有关知识
当地地理坐标系的绝对角速度
第五章 惯性导航系统
一、概 述
第五章 惯性导航系统
一、概 述
实际惯导系统不仅能提供即时速度和即时位置,还可以测量飞机 的姿态。在捷联式惯导系统中可提供多达35个参数,构成惯性基 准系统。
35个参数中主要有:即时经度和纬度;飞机地速,航迹角;飞机 三个姿态角和角速度;沿机体轴的三个线加速度;垂直速度;惯 性高度。此外,在由大气数据系统提供真空速条件下,还输出风 速风向(角)等。
OENζ相对惯性坐标系的转动 角速度应包括两个部分:相 对角速度,它是由于飞机相 对于地球运动而形成的;牵 连角速度,它是地球相对惯 性坐标系运动形成的。
第五章 惯性导航系统
一、概 述
用一种叫加速度计的仪表测量到飞机(物体)的运动加速度后,飞
第五章 惯性导航系统
所谓导航,是指在某参考系内将运动物体以一点引导到 另一点的过程。
惯性导航所要解决的基本问题是不断确定载体的姿态、 速度和位置。
任何物质的运动和变化,都是在空间和时间中进行的。物 体的运动或静止及其在空间的位置,是指它相对另一物体而 言。这就是说,在描述物体的运动时,必须选定一个或几个 物体作为参考系。当物体对于参考系的位置有了变化时,就 说明该物体发生了运动。
速度分解为沿地理北向和地理东向两
个分量
vN v cos
vE v sin
飞行速度北向分量vN引起地理坐标系绕 平行于地理东西方向的地心轴转动,其
转动角速度为
vN v cos Rh Rh
飞行速度引起地理坐标系转动
第五章 惯性导航系统
二、有关知识
当地地理坐标系的绝对角速度
第五章 惯性导航系统
一、概 述
第五章 惯性导航系统
一、概 述
实际惯导系统不仅能提供即时速度和即时位置,还可以测量飞机 的姿态。在捷联式惯导系统中可提供多达35个参数,构成惯性基 准系统。
35个参数中主要有:即时经度和纬度;飞机地速,航迹角;飞机 三个姿态角和角速度;沿机体轴的三个线加速度;垂直速度;惯 性高度。此外,在由大气数据系统提供真空速条件下,还输出风 速风向(角)等。
OENζ相对惯性坐标系的转动 角速度应包括两个部分:相 对角速度,它是由于飞机相 对于地球运动而形成的;牵 连角速度,它是地球相对惯 性坐标系运动形成的。
捷联惯导系统算法.ppt
b Eby
cos
b Ebz
注意事项:当 θ= 90 度时,方程出现奇点
姿态计算 矩阵方程精确解1
二、方向余弦矩阵微分方程及其解 C C
其中
C bE
CbE
b Eb
0
b Eb
z
z
0
y
x
y x
0
由于陀螺仪直接测得的是载体 相对惯性空间的角速度,所以:
CbE
b ib
E iE
C
E b
或四元数微分方程:
q(t)
(
b ib
b iE
)q(t)
注意事项: 1、上述两个方程中的角速度表达式不一样 2、方程第二项较小,计算时速度可以低一些
增量算法 矩阵方程精确解
一、角增量算法
角增量:陀螺仪数字脉冲输出,每个脉冲代表一个角增量
一个采样周期内,陀螺输出脉冲数对应的角增量为:
C
0
0
c os
0 0 0 sin
sin
sin
c os
cos cos
求解欧拉角速率得
1 0
0
cos
0 sin
惯性器件的误差补偿
姿态计算 欧拉角微分方程1
姿态矩阵的计算 假设数学坐标系模拟地理坐标系 飞行器姿态的描述:
航向角ψ、俯仰角θ、滚动角γ 一、欧拉微分方程
从地理坐标系到载体坐标系 的旋转顺序:
Ψ →θ →γ
cos
b Ebz
注意事项:当 θ= 90 度时,方程出现奇点
姿态计算 矩阵方程精确解1
二、方向余弦矩阵微分方程及其解 C C
其中
C bE
CbE
b Eb
0
b Eb
z
z
0
y
x
y x
0
由于陀螺仪直接测得的是载体 相对惯性空间的角速度,所以:
CbE
b ib
E iE
C
E b
或四元数微分方程:
q(t)
(
b ib
b iE
)q(t)
注意事项: 1、上述两个方程中的角速度表达式不一样 2、方程第二项较小,计算时速度可以低一些
增量算法 矩阵方程精确解
一、角增量算法
角增量:陀螺仪数字脉冲输出,每个脉冲代表一个角增量
一个采样周期内,陀螺输出脉冲数对应的角增量为:
C
0
0
c os
0 0 0 sin
sin
sin
c os
cos cos
求解欧拉角速率得
1 0
0
cos
0 sin
惯性器件的误差补偿
姿态计算 欧拉角微分方程1
姿态矩阵的计算 假设数学坐标系模拟地理坐标系 飞行器姿态的描述:
航向角ψ、俯仰角θ、滚动角γ 一、欧拉微分方程
从地理坐标系到载体坐标系 的旋转顺序:
Ψ →θ →γ
《惯性导航系统》课件

软件温度补偿
通过算法对温度变化引起的误差进 行估计和补偿,提高导航精度。
混合温度补偿
结合硬件和软件温度补偿的优势, 进一步提高导航精度。
05
惯性导航系统发展现状与 趋势
国内外研究现状
国内研究现状
国内在惯性导航系统领域的研究起步较晚,但近年来发展迅速,取得了一系列重要成果。国内的研究 主要集中在技术研发、系统集成和实际应用等方面,涉及的领域包括航空、航天、航海、机器人等。
陀螺仪的精度和稳定性对惯性导航系 统的性能有着至关重要的影响。
它通过高速旋转的陀螺仪能够感知方 向的变化,并将这些变化转化为电信 号,以供其他组件使用。
不同类型的陀螺仪(如机械陀螺仪、 光纤陀螺仪、激光陀螺仪等)具有不 同的特点和应用场景。
加速度计
01
加速度计用于测量物体在惯性参 考系下的加速度。
动态调整初始对准过程中的参数。
动态误差与扰动误差
要点一
动态误差与扰动误差
在动态环境下,惯性导航系统会受到各种扰动因素的影响 ,如车辆颠簸、气流扰动等。这些扰动因素会导致系统输 出数据出现偏差,从而影响导航精度。为了减小这些误差 ,可以采用多种技术手段,如滤波算法、卡尔曼滤波等。
要点二
卡尔曼滤波
卡尔曼滤波是一种基于状态方程和观测方程的递归滤波算 法,可以对系统状态进行最优估计。通过将卡尔曼滤波算 法应用于惯性导航系统中,可以有效减小由于动态环境和 扰动因素引起的误差。此外,还可以采用其他先进的滤波 算法,如扩展卡尔曼滤波、粒子滤波等,根据实际情况选 择最适合的算法来减小动态误差与扰动误差。
案例分析:无人机导航系统
案例背景介绍
介绍无人机导航系统的应用场景和需求,阐述其重要性和挑战。
捷联惯性导航系统的解算方法课件

02
CATALOGUE
捷联惯性导航系统组成及工作 原理
主要组成部分介绍
惯性测量单元
包括加速度计和陀螺仪,用于测量载体在三个正交轴上的加速度 和角速度。
导航计算机
用于处理惯性测量单元的测量数据,解算出载体的姿态、速度和 位置信息。
控制与显示单元
用于实现人机交互,包括设置导航参数、显示导航信息等。
工作原理简述
学生自我评价报告
知识掌握情况
学生对捷联惯性导航系统的基本原理、解算 方法和实现技术有了深入的理解和掌握。
实践能力提升
通过实验和仿真,学生的动手实践能力得到了提升 ,能够独立完成相关的实验和仿真验证。
团队协作能力
在课程项目中,学生之间的团队协作能力得 到了锻炼和提升,能够相互协作完成项目任 务。
对未来发展趋势的预测和建议
捷联惯性导航系统的解算 方法课件
CATALOGUE
目 录
• 捷联惯性导航系统概述 • 捷联惯性导航系统组成及工作原理 • 捷联惯性导航系统解算方法 • 误差分析及补偿策略 • 实验验证与结果展示 • 总结与展望
01
CATALOGUE
捷联惯性导航系统概述
定义与基本原理
定义
捷联惯性导航系统是一种基于惯性测量元件(加速度计和陀螺仪)来测量载体(如飞机、导弹等)的加速度和角 速度,并通过积分运算得到载体位置、速度和姿态信息的自主导航系统。
01
高精度、高可靠性
02
多传感器融合技术
随着科技的发展和应用需求的提高, 捷联惯性导航系统需要进一步提高精 度和可靠性,以满足更高层次的应用 需求。
为了克服单一传感器的局限性,可以 采用多传感器融合技术,将捷联惯性 导航系统与其他传感器进行融合,提 高导航系统的性能和鲁棒性。
惯性导航原理ppt课件

代入上述投影变换式
Ve ' x'i y' j z' k q 1 P1i P2 j P3k
x'i y' j z'k
( P1i P2 j P3k) (xi yj zk) ( P1i P2 j P3k)
进行四元数乘法运算,整理运算结果可得
20
四元数表示转动 方向余弦
或简单表示为
q M v, P
12
四元数基本性质 乘法
2.四元数乘法
q M ( P1i P2 j P3k)(v 1i 2 j 3k)
(v P11 P2 2 P33 )
( 1 P1v P2 3 P32 )i
( 2 P2v P31 P13 ) j
( 3 P3v P12 P2 1 )k
7
6. 机体坐标系——
Oxb yb zb
机体坐标系是固连在机体上的坐标系。机 体坐标系的坐标原点o位于飞行器的重心处, x沿机体横轴指向右,y沿机体纵轴指向前, z垂直于oxy,并沿飞行器的竖轴指向上。
8
3.2四元数理论
9
四元数 表示
四元数:描述刚体角运动的数学工具 (quaternions) 针对捷联惯导系统,可弥补欧拉参数在描述和解算方面的不足。
四元数 映象图解
V xi yj zk
V x'i' y' j'z'k'
Ve xi yj zk Ve ' x'i y' j z' k
19
四元数表示转动 方向余弦
Ve ' q 1Ve q 将该投影变换式展开,也就是把
Ve xi yj zk q P1i P2 j P3k
Ve ' x'i y' j z' k q 1 P1i P2 j P3k
x'i y' j z'k
( P1i P2 j P3k) (xi yj zk) ( P1i P2 j P3k)
进行四元数乘法运算,整理运算结果可得
20
四元数表示转动 方向余弦
或简单表示为
q M v, P
12
四元数基本性质 乘法
2.四元数乘法
q M ( P1i P2 j P3k)(v 1i 2 j 3k)
(v P11 P2 2 P33 )
( 1 P1v P2 3 P32 )i
( 2 P2v P31 P13 ) j
( 3 P3v P12 P2 1 )k
7
6. 机体坐标系——
Oxb yb zb
机体坐标系是固连在机体上的坐标系。机 体坐标系的坐标原点o位于飞行器的重心处, x沿机体横轴指向右,y沿机体纵轴指向前, z垂直于oxy,并沿飞行器的竖轴指向上。
8
3.2四元数理论
9
四元数 表示
四元数:描述刚体角运动的数学工具 (quaternions) 针对捷联惯导系统,可弥补欧拉参数在描述和解算方面的不足。
四元数 映象图解
V xi yj zk
V x'i' y' j'z'k'
Ve xi yj zk Ve ' x'i y' j z' k
19
四元数表示转动 方向余弦
Ve ' q 1Ve q 将该投影变换式展开,也就是把
Ve xi yj zk q P1i P2 j P3k
捷联惯导

捷联惯导数学模型及惯导解算原理
坐标系的定义
1. 地理坐标系(下标为t)—— OXtYtZt :O 取载体质心,Xt 轴指向东,Yt 轴指向北,Zt 轴沿垂线指向天。 2. 导航坐标系(下标为n)—— OX nYnZn :O 取载体质心,Zn与 Zt 重合,Xn 与 Xt,Yn 与 Yt 相差一个游动方
C13
C23
C33
位置速率
p ep
位置速率是由飞行器地速的水平分量引起的,由于平台坐标系与地理坐标系相差 一个游动方位角,
可得:
VVENtt
cos sin
sin cos
VEp VNp
p ep
可写成
p epE
C32 C31
180 ,180
1.求纬度的真值L
L L 反正弦函数的主值域与L的定义域一致,因此:
主
2.求经度的真值
反正切函数的主值域是 90 ,90 与 的定义域不一致,因此需要在 的定义域内确定经度的真值。
由: 主
tan 1
C32 C31
tan 1
cos L sin cos L cos
其中:
.
V ep 平台系相对地球的加速度向量
f 加速度计测量的比力向量
2ie ep V ep 无明显物理意义,又称有害加速度
g 重力加速度向量
整理上式可得:
.
VEp
.
VNp
.
VUp
f
p E
坐标系的定义
1. 地理坐标系(下标为t)—— OXtYtZt :O 取载体质心,Xt 轴指向东,Yt 轴指向北,Zt 轴沿垂线指向天。 2. 导航坐标系(下标为n)—— OX nYnZn :O 取载体质心,Zn与 Zt 重合,Xn 与 Xt,Yn 与 Yt 相差一个游动方
C13
C23
C33
位置速率
p ep
位置速率是由飞行器地速的水平分量引起的,由于平台坐标系与地理坐标系相差 一个游动方位角,
可得:
VVENtt
cos sin
sin cos
VEp VNp
p ep
可写成
p epE
C32 C31
180 ,180
1.求纬度的真值L
L L 反正弦函数的主值域与L的定义域一致,因此:
主
2.求经度的真值
反正切函数的主值域是 90 ,90 与 的定义域不一致,因此需要在 的定义域内确定经度的真值。
由: 主
tan 1
C32 C31
tan 1
cos L sin cos L cos
其中:
.
V ep 平台系相对地球的加速度向量
f 加速度计测量的比力向量
2ie ep V ep 无明显物理意义,又称有害加速度
g 重力加速度向量
整理上式可得:
.
VEp
.
VNp
.
VUp
f
p E
6.7 捷联式惯性导航系统

稳定平台
加速度信息
位置信息
导航计算机
陀螺旋矩信息
速度信息
陀螺输出信息
控制平台 信息
稳定回路
变态信息
捷联式惯性导航系统
捷联式惯性导航系统特点
• 由于将陀螺仪和加速度计直接固连于运载体,省去复杂的框架系 统、电气稳定系统及接触滑环等,所以其可靠性高于平台式惯导 系统。
• 由于直接将惯性元件固连在运载体上,所以惯性元件测量范围大, 工作环境恶劣,要求苛刻,要求惯性元件的动态特性要好。
cos
0
sin
0
1 0
H
sin
纵摇横摇航向角
H
1 cos
sin
sin sin
0 0 cos
cos x
sin cos
y
载体相对地理坐标系角速度
H y0
捷联式惯性导航系统
捷联姿态矩阵
cos cos H sin sin sin H
Tbt cos sin H sin sin cos H
sin cos
cos sin H cos cos H
sin
sin cos H cos sin sin H
3
捷联式惯性导航系统
从算法的角度看,捷联式惯导系统必须根据陀螺输出的角速度或 角增量计算维持一个数学平台。
sin cos z
3
捷联式惯导系统工作原理
加速度计
载体
陀螺
由机体坐标系至 平台坐标系的方
向余弦矩阵
沿平台坐标系 的比力分量 导航
加速度信息
位置信息
导航计算机
陀螺旋矩信息
速度信息
陀螺输出信息
控制平台 信息
稳定回路
变态信息
捷联式惯性导航系统
捷联式惯性导航系统特点
• 由于将陀螺仪和加速度计直接固连于运载体,省去复杂的框架系 统、电气稳定系统及接触滑环等,所以其可靠性高于平台式惯导 系统。
• 由于直接将惯性元件固连在运载体上,所以惯性元件测量范围大, 工作环境恶劣,要求苛刻,要求惯性元件的动态特性要好。
cos
0
sin
0
1 0
H
sin
纵摇横摇航向角
H
1 cos
sin
sin sin
0 0 cos
cos x
sin cos
y
载体相对地理坐标系角速度
H y0
捷联式惯性导航系统
捷联姿态矩阵
cos cos H sin sin sin H
Tbt cos sin H sin sin cos H
sin cos
cos sin H cos cos H
sin
sin cos H cos sin sin H
3
捷联式惯性导航系统
从算法的角度看,捷联式惯导系统必须根据陀螺输出的角速度或 角增量计算维持一个数学平台。
sin cos z
3
捷联式惯导系统工作原理
加速度计
载体
陀螺
由机体坐标系至 平台坐标系的方
向余弦矩阵
沿平台坐标系 的比力分量 导航
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
H
'
N
16
cos P sin
惯性导航系统原理
3 捷联式惯导系统 程向红 2010.03.19
3 捷联式惯导系统
3.1 捷联式惯导算法概述 3.2 姿态矩阵的计算 3.3 姿态矩阵计算机执行算法
2010-03-19
2
3.1 捷联式惯导算初法始条概件 述
加速度计组
SFb
陀 螺仪组 ibb
Cbn
SFn inb
姿态矩 阵 计 算
2010-03-19
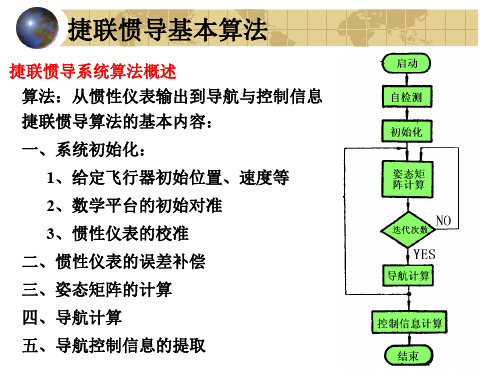
接联式惯导的算法的基本内容
(1)系统的启动和自检 测 (2)系统初始化 (3)惯性仪表的误差补 偿 (4)姿态矩阵的计算 (5)导航计算 (6)制导和控制信息的 提取
2010-03-19
(1)系统的启动和自检测
系统启动后,各个部分的工作是否正常,要 通 过自检测程序加以检测,其中包括电源、惯 性仪 表、计算机以及计算机软件。
如把OXbYbZb作为动坐标系, ENU作为参考坐标系,则航向 角H,纵摇角(俯仰角)P和横 摇角(横滚角、倾斜角)R。就 是一组欧拉角。
Zb Zb'' U Zb' P
欧拉角没有严格的定义,根 据
需要,可以选用不同的欧拉 角
组。第一次转动,可以绕三 个
轴中的任一个转动,故有3种 可
能,第二次有2种可能,第三 次
也有2种可能。总共有12种可 能。
ER
Xb'' Xb'
Xb
2010-03-19
H. R.
O
P.
Yb'' Yb Yb'
H N
用欧拉角表示的姿态矩阵
Xb'
Y
' b
Z
' b
cos H sin H
sin H cos
0 H0
-
v-
CH
___
0 E
0 N
1U
Zb
Zb
''
U Zb'
P
H .
X b''
P, R,
H, E N
L,V ,V
根据捷联式惯导的应用和功能要求不同,计算的内容和要 求,有很大的差别。常有
SINS——Strapdown Inertial Navigation Systems SVRU—— Strapdown Vertical Reference Uint SAHRS——Strapdown Attitude and Heading Reference Systems IMU——Inertial measurement Unit
''
Y bZb''
1 00 -
0
cos P v- sYinbP
0 sin
P
X
' b
'
cos
P___
Z
' b
CP
b cos R
XYb
b Z
sin vR-
0 0
1
sin 0
Rቤተ መጻሕፍቲ ባይዱX Yb
''
b ''
0
cos
R___Z
'' b
CR
ER
Xb
Xb '
''
Xb
O
P .
HPR
010-03-19
三参数法 欧拉角法 ,是欧拉在1776年提出的。
四元数法。威廉.哈密顿(William Hamilton) 四参数法 1在843年发明的,首先在数学中引入四元数,以
后用在刚体定位问题。凯里.克莱茵(CayleyKlein)参数法,是在1897年提出的。 九参数法 基于方向余弦的概念,也称 方向余弦法。
2010-03-19
(6)制导和控制信息的提取
制导和控制信息的提取,载体的姿态既可用来 显示也是控制系统最基本的控制信息。 此外,载体的角速度和线速度信息也都是控制 载体所需要的信息。 这些信息可以从姿态矩阵的元素和陀螺加速度 计的输出中提取出来。
2010-03-19
2010-03-19
捷联式惯导系统算法流程图
2010-03-19
等效转动矢量法
13
3.2 姿态矩阵的计算
3.2.1 欧拉角法 3.2.2 方向余弦法 3.2.3 四元数法 3.2.4 等效转动矢量法
2010-03-19
3.2.1 欧拉角法
一个动坐标系相对参考坐标系的方位,完全可以由动坐 标系依次绕3个不同的轴转动的3个转角来确定。
启动
自检 测
初始 化
返回9
姿态
迭 数
代
次阵计 算
N O
YES
导 航 计 控 制 信 息算提 取
3.2 姿态矩阵的计算
捷联式惯导中,载体地理位置就是地理坐标系相对 地球坐标系的方位。而载体的姿态和航向则是载体 坐标系相对于地理坐标系的方位关系。确定两个坐 标系的方位关系问题,是力学中的刚体定点转到理 论。在刚体定点转动理论中,描述动坐标系相对参 考坐标系方位关系的方法有多种。
2010-03-19
(4)姿态矩阵的计算
姿态矩阵的计算是捷联式惯导算法中最重要的一 部分,也是捷联式系统所特有的。 不管捷联式惯导应用和功能要求如何,姿态矩阵 的计算却是不可少的。姿态矩阵算法是本章重点 讨论的内容。
2010-03-19
(5)导航计算
导航计算就是把加速度计的输出信息变换到导航坐 标系,然后,计算载体速度、位置等导航信息。
通过自检测,发现有不正常,则发出告警信息 (或 故障码)。系统的自检测是保证系统进入导航 状态 后能正常工作、提高系统可靠性的措施。
2010-03-19
为何要初始化?
(2)系统初始化
给定载体(舰船、飞行器、车辆等)的初始位置 (经度和纬度)和初始速度等初始信息。
导航平台的初始对准 平台式 用物理的方法来实现
导 航 计算 机
H
Pt
R
VE VN
ibb
捷联式惯
f ibb
导算法
P, R, H
,
L,VE ,VN
捷联式惯导航系统是一个信息处理系统,就是将载体上安装的惯性 仪表所测量的载体运动信息,经过计算处理成所需要的导航信息。
2010-03-19
3
捷联式惯性导航系统=信息处理系统
ibb
fibb
捷联式惯 导算法
Cnb
2
cos H
R
cos H cos
sin P P sin
sin
R
sin
sin R cos HH sin P cos R sin
H
cos R sin H sin P sin R cos H
cos P cos H sin R sin H sin P cos R cos
R
YYbb''
.
Yb
惯性仪表的校准 Calibration
捷联式 姿态矩阵的初始值 陀螺仪
标度系数 漂移 进行测定 加速度计 偏置
2010-03-19
(3)惯性仪表的误差补偿
对捷联式惯导系统来说,由于惯性仪表直接安装 在载体上,因此,载体的线运动和角运动都引起 较大的误差。 为了保证系统的精度,必须对惯性仪表的误差进 行 补偿,最好的补偿方法是计算机补偿。 在计算机中通过专用的软件来实现误差补偿。
