结构力学(包世华)第四版课件ppt
合集下载
结构力学基础讲义PPT(共270页,图文)

alMM
B bM l
a l
b M
l
17
2. 多跨静定梁: 关键在于正确区分基本部分和附
属部分,熟练掌握截面法求控制截面 弯矩,熟练掌握区段叠加法作单跨梁 内力图。
多跨静定梁——由若干根梁用铰相连, 并用若干支座与基础相连而组成的静 定结构。
17:11
18
附属部分--依赖基本 部分的存在才维持几 何不变的部分。
17:11
24
3. 静定平面刚架 (1) 求反力。
切断C铰,考虑右边平衡,再分析左 边部分。求得反力如图所示:
C
17:11
25
3. 静定平面刚架
(2)作M图 (3)做Q、N图 (4) 校核
17:11M图
N图
Q图
26
§1-4 静定桁架
17:11
27
§1-4 静定桁架
* 桁架的定义:
——由若干个以铰(Pins)结点连接而成的 结构,外部荷载只作用在结点上。
对只有轴力的结构(桁架):
1组7:1合1 结构则应分别对待。
61
§1-5静定结构位移计算
3. 荷载作用下的位移计算
例:求△cy 1. 建立力状态,在C点加单位 EI
竖向力。
2. 建立各杆内力方程:
EI
3. 求位移:
17:11
62
§1-5静定结构位移计算
3. 荷载作用下的位移计算
积分注意事项:
⒈ 逐段、逐杆积分。 ⒉ 两状态中内力函数服从同一坐标系。 ⒊ 弯矩的符号法则两状态一致。
2. 三铰拱的数解法
* 内力计算: ⑴任一截面K(位置):KK截 截面 面形 形心 心处 坐拱 标X轴K切、线YK的倾角 K
结构力学课件 第十四章 结构动力学(1)
l/2
EI
EI P(t)
P(t)
R(t) 0
k11 y(t) R1P (t) 0
k11 24 EI / l3 R1P my P / 2
my(t)
1
k11
P(t)
R1P (t)
层间侧移刚度
对于带刚性横梁的刚架(剪切型刚架),
当两层之间发生相对单位水平位移时,两
层之间的所有柱子中的剪力之和称作该
P(t)
my(t)
形式上2的.求平外衡力方和程惯,性实力质引上起的的运位动移方;程 3.令该位移等于体系位移。
一、柔度法
P(t) m my(t) =1 11
y(t)
l EI
11[P(t) my(t)]
P(t) my(t)
y(t) 11[P(t) my(t)]
11
l3 3EI
柔度系数
l
my(t)
3EI l3
y(t)
P(t)
二、刚度法
P(t)
m
1
my(t)
y(t)
l EI
y
k11
k11y(t) P(t) my(t)
k11 y(t )
k11
3EI l3
刚度系数
my(t)
3EI l3
y(t)
P(t)
k11 11 1
刚度法步骤:
柔度法步骤:
1.在质量上沿位移正向加惯性力;
1.在质量上沿位移正向加惯性力;
三、列运动方程例题
例3.P(t)
m
P(t)
my(t)
1 k11
EI1
y(t)
l EI
EI
k11
l
k11 24 EI / l3
结构力学课件 第十四章 结构动力学

21
11
[
P1
m1
y1
]
22
[
12
P2
m2
y2
]
例7. P2 (t) P1(t)
m2
EI1
k2 m1
EI1
k1
y2 (t) y1(t)
P1(t) m1y1 k1 y1 k2 ( y2 y1)
P2 (t) P1(t) P2 (t)
y2 (t) m2 y2 (t) y1(t) m1y1(t)
1) 集中质量法 将实际结构的质量看成(按一定规则)
集中在某些几何点上,除这些点之外物体是 无质量的。这样就将无限自由度系统变成一 有限自由度系统。
m y(x)
广义坐标个数即 为自由度个数
m
结点位移个数即 为自由度个数
m
二. 自由度的确定
4)
1) 平面上的一个质点
y1
W=1
y2
y1 W=2
5)
2) W=2
§14-1. 概述
1.1 动荷载及其分类
一.动荷载的定义 大小、方向和作用点随时间变化;在其作用下,结构上的惯性力
与外荷比不可忽视的荷载。
自重、缓慢变化的荷载,其惯性力与外荷比很小,分析时仍视作
静荷载。 静荷只与作用位置有关,而动荷是坐标和时间的函数。
二.动荷载的分类 确定
动荷载
简谐荷载 周期 非简谐荷载
层之间的所有柱子中的剪力之和称作该
层的层间侧移刚度.
24EI
k l3
1
11
k
11
1 k
EI1
l EI
k2
EI
l
EI
EI1
k1
结构力学(虚功原理和结构位移计算)ppt课件

A
i
δij
j Pj=1
B
δjj
δjj --直接柔度 δij --间接柔度
δjj >0
>0 δij <0
=0
完整版课件
9
5、计算位移的有关假定
1)、结构材料服从“虎克定律”,即应力、应变成线形关系。
2)、小变形假设。变形前后荷载作用位置不变。
3)、结构各部分之间为理想联结,不计摩擦阻力。
4)、当杆件同时承受轴力与横向力作用时, 不考虑由于杆弯曲 所引起的杆端轴力对弯矩及弯曲变形的影响。
由平衡条件知:
A
R1
b 未知力与已知力 a 之间的几何方程
由虚功方程:
R1
C
a
b
图(a)
C
图(b)
Δ1c1ab0
即
完整版课件
Δ
c1
•
b a
B
B' P=1 B
14
应用虚力原理求未知位移的关键是沿拟求位移Δ方向虚设单 位荷载,并利用平衡条件求与已知位移c1对应的支反力 R1 这种解法称为单位荷载法。
特点:利用静力平衡,通过虚功方程来解几何问题。 适用范围: 刚体体系的位移计算,
若求桁架中AB杆的角位移,应加 一单位力偶,构成这一力偶的两个 集中力的值取 1/d。作用于杆端 且垂直于杆(d 为杆长)。
完整版课件
32
3) 若要求结构上两点(A、B)沿其连线的相对位移,可在 该两点沿其连线加上两个方向相反的单位力。
完整版课件
33
4) 若求梁或刚架上两个截面的相对角位移,可在两个截 面上加两个方向相反的单位力偶。
当静力加载时,即:
P
P由0增加至P
结构力学第4章(2024版)
1 qa 2 2
MP
1
8
qa
2
qa
(2) 在C 截面加单位力偶作 M图1 ,如图b所示。
2
m =1 (c)
2
1 1
3
2
1
a
M1
烟台大学 烟台大学
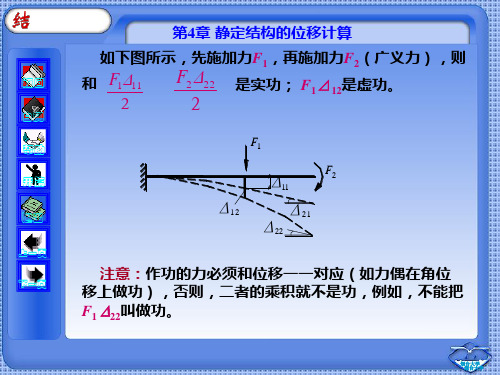
第4章 静定结构的位移计算
返回
c
M 1MP ds EI
RM
RM P
1 k1
R
N
RNP
1 k2
自测
1 [ 2 1 qa2 a 1 1 2a qa2 ( 2 3 1 1)
烟台大学 烟台大学
第4章 静定结构的位移计算
5. 具有弹性支撑或弹性约束的结构的位移计算
返回
弹性支承或弹性约束有以下几种类型:
自测
(a)
(b)
(c)
(d)
帮助
开篇
已知弹簧的刚度系数为k(或已知柔度系数为f,其中
退出 f=1/k)
图a和图b的弹簧会产生线位移⊿,从而产生反力k⊿。
上一页
注意:弹簧的反力与位移⊿方向相反。
第4章 静定结构的位移计算
3. 支座移动时的位移计算
返回
静定结构当支座产生移动时,整个结构发生刚体位移,
自测 因而不产生变形,应用刚体的虚功原理We=0,得
Δ1 Rc 0
帮助
式中,R为虚单位力引起的支座反力,c 为实际支座位
开篇 移,当二者方向一致时,其乘积取正值,相反时取负值。若
结构是超静定的,则当支座移动时,将会产生内力和变形,
应的位移影响系数21等于由荷载F2引起的与荷载F1相应
上一页 的位移影响系数12。
这里的荷载可以是广义荷载,而位移则是相应的广义位
