经典__材料力学结构力学弯矩图 ppt课件
合集下载
《轴力剪力弯矩》课件
剪力：平行于截面的力，用于描述物体在剪切方向受到的力
弯矩：垂直于截面的力矩，用于描述物体在弯曲方向受到的力矩 关系：轴力、剪力和弯矩是相互关联的，它们共同作用于物体，影响物 体的变形和破坏。
Part Six
轴力剪力弯矩的应 用
在工程结构中的应用
轴力：用于计算梁、柱等构件的承载能力 剪力：用于计算梁、板等构件的抗剪强度 弯矩：用于计算梁、柱等构件的抗弯强度 轴力剪力弯矩的综合应用：用于计算复杂结构的承载能力和稳定性
剪力符号：F
剪力方向：垂直于截面
剪力作用：使物体发生剪 切变形
Part Four
弯矩
定义
弯矩是物体受力后产生的一种内力，通常用M表示 弯矩的大小与力的大小、力的方向、力的作用点有关 弯矩的方向与力的方向垂直，与力的作用点所在的平面平行 弯矩的作用效果是使物体产生弯曲变形
计算方法
截面法：将结构简化为平面截面，计算截面上的弯矩 积分法：将结构简化为连续体，通过积分计算弯矩 矩阵法：将结构简化为有限元模型，通过矩阵计算弯矩 数值法：通过数值模拟计算弯矩，如有限元分析、边界元分析等
符号规定
弯矩：表示弯 曲变形时截面
上的内力
符号：M，表 示弯矩
单位：牛顿·米 （N·m）
计算公式： M=F*L，其中 F为作用力，L
为力臂长度
单位
弯矩的单位是牛顿·米（N·m） 弯矩是衡量物体弯曲程度的物理量 弯矩的大小与物体的材料、截面形状、受力情况等因素有关 弯矩的计算公式为：弯矩=力×力臂
应变：单 位为m/m （米/米）
弹性模量： 单位为Pa （帕斯卡）
Part Three
剪力
定义
剪力：物体受到的平行于其表面的力 剪力方向：与受力面垂直 剪力作用：使物体发生剪切变形 剪力计算：通过剪力公式进行计算，如F=P*L
弯矩：垂直于截面的力矩，用于描述物体在弯曲方向受到的力矩 关系：轴力、剪力和弯矩是相互关联的，它们共同作用于物体，影响物 体的变形和破坏。
Part Six
轴力剪力弯矩的应 用
在工程结构中的应用
轴力：用于计算梁、柱等构件的承载能力 剪力：用于计算梁、板等构件的抗剪强度 弯矩：用于计算梁、柱等构件的抗弯强度 轴力剪力弯矩的综合应用：用于计算复杂结构的承载能力和稳定性
剪力符号：F
剪力方向：垂直于截面
剪力作用：使物体发生剪 切变形
Part Four
弯矩
定义
弯矩是物体受力后产生的一种内力，通常用M表示 弯矩的大小与力的大小、力的方向、力的作用点有关 弯矩的方向与力的方向垂直，与力的作用点所在的平面平行 弯矩的作用效果是使物体产生弯曲变形
计算方法
截面法：将结构简化为平面截面，计算截面上的弯矩 积分法：将结构简化为连续体，通过积分计算弯矩 矩阵法：将结构简化为有限元模型，通过矩阵计算弯矩 数值法：通过数值模拟计算弯矩，如有限元分析、边界元分析等
符号规定
弯矩：表示弯 曲变形时截面
上的内力
符号：M，表 示弯矩
单位：牛顿·米 （N·m）
计算公式： M=F*L，其中 F为作用力，L
为力臂长度
单位
弯矩的单位是牛顿·米（N·m） 弯矩是衡量物体弯曲程度的物理量 弯矩的大小与物体的材料、截面形状、受力情况等因素有关 弯矩的计算公式为：弯矩=力×力臂
应变：单 位为m/m （米/米）
弹性模量： 单位为Pa （帕斯卡）
Part Three
剪力
定义
剪力：物体受到的平行于其表面的力 剪力方向：与受力面垂直 剪力作用：使物体发生剪切变形 剪力计算：通过剪力公式进行计算，如F=P*L
材料力学基础—结构力学弯矩图
一 、 梁
q 2 q P
MM == P q L P L 2 =qL
L L L L L/2
( ( (1 19 0 )) ( ) 1)
P作用下的M图： qL2
2PL
qP
PL
qM=qL 2 q P=qL
LL
P=qL L
P=2qL
LL
L
( (21)1 () 2)
P作用下的M图：
( (( 31 3 )2 ))
先计算支反M= 力qL 2，再q作MP 图=q：L
(15) 1 M
(13)
2
L
q q qL
( L 1211 M)
L L (7)
P=qL
1 qL LP P= =q qL L 4
L M M L= =q qL L 142 2( qM L12 2q q )L81LqLP P= 2=q qL L
L L (8)L L
P作用下的M图：
4 qL 2
qL
1 2
M=qL 2 q
q作用q下的M图：
P=qP L
P
qL 2
L
L
L
L
(4)
qL2
q
q作q用下的M图：
1 qL 2 2
L
L
(5)
(12)
P与q作用下的M图：
3 qL 2 L
q
2
(13)
qL L L
(7)
P与q作用下的M图：
L
M
L/4
1
qL
(14)
2
L
L
2
(8)
P 2P
q LL L q q
(7)
L L L L L L
L ( ( (77 7 )) )
q 2 q P
MM == P q L P L 2 =qL
L L L L L/2
( ( (1 19 0 )) ( ) 1)
P作用下的M图： qL2
2PL
qP
PL
qM=qL 2 q P=qL
LL
P=qL L
P=2qL
LL
L
( (21)1 () 2)
P作用下的M图：
( (( 31 3 )2 ))
先计算支反M= 力qL 2，再q作MP 图=q：L
(15) 1 M
(13)
2
L
q q qL
( L 1211 M)
L L (7)
P=qL
1 qL LP P= =q qL L 4
L M M L= =q qL L 142 2( qM L12 2q q )L81LqLP P= 2=q qL L
L L (8)L L
P作用下的M图：
4 qL 2
qL
1 2
M=qL 2 q
q作用q下的M图：
P=qP L
P
qL 2
L
L
L
L
(4)
qL2
q
q作q用下的M图：
1 qL 2 2
L
L
(5)
(12)
P与q作用下的M图：
3 qL 2 L
q
2
(13)
qL L L
(7)
P与q作用下的M图：
L
M
L/4
1
qL
(14)
2
L
L
2
(8)
P 2P
q LL L q q
(7)
L L L L L L
L ( ( (77 7 )) )
经典材料力学结构力学弯矩图课件
L
L
(25)
(2(53)5)
L
L
L
L
(24) (24)
qa 2
qa
qa
1
qa
q 2q
8
1 qa2 2
a a
(26) ((2366))
aa
2L2L
qa
q
与杆件轴 线相切
qa
qa 2
q
qa 2 qa2
1 qa2 2
a
(27)
(37)
a/2
a/2பைடு நூலகம்
2a
q
1 qa2
2
1 qa2 2
q
qa 2
a
a
(28)
(38)
利用L反对称性q 作LM/图4 ：
(15)1 M 2q
qq L
L
(L1211M)
LL(7)
P=qL L PP==qqLL
2PL L L PP
PL L L PL
(((22166PP)0))
L
L
从右向左作M图：
LL
LL (2) LL
PL ((66)) q
P=qL
q qq L q
(9)
PL
PP==qqLL
PL 2 3PL 2
M=PL
300 P
2qa2
2a
4a
用“局部悬臂梁法”直接作M 图，P力通过截面弯矩为0
L/2
PL
2
PL 2
PL 2
P
L/2
3PL 3PL 2
L
(19)
(27)
PL
PL
L/2
L/2
(20)
(28)
q
结构力学 PPT课件
总复习
1
NaA 2
1 1m×4＝4m
解：取1-1以右为分离体 ∑Y=0 NC=－10kN 取2-2以右为分离体
O
∑Y=6+YB+YC=0
6kN
YB=0
∑MO=0 NA=0
a
2
6kN
8kN
6kN
总复习
第八章 静定结构影响线
一、影响线的定义：
定义：当单位荷载（P=1）在结构上移动时，表示结构某一指
定截面中某项内力变化规律的曲线，称为该项内力的影响线。
二、叠加法绘制弯矩图
Q M AB M BA Q0
AB
l
AB
•首先求出两杆端弯矩，连一虚线， •然后以该虚线为基线， •叠加上简支梁在跨间荷载作用下的弯矩图。
三、内力图形状特征 1、在自由端、铰支座、铰结点处，无集中力偶作用，截
面弯矩等于零，有集中力偶作用，截面弯矩等于集中力偶的值。
总复习
M M 0 Hy
Q Q0 cos H sin N Q0 sin H cos
2、在拱的左半跨取正右半跨取负；
3、仍有 Q=dM/ds 即剪力等零处弯矩达极值；
4、 M、Q、N图均不再为直线。
5、集中力作用处Q图将发生突变。
6、集中力偶作用处M图将发生突变。
四、三铰拱的合理轴线 在给定荷载作用下使拱内各截面弯矩
2、刚结点上各杆端弯矩及集中力偶应满足结点的力矩平 衡。两杆相交刚结点无m作用时，两杆端弯矩等值，同侧受拉。
3、具有定向连结的杆端剪力等于零，如无横向荷载作用， 该端弯矩为零。
4.无何载区段 5.均布荷载区段 6.集中力作用处 7.集中力偶作用处
平行轴线
Q图
结构力学课件--6力法
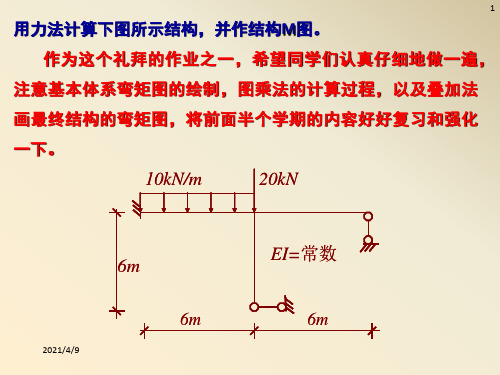
2m 2m
4m
1
4m
125
15
11.3
15
M kN m
Q kN
3.7 75
200
15 147.5
11.3 22.5
11.3 3.7
22.5
2021/4/9竖向力不平衡
147.5
N kN
二、变形条件的校核
25
200
100 60
2
2 30
1
40
1
150
4m
1
1
20 2m 2m
15 4m
11
M kN m
2) 3
4a 3EI
X2 1
22
1 EI
(1 2
a 1
2) 3
a 3EI
M2
12
1 EI
(1 2
a 1 1) 3
a 6EI
1 1 Pa
1 Pa 2 5Pa2
1P
EI
( 2
2
a1 2
2
a ) 3 12EI
2P
1 EI
1 2
Pa 2
a
1) 3
Pa 2 12EI
Pa 2
P 2 MP 1
X1 1 M1
EA
0 E1A1
1P
M1M P EI
ds
=
1P
l N12 dx l 12 dx l
0 E1A1
0 E1A1
E1 A1
11
M12 ds EI
N12 ds EA
l E1 A1
11
l E1 A1
两类拱的比较： 无拉杆 H 1P
11
E1A1 H H 相当于无拉杆
《船舶结构力学》0预备知识-弯矩图、剪力图复习
x
FS x＝qx
0 x l
FS x
ql
M x＝qx2 / 2 0 x l
依方程画出剪力图和弯矩图
x
ql2 / 2 由剪力图、弯矩图可见。最
大剪力和弯矩分别为
ql 2 / 8
FS max＝ql M max＝ql 2 / 2
x
目录
(Internal Forces in Beams)
例题5-3
F
a
b
A
C
x1 x2
FAY
l
FS Fb / l
图示简支梁C点受集中力作用。
B 试写出剪力和弯矩方程，并画 出剪力图和弯矩图。
FBY 解：1．确定约束力
M A＝0， MB＝0
FAy＝Fb/l FBy＝Fa/l
2．写出剪力和弯矩方程
Fa / l
Fab/ l
M
x AC
FS x1＝Fb / l 0 x1 a
M x1＝Fbx1 / l 0 x1 a
CB FS x2 ＝ Fa / l a x2 l
M x2 ＝Fal x2 / l a x2 l
x 3. 依方程画出剪力图和弯矩图。
目录
(Internal Forces in Beams)
例题5-4
a
b
图示简支梁C点受集中力偶作用。
M
A
C
x1
试写出剪力和弯矩方程，并画
M x2 ＝ Mx2 / l 0 x2 b
3. 依方程画出剪力图和弯矩图。
目录
(Internal Forces in Beams)
二、q(x)、Fs(x)图、 M（x）图三者间的关系 (relationships between load,shear force,and bending moment diagrams)
材料力学和结构力学课件
材料力学1.材料力学研究内容⑴研究物体在外力作用下的应力、变形和能量，统称为应力分析；研究对象仅限于杆、轴、梁等物体，其几何特征是纵向尺寸远大于横向尺寸，这类物体统称为杆或杆件。
⑵研究材料在外力和温度作用下所表现出的力学性能和失效行为；研究对象仅限于材料的宏观力学行为，不涉及材料的微观机理。
研究目的设计出杆件或零部件的合理形状和尺寸，以保证它们具有足够的强度、刚度和稳定性。
2.杆件的受力与变形形式⑴拉伸或压缩 ⑵剪切 ⑶扭转 ⑷弯曲⑸组合受力和变形拉杆、压杆或柱、轴、梁受力特点3.材料的基本假定⑴各向同性假定 ⑵均匀连续性假定 ⑶平截面假定4.受力分析方法⑴截面法：应用假想截面将弹性体截开，分成两部分，考虑其中任意一部分平衡，从而确定截面上的内力的方法。
弹性体受力、变形的第二特征是变形协调。
P9［例题1-1］ 平衡方程+变形协调方程0x F =∑ 0y F =∑ 0cM =∑P31［例题2-6］5.应力应变相互关系E σε=、G τγ=6.轴力与轴力图正负号规定：拉正，压负。
⑴确定约束力。
⑵根据杆件上作用的荷载及约束力确定控制面，也就是轴力图的分段点。
⑶应用截面法，对截开的部分杆件建立平衡方程，确定控制面上的轴力数值。
⑷建立N x F -坐标系，将所求得的轴力值标在坐标系中，画出轴力图。
P21［例题2-1］7.变形计算变形N F ll EA∆=±应变N F l l EA Eσε∆===横向变形y x ευε=- υ泊松比 P25［例题2-2］8.拉伸与压缩杆件的强度设计⑴强度校核[]max σσ≤⑵尺寸设计[][][]max N N F FA A σσσσ≤⇒≤⇒≥ ⑶确定杆件或结构所能承受的许用荷载[][][][]max NN P F F A F Aσσσσ≤⇒≤⇒≤⇒ P28［例题2-4/5］9.拉伸与压缩杆件斜截面上的应力2cos =cos N P x F F A A θθθθσσθ==()sin 1=sin 22Q P x F F A A θθθθτσθ== 10.连接件强度的强度计算铆接件的破坏形式：剪切破坏、挤压破坏、连接板拉断以及铆钉后面连接板的剪切破坏。
剪力以及弯矩剪力图以及弯矩图
剪力图和弯矩图在工程管理中的应用
结构设计：用于计 算结构受力确定结 构尺寸和材料
施工管理：用于 指导施工确保施 工质量和安全
维护管理：用于 评估结构状态制 定维护计划
优化设计：用于 优化结构设计降 低成本和能耗
剪力图和弯矩图的注意 事项
绘制剪力图和弯矩图时应注意的事项
确保数据准确无误 注意单位换算确保单位一致 绘制过程中注意比例尺和坐标轴的设置 绘制完成后检查图例、标题、标注等是否清晰明确
添加副标题
剪力和弯矩剪力图以及弯矩 图
汇报人：
目录
CONTENTS
01 添加目录标题
02 剪力和弯矩的基本 概念
03 剪力图和弯矩图的 绘制
04 剪力图和弯矩图的 解读
05 剪力图和弯矩图的 应用
06 剪力图和弯矩图的 注意事项
添加章节标题
剪力和弯矩的基本概念
剪力和弯矩的定义
剪力：作用在物体表面上的力使物体发生剪切变形 弯矩：作用在物体表面上的力使物体发生弯曲变形 剪力图：表示剪力在物体表面上的分布情况 弯矩图：表示弯矩在物体表面上的分布情况
剪力和弯矩的计算方法
剪力：作用在物体上的力使物体发生剪切变形 弯矩：作用在物体上的力使物体发生弯曲变形 剪力计算方法：根据力的平衡原理利用剪力公式进行计算 弯矩计算方法：根据力的平衡原理利用弯矩公式进行计算
剪力和弯矩的单位和符号
剪力：单位为牛顿（N） 符号为F
弯矩：单位为牛顿·米 （N·m）符号为M
证结构安全
剪力图和弯矩图在施工中的应用
确定结构受力情况： 通过剪力图和弯矩图 可以了解结构的受力 情况为施工提供依据。
优化施工方案：根据 剪力图和弯矩图可以 优化施工方案提高施 工效率和质量。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
L
MM(8)
P
L/2
P
LL L
LL L
(((888()))4)
利用反L 对称性q 作LM/4图：
(15)1 M 2q
qq L
L
PLL((PL7121T)1M课) 件 L
P=qL PP==qqLL
2PL L L PP
PL L L PL
(((22616PP) 0))
从LL 右L向LL左(2作) MLL图L ：
1 q3a2
8
8.5qa2
8qa2
4qa2 相切
二、悬臂式刚架
M=PL
PPT课件
15qa2 16qa2
1 q4a2
8
5
(11)
qL2
qL2
2
2
L
L
L
L
L
斜梁各截面弯矩值与所对应简支梁一样(8，) 作M图：
(7)
q
q
pL
2P
M=PL
5qL2
q
2
qL2 L 8 L pL
L (10)
(13)
qL2
只影响AC段,作M图：
qa2
qa2
2
不与水平线相切 4
m q=10 a
2m
60
15
aa a
2m
2m
2m
从附属部分开(始16)，直接作M图(：22)
m
q
M=2qa
a aa
a
2a
a
(17)
m
m
q
P=qa M=qa2
P=2qa
m
q
3a
a
2a
2a
aa
2a
4a
(23) (18)
从附属部分开始，用“局部悬臂梁法”直接作M图：
(33)
2L 2L
LL
用“局部悬臂梁法”直接作M图：
P P
PL PL
3PL
L
L
L
L
((3244))
(24)
2PL 2PL
P P
PPT课件
qa 10 qa
L
LL
2PL 2PL
P P
PL 2PL
3PL
L
L
L
L
(25)
(2(355))
LLLຫໍສະໝຸດ L(24) (24)
qa2
qa
qa
1
qa
q 2q
8
1 qa2 2
qL2 8
L
5qL2 32
L/4
6
L
3a
a
2a
2a
aa
15qa2 16qa2
(18)
用“局部悬臂梁法”直接作M 图，P力通过截面以上部分还 二、有悬力臂偶式，刚所架以弯矩不为0：
PL 2 3PL 2
M=PL
300 P
2qa2
2a
4a
用“局部悬臂梁法”直接作M 图，P力通过截面弯矩为0
L/2
PL
2
PL 2
4.5qL2L 直线q与曲L线/4 相切P=qL
(15)
2qL2
L
(9) 1
L
((11)) q P
P LL L
P=qL
(((41)41))
PP
从右LL向左作PP MLL图：
PL
((4P4q))L
q
L
L
L
(7)
LL
LL
LL
L
(((777)))
利(14用) 对称性2P 作M图M=：LP/L4
1
L
qL2
PPT课件
8
用“局部悬臂梁法”直接作M图：用“局部悬臂梁法”直接作M图：
1 Pl 2
1 Pl
2Pl 2Pl
2
Pl
Pl
1 Pl 2
(31)
注：P力通过点弯矩为0
(32)
注：P力通过点弯矩为0
PPT课件
9
aa
用“局部悬臂梁法”直接作M图：
P
P
P
Pa
P
2Pa
A Pa
a Ba
a
a
(23)
注：AB段弯矩(2为3)常数。
30
3
30
(16)
(17)
先计算支反力，再作M图： 直接作M图：
Fa
qa2
1 Fa 3
1F
3
9 qa2 8
(18)
直接作M图：
10
60
20
(19)
CD段直接作M图， AC段采用叠加法：
qa2
1 qa2 2
相切
(20)
力偶只影响BD段,直 接用叠加法作M图：
qa2 qa2
PPT课件
(21)
力偶只影响BC段,力
2
81(1q220LPP)2
12LqLMM2 ==PPLL
LL
LL
L
L
((M22=))qL2 qq
P=qL
一、梁
L
L
((P33))
2P
2P
M=PL
LL q
LLM=qL2
((51)(25)qq)
5 2
q从L2 右LL 向左(L((23155)))作qLM2MLLL图/812：qL2
q L
1 qL2 2
PL ((66)) q
P=qL
q qq L q
(9)
PL
PP==qqLL
L LL
L
((L99))((59))
先计算支反M=力qL2，再q 作MP图=q：L
(13)
1 qL 4
MML==qqLL22 M qq
L
1 (q1L22) 4
L
1
PP==qqLL
qL2
L8
LL
(8) LL
2
2PL
Pq
PL
LL
LL
qL2
2
8
qL2
L
L8
(11) (14)
P=qL
5qL2 L/4 32
(24)
(25)
L (9)
q
qL2 2
3qL2 2
q
5qL2
qL2 M=qL2 32
LqL22
L
8
(12)
L
L/4
((2165))
L/2
P=qL
所对应简支梁为：
q
q
q
L/2
qL2 8 L
(13)
qL2 8 L
PPT课件 (14)
5qL2 L/4 32
P=qPL
1 qL2 2
L
L
P L
L
(4)
qL2
q
q作q 用下的M图：
1 qL2 2
L
L
(5)
(12)
P与q作用下的M图：
3 qL2 L
q
2
(13)
qL
L
L
(7)
P与q作用下的M图：
L
M
L/4
1
(14)
qL2
L
L
2
(8)
PPT课件
P
2P
q作q 用下的M图：
1 qL2 L
L
L
2
(6)
P与q作用下的M图：
a a
(26) ((3266))
aa
2L2L
PPT课件
11
qa
q
与杆件轴 线相切
一、梁
q2qP
MM==PqLPL2=qL
L
LL L L/2
(((1190))()1)
P作用下的M图： qL2
2PL
qP
PL
q M=qL2 q
P=qL
P=qL
LL
L
P=2qL
LL
L
((21)1()2)
P作用下的M图：
(((313) 2))
P作用下的M图： 4qL2
/2 L/2
L
M=qL2 q
q作用q下的M图：
(6)
1.6 0.6kN
1.6 2.4 0.1
1.4kN
qM
(13)
作M图,只需计算C P=qL 截面弯L 矩 L L
1 Fl ((181)) 2
M=qqL2 q
(14)
PP==qqLL
作M图,只需计算C
截面弯L 矩 L
(192))
1 2
L
qa
21
qa
2
8
曲线在B点PP与T课水件平线相切
(15)
不用计算支反力， 可快速作M图
PL 2
P
L/2
3PL 3PL 2
L
(19)
(27)
PL
PL
PPT课件
L/2
L/2
(20)
(28)
q
7
3PL 3PL 2
L
(19)
用“局部悬臂梁法”直接作M 图，P力通过截面弯矩为0
PL
PL
L
P L
((2291))
L/2
L/2
(20)
用“局部悬臂梁法”直接作M 图
q
与杆件轴 线相切
qL2 2
L
(2(320))
((1(205)) )
叠加法作M图： 1.先考虑力偶作用
2.再叠加MP的q 作用
2PL L
PL
L
L 14(8P)L L
(5)
qP
2P
LL L
P=2qL LL
(1((136)))
(12)
先计算支反力，再作M图： 先计算支反力，再作M图：