6.8 平面衍射光栅解析
第四章衍射光栅
d ：光栅常数
每毫米光栅的狭缝数目： 数百条～两千左右条。
2）多缝夫琅禾费衍射图样
3）衍射图样的特征
（1）有一系列主极强、次极强和极小值。
（2）主极强的位置与缝数N无关， 宽度随N增加减小（更细锐）。
（3）相邻主极强间有 (N 1)条暗纹（极小）
I
0
(
sin
)2
（1）单缝的调制作用
（2）缺级
a sin m m 1,2, 由d sin k k 0,1,2,
，
缺级级次： k m d
a
，
m 1,2,
§2 光栅光谱仪
1、光栅的分光原理
由光栅方程
d sin k
可知： 光栅衍射的零级光谱 是白色的，其余各个 级次均为彩色光谱。
eNi ei
E
a0
sin
sin N sin
eikr0
其中：r0 r01 [(N 1)d sin ]/ 2
，
是整个光栅中心到观察点P的光程。
，
a0IaCI~0，(sina) 2si(nssinin，N
d
)2
sin
4．缝间干涉因子的特点
(sin )2：衍射因子
(sin N )2：干涉因子 sin
和 (N 2)个次极强。
（4）外部轮廓呈单缝衍射的曲线包络
3．多缝夫琅禾费衍射的复振幅和光强分布
1）不同单缝衍射的差异
n （1）第 个单缝的复振幅分布：
E
n(
E
P)
rn
n (P)
i E(Q)eikrd C
r0
r －x (0 ) 0n
第二章之5 平面衍射光栅
jN 1l 最小值位置sinq q
Nd
jN 1l sinq q sin q
Nd
l l j d Nd
由于△θ的值非常小，上式可变为
l sinq q sin q sin q cos q q Nd
l q Nd cos q
0 x f
由光栅方程可得其重叠条件为：
jl j l
1 1 2
2
六 衍射光谱
入射光为白光时， q k不同，按波长分开形成光谱. l不同，
( b a ) sin q kl
( k 0 ,1 ,2 , )
I
sin q
l ba
0
一级光谱
三级光谱 二级光谱
I
sin q
l ba
从物理上看，处理方法都是从位相差着手。
从数学上，干涉是有限求和， 衍射是无限积分。
光栅衍射实验装置
衍射角
L
P
Q
b
q
a
ba
光栅常数
o
f
二 光栅衍射条纹的形成 光栅的衍射条纹是单 缝衍射和多光束干涉的总 效果.
光栅常数：105 ~ 106 m 衍射角
q
( b a ) sin q
E10 E20 E30 E40 E50
kl , k 1, q 38
1 N 9729 条 ba
o
( b a ) 1.028μm
o
( b a ) sin q （2） q 90 k 1.6 2 l
只能看到第一
级衍射明纹
六. 光栅光谱
复色光 如果有几种 单色光同时投射在 光栅上，在屏上将 出现光栅光谱。 中央主极大（零级谱）仍为 白色，无色散，其余各级光 谱对称地分列两旁。 屏
甲型光学第六章衍射光栅解析PPT教学课件
5
6.1.1 黑白型光栅的衍射强度
• 是多缝夫琅禾费衍射
• 满足近轴条件
• 每一狭缝的衍射是相同的，即具有相似的单元 衍射因子，相邻衍射单元的复振幅光程差相等
U n()U 0 (n)siu nua(n)
u asin
d
U(n) 0
aKUn(Q)eikfrn0
a
a (n1)
a (n)
a (n1)
f
u sin
I(P )I0(su iu)n 2(ssiN in n)2
I0
aKU~0 f
(Q)
2
shi满足近轴条件时，单个狭缝在像方焦点处的光 强
2020/10/16
12
2020/10/单16 元衍射与N元干涉曲线周期之比为d/a
13
N=4 d=3a
2020/10/16
I (sinu/u)2 0
19
• 5．谱线的缺级
当干涉的最大值与衍射的极小值重合时，出现缺级
干涉极大位置sinθ=jλ/d 衍射极小位置sinθ=nλ/a j/d= n/a，即 j=nd/a。谱线级数缺。
2020/10/16
20
j=-3 j=-2 j=-1j=0 j=1 j=2 j=3
N=6,d=5a
2020/10/16
(sinNβ/sinβ)2
u=πasinθ/λ
14
N=6,d=5a
2020/10/16
15
N=20,d=3a
2020/10/16
16
6.1.2 衍射花样的特点
• 1．衍射极大值位置
I(P )I0(su iu)n 2(ssiN in n)2
极大值 j dsinj
I(j)I0(siu nu)2N2 NN!!
平面衍射光栅
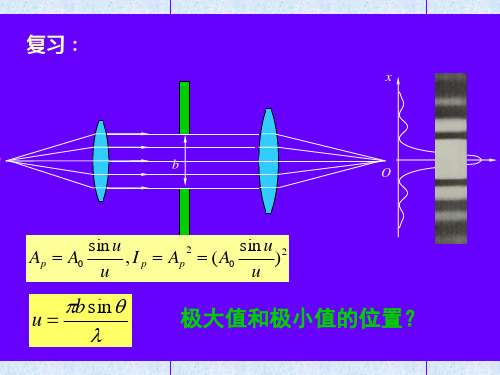
讨论
Multiple rays interference
d d
a a a b b a b
B
I
C C C B B
BC (a b) sin d sin
2
BC
1) Grating equation 光栅方程
principal maxima 主明纹
屏 （4）强度分布中保留了单缝衍射因子， 幕
就是曲线的包迹（轮廓），与单缝衍射曲 线形势一样
三、强度分布
缝间多(N)光束 干涉干涉因子
P点的光强
b sin u
sin u sin Nv I (P) I0 2 2 u sin v
单缝衍射 衍射因子
2
2
d sin v
结论：多缝衍射光强分布是多光束干涉光强分布受 单缝衍射光强分布调制的结果。
缺 级 缺 级
2 4 5
-5 -4
-2 -1
1
2
3) Lack of the order 缺级：
：
(a b) sin j (1)
j 0 1. 2. 3...
b sin k (2)
k 1. 2. 3...
ab d jk k (3) b b k 1. 2. 3...
I
-2 -5 -4
缺 级
缺 级
2 4 5
-2 -1
1
2
3) Lack of the order 缺级
Only is there diffraction 只考虑单缝衍射:
I
-2
-1
1
2
Only is there interference 只考虑多光束干涉 ： I
衍射光栅实验原理
衍射光栅实验原理衍射光栅实验是一种重要的实验方法，它能够帮助我们深入理解光的衍射现象。
衍射光栅实验原理主要涉及到光的衍射现象、光栅的结构和原理以及实验过程和结果分析等内容。
首先，让我们来了解一下光的衍射现象。
光的衍射是指光波遇到障碍物或通过狭缝后，波的传播方向发生改变并产生干涉现象的现象。
在衍射光栅实验中，光波通过光栅的狭缝后，会产生明暗条纹的衍射图样，这是由于光波在通过光栅狭缝后发生了衍射现象所致。
其次，光栅的结构和原理也是衍射光栅实验原理中的重要内容。
光栅是一种具有周期性结构的光学元件，它由许多平行的透射或反射狭缝组成。
当光波通过光栅时，会根据光栅的周期性结构产生衍射现象，形成衍射图样。
光栅的衍射图样可以帮助我们研究光的波动性质，进而深入理解光的本质。
在进行衍射光栅实验时，我们需要准备一台光源、一块光栅和一块屏幕。
首先，我们将光源照射到光栅上，光波通过光栅的狭缝后将在屏幕上形成衍射图样。
通过观察衍射图样的形状和特点，我们可以分析光波的衍射现象，并进一步研究光的波动特性。
衍射光栅实验原理的研究对于光学领域具有重要意义。
通过衍射光栅实验，我们可以深入理解光的波动性质和衍射现象，为光学理论的研究提供重要的实验数据。
同时，衍射光栅实验也在光学仪器的设计和应用中具有重要的作用，例如在光谱仪、激光器等光学仪器中都广泛应用了衍射光栅原理。
总之，衍射光栅实验原理涉及到光的衍射现象、光栅的结构和原理以及实验过程和结果分析等内容。
通过对衍射光栅实验原理的研究，我们可以更深入地理解光的本质和光的波动性质，为光学领域的发展和应用提供重要的理论基础和实验数据。
平面衍射光栅
sin N
物理科学与信息工程学院 11
或 式中
sin u sin N I I0 . 2 2 u sin a sin d sin u , ,
2 2
光强公式中
sin 2 u 2 u 2 sin N 2 sin
称为衍射因子, 称为缝间干涉因子.
可见光栅衍射的光强是单缝衍射图样和缝间干涉因 子的乘积。单缝衍射因子对干涉主最大起调制作用。
造成这种情况的原因是单缝衍射因子的零级与缝间 干涉因子的零级主最大重叠。实际使用光栅时，通 常只使用它的某一级光谱。
因此，只需设法把光能集中到这一光谱上来即可。 用闪耀光栅即可解决这个问题。
物理科学与信息工程学院 28
目前在分光仪器中使用的光栅几乎都是反射式的闪 耀光栅。它的优点是：能将单缝的中央最大值的位 置从没有色散的零级光谱转移到其他有色散的光谱 级上。如图所示：
即
k ' 0, N ,2 N ,3N ,
的整数。
否则上式就变成决定主最大角位置的光栅方程了。 因此,两个干涉主极大之间有(N-1)个由于干涉产生 的光强为零的最小值.
物理科学与信息工程学院 18
3. 次最大的角位置和数目 次最大的角位置可由
d sin N 0 d sin
若平行光斜入射到光栅上，入射方向和光栅平面法 线方向的夹角为0，则光栅方程为：
d (sin sin 0 ) k
k 0, 1, 2,
其角度均取正值， 和0 在法线同侧时上式左边
括号中取加号；在法线异侧是取减号。
物理科学与信息工程学院 16
2. 光强为零（暗纹）的角位置和数目 在光强公式中，两因子中任一因子为零，P点的光 强都会为零. 对于干涉因子, 当
光栅衍射现象衍射光栅
k 解: (1) (a b) sin k (a b) 6 m sin
(a b ) (2)k k a k 4, 取k 1
amin
ab 1.5m b d amin 4.5m 4
(3)由光栅方程 sin 1，k kmax ab 6 m k max 10 0.6m
X射线管
阴极
阳极 （对阴极）
10
4
~10 V
+
5
X 射线衍射---劳厄实验
X 射 线 管 铅 屏 底 片 晶体 晶体可看作三维 立体光栅。 根据劳厄斑点的分 布可算出晶面间距，掌 握晶体点阵结构。
劳 厄 斑 点
布喇格父子(W.H.Bragg, W.L.Bragg)对伦琴射线衍射 的研究：
O . d . . φ A . B C
2 a
其他明条纹的角宽度：
I
a
5 3 2a 2a
0
3 2a
5 sin 2a
2、条纹的光强随着级次的增大而减小。
I
5 3 2a 2a
0
3 2a
5 sin 2a
当 角增加时，半波带数增加，未被抵消的半 波带面积减少，所以光强变小。
3 、当用白光照射时，除中央明纹仍为白色外， 其它明纹均为由紫到红的彩色条纹。不同波长， 不同级次的条纹可能产生重叠现象。
A
(1 ) (1 ) (1 )
a
B
P0
f
菲涅耳半波带法
A
A1 A2 A3
C
两个相邻的半波带 上对应点发出的子 波会聚于 P 点时，其 光 程 差 恰 好 为 λ/2 ， 因此干涉相消。
B
平面光栅的工作原理
平面光栅的工作原理平面光栅是一种基于干涉原理的光学元件，是由一系列平行等间距的透明和不透明条纹组成的。
它的工作原理可以通过光的干涉和衍射来解释。
首先让我们来了解一下光的干涉。
干涉是指两束或多束光波相遇时相互作用的现象。
当光波相遇时，它们的波动性使得它们可以相互增强或抵消。
如果两束光波的相位差为整数倍的波长（即相位相同），它们会互相加强，形成明亮的干涉条纹。
而如果相位差为半整数倍的波长（即相位相反），则它们会互相抵消，形成暗亮的干涉条纹。
接下来是光的衍射。
衍射是光波通过障碍物或缝隙时发生偏离的现象。
当光波通过一个缝隙或条纹时，会沿着不同方向传播，形成特定的角度和强度分布。
这样的现象被称为衍射，通过衍射可以使光波的传播方向和能量分布发生改变。
平面光栅利用了光的干涉和衍射现象。
当入射平行光通过平面光栅时，光波将被分为若干个具有特定角度的光波组。
这是因为平面光栅上的条纹起到了类似于缝隙的作用，光波通过条纹时会发生衍射。
光栅的条纹间距是一定的，决定了不同衍射光波的角度。
根据光的波长和入射角度不同，通过衍射光波角度也会有所不同。
平面光栅的工作原理可以通过狭缝衍射公式来计算。
狭缝衍射公式可以描述入射光波经过狭缝时的衍射角度及强度分布。
基本上，平面光栅可以看作由复制了许多小狭缝的组成，每个小狭缝产生一组衍射光波。
平面光栅还有一个重要的参数叫作光栅常数，表示单位长度内的条纹数。
光栅常数越大，条纹间距就越小，形成的衍射角度也就越大。
通过调节光栅常数，可以控制所产生的衍射角度和强度分布。
利用平面光栅的这种工作原理，可以用于光谱分析、光学仪器的校准和光学通信等领域。
例如，在光谱分析中，平面光栅可以将入射光波分散成具有不同波长的光波，从而得到光谱信息。
在光学通信中，平面光栅可以用于分波复用和解复用，实现多路光信号的传输。
总之，平面光栅是一种基于干涉和衍射原理的光学元件，利用条纹的干涉和衍射现象，将入射光波分散成具有特定角度的光波组。
§2.4-平面衍射光栅概述
nd
A0
2i bsin
2i n d sin 2i b sin e e
2i n d sin
e
A0
sin
b
sin
bsin
i
e
b sin
2i
e
n d sin
（2）
将各项相加
Ep
A0
sin
b
sin
bsin
ei
(
kt
)
i
e
b
sin
i 2 d sin
1 e
2i 2 d sin
I M
lim v j
sin2 Nv sin2 v
N2
主极大条纹的位置—光栅方程
d sin j, j 0, 1, 2,
（7） （8）
（2）最小值（零点）的位置和此极大的数目.
Nv N d sin k
v d sin j
d
sin
k N
d k
sin
jN
k
N 0, N, 2N
1、联系：本质相同，干涉和衍射两者的本质都是波的相干叠 加的结果。 2、区别： （1）形成条件不同。参与相干叠加的对象有所区别，干涉是 有限几束光的叠加（离散相干光波的叠加），而衍射则是无穷 多次波的相干叠加（连续相干光波的叠加），前者是粗略的， 后者是精细的叠加。 （2）图样分布特点不同。干涉和衍射花样都是明暗相间的条 纹，但在光强分布上有间距均匀与相对集中的不同。 （3）在处理问题的方法上不同。从物理角度来看，考虑叠加 时的中心问题都是位相差，但位相差由分立（离散）变化到连 续变化；从数学角度来看，相干叠加的矢量图由干涉的折线过 渡到衍射的连续弧线，由有限项求和过渡到积分运算。
衍射光栅_精品文档
衍射光栅衍射光栅（Diffraction Grating）是一种用于分散光束及研究光波性质的光学器件。
它是由透明的平行斑纹组成的光学元件，其中每个斑纹都具有相等的宽度，并且间隔均匀。
衍射光栅的主要作用是将入射的光束分解成不同波长的光，并使它们以不同的角度进行衍射。
光的波动性是光学研究中的一个重要方面。
光在传播过程中会受到衍射现象的影响，即光通过一个物体的边缘或孔洞时，会发生偏离传播方向的现象。
而光栅正是基于衍射现象而设计出来的光学器件。
一维衍射光栅是最简单的光栅形式，它由一系列平行的凹槽或凸起构成。
这些凹槽或凸起被等间距地排列，其间距称为衍射光栅的线密度，用单位长度中所含凹槽或凸起的数量来表示。
常见的线密度单位是每毫米凹槽或凸起的数量。
当光束通过衍射光栅时，光波会在每个凹槽或凸起上发生衍射，形成一系列的衍射波。
由于各个波长的光波具有不同的传播速度，因此它们在通过衍射光栅后会以不同的角度进行衍射。
这样，不同波长的光将会分散开来，从而实现对光的分光。
衍射光栅的分光效果可以通过光波的干涉来解释。
当光波通过衍射光栅时，每个凹槽或凸起上的光波会形成一组衍射波，这些衍射波在空间中相互干涉。
具体来说，通过干涉效应，分布在不同位置的衍射波会相互加强或相互抵消，从而形成一系列明暗相间的条纹。
这些条纹被称为衍射顺序，而每个顺序对应着不同的角度和波长。
衍射光栅的分光效果可以应用于许多领域，特别是光谱学和光学测量。
通过分散光束，衍射光栅可以将复杂的光信号分解成不同波长的成分，从而使我们能够对光进行精确的分析和研究。
此外，衍射光栅还被广泛应用于激光和光纤通信领域，用于解调和发射光信号。
除了一维衍射光栅外，还存在二维和三维衍射光栅。
二维衍射光栅在一个平面上具有两个正交的衍射方向，可以实现更复杂的分光效果。
而三维衍射光栅则可以在三个坐标方向上进行分光，具有更高的分光分辨率。
总结起来，衍射光栅是一种用于分散光束以及研究光波性质的重要光学器件。
光栅衍射知识点总结课件
光栅衍射知识点总结课件光栅衍射是一种利用光栅产生衍射效应的现象，是一种重要的光学现象。
通过光栅衍射，我们可以了解到光的波动特性以及光波通过光栅的衍射规律。
在实际应用中，光栅衍射被广泛应用于光学仪器、激光技术、光谱分析等领域。
本文将对光栅衍射的知识点进行总结，包括光栅的原理与特性、光栅衍射的规律、光栅衍射的应用等内容。
一、光栅的原理与特性1. 光栅的定义光栅是一种光学元件，是由许多等间距的平行条纹组成的平面或曲面。
光栅通常是由金属、玻璃等材料制成，其间距和条纹数目是确定的，可以分为透射光栅和反射光栅两种类型。
2. 光栅的特性光栅具有几何光学特性和衍射光学特性。
在几何光学中，光栅可以用来分束、合束和分光；在衍射光学中，光栅可以产生衍射效应，使光的波动性显现出来。
3. 光栅的构造光栅由一系列等间距的透明或不透明条纹组成，这些条纹可以是平行的，也可以是曲线的。
光栅的构造决定了其对入射光的衍射效应。
4. 光栅的作用光栅可以将入射光分散成各个波长的光，从而进行光谱分析；也可以用于制备激光器、衍射仪、干涉仪等光学仪器；同时，光栅也被广泛应用于激光技术、光通信等领域。
二、光栅衍射的规律1. 光栅衍射的基本原理光栅衍射是指入射光通过光栅后产生衍射效应的现象。
当入射光照射到光栅上时，光栅上的条纹会对入射光进行衍射，产生出多个次级光源，形成衍射图样。
2. 光栅衍射的数学描述光栅衍射的数学描述可以利用菲涅尔衍射理论、惠更斯-菲涅尔原理等方法进行描述。
通过数学模型，可以求解出光栅衍射的衍射角、衍射级数、衍射图样等参数。
3. 光栅衍射的表达式光栅衍射的强度分布可以用衍射方程来描述，通常可以采用菲涅尔衍射积分或者费涅尔积分来进行数值计算。
通过衍射方程的计算，可以得到光栅衍射的强度分布图。
4. 光栅衍射的规律光栅衍射的规律包括主极大和次级极大、衍射级数、衍射角、衍射图样等规律。
这些规律可以帮助我们理解光栅衍射的特性，并且可以应用于光栅的设计和光学仪器的优化。
初二物理光栅衍射定律推导
初二物理光栅衍射定律推导光栅衍射是光的一种特殊现象，它可以通过光线在光栅上的衍射来解释。
本文将对初二物理中关于光栅衍射定律的推导进行详细介绍。
1. 光栅衍射的基本原理光栅是一种由等距、等宽、相同透过率的平行透光狭缝组成的光学元件。
当平行的单色平面波（即单色光）垂直入射到光栅上时，光栅会改变光的传播方向，导致光在垂直于光栅的平面上发生衍射。
2. 单缝衍射定律回顾在介绍光栅衍射定律前，先回顾一下单缝衍射定律。
当单色光通过一个狭缝时，根据夫琅禾费衍射公式，可以得到衍射角θ和狭缝宽度d 的关系公式为：d·sin(θ)=n·λ其中，d表示狭缝的宽度，θ表示衍射角，n表示衍射级次，λ表示光的波长。
3. 光栅衍射定律的推导对于由N个宽度相等、间距相等的狭缝组成的光栅，我们来推导光栅衍射定律。
首先假设入射光波垂直于光栅，经过光栅后衍射光线的角度为θ。
根据衍射定律，衍射光线满足光栅中各个缝隙中传播的光程差相等的条件。
光程差是指从光栅上一个狭缝到另一个狭缝路径的差值。
根据几何关系，可以得到光程差Δl和衍射角θ的关系公式为：Δl=d·sin(θ)其中，d表示光栅缝隙的间距。
此外，由于光栅是由N个缝隙组成，因此总的光程差ΔL等于单个狭缝的光程差Δl乘以缝隙数量N。
即：ΔL=N·Δl=N·d·sin(θ)根据波程差等于光的波长的整数倍的条件，可得到光栅衍射定律：d·sin(θ)=n·λ其中，d表示光栅缝隙的间距，θ表示衍射角，n表示衍射级次（即亮纹的序号），λ表示入射光的波长。
通过上述推导，我们得到了光栅衍射定律。
这个定律可以帮助我们计算光栅衍射现象中衍射角和光栅参数之间的关系，从而更好地理解和分析光栅衍射现象。
4. 光栅衍射的应用光栅衍射定律在实际应用中有着广泛的应用，例如光谱仪、激光器、衍射光栅等装置都利用了光栅衍射的原理。
通过精确地控制光栅的参数，可以实现对入射光的激发和分离，使得光栅的应用在科学研究、通信技术、光学仪器等领域发挥重要作用。
光栅的衍射
d
o
f
d sin
x sin tan (＜5 ) f 思考:光栅第五级明纹的第1条缝与第N条缝衍射光的光程差是 多少? (N-1)5
2)主极大的位置:
观察屏
f xk d
k=0,±1,±2, ......
多光束干涉主极大的位置与缝的个数无关。
3. 暗纹条件 1) 满足单缝衍射暗纹的位置必为光栅衍射的暗纹
从 k = 2 开始重叠。
也可用公式：kΔ < 紫，得到 k<4/3 时光谱完整，则 k=2 时开始重叠。
(2)设1=4000Å的第k+1 级与2=7000Å的第k级 开始重叠
-3 -2 -1
0
( k 1)1 1的第k+1级角位置: sin1 2 10 2 ( k 1) ab
1
2
3
当 k = 2, sin 2 sin1 (3) (a b) sin
k2 2 3.5 10 k 2的第k级角位置: sin 2 ab
解: (1) (a b) sin
3
3 f1 x1 f tan 1 f sin1 ab 3 f 2 x2 ab
31 sin 1 ab 32 sin 2 ab
3 f (2 1 ) Δx x2 x1 6[mm ] ab
(a b) sin k2
a b 0.002 10 2 能出现28级完整光谱 kmax 28 . 6 2 7000 1010
sin 1 2
作业2： 6-20，6-21，6-24
6.7.3 光栅光谱(grating spectrum)(又叫衍射光谱)
I
衍射光栅公式 解释说明以及概述
衍射光栅公式解释说明以及概述1. 引言1.1 概述衍射光栅公式是一种描述光通过衍射光栅时产生的干涉和衍射现象的数学公式。
衍射光栅是一种具有规则排列的透明或不透明条纹，当入射光通过光栅时，会发生干涉和衍射现象。
这些现象在光学领域中具有重要的理论与实际应用价值。
1.2 文章结构本文将按照以下结构进行说明与探讨。
首先，在引言部分，我们将概述本文所要介绍的内容，并解释为什么这些内容对于理解和应用衍射光栅公式至关重要。
其次，在第二部分“衍射光栅公式解释说明”中，我们将详细介绍衍射现象的基本原理以及光栅的结构特点。
随后，我们将推导并解释衍射光栅公式，深入探讨其各个参数对于干涉和衍射效应的影响。
第三部分是“衍射光栅应用领域概述”，我们将阐述不同领域中利用衍射光栅的应用。
其中包括光谱分析、光学显微镜以及激光干涉仪等领域，展示衍射光栅在这些领域中所发挥的重要作用。
第四部分是“实验与结果分析”，我们将介绍设计的实验以及步骤，并详细描述数据采集与分析方法。
通过对实验结果的分析和讨论，我们将进一步验证和解释衍射光栅公式的有效性和准确性。
最后，在“结论与展望”部分，我们将总结研究成果，并提出可能的扩展研究方向，为进一步深入研究衍射光栅提供参考。
1.3 目的本文旨在全面解释与阐述衍射光栅公式，深入探讨其原理、推导过程以及应用领域。
通过本文的阅读和理解，读者将能够更好地理解与运用衍射光栅公式，并且了解到该公式在不同领域中的广泛应用和重要意义。
希望本文能够达到科普教育和引导学术研究的目标，为相关领域的研究者和学习者提供有价值的参考。
2. 衍射光栅公式解释说明:2.1 衍射现象介绍衍射是光通过物体边缘或孔径时发生偏转和扩散的现象。
它是波动性质的一种表现，当光传播过程中遇到不同介质的边界或有一定周期的结构时，会发生衍射现象。
2.2 光栅原理及结构光栅是具有平行排列的凹槽或透明间隙的光学元件。
它可以将入射光束分散成多个次级光束，并形成特定方向上干涉条纹。
衍 射 光 栅
d sin k
asin k
即 k d k a
上式表明，当光栅常数d与缝宽a之比为整数时，就会发生 缺级现象。例如，d＝4a时，在k＝±4，±8，…处的明纹将发 生缺级现象。
3.4
k取3，即最多能看到第三级条纹。
【例12-9】用白光垂直照射光栅常数为2.0×10-4cm的光栅， 求第一级光谱的张角有多大？（白光波长范围为400～760nm）
【解】第一级光谱的最小衍射角θ1由紫光决定：
s in 1
1
d
400 10 7 2.010 4
0.2
θ1≈11.54° 第一级光谱的最大衍射角θ2由红光决定：
1.1 光栅衍射条纹的形成
如下图所示，若只开放缝A，则由缝A上发出的与透镜主轴 平行的光将会聚到O点，与主轴成θ角的光将会聚到P点；若只 开放缝B，则由缝B上发出的与透镜主轴平行的光也将会聚到O 点，与主轴成θ角的光也将会聚到P点，即同方向的衍射光线在 屏上的会聚点相同。又因两缝等宽，对同一θ角，两缝分成的半 波带数相同，所以，上述两种情况中，O点和P点的光强也相同。
s in 2
2
d
760 10 7 2.010 4
0.38
θ2≈22.33° 所以，白光第一级衍射光谱的张角为：
θ2－θ1＝22.33°－11.54°＝10.79°
物理学
1.3 光栅光谱
由光栅方程式（12–36）可知，光栅常数d一定时，除中央明 纹（k＝0）外，其它各明纹的位置都与入射光的波长λ有关。当 一束平行白光垂直照射到光栅上时，中央明纹仍为白色，其余各 级中不同波长的光将产生各自分开的条纹，形成光栅的各级衍射 光谱，称为光栅光谱。
衍射光栅原理
衍射光栅原理衍射光栅是一种利用衍射现象制造的光学元件，它可以对光进行衍射，从而产生干涉条纹，广泛应用于光谱仪、激光器、光学通信等领域。
衍射光栅原理是基于光的波动性和干涉现象，下面我们将详细介绍衍射光栅的原理。
首先，衍射光栅是由一系列平行的透明条纹组成的，这些条纹可以是等宽的透明条纹，也可以是透明-不透明的周期性结构。
当入射光线照射到光栅上时，光波会受到衍射现象的影响，发生弯曲和干涉，最终形成衍射图样。
其次，衍射光栅的原理可以用赫布理论来解释。
赫布理论认为，光波通过光栅时，会被分成许多个次波，这些次波在空间中相互干涉，形成明暗相间的衍射图样。
根据赫布理论，我们可以计算出不同波长的光在衍射光栅上的衍射角度，从而实现光谱分析和波长测量。
另外，衍射光栅原理还涉及到光栅常数和衍射级数的概念。
光栅常数是指光栅上相邻两个透明条纹之间的距离，它决定了衍射光栅对入射光的衍射效果。
而衍射级数则表示在衍射图样中的明暗条纹的级数，它与光波的波长和光栅常数有关。
最后，衍射光栅原理在实际应用中具有重要意义。
通过精确控制光栅的结构和参数，可以实现对入射光的波长、偏振状态等特性的精确调控，从而广泛应用于光谱仪、激光器、光学通信等领域。
同时，衍射光栅还可以用于光学成像、光学信息处理等方面，为光学技术的发展提供了重要支持。
总之，衍射光栅原理是基于光的波动性和干涉现象，利用光栅的周期结构对光进行衍射，从而实现对光波特性的精确调控。
它在光学技术领域具有重要应用，对光学仪器的性能和功能起着关键作用。
希望通过本文的介绍，读者能够更加深入地理解衍射光栅原理，并进一步应用于实际工程中。
衍射光栅_精品文档
20
总结：极大和极小位置：
单缝衍射极大、极小位置 共同决定多缝衍射极大极小位置。
多缝干涉极大、极小位置
单缝衍射
中央极大： 0
极小： sin k
b
其它极大：sin (k 1)
2b
(k 1,2) (k 1,2)
将多光束干涉极大极小的结果列表如下：
单缝衍射极小位置
sin
k
b
b
可见光栅衍射的光强是单缝衍射图样和缝间干涉因子的乘积。 单缝衍射因子对干涉主最大起调制作用。
如右图示：相邻两缝上任一对应点到观察点P的
光程差: d sin 位相差: 2 d sin 2
a
sin 2 1 N
光强公式变为
I P A02 sin c2u
2
sin 2 1
d
θ b
θ
2、讨论：
槽面法线
B
光栅平面法线
因此，只需设法把光能集中到这一光谱上来即可。 用闪耀光栅即可解决这个问题。
35
目前在分光仪器中使用的光栅几乎都是反射式的闪 耀光栅。它的优点是：能将单缝的中央最大值的位 置从没有色散的零级光谱转移到其他有色散的光谱 级上。如图所示：
在一块玻璃板上镀一层反射 率很高的金属层，然后用钢 刀在金属层上等间隔地刻画 很密的锯齿形沟槽，即形成 了闪耀光栅。每个反射面相 对于光栅平面有一定倾角B， 称闪耀角。
j, k.
-2
-1
光栅衍射 光强曲线
0
1
2
I
单缝衍射 轮廓线
-8
-4
0
4
8
26
由上面两方程, 得： k d j. b
第级干涉主极大被 j级衍射极小调制掉
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
（ Diffraction of light） §6.8 光栅衍射 grating diffraction
衍射光栅的定义：
广义的说，任何具有空间周期性的衍射屏都可称
为衍射光栅。这些具有空间周期性的衍射屏能等宽 度、等间隔地分割入射光的波面。
物理科学与信Байду номын сангаас工程学院 1
例如在一块不透明的板上刻划出一系列等宽度又等 间距的平行狭缝。就是一种简单的一维透射式光栅。
a不透光
b透光
在一张透明胶片上因曝光而记录的一系列等宽度又 等间距的平行干涉条纹。便是一块一维的正弦光栅。 又如在一块很平的铝板上刻 上一系列等间隔的平行槽纹， 就是一块反射式光栅。
反射光栅
a b
d
物理科学与信息工程学院 2
晶体由于内部原子排列具有空间周期性而成为天然的 的三维光栅。 光栅种类很多，有透射光栅和反射光栅。有平面光栅 和凹面光栅，有黑白光栅和正弦光栅，有一维、二维和 三维光栅。 光栅的种类虽然很多但其基本原理是相似的，下面以 平面透射光栅为例讨论光栅衍射的基本原理。
~ i ( N 1) E N c a sin cu e .
物理科学与信息工程学院 9
~
于是P点的复振幅为
~ EP
n N 1 n 0
in ~ ~ c a sin cu e c a sin cu
n N 1 n 0
e
in
1 e ~ c a sin cu . i 1 e iN 2 iN 2 i ( N 1) e e ~a sin cu 2 c e i 2 i 2 e e
sin N
物理科学与信息工程学院 12
或 式中
sin u sin N I I0 . 2 2 u sin a sin d sin u , ,
2 2
光强公式中
sin 2 u 2 u 2 sin N 2 sin
称为衍射因子, 称为缝间干涉因子.
可见光栅衍射的光强是单缝衍射图样和缝间干涉因 子的乘积。单缝衍射因子对干涉主最大起调制作用。
物理科学与信息工程学院 6
但是实际上，还必须考虑由各缝发出的多光束 之间产生的干涉。
因此，如果相邻各缝间不透明部分的宽度也是严 格相等的。那么各相邻光束在叠加时有相同的相位 差，因而同时将出现多光束干涉图样，即宽大的黑 暗背景中出现明晰锐利的亮条纹。 如果照射的光是复色光，则每一波长都将产生 和它对应的细窄亮条纹。通常称为光谱线。
物理科学与信息工程学院 7
光栅有N条狭缝，缝宽为b，光栅 常数为d。 由于透镜 L2 的作用，来自不同的 狭缝的方向衍射光会聚在屏幕上同 一点，形成多光束干涉．
d
d sin
在夫琅和费远场条件下，各缝在 P 点产生的振动， 振幅相同，相位不同.相邻两缝在方向上的光程差为
d sin ,
sin u ~ ~ 2 ei ( N 1) . 所以 EP c a u sin 2 2 sin N 2 sin u ~ 2 ~ ~ 2 I EP EP EP I 0 u2 2 sin 2 d sin 2 a sin 2 sin sin N I I0 . a sin 2 2 d sin ( ) sin
物理科学与信息工程学院 8
相位差为
2
d sin .
设最上面的狭缝在P点的光振动相位为零,则各点 P点产生的复振幅分别为
~ ~ i E 2 c a sin cu e ,
~ ~ i0 E1 c a sin c u e ,
~ ~ i ( n 1) E n c a sin cu e ,
~ c a sin cu sin N sin
iN
2e
i ( N 1)
2
2
物理科学与信息工程学院 10
上式的推导中,应用了等比数列前N项和公式
a1 (1 r ) SN 1 r
N
式中
a1 1,
e e
i
r e
i
i
以及欧拉公式
2i sin .
物理科学与信息工程学院 11
2
当
k
时
(k 0, 1, 2 )
－称为光栅方程
物理科学与信息工程学院 14
即
d sin k
时,
由
sin N 2 lim N . 2 k sin
2
在满足 dsin = k 的衍射方向上， 光强为
sin u I N I0 . 2 u
2
2
在屏幕的中心
0,
sin u lim 1 , 2 0 u
2
2
光强取得最大值:
I max N I 0 .
物理科学与信息工程学院 15
主最大的数目: 由
一、实验装置
S
*
屏 幕
3
设光栅各缝的宽度都等于b，相邻两缝间不透明 部分的宽度都等于a，则相邻狭缝上对应点之间的 距离为：
d a b
－称为光栅常量（数）
它反映光栅的空间周期性，其倒数表示每毫米 内有多少条狭缝，称为光栅密度，实验室内常用 （600~1200）/mm的光栅。
物理科学与信息工程学院 4
二、光栅衍射的强度分布
L1
F1
L2
屏 幕
S
F
P
2
f1
f 2
当平行光来照射到一条细长狭缝上出现衍射图 样时，其光强分布满足 下式：
物理科学与信息工程学院 5
sin u 2 I I0 ( ) u
其中
b sin u
光屏上所有最大值和最小值的位置分布仅取决于 相应的衍射角，并不随缝的位置的改变而改变。 也就是说，当狭缝平行于自身做平动时，光屏上 出现的图样仍维持原状，并不跟着移动。 如果在平面上开了许多相互平行的同样宽度的细 长狭缝，则它们会给出与单缝同样的相互重叠的衍 射图样，各最大值都在原来位置得到相应的加强。
物理科学与信息工程学院 13
三、光栅衍射图样的主要特征 根据
sin u sin N I I0 . 2 2 u sin
2 2
可得出光栅衍射花样的主要特征是：一系列的主最 大、次最大和光强为零的条纹有规律的分布。 1. 主最大的角位置、光强和数目 由缝间干涉因子
sin N , 2 sin