第24章 圆一课一练
《第24章_圆》复习课件 上课用

.A. 点在圆内
d<r
.
点在圆上
d=rC. 点在源自外d>rB7.在Rt△ ABC中,∠C=90°,BC=3cm,AC=4cm,D 为AB的中点,E为AC的中点,以B为圆心,BC为
半径作⊙B, 问:(1)A、C、D、E与⊙B的位置关系如何?
A
1.如图,在以O为圆心的
O.
ED
B
两个同心圆中,大圆的弦 AB交小圆于C、D,则:
AC=BD
∟ ∟
O
.
C
B
若大圆的弦切小圆于C,则 AC=BC
两圆之间的环形面积 S= 1 πAB2
4
2.如图,以等腰△ABC的腰AB为直径作 ⊙O交底边BC于点D,则:
A
点D是BC的中点.
O
B DC
3.如图,已知PA、PB切圆O于点A,B, 过弧AB上任一点E作圆O的切线,交 PA,PB于点C,D,则:
A
B
•
O C
D
1. 在⊙O中,弦AB所对的圆心角∠AOB=100°,则
弦AB所对的圆周角为__5__0_0或___1_3_0_0_.(05年上海)
2.如图,AB是⊙O的直径,BD是
⊙O的弦,延长BD到点C,使
DC=BD,连接AC交⊙O与点F.
(1)AB与AC的大小有什么关
A
系?为什么?
F
(2)按角的大小分类, 请你判断
于F点,然后证明
F
DF等于圆D的半
径BD
5、如图,AB是圆O的直径,圆O过 AC的中点D,DE⊥BC于E.
证明:DE是圆O的切线.
D
A
. O
《第24章-圆》复习课件

A
B
•
O C
D
1. 在⊙O中,弦AB所对的圆心角∠AOB=100°,则
弦AB所对的圆周角为__5__0_0或___1_3_0_0_.(05年上海)
2.如图,AB是⊙O的直径,BD是
⊙O的弦,延长BD到点C,使
DC=BD,连接AC交⊙O与点F.
(1)AB与AC的大小有什么关
A
系?为什么? (2)按角的大小分类, 请你判断
F O
△ABC属于哪一类三角形,
并说明理由.(05宜昌)
B
D
C
3.如图在比赛中,甲带球向对方球门 PQ进攻,当他带球冲到A点时,同伴乙 已经助攻冲到B点,此时甲是直接射门 好,还是将球传给乙,让乙射门好?为什 么?
P
Q
·
A
B
三.与圆有关的位置关系:
1.点和圆的位置关系
(1)点在圆内 (2)点在圆上 (3)点在圆外
A
D P
C
.o
F
E
B
5 . 如 图 , 已 知 △ABC 的 三 边 长 分 别 为 AB=4cm , BC=5cm,AC=6cm,⊙O是△ABC的内切圆,切点分 别是E、F、G,则AE= ,BF= ,CG= 。
7.如图,⊙M与x 轴相交于点A(2,0),B
(8,0),与y轴相切于点C,求圆心M的坐
2.半径:正多边形外接圆的半径叫做这
个正多边形的半径.
EG
3.中心角:正多边形每一边所对的外接圆 的圆心角叫做这个正多边形的中心角.
4.边心距:中心到正多边形一边的距离 叫做这个正多边形的边心距.
C
D
四.圆中的有关计算:
1.圆的周长和面积公式
周长C=2πr 面积s=πr2
最新第24章《圆》复习课ppt课件培训讲学

所以∠OCB=90°-∠ACO=90°-70°=20°.
答案:20
主题3 切线的性质和判定 【主题训练3】(2013·昭通中考)如图,已知AB是☉O的直径,点 C,D在☉O上,点E在☉O外,∠EAC =∠B =60°. (1)求∠ADC的度数. (2)求证:AE是☉O的切线.
【自主解答】(1)∵∠B与∠ADC都是 A 所C 对的圆周角,且∠B =60°, ∴∠ADC=∠B =60°. (2)∵AB是☉O的直径, ∴∠ACB=90°, 又∠B =60°,∴∠BAC=30°, ∵∠EAC =∠B =60°, ∴∠BAE =∠BAC+∠EAC=30°+60°=90°, ∴BA⊥AE,∴AE是☉O的切线.
【主题升华】 切线的性质与判定
1.切线的判定的三种方法:(1)根据定义观察直线与圆公共点的 个数.(2)由圆心到直线的距离与半径的大小关系来判断.(3)应 用切线的判定定理.应用判定定理时,要注意仔细审题,选择合适 的证明思路:①连半径,证垂直;②作垂直,证半径.
2.切线的性质是求角的度数及垂直关系的重要依据,辅助线的作 法一般是连接切点和圆心,构造垂直关系来证明或计算.切线长 定理也为线段或角的相等提供了丰富的理论依据.
1.位置关系:(1)点与圆的位置关系;(2)直线与圆的位置关系. 2.判定方法:(1)利用到圆心的距离和半径作比较; (2)利用交点的个数判断直线与圆的位置关系.
OC=R-3;由勾股定理,得:OA2=AC2+OC2,即:R2=16+(R-3)2,解得 R=2 5 cm,所以选A.
6
【主题升华】 垂径定理及推论的四个应用
1.计算线段的长度:常利用半径、弦长的一半、圆心到弦的距离 构造直角三角形,结合勾股定理进行计算. 2.证明线段相等:根据垂径定理平分线段推导线段相等. 3.证明等弧. 4.证明垂直:根据垂径定理的推论证明线段垂直.
九年级数学上册第24章圆24.1圆的有关性质24.1.1圆24.1.2垂直于弦的直径习题课件(新版)

24.1 圆的有关性质
第二十四章 圆
圆
垂直于弦的直径
考场对接
考场对接
题型一 圆周角定理及其推论的应用
例题1 如图24-1-47, 在 ⊙O中, AC∥OB, ∠BAO=25°. 则∠BOC的度数
为(
). B
A.25°
B.50°
C.60°
D.80°
分析 ∵OA=OB, ∴∠B=∠BAO=25°.
证明.
例题4 如图24-1-50, 在 ⊙O中, C, D是直径AB上两点, 且AC=BD,
MC⊥AB, ND⊥AB, 点M, N在⊙O上.
(1)求证:AM =BN ;
(2)若C, D分别为OA, OB的中点, 则AM =MN =
NB 成立吗?请说明理由.
解 证明:如图24-1-50, 连接OM, ON.
点C, 使AC=AB. 求证:BD=CD.
证明
如图24-1-48, 连接AD.
∵AB是⊙O的直径, ∴∠ADB=90°,
即AD⊥BC.
又AC=AB, ∴BD=CD.
锦囊妙计
连弦构造直角三角形
在圆中, 遇到直径时, 可以构造直径所对的圆 周角, 遇到
90°的圆周角时, 可以作出直径, 进而得 到直角三角形, 再利用
圆内接四边形中角的“三种关系”
(1)对角互补, 即若四边形ABCD为⊙O的内 接四边形, 则
∠A+∠C=180°, ∠B+∠D=180°;
(2)四个角的和是360°, 即若四边形ABCD 为⊙O的内接四边形,
则∠A+∠B+∠C+∠D= 360°;
(3)圆内接四边形的外角等于其内对角.
D
第24章 圆单元复习1及答案.docx
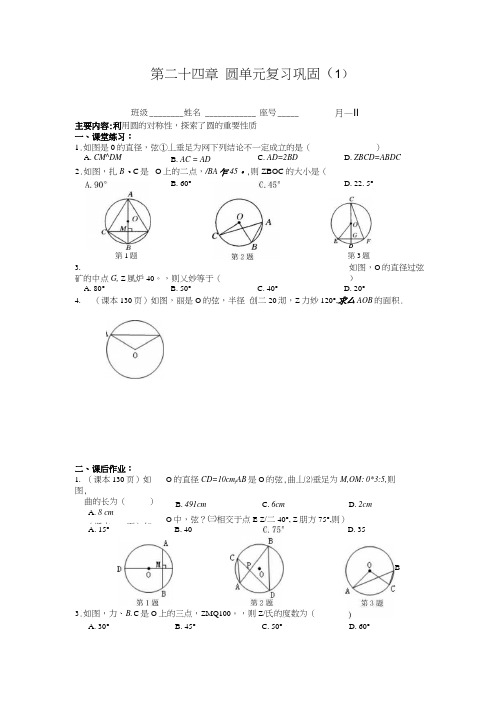
第二十四章 圆单元复习巩固(1)主要内容:利用圆的对称性,探索了圆的重要性质一、课堂练习:1.如图是0的直径,弦①丄垂足为网下列结论不一定成立的是() 3. 如图,O 的直径过弦矿的中点G, Z 風炉40。
,则乂妙等于( )4. (课本130页)如图,丽是O 的弦,半径 创二20沏,Z 力妙120°,求厶AOB 的面积.班级 ________ 姓名 ____________ 座号 _____月—II A. CM^DM B. AC = ADC. AD=2BDD. ZBCD=ABDC O 上的二点,/BA 乍45。
,则ZBOC 的大小是(B. 60° D. 22. 5°A. 80°B. 50°C. 40°D. 20°二、课后作业:1. (课本130页)如图,曲的长为( ) A. 8 cm 2. (课本130页)如O 的直径CD=10cm f AB 是O 的弦,曲丄⑵垂足为M,OM: 0*3:5,则 B. 491cm C. 6cm D. 2cm O 中,弦?㈢相交于点E Z/二40°, Z 朋方75°,则) A. 15° B. 40 3.如图,力、B. C 是O 上的三点,ZMQ100。
,则Z/氏的度数为(A. 30°B. 45°C. 50° 2.如图,扎B 、C 是 第1题 D第3题D. 35BD. 60°4.(课本130页)如K, AC = CB,D,£分别是半径%血的中点,求证:仞=处5.(课木131页)如图估计三段弧的半径的大小关系,再用圆规检验你的结论.6.(课木132页)在直径为650mm的圆柱形油槽内装入一些油以后,截面如图所示,若油面宽AB=600"“",求油的最大深度.7.(课本132页)如图,在足球比赛中,甲带球向对方球门%进攻,当他带球冲到A点时,同伴乙已经助攻冲到B点、,此时甲是直接射门好,还是将球传给乙,山乙射门好?(仅从射门角度考虑)参考答案一、课堂练习:1.如图,他是0的直径,弦G9丄肋;垂足为必下列结论不一定成立的是(C )4.(课本130页)如S, AC = CB,D, E 分别是半径创、血的中点,求证:血二宓 证明:连接%I AC = CB:.ACOD^ACOE•:D 、E 分别是半径创、加的中点B. AC = ADC. AD^IBDD. ^BCL^ABDC 2.如图B 、C 是O 上的三点,Z 场745°,则Z/加的大小是( A. 90°B. 603.如图,O 的直径 仞过弦EF 的中点G, Z 仅炉40°,则等于(D )A. 80°B. 50°C. 40°D. 20°4.(课本130页)如图,曲是O 的弦,半径OA=20cm, "03=120。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
新世纪教育网 www.xsjjyw.com 精品资料 版权所有@新世纪教育网 新世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@新世纪教育网 1 人教版数学第二十四章圆经典训练题 24.1 圆 一、选择题. 1.如图1,如果AB为⊙O的直径,弦CD⊥AB,垂足为E, 那么下列结论中,•错误的是( ).
A.CE=DE B.BCBD C.∠BAC=∠BAD D.AC>AD
BA
CED
O
BA
O
M BA
C
DPO
(1) (2) (3) 2.如图2,⊙O的直径为10,圆心O到弦AB的距离OM的长为3,则弦AB的长是( ) A.4 B.6 C.7 D.8
3.如图3,在⊙O中,P是弦AB的中点,CD是过点P的直径,•则下列结论中不正确的是( )
A.AB⊥CD B.∠AOB=4∠ACD C.ADBD D.PO=PD
二、填空题 1.如图4,AB为⊙O直径,E是BC中点,OE交BC于点D,BD=3,AB=10,则AC=_____.
BA
CED
O
BAC
E
DOF (4) (5) 2.P为⊙O内一点,OP=3cm,⊙O半径为5cm,则经过P点的最短弦长为________;•最长弦长为_______.
3.如图5,OE、OF分别为⊙O的弦AB、CD的弦心距,如果OE=OF, 新世纪教育网 www.xsjjyw.com 精品资料 版权所有@新世纪教育网 新世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@新世纪教育网 2 那么_______________(只需写一个正确的结论) 三、综合提高题 1.如图24-11,AB为⊙O的直径,CD为弦,过C、D分别作CN⊥CD、DM•⊥CD,•分别交AB于N、M,请问图中的AN与BM是否相等,说明理由.
BACD
ON
M
2.如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长. BAC
E
DO
3.(开放题)AB是⊙O的直径,AC、AD是⊙O的两弦,已知AB=16,AC=8,AD=•8,•求∠DAC的度数. 新世纪教育网 www.xsjjyw.com 精品资料 版权所有@新世纪教育网
新世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@新世纪教育网 3 新课 标 第 一网24.1 圆(第2课时) 一、选择题. 1.如果两个圆心角相等,那么( ) A.这两个圆心角所对的弦相等; B.这两个圆心角所对的弧相等 C.这两个圆心角所对的弦的弦心距相等; D.以上说法都不对
2.在同圆中,圆心角∠AOB=2∠COD,则两条弧AB与CD关系是( ) A.AB=2CD B.AB>CD C.AB<2CD D.不能确定
3.如图5,⊙O中,如果AB=2AC,那么( ). A.AB=AC B.AB=AC C.AB<2AC D.AB>2AC
OB
AC OBA
CE
D 二、填空题 1.交通工具上的轮子都是做圆的,这是运用了圆的性质中的__________________.
2.一条弦长恰好为半径长,则此弦所对的弧是半圆的__________________. 3.如图6,AB和DE是⊙O的直径,弦AC∥DE,若弦BE=3,则弦CE=________. 三、解答题 1.如图,在⊙O中,C、D是直径AB上两点,且AC=BD,MC⊥AB,ND⊥AB,M、N•在⊙O上.
(1)求证:AM=BN;
(2)若C、D分别为OA、OB中点,则AMMNNB成立吗?
OBACD
www.czsx.com.cn
NM新世纪教育网 www.xsjjyw.com 精品资料 版权所有@新世纪教育网 新世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@新世纪教育网 4 2.如图,以ABCD的顶点A为圆心,AB为半径作圆,分别交BC、AD于E、F,若∠D=50°,求BE的度数和EF的度数.
3.如图,∠AOB=90°,C、D是AB三等分点,AB分别交OC、OD于点E、F,求证:AE=BF=CD.
BACE
D
www.czsx.com.cnF
OB
AC
ED
www.czsx.com.cnF新世纪教育网 www.xsjjyw.com 精品资料 版权所有@新世纪教育网
新世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@新世纪教育网 5 OBACD
21
4
3
24.1 圆(第3课时)
一、选择题 1.如图1,A、B、C三点在⊙O上,∠AOC=100°,则∠ABC等于( ). A.140° B.110° C.120° D.130°
(1) (2) (3)
2.如图2,∠1、∠2、∠3、∠4的大小关系是( ) A.∠4<∠1<∠2<∠3 B.∠4<∠1=∠3<∠2 C.∠4<∠1<∠3∠2 D.∠4<∠1<∠3=∠2
3.如图3,AD是⊙O的直径,AC是弦,OB⊥AD,若OB=5,且∠CAD=30°,则BC等于( ).
A.3 B.3+3 C.5-123 D.5 二、填空题 1.半径为2a的⊙O中,弦AB的长为23a,则弦AB所对的圆周角的度数是________.
2.如图4,A、B是⊙O的直径,C、D、E都是圆上的点,则∠1+∠2=_______.•
OBA
C21
E
D OBACwww.czsx.com.cn (4) (5)
3.如图5,已知△ABC为⊙O内接三角形,BC=•1,•∠A=•60•°,•则⊙O•半径为_______.
OBA
Cwww.czsx.com.cn新世纪教育网 www.xsjjyw.com 精品资料 版权所有@新世纪教育网
新世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@新世纪教育网 6
三、综合提高题 1.如图,弦AB把圆周分成1:2的两部分,已知⊙O半径为1,求弦长AB.
OBA
2.如图,已知AB=AC,∠APC=60° (1)求证:△ABC是等边三角形. (2)若BC=4cm,求⊙O的面积.
OB
ACP
3.如图,⊙C经过坐标原点,且与两坐标轴分别交于点A与点B,点A的坐标为(0,4),M是圆上一点,∠BMO=120°. (1)求证:AB为⊙C直径. (2)求⊙C的半径及圆心C的坐标.
OB
AC
y
xM新世纪教育网 www.xsjjyw.com 精品资料 版权所有@新世纪教育网
新世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@新世纪教育网 7 24.2 与圆有关的位置关系(第1课时) 一、选择题. 1.下列说法:①三点确定一个圆;②三角形有且只有一个外接圆;•③圆有且只有一个内接三角形;④三角形的外心是各边垂直平分线的交点;⑤三角形的外心到三角形三边的距离相等;⑥等腰三角形的外心一定在这个三角形内,其中正确的个数有(• ) A.1 B.2 C.3 D.4
2.如图,Rt△ABC,∠C=90°,AC=3cm,BC=4cm,则它的外心与顶点C的距离为( ). A.2.5 B.2.5cm C.3cm D.4cm
3.如图,△ABC内接于⊙O,AB是直径,BC=4,AC=3,CD平分∠ACB,则弦AD长为( )
A.522 B.52 C.2 D.3 二、填空题. 1.经过一点P可以作_______个圆;经过两点P、Q可以作________•个圆,•圆心在_________上;经过不在同一直线上的三个点可以作________个圆,•圆心是________的交点.
2.边长为a的等边三角形外接圆半径为_______,圆心到边的距离为________. 3.直角三角形的外心是______的中点,锐角三角形外心在三角形______,钝角三角形外心在三角形_________. 三、综合提高题. 1.如图,通过防治“非典”,人们增强了卫生意识,大街随地乱扔生活垃圾的人少了,人们自觉地将生活垃圾倒入垃圾桶中,如图24-49所示,A、B、C•为市内的三个住宅小区,环保公司要建一垃圾回收站,为方便起见,•要使得回收站建在三个小区都相等的某处,请问如果你是工程师,你将如何选址.
. . .
BACDOBAC
