【数学】1.1《关于“球”的常见问题》教案(新人教A版必修2)
新课标人教A版数学必修2教案完整版

新课标人教A版数学必修2教案完整版第一章:空间几何体1.1.1柱、锥、台、球的结构特征一、教学目标1.知识与技能(1)通过实物操作,增强学生的直观感知。
(2)能根据几何结构特征对空间物体进行分类。
(3)会用语言概述棱柱、棱锥、圆柱、圆锥、棱台、圆台、球的结构特征。
(4)会表示有关于几何体以及柱、锥、台的分类。
2.过程与方法(1)让学生通过直观感受空间物体,从实物中概括出柱、锥、台、球的几何结构特征。
(2)让学生观察、讨论、归纳、概括所学的知识。
3.情感态度与价值观(1)使学生感受空间几何体存在于现实生活周围,增强学生学习的积极性,同时提高学生的观察能力。
(2)培养学生的空间想象能力和抽象括能力。
二、教学重点、难点重点:让学生感受大量空间实物及模型、概括出柱、锥、台、球的结构特征。
难点:柱、锥、台、球的结构特征的概括。
三、教学用具(1)学法:观察、思考、交流、讨论、概括。
(2)实物模型、投影仪四、教学思路(一)创设情景,揭示课题1.教师提出问题:在我们生活周围中有不少有特色的建筑物,你能举出一些例子吗?这些建筑的几何结构特征如何?引导学生回忆,举例和相互交流。
教师对学生的活动及时给予评价。
2.所举的建筑物基本上都是由这些几何体组合而成的,(展示具有柱、锥、台、球结构特征的空间物体),你能通过观察。
根据某种标准对这些空间物体进行分类吗?这是我们所要学习的内容。
(二)、研探新知1.引导学生观察物体、思考、交流、讨论,对物体进行分类,分辩棱柱、圆柱、棱锥。
2.观察棱柱的几何物件以及投影出棱柱的图片,它们各自的特点是什么?它们的共同特点是什么?3.组织学生分组讨论,每小组选出一名同学发表本组讨论结果。
在此基础上得出棱柱的主要结构特征。
(1)有两个面互相平行;(2)其余各面都是平行四边形;(3)每相邻两上四边形的公共边互相平行。
概括出棱柱的概念。
4.教师与学生结合图形共同得出棱柱相关概念以及棱柱的表示。
5.提出问题:各种这样的棱柱,主要有什么不同?可不可以根据不同对棱柱分类?请列举身边具有已学过的几何结构特征的物体,并说出组成这些物体的几何结构特征?它们由哪些基本几何体组成的?6.以类似的方法,让学生思考、讨论、概括出棱锥、棱台的结构特征,并得出相关的概念,分类以及表示。
高中数学1.3.2球的体积与表面积教案新人教A版必修2

必修2第1章第3节《球的体积和表面积》第1课时教学设计【课标解读】由于球的体积和表面积公式在推导证明上比较繁琐,先生在理解掌握上也比较困难,根据新的《数学课程标准》要求,本节的公式证明和推导应淡化处理,只需让先生简单了解推导过程,领会其中所包含的数学思想和方法,和它们在后续学习中的作用,不要求先生掌握其证明。
在球的体积和表面积公式运用和球与几何体组合体的求解过程中,进步先生的空间想象、抽象概括、推理论证、运算求解、数据处理等基本能力。
经过运用预设和相应的运用练习进步先生的提出、分析和解决成绩(包括简单的理论成绩)的能力,利用先生身旁熟知的成绩预设进步先生学习数学的兴味,建立学好数学的决心,进而构成锲而不舍的研讨精神和科学态度。
【教材分析】本节课是人教A版高中数学(课程标准实验教材)必修2第一章“空间几何体”第三节“球的体积和表面积”,是在学习了柱体、锥体、台体等基本几何体的基础上,经过空间度量方式了解另一种基本几何体的结构特点。
从知识上讲,球是一种高度对称的基本空间几何体,同时它也是进一步研讨空间组合体结构特点的基础;从方法上讲,它为我们提供了另外一种求空间几何体体积和表面积的思想方法;从教材编排上,更注重先生的直观感知和操作确认,为螺旋式上升的学习奠定了基础。
【学情分析】先生刚学习立体几何不久,具备的图形言语表达及空间想象能力绝对不足,几何体的内切球、外接球的地位关系较难想象,很难顺利作出正确的直观图,空间图构成绩向平面图构成绩的转化认识也不够,对于解决组合体的体积和表面积的成绩有必然的困难,而且先生的归纳总结能力不够,独立完成自主学习任务有必然困难,还不能从必然高度去体会和感悟数学思想。
这些都是摆在先生面前的难题,也是教学中迫切需求解决的成绩。
【教学目标】1.掌握球的体积、表面积公式及其运用。
2会用球的表面积公式、体积公式解决相关成绩,培养先生运用数学的能力,发展逻辑思想能力,加强辩证唯物主义观点。
2015高中数学1.1.1柱、锥、台、球的结构特征学案新人教A版必修2
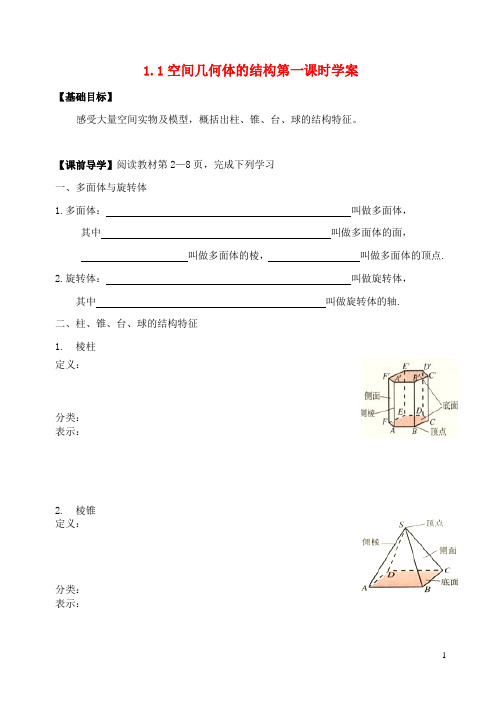
1.1空间几何体的结构第一课时学案
【基础目标】
感受大量空间实物及模型,概括出柱、锥、台、球的结构特征。
【课前导学】阅读教材第2—8页,完成下列学习
一、多面体与旋转体
1.多面体:叫做多面体,
其中叫做多面体的面,
叫做多面体的棱,叫做多面体的顶点.
2.旋转体:叫做旋转体,
其中叫做旋转体的轴.
二、柱、锥、台、球的结构特征
1.棱柱
定义:
分类:
表示:
2.棱锥
定义:
分类:
表示:
3.棱台定义:.
分类:表示:
4.圆柱定义:
表示:
5. 圆锥
定义:表示:
6.圆台定义:
表示:
7.球
定义:
.
表示:
【基础自测】
1.下列命题中正确的是()
A.由五个平面围成的多面体一定是四棱锥
B.棱锥的高线可能在几何体之外
C.仅有一组对面平行的六面体是棱台
D.有一个面是多边形,其余各面是三角形的几何体是棱锥
2.下列命题中正确的是()
A.有两个面平行,其余各面都是四边形的几何体叫棱柱
B.有两个面平行,其余各面都是平行四边形的几何体叫棱柱
C.有两个面平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行的几何体是棱柱
D.用一个平面去截棱锥,底面与截面之间的部分组成的几何体叫棱台
3.直角三角形绕其一边旋转一周所形成的几何体是否是圆锥?。
高中数学 第一章球的体积和表面积导学案 新人教A版必修2推荐

1.3.2 球的体积和表面积 问题导学 一、球的表面积与体积 活动与探究1 (1)已知球的直径为8 cm,求它的表面积和体积; (2)已知球的表面积为144π,求它的体积;
(3)已知球的体积为5003π,求它的表面积. 迁移与应用 1.两个球的体积之比为1∶27,那么两个球的表面积之比为( ) A.1∶9 B.1∶27 C.1∶3 D.1∶1 2.三个球的半径比是1∶2∶3,那么最大球的体积是其余两球体积和的( ) A.1倍 B.2倍 C.3倍 D.8倍
(1)与球的体积、表面积有关的问题就是与球的半径有关的问题,设出球的半径或求出球的半径,一切问题都迎刃而解. (2)两个球的表面积之比等于这两个球的半径之比的平方,两个球的体积之比等于这两个球的半径之比的立方. 二、球的截面问题 活动与探究2 已知球的两平行截面的面积为5π和8π,它们位于球心的同一侧,且相距为1,求这个球的表面积和体积. 迁移与应用
已知过球面上三点A,B,C的截面到球心的距离等于球半径的32倍,且AC=8,BC=6,AB=10,求球的表面积与球的体积.
设球的截面圆上一点A,球心为O,截面圆心为O1,则△AO1O是以O1为直角顶点的直角三角形,解答球的截面问题时,常用该直角三角形求解,并常用过球心和截面圆心的轴截面. 三、有关几何体的外接球与内切球 活动与探究3 有三个球,第一个球内切于正方体;第二个球与这个正方体各条棱相切,第三个球过这个正方体的各个顶点,求这三个球的表面积之比. 迁移与应用 1.长方体的一个顶点上三条棱的长分别为3,4,5,且它的八个顶点都在同一个球面上,求这个球的表面积. 2.在球面上有四个点A,B,C,P,且PA,PB,PC两两垂直,PA=a,PB=2a,PC=a.求球的体积.
(1)球内接长方体的体对角线长等于球的直径. (2)注意“迁移与应用2”的解法:补形法的应用,即遇到类似问题时,可补形为一个长方体,利用长方体的外接球求解. 当堂检测 1.把球的表面积扩大到原来的2倍,那么体积扩大到原来的( ) A.2倍 B.22倍 C.2倍 D.32倍 2.设正方体的表面积为24 cm2,一个球内切于该正方体,那么这个球的体积是( ) A.6π cm3 B.6 cm3
高中数学第一章.2球的体积和表面积学案含解析新人教A版必修01

1.3.2 球的体积和表面积球的体积和表面积[提出问题]从生活经验中我们知道,不能将橘子皮展成平面,因为橘子皮近似于球面,这种曲面不能展成平面图形.那么,人们又是怎样计算球面的面积的呢?古人在计算圆周率时,一般是用割圆术,即用圆的内接或外切正多边形来逼近圆的周长.理论上,只要取得圆内接正多边形的边数越多,圆周率越精确,直到无穷.这种思想就是朴素的极限思想.问题1:运用上述思想能否计算球的表面积和体积? 提示:可以.问题2:求球的表面积和体积需要什么条件? 提示:已知球的半径即可. [导入新知] 1.球的体积设球的半径为R ,则球的体积V =43πR 3.2.球的表面积设球的半径为R ,则球的表面积S =4πR 2,即球的表面积等于它的大圆面积的4倍. [化解疑难] 1.一个关键把握住球的表面积公式S 球=4πR 2,球的体积公式V 球=43πR 3是计算球的表面积和体积的关键,半径与球心是确定球的条件.把握住公式,球的体积与表面积计算的相关题目也就迎刃而解了.2.两个结论(1)两个球的体积之比等于这两个球的半径之比的立方. (2)两个球的表面积之比等于这两个球的半径之比的平方.球的体积与表面积[例1] 求圆锥侧面积与球面面积之比.[解] 设圆锥的底面半径为r ,高为h ,母线长为l ,球的半径为R , 则由题意得⎩⎪⎨⎪⎧13πr 2·h =43πR 3,r =2R .∴13π(2R )2·h =43πR 3,∴R =h ,r =2h , ∴l =r 2+h 2= 5h ,∴S 圆锥侧=πrl =π×2h ×5h =25πh 2,S 球=4πR 2=4πh 2,∴S 圆锥侧S 球=25πh 24πh 2=52. [类题通法]求球的体积与表面积的方法(1)要求球的体积或表面积,必须知道半径R 或者通过条件能求出半径R ,然后代入体积或表面积公式求解.(2)半径和球心是球的最关键要素,把握住了这两点,计算球的表面积或体积的相关题目也就易如反掌了.[活学活用]球的体积是32π3,则此球的表面积是( )A .12πB .16π C.16π3D.64π3答案:B根据三视图计算球的体积与表面积[例2] 表面积是________cm 2.[答案] 4π+12 [类题通法]1.由三视图计算球或球与其他几何体的组合体的表面积或体积,最重要的是还原组合体,并弄清组合体的结构特征和三视图中数据的含义.根据球与球的组合体的结构特征及数据计算其表面积或体积.此时要特别注意球的三种视图都是直径相同的圆.2.计算球与球的组合体的表面积与体积时要恰当地分割与拼接,避免重叠和交叉.[活学活用]如图是一个几何体的三视图,根据图中的数据可得该几何体的表面积为( )A.18πB.30πC.33πD.40π答案:C球的截面问题[例3] 且相距为1,求这个球的表面积.[解] 如图所示,设以r1为半径的截面面积为5π,以r2为半径的截面面积为8π,O1O2=1,球的半径为R,OO2=x,那么可得下列关系式:r22=R2-x2且πr22=π(R2-x2)=8π,r21=R2-(x+1)2且πr21=π[R2-(x+1)2]=5π,于是π(R2-x2)-π[R2-(x+1)2]=8π-5π,即R2-x2-R2+x2+2x+1=3,∴2x=2,即x=1.又∵π(R2-x2)=8π,∴R2-1=8,R2=9,∴R=3.球的表面积为S=4πR2=4π×32=36π.[类题通法]球的截面问题的解题技巧(1)有关球的截面问题,常画出过球心的截面圆,将问题转化为平面中圆的问题.(2)解题时要注意借助球半径R,截面圆半径r,球心到截面的距离d构成的直角三角形,即R2=d2+r2.[活学活用]已知过球面上三点A,B,C的截面到球心的距离等于球半径的一半,且AC=BC=6,AB =4,求球的表面积与球的体积.解:如图,设球心为O,球半径为R,作OO1垂直平面ABC于O1,由于OA=OB=OC=R,则O1是△ABC的外心.设M是AB的中点,由于AC=BC,则O1在CM上.设O 1M =x ,易知O 1M ⊥AB ,设O 1A =22+x 2,O 1C =CM -O 1M =62-22-x .又O 1A =O 1C ,∴22+x 2=62-22-x . 解得x =724.则O 1A =O 1B =O 1C =924.在Rt △OO 1A 中,O 1O =R 2,∠OO 1A =90°,OA =R .由勾股定理得⎝ ⎛⎭⎪⎫R 22+⎝ ⎛⎭⎪⎫9242=R 2.解得R =362. 故S 球=4πR 2=54π,V 球=43πR 3=276π.1.探究与球有关的组合问题[典例] 一个长方体的各个顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为1,2,3,则此球的表面积为________.[解析] 长方体外接球直径长等于长方体体对角线长,即2R =12+22+32=14,所以球的表面积S =4πR 2=14π.[答案] 14π [多维探究]1.球的内接正方体问题若棱长为2的正方体的各个顶点均在同一球面上,求此球的体积. 解:正方体的外接球直径等于正方体的对角线长, 即2R =3×2,所以R =3, 所以V 球=43·π·(3)3=43π.2.球内切于正方体问题将棱长为2的正方体木块削成一个体积最大的球,则该球的体积为( ) A.4π3 B.2π3 C.3π2D.π6答案:A3.球的内接正四面体问题若棱长为a 的正四面体的各个顶点都在半径为R 的球面上,求球的表面积. 解:把正四面体放在正方体中, 设正方体棱长为x ,则a =2x , 由题意2R=3x =3×2a 2=62a , ∴S 球=4πR 2=64a π=32a π.4.球的内接圆锥问题球的一个内接圆锥满足:球心到该圆锥底面的距离是球半径的一半,则该圆锥的体积和此球体积的比值为________.解析:①当圆锥顶点与底面在球心两侧时,如图所示,设球半径为r ,则球心到该圆锥底面的距离是r2,于是圆锥的底面半径为r 2-⎝ ⎛⎭⎪⎫r 22=3r 2,高为3r 2.该圆锥的体积为13×π×⎝ ⎛⎭⎪⎫3r 22×3r 2=38πr 3,球体积为43πr 3,∴该圆锥的体积和此球体积的比值为38πr 343πr 3=932.②同理,当圆锥顶点与底面在球心同侧时,该圆锥的体积和此球体积的比值为332. 答案:932或3325.球的内接直棱柱问题设三棱柱的侧棱垂直于底面,所有棱的长都为a ,顶点都在一个球面上,则该球的表面积为( )A .πa 2B.73πa 2C.113πa 2D .5πa 2答案:B[方法感悟] 1.正方体的内切球球与正方体的六个面都相切,称球为正方体的内切球,此时球的半径为r 1=a2,过在一个平面上的四个切点作截面,如图(1).2.球与正方体的各条棱相切球与正方体的各条棱相切于各棱的中点,过球心作正方体的对角面有r 2=2a2,如图(2). 3.长方体的外接球长方体的八个顶点都在球面上,称球为长方体的外接球,根据球的定义可知,长方体的体对角线是球的直径,若长方体过同一顶点的三条棱长为a ,b ,c ,则过球心作长方体的对角面有球的半径为r 3=12a 2+b 2+c 2,如图(3).4.正方体的外接球正方体棱长a 与外接球半径R 的关系为2R =3a . 5.正四面体的外接球正四面体的棱长a 与外接球半径R 的关系为:2R =62a .[随堂即时演练]1.两个球的半径之比为1∶3,那么两个球的表面积之比为( )A .1∶9B .1∶27C .1∶3D .1∶1答案:A2.棱长为2的正方体的外接球的表面积是( ) A .8π B .4π C .12π D .16π 答案:C3.火星的半径约是地球半径的一半,则地球的体积是火星体积的________倍.答案:84.已知OA 为球O 的半径,过OA 的中点M 且垂直于OA 的平面截球面得到圆M .若圆M 的面积为3π,则球O 的表面积等于________.答案:16π5.(1)已知球的直径为2,求它的表面积和体积. (2)已知球的体积为36π,求它的表面积. 答案:(1)表面积:4π,体积:43π. (2)36π.[课时达标检测]一、选择题1.两个球的体积之比为8∶27,那么这两个球的表面积之比为( ) A .2∶3 B .4∶9 C.2∶ 3 D.8∶27答案:B2.设长方体的长、宽、高分别为2a ,a ,a ,其顶点都在一个球面上,则该球的表面积为( )A .3πa 2B .6πa 2C .12πa 2D .24πa 2答案:B3.如果一个球的外切圆锥的高是这个球的半径的3倍,则圆锥的侧面面积和球的表面积之比为( )A .4∶3B .3∶1C .3∶2D .9∶4答案:C4.(全国乙卷)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是28π3,则它的表面积是( )A .17πB .18πC .20πD .28π答案:A5.(山东高考)一个由半球和四棱锥组成的几何体,其三视图如图所示,则该几何体的体积为( )A.13+23π B.13+23π C.13+26π D .1+26π 答案:C 二、填空题6.圆柱形容器的内壁底半径是10 cm ,有一个实心铁球浸没于容器的水中,若取出这个铁球,测得容器的水面下降了53cm ,则这个铁球的表面积为________ cm 2.答案:100π7.正四棱锥的顶点都在同一球面上.若该棱锥的高为4,底面边长为2,则该球的表面积为________.答案:814π8.(天津高考)一个几何体的三视图如图所示(单位:m),则该几何体的体积为________m 3.答案:18+9π 三、解答题9.某组合体的直观图如图所示,它的中间为圆柱形,左右两端均为半球形,若图中r =1,l =3,试求该组合体的表面积和体积.解:该组合体的表面积S =4πr 2+2πrl =4π×12+2π×1×3=10π,该组合体的体积V =43πr 3+πr 2l =43π×13+π×12×3=13π3.10.用两个平行平面去截半径为R 的球面,两个截面圆的半径为r 1=24 cm ,r 2=15 cm ,两截面间的距离为d =27 cm ,求球的表面积.解:设垂直于截面的大圆面交两截面圆于A 1B 1,A 2B 2,上述大圆的垂直于A 1B 1的直径交两截面圆于O 1,O 2,设球心到两截面的距离分别为d 1,d 2,则⎩⎪⎨⎪⎧d 1+d 2=27, ①d 21+242=R 2, ②d 22+152=R 2, ③解得R =25.当|d 1-d 2|=27时,其与②③组成的方程组无解. ∴S 球=4πR 2=2 500π(cm 2).。
【高中数学】立体几何中外接球内切球 专题课件 高一下学期数学人教A版(2019)必修第二册

答案 A 解析 由已知, 2R 12 12 ( 2)2 2 , S球 4 R2 4 π.
(4)在正三棱锥 S-ABC 中,M,N 分别是棱 SC,BC 的中点,
且 AM MN ,若侧棱 SA 2 3 ,则正三棱锥 S-ABC 外接球的表面
积是________.
2
空间几何体的外接球与内切球十大模型
1.墙角模型; 2.对棱相等模型; 3.汉堡模型; 4.垂面模型; 5.切瓜模型; 6.斗笠模型; 7.鳄鱼模型; 8.已知球心或球半径模型; 9.最值模型; 10.内切球模型.
3
一、墙角模型 墙角模型是三棱锥有一条侧棱垂直于底面且底面是直角三角形模
型,用构造法(构造长方体)解决.外接球的直径等于长方体的体对角线 长(在长方体的同一顶点的三条棱长分别为 a,b,c,外接球的半径为 R, 则 2R= a2+b2+c2.),秒杀公式:R2=a2+b2+c2。可求出球的半径
4
2
7a 2
7
, a 2
.在正四面体
A BCD 的边长为 2,外接球的半径 R
6a 4
6
2 ,外接球的体积
V 4 R3
3
6 .
12
(5) 已 知 三 棱 锥 A BCD , 三 组 对 棱 两 两 相 等 , 且
AB CD 1 , AD BC 3 ,若三棱锥 A BCD 的外接球表面
足为 BC 的中点 M.又 AM=12BC=52,OM=12AA1=6,
所以球 O 的半径 R=OA=
5 2
2+62=13. 2
另解 过 C 点作 AB 的平行线,过 B 点作 AC 的
平行线,交点为 D,同理过 C1 作 A1B1 的平行线,过 B1 作 A1C1 的 平行线,交点为 D1,连接 DD1,则 ABCD-A1B1C1D1 恰好成为球
高中数学教案之高数学人教版必修二球的表面积和体积
高一数学必修二教案科目:数学课题§1.3.2球的表面积和体积课型新课教学目标(1)了解球的表面积与体积公式(不要求记忆公式).(2)培养学生空间想象能力和思维能力.(3)通过作轴截面,寻找旋转体类组合体中量与量之间的关系.(4)让学生更好地认识空间几何体的结构特征,培养学生学习的兴趣.教学过程教学内容备注一、自主学习1.柱体、锥体、台体的体积公式分别是什么圆柱、圆锥、圆台的表面积公式分别是什么2.球是一个旋转体,它也有表面积和体积,怎样求一个球的表面积和体积也就成为我们学习的内容.二、质疑提问思考1:从球的结构特征分析,球的大小由哪个量所确定思考2:底面半径和高都为R的圆柱和圆锥的体积分别是什么思考3:如图,对一个半径为R的半球,其体积与上述圆柱和圆锥的体积有何大小关系思考4:根据上述圆柱、圆锥的体积,你猜想半球的体积是什么思考5:由上述猜想可知,半径为R的球的体积334Rπ=球V,这是一个正确的结论,你能提出一些证明思路吗祖暅原理幂势既同,则积不容异夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等.三、问题探究思考1:半径为r的圆面积公式是什么它是怎样得出来的思考2:把球面任意分割成n个“小球面片”,它们的面积之和等于什么思考3:以这些“小球面片”为底,球心为顶点的“小锥体”近似地看成棱锥,那么这些小棱锥的底面积和高近似地等于什么它们的体积之和近似地等于什么思考4:你能由此推导出半径为R的球的表面积公式吗思考5:经过球心的截面圆面积是什么它与球的表面积有什么关系球的表面积等于球的大圆面积的4倍例1:如图,圆柱的底面直径与高都等于球的直径,求证:(1)球的体积等于圆柱体积的;(2)球的表面积等于圆柱的侧面积.例2:已知正方体的八个顶点都在球O的球面上,且正方体的表面积为a2,求球O的表面积和体积.例3:有一种空心钢球,质量为142g(钢的密度为cm3),测得其外径为5cm,求它的内径(精确到).四、课堂检测将一个气球的半径扩大1倍,它的体积扩大到原来的几倍已知A、B、C为球面上三点,AC=BC=6,AB=4,球心O与△ABC的外心M的距离等于球半径的一半,求这个球的表面积和体积.五、小结评价本节课主要学习了球的体积和球的表面积公式的推导,以及利用公式解决相关的球的问题。
球的表面积和体积(第2课时) 课件-高中数学人教A版(2019)必修第二册
64
B.
3
C.32
).
32
D.
3
答案:D.
解:设球的半径为,则由题意可知42 = 16,故 = 2.
4
3
所以球的体积 = 3 =
32
.故选D.
3
练习
例1.(2)已知球的体积为
500
,则它的表面积为_____.
3
答案:100.
4
解:设球的半径为,由已知得 3
如图所示.在∆1 中,1 = 5 ,1 = 2 ,
∴球的半径 = =
4
3
22 + ( 5)2 = 3(),
∴球的体积 = × 33 = 36(3 ).故选B.
练习
例2.(2)已知一个球内有相距9 的两个平行截面,它们的面积分别为49 2 和
性质知1 //2 ,且1 ,2 为两截面圆的圆心,则1 ⊥ 1 ,
2 ⊥ 2 .设球的半径为,
∵ ∙ 2 2 = 49,∴2 = 7 .同理,得1 = 20 .
设1 = ,则2 = (9−) .
在∆1 中,2 = 2 + 400.在∆2 中,2 = (9−)2 +49,
2
=
3
,
3
=
1
,所以球的半径
2
3
1
7 2
2
2
) +( ) = ,故球
3
2
12
=
42
=
= 满足
7
2 .故选B.
3
练习
例3.(2)球的一个内接圆锥满足:球心到该圆锥底面的距离是球半径的一半,则该
圆锥的体积和此球体积的比值为________.
高中数学:.2《球的表面积和体积》【新人教A版必修2】PPT完美课件
高中数学:.2《球的表面积和体积》 【新人 教A版必 修2】P PT完美 课件
高中数学:.2《球的表面积和体积》 【新人 教A版必 修2】P PT完美 课件
球的表面积
第 一 步: 分 割
高中数学:.2《球的表面积和体积》 【新人 教A版必 修2】P PT完美 课件
高中数学:.2《球的表面积和体积》 【新人 教A版必 修2】P PT完美 课件
•
1应该认识到,阅读是学校教育的重要 组成部 分,一 个孩子 如果在 十多年 的教育 历程中 没有养 成阅读 的习惯 、兴趣 和能力 ,一旦 离开校 园,很 可能把 书永远 丢弃在 一边, 这样的 结果一 定是我 们所有 的教育 工作者 不想看 到的。
•
10保尔身上的人格特征或完美的精神 操守: 自我献 身的精 神、坚 定不移 的信念 、顽强 坚韧的 意志
•
11把记叙、描写、抒情和议论有机地 融合为 一体, 充满诗 情画意 。如描 写百草 园的景 致,绘 声绘色 ,令人 神往。
•
12简·爱人生追求有两个基本旋律:富 有激情 、幻想 、反抗 和坚持 不懈的 精神; 对人间 自由幸 福的渴 望和对 更高精 神境界 的追求 。
温故知新
回顾圆面积公式的推导
n=6
O
假设将圆n等分,则
A1
n=12 An
A2 S 正多 S A 1 O 边 2 A S 形 A 2 O 3 A S A n O 1
1 2p(A 1A2A2A3 AnA 1) 1
2 pC正多边形
O
当 n 时 p , R ,C 正多 边 C 圆形
p A3 A1 A2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【关于“球”的常见问题】
常见问题1: 问题:怎样把圆和球的主要性质进行对照?
解答:
答:
圆的主要性质球的主要性质
1 平面内与定点距离等于定长的点集
(轨迹)
空间与定点距离等于定长的点集(轨迹)
2 同圆(或等圆)的半径相等,直径是半径的2倍同球(或等球)的半径相等,直径是半径的2倍
3 与弦垂直的直径过弦的中点,圆半径2=圆心到弦距
离2+弦长的一半2与截面积垂直的直径过截面圆的圆心,球半径2=球心到截面圆距离2+截面圆的半径2
4 不过圆心的弦小于直径;经过圆心的弦是直径,是
最大的弦不过球心的截得的是球的小圆,其半径和面积都小于球的大圆的半径和面积;经过球心的截面截得的是球的大圆,是最大的截面圆
5 过切点的圆半径垂直于圆的切线过切点的球半径垂直于球的切面[注]
6 圆周长=2π×圆半径
圆面积==π×圆半径2大圆周长=2π×球半径球面积=4π×球半径2
球体积=
[注] 与球面只有一个公共点的平面叫做球的切面,这个公共点叫做切点。
类似的,与球面只有一个公共点的直线叫做球的切线,这个公共点也叫做切点。
球的切线有以下主要性质:
1. 过切点的球半径垂直于球的切线;
2. 过球面上一点的切线有无限多条,这些切线都在这一点的球的切面内。
常见问题2: 球
问题:
地球半径为R ,A 、B 两地都在北纬45°线上,且A 、B 的球面距离为 ,求A 、B 两地经度的差.
解答:
分析:如图,O 为球心,O 1为北纬45°小圆的圆心,知A 、B 的球面距离,就可求得∠AOB 的弧度数,进而求得线段AB 的长,在ΔAO 1B 中,∠AO 1B 的大小就是A 、B 两地的经度差.
解 设O 1是北纬45°圈的中心, ∵A、B 都在此圈上,
∴O 1A =O 1B = R.
∵A、B 的球面距离为 ,
∴∠AOB= = = ,ΔAOB 为等边三角形.
AB =R ,在ΔAO 1B 中,
∵O 1A 2+O 1B 2
=
R 2
+
R 2=R 2=AB 2
,
∴∠AO 1B =90°.
∴A、B 两地的经度差是90°.
评析:注意搞清纬度和经度的问题,球面距离三步骤的运用是非常重要的问题.
常见问题3: 球
问题:
已知圆锥的母亲长为l,母线对圆锥底面的倾角为θ,在这个圆锥内有一内切球,球内又有一个内接的正方体,求这个内接正方体的体积.
解答:
解设球半径为R,以内接正方体对角面为轴截面,如图.连接OA,∠OAD=,R=OD=AD·tan
,VA=l,AD=lcosθ,∴R=lcosθtan ,又设正方体棱长为x,则3x2=EG2=4R2,x=R.∴V
正方
=(lcosθtan )3.
体
常见问题4: 球
问题:
如图,过半径为R的球面上一点P作三条两两垂直的弦PA、PB、PC,(1)求证:PA2+PB2+PC2为定值;
(2)求三棱锥P—ABC的体积的最大值.
解答:
分析:先选其中两条弦PA 、PB ,设其确定的平面截球得⊙O 1,AB 是⊙O 1的直径,连PO 1并延长交⊙O 1
于D ,PADB 是矩形,PD 2=AB 2=PA 2+PB 2,然后只要证得PC 和PD 确定是大圆就可以了.
解 (1)设过PA 、PB 的平面截球得⊙O 1,∵PA⊥PB,
∴AB 是⊙O 1的直径,连PO 1并延长交⊙O 1于D ,则PADB 是矩形,PD 2=PA 2+PB 2. 设O 为球心,则OO 1⊥平面⊙O 1, ∵PC⊥⊙O 1平面,
∴OO 1∥PC,因此过PC 、PD 的平面经过球心O ,截球得大圆,又PC⊥PD. ∴CD 是球的直径.
故 PA 2+PB 2+PC 2=PD 2+PC 2=CD 2=4R 2定值.
(2)设PA 、PB 、PC 的长分别为x 、y 、z ,则三棱锥P —ABC 的体积V = xyz ,
V 2= x 2y 2z 2≤ ( )3= · = R 6.
∴V≤ R 3.
即 V 最大= R 3.
评析:定值问题可用特殊情况先“探求”,如本题(1)若先考虑PAB 是大圆,探求得定值4R 2可为(1)的证明指明方向.
球面上任一点对球的直径所张的角等于90°,这应记作很重要的性质.
常见问题5: 球
问题:
求棱长为a 的正四面体的外接球和内切球的半径.
解答:
解如图,作A H⊥底面BCD于H,则AH=a,设内切球的球心为O,半径为r,O点与A、B、C、
D相连,得四个锥体,设底面为S,则每个侧面积为S,有4· ·Sr=S·AH,∴r=AH=a,
设外接球心为O,半径R,过A点作球的半径交底面ΔCD于H,则H为圆BCD的圆心,求得BH=a,AH
=a,由相交弦定理得a×(2R- a)=( a)2.
解得R= a.
常见问题6: 球
问题:
球面上有3个点,其中任意两点的球面距离都等于大圆周长的,经过3个点的小圆的周长为4π,那么这个球的半径为( )
A.4
B.2
C.2
D.
解答:
解设球半径为R,小圆半径为r,则2πr=4π,∴r=2.如图,设三点A、B、C,O为球心,∠AOB
=∠BOC=∠COA=,又∵OA=OB
∴ΔAOB是等边三角形
同理,ΔBOC、ΔCOA都是等边三角形,得ΔABC为等边三角形.
边长等于球半径R,r为ΔABC的外接圆半径.
r=AB=R
R=r=2
∴应选B.
常见问题7: 球
问题:
已知球面上A、B、C三点的截面和球心的距离都是球半径的一半,且AB=BC=CA=2,则球表面积是( )
A. π
B. π
C.4π
D. π
解答:
解如图,过ABC三点的截面圆的圆心是O′,球心是O,连结AO′、OO′,则OO′⊥AO′.ΔABC 中,AB=BC=CA=2,故ΔABC为正三角形.
∴AO′=×2=
设球半径为R,则OA=R,OO′=
在RtΔOAO′中,OA2=O′O2+O′A2,即R2=+( )2
∴R=
∴球面面积为4πR2=π
∴应选A.
说明因为R=OA>O′A>AB=1,所以球面积S=4πR2>4π.从而选A.
常见问题8: 球
问题:
长方体的一个顶点上的三条棱分别是3、4、5,且它的八个顶点都在同一球面上,这个球的表面积是( )
A.20 π
B.25 π
C.50π
D.200π
解答:
解正方体的对角线为l,球的半径为R,则l=2R.
得:l2=4R2=32+42+52=50
=4πR2=50π
从而 S
球
∴应选C.
常见问题9: 球
问题:
在球面上有四个点P、A、B、C.如果PA、PB、PC两两互相垂直,且PA=PB=PC=a,那么这个球的表面积是 .
解答:
解由已知可得PA、PB、PC实际上就是球内接正方体中交于一点的三条棱,正方体的对角线长就是
球的直径,连结过点C的一条对角线CD,则CD过球心O,对角线CD= a.
∴S
球表面积
=4π·( a)2=3πa2.
常见问题10: 球
问题:
圆柱形容器的内壁底半径为5cm,两个直径为5cm的玻璃小球都浸没于容器的水中,若取出这两个小球,则容器内的水面将下降 cm.
解答:
分析:球的体积等于它在容器中排开水的体积.
解设取出小球后,容器水平面将下降hcm,两小球体积为V
球=2× π×52×h,V
1
= V
球
即 25πh=π∴h=cm.
∴应填.
常见问题11: 球
问题:
湖结冰时,一个球漂在其上,取出后(未弄破冰),冰面上留下了一个直径为24cm,深为8cm的空穴,求该球的半径.
解答:
解设球的半径为R,依题意知截面圆的半径r=12,球心与截面的距离为d=R-8,由截面性质得:r2+d2=R2,即122+(R-8)2=R2.
得R=13 ∴该球半径为13cm.
常见问题12: 球
问题:
在有阳光时,一根长为3米的旗轩垂直于水平地面,它的影长为米,同时将一个半径为3米的球放在这块水平地面上,如图所示,求球的阴影部分的面积(结果用无理数表示).
解答:
解:由题意知,光线与地面成60°角,设球的阴影部分面积为S,垂直于光线的大圆面积为S′,则Sc os30°=S′,并且S′=9π,所以S=6 π(米2)
常见问题13: 球
问题:
设棱锥M—ABCD的底面是正方形,且MA=MD,MA⊥AB,如果ΔAMD的面积为1,试求能够放入这个棱锥的最大球的半径.
解答:
解∵AB⊥AD,AB⊥MA,
∴AB⊥平面MAD,
由此,面MAD⊥面AC.
记E是AD的中点,
从而ME⊥AD.
∴ME⊥平面AC ME⊥EF
设球O是与平面MAD、AC、平面MBC都相切的球.
不妨设O∈平面MEF,于是O是ΔMEF的内心.
设球O的半径为r,则r=
设AD=EF=a,∵S
ΔAMD=1.
∴ME=.MF=,
r=≤ =-1
当且仅当a=,即a=时,等号成立.
∴当AD=ME=时,满足条件的球最大半径为-1.。
