圆锥曲线复习课演示文稿
合集下载
圆锥曲线的复习课说课课件-高二上学期数学人教A版(2019)选择性必修第一册
教学策略分析
第一章
教师引导，学生思考
发现问题，解决问题
教学设计
教学过程
动手实践，抽象概括
回忆联想，类比分析
重难点分析
重点
重点
圆锥曲线统一定义的
生成、理解、应用
难 点
圆锥曲线的统一定义的
生成以及对对统一性深
层次的理解
教学过程
教学过程
提出问题
定义比较
提出猜想
动态直观让学生直观感知，
培养学生直观想象、数形
结合的核心素养。
.
.
.
.
03 .探究思考，生成定义
问题3:为了研究问题的方便，不妨从标准方程入手，若椭圆方
程
+
= （ > > ）上一点(, ),与定点为（, ）的
距离和它到定直线： = 的距离之比是常数e，你能寻求定
02
定义比较，提出猜想
问题2：点M与定点F（2，0）的距离和它到定直线: = 8的
距离的比是1：2，求M点的轨迹方程，并说明轨迹是什么图
形？
教学过程
03
探究思考，生成定义
设计意图：让学生类
比，大胆猜想，不断提出
自己主张，完善自己的想
法，过程，由此主观能动
性得以较好的体现。通过
GGB软件演示，生动形象、
直线的方程吗？
.
教学过程
.
教学过程
03
探究思考，生成定义
设计意图：通过发挥学
生主观能动性，大胆探索，
主动求知，真相展示自己
的见解，不乏新的想法，
显示了学生的思维广阔，
达到了学生的最近发展区。
高二数学圆锥曲线复习课PPT课件演示文稿
第38页，共129页。
(2)设椭圆方程为 mx2＋ny2＝1(m>0，n>0 且 m≠n)． ∵椭圆经过 P1、P2 点，将 P1，P2 两点坐标代入椭圆方程， 得63mm＋ ＋n2n＝＝1， 1. 解得 m＝19，n＝13. ∴所求椭圆方程为x92＋y32＝1.
b2 1
消元
一元二次方程
消y
消x
f (x) 0
g( y) 0
y
SABC
1 2
AB
•d
1 SABC 2 OC • y1 y2
B
c
O
x
A
第10页，共129页。
(3)直线与圆锥曲线有关弦的中点问题
解 题
思 路
直线与圆锥曲线联立消元得到一元二次方程
点差法
点的对称性
：
第11页，共129页。
5、焦点三角y形性质：
高二数学圆锥曲线复习课PPT 课件演示文稿
第1页，共129页。
（优质）高二数学圆
锥曲线复习课PPT课 件
第2页，共129页。
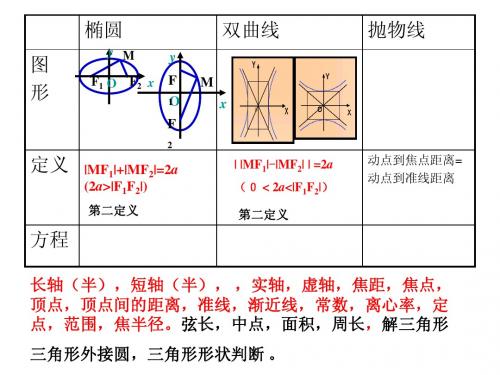
二、基础知识点梳理
1、圆锥曲线的定义
椭圆的定义：
双曲线的定义： 圆锥曲线的统一定义（第二定义） ：
l
d . .M F
l d .M .
F
l d.M .
F
第3页，共129页。
2、圆锥曲线的标准方程
Image (2)（20191·新1课6标全国高考）在平面直角1坐6标系9xOy中，椭圆
C的中心为原点，焦点F1，F2在x轴上，离心率为 过F1的2直. 线l交C于A，B两点，且△ABF2的周长为16，那么C的方程2为____．
第33页，共129页。
【解析】(1)选C.不妨设E（-c,0），F（c,0），则
(2)设椭圆方程为 mx2＋ny2＝1(m>0，n>0 且 m≠n)． ∵椭圆经过 P1、P2 点，将 P1，P2 两点坐标代入椭圆方程， 得63mm＋ ＋n2n＝＝1， 1. 解得 m＝19，n＝13. ∴所求椭圆方程为x92＋y32＝1.
b2 1
消元
一元二次方程
消y
消x
f (x) 0
g( y) 0
y
SABC
1 2
AB
•d
1 SABC 2 OC • y1 y2
B
c
O
x
A
第10页，共129页。
(3)直线与圆锥曲线有关弦的中点问题
解 题
思 路
直线与圆锥曲线联立消元得到一元二次方程
点差法
点的对称性
：
第11页，共129页。
5、焦点三角y形性质：
高二数学圆锥曲线复习课PPT 课件演示文稿
第1页，共129页。
（优质）高二数学圆
锥曲线复习课PPT课 件
第2页，共129页。
二、基础知识点梳理
1、圆锥曲线的定义
椭圆的定义：
双曲线的定义： 圆锥曲线的统一定义（第二定义） ：
l
d . .M F
l d .M .
F
l d.M .
F
第3页，共129页。
2、圆锥曲线的标准方程
Image (2)（20191·新1课6标全国高考）在平面直角1坐6标系9xOy中，椭圆
C的中心为原点，焦点F1，F2在x轴上，离心率为 过F1的2直. 线l交C于A，B两点，且△ABF2的周长为16，那么C的方程2为____．
第33页，共129页。
【解析】(1)选C.不妨设E（-c,0），F（c,0），则
圆锥曲线复习-ppt课件经典
(2)
x b
2 2
y2 a2
=1 (a＞b＞0),其中a2=b2+c2，焦点
坐标为⑤ F1(0,-c),F2(0,c).
采用PP管及配件：根据给水设计图配 置好PP管及配 件，用 管件在 管材垂 直角切 断管材 ，边剪 边旋转 ，以保 证切口 面的圆 度，保 持熔接 部位干 净无污 物
4.椭圆
x2 a2
近线方(5)程渐为近1线3 y：=±双b 曲x 线;双ax 22 曲 by线22
两条渐近线方程为
a
14
y=± a x
1 x2
a2
.
的两条渐
y2 b2
1
的
b
采用PP管及配件：根据给水设计图配 置好PP管及配 件，用 管件在 管材垂 直角切 断管材 ，边剪 边旋转 ，以保 证切口 面的圆 度，保 持熔接 部位干 净无污 物
A.椭圆 C.线段F1F2
B.圆 D.直线F1F2
采用PP管及配件：根据给水设计图配 置好PP管及配 件，用 管件在 管材垂 直角切 断管材 ，边剪 边旋转 ，以保 证切口 面的圆 度，保 持熔接 部位干 净无污 物
(2)定义法：某动点的轨迹符合某一基 本轨迹(如直线、圆锥曲线)的⑤ 定义 ,则可 根据定义采用设方程求方程系数得到动点 的轨迹方程；
(3)代入法(相关点法)：当所求动点M 是随着另一动点P(称之为相关点)而运动， 如果相关点P满足某一曲线方程，这时我 们可以用动点坐标表示相关点坐标，再把 相关点代入曲线方程，就把相关点所满足 的方程转化为动点的轨迹方程；
a2
y2 b2
0
近线方程.
就是双曲线x 2
a2
y2 b2
1
的两条渐
圆锥曲线复习 演示文稿
则点M的轨迹为 椭圆
y2 x2 1 其标准方程为 25 16
。
定义的再认识 已知双曲线的焦点为F1(-5,0), F2(5,0)双曲线上 一点到焦点的距离差的绝对值等于6，则 5 4 3 (1) a=_______ , c =_______ , b =_______
(2) 双曲线的标准方程为______________ (3)双曲线上一点Ｐ， |PF1|=10, 4或16 则|PF2|=_________
定义的再认识
例 2.化简: x ( y 3)
2 2
x ( y 3) 4 ,使结
2 2
y x 1 ( y 0) 果不含根式得： ___________________________ 4 5
2
2
练习巩固:
下列方程各表示什么曲线?
(1)
( x 3) y ( x 3) y 4
2
k 8
1 5 1 k 1 e ，即 k ． 由 ，得 9 4 2 4
5 ∴满足条件的 k 4 或 k ． 4
方程再认识----区分椭圆与双曲线 2 2 x y 1 表示双曲线 例1.如果方程 2 m m 1
（椭圆），求m的取值范围.
解:∴ m 的取值范围为 (, 2) (1, )
x y 9 16 2.已知方程 1 9k k 3 3 k 9且 k 6； (1)方程表示椭圆，则 k的取值范围是 __________ ______
k 3或k 9 . (2)方程表示双曲线，则 k的取值范围是 __________ _____
3.已知双曲线8kx 2 ky 2 8的一个焦点为（ 0,3 ）， 则k的值为 （ ） B 65 65 A.1 B.－1 C. D.－ 3 3
高三数学二轮复习圆锥曲线 课件
考查
内容
难度
中等
圆锥曲线的方程与性质、弦
长问题.
考点1：圆锥曲线的定义及
标准方程
【例1】（1）已知P是抛物线 y2＝4x上的一个动点，Q是圆(x‒3)2＋(y‒1)2＝1上
的一个动点，N(1，0)是一个定点，则|PQ|＋|PN|的最小值为( A )
A．3
B．4
y
C．5
Pபைடு நூலகம்
H
Q
1
O
x=-1
N
3
x
D． 2 ＋1
2
2
2
− 2
= 1 (a>0，
b>0)的右顶点为A，以A为圆心，b为半径作圆
A，圆A与双曲线C的一条渐近线交于M，N两
点．若∠MAN＝60°，则C的离心率为
2 3
________．
3
M
N
A
x
（2）在平面直角坐标系xOy中，双曲线
2
2
2
− 2
y
B
= 1 (a＞0，b＞0)的右支与焦点为F
•
计算，即利用待定系数法求出方程中的a 2 ，b 2 或p．另外，当焦点位置无法确定时，
抛物线常设为y 2 ＝2px或x 2 ＝2py(p≠0)，椭圆常设为mx 2 ＋ny 2 ＝1(m>0，n>0)，双
曲线常设为mx 2 －ny 2 ＝1(mn>0)．
考点2：圆锥曲线的几何性质
y
【例2】（1）已知双曲线C：
2
（2）已知双曲线 2
2
− 2
= 1 (a>0，b>0)的左焦点为F，离心率为 2 .若经过F
和P(0，4)两点的直线平行于双曲线的一条渐近线，则双曲线的方程为( B )
内容
难度
中等
圆锥曲线的方程与性质、弦
长问题.
考点1：圆锥曲线的定义及
标准方程
【例1】（1）已知P是抛物线 y2＝4x上的一个动点，Q是圆(x‒3)2＋(y‒1)2＝1上
的一个动点，N(1，0)是一个定点，则|PQ|＋|PN|的最小值为( A )
A．3
B．4
y
C．5
Pபைடு நூலகம்
H
Q
1
O
x=-1
N
3
x
D． 2 ＋1
2
2
2
− 2
= 1 (a>0，
b>0)的右顶点为A，以A为圆心，b为半径作圆
A，圆A与双曲线C的一条渐近线交于M，N两
点．若∠MAN＝60°，则C的离心率为
2 3
________．
3
M
N
A
x
（2）在平面直角坐标系xOy中，双曲线
2
2
2
− 2
y
B
= 1 (a＞0，b＞0)的右支与焦点为F
•
计算，即利用待定系数法求出方程中的a 2 ，b 2 或p．另外，当焦点位置无法确定时，
抛物线常设为y 2 ＝2px或x 2 ＝2py(p≠0)，椭圆常设为mx 2 ＋ny 2 ＝1(m>0，n>0)，双
曲线常设为mx 2 －ny 2 ＝1(mn>0)．
考点2：圆锥曲线的几何性质
y
【例2】（1）已知双曲线C：
2
（2）已知双曲线 2
2
− 2
= 1 (a>0，b>0)的左焦点为F，离心率为 2 .若经过F
和P(0，4)两点的直线平行于双曲线的一条渐近线，则双曲线的方程为( B )
圆锥曲线复习课件
圆锥曲线复习PPT课件
本次课程将为您复习圆锥曲线的基本概念、分类、通式以及应用。我们会讨 论每种曲线的方程和性质，以及它们在不同领域中的应用。在这个PPT课件中， 您将学到一些基础概念，发现领域内的巧妙用法，甚至可以了解到曲线中的 美学和艺术价值。
圆锥曲线基本定义和分类
定义
圆锥曲线是平面上的一条曲线，由一条平面直线与一个圆锥相交而成。
学习要点回顾
你学习了圆锥曲线的定义和分 类，以及每个曲线的一般方程 和基本性质。
下一步学习计划
你可以通过进一步研究领域内 的应用，来深入了解曲线的美 学和艺术方面。你也可以拓展 学习更高级的曲线和更复杂的 几何概念。
分类
圆锥曲线分为三类：椭圆、双曲线和抛物线。
通式
通式是描述圆锥曲线的一般方程，可以用来表示三种曲线的具体形态。
椭圆的定义和方程
1
定义
椭圆是圆锥曲线的一种。它是焦点到直线距离之和为常数的(x-h)²/a²+ (y-k)²/b²= 1，其中(h, k)是坐标系中椭圆中心的坐标， a和b分别是椭圆的长半轴和短半轴。
图形特征
双曲线不具有对称性，它的两 个分支向外扩张。与椭圆不同， 它不会相交而是会进一步分离。
抛物线的定义和方程
1
定义
抛物线是圆锥曲线的一种。它是从一点出发，做抛物线运动，所有位置在同一高 度的轨迹。
2
抛物线方程
抛物线的一般方程是y = ax²+bx+c，a、b、c是常数。
3
图形特征
抛物线具有轴对称性，是一个U形的曲线，有两个方向。抛物线也可以是开口向 下的。
对于每个圆锥曲线，具有一对焦点和一条 直线，它们决定了曲线的位置和形状。
圆锥曲线的应用
本次课程将为您复习圆锥曲线的基本概念、分类、通式以及应用。我们会讨 论每种曲线的方程和性质，以及它们在不同领域中的应用。在这个PPT课件中， 您将学到一些基础概念，发现领域内的巧妙用法，甚至可以了解到曲线中的 美学和艺术价值。
圆锥曲线基本定义和分类
定义
圆锥曲线是平面上的一条曲线，由一条平面直线与一个圆锥相交而成。
学习要点回顾
你学习了圆锥曲线的定义和分 类，以及每个曲线的一般方程 和基本性质。
下一步学习计划
你可以通过进一步研究领域内 的应用，来深入了解曲线的美 学和艺术方面。你也可以拓展 学习更高级的曲线和更复杂的 几何概念。
分类
圆锥曲线分为三类：椭圆、双曲线和抛物线。
通式
通式是描述圆锥曲线的一般方程，可以用来表示三种曲线的具体形态。
椭圆的定义和方程
1
定义
椭圆是圆锥曲线的一种。它是焦点到直线距离之和为常数的(x-h)²/a²+ (y-k)²/b²= 1，其中(h, k)是坐标系中椭圆中心的坐标， a和b分别是椭圆的长半轴和短半轴。
图形特征
双曲线不具有对称性，它的两 个分支向外扩张。与椭圆不同， 它不会相交而是会进一步分离。
抛物线的定义和方程
1
定义
抛物线是圆锥曲线的一种。它是从一点出发，做抛物线运动，所有位置在同一高 度的轨迹。
2
抛物线方程
抛物线的一般方程是y = ax²+bx+c，a、b、c是常数。
3
图形特征
抛物线具有轴对称性，是一个U形的曲线，有两个方向。抛物线也可以是开口向 下的。
对于每个圆锥曲线，具有一对焦点和一条 直线，它们决定了曲线的位置和形状。
圆锥曲线的应用
高三复习圆锥曲线复习1PPT课件
课 堂 题 型 设 计
3．已知椭圆
规
律 方
________.
法
提
炼
的离心率
则k＝
课 后 强 化 作 业
首页
上页
下页
末页
第8章 圆锥曲线方程
高
考
导
航
解题思路：由于椭圆的焦点位置不确定，应分两种情
况进行讨论．
知
识 梳
(1)当椭圆的焦点在x轴上时，
理
∵a2＝k＋8，b2＝9.
课
堂 题
∴c2＝a2－b2＝(k＋8)－9＝k－1.
律
方 法
重点，所以要熟练掌握求曲线方程的一般方法：直接法、
提
炼 定义法、待定系数法、相关点法、参数法等．
课 后 强 化 作 业
首页
上页
下页
末页
第8章 圆锥曲线方程
高 考 导 航
3．关注“热点”问题，直线与圆锥曲线的位置关系
知
识 梳
问题一直是高考命题的热点，这类问题常涉及圆锥曲线的
理
性质和直线的基本知识点，分析问题时要注意数形结合思
高 考 导 航
知
识 梳
5．着力抓好“运算关”．解析几何问题的解题思路
理
容易分析出来，但往往由于运算不过关而半途而废．因
课
堂 题
此，在复习中要注意寻求合理的运算方案，以及简化运算
型
设 计
的基本途径与方法，亲身经历运算困难的发生与克服困难
规 的完整过程，增强解决复杂问题的信心.
律 方 法 提 炼
课 后 强 化 作 业
高
考
导
航
备考指南：
1．注重“三基”训练．重点掌握椭圆、双曲线、抛
第3章圆锥曲线的方程(复习课件)高二数学(人教A版选择性必修第一册)
x＝ty＋a，
由 2
y ＝2x，
消去 x，得 y2－2ty－2a＝0.
设A(x1，y1)，B(x2，y2)，则y1＋y2＝2t，y1y2＝－2a.
y21y22
因为 OA⊥OB，所以 x1x2＋y1y2＝0，即 4 ＋y1y2＝0，
解得y1y2＝0(舍去)或y1y2＝－4.
所以－2a＝－4，解得a＝2.
我们把平面内与两个定点F1，F2的距离之和（2a）等于常数
（大于|F1F2|）的点的轨迹叫做椭圆。这两个定点叫做椭圆的
焦点，两焦点间的距离叫做椭圆的焦距，焦距的一半称为半焦
距。
对椭圆定义的理解
①当2a=|F1F2|时，其轨迹为线段；
②当2a<|F1F2|时，其轨迹不存在.
椭圆的简单几何性质：
焦点位置
x2 y2
∴椭圆的方程为 4 ＋ 3 ＝1.
1
(2)若直线 l：y＝－2x＋m 与椭圆交于 A，B 两点，与以 F1F2 为直径的圆交于 C，
|AB| 5 3
D 两点，且满足|CD|＝ 4 ，求直线 l 的方程.
解
由(1)知，以F1F2为直径的圆的方程为x2＋y2＝1，
2|m|
∴圆心到直线 l 的距离 d＝
焦点坐标
y 2 2 px ( p 0)
p
F ( ,0)
2
y 2 2 px ( p 0)
F (
x 2 py( p 0)
p
F (0, )
2
y
p
F (0, )
2
y
2
x 2 2 py( p 0)
p
,0)
2
准线方程
x
x
p
《圆锥曲线》章末复习课件精选全文
的斜率,交点A x1, y1 , B x2 , y2 .
2
1
2
(2)处理中点弦问题时,一般有两种思路,思路一:联立方程组,消元,利用根与系数的关系
进行“设而不求”;思路二:利用“点差法”
知识要点整合
高中数学
GAOZHONGSHUXUE
四、圆锥曲线中的弦长、中点弦问题
例4
x2 y 2
已知椭圆 a 2 b2 1(a b 0) 的一个顶点为A(0,1),离心率为
一、圆锥曲线的定义及应用
2
2
例1 (1)一动圆与两圆: x 2 y 2 1和 x y 6 x 5 0都外切,则动圆圆心的轨迹为( )
A.抛物线
B.双曲线
C.双曲线的一支
D.椭圆
(2)在平面直角坐标系xOy中,椭圆C的中心为原点,焦点F1,F2在x轴上,离心率为
2
.
2
过F1的直线l交椭圆C于A,B两点,且△ABF2的周长为16,那么椭圆C的方程为______.
例2
x2 y 2
3
(1)若椭圆 2 2 1(a b 0) 的离心率为
2
a
b
1
A. y 2 x
B. y 2 x
C. y 4 x
x2 y 2
,则双面线 2 2 1的渐近线方程为(
a
b
1
y
x
D.
4
x2 y 2
(2)已知双曲线 a 2 b2 1(a 0, b 0) 的左焦点为F,离心率为
,且
a
2
x2
2
y
1
2, c 1.易得椭圆方程为
2
1
2
(2)处理中点弦问题时,一般有两种思路,思路一:联立方程组,消元,利用根与系数的关系
进行“设而不求”;思路二:利用“点差法”
知识要点整合
高中数学
GAOZHONGSHUXUE
四、圆锥曲线中的弦长、中点弦问题
例4
x2 y 2
已知椭圆 a 2 b2 1(a b 0) 的一个顶点为A(0,1),离心率为
一、圆锥曲线的定义及应用
2
2
例1 (1)一动圆与两圆: x 2 y 2 1和 x y 6 x 5 0都外切,则动圆圆心的轨迹为( )
A.抛物线
B.双曲线
C.双曲线的一支
D.椭圆
(2)在平面直角坐标系xOy中,椭圆C的中心为原点,焦点F1,F2在x轴上,离心率为
2
.
2
过F1的直线l交椭圆C于A,B两点,且△ABF2的周长为16,那么椭圆C的方程为______.
例2
x2 y 2
3
(1)若椭圆 2 2 1(a b 0) 的离心率为
2
a
b
1
A. y 2 x
B. y 2 x
C. y 4 x
x2 y 2
,则双面线 2 2 1的渐近线方程为(
a
b
1
y
x
D.
4
x2 y 2
(2)已知双曲线 a 2 b2 1(a 0, b 0) 的左焦点为F,离心率为
,且
a
2
x2
2
y
1
2, c 1.易得椭圆方程为
圆锥曲线复习课课件
函数思想法
将问题转化为函数问题，利用函数的性质和图像，求解相关 问题。
05
圆锥曲线的问题与挑战
圆锥曲线中的难题与挑战
圆锥曲线中的复杂计算
圆锥曲线问题往往涉及大量的计算和复杂的数学公式，需要学生 具备较高的数学计算能力和逻辑思维能力。
圆锥曲线中的抽象概念
圆锥曲线问题常常涉及到抽象的概念和性质，需要学生具备较好的 数学基础和空间想象力。
利用圆锥曲线的参数方程，将问 题转化为参数的取值范围或最值 问题，简化计算。
圆锥曲线的特殊解题方法
焦点三角形法
利用圆锥曲线的焦点三角形，结合正 弦定理、余弦定理等，求解相关问题 。
切线法
通过圆锥曲线的切线性质，结合导数 和切线斜率，求解相关问题。
圆锥曲线的综合解题方法
数形结合法
将几何性质与代数表达式相结合，通过数形结合的方法，直 观地解决问题。
作用。
光线的弯曲程度与圆锥曲线的离 心率有关，离心率越大，光线弯
曲程度越明显。
圆锥曲线的对称性质
圆锥曲线具有对称性，包括中 心对称、轴对称和面对称等。
圆具有中心对称和轴对称，椭 圆和双曲线只有中心对称，抛 物线只有轴对称。
对称性是圆锥曲线的一个重要 性质，在解决几何问题时具有 广泛应用。
03
圆锥曲线的应用
路，提高解题能力。
培养数学思维
学生应注重培养数学思维，提高 逻辑推理能力和空间想象力，以
便更好地解决圆锥曲线问题。
如何进一步深化对圆锥曲线的研究
研究圆锥曲线的性质
01
学生可以进一步研究圆锥曲线的性质和特点，探索其内在规律
和数学之美。
探索圆锥曲线与其他数学领域的联系
02
学生可以探索圆锥曲线与其他数学领域之间的联系，例如与代
将问题转化为函数问题，利用函数的性质和图像，求解相关 问题。
05
圆锥曲线的问题与挑战
圆锥曲线中的难题与挑战
圆锥曲线中的复杂计算
圆锥曲线问题往往涉及大量的计算和复杂的数学公式，需要学生 具备较高的数学计算能力和逻辑思维能力。
圆锥曲线中的抽象概念
圆锥曲线问题常常涉及到抽象的概念和性质，需要学生具备较好的 数学基础和空间想象力。
利用圆锥曲线的参数方程，将问 题转化为参数的取值范围或最值 问题，简化计算。
圆锥曲线的特殊解题方法
焦点三角形法
利用圆锥曲线的焦点三角形，结合正 弦定理、余弦定理等，求解相关问题 。
切线法
通过圆锥曲线的切线性质，结合导数 和切线斜率，求解相关问题。
圆锥曲线的综合解题方法
数形结合法
将几何性质与代数表达式相结合，通过数形结合的方法，直 观地解决问题。
作用。
光线的弯曲程度与圆锥曲线的离 心率有关，离心率越大，光线弯
曲程度越明显。
圆锥曲线的对称性质
圆锥曲线具有对称性，包括中 心对称、轴对称和面对称等。
圆具有中心对称和轴对称，椭 圆和双曲线只有中心对称，抛 物线只有轴对称。
对称性是圆锥曲线的一个重要 性质，在解决几何问题时具有 广泛应用。
03
圆锥曲线的应用
路，提高解题能力。
培养数学思维
学生应注重培养数学思维，提高 逻辑推理能力和空间想象力，以
便更好地解决圆锥曲线问题。
如何进一步深化对圆锥曲线的研究
研究圆锥曲线的性质
01
学生可以进一步研究圆锥曲线的性质和特点，探索其内在规律
和数学之美。
探索圆锥曲线与其他数学领域的联系
02
学生可以探索圆锥曲线与其他数学领域之间的联系，例如与代
圆锥曲线复习ppt课件
复习目标
1)掌握椭圆的定义，标准方程和椭圆的几 何性质
2)掌握双曲线的定义，标准方程和双曲线 的几何性质
3)掌握抛物线的定义，标准方程和抛物线 的几何性质
4)能够根据条件利用工具画圆锥曲线的图 形，并了解圆锥曲线的初步应用.
资金是运动的价值，资金的价值是随 时间变 化而变 化的， 是时间 的函数 ，随时 间的推 移而增 值，其 增值的 这部分 资金就 是原有 资金的 时间价 值
x轴，长轴长2a， x轴，实轴长2a， y轴，短轴长2b y轴，虚轴长2b
(±c，0)
(±c，0)
c2=a2-b2
c2=a2+b2
0<e<1
e>1
x轴 (p/2，0)
e=1
x=±a2/c x=±a2/c x=-p/2
渐近线方程
y=±(b/a) x
资金是运动的价值，资金的价值是随 时间变 化而变 化的， 是时间 的函数 ，随时 间的推 移而增 值，其 增值的 这部分 资金就 是原有 资金的 时间价 值
A．k＜1 B．k＞2 C．k＜1或k＞2 D．1＜k＜2
2、已知方程 a x 2 b y 2 a b 和 a x b y c 0 ( 其 中 a b 0 , a b , c 0 ) 它们所表示的曲线可能是( B)
x1
和
A
B
C
D
3、双曲线 x 2 y 2 1 的两条渐近线所成的锐角是 ( C )
y
A
O
x
B
资金是运动的价值，资金的价值是随 时间变 化而变 化的， 是时间 的函数 ，随时 间的推 移而增 值，其 增值的 这部分 资金就 是原有 资金的 时间价 值
5、设F1、F2分别是椭 圆
1)掌握椭圆的定义，标准方程和椭圆的几 何性质
2)掌握双曲线的定义，标准方程和双曲线 的几何性质
3)掌握抛物线的定义，标准方程和抛物线 的几何性质
4)能够根据条件利用工具画圆锥曲线的图 形，并了解圆锥曲线的初步应用.
资金是运动的价值，资金的价值是随 时间变 化而变 化的， 是时间 的函数 ，随时 间的推 移而增 值，其 增值的 这部分 资金就 是原有 资金的 时间价 值
x轴，长轴长2a， x轴，实轴长2a， y轴，短轴长2b y轴，虚轴长2b
(±c，0)
(±c，0)
c2=a2-b2
c2=a2+b2
0<e<1
e>1
x轴 (p/2，0)
e=1
x=±a2/c x=±a2/c x=-p/2
渐近线方程
y=±(b/a) x
资金是运动的价值，资金的价值是随 时间变 化而变 化的， 是时间 的函数 ，随时 间的推 移而增 值，其 增值的 这部分 资金就 是原有 资金的 时间价 值
A．k＜1 B．k＞2 C．k＜1或k＞2 D．1＜k＜2
2、已知方程 a x 2 b y 2 a b 和 a x b y c 0 ( 其 中 a b 0 , a b , c 0 ) 它们所表示的曲线可能是( B)
x1
和
A
B
C
D
3、双曲线 x 2 y 2 1 的两条渐近线所成的锐角是 ( C )
y
A
O
x
B
资金是运动的价值，资金的价值是随 时间变 化而变 化的， 是时间 的函数 ，随时 间的推 移而增 值，其 增值的 这部分 资金就 是原有 资金的 时间价 值
5、设F1、F2分别是椭 圆
圆锥曲线复习+课件
圆锥曲线在解决几何问题中具有广泛应用，例如求图形的面积、体积、角度、线 段长度等问题。
在其他数学分支中的地位和作用
圆锥曲线在解析几何、微积分、线性代数等数学分支中都有 重要应用。
圆锥曲线在解决物理、工程、经济等领域的问题中也有广泛 应用，例如物理学中的光学、力学问题，经济学中的供需关 系、最优问题等。
物体运动轨迹
在物理学中，圆锥曲线被用来描述各种 物体的运动轨迹。例如，当物体在重力 的作用下自由下落时，其运动轨迹可能 是一个抛物线；当物体沿着斜面滑下时 ，其运动轨迹可能是一个螺旋线。
VS
粒子运动
在量子力学和粒子物理学中，粒子在强磁 场中的运动轨迹通常被描述为复杂的曲线 ，这些曲线的形状和变化规律对于理解粒 子的性质和行为至关重要。
THANKS
感谢观看
圆锥曲线在几何学中的应 用
在几何学中，圆锥曲线被广泛应用于解决各 种问题，如轨迹问题、最值问题等。
现代圆锥曲线的研究方向和成果
圆锥曲线与代数几何的结合
现代数学家将圆锥曲线与代数几何相结合，研究了一些深层次的问题，如圆锥曲线的分类、几何不变量等。
圆锥曲线在物理学中的应用
在物理学中，圆锥曲线被应用于解决一些实际问题，如行星运动轨迹的计算、光学问题等。
• 解析
首先求出圆心A到抛物线准线的距离，然后与圆的半径进行比较，得 出圆与抛物线的位置关系。
解答题2
已知椭圆C的中心在原点，焦点在x轴上，且经过两个点$P_1(1,1)$和 $P_2( - frac{1}{5}, - frac{9}{5})$，求椭圆C的标准方程。
• 解析
根据椭圆的性质和给定的两个点，我们可以列出方程组解出椭圆的标 准方程。
06
圆锥曲线复习题及解析
在其他数学分支中的地位和作用
圆锥曲线在解析几何、微积分、线性代数等数学分支中都有 重要应用。
圆锥曲线在解决物理、工程、经济等领域的问题中也有广泛 应用，例如物理学中的光学、力学问题，经济学中的供需关 系、最优问题等。
物体运动轨迹
在物理学中，圆锥曲线被用来描述各种 物体的运动轨迹。例如，当物体在重力 的作用下自由下落时，其运动轨迹可能 是一个抛物线；当物体沿着斜面滑下时 ，其运动轨迹可能是一个螺旋线。
VS
粒子运动
在量子力学和粒子物理学中，粒子在强磁 场中的运动轨迹通常被描述为复杂的曲线 ，这些曲线的形状和变化规律对于理解粒 子的性质和行为至关重要。
THANKS
感谢观看
圆锥曲线在几何学中的应 用
在几何学中，圆锥曲线被广泛应用于解决各 种问题，如轨迹问题、最值问题等。
现代圆锥曲线的研究方向和成果
圆锥曲线与代数几何的结合
现代数学家将圆锥曲线与代数几何相结合，研究了一些深层次的问题，如圆锥曲线的分类、几何不变量等。
圆锥曲线在物理学中的应用
在物理学中，圆锥曲线被应用于解决一些实际问题，如行星运动轨迹的计算、光学问题等。
• 解析
首先求出圆心A到抛物线准线的距离，然后与圆的半径进行比较，得 出圆与抛物线的位置关系。
解答题2
已知椭圆C的中心在原点，焦点在x轴上，且经过两个点$P_1(1,1)$和 $P_2( - frac{1}{5}, - frac{9}{5})$，求椭圆C的标准方程。
• 解析
根据椭圆的性质和给定的两个点，我们可以列出方程组解出椭圆的标 准方程。
06
圆锥曲线复习题及解析
圆锥曲线复习1 人教课标版精品公开PPT课件
四、几个重要结论：
设P是椭圆
x2 a2
by22
1ab0上 的点，F1，F2是椭
圆的焦点，∠F1PF2=θ,则
B2
P
1、当P为短轴端点时， A1 F1
F2 A2
x
B1
S△PF1F2有最大值=bc
2、当P为短轴端点时，∠F1PF2为最大
3、椭圆上的点A1距F1最近，A2距F1最远
4、过焦点的弦中，以垂直于长轴的弦为最短
A1 F1
F2 A2
x
B1
y2 x2 1ab0
a2 b2
A2 y
F2 B1
B2 x
F1 A1
中心
(0,0)
(0,0)
焦点 F1(-c,0),F2(c,0) F1(0,-c),F2(0,c)
(±a,0),
顶点
(0, ±b)
(±b,0), (0, ±a)
轴长
长轴2a，短轴2b，a2=b2+c2， |B2O|=b,|OF2|=c,|B2F2|=a
x2 a2
y2 b2
1,(ab0)
的两焦点，过F1的弦AB与F2组成等腰直 角三角形ABF2，其中∠BAF2=90°，则椭 圆离心率是____6___.3
6、一个椭圆的离心率 e 1 ，准线方程 2
是x=4，对应的焦点F(2,0)，则椭圆
的方程是__3_x_2_+_4_y_2_-_8_x_=_0____________.
法二：焦点弦： AB 2ae(x1x2)
22、、已已知知椭椭圆圆1x16x262
yy22 99
11
求求以以点点PP（（22，，11））为为中中点点的的
弦弦所所在在直直线线的的方方程程。。
选修21人教版圆锥曲线复习课共15张PPT
x轴、y轴、 原点对称
(+a,0)
(0,+a)
e c a
e c a
e 1
ybx a
yax b
图像 标准方程
抛物线
ly
ox
yl
ox
y
o lx
y
o
l
x
y2 2 px( p 0) y2 2 px( p 0) x2 2 py( p 0) x2 2 py( p 0)
范围 焦点 准线 对称性 离心率
A
11
22
o
P
x B
联立方程
y
x2 4
kx 1 k + y2 =1
2
消去y, 得 (1 2k 2 )x2
4k(k
1)x
2(k
2
2k
1)
0
令 0,即16k2(k 1)2 8(1 2k2) k2 2k 1 0, 恒成立。
由韦达定理得x1
x2
4k(k 1) 1 2k 2
.
又P平分AB， x1 x2 2
4k(k 1) 2,解得k 1 , 又直线过P点，直线方程为y-1=- 1 (x 1),
1 2k 2
2
2
即x+2y-3=0
注2： (1)联立方程组
例3 P(1,1)为椭圆 x2 + y2 =1内一定点，经过P引一弦，使此弦
42
在P点被平分，求此弦所在的直线方程。
解：法2：点差法 设弦的两个端点 A(x1, y1), B(x2, y2 )
（
）
A2
B3
C6
D9
A (2)直线y kx k 1与椭圆 x2 y2 1恒有（ ）个交点。 94
圆锥曲线复习课市公开课金奖市赛课一等奖课件
(2)点A5，0到双曲线上动点 P的距离的
最小值为 6.
第44页
B两点， （1）若以AB为直径的圆过原点，求 实数a的值 （2）是否存在这样的实数 a，使双曲线上能找
到两点M，N关于直线y ax 1对称？若存在， 求a的范围.
第41页
例9、抛物线y2 4ax与圆( x a r )2 y2 r 2
(2a r )的上半部分交于 M , N两点,抛物线 2
使 BN BM ？若存在，求k的取值范围；若不存在 ， 说明理由.
第39页
例7 、椭圆
x2 a2
y2 b2
1(a
b
0)与x轴，y轴正方向
交于A，B两点, 在劣弧AB上取一点 C , 使四边形
OACB的面积最大 .求最大面积 .
y
B
C
o
Ax
第40页
例8、已知直线y ax 1与双曲线3x2 y2 1交于A，
y
4.焦点弦性质 A1
A(x1,y1)
(1)x1 x2
p2 4
(2) y1 y2 p2
2 11
O
(3)
p mn
(设AF=m, BF=n)
B1
(4) A、O、B1
三点共线
x
p
2
y2 2 px( p 0)
F( P ,0)
x
2
B(x2,y2)
第25页
y
A1
(5) 以AB为直径圆与 准线相切
x2 a2
y2 b2
1
消元
(b2 a2k 2 ) x2 2kma 2 x a2m 2 a2b2 0
b2 a2k2 0
a2m2 a2b2 x 2kma 2
一交点
最小值为 6.
第44页
B两点， （1）若以AB为直径的圆过原点，求 实数a的值 （2）是否存在这样的实数 a，使双曲线上能找
到两点M，N关于直线y ax 1对称？若存在， 求a的范围.
第41页
例9、抛物线y2 4ax与圆( x a r )2 y2 r 2
(2a r )的上半部分交于 M , N两点,抛物线 2
使 BN BM ？若存在，求k的取值范围；若不存在 ， 说明理由.
第39页
例7 、椭圆
x2 a2
y2 b2
1(a
b
0)与x轴，y轴正方向
交于A，B两点, 在劣弧AB上取一点 C , 使四边形
OACB的面积最大 .求最大面积 .
y
B
C
o
Ax
第40页
例8、已知直线y ax 1与双曲线3x2 y2 1交于A，
y
4.焦点弦性质 A1
A(x1,y1)
(1)x1 x2
p2 4
(2) y1 y2 p2
2 11
O
(3)
p mn
(设AF=m, BF=n)
B1
(4) A、O、B1
三点共线
x
p
2
y2 2 px( p 0)
F( P ,0)
x
2
B(x2,y2)
第25页
y
A1
(5) 以AB为直径圆与 准线相切
x2 a2
y2 b2
1
消元
(b2 a2k 2 ) x2 2kma 2 x a2m 2 a2b2 0
b2 a2k2 0
a2m2 a2b2 x 2kma 2
一交点
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
[解析] (1)P 到 F(0,2)的距离比它到 y＋4＝0 的距离小 2， 因此 P 到 F(0,2)的距离与它到直线 y＋2＝0 的距离相等， 故 P 的轨迹是以 F 为焦点，y＝－2 为准线的抛物线，∴P 的轨迹方程为 x2＝8y. (2)设椭圆方程为xa22＋by22＝1(a＞b＞0)，因为 AB 过 F1 且 A， B 在椭圆上，如图，则△ABF2 的周长为|AB|＋|AF2|＋|BF2| ＝|AF1|＋|AF2|＋|BF1|＋|BF2|＝4a＝16，∴a＝4.
k＜－
23或
k＞
3 2.
当∠AOB 为锐角时，O→A·O→B＞0，则 x1x2＋y1y2＞0， 即1＋124k2＋41－ ＋44kk22＞0，解得－2＜k＜2，
故当∠AOB 为锐角时，k∈(－2，－ 23)∪( 23，2)．
曲线与方程
求曲线方程的常用方法有： (1)直接法：建立适当的坐标系，设动点为(x，y)，根据几 何条件直接寻求x、y之间的关系式． (2)代入法：利用所求曲线上的动点与某一已知曲线上的 动点的关系，把所求动点转换为已知动点．具体地说， 就是用所求动点的坐标x、y来表示已知动点的坐标并代 入已知动点满足的曲线的方程，由此即可求得所求动点 坐标x、y之间的关系式． (3)定义法：如果所给几何条件正好符合圆、椭圆、双曲 线、抛物线等曲线的定义，则可直接利用这些已知曲线 的方程写出动点的轨迹方程．
圆锥曲线复习课演示文稿
优选圆锥曲线复习课
圆锥曲线定义的应用
圆锥曲线的定义是相应标准方程和几何性质的“源”，对 于圆锥曲线的有关问题，要有运用圆锥曲线定义解题的意 识，“回归定义”是一种重要的解题策略． 研究有关点间的距离的最值问题时，常用定义把曲线上的 点到焦点的距离转化为到另一焦点的距离或利用定义把曲 线上的点到焦点的距离转化为其到相应准线的距离，再利 用数形结合的思想去解决有关的最值问题．
0， 由根与系数的关系得 x1＋x2＝1－＋146kk2，x1x2＝1＋124k2，
∴y1y2＝(kx1＋2)(kx2＋2)＝k2x1x2＋2k(x1＋x2)＋4＝11＋2k42k2 ＋－ 1＋324kk22＋4＝41－ ＋44kk22， ∵直线 l 与椭圆 C 交于不同两点，则 Δ＞0，
即
256k2－48(1＋4k2)＞0，解得
A. 2 C.32
B. 3
D.
6 2
[解析] (1)由抛物线 y2＝4x，有 2p＝4⇒p＝2，焦点坐标
为(1,0)，双曲线的渐近线方程为 y＝± 3x，不妨取其中一
条
3x－y＝0，由点到直线的距离公式，有 d＝|
3×1－0| 3＋1
＝ 23.故选 B.
(2)焦点 F1(－ 3，0)，F2( 3，0)，在 Rt△AF1F2 中，|AF1| ＋|AF2|＝4，|AF1|2＋|AF2|2＝12，所以可解得|AF2|－|AF1|
[解析] (1)⊙C2的圆心为C2(4,0)，半径为2，设动圆的圆 心为M，半径为r，因为动圆与⊙C1外切，又与⊙C2内切， 所以r＞2，|MC1|＝r＋1①，|MC2|＝r－2②. 由①－②得|MC1|－|MC2|＝3＜|C1C2|＝4. 根据双曲线的定义知，动圆圆心的轨迹是以C1，C2为焦 点的双曲线靠近C2的一支．
又离心率 e＝ac＝ 22，
∴c＝2 2，∴b2＝a2－c2＝8， ∴椭圆 C 的方程为1x62＋y82＝1.
圆锥曲线的方程与性质
椭圆、双曲线、抛物线的几何性质，主要指图形的范围、
对称性，以及顶点坐标、焦点坐标、中心坐标、离心率、
准线、渐近线以及几何元素a，b，c，e之间的关系等．
(1)(2013·高考四川卷)抛物线 y2＝4x 的焦点到双曲
(1)若点 P 到点 F(0,2)的距离比它到直线 y＋4＝0的距离小 2则 P 的轨迹方程为( C )
A．y2＝8x
B．y2＝－8x
C．x2＝8y
D．x2＝－8y
(2)(2014·湖南岳阳质检)在平面直角坐标系 xOy 中，椭圆 C
的中心为原点，焦点 F1，F2 在 x 轴上，离心率为 22.过 F1 的直线 l 交 C 于 A，B 两点，且△ABF2 的周长为 16，那 么 C 的方程为__1x_62_＋__y8_2_＝__1______．
线 x2－y32＝1 的渐近线的距离是( B )
1
3
A.2
B. 2
C．1
D. 3
(2)(2013·高考浙江卷)如图，F1，F2 是椭圆 C1：x42＋y2＝1
与双曲线 C2 的公共焦点，A，B 分别是 C1，C2 在第二、 四象限的公共点．若四边形 AF1BF2 为矩形，则 C2 的离心 率是( D )
[解] (1)依题意知 ac＝ 23， a2＝b2＋c2，
解得a＝2， b＝1，
故椭圆 C 的方程为x42＋y2＝1.
(2)如图，依题意知，直线 l 的斜率必存在，
设直线 l 的方程为 y＝kx＋2，A(x1，y1)，B(x2，y2)，
y＝kx＋2，
联立x42＋y2＝1
消去 y 整理得(1＋4k2)x2＋16kx＋12＝
(1)(2014·云南保山质检)动圆与⊙C1：x2＋y2＝1 外 切，与⊙C2：x2＋y2－8x＋12＝0 内切，则动圆圆心的轨 迹是__以__C_1_，__C_2_为__焦__点__的__双__曲__线__的__右__支__________． (2)(2014·四川成都质检)P 是椭圆xa22＋by22＝1 上的任意一点， F足1、O→QF＝2 是P→F它1＋的P两→F个2，焦则点动，点OQ为的坐轨标迹原方点程，是有_4一x_a2_2动＋__点4_yb_22_Q＝．满1
＝2
2，故双曲线的离心率 e＝
3＝ 2
26，选
D.
直线与圆锥曲线的位置关系
直线与圆锥曲线的位置关系主要有： (1)有关直线与圆锥曲线公共点的个数问题，应注意数形结合； (2)有关弦长问题，应注意运用弦长公式及根与系数的关系； (3)有关垂直问题，应注意运用斜率关系及根与系数的关系，尽 量设而不求，简化运算．
已知椭圆 C：xa22＋by22＝1(a＞b＞0)．
(1)若椭圆的长轴长为 4，离心率为 23，求椭圆 C 的标准方 程； (2)在(1)的条件下，设过定点 M(0,2)的直线 l 与椭圆 C 交 于不同的两点 A，B，且∠AOB 为锐角(O 为坐标原点)， 求直线 l 的斜率 k 的取值范围．
2a＝4，