历届数学数列理(2007-2012)教师版

合集下载

07-13年广东高考数学理科数列真题(含答案)

07-13年广东高考数学理科数列真题(含答案)-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN5.已知数列{a n }的前n 项和29n S n n =-，第k 项满足58k a <<,则k = A. 9 B. 8 C. 7 D. 621.（本小题满分14分）已知函数2()1, f x x x αβ=+-、是方程()0f x =的两个根()αβ>,()f x '是()f x 的导数.设11()1,(1,2,)()n n n n f a a a a n f a +==-=', (1)求αβ、的值；(2)证明：对任意的正整数n ，都有n a α>; (3)记ln(1,2,)n n n a b n a βα-==-,求数列{}n b 的前n 项和n S .2．记等差数列{}n a 的前n 项和为n S ，若112a =，420S =，则6S =（）A ．16B ．24C ．36D ．4821．（本小题满分12分）设p q ，为实数，αβ，是方程20x px q -+=的两个实根，数列{}n x 满足1x p =，22x p q =-，12n n n x px qx --=-（34n =，，…）．（1）证明：p αβ+=，q αβ=；（2）求数列{}n x 的通项公式；（3）若1p =，14q =，求{}n x 的前n 项和n S ．４．巳知等比数列{}n a 满足0,1,2,n a n >=，且25252(3)n n a a n -⋅=≥，则当1n ≥时，2123221log log log n a a a -+++=（）Ａ．(21)n n - Ｂ．2(1)n + Ｃ．2n Ｄ．2(1)n -21．（本小题满分14分）已知曲线22:20(1,2,)n C x nx y n -+==．从点(1,0)P -向曲线n C 引斜率为(0)n n k k >的切线n l ，切点为(,)n n n P x y ．（１）求数列{}{}n n x y 与的通项公式；（２）证明：13521n n nxx x x x y -⋅⋅⋅⋅<<4.已知{}n a 为等比数列,n S 是它的前n 项和.若2312a a a ⋅=, 且4a 与72a 的等差中项为54,则5S =A.35B.33C.31D.292011年广东高考理科卷11. 等差数列{}n a 前9项的和等于前4项的和. 若141,0k a a a =+=，则k=____________.20.（本小题共14分）设b>0,数列{}n a 满足a 1=b ，11(2)22n n n nba a n a n --=≥+-.（1）求数列{}n a 的通项公式；（2）证明：对于一切正整数n ，11 1.2n n n b a ++≤+11.已知递增的等差数列{}n a 满足21321,4a a a ==-，则n a =_____________19. （本小题满分14分）设数列{a n }的前n 项和为S n ，满足2S n =an+1-2n+1，n ∈N ﹡,且a 1，a 2+5，a 3成等差数列。

2007-2012年高考新课标全国卷(文理科数学)考点分布统计表

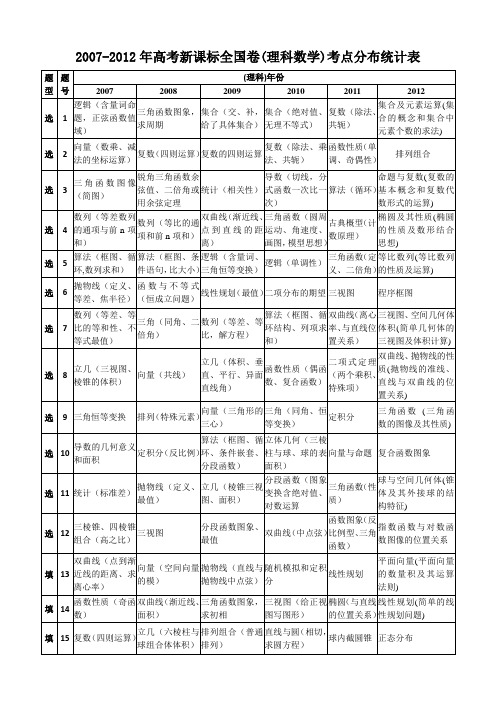
2007-2012年高考新课标全国卷(理科数学)考点分布统计表2007-2012年高考新课标全国卷(文科数学)考点分布统计表总结07-12年（共6年）高考新课标全国卷试题，结合2013年考纲，对文科数学每部分考点分析如下：1、集合（5分）：每年1题，交并补子集运算为主，常与一、二次不等式（也有简单绝对值不等式，简单根式不等式）等交汇，新定义运算也有较小的可能，但是难度较低；基本上每年都是送分题，相信大幅变动的可能性不大。

2、简易逻辑（0-5分）：2010、2011、2012三年没有直接考查，前三年考查“任意”与“存在”类命题的否定、判断真假等。

2013年直接考查很有可能，热点是“充要条件”，注意区分否定与否命题，同样相信难度不会大。

3、算法（5分）：每年一个框图，其中五年考查输出值，只有08年判断条件。

送分题，难度较低，注意与数列求和、整数解、大小比较的融合。

4、复数（5分）：每年1题，四则运算为主，难度较小，送分题。

注意看清实部？虚部？共轭复数？5、三角函数与解三角形（15-20分）：基本每年至少两题，主要考查三角求值，三角恒等变换及性质，图象变换是难点，前三年17题位置以大题考查，其中两年考查解三角形，08、12年直接解三角形。

不管大题小题，难度不大，但学生不容易得分，主要是对三角函数基础知识应用不熟练。

2013年估计仍以前几年考查方向为主线，在17题位置以大题考查有可能，本节知识较碎，复习时注重练习各个击破。

6、平面向量（5分）：基本上每年1题，难度都不大，简单的代数或坐标运算，考查向量共线、垂直、求夹角等，2013年难度应该不会太大，要明白向量是一种解题工具，注意向量相关的几何意义（模、加减法、数量积）。

7、线性规划（0-5分）：除了07年，每年1题，都是常规的线性区域找最优解，难度不大，2013年估计会有1题，注意实际背景下的线性规划问题，特别是“整数解”容易忽视，小心通过目标函数的最值作为条件反求可行域内的参数问题（对文科生来说是难点）。

【最新经典专题】高考数学讲练测系列专题03 数列(教师版).pdf

【专项冲击波】2013年高考数学讲练测系列专题03 数列（教师版）【考纲解读】 1.理解数列的概念，了解数列通项公式的意义，了解递推公式是给出数列的一种方法，并能根据递推公式写出数列的前几项. 2.理解等差数列的概念，掌握等差数列的通项公式与前n项和公式，并能运用公式解答简单的问题. 3.理解等比数列的概念，掌握等比数列的通项公式与前n项和公式，并能运用公式解决简单的问题. 【考点预测】 1.等差（比）数列的基本知识是必考内容，这类问题既有选择题、填空题，也有解答题；难度易、中、难三类皆有. 2.数列中an与Sn之间的互化关系也是高考的一个热点. 3.函数思想、方程思想、分类讨论思想等数学思想方法在解决问题中常常用到，解答试题时要注意灵活应用. 4.解答题的难度有逐年增大的趋势,还有一些新颖题型,如与导数和极限相结合等. 因此复习中应注意： 1.数列是一种特殊的函数，学习时要善于利用函数的思想来解决.如通项公式、前n项和公式等. 2.运用方程的思想解等差（比）数列，是常见题型，解决此类问题需要抓住基本量a1、d（或q），掌握好设未知数、列出方程、解方程三个环节，常通过“设而不求，整体代入”来简化运算. 3.分类讨论的思想在本章尤为突出.学习时考虑问题要全面，如等比数列求和要注意q=1和q≠1两种情况等等. 4.等价转化是数学复习中常常运用的，数列也不例外.如an与Sn的转化；将一些数列转化成等差（比）数列来解决等.复习时，要及时总结归纳. 5.深刻理解等差（比）数列的定义，能正确使用定义和等差（比）数列的性质是学好本章的关键. 6.解题要善于总结基本数学方法.如观察法、类比法、错位相减法、待定系数法、归纳法、数形结合法，养成良好的学习习惯，定能达到事半功倍的效果. . 【要点梳理】 1.证明数列是等差数列的两种基本方法：（1）定义法：为常数；（2）等差中项法：. 2.证明数列是等比数列的两种基本方法：（1）定义法：(非零常数)；（2）等差中项法：. 3.常用性质:(1)等差数列中,若,则; (2)等比数列中,若,则. 4.求和: (1)等差等比数列,用其前n项和求出; (2)掌握几种常见的求和方法:错位相减法、裂项相消法、分组求和法、倒序相加法; (3)掌握等差等比数列前n项和的常用性质. 【考点在线】考点1 等差等比数列的概念及性质在等差、等比数列中，已知五个元素或，中的任意三个，运用方程的思想，便可求出其余两个，即“知三求二”。

历届高考数学真题汇编专题4数列理

精品文档，知识共享，下载后可随意编辑!【2012高考试题】一、选择题1.【2012高考真题重庆理1】在等差数列｛a n｝中，a2 =1，a^5则｛务｝的前5项和S s =A. 7B.15C.20D.25【答案】B【岸析】因为的=1 •= 5 »所以还*逐=还+化=6 *所以数列的前 '项和二処5)代6皿选玫2.【2012高考真题浙江理7】设S n是公差为d ( d丰0)的无穷等差数列｛a n｝的前n项和，则下列命题错误的是A. 若d v 0,则数列｛S ｝有最大项B. 若数列｛S ｝有最大项，则d v 0C. 若数列｛S ｝是递增数列，则对任意n • N*，均有S n 0D. 若对任意n • N*，均有S n- 0，则数列｛S ｝是递增数列【答案】C【解析】选项C显然是错的，举出反例：一1, 0, 1,真3,...满足数列◎«｝是超增数列*但是X A 0不成立.故选C；3.【2012高考真题新课标理5】已知订爲为等比数列，a4• a7 = 2，a5a^ -8，则a1 s t二( )(A) 7 (B) 5 (C)」(D)-【答案】D【解析】因为｛a n｝为等比数列，所以a5a6二a4a7 = -8，又a4 a^ 2，所以精品文档，知识共享，下载后可随意编辑!a4 =4，a? - -2 或印- -2，a? =4 .若a^4，a^ -2，解得印- -8, a® =1，7.【2012高考真题湖北理7】定义在(-：：,0) (0,；)上的函数f (x)，如果对于任意给定的等精品文档，知识共享，下载后可随意编辑!a 1 ■ aw - -7 ；若印--2, a 7 - 4，解得a 1^ - -8, a 1 = 1，仍有 a 1 a 1^ - -7，综上选D.中，正数的个数是(【答案】D【解析】当1S<24时・a,. >0,当26<R <49时,但其绝对值要小于l<w<24 Bl时相应的值，二当l<n<100时，均有S. >0«(A)58 (B)88(C)143(D)176【答案】B11x(a“ + a“)【解析】在等差数列中，；a 1 a 1^a 4 a^16r s 1111188，答案为B26.【2012高考真题四川理12】设函数f (x) =2x -cosx ，｛a n ｝是公差为'的等差数列,82f(aj f®)…_f ©5)=5二，则［f®)］ —a^ =()1 2、 ■:16【答案】D 【解析】/(^) ------- /(^)-(2^-COS ^)-(2A 一8$还) -------- (2A 一COM 逐)■ 即©+幻+ 码)-(cos^ +cos 勺+…+匚6碍)而SJ 是公差为—的等差数列,代入2(玛 + 碍 +---+d7j)—(cos^ +cosa 3 +-- -l-cos^) = 5^i BP 10碍一［com (込——)+ cosffl-+ cos a- + co 或口： + —} + cos(a- + —)］二 (2cos —+ 2COJ —+ l)casa ?g - g ' 4 4 8 -不是丁的倍数，：10冬=5^t a 3= — . A= (2x —-0)a -(— - —)(— -IM土2«」■r13T=—,故选D4.【2012高考真题上海理18】设a n =〔sin 兰n 25 ，S n• a^- - a n ，在 S 2,…,S 100A . 25.50 .75 .100相应的值，当51S^<74时，当7幺打兰四时,乩: <山但其绝对值要小于51S?; <745.【2012高考真题辽宁理6】在等差数列｛a n ｝中，已知34+38=16,则该数列前 11项和S 11 =132、 ■:16精品文档，知识共享，下载后可随意编辑!167.【2012高考真题湖北理7】定义在(-：：,0) (0,；)上的函数f (x)，如果对于任意给定的等精品文档，知识共享，下载后可随意编辑!比数列｛a n ｝ , ｛f(a n )｝仍是等比数列，则称 f(x)为“保等比数列函数” •现有定义在(-； 0)(0,；)上的如下函数：① f(x)r x 2 ； ② f(x)=2x ；③ f(x)=J i T | ； ④ f(x)=ln|x|.贝淇中是“保等比数列函数”的f(x)的序号为A .①②B .③④C.①③D.②④ 【答案】C【解析】等上匕数列性质，冬2心=迂1 -①/qSa ：应詁乙=J =产匕一 ② 于 Si)f (务 J H 2 4- = f' 3*4)!③)f (务-J =少/爲=7K-ii④ /'©少匕二尸(％J •选 C8. 【2012高考真题福建理2】等差数列｛a n ｝中，a i +a 5=10,a 4=7,则数列｛a n ｝的公差为A.1B.2C.3D.4【答案】B.【解析】由等差中项的性质知 a 3二埜旦=5，又；a 4 = 7,. d = a 4 - a 3 = 2.故选B.29. 【2012高考真题安徽理 4】公比为3 2等比数列｛a n ｝的各项都是正数，且 a 3an =16，则也步()(A) 4(B)5 (C)「 (D)【答案】Ba 2 = 16 二 a 7 = 4= a 16 = a 7 q 9 = 32 二 log 2 a 16 = 5.已知等差数列｛a n ｝的前n 项和为S ，a 5=5，S 5=15，则数列【答案】A【解析】a 3a |^16 — 10.【2012高考真题全国卷理的前 100项和为(A) 100(B)10199竺(C)10199 100(D)101100精品文档，知识共享，下载后可随意编辑!22【解析】由乞二見Sw = 1二得白：=M = 1 ’所以口 t = 1+07-二I 二吃，所以11 1 1------- = ---------- =—— --------亚理-1科（拧+ 1） n 冲+ 1亠丄二竺选A100 101 101 101、填空题11. [ 2012高考真题浙江理13】设公比为q(q > 0)的等比数列｛a n ｝的前n 项和为S 。

备战历届高考数学真题汇编专题14_复数_理(2007-2012).pptx

12.【2012 高考真题安徽理 1】复数 z 满足： (z i)(2 i) 5 ；则 z （） ( A) 2 2i (B) 2 2i (C) i (D) i
13．【2012 高考真题天津理 1】i 是虚数单位，复数 7 i = 3i
（A） 2 + i （B）2 – i （C）-2 + i （D）-2 – i 【答案】B
学海无涯
3、(2011 年高考安徽卷江苏 3)设复数 i 满足i(z 1) 3 2i （i 是虚数单位），则 z 的实部
是【答案】1
【解析】因为 z 1 3 2i (3 2i)(i) 2 3i ，所以 z 1 3i ,故 z 的实部是 1. i
三、解答题: 1．(2011 年高考上海卷理科 19)（12 分）已知复数 z1 满足(z1 2)(1 i) 1 i（i 为虚数单位），
学海无涯
n=1 n=2 n=3 n=4 由此推断，当 n=6 时，黑色正方形互不相邻的着色方案共有种，至少有两个黑色正方形相邻的着色方案共有种.（结果用数值表示）
4 ．(2011 年高考陕西卷理科 13)观察下列等式
照此规律，第 n 个等式为【答案】 n (n 1) (n 2) L (3n 2) (2n 1)2
当 n N 且 n 2 时， f (x) f ( f (x)) .
n
n1
学海无涯
【答案】
x
(2n 1)x 2n
【解析】观察知:四个等式等号右边的分母为 x 2,3x 4, 7x 8,15x 16 ,即
(2 1)x 2,(4 1)x 4,(8 1)x 8,(16 1)x 16 ,所以归纳出分母为 fn (x) f ( fn1(x)) 的
虚数”的（）

十年真题(2010-2019)高考数学(理)分类汇编专题07 数列(新课标Ⅰ卷)(原卷版)

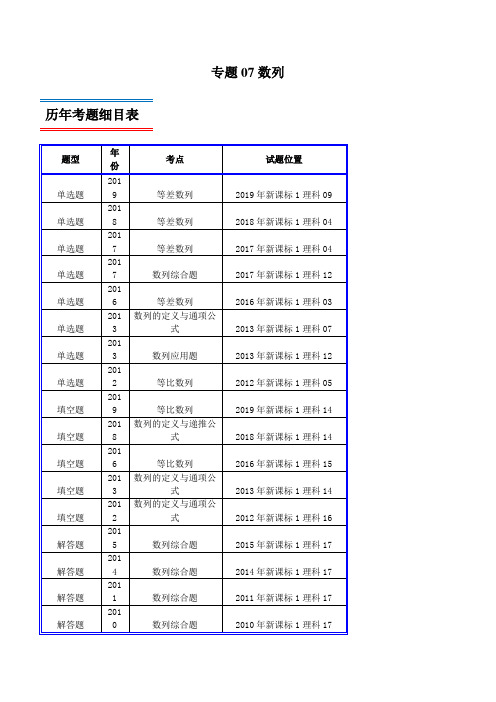
专题07数列历年考题细目表历年高考真题汇编1．【2019年新课标1理科09】记S n为等差数列{a n}的前n项和．已知S4＝0，a5＝5，则（）A．a n＝2n﹣5 B．a n＝3n﹣10 C．S n＝2n2﹣8n D．S n n2﹣2n2．【2018年新课标1理科04】记S n为等差数列{a n}的前n项和．若3S3＝S2+S4，a1＝2，则a5＝（）A．﹣12 B．﹣10 C．10 D．123．【2017年新课标1理科04】记S n为等差数列{a n}的前n项和．若a4+a5＝24，S6＝48，则{a n}的公差为（）A．1 B．2 C．4 D．84．【2017年新课标1理科12】几位大学生响应国家的创业号召，开发了一款应用软件．为激发大家学习数学的兴趣，他们推出了“解数学题获取软件激活码”的活动．这款软件的激活码为下面数学问题的答案：已知数列1，1，2，1，2，4，1，2，4，8，1，2，4，8，16，…，其中第一项是20，接下的两项是20，21，再接下的三项是20，21，22，依此类推．求满足如下条件的最小整数N：N＞100且该数列的前N项和为2的整数幂．那么该款软件的激活码是（）A．440 B．330 C．220 D．1105．【2016年新课标1理科03】已知等差数列{a n}前9项的和为27，a10＝8，则a100＝（）A．100 B．99 C．98 D．976．【2013年新课标1理科07】设等差数列{a n}的前n项和为S n，若S m﹣1＝﹣2，S m＝0，S m+1＝3，则m＝（）A．3 B．4 C．5 D．67．【2013年新课标1理科12】设△A n B n∁n的三边长分别为a n，b n，c n，△A n B n∁n的面积为S n，n＝1，2，3…若b1＞c1，b1+c1＝2a1，a n+1＝a n，，，则（）A．{S n}为递减数列B．{S n}为递增数列C．{S2n﹣1}为递增数列，{S2n}为递减数列D．{S2n﹣1}为递减数列，{S2n}为递增数列8．【2012年新课标1理科05】已知{a n}为等比数列，a4+a7＝2，a5a6＝﹣8，则a1+a10＝（）A．7 B．5 C．﹣5 D．﹣79．【2019年新课标1理科14】记S n为等比数列{a n}的前n项和．若a1，a42＝a6，则S5＝．10．【2018年新课标1理科14】记S n为数列{a n}的前n项和．若S n＝2a n+1，则S6＝．11．【2016年新课标1理科15】设等比数列{a n}满足a1+a3＝10，a2+a4＝5，则a1a2…a n的最大值为64．12．【2013年新课标1理科14】若数列{a n}的前n项和为S n a n，则数列{a n}的通项公式是a n＝．13．【2012年新课标1理科16】数列{a n}满足a n+1+（﹣1）n a n＝2n﹣1，则{a n}的前60项和为．14．【2015年新课标1理科17】S n为数列{a n}的前n项和，已知a n＞0，a n2+2a n＝4S n+3（I）求{a n}的通项公式：（Ⅱ）设b n，求数列{b n}的前n项和．15．【2014年新课标1理科17】已知数列{a n}的前n项和为S n，a1＝1，a n≠0，a n a n+1＝λS n﹣1，其中λ为常数．（Ⅰ）证明：a n+2﹣a n＝λ（Ⅱ）是否存在λ，使得{a n}为等差数列？并说明理由．16．【2011年新课标1理科17】等比数列{a n}的各项均为正数，且2a1+3a2＝1，a32＝9a2a6，（Ⅰ）求数列{a n}的通项公式；（Ⅱ）设b n＝log3a1+log3a2+…+log3a n，求数列{}的前n项和．17．【2010年新课标1理科17】设数列满足a1＝2，a n+1﹣a n＝3•22n﹣1（1）求数列{a n}的通项公式；（2）令b n＝na n，求数列{b n}的前n项和S n．考题分析与复习建议本专题考查的知识点为：数列的概念与简单表示法，等差数列及其前n项和，等比数列及其前n项和，数列求和，数列求通项等.历年考题主要以选择填空或解答题题型出现.重点考查的知识点为：等差数列及其前n项和，等比数列及其前n项和，数列求和，数列求通项等.预测明年本考点题目会比较稳定，备考方向以知识点等差数列及其前n 项和，等比数列及其前n 项和，数列求和，数列求通项为重点较佳.最新高考模拟试题1．等差数列{}n a ，等比数列{}n b ，满足111a b ==，53a b =，则9a 能取到的最小整数是（） A ．1-B ．0C ．2D ．32．中国古代数学名著《九章算术》中有这样一个问題今有牛、马、羊食人苗，苗主责之粟五斗，羊主曰“我羊食半马、“马主曰“我马食半牛，”今欲衰偿之，问各出几何?此问题的译文是今有牛、马、羊吃了别人的禾苗，禾苗主人要求赔偿5斗粟、羊主人说“我羊所吃的禾苗只有马的一半，”马主人说“我马所吃的禾苗只有牛的一半，“打算按此比例偿还，他们各应偿还多少？该问题中，1斗为10升，则马主人应偿还( )升粟？ A ．253B ．503C ．507D ．10073．我国古代的《洛书》中记载着世界上最古老的一个幻方：如图，将1，2，…，9填入33⨯的方格内，使三行，三列和两条对角线上的三个数字之和都等于15.一般地，将连续的正整数21,2,3,,n L 填入n n ⨯个方格中，使得每行，每列和两条对角线上的数字之和都相等，这个正方形叫做n 阶幻方.记n 阶幻方的对角线上的数字之和为n N ，如图三阶幻方的315N =，那么 9N 的值为（）A ．41B ．45C ．369D ．3214．设数列{}n a 的前n 项和为n S ，且11a = 2(1)()nn S a n n N n *=+-∈，则数列13n S n ⎧⎫⎨⎬+⎩⎭的前10项的和是（） A ．290B ．920C ．511D ．10115．意大利数学家列昂那多·斐波那契以兔子繁殖为例，引入“兔子数列”：1,1,2,3,5,8,13,21,34,55,L L ，即()()()()()121,12F F F n F n F n ===-+-()3,n n N*≥∈，此数列在现代物理“准晶体结构”、化学等都有着广泛的应用．若此数列被2整除后的余数构成一个新数列{}n a ，则数列{}n a 的前2019项的和为（） A ．672B ．673C ．1346D ．20196．已知数列{}n a 是等比数列，数列{}n b是等差数列，若2610a a a ⋅⋅=16117b b b π++=，则21039tan1b b a a +-⋅的值是（）A ．1BC． D．7．已知数列{}n a 满足2*123111()23n a a a a n n n N n++++=+∈L ，设数列{}n b 满足：121n n n n b a a ++=，数列{}n b 的前n 项和为nT，若*()1n n N T n nλ<∈+恒成立，则实数λ的取值范围为（） A ．1[,)4+∞B ．1(,)4+∞ C ．3[,)8+∞ D ．3(,)8+∞8．已知函数()y f x =的定义域为R ，当0x <时()1f x >，且对任意的实数,x y R ∈，等式()()()f x f y f x y =+成立，若数列{}n a 满足()()1111n n f a f n N a *+⎛⎫=∈ ⎪+⎝⎭，且()10a f =，则下列结论成立的是（） A ．()()20162018f a f a > B ．()()20172020f a f a > C ．()()20182019f a f a > D ．()()20162019f a f a >9．在数列{}n a 中，1111,,(*)2019(1)n n a a a n N n n +==+∈+，则2019a 的值为______． 10．已知正项等比数列{}n a 满足5432a a a +=，若存在两项m a ，n a，使得1a =，则91m n+的最小值为__________． 11．已知数列{}n a 满足对*,m n N ∀∈，都有m n m n a a a ++=成立，72a π=，函数()f x =2sin 24cos2x x +，记()n n y f a =，则数列{}n y 的前13项和为______．12．已知数列{}n a 的前n 项和为n S ，满足22()n n S a n n N *=+∈，则n a =_____．13．等差数列{}n a 中，410a =且3a ，6a ，10a 成等比数列，数列{}n a 前20项的和20S =____ 14．已知正项等比数列{}n a 的前n 项和为n S ．若9362S S S =+，则631S S +取得最小值时，9S 的值为_______．15．设数列{}n a 的前n 项和为n S ，且满足11222n n a a a n -++⋯+=，则5S =____．16．已知数列{}n a 满足112(1)0,4n n n a na a ++-==，则数列(1)(2)na n n ⎧⎫⎨⎬++⎩⎭的前n 项和为___________.17．定义：从数列{}n a 中抽取(,3)m m N m ∈≥项按其在{}n a 中的次序排列形成一个新数列{}n b ，则称{}n b 为{}n a 的子数列；若{}n b 成等差（或等比），则称{}n b 为{}n a 的等差（或等比）子数列. （1）记数列{}n a 的前n 项和为n S ，已知21n n S =-. ①求数列{}n a 的通项公式；②数列{}n a 是否存在等差子数列，若存在，求出等差子数列；若不存在，请说明理由. （2）已知数列{}n a 的通项公式为()n a n a a Q +=+∈，证明：{}n a 存在等比子数列. 18．在等差数列{}n a 中，已知公差2d =，2a 是1a 与4a 的等比中项（1）求数列{}n a 的通项公式；（2）若数列{}n b 满足3122331313131n n n b b b ba =++++++++L ，求数列{}nb 的通项公式；（3）令()*4n nn a b c n N =∈，数列{}n c 的前n 项和为n T . 19．已知等差数列{}n a 满足32421,7a a a =-=，等比数列{}n b 满足()35242b b b b +=+，且()2*22n n b b n =∈N .（1）求数列{}n a ，{}n b 的通项公式；（2）记数列{}n a 的前n 项和为n S ，若数列{}n c 满足()*1212n n nc c c S n b b b ++⋯+=∈N ，求{}n c 的前n 项和为n T .20．等差数列{}n a 前n 项和为n S ，且432S =，13221S =．（1）求{}n a 的通项公式n a ；（2）数列{}n b 满足()*1n n n b b a n N+-=∈且13b =，求1n b ⎧⎫⎨⎬⎩⎭的前n 项和n T ． 21．设{}n a 是单调递增的等比数列，n S 为数列{}n a 的前n 项和．已知313S =，且13a +，23a ，35a +构成等差数列．（1）求n a 及n S ；（2）是否存在常数λ．使得数列{}n S λ+是等比数列?若存在，求λ的值；若不存在，请说明理由． 22．对于无穷数列{}n a ，{}n b ，若{}{}1212max ,,,min ,,,k k k b a a a a a a =-L L ，1,2,3,k =L ，则称{}n b 是{}n a 的“收缩数列”.其中{}12max ,,,k a a a L ，{}12min ,,,k a a a L 分别表示12,,,k a a a L 中的最大数和最小数.已知{}n a 为无穷数列，其前n 项和为n S ，数列{}n b 是{}n a 的“收缩数列”. （1）若21n a n =+，求{}n b 的前n 项和；（2）证明：{}n b 的“收缩数列”仍是{}n b ；（3）若121(1)(1)(1,2,3,)22n n n n n n S S S a b n +-+++=+=L L 且11a =，22a =，求所有满足该条件的{}n a .。

数列求和教师版

数列求和教师版数列求和教师版⼀、错位相减法（2009全国卷Ⅰ理）在数列{}n a 中，11111,(1)2n n n n a a a n ++==++ （I ）设nn a b n=，求数列{}n b 的通项公式（II ）求数列{}n a 的前n 项和n S 分析：（I ）由已知有1112n n n a a n n +=++11 2n n n b b +∴-=利⽤累差迭加即可求出数列{}n b 的通项公式: 1122n n b -=-(*n N ∈)（II ）由（I ）知122n n n a n -=-,∴n S =11(2)2n k k k k -=-∑111(2)2n nk k k kk -===-∑∑⽽1(2)(1)nk k n n ==+∑,⼜112nk k k-=∑是⼀个典型的错位相减法模型，易得1112422nk n k k n --=+=-∑ ∴n S =(1)n n +1242n n -++- (2009湖北卷理)已知数列{}n a 的前n 项和11()22n n n S a -=--+（n 为正整数）。

（Ⅰ）令2n n n b a =，求证数列{}n b 是等差数列，并求数列{}n a 的通项公式；(Ⅱ）令1n n n c a n +=，12........n n T c c c =+++试⽐较n T 与521nn +的⼤⼩，并予以证明。

解（I ）在11()22n n n S a -=--+中，令n=1，可得1112n S a a =--+=，即11 2a =当2n ≥时，21111111()2()22n n n n n n n n n S a a S S a a ------=--+∴=-=-++，， 11n 1112a (),212n n n n n a a a ----∴=+=+n 即2.112,1,n 21n n n n n n b a b b b --=∴=+≥-= n 即当时，b . ⼜1121,b a ==∴数列}{n b 是⾸项和公差均为1的等差数列. 于是1(1)12,2nn n n n n b n n a a =+-?==∴=. (II)由（I ）得11(1)()2n n n n c a n n +==+，所以 23111123()4()(1)()2222n n T n =?+?+?+++K2341111112()3()4()(1)()22222n n T n +=?+?+?+++K由①-②得231111111()()()(1)()22222nn n T n +=++++-+K11111[1()]133421(1)()122212332n n n n nn n n T -++-+=+-+=--+∴=- 535(3)(221)3212212(21)n n n n n n n n n T n n n ++---=--=+++ 于是确定521n n T n +与的⼤⼩关系等价于⽐较221nn +与的⼤⼩由23452211;2221;2231;2241;225;可猜想当322 1.nn n ≥>+时，证明如下：证法1：（1）当n=3时，由上验算显⽰成⽴。

2007-2019年新课标全国卷理——数列

2007－2019年新课标全国卷数列题（2007宁夏卷）4．已知{}n a 是等差数列，1010a =，其前10项和1070S =，则其公差d =（）Ａ．23-Ｂ．13-Ｃ．13Ｄ．237．已知0x >，0y >，x a b y ，，，成等差数列，x c d y ，，，成等比数列，则2()a b cd+的最小值是（）Ａ．0 Ｂ．1 Ｃ．2 Ｄ．4（无数列解答题）（2008宁夏卷）4、设等比数列{}n a 的公比2q =，前n 项和为n S ，则42S a =（） A. 2B. 4C.152D. 17217、（本小题满分12分）已知数列{}n a 是一个等差数列，且21a =，55a =-。

（1）求{}n a 的通项n a ；（2）求{}n a 前n 项和n S 的最大值。

（2009宁夏卷）（7）等比数列{}n a 的前n 项和为n s ，且41a ，22a ，3a 成等差数列。

若1a =1，则4s =（A ）7 （B ）8 （3）15 （4）16 （16）等差数列{n a }前n 项和为n S 。

已知1m a -+1m a +-2ma =0，21m S -=38,则m=_______（无数列解答题）（2010课标全国卷）（无数列小题）17.（本小题满分12分）设数列{}n a 满足21112,32n n n a a a -+=-=(I)求数列{}n a 的通项公式；(II)令n n b na =，求数列的前n 项和n S .（2011课标全国卷）（无数列小题）17．（本小题满分12分）等比数列{}n a 的各项均为正数，且212326231,9a a a a a +==．（Ⅰ）求数列{}n a 的通项公式．（Ⅱ）设31323log log log n n b a a a =++⋅⋅⋅+求数列1n b ⎧⎫⎨⎬⎩⎭的前n 项和．（2012课标全国卷）5．已知{}n a 为等比数列，472a a +=，568a a =-，则110a a +=( )A ．7B ．5C ．-5D ．-716．数列{}n a 满足1(1)21nn n a a n ++-=-，则{}n a 的前60项和为_______（无数列解答题）（2013课标全国I 卷）7、设等差数列{a n }的前n 项和为S n ，1m S -＝－2，m S ＝0，1m S +＝3，则m ＝ ( ) A 、3 B 、4 C 、5 D 、612、设△A n B n C n 的三边长分别为a n ,b n ,c n ，△A n B n C n 的面积为S n ，n =1,2,3,…若b 1＞c 1，b 1＋c 1＝2a 1，a n ＋1＝a n ，b n ＋1＝c n ＋a n 2，c n ＋1＝b n ＋a n2，则( ) A 、{S n }为递减数列 B 、{S n }为递增数列 C 、{S 2n －1}为递增数列，{S 2n }为递减数列 D 、{S 2n －1}为递减数列，{S 2n }为递增数列 14、若数列{n a }的前n 项和为S n ＝2133n a +，则数列{n a }的通项公式是n a =______. （无数列解答题）（2013课标全国II 卷）（3）等比数列{a n }的的前n 项和为S n ，已知S 3 = a 2 +10a 1 ，a 5 = 9，则a 1 =（A ）13 （B ）- 13 （C ）19 （D ）- 19（16）等差数列{a n }的前n 项和为S n ，已知S 10 = 0，S 15 = 25，则nS n 的最小值为 . （无数列解答题）（2014课标全国Ⅰ卷）17. (本小题满分12分)已知数列{n a }的前n 项和为n S ，1a =1，0n a ≠，11n n n a a S λ+=-，其中λ为常数. （Ⅰ）证明：2n n a a λ+-=；（Ⅱ）是否存在λ，使得{n a }为等差数列？并说明理由.（2014课标全国Ⅱ卷）(无数列小题)17.（本小题满分12分）已知数列{}n a 满足1a =1，131n n a a +=+.（Ⅰ）证明{}12n a +是等比数列，并求{}n a 的通项公式；（Ⅱ）证明：1231112na a a ++<…+.（2015课标全国Ⅰ卷）（17）（本小题满分12分）n S 为数列{}n a 的前n 项和.已知20,243n n n n a a a S >+=+，（Ⅰ）求{}n a 的通项公式：（Ⅱ）设11n n n b a a +=,求数列{}n b 的前n 项和。

【六年中考】2007-2012全国各地中考数学试题分类汇编第1章有理数

2007-2012全国各地中考数学试题分类汇编第1章有理数2012年全国各地50份中考数学试题分类解析汇编一、选择题1．（2012福州）3的相反数是A ．－3B ．13C ．3D ．－13考点：相反数．专题：存在型．分析：根据相反数的定义进行解答．解答：解：由相反数的定义可知，3的相反数是－3．故选A ．点评：本题考查的是相反数的定义，即只有符号不同的两个数叫做互为相反数．2．（2012福州）今年参观“5·18”海交会的总人数约为489000人，将489000用科学记数法表示为A ．48.9×104B ．4.89×105C ．4.89×104D ．0.489×106 考点：科学记数法—表示较大的数．分析：科学记数法的表示形式为a ×10n 的形式，其中1≤|a |＜10，n 为整数．确定n 的值时，要看把原数变成a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n 是正数；当原数的绝对值＜1时，n 是负数．解答：解：489000＝4.89×105．故选B ．点评：此题考查科学记数法的表示方法．科学记数法的表示形式为a ×10n 的形式，其中1≤|a |＜10，n 为整数，表示时关键要正确确定a 的值以及n 的值． 3、（2012•广州）实数3的倒数是（） A ．﹣ B ． C ．﹣3 D ．3 考点：实数的性质。

专题：常规题型。

分析：根据乘积是1的两个数互为倒数解答．解答：解：∵3×=1，∴3的倒数是．故选B ．点评：本题考查了实数的性质，熟记倒数的定义是解题的关键． 4. （2012广东湛江）2的倒数是（） A ．2 B ．﹣2 C ．D ．﹣解析：：∵2×=1，∴2的倒数是．故选C．5. （2012广东湛江）国家发改委已于2012年5月24日核准广东湛江钢铁基地项目，项目由宝钢湛江钢铁有限公司投资建设，预计投产后年产10200000吨钢铁，数据10200000用科学记数法表示为（）A．102×105 B．10.2×106 C．1.02×106 D．1.02×107解析：将10200000用科学记数法表示为：1.02×107．故选：D．6．（2012广东）﹣5的绝对值是（）A． 5 B．﹣5 C．D．﹣考点：绝对值。

专题07 数列及其应用-十年(2012-2021)高考数学真题分项详解(全国通用)(解析版)

专题07 数列及其应用【2021年】1．（2021年全国高考甲卷数学（文）试题）记n S 为等比数列{}n a 的前n 项和.若24S =，46S =，则6S =（） A ．7 B ．8C ．9D ．10【答案】A【分析】∵n S 为等比数列{}n a 的前n 项和， ∵2S ，42S S -，64S S -成等比数列 ∵24S =，42642S S -=-= ∵641S S -=， ∵641167S S =+=+=. 故选：A.二、解答题2．（2021年全国高考乙卷数学（文）试题）设{}n a 是首项为1的等比数列，数列{}n b 满足3nn na b =．已知1a ，23a ，39a 成等差数列．（1）求{}n a 和{}n b 的通项公式；（2）记n S 和n T 分别为{}n a 和{}n b 的前n 项和．证明：2nn S T <．【答案】（1）11()3n n a -=，3n n n b =；（2）证明见解析.【分析】因为{}n a 是首项为1的等比数列且1a ，23a ，39a 成等差数列，所以21369a a a =+，所以211169a q a a q =+，即29610q q -+=，解得13q =，所以11()3n n a -=，所以33n n n na nb ==.（2）证明：由（1）可得11(1)313(1)12313nn n S ⨯-==--，211213333n n n n nT --=++++，∵231112133333n n n n nT +-=++++，∵ ∵-∵得23121111333333n n n n T +=++++- 1111(1)1133(1)1323313n n n n n n ++-=-=---，所以31(1)4323n n n n T =--⋅，所以2n n S T -=3131(1)(1)043234323n n n n n n----=-<⋅⋅，所以2n n ST <.3．（2021年全国高考乙卷数学（理）试题）记n S 为数列{}n a 的前n 项和，n b 为数列{}n S 的前n 项积，已知212n nS b +=．（1）证明：数列{}n b 是等差数列; （2）求{}n a 的通项公式．【答案】（1）证明见解析；（2）()3,121,21n n a n n n ⎧=⎪⎪=⎨⎪-≥+⎪⎩. 【分析】（1）由已知212n n S b +=得221n n n b S b =-,且0n b ≠，12n b ≠, 取1n =,由11S b =得132b =, 由于n b 为数列{}n S 的前n 项积，所以1212222212121n n n b b b b b b b ⋅⋅⋅⋅=---,所以1121121222212121n n n b b b b b b b +++⋅⋅⋅⋅=---，所以111221n n n nb bb b +++=-,由于10n b +≠所以12121n n b b +=-，即112n n b b +-=,其中*n N ∈ 所以数列{}n b 是以132b =为首项，以12d =为公差等差数列; （2）由（1）可得，数列{}n b 是以132b =为首项，以12d =为公差的等差数列，()3111222n nb n ∴=+-⨯=+, 22211n n n b nS b n+==-+,当n =1时，1132a S ==, 当n ≥2时,()121111n n n n n a S S n n n n -++=-=-=-++,显然对于n =1不成立, ∵()3,121,21n n a n n n ⎧=⎪⎪=⎨⎪-≥+⎪⎩.4．（2021年全国高考甲卷数学（文）试题）记n S 为数列{}n a 的前n 项和，已知210,3n a a a >=，且数列是等差数列，证明：{}n a 是等差数列. 【答案】证明见解析. 【分析】∵数列是等差数列，设公差为d(n =-=，()n *∈N∵12n S a n =，()n *∈N∵当2n ≥时，()221111112n n n a S S a n a n a n a -=-=--=-当1n =时，11121=a a a ⨯-，满足112n a a n a =-， ∵{}n a 的通项公式为112n a a n a =-，()n *∈N ∵()()111111221=2n n a a a n a a n a a --=----⎡⎤⎣⎦ ∵{}n a 是等差数列.5．（2021年全国高考甲卷数学（理）试题）已知数列{}n a 的各项均为正数，记n S 为{}n a 的前n 项和，从下面∵∵∵中选取两个作为条件，证明另外一个成立．∵数列{}n a 是等差数列：∵数列是等差数列；∵213aa =．注：若选择不同的组合分别解答，则按第一个解答计分．【答案】答案见解析【分析】选∵∵作条件证明∵：(0)an b a =+>，则()2n S an b =+，当1n =时，()211a S a b ==+；当2n ≥时，()()221n n n a S S an b an a b -=-=+--+()22a an a b =-+；因为{}n a 也是等差数列，所以()()222a b a a a b +=-+，解得0b =；所以()221n aa n =-，所以213a a =.选∵∵作条件证明∵：因为213a a =，{}n a 是等差数列，所以公差2112d a a a =-=，所以()21112n n n S na d n a -=+==，)1n +=所以是等差数列.选∵∵作条件证明∵：(0)an b a =+>，则()2n S an b =+，当1n =时，()211a S a b ==+；当2n ≥时，()()221n n n a S S an b an a b -=-=+--+()22a an a b =-+；因为213a a =，所以()()2323a a b a b +=+，解得0b =或43a b =-；当0b =时，()221,21n a a a a n ==-，当2n ≥时，2-1-2n n a a a =满足等差数列的定义，此时{}n a 为等差数列；当43a b =-4=3an b an a =+-03a=-<不合题意，舍去.综上可知{}n a 为等差数列.6．（2021年全国新高考∵卷数学试题）已知数列{}n a 满足11a =，11,,2,.n n na n a a n ++⎧=⎨+⎩为奇数为偶数（1）记2n n b a =，写出1b ，2b ，并求数列{}n b 的通项公式；（2）求{}n a 的前20项和.【答案】（1）122,5b b ==；（2）300.【分析】（1）由题设可得121243212,1215b a a b a a a ==+===+=++=又22211k k a a ++=+，2122k k a a +=+，*()k N ∈故2223k k a a +=+，即13n n b b +=+，即13n n b b +-= 所以{}n b 为等差数列，故()21331n b n n =+-⨯=-. （2）设{}n a 的前20项和为20S ，则2012320S a a a a =++++，因为123419201,1,,1a a a a a a =-=-=-，所以()20241820210S a a a a =++++-()1291091021021023103002b b b b ⨯⎛⎫=++++-=⨯⨯+⨯-= ⎪⎝⎭.【2012年——2020年】1．（2020年全国统一高考数学试卷（文科）（新课标∵））设{}n a 是等比数列，且1231a a a ++=，234+2a a a +=，则678a a a ++=（） A ．12 B ．24C ．30D ．32【答案】D【分析】设等比数列{}n a 的公比为q ，则()2123111a a a a q q++=++=，()232234111112a a a a q a q a q a q q q q ++=++=++==，因此，()5675256781111132a a a a q a q a q a q q q q++=++=++==.故选：D.2．（2020年全国统一高考数学试卷（文科）（新课标∵））如图，将钢琴上的12个键依次记为a 1，a 2，…，a 12.设1≤i <j <k ≤12．若k –j =3且j –i =4，则称a i ，a j ，a k 为原位大三和弦；若k –j =4且j –i =3，则称a i ，a j ，a k 为原位小三和弦．用这12个键可以构成的原位大三和弦与原位小三和弦的个数之和为（）A ．5B ．8C ．10D ．15【答案】C【分析】根据题意可知，原位大三和弦满足：3,4k j j i -=-=．∵1,5,8i j k ===；2,6,9i j k ===；3,7,10i j k ===；4,8,11i j k ===；5,9,12i j k ===．原位小三和弦满足：4,3k j j i -=-=．∵1,4,8i j k ===；2,5,9i j k ===；3,6,10i j k ===；4,7,11i j k ===；5,8,12i j k ===．故个数之和为10．故选：C ．3．（2020年全国统一高考数学试卷（文科）（新课标∵））记S n 为等比数列{a n }的前n 项和．若a 5–a 3=12，a 6–a 4=24，则nnS a =（） A ．2n –1 B ．2–21–nC ．2–2n –1D ．21–n –1【答案】B【分析】设等比数列的公比为q ，由536412,24a a a a -=-=可得：421153111122124a q a q q a a q a q ⎧-==⎧⎪⇒⎨⎨=-=⎪⎩⎩，所以1111(1)122,21112n nn n n n n a q a a qS q ----=====---，因此1121222n n n n n S a ---==-. 故选：B.4．（2020年全国统一高考数学试卷（理科）（新课标∵））北京天坛的圜丘坛为古代祭天的场所，分上、中、下三层，上层中心有一块圆形石板(称为天心石)，环绕天心石砌9块扇面形石板构成第一环，向外每环依次增加9块，下一层的第一环比上一层的最后一环多9块，向外每环依次也增加9块，已知每层环数相同，且下层比中层多729块，则三层共有扇面形石板(不含天心石)（）A ．3699块B ．3474块C ．3402块D ．3339块【答案】C【分析】设第n 环天石心块数为n a ，第一层共有n 环，则{}n a 是以9为首项，9为公差的等差数列，9(1)99n a n n =+-⨯=，设n S 为{}n a 的前n 项和，则第一层、第二层、第三层的块数分别为232,,n n n n n S S S S S --，因为下层比中层多729块，所以322729n n n n S S S S -=-+，即3(927)2(918)2(918)(99)7292222n n n n n n n n ++++-=-+即29729n =，解得9n =，所以32727(9927)34022n S S +⨯===.故选：C5．（2020年全国统一高考数学试卷（理科）（新课标∵））数列{}n a 中，12a =，m n m n a a a +=，若155121022k k k a a a ++++++=-，则k =（）A ．2B ．3C ．4D ．5【答案】C【分析】在等式m n m n a a a +=中，令1m =，可得112n n n a a a a +==，12n na a +∴=，所以，数列{}n a 是以2为首项，以2为公比的等比数列，则1222n nn a -=⨯=，()()()()1011011105101210122122212211212k k k k k k a a a a ++++++⋅-⋅-∴+++===-=---，1522k +∴=，则15k +=，解得4k =.故选：C.6．（2019年全国统一高考数学试卷（理科）（新课标∵））记n S 为等差数列{}n a 的前n 项和．已知4505S a ==，，则A ．25n a n =-B ． 310n a n =-C ．228n S n n =-D ．2122n S n n =- 【答案】A【分析】由题知，41514430245d S a a a d ⎧=+⨯⨯=⎪⎨⎪=+=⎩，解得132a d =-⎧⎨=⎩，∵25n a n =-，故选A ． 7．（2019年全国统一高考数学试卷（文科）（新课标∵））已知各项均为正数的等比数列{}n a 的前4项和为15，且53134a a a =+，则3a = A ．16 B ．8C ．4D ．2【答案】C【分析】设正数的等比数列{a n }的公比为q ，则2311114211115,34a a q a q a q a q a q a ⎧+++=⎨=+⎩，解得11,2a q =⎧⎨=⎩，2314a a q ∴==，故选C ．8．（2018年全国普通高等学校招生统一考试理科数学（新课标I 卷））设n S 为等差数列{}n a 的前n 项和，若3243S S S =+，12a =，则5a = A ．12- B ．10-C ．10D ．12【答案】B【详解】：设该等差数列的公差为d ，根据题中的条件可得32433(32)224222d d d ⨯⨯⨯+⋅=⨯++⨯+⋅，整理解得3d =-，所以51421210a a d =+=-=-，故选B.9．（2017年全国普通高等学校招生统一考试理科数学（新课标1卷））（2017新课标全国I 理科）记n S 为等差数列{}n a 的前n 项和．若4524a a +=，648S =，则{}n a 的公差为 A ．1 B ．2 C ．4 D ．8【答案】C 【解析】设公差为d ，45111342724a a a d a d a d +=+++=+=，611656615482S a d a d ⨯=+=+=，联立112724,61548a d a d +=⎧⎨+=⎩解得4d =，故选C. 10．（）等差数列{}n a 的首项为1，公差不为0．若2a 、3a 、6a 成等比数列，则{}n a 的前6项的和为（） A ．24- B ．3-C ．3D ．8【答案】A【分析】设等差数列{}n a 的公差为d ，由2a 、3a 、6a 成等比数列可得2326a a a =，即2(12)(1)(15)d d d +=++，整理可得220d d +=，又公差不为0，则2d =-，故{}n a 前6项的和为616(61)6(61)661(2)2422S a d ⨯-⨯-=+=⨯+⨯-=-. 故选：A11．（2016年全国普通高等学校招生统一考试理科数学）定义“规范01数列”{a n }如下：{a n }共有2m 项，其中m 项为0，m 项为1，且对任意2k m ≤，12,,,,k a a a 中0的个数不少于1的个数.若m =4，则不同的“规范01数列”共有 A ．18个 B ．16个 C ．14个 D ．12个【答案】C 【详解】试题分析：由题意，得必有10a =，81a =，则具体的排法列表如下：,01010011;010101011,共14个12．（2016年全国普通高等学校招生统一考试）已知{}n a 是公差为1的等差数列，n S 为{}n a 的前n 项和，若844S S =，则10a = A ．172B ．192C ．10D ．12【答案】B【详解】：由844S S =得()11828446a d a d +=+，解得1101119,922a a a ==+=.13．（2015年全国普通高等学校招生统一考试文科数学（新课标∵））设n S 是等差数列{}n a 的前n 项和,若1353a a a ++=,则5S =A ．5B ．7C ．9D ．11【答案】A 【详解】1353333,1a a a a a ++===，5153355()25522S a a a a =+=⨯==，选A.14．（2015年全国普通高等学校招生统一考试文科数学（新课标∵））已知等比数列{}n a 满足114a =,()35441a a a =-,则2a =（）A ．2B ．1C ．12D ．18【答案】C【详解】：由题意可得()235444412a a a a a ==-⇒=,所以34182a q q a ==⇒= ,故2112a a q == ,选C.15．（2015年全国普通高等学校招生统一考试理科数学（新课标∵））已知等比数列{}n a 满足13a =，13521a a a ++=，则357a a a ++=A ．21B ．42C ．63D ．84【答案】B 【详解】由a 1+a 3+a 5=21得242421(1)21172a q q q q q ++=∴++=∴=∴ a 3+a 5+a 7=2135()22142q a a a ++=⨯=，选B.16．（2013年全国普通高等学校招生统一考试文科数学（新课标1卷））设首项为1，公比为23的等比数列{}n a的前n 项和为n S ，则 A ．21n n S a =- B ．32n n S a =-C ．43n n S a =-D ．32n n S a =-【答案】D 【详解】S n ＝()111na q q--＝11n a q a q -⋅-＝21313na -＝3－2a n .17．（2013年全国普通高等学校招生统一考试理科数学（新课标1卷））设等差数列{}n a 的前n 项和为n S ，若112,0,3m m m S S S -+=-==，则m =( ) A ．3 B ．4C ．5D ．6【答案】C 【分析】{}n a 是等差数列()102ms m m a a S +∴==()112m m m a a S S -⇒=-=--=-又113m m m a S S ++=-=， ∵公差11m m d a a +=-=，11325m a a m m m +==+=-+⇒=，故选C ．18．（2013年全国普通高等学校招生统一考试理科数学（新课标1卷））设∵A n B n C n 的三边长分别为a n ,b n ,c n ，∵A n B n C n 的面积为S n ，n=1,2,3,… 若b 1＞c 1，b 1＋c 1＝2a 1，a n ＋1＝a n ，b n ＋1＝2n n c a +，c n ＋1＝2n nb a +，则 A ．{S n }为递减数列 B ．{S n }为递增数列C ．{S 2n －1}为递增数列，{S 2n }为递减数列D ．{S 2n －1}为递减数列，{S 2n }为递增数列【答案】B【详解】1112b a c =-且11b c >，1112a c c ∴->，11a c ∴>， 111111120b a a c a a c ∴-=--=->，111b a c ∴>>，又111b c a -<，11112a c c a ∴--<，112c a ∴>，∴112a c >，由题意，112n n n n nbc b c a ++++=+，1112(2)2n n n n n n b c a b c a ++∴+-=+-， 1112b c a +=，11120b c a ∴+-=，20n n n b c a ∴+-=，122n n n b c a a ∴+==，12nn b c a +∴=，由此可知顶点n A 在以n B 、n c 为焦点的椭圆上，又由题意，112n n n n c b b c ++--=，∴111112(2)2n n n n n a b bb a b a b ++----==-， 1111()2n n b a a b +∴-=-，111()2n n b a -∴-=-，∴11111()()2n n b a b a -=+--，1111112()()2n n n c a b a b a -=-=---， ∴21111111111111333311()[()()][()()]222222n n n a a a a S a a b a a b a --=------+-- 2212111131[()()]424n a a b a -=--单调递增（可证当1n =时22111()0)4a b a --> 故选：B ．19．（2013年全国普通高等学校招生统一考试理科数学（新课标2））等比数列｛a n ｝的前n 项和为S n ，已知S 3 = a 2 +10a 1 ，a 5 = 9，则a 1= A ． B ．- C ． D ．-【答案】C 【详解】由S 3 = a 2 +10a 1得，1a +a 2 +a 3= a 2 +10a 1，即a 3= 9a 1，即21a q = 9a 1，解得2q = 9，又因为a 5 = 9，所以41a q =9，解得119a =，故选C. 20．（2012年全国普通高等学校招生统一考试文科数学））数列{a n }满足a n+1+（﹣1）n a n =2n ﹣1，则{a n }的前60项和为（） A ．3690 B ．3660C ．1845D ．1830【答案】D 【详解】由于数列{a n }满足a n+1+（﹣1）n a n =2n ﹣1，故有 a 2﹣a 1=1，a 3+a 2=3，a 4﹣a 3=5， a 5+a 4=7，a 6﹣a 5=9，a 7+a 6=11，…a 50﹣a 49=97．从而可得 a 3+a 1=2，a 4+a 2=8，a 7+a 5=2，a 8+a 6=24，a 9+a 11=2，a 12+a 10=40，a 13+a 15=2，a 16+a 14=56，… 从第一项开始，依次取2个相邻奇数项的和都等于2，从第二项开始，依次取2个相邻偶数项的和构成以8为首项，以16为公差的等差数列． {a n }的前60项和为 15×2+（15×8+）=1830，故选D ．21．（2012年全国普通高等学校招生统一考试）已知{}n a 为等比数列,472a a +=,568a a =-,则110a a +=（） A ．7 B ．5C ．5-D ．7-【答案】D【分析】56474747822,4a a a a a a a a ==-+=∴=-=或474,2a a ==-.由等比数列性质可知2274101478,1a a a a a a ==-==或2274101471,8a a a a a a ====-1107a a ∴+=-故选D.二、填空题22．（2020年全国统一高考数学试卷（文科）（新课标∵））数列{}n a 满足2(1)31nn n a a n ++-=-，前16项和为540，则1a = ______________. 【答案】7【分析】2(1)31nn n a a n ++-=-，当n 为奇数时，231n n a a n +=+-；当n 为偶数时，231n n a a n ++=-. 设数列{}n a 的前n 项和为n S ，16123416S a a a a a =+++++13515241416()()a a a a a a a a =+++++++111111(2)(10)(24)(44)(70)a a a a a a =++++++++++ 11(102)(140)(5172941)a a ++++++++ 118392928484540a a =++=+=， 17a ∴=.故答案为：7.23．（2020年全国统一高考数学试卷（文科）（新课标∵））记n S 为等差数列{}n a 的前n 项和．若1262,2a a a =-+=，则10S =__________．【答案】25 【分析】{}n a 是等差数列，且12a =-，262a a +=设{}n a 等差数列的公差d根据等差数列通项公式：()11n a a n d +-= 可得1152a d a d +++= 即：()2252d d -++-+= 整理可得：66d = 解得：1d =根据等差数列前n 项和公式：*1(1),2n n n S na d n N -=+∈ 可得：()1010(101)1022045252S ⨯-=-+=-+=∴1025S =.故答案为：25.24．（2019年全国统一高考数学试卷（文科）（新课标∵））记S n 为等比数列{a n }的前n 项和.若13314a S ==，，则S 4=___________．【答案】58. 【分析】：设等比数列的公比为q ，由已知223111314S a a q a q q q =++=++=，即2104q q ++= 解得12q =-，所以441411()(1)521181()2a q S q ---===---．25．（2019年全国统一高考数学试卷（理科）（新课标∵））记S n 为等比数列{a n }的前n 项和．若214613a a a ==，，则S 5=____________．【答案】1213. 【分析】设等比数列的公比为q ，由已知21461,3a a a ==，所以32511(),33q q =又0q ≠，所以3,q =所以55151(13)(1)12131133a q S q --===--． 26．（2019年全国统一高考数学试卷（文科）（新课标∵））记n S 为等差数列{}n a 的前n 项和，若375,13a a ==，则10S =___________. 【答案】100 【分析】317125,613a a d a a d =+=⎧⎨=+=⎩得11,2a d =⎧⎨=⎩101109109101012100.22S a d ⨯⨯∴=+=⨯+⨯= 27．（2019年全国统一高考数学试卷（理科）（新课标∵））记S n 为等差数列{a n }的前n 项和，12103a a a =≠，，则105S S =___________. 【答案】4.【分析】因213a a =，所以113a d a +=，即12a d =，所以105S S =11111091010024542552a d a a a d⨯+==⨯+． 28．（2018年全国普通高等学校招生统一考试理科数学（新课标I 卷））记n S 为数列{}n a 的前n 项和，若21n n S a =+，则6S =_____________．【答案】63-【分析】根据21n n S a =+，可得1121n n S a ++=+，两式相减得1122n n n a a a ++=-，即12n n a a +=，当1n =时，11121S a a ==+，解得11a =-，所以数列{}n a 是以-1为首项，以2为公比的等比数列，所以66(12)6312S --==--，故答案是63-.29．（2017年全国普通高等学校招生统一考试理科数学（新课标2卷））等差数列{}n a 的前n 项和为n S ，33a =，410S =，则11nk kS ==∑____________．【答案】21n n + 【详解】设等差数列的首项为1a ，公差为d ，由题意有1123434102a d a d +=⎧⎪⎨⨯+=⎪⎩，解得111a d =⎧⎨=⎩ ，数列的前n 项和()()()111111222n n n n n n n S na d n --+=+=⨯+⨯=，裂项可得12112()(1)1k S k k k k ==-++，所以1111111122[(1)()()]2(1)223111nk knS n n n n ==-+-++-=-=+++∑．30．（2017年全国普通高等学校招生统一考试理科数学（新课标3卷））设等比数列{}n a 满足a 1 + a 2 = –1, a 1 – a 3 = –3，则a 4 = ___________．【答案】-8【解析】设等比数列{}n a 的公比为q ，很明显1q ≠-，结合等比数列的通项公式和题意可得方程组：()()12121311113a a a q a a a q ⎧+=+=-⎪⎨-=-=-⎪⎩，①，②，由②①可得：2q =-，代入∵可得11a =，由等比数列的通项公式可得3418a a q ==-.31．（2016年全国普通高等学校招生统一考试）设等比数列{}n a 满足a 1+a 3=10，a 2+a 4=5，则a 1a 2 …a n 的最大值为___________．【答案】64【详解】：设等比数列的公比为q ，由132410{5a a a a +=+=得，2121(1)10{(1)5a q a q q +=+=，解得1812a q =⎧⎪⎨=⎪⎩.所以2(1)1712(1)22212118()22n n n n n n nn a a a a q--++++-==⨯=，于是当3n =或4时，12n a a a 取得最大值6264=.32．（2015年全国普通高等学校招生统一考试文科数学（新课标∵））数列{}n a 中112,2,n n n a a a S +==为{}n a 的前n 项和，若126n S =，则n =_______. 【答案】6【解析】：由题意得，因为12n n a a +=，即12n na a +=，所以数列{}n a 构成首项12a =，公比为2的等比数列，则2(12)12612n n S -==-，解得6n =．33．（2015年全国普通高等学校招生统一考试）设n S 是数列{}n a 的前n 项和，且11a =-，11n n n a S S ++=，则n S =__________．【答案】1n-【解析】原式为1111n n n n n n n a S S S S S S ++++=⇔-=，整理为：1111n n S S +-= ，即1111n n S S +-=-，即数列1n S ⎧⎫⎨⎬⎩⎭是以-1为首项，-1为公差的等差的数列，所以()()1111nn n S =-+--=- ，即1n S n=- .34．（2014年全国普通高等学校招生统一考试文科数学（全国∵卷））数列满足，则________．【答案】12．【详解】：由已知得，111n n a a +=-，82a =，所以781112a a =-=，67111a a =-=-，56112a a =-=， 451112a a =-=，34111a a =-=-，23112a a =-=，．35．（2013年全国普通高等学校招生统一考试理科数学（新课标1））若数列{a n }的前n 项和为S n ＝23a n ＋13，则数列{a n }的通项公式是a n =______.【答案】1(2)n n a -=-；【详解】：解：当n=1时，a 1=S 1=23a 1+13，解得a 1=1,当n≥2时，a n =S n -S n -1=（2133n a +）-（12133n a -+）=23n a -123n a -整理可得13a n ＝−23a n−1，即1n n a a -=-2，故数列{a n }是以1为首项，-2为公比的等比数列，故a n =1×（-2）n -1=（-2）n -1故答案为（-2）n -1．36．（2013年全国普通高等学校招生统一考试理科数学（新课标2卷））等差数列{a n }的前n 项和为S n ，已知S 10＝0，S 15＝25，则nS n 的最小值为________．【答案】－49【详解】由条件得1323a d =-⎧⎪⎨⎪⎩＝nS n ＝321033n n -，对f (x )＝321033x x -求导可得f (x )在20,3⎛⎫ ⎪⎝⎭上递减，在20,3⎛⎫+∞ ⎪⎝⎭上递增，分别计算n ＝6和n ＝7可得，当n ＝7时nS n ＝321033n n -最小为－49.37．（2012年全国普通高等学校招生统一考试文科数学（课标卷））等比数列{a n }的前n 项和为S n ，若S 3+3S 2=0，则公比q=_______ 【答案】【详解】显然公比，设首项为，则由，得，即，即，即，所以，解得.38．（2012年全国普通高等学校招生统一考试理科数学）数列{}n a 满足1(1)21nn n a a n ++-=-，则{}n a 的前60项和为____ 【答案】1830 【解析】：()()11121211n nn n n n a a n a n a +++--∴---＝，＝，令1414243444143434242412n n n n n n n n n n n b a a a a a a a a a a +++++++++++=++++=+--=，（）（），424444434342168n n n n n n a a a a a a n +++++++=-++=+（）（），则14142434443424141616n n n n n n n n n n b a a a a a a a a b +++++---=+++=++++=+，即数列{}n b 是以16为公差的等差数列，{}n a 的前60项和为即为数列{b n }的前15项和1123415141010151618302b a a a a S ⨯=+++=∴⨯+⨯=＝三、解答题39．（2020年全国统一高考数学试卷（理科）（新课标∵））设{}n a 是公比不为1的等比数列，1a 为2a ，3a 的等差中项．（1）求{}n a 的公比；（2）若11a =，求数列{}n na 的前n 项和．【答案】（1）2-；（2）1(13)(2)9nn n S -+-=. 【分析】（1）设{}n a 的公比为q ，1a 为23,a a 的等差中项，212312,0,20a a a a q q =+≠∴+-=，1,2q q ≠∴=-；（2）设{}n na 的前n 项和为n S ，111,(2)n n a a -==-，21112(2)3(2)(2)n n S n -=⨯+⨯-+⨯-++-，∵23121(2)2(2)3(2)(1)(2)(2)n n n S n n --=⨯-+⨯-+⨯-+--+-，∵∵-∵得，2131(2)(2)(2)(2)n n n S n -=+-+-++---1(2)1(13)(2)(2)1(2)3n n n n n ---+-=--=--， 1(13)(2)9nn n S -+-∴=. 40．（2020年全国统一高考数学试卷（文科）（新课标∵））设等比数列{a n }满足124a a +=，318a a -=．（1）求{a n }的通项公式；（2）记n S 为数列{log 3a n }的前n 项和．若13m m m S S S +++=，求m ．【答案】（1）13-=n n a ；（2）6m =. 【分析】（1）设等比数列{}n a 的公比为q ，根据题意，有1121148a a q a q a +=⎧⎨-=⎩，解得113a q =⎧⎨=⎩，所以13-=n n a ；（2）令313log log 31n n n b a n -===-，所以(01)(1)22n n n n n S +--==，根据13m m m S S S +++=，可得(1)(1)(2)(3)222m m m m m m -++++=，整理得2560m m --=，因为0m >，所以6m =，41．（2020年全国统一高考数学试卷（理科）（新课标∵））设数列{a n }满足a 1=3，134n n a a n +=-．（1）计算a 2，a 3，猜想{a n }的通项公式并加以证明；（2）求数列{2n a n }的前n 项和S n ．【答案】（1）25a =，37a =，21n a n =+，证明见解析；（2）1(21)22n n S n +=-⋅+.【分析】（1）由题意可得2134945a a =-=-=，32381587a a =-=-=，由数列{}n a 的前三项可猜想数列{}n a 是以3为首项，2为公差的等差数列，即21n a n =+，证明如下：当1n =时，13a =成立；假设n k =时，21k a k =+成立.那么1n k =+时，1343(21)4232(1)1k k a a k k k k k +=-=+-=+=++也成立. 则对任意的*n N ∈，都有21n a n =+成立；（2）由（1）可知，2(21)2nnn a n ⋅=+⋅231325272(21)2(21)2n n n S n n -=⨯+⨯+⨯++-⋅++⋅，∵ 23412325272(21)2(21)2n n n S n n +=⨯+⨯+⨯++-⋅++⋅，∵由∵-∵得：()23162222(21)2n n n S n +-=+⨯+++-+⋅()21121262(21)212n n n -+-=+⨯-+⋅⨯-1(12)22n n +=-⋅-，即1(21)22n n S n +=-⋅+.42．（2019年全国统一高考数学试卷（文科）（新课标∵））记S n 为等差数列{a n }的前n 项和，已知S 9=－a 5．（1）若a 3=4，求{a n }的通项公式；（2）若a 1>0，求使得S n ≥a n 的n 的取值范围．【答案】（1）210n a n =-+；（2）110()n n N *≤≤∈.【分析】（1）设等差数列{}n a 的首项为1a ，公差为d ，根据题意有111989(4)224a d a d a d ⨯⎧+=-+⎪⎨⎪+=⎩，解答182a d =⎧⎨=-⎩，所以8(1)(2)210n a n n =+-⨯-=-+，所以等差数列{}n a 的通项公式为210n a n =-+；（2）由条件95S a =-，得559a a =-，即50a =，因为10a >，所以0d <，并且有5140a a d =+=，所以有14a d =-，由n n S a ≥得11(1)(1)2n n na d a n d -+≥+-，整理得2(9)(210)n n d n d -≥-，因为0d <，所以有29210n n n -≤-，即211100n n -+≤，解得110n ≤≤，所以n 的取值范围是：110()n n N *≤≤∈43．（2019年全国统一高考数学试卷（文科）（新课标∵））已知{}n a 是各项均为正数的等比数列，1322,216a a a ==+.（1）求{}n a 的通项公式；（2）设2log n n b a =，求数列{}n b 的前n 项和. 【答案】（1）212n na -=；（2）2n S n =.【分析】(1)因为数列{}n a 是各项均为正数的等比数列，32216a a ，12a =，所以令数列{}n a 的公比为q ，2231=2a a q q ，212a a qq ，所以22416qq ，解得2q =-(舍去)或4，所以数列{}n a 是首项为2、公比为4的等比数列，121242n n n a --=⨯=．(2)因为2log n n b a =，所以21n b n =-，+121n b n ，12n nb b ，所以数列{}n b 是首项为1、公差为2的等差数列，21212n nS n n ．44．（2019年全国统一高考数学试卷（理科）（新课标∵））已知数列{a n }和{b n }满足a 1=1，b 1=0，1434n n n a a b +-=+ ，1434n n n b b a +-=-. （1）证明：{a n +b n }是等比数列，{a n –b n }是等差数列；（2）求{a n }和{b n }的通项公式. 【答案】（1）见解析；（2）1122nna n，1122nnb n．【分析】(1)由题意可知1434n n n a a b +-=+，1434n n n b b a +-=-，111a b ，111a b -=，所以1144323442nn n n n n n n a b a b b a a b ，即1112n n n n a b a b ，所以数列{}n n a b +是首项为1、公比为12的等比数列，112n n n a b ，因为11443434448n n n n n n n n a b a b b a a b ，所以112nn n n a b a b ，数列{}n n a b -是首项1、公差为2的等差数列，21n na b n ．(2)由(1)可知，112n n n a b ，21n na b n ，所以111222nnn n n na ab a b n，111222nn n n n nb a b a b n．45．（2018年全国普通高等学校招生统一考试文科数学（新课标I 卷））已知数列{}n a 满足11a =，()121n n na n a +=+，设nn a b n=．（1）求123b b b ，，；（2）判断数列{}n b 是否为等比数列，并说明理由；（3）求{}n a 的通项公式．【答案】（1）11b =，22b =，34b =；（2）{}n b 是首项为1，公比为2的等比数列．理由见解析；（3）12n n a n -=⋅. 【分析】（1）由条件可得()121n n n a a n++=．将1n =代入得，214a a =，而11a =，所以，24a =．将2n =代入得，323a a =，所以，312a =．从而11b =，22b =，34b =；（2）{}n b 是首项为1，公比为2的等比数列．由条件可得121n na a n n+=+，即12n n b b +=，又11b =，所以{}n b 是首项为1，公比为2的等比数列；（3）由（2）可得11122n n nn a b n--==⨯=，所以12n n a n -=⋅． 46．（2018年全国普通高等学校招生统一考试理数（全国卷II ））记n S 为等差数列{}n a 的前n 项和，已知17a =-，315S =-．（1）求{}n a 的通项公式；（2）求n S ，并求n S 的最小值．【答案】（1）a n =2n –9，（2）S n =n 2–8n ，最小值为–16．【详解】：（1）设{a n }的公差为d ，由题意得3a 1+3d =–15．由a 1=–7得d =2．所以{a n }的通项公式为a n =2n –9．（2）由（1）得S n =n 2–8n =（n –4）2–16．所以当n =4时，S n 取得最小值，最小值为–16．47．（2018年全国卷∵文数高考试题）等比数列{}n a 中，15314a a a ==，．（1）求{}n a 的通项公式；（2）记n S 为{}n a 的前n 项和．若63m S =，求m ．【答案】（1）()12n n a -=-或12n n a -= .（2）6m =.【详解】：（1）设{}n a 的公比为q ，由题设得1n n a q -=．由已知得424q q =，解得0q =（舍去），2q =-或2q =．故()12n n a -=-或12n n a -=．（2）若()12n n a -=-，则()123nnS --=．由63m S =得()2188m-=-，此方程没有正整数解．若12n n a -=，则21nn S =-．由63m S =得264m =，解得6m =．综上，6m =．48．（2017年全国普通高等学校招生统一考试文科数学（新课标1卷））记S n 为等比数列{}n a 的前n 项和，已知S 2=2，S 3=-6.（1）求{}n a 的通项公式；（2）求S n ，并判断S n +1，S n ，S n +2是否成等差数列．【答案】（1）(2)n n a =-；（2）见解析.【详解】：（1）设{}n a 的公比为q .由题设可得()()1211216a q a q q ⎧+=⎪⎨++=-⎪⎩ ，解得2q =-，12a =-. 故{}n a 的通项公式为()2nn a =-. （2）由（1）可得()()111221133nn nn a q S q+-==-+--. 由于()()321214222212123333n n n n n n n n S S S +++++⎡⎤-+=-+-=-+-=⎢⎥⎣⎦，故1n S +，n S ，2n S +成等差数列.49．（2017年全国普通高等学校招生统一考试文科数学）已知等差数列{}n a 的前n 项和为n S ，等比数列{}n b 的前n 项和为n T ，且11a =，11b =，224a b +=. （1）若337a b +=，求{}n b 的通项公式；（2）若313T =，求5S .【答案】（1）12n n b -=；（2）5或75.【分析】设等差数列{}n a 公差为d ，等比数列{}n b 公比为()0q q ≠有()14d q ++=，即3d q +=. （1）∵()2127d q ++=，结合3d q +=得2q =，∵12n n b -=.（2）∵23113T q q =++=，解得4q =-或3，当4q =-时，7d =，此时55457752S ⨯=+⨯=；当3q =时，0d =，此时5155S a ==.50．（2017年全国普通高等学校招生统一考试文科数学）设数列{}n a 满足123(21)2n a a n a n ++⋯+-=. （1）求{}n a 的通项公式（2）求数列21n a n ⎧⎫⎨⎬+⎩⎭的前n 项和．【答案】(1) 221n a n =-；(2)221n n +. 【分析】（1）数列{}n a 满足()123212=n a a n a n ++⋯+-2n ≥时,()()12132321n a a n a n ++⋯+--﹣＝ ∵()212n n a -= ∵221n a n =- 当1n =时,12a =,上式也成立 ∵221n a n =- （2）21121(21)(21)2121n a n n n n n ==-+-+-+ ∵数列21n a n ⎧⎫⎨⎬+⎩⎭的前n 项和 1111113352121n n ⎛⎫⎛⎫⎛⎫=-+-++- ⎪ ⎪ ⎪-+⎝⎭⎝⎭⎝⎭1212121nn n =-=++ 51．（2016年全国普通高等学校招生统一考试文科数学（全国1））已知{}n a 是公差为3的等差数列，数列{}n b 满足12111==3n n n n b b a b b nb +++=1，，．（∵）求{}n a 的通项公式；（∵）求{}n b 的前n 项和．【答案】(∵)3n-1;(∵)见解析.【详解】：（∵）由已知，1221121,1,,3a b b b b b +===得12a =，所以数列{}n a 是首项为2，公差为3的等差数列，通项公式为31n a n =-.（∵）由（∵）和11n n n n a b b nb +++= 得13n n b b +=，因此{}n b 是首项为1，公比为13的等比数列.记{}n b 的前n 项和为n S ，则111()313.122313nn n S --==-⨯-52．（2016年全国普通高等学校招生统一考试）等差数列{n a }中，34574,6a a a a +=+=. （∵）求{n a }的通项公式；（∵）设[]n n b a =，求数列{}n b 的前10项和，其中[]x 表示不超过x 的最大整数，如[0.9]=0,[2.6]=2. 【答案】（∵）235n n a +=；（∵）24. 【解析】：（∵）设数列{}n a 的公差为d ，由题意有112+54,+53a d a d ==. 解得121,5a d ==. 所以{}n a 的通项公式为235n n a +=. （∵）由（∵）知235n n b +⎡⎤=⎢⎥⎣⎦. 当n=1,2,3时，2312,15n n b +≤<=；当n=4,5时，2323,25n n b +≤<=；当n=6,7,8时，2334,35n n b +≤<=；当n=9,10时，2345,45n n b +≤<=. 所以数列{}n b 的前10项和为1322334224⨯+⨯+⨯+⨯=.53．（2016年全国普通高等学校招生统一考试数学）n S 为等差数列{}n a 的前n 项和，且17=128.a S =，记[]=lg n n b a ，其中[]x 表示不超过x 的最大整数，如[][]0.9=0lg99=1，.（∵）求111101,,b b b ；（∵）求数列{}n b 的前1000项和.【答案】（∵）1111010,1, 2.b b b ===（∵）1893.【详解】：（∵）设{}n a 的公差为d ，据已知有72128d +=，解得 1.d = 所以{}n a 的通项公式为.n a n =111101[lg1]0,[lg11]1,[lg101] 2.b b b ======（∵）因为0,110,1,10100,{2,1001000,3,1000.n n n b n n ≤<≤<=≤<=所以数列{}n b 的前1000项和为1902900311893.⨯+⨯+⨯=54．（2016年全国普通高等学校招生统一考试数学）已知各项都为正数的数列{}n a 满足11a =，211(21)20n n n n a a a a ++---=.（∵）求23,a a ；（∵）求{}n a 的通项公式. 【答案】（∵）；（∵）．【详解】：（∵）由题意，得.（∵）由得.因为的各项都为正数，所以.故是首项为，公比为的等比数列，因此.55．（2015年全国普通高等学校招生统一考试文科数学）已知数列{}n a 的前n 项和1n n S a λ=+，其中0λ≠．（∵）证明{}n a 是等比数列，并求其通项公式；（∵）若53132S =，求λ．【答案】（∵）；（∵）1λ=-．【详解】：（∵）由题意得，故，，. 由，得，即.由，得，所以.因此{}n a 是首项为，公比为的等比数列，于是.（∵）由（∵）得.由得，即.解得1λ=-.56．（2015年全国普通高等学校招生统一考试理科数学（新课标∵）n S 为数列{n a }的前n 项和.已知n a ＞0，22n n a a +=43n S +.（∵）求{n a }的通项公式；（∵）设11n n n b a a +=,求数列{n b }的前n 项和. 【答案】（∵）21n （∵）11646n -+ 【分析】：（I ）由a n 2+2a n ＝4S n +3，可知a n +12+2a n +1＝4S n +1+3 两式相减得a n +12﹣a n 2+2（a n +1﹣a n ）＝4a n +1，即2（a n +1+a n ）＝a n +12﹣a n 2＝（a n +1+a n ）（a n +1﹣a n ）， ∵a n ＞0，∵a n +1﹣a n ＝2， ∵a 12+2a 1＝4a 1+3， ∵a 1＝﹣1（舍）或a 1＝3，则{a n }是首项为3，公差d ＝2的等差数列， ∵{a n }的通项公式a n ＝3+2（n ﹣1）＝2n +1：（∵）∵a n ＝2n +1，∵b n ()()111121232n n a a n n +===++（112123n n -++）， ∵数列{b n }的前n 项和T n 12=（11111135572123n n -+-++-++）12=（11323n -+）11646n =-+. 57．（2014年全国普通高等学校招生统一考试文科数学（新课标∵））已知{}n a 是递增的等差数列，2a ，4a 是方程的根.（1）求{}n a 的通项公式；（2）求数列2n n a ⎧⎫⎨⎬⎩⎭的前n 项和. 【答案】（1）112n a n =+;（2）1422n n n S ++=-. 【分析】方程x 2－5x ＋6＝0的两根为2，3.由题意得a 2＝2，a 4＝3.设数列{a n }的公差为d ，则a 4－a 2＝2d ，故d ＝12，从而得a 1＝32. 所以{a n }的通项公式为a n ＝12n ＋1. （2）设2n n a ⎧⎫⎨⎬⎩⎭的前n 项和为S n ，由（1）知2n n a ＝122n n ++，则S n ＝232＋342＋…＋12n n +＋122n n ++， 12S n ＝332＋442＋…＋112n n ++＋222n n ++，两式相减得12S n ＝34＋311122n +⎛⎫+⋅⋅⋅+ ⎪⎝⎭－222n n ++ ＝34＋111142n -⎛⎫- ⎪⎝⎭－222n n ++，所以S n ＝2－142n n ++.58．（2014年全国普通高等学校招生统一考试理科数学（新课标∵））已知数列{}n a 的前n 项和为11,1,0,1n n n n n S a a a a S λ+=≠=-，其中λ为常数．（1）证明：2n n a a λ+-=；（2）是否存在λ，使得{}n a 为等差数列？并说明理由．【答案】（1）证明见解析；（2）4λ=.【详解】：（I ）由题设，11n n n a a S λ+=-，1211n n n a a S λ+++=-．两式相减得，121()n n n n a a a a λ+++-=．由于10n a +≠，所以2n n a a λ+-=．（II ）由题设，11a =，1211a a S λ=-，可得21a λ=-，由（I ）知，31a λ=+．令2132a a a =+，解得4λ=．故24n n a a +-=，由此可得，{}21n a -是首项为1，公差为4的等差数列，211(1)443n a n n -=+-⋅=-； {}2n a 是首项为3，公差为4的等差数列，23(1)441n a n n =+-⋅=-．所以21n a n =-，12n n a a +-=．因此存在4λ=，使得{}n a 为等差数列．59．（2014年全国普通高等学校招生统一考试理科数学（全国∵卷））已知数列{}n a 满足111,31n n a a a +==+.(1)证明12n a ⎧⎫+⎨⎬⎩⎭是等比数列，并求{}n a 的通项公式； (2)证明： 121113 (2)n a a a +++<. 【答案】（1）证明见解析，113322n n a -+=；（2）证明见解析. 【详解】：（1）证明：由131n n a a +=+得1113()22n n a a ++=+，所以112312n n a a ++=+，所以12n a ⎧+⎫⎨⎬⎩⎭是等比数列，首项为11322a +=，公比为3，所以12n a +=1332n -⋅，解得n a =312n -.（2）由（1）知：n a =312n -，所以1231n na =-，因为当1n ≥时，13123n n --≥⋅，所以1113123n n -≤-⋅，于是11a +21a +1n a 111133n -≤+++=31(1)23n -32<，所以11a +21a +1n a 32<.60．（2013年全国普通高等学校招生统一考试文科数学（新课标1卷））已知等差数列{}n a 的前n 项和n S 满足30S =，55S =-．（1）求{}n a 的通项公式；（2）求数列21211n n a a -+⎧⎫⎨⎬⎩⎭的前n 项和．【答案】(1)2n a n =-；（2）12n n-. 【分析】：（1）由等差数列的性质可得1133054552a d a d +=⎧⎪⎨⨯+=-⎪⎩，即11021a d a d +=⎧⎨+=-⎩，解得a 1＝1，d ＝﹣1，则{a n }的通项公式a n ＝1﹣（n ﹣1）＝2﹣n ；（2）()()()()21211111321221232n n a a n n n n -+===⨯----（()()()21232123n n n n -----）12=（112321n n ---），则数列{21211n n a a -+⨯}的前n 项和S n 12=（11111132321n n --+-++---） 12=（﹣1121n --）12n n=-． 61．（2013年全国普通高等学校招生统一考试文科数学（新课标2卷））已知等差数列｛a n ｝的公差不为零，a 1=25，且1a ，11a ，13a 成等比数列.（∵）求{}n a 的通项公式；（∵）求1a +a 4+a 7+…+a 3n -2.【答案】（∵）227n a n =-+；（∵）2328n n -+.【详解】(1)设{a n }的公差为d.由题意， a 112＝a 1a 13，即(a 1＋10d)2＝a 1(a 1＋12d)，于是d(2a 1＋25d)＝0. 又a 1＝25，所以d ＝0(舍去)，或d ＝－2. 故a n ＝－2n ＋27.(2)令S n ＝a 1＋a 4＋a 7＋…＋a 3n －2. 由(1)知a 3n －2＝－6n ＋31，故{a 3n －2}是首项为25，公差为－6的等差数列．从而S n ＝2n (a 1＋a 3n －2)＝2n (－6n ＋56)＝－3n 2＋28n.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

【2012高考试题】一、选择题 1.【2012重庆理1】在等差数列}{na中，12a，54a则}{na的前5项和5S=（ B） A.7 B.15 C.20 D.25 2.【2012浙江理7】设nS是公差为d（d≠0）的无穷等差数列﹛an﹜的前n项和，则下列命题错误的是（ C） A.若d＜0，则数列﹛Sn﹜有最大项B.若数列﹛Sn﹜有最大项，则d＜0 C.若数列﹛Sn﹜是递增数列，则对任意*Nn，均有0nS D. 若对任意*Nn，均有0nS，则数列﹛Sn﹜是递增数列 3.【2012新课标理5】已知na为等比数列，472aa，568aa，则110aa（ D ） ()A7 ()B 5 ()C ()D 4.【2012江西理12】设数列{an},{bn}都是等差数列，若711ba，2133ba，则55ba____35______。【解析】设数列}{},{nnba的公差分别为bd,，则由2133ba，得21)(211dbba，即14721)(2db，所以7db，所以35747)(41155dbbaba。 5.【2012辽宁理6】在等差数列{an}中，已知a4+a8=16，则该数列前11项和S11=( B ) (A)58 (B)88 (C)143 (D)176 6.【2012四川理12】设函数()2cosfxxx，{}na是公差为8的等差数列，125()()()5fafafa，则5123)]([aaaf（）A、0 B、2116 C、218 D、21316

7.【2012湖北理7】定义在(,0)(0,)上的函数()fx，如果对于任意给定的等比数列{}na， {()}nfa仍是等比数列，则称()fx为“保等比数列函数”. 现有定义在(,0)(0,)上的如下函数：①2()fxx； ②()2xfx； ③()||fxx； ④()ln||fxx.则其中是“保等比数列函数”的()fx的序号为（ C ） A.① ② B．③ ④ C．① ③ D．② ④ 8.【2012福建理】等差数列{an}中，a1+a5=10,a4=7,则数列{an}的公差为（ B ）A.1 B.2 C.3 D.4 9.【2012安徽理】公比为32等比数列{}na的各项都是正数，且31116aa，则162loga=（ B ） ()A4 ()B5 ()C ()D 【解析】29311771672161616432log5aaaaaaqa．

10.【2012全国理】已知等差数列{an}的前n项和为Sn，a5=5，S5=15，则数列的前100项和为（ A ） (A)100101 (B) 99101 (C) 99100 (D) 101100

11.【2012浙江理】设公比为q（q＞0）的等比数列{an}的前n项和为Sn。若S2=3a2+2，S4=3a4+2，则q=____32_____。【解析】将2232Sa，4432Sa两个式子全部转化成用1a，q表示的式子．

即111233111113232aaqaqaaqaqaqaq，两式作差：2321113(1)aqaqaqq，即：2230qq，解之得：312qq或(舍去)． 12.【2012辽宁理】已知等比数列｛an｝为递增数列，且251021,2()5nnnaaaaa，则数列｛an｝的通项公式an =___2n______ 解2429510111,(),,,nnaaaqaqaqaq 222112()5,2(1)5,2(1)5,2(22nnnnnnnaaaaqaqqqqqa解得或舍去），

13.【2012北京理】已知}{na等差数列nS为其前n项和，若211a，32aS，则2a=_______，nS=_______ 14.【2012重庆理】nnnn51lim2 52 . 【解析】)5)(5(5lim51lim2222nnnnnnnnnnnnnn525115151lim55lim2nnnnnnn 15.【2012上海理】有一列正方体，棱长组成以1为首项、21为公比的等比数列，体积分别记为，，，，nVVV21，则)(lim21nnVVV 。【解析】由题意可知，该列正方体的体积构成以1为首项，81为公比的等比数列，

∴1V+2V+„+nV=811811n=)811(78n，∴)(lim21nnVVV78。

16.【2012福建理】数列{an}的通项公式，前n项和为Sn，则S2012=___________.

17.【2012湖北理18】已知等差数列{}na前三项的和为3，前三项的积为8. （Ⅰ）求等差数列{}na的通项公式；（Ⅱ）若2a，3a，1a成等比数列，求数列{||}na的前n项和.

（Ⅱ）当35nan时，2a，3a，1a分别为1，4，2，不成等比数列；

当37nan时，2a，3a，1a分别为1，2，4，成等比数列，满足条件.故37,1,2,|||37|37,3.nnnannn 记数列{||}na的前n项和为nS.当1n时，11||4Sa；当2n时，212||||5Saa；当3n时，234||||||nnSSaaa5(337)(347)(37)n

2(2)[2(37)]311510222nnnn. 当2n时，满足此式.综上，24,1,31110,1.22nnSnnn 18.【2012广东理】设数列{an}的前n项和为Sn，满足12211nnnaS，n∈N﹡,且a1，a2+5，a3成等差数列．（1）求a1的值；（2）求数列{an}的通项公式．

19.【2012高考真题江西理17】已知数列{an}的前n项和knnSn221，*Nk,且Sn的最大值为8. （1）确定常数k，求an；（2）求数列}229{nna的前n项和Tn。

20.【2012天津理】已知}{na是等差数列，其前n项和为Sn，}{nb是等比数列，且27,24411baba， 1044bS.（Ⅰ）求数列}{na与}{nb的通项公式；（Ⅱ）记nnnnbababaT1211，*Nn，

证明nnnbaT10212（*Nn）. - 5 -

【2011年高考试题】 1. (2011年四川理)数列na的首项为3，nb 为等差数列且1(*)nnnbaanN .若则32b，1012b，则8a( B )（A）0 （B）3 （C）8 （D）11解析：128,28,nnnbnaan由叠加法

21328781()()()642024603aaaaaaaa.

2.(2011年全国理)设nS为等差数列na的前n项和，若11a，公差2d， Sk+2-Sk=24，可则k（ D ）（A）8 （B）7 （C）6 （D）5

3. (2011广东理)等差数列na前9项的和等于前4项的和.若141,0kaaa，则k 10 . 【解析】由题得1061031)1(123442899kdddkdd 4. (2011年重庆理)在等差数列na中，3737aa，则2468aaaa 解析：74. 28463737aaaaaa，故246823774aaaa 5. (2011年北京理)在等比数列{an}中，a1=12，a4=-4，则公比q=_—2 ，_12...naaa___2121n______。 6.(2011年辽宁理)已知等差数列{an}满足a2=0，a6+a8= -10 （I）求数列{an}的通项公式；（II）求数列12nna的前n项和.

所以12nnnS.综上，数列12nna的前n项和为12nnnS. 7.(2011年重庆理)设实数数列na的前n项和nS满足*11nnnSaSnN （Ⅰ）若122,,2aSa成等比数列，求2S和3a

解析：（Ⅰ）由题意2212221122SaaSaSaa，得2222SS，由2S是等比中项知20S，因此22S，由23332SaSaS，解得，232213SaS 8.(2011年全国理)设数列na满足10a且1111.11nnaa （Ⅰ）求na的通项公式；（Ⅱ）设111,,1.nnnnknkabbSn记S证明：【解析】：（Ⅰ）由1111.11nnaa得11na为等差数列，前项为1111,1,1(1)111ndnnaa于是，111,1nnaann （Ⅱ）111111nnnanbnn11111nnnnnn 1111111()()()12231nnkkSbnn



1111n



9．(2011年福建理) 已知等比数列{an}的公比q=3，前3项和S3=133。（I）求数列{an}的通项公式；（II）若函数()sin(2)(0,0)fxAxAp在6x处取得最大值，且最大值为a3，求函数f（x）的解析式。

【2010年高考试题】 1.（2010浙江理数）（3）设nS为等比数列na的前n项和，2580aa，则52SS（ D ）（A）11 （B）5 （C）8 （D）11 解析：解析：通过2580aa，设公比为q，将该式转化为08322qaa，解得q=-2，带入所求式可知答案选D， 2.（2010全国理）（4）.如果等差数列na中，34512aaa，那么127...aaa( C ) （A）14 （B）21 （C）28 （D）35

3.（2010辽宁理数）（6）设{an}是有正数组成的等比数列，nS为其前n项和。已知a2a4=1, 37S,则5S( B ) （A）152 (B)314 (C)334 (D)172