五年级奥数-数列与数表
高思奥数导引小学五年级含详解答案第17讲:计算综合一

第17讲计算综合一内容概述了解等比数列的基本概念,学会利用错位相减的方法进行求和;灵活使用各种方法简化比较复杂的分数算式;具有一定综合性的“定义新运算”问题;较复杂的数列与数表问题。
典型问题兴趣篇1.计算:(1)1248163264128256++++++++;(2)111111111248163264128256 ++++++++。
2.计算:23456333333+++++。
3.计算:199519951995199519951995 200920092009200920092009 ++++。
4.计算:131435 415263 342556⨯+⨯+⨯。
5.计算:1111111111 123456789100 2342342342+-++-++-++。
6.规定新运算“*”为:*32a b a b=⨯-⨯。
(1)计算:456**345⎛⎫⎪⎝⎭;(2)已知456**345x⎛⎫=⎪⎝⎭,求x。
7.图17-1中除了每行两端的数之外,其余每个数都是与它相连的上一行的两个数的平均数,例如:2.75是2.5和3的平均数。
请问:第100行中的各数之和是多少?8.有这样一列数,前两个数分别是0和1,从第三个数开始,每一个数都是前两个数的和:0,1,1,2,3,5,8,13,21,34,…。
请问:这个数列的第1000个数除以8所得的余数是多少?9.观察下面的数阵:根据前五行数所表达的规律,求(1)3367这个数在由上至下的第几行?在这一行中,它是由左向右第几个?(2)第28行第19个数是什么?10.观察数列11,12,22,12,13,23,33,13,14,24,34,44,34,24,14,…,求:(1)数列中第150项;(2)数列中前300项的和。
拓展篇1.如图17-2,有一个边长为81厘米的等边三角形,将它每条边三等分,以中间那一份为边向外作等边三角形,得到图17-3。
由图17-3通过同样方法又得到图17-4。
小学五年级数学奥数题100道及答案(完整版)

小学五年级数学奥数题100道及答案(完整版)题目1:计算:1 + 2 + 3 + 4 + 5 + …+ 99 + 100答案:5050解析:这是一个等差数列求和,公式为(首项+ 末项)×项数÷ 2 ,即(1 + 100)×100 ÷2 = 5050题目2:有三个连续自然数,它们的乘积是60,求这三个数。
答案:3、4、5解析:将60 分解质因数60 = 2×2×3×5 = 3×4×5题目3:一个数除以5 余3,除以6 余4,除以7 余5,这个数最小是多少?答案:208解析:这个数加上 2 就能被5、6、7 整除,5、6、7 的最小公倍数是210,所以这个数是210 - 2 = 208题目4:甲、乙两车同时从A、B 两地相向而行,在距A 地60 千米处第一次相遇。
各自到达对方出发地后立即返回,途中又在距A 地40 千米处相遇。
A、B 两地相距多少千米?答案:110 千米解析:第一次相遇时,两车共行了一个全程,甲行了60 千米。
第二次相遇时,两车共行了三个全程,甲行了60×3 = 180 千米。
此时甲距离 A 地40 千米,所以两个全程是180 + 40 = 220 千米,全程为110 千米。
题目5:鸡兔同笼,共有头48 个,脚132 只,鸡和兔各有多少只?答案:鸡30 只,兔18 只解析:假设全是鸡,有脚48×2 = 96 只,少了132 - 96 = 36 只脚。
每把一只鸡换成一只兔,脚多4 - 2 = 2 只,所以兔有36÷2 = 18 只,鸡有48 - 18 = 30 只。
题目6:小明从一楼到三楼用了18 秒,照这样计算,他从一楼到六楼需要多少秒?答案:45 秒解析:一楼到三楼走了 2 层楼梯,每层用时18÷2 = 9 秒。
一楼到六楼走5 层楼梯,用时5×9 = 45 秒。
小学奥数1-2-1-3 等差数列应用题.专项练习及答案解析

【例 1】 100以内的自然数中。
所有是3的倍数的数的平均数是 。
【考点】等差数列应用题 【难度】1星 【题型】填空 【关键词】希望杯,五年级,复赛,第3题,5分 【解析】 100以内的自然数中是3的倍数的数有0,3,6,9,99共33个,他们的和是()09934179916832+⨯=⨯=,则他们的平均数为1683÷34=49.5。
【答案】49.5【例 2】 一群小猴上山摘野果,第一只小猴摘了一个野果,第二只小猴摘了2个野果,第三只小猴摘了3个野果,依次类推,后面的小猴都比它前面的小猴多摘一个野果。
最后,每只小猴分得8个野果。
这群小猴一共有_________只。
【考点】等差数列应用题 【难度】2星 【题型】填空 【关键词】希望杯,四年级,二试,第7题【解析】 平均每只猴分8个野果,所以最后一只猴摘了821=15⨯-只果,共有15只猴. 【答案】15只猴子【例 3】 15位同学排成一队报数,从左边报起思思报10.从右边报起学学报12.那么学学和思思中间排着有 位同学.【考点】等差数列应用题 【难度】2星 【题型】填空 【关键词】学而思杯,1年级【解析】 因为从左边起思思报10,所以,思思的右边还有15105-=(个);又因为从右边起学学报12,所以,学学的左边还有15123-=(个),15645--=(个)学学和思思中间排着5位同学.<考点> 排队问题 【答案】5位【例 4】 体育课上老师指挥大家排成一排,冬冬站排头,阿奇站排尾,从排头到排尾依例题精讲等差数列应用题次报数。
如果冬冬报17,阿奇报150,每位同学报的数都比前一位多7,那么队伍里一共有多少人?【考点】等差数列应用题【难度】2星【题型】解答【解析】首项=17,末项=150,公差=7,项数=(150-17)÷7+1=20【答案】20【例 5】一个队列按照每排2,4,6,8人的顺序可以一直排到某一排有100人,那么这个队列共有多少人?【考点】等差数列应用题【难度】2星【题型】解答【解析】(方法一)利用等差数列求和公式:通过例1的学习可以知道,这个数列一共有50个数,再将和为102的两个数一一配对,可配成25对.所以2469698100++++++=2+10025=10325=2550()⨯⨯(方法二)根据12398991005050+++++的++++++=,从这个和中减去1357 (99)和,就可得出此题的结果,这样从“反面求解”的思想可以给学生灌输一下,为今后的学习作铺垫.【答案】2550【例 6】有一个很神秘的地方,那里有很多的雕塑,每个雕塑都是由蝴蝶组成的.第一个雕塑有3只蝴蝶,第二个雕塑有5只蝴蝶,第三个雕塑有7只蝴蝶,第四个雕塑有9只蝴蝶,以后的雕塑按照这样的规律一直延伸到很远的地方,学学和思思看不到这排雕塑的尽头在哪里,那么,第102个雕塑是由多少只蝴蝶组成的呢?由999只蝴蝶组成的雕塑是第多少个呢?【考点】等差数列应用题【难度】2星【题型】解答【解析】也就是已知一个数列:3、5、7、9、11、13、15、……,求这个数列的第102项是多少?999是第几项?由刚刚推导出的公式——第n项=首项+公差(),⨯-n1所以,第102项321021205(-);由“项数=(末项-首项)÷公差1=+⨯=+”,999所处的项数是:()-÷+=÷+=+=999321996214981499【答案】499【例 7】如右图,用同样大小的正三角形,向下逐次拼接出更大的正三角形。
小学五年级奥数550数列数表(学生版)专项练习题

学科培优数学“数列数表”学生姓名授课日期教师姓名授课时长日常生活中,我们经常接触到许多按一定顺序排列的数,如:自然数:1,2,3,4,5,6,7, (1)年份:1990,1991,1992,1993,1994,1995,1996 (2)某年级各班的学生人数(按班级顺序一、二、三、四、五班排列)45,45,44,46,45 (3)像上面的这些例子,按一定次序排列的一列数就叫做数列.数列中的每一个数都叫做这个数列的项,其中第1个数称为这个数列的第1项,第2个数称为第2项,…,第n个数就称为第n项.如数列(3)中,第1项是45,第2项也是45,第3项是44,第4项是46,第5项45。
根据数列中项的个数分类,我们把项数有限的数列(即有有穷多个项的数列)称为有穷数列,把项数无限的数列(即有无穷多个项的数列)称为无穷数列,上面的几个例子中,(2)(3)是有穷数列,(1)是无穷数列。
一、数列规律等差数列,简单的等比数列,周期规律,递推规律是数列中常见的形式,在小学阶段的奥数题中,比较多的项数进行计算基本都是可以找到相应规律的。
二、数表规律通过观察数表中的已知数据,发现规律并进行补填与计算的问题.这里要注意数表结构的差异,它们通常是按行、按列、沿斜线或螺旋线逐步形成的.涉及小数的,或与其他方面知识相综合的数列问题.三、递推思想奥数学习需要的是思维的积累,其中递推归纳的思想应用十分广泛。
而在数列数表中,递推的规律体现的淋漓尽致,需要学生用心体会。
注意:1.等差数列及相对应的数学解题思想,倒序相加,递推,对应等。
2.数列求和技巧,简单等比数列求和中措项相消得思想。
3.数表中如何发现规律并转化成已知知识。
4.措项相消思想的运用5.数表与计数数论相联系6.分数数列的计算7.数表的求和例题精讲【试题来源】【题目】0,1,2,3,6,7,14,15,30,________,________,________。
上面这个数列是小明按照一定的规律写下来的,他第一次先写出0,1,然后第二次写出2,3,第三次接着写6,7,第四次又接着写14,15,依次类推。
五年级奥数等差数列的认识与公式运用教师版

五年级奥数等差数列的认识与公式运用教师版一、等差数列的定义⑴ 先介绍一下一些定义和表示方法定义:从第二项起,每一项都比前一项大(或小)一个常数(固定不变的数),这样的数列我们称它为等差数列.譬如:2、5、8、11、14、17、20、 从第二项起,每一项比前一项大3 ,递增数列100、95、90、85、80、 从第二项起,每一项比前一项小5 ,递减数列⑵ 首项:一个数列的第一项,通常用1a 表示末项:一个数列的最后一项,通常用n a 表示,它也可表示数列的第n 项。
项数:一个数列全部项的个数,通常用n 来表示;公差:等差数列每两项之间固定不变的差,通常用d 来表示;和 :一个数列的前n 项的和,常用n S 来表示 .二、等差数列的相关公式(1)三个重要的公式① 通项公式:递增数列:末项=首项+(项数1-)⨯公差,11n a a n d =+-⨯() 递减数列:末项=首项-(项数1-)⨯公差,11n a a n d =--⨯()回忆讲解这个公式的时候可以结合具体数列或者原来学的植树问题的思想,让学生明白 末项其实就是首项加上(末项与首项的)间隔个公差个数,或者从找规律的情况入手.同时还可延伸出来这样一个有用的公式:n m a a n m d -=-⨯(),n m >() ② 项数公式:项数=(末项-首项)÷公差+1由通项公式可以得到:11n n a a d =-÷+() (若1n a a >);11n n a a d =-÷+() (若1n a a >).找项数还有一种配组的方法,其中运用的思想我们是常常用到的.譬如:找找下面数列的项数:4、7、10、13、、40、43、46 ,分析:配组:(4、5、6)、(7、8、9)、(10、11、12)、(13、14、15)、、(46、47、48),注意等差是3 ,那么每组有3个数,我们数列中的数都在每组的第1位,所以46应在最后一组第1位,4到48有484145-+=项,每组3个数,所以共45315÷=组,原数列有15组. 当然还可以有其他的配组方法.③ 求和公式:和=(首项+末项)⨯项数÷2对于这个公式的得到可以从两个方面入手:(思路1) 1239899100++++++11002993985051=++++++++共50个101()()()()101505050=⨯= 知识点拨教学目标五年级奥数等差数列的认识与公式运用教师版(思路2)这道题目,还可以这样理解:23498991001009998973212101101101101101101101+++++++=+++++++=+++++++和=1+和倍和即,和 (1001)1002101505050=+⨯÷=⨯=(2) 中项定理:对于任意一个项数为奇数的等差数列,中间一项的值等于所有项的平均数,也等于首项与末项和的一半;或者换句话说,各项和等于中间项乘以项数.譬如:① 48123236436922091800+++++=+⨯÷=⨯=(),题中的等差数列有9项,中间一项即第5项的值是20,而和恰等于209⨯;② 65636153116533233331089++++++=+⨯÷=⨯=(),题中的等差数列有33项,中间一项即第17项的值是33,而和恰等于3333⨯.模块一、等差数列基本概念及公式的简单应用等差数列的基本认识【例 1】下面的数列中,哪些是等差数列?若是,请指明公差,若不是,则说明理由。
五六年级奥数题及答案经典

五六年级奥数题及答案经典五、六年级奥数题及答案_经典五年级奥数题每类型一道,问题+思路+答案9.有7个数,它们的平均数是18。
去掉一个数后,剩下6个数的平均数是19;再去掉一个数后,剩下的5个数的平均数是20。
求去掉的两个数的乘积。
解:7某18-6某19126-114126某19-5某20114-10014去掉的两个数是12和14它们的乘积是12某1416810.有七个排成一列的数,它们的平均数是30,前三个数的平均数是28,后五个数的平均数是33。
求第三个数。
解:28某3+33某5-30某739。
11.有两组数,第一组9个数的和是63,第二组的平均数是11,两个组中所有数的平均数是8。
问:第二组有多少个数?解:设第二组有某个数,则63+11某8某(9+某),解得某3。
12.小明参加了六次测验,第三、第四次的平均分比前两次的平均分多2分,比后两次的平均分少2分。
如果后三次平均分比前三次平均分多3分,那么第四次比第三次多得几分?解:第三、四次的成绩和比前两次的成绩和多4分,比后两次的成绩和少4分,推知后两次的成绩和比前两次的成绩和多8分。
因为后三次的成绩和比前三次的成绩和多9分,所以第四次比第三次多9-81(分)。
13.妈妈每4天要去一次副食商店,每5天要去一次百货商店。
妈妈平均每星期去这两个商店几次?用小数表示解:每20天去9次,9÷20某73.15(次)。
14.乙、丙两数的平均数与甲数之比是137,求甲、乙、丙三数的平均数与甲数之比。
解:以甲数为7份,则乙、丙两数共13某2=26(份)所以甲乙丙的平均数是(26+7)/311(份)因此甲乙丙三数的平均数与甲数之比是11:7。
15.五年级同学参加校办工厂糊纸盒劳动,平均每人糊了76个。
已知每人至少糊了70个,并且其中有一个同学糊了88个,如果不把这个同学计算在内,那么平均每人糊74个。
糊得最快的同学最多糊了多少个?解:当把糊了88个纸盒的同学计算在内时,因为他比其余同学的平均数多88-74=14(个),而使大家的平均数增加了76-742(个),说明总人数是14÷2=7(人)。
小学五年级奥数题100题(附答案)

小学五年级奥数题100题(附答案)1.解题思路:先按照乘除法的优先级计算,再按照加减法的顺序计算。
将原式化简后得到答案.2.解题思路:利用等差数列求和公式,先计算出1到XXX的和,再计算出9001到9999的和,两者相减即可得到答案xxxxxxx。
3.解题思路:将式子展开,利用差平方公式化简后得到答案.4.解题思路:将等式左右两边的式子进行化简,得到873×477-198=476×874+199,因此原式等于1.5.解题思路:将原式进行拆分,每两项作为一组进行化简,得到1999×2+1997×2+1995×2+…+3×2+1×2=2×(1999+1997+…+3+1),化简得到答案xxxxxxx。
6.解题思路:利用等差数列求和公式,将297和209看作首项和末项,公差为-4,求得答案5819.7.解题思路:将分式中的分子和分母进行配对相消,最终得到答案50/99.8.解题思路:将原式进行化简,得到1/4.9.解题思路:设去掉的两个数分别为x和y,根据题意列出方程组求解得到x=12,y=14,因此它们的乘积为168.10.解题思路:设第三个数为x,根据题意列出方程组求解得到x=39-28×3-33×5+30×7=39,因此第三个数为39.11.解题思路:设第二组数的个数为x,根据题意列出方程求解得到x=12,因此第二组数的个数为12.12.XXX参加了六次测验,其中第三、第四次的平均分比前两次的平均分高2分,比后两次的平均分低2分。
如果后三次平均分比前三次平均分高3分,那么第四次得分比第三次高几分?解:第三、四次的成绩和比前两次的成绩和高4分,比后两次的成绩和低4分,推知后两次的成绩和比前两次的成绩和高8分。
因为后三次的成绩和比前三次的成绩和高9分,所以第四次得分比第三次高9-8=1分。
13.妈妈每4天要去一次副食商店,每5天要去一次百货商店。
奥数1-6年级课表及学费 (学而思)
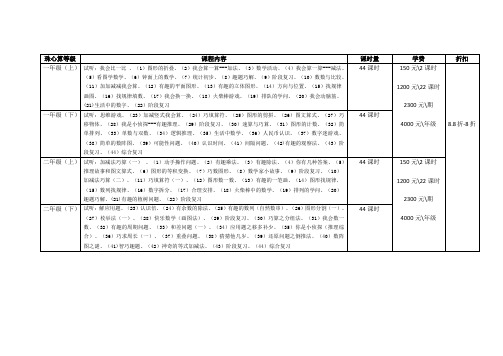
170元\2课时
1500元\22课时
2500元\期
4300元\年级
四年级(下)
试听:环形跑道(一)、(23)环形跑道(二)、(24)加乘原理与归纳递推、(25)操作问题、(26)流水行船初步、(27)构造与论证之奇偶分析(一)、(28)构造与论证之奇偶分析(二)、(29)多位数计算、(30)容斥原理初步(一)、(31)容斥原理初步(二)、(32)应用题综合、(33)数列与数表(一)、(34)排列(一)、(35)排列(二)、(36)组合(一)、(37)组合(二)、(38)统筹与最优化、(39)小数计算(春季课程)、(40)几何计数、(41)格点与割补、(42)等积变形(一)、(43)等积变形(二)、(44)综合复习
四年级、五年级、六年级学生每次课2小时(2课时,每课时60分钟)
44课时
注意:
奥数学费折扣说明
(1)报22课时可打8.8折
(2)报一学期可打8.5折
(3)报一学年可打8折
奥数特惠试听班399元=6课时(3次课),随同年龄正课班同学试听学习!若试听后满意,需要报正课的同学,399元可以抵扣正课学费!
上课时间说明:一年级、二年级、三年级学生每次课1.5小时(2课时,每课时45分钟)
44课时
二年级(上)
试听:加减法巧算(一) 、(1)动手操作问题、(2)有趣乘法、(3)有趣除法、(4)你有几种答案、(5)推理故事和图文算式、(6)图形的等积变换、(7)巧数图形、(8)数学家小故事、(9)阶段复习、(10)加减法巧算(二)、(11)巧填算符(一)、(12)图形数一数、(13)有趣的一笔画、(14)图形找规律、(15)数列找规律、(16)数字拆分、(17)合理安排、(18)火柴棒中的数学、(19)排列的学问、(20)趣题巧解、(21)有趣的植树问题、(22)阶段复习
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
五年级奥数-数列与数表
1.计算:(2+5+8+......+194)÷(4+7+ (196)
2.一本600页的书,小明每天都比前一天多读一页,16天刚好读完这本书,那
么他最后一天读了多少页?
3.有一列数,前两个数分别是0和1,从第三个数开始,每一个数都是前两个数
的和:0,1,1,2,3,5,8,13,21,34,……。
那么这个数列的第2005个数除以8所得的余数是多少?
4.把自然数按照下列规则排列,那么2008应该排在左起第几列?
1 2 3 4 5
9 8 7 6
10 11 12 13
17 16 15 14
18 19 20 21
25 24 23 22
26 27 28 29
…… ……
5.观察下面的一列有规律的算式:5+3,7+6,9+9,11+12,……则按照规律第
2008个算式的结果应该是多少?
五年级奥数-数列与数表答案
1.解析:
2,5,8,......,194是以3为公差的等差数列,共有(194-2)÷3+1=64项,则2+5+8+......+194=(2+194)×64÷2=98×64。
4,7,10, (196)
每一项都比上面的等差数列中每一项多2,因此4+7+10+……+196=98×64+2×64=100×64。
因此原式=98÷100=0.98。
2.解析:
设小明最后一天读了x页,则第一天读了x-15页,由题意可得方程:(x-15+x)×16÷2=600,解得,x=45。
3.解析:
这串除以8所得的余数依次是:0,1,1,2,3,5,0,5,5,2,7,1,0,1,1,2,……。
余数数列从第1个开始,以0、1、1、2、3、5、0、5、5、
2、7、1这12个数为一组依次循环出现的,又2008=12×167+4,所以第2008
个数除以8所得的余数与第4个余数相同,即为2。
4.解析:
观察数列可知,除了前5个数之外,后面的数以8为周期,由2008=8×250=8+8×249,所以2008与8在同一列,即2008在左边第2列。
5.解析:
通过观察可以发现,题目中出现的算式的规律是:每一个算式的第一个加数比上一个算式的第一个加数多2,而每一个算式的第二个加数比上一个算式的第二个加数多3。
以此推断,第2008个算式的两个加数分别是5+2×2007和3+3×2007,所以该算式的结果为5+2×2007+3+3×2007=10043。
