2017年春季新版北师大版八年级数学下学期6.3、三角形的中位线同步练习17
八年级数学下册6.3三角形的中位线能力提升(新版)北师大版
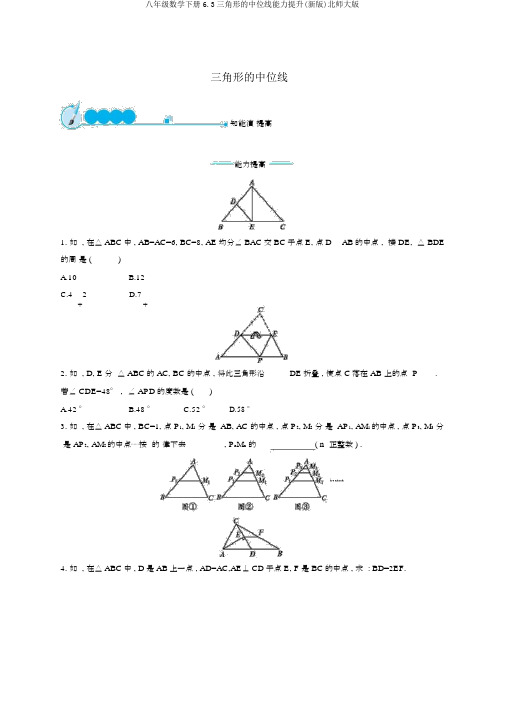
三角形的中位线知能演提高能力提高1.如 , 在△ABC中 , AB=AC=6, BC=8, AE均分∠BAC交BC于点E, 点D AB的中点,接 DE,△ BDE 的周是 ()A.10B.12C.42D.7++2.如 , D, E分△ABC的AC, BC的中点 , 将此三角形沿DE折叠,使点 C落在 AB上的点 P.若∠ CDE=48°,∠ APD的度数是()A.42 °B.48 °C.52 °D.58 °3.如 , 在△ABC中 , BC=1, 点P1, M1分是AB, AC的中点 , 点P2, M2分是AP1, AM1的中点 , 点P3, M3分是 AP2, AM2的中点⋯⋯按的律下去, P n M n的( n正整数 ) .4.如 , 在△ABC中 , D是AB上一点 , AD=AC,AE⊥CD于点E, F是BC的中点 , 求 : BD=2EF.5.如图 , 已知随意四边形ABCD,且线段 AB, BC, CD, DA, AC, BD的中点分别是E, F, G, H, P, Q.(1)按序连结 EF, FG, GH, HE,求证:四边形 EFGH是平行四边形;(2)按序连结 EQ, QG,GP, PE必定获得平行四边形吗?(只判断,不证明)6.如图 , 在四边形ABCD中, P是对角线 BD的中点, E, F 分别是 AB, CD的中点, AD=BC,∠ PEF=18°,求∠PFE的度数 .创新应用7.如图①, 在四边形ABCD中 , AB=CD,E, F分别是BC, AD的中点 , 连结EF并延伸 , 分别与BA, CD的延伸线交于点 M, N,则∠ BME=∠ CNE(不需证明) .小明的思路是 : 在图①中 , 连结BD, 取BD的中点H, 连结HE, HF, 依据三角形中位线定理和平行线性质,可证得∠ BME=∠ CNE.问题 : 如图② , 在△ABC中 , AC>AB,D点在AC上 , AB=CD,E, F分别是BC, AD的中点 , 连结EF并延伸 , 与BA的延伸线交于点G,若∠ EFC=60°,连结 GD,判断△ AGD的形状并证明 .答案:能力提高1.A2.B3.4.证明 : ∵AD=AC,AE⊥CD, ∴CE=DE.∵F是 BC的中点,∴EF是△ CDB的中位线 .∴BD=2EF.5. (1) 证明 : ∵E, F分别是AB, BC的中点 ,∴EF是△ ABC的中位线 . ∴EF∥ AC, EF=AC.同理 HG∥ AC, HG=AC.∴EF∥HG, EF=HG∴.四边形 EFGH是平行四边形 .(2)解 : 四边形EQGP是平行四边形.6.解 : ∵PF是△DBC的中位线 , PE是△BAD的中位线 ,∴PF=BC,PE=AD.∵AD=BC,∴PF=PE,∴∠ PFE=∠ PEF=18° .创新应用7.解 : △AGD是直角三角形.证明以下 :如图 , 连结BD, 取BD的中点H, 连结HF, HE.∵F是 AD的中点,∴HF∥AB, HF=AB,∴∠ 1=∠ 3.同理HE∥CD, HE=CD,∴∠ 2=∠EFC.∵AB=CD,∴HF=HE,∴∠1=∠2.∵∠ EFC=60°,∴∠3=∠ EFC=∠ AFG=60°,∴△ AGF为等边三角形 .∵AF=FD,∴GF=FD,∴∠ FGD=∠ FDG=30°,∴∠ AGD=90°,即△ AGD是直角三角形 .。
2017年春季新版北师大版八年级数学下学期6.3、三角形的中位线导学案8

6.3 三角形的中位线【学习目标】1、了解三角形中位线的概念。
2、探索并掌握三角形中位线的性质,并能应用其性质解决有关问题。
【学习重难点】重点:三角形中位线定理;难点:三角形中位线定理的运用【学习过程】一、学习准备:1、平行四边形的判定方法:①两组对边 的四边形是平行四边形。
②两组对边_____________________ 的四边形是平行四边形。
③一组对边 的四边形是平行四边形。
④两组对角_____________________ 的四边形是平行四边形。
⑤两条对角线 的四边形是平行四边形。
2、三角形的中线:在三角形中,连接一个________与它__________的线段 _________________________叫做这个三角形的中线.3、三角形的中位线:连接三角形____________的线段叫做三角形的中位线.如图,在∆ABC 中,D 为AB 的中点,E 为AC 的中点,则线段_____是∆ABC的中位线. 线段_________是∆ABC 的中线.4、三角形中位线定理:三角形的中位线__________第三边,且________第三边的________.二、教材精读:已知:如图,DE 是∆ABC 的中位线。
求证:DE ∥BC ,DE=21BC.合作探究如图:任意画一个四边形,以四边的中点为顶点组成一个新四边形,这个新四边形的形状有什么特征?请证明你的结论,并与同伴交流。
三、课堂练习:5、(福建厦门中考)如图,在∆ABC 中,DE 是∆ABC 的中位线,若DE=2,则BC=_______.6、(2012.浙江)如图,点D,E,F 分别为∆ABC 三边的中点,若∆DEF 的周长为10,则∆ABC 的周长为( )分析:三角形中位线定理可得到BC DF AB EF AC DE 21,21,21=== A.5 B.10 C.20 D.40总结:由三角形的三条中位线,可以得出以下结论:(1)三条中位线组成一个三角形,其周长为原三角形组成的__________;(2)三条中位线将原三角形分割成四个____________的三角形;(3)三条中位线将原三角形划分出__________个面积相等得平行四边形。
【课件】北师大版八年级下册6.3三角形的中位线-刘文

方法3:连接AC、BD EF∥HG,EH ∥FG (或EH=FG,EF=HG)
HD A
G E
四边形EFGH是平行四边形 B
F
C
你的结论对所有的四边形ABCD都成立吗? 成立
顺次连接任意四边形的四边中点得到平行四边形。
这样的四边形也叫中点四边形
感悟收获
为证明平行关系以及一条
同学们,通过本节课的学习,你都有线哪段些是另收一获条线?段的2倍或 一半提供了一个新的途径
CD = 1 AB角形300角所对的 B
直角边等于斜边的一半。
1
BC = AB
C
2
300 A
课堂练习 暂停视频,做一做
1、如图:在△ABC中,DE是中位线.
A
(1)若∠ADE=60°,则∠B= 60°;
(2)若BC=8cm,则DE= 4 cm;
D
E
(3)若DE=8cm,则BC= 16 cm.
若MN之间还有阻隔呢? 你有什么办法解决?
暂停视频,做一做 P
Q
分析:将四边形ABCD分割为三角形,利 用三角形的中位线可转化两组对边分 别平行或一组对边平行且相等来证明.
如图,四边形ABCD四边的中点分别为E,F,G,H,四边形EFGH是怎样四 边形?请你猜想一下。
已知:如图,在四边形ABCD中, E,F,G,H分别为各边的中点.
E
1
∴ DE∥BC , DE= BC
2
C
(位置关系)(数量关系)
作用:1、证明两条线段平行;
1 2、证明一条线段是另一条线段的2倍或 2 ;
方法总结
证明线段倍分关系的方法常有三种: A
三角形的中位线(分层练习)(解析版)-八年级数学 下册

第六章平行四边形6.3三角形的中位线一、单选题A.1【答案】C【分析】根据三角形的中位线等于第三边的一半进行计算即可.【详解】解:∵D,EA.20m B【答案】D【分析】根据中位线定理可得:【详解】解:D∵是ACA.5B【答案】D的长,再根据中位线的性质即可求解.A.4B.6【答案】AABCA.1.5B.2【答案】B【分析】根据三角形中位线定理解答即可.A.6米B.7米【答案】C【分析】直接使用中位线定理得出结果.【详解】E∵、F分别是边AB、二、填空题7.(2022秋·八年级单元测试)如图,在ABC 中,D ,E 分别为AB ,AC 边的中点,若3DE ,则BC 的长为______.【答案】6【分析】直接根据三角形中位线定理即可得.【详解】解:∵在ABC 中,D ,E 分别为AB ,AC 边的中点,且3DE ,26BC DE 故答案为:6.【点睛】本题考查了三角形中位线定理,熟练掌握三角形中位线定理是解题关键.8.(2022春·湖南常德·八年级统考期中)如图,A ,B 两地被一座小山阻隔,为测量A ,B 两地之间的距离,在地面上选一点C ,连接CA ,CB ,分别取CA ,CB 的中点D ,E ,测得DE 的长度为380米,则A ,B 两地之间的距离是________米.【答案】760【分析】利用三角形中位线定理解决问题即可.【详解】解:∵D 、E 分别是CA ,CB 的中点,【答案】1【分析】利用三角形中位线定理解答即可.【详解】解:∵F ,M 分别为边∴11FM AB ,【答案】4【分析】根据三角形中位线定理即可求出四边形周长.【详解】解:∵点E,F分别是三、解答题∴A CDE ,在ABC 和DCE △中,AB CD A CDE AC DE,∴()ABC DCE SAS △△,∴BC CE .【点睛】本题考查了三角形中位线定理、平行线的性质、三角形全等的判定定理与性质,熟练掌握三角形中位线定理是解题关键.一、填空题1.(2023春·陕西西安·八年级高新一中校考阶段练习)如图,M 是ABC 的边BC 的中点,AN 平分BAC ,BN AN 于点N ,延长BN 交AC 于点D ,已知10AB ,15BC ,4MN ,则ABC 的周长是__________.【答案】43【分析】证明ABN ADN ≌ ,得到10AD AB ,BN DN ,根据三角形中位线定理求出CD ,计算即可.【详解】解:∵AN 平分BAC ,∴BAN DAN ,在ABN 和ADN △中,【答案】4【分析】利用三角形的中位线定理并结合条件可证明进而证明四边形AEFD∴AD EF ∥,1AD EF ,∴四边形AEFD 是平行四边形,∴1AE DF ,∴四边形AEFD 的周长为11114AE EF DF AD .故答案为:4.【点睛】本题考查了三角形的中位线定理,平行四边形的判定与性质等知识,证明四边形AEFD 是平行四边形是解题的关键.3.(2023·山东烟台·统考二模)如图,ABCD Y 中,4660AB AD A ,,,点E 在AB 的延长线上,F 为DE 的中点,连接CF ,若10BE ,则CF 的长为__________.【答案】3【分析】延长BC 至G ,使10BG BE ,连接GE ,延长DC 交GE 于点H ,得到GBE 是等边三角形,推出GCH △是边长为4等边三角形,证明CF 是DEH △的中位线,根据三角形中位线定理即可求解.【详解】解:∵ABCD Y 中,60A ,∴60GBE A ,延长BC 至G ,使10BG BE ,连接GE ,延长DC 交GE 于点H ,∵60GBE ,∴GBE 是等边三角形,∴10BG BE GE ,【答案】5【分析】取AB的中点G,连接边的一半求出EG、FG,并求出【详解】解:如图,取AB的中点【答案】201612【分析】根据三角形中位线定理求出第二个三角形的周长、得到答案.【详解】解:根据三角形中位线定理得到第二个三角形三边长是即第二个三角形的周长为12二、解答题6.(2022秋·八年级单元测试)如图所示,在四边形ABCD 中,对角线AC 、BD 交于点O ,E ,F 分别是AB 、CD 的中点,且AC BD .求证:OM ON .【答案】见解析【分析】取AD 的中点G ,连接EG ,FG ,构造三角形的中位线,根据三角形的中位线定理进行证明即可.【详解】证明:如图所示,取AD 的中点G ,连接EG ,FG ,G ∵、F 分别为AD 、CD 的中点,GF 是ACD 的中位线,12GF AC ,同理可得,12GE BD ,AC BD ∵,1122GF GE AC BD .GFN GEM ,(1)求证:BD CE ;(2)若2AB ,且CE AD ,求【答案】(1)见解析(2)3。
北师大版八下数学《三角形的中位线》即时练习

求证:四边形EFGH是平行四边形.
AH E
D 分析 : 由E,F,G,H分别
是四边形ABCD各边的中
G 点,联想到应用三角形的
中位线 定理来证明.
《三角形的中位线》 即时练习
1、已知:三角形的各边分别为6cm,8cm, 10cm,则连结各边中点所成三角形的周 长为 —12—cm.
3 10
8 E5 4
F
6
2、己知: E、F分别三角形ABC为AB、AC的中点 (1)∵ E、F分别为AB、AC的中点。
∴ EF∥BC的根据:三角形中位线定理 (2)若BC =10cm,
B
F
C
证明: 连结AC BD
∵ EF和HG分别是⊿ABC 和
A
⊿ADC的中位线
∴ EF//AC HG//AC(三角形的中
位线平行于第三边,并且等于张三 E
边的一半)
∴ EF//HG 同理可证 EH//FG
B
∴四边形EFGH是平行四边形
(两组对边分别平行的四边形是平
行四边形).
H D G
F
C
结束
6.3三角形的中位线同步练习2020-2021学年北师大版八年级下册数学

6.3三角形的中位线一.选择题1.如图所示,在△ABC中,∠ACB=90°,AC=5,AB=13,点D是AC的中点,过点D 作DE∥BC,交AB于E点,则DE的长为()A.8B.7C.6D.52.如图,BD、CE是△ABC的中线,P、Q分别是BD、CE的中点,则PQ:BC等于()A.1:4B.1:5C.1:6D.1:73.如图,平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为()A.3cm B.6cm C.9cm D.12cm4.如图,BD为△ABC的中线,E为BD的中点,连接AE并延长交BC于点F,若BC的长为7,则BF的长为()A.B.C.D.5.如图,D,E分别是△ABC的边AC,BC的中点,则下列说法不正确的是()A.DE是△BCD的中线B.BD是△ABC的中线C.AD=DC,BE=EC D.DE是△ABC的中线6.如图,在△ABC中,点D,E,F分别是边AB,AC,BC的中点,已知∠A=65°,则∠DFE=()A.60°B.62°C.64°D.65°7.如图,AH是△ABC的高,D,E,F分别是三边中点,则DE与FH的大小关系是()A.DE<FH B.DE>FH C.DE=FH D.不能确定8.如图,在△ABC中,点D,E分别是边AB,AC的中点,点F是线段DE上的一点.连接AF,BF,∠AFB=90°,且AB=8,BC=14,则EF的长是()A.2B.3C.4D.59.如图,△ABC的周长为32,点D、E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=12,则PQ的长为()A.3B.4C.5D.610.如图,△ABC中,AB=4,AC=3,AD,AE分别是其角平分线和中线,过点C作CG ⊥AD于F,交AB于G,连接EF,则线段EF的长为()A.1B.C.D.二.填空题11.如图,在△ABC中,D,E分别是边AB,AC的中点,如果BC=7,那么DE=.12.如图,已知线段AB,将线段AB沿某个方向平移4个单位得到线段DC,其中点D是A 的对应点,且点D不在直线AB上.连接AC,BD交于点O,若E是CD中点,则OE 的长度值是.13.如图,△ABC中,BD平分∠ABC,AD⊥BD于点D,AD的延长线交BC于点E,F是AC中点,连接DF,若AB=10,BC=24,则DF的长为.14.如图,△ABC中,若D、E、F分别是AB、AC、CD的中点,连接BF,若四边形BDEF 的面积为6,则△ABC的面积=.15.如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是.三.解答题16.如图,等边△ABC的边长是4,D、E分别为AB、AC的中点,延长BC至点F,使CF =BC,连接CD和EF.(1)求证:DE=CF;(2)求EF的长.17.在△ABC中,E是AC边上一点,线段BE垂直∠BAC的平分线于D点,点M为BC边的中点,连接DM.(1)求证:DM=CE;(2)若AD=6,BD=8,DM=2,求AC的长.18.如图,在△ABC中,AE平分∠BAC,BE⊥AE于点E,点F是BC的中点.(1)如图1,BE的延长线与AC边相交于点D,求证:EF=(AC﹣AB);(2)如图2,请直接写出线段AB、AC、EF的数量关系.参考答案一.选择题1.解:∠ACB=90°,AC=5,AB=13,∴BC==12,∵DE∥BC,D是AC的中点,∴DE=BC=6,故选:C.2.解:连接DE,连接并延长EP交BC于点F,∵DE是△ABC中位线,∴DE=BC,AE=BE,AD=CD,∴∠EDB=∠DBF,∵P、Q是BD、CE的中点,∴DP=BP,∵在△DEP与△BFP中,,∴△DEP≌△BFP(ASA),∴BF=DE=BC,P是EF中点,∴FC=BC,PQ是△EFC中位线,PQ=FC,∴PQ:BC=1:4.故选:A.3.解:∵四边形ABCD是平行四边形,∴OA=OC;又∵点E是BC的中点,∴BE=CE,∴AB=2OE=2×3=6(cm)故选:B.4.解:取FC的中点H,连接DH,∵CD=DA,∴DH是△ACF的中位线,∴DH∥AF,∵BE=ED,∴BF=FH,∴BF=FH=HC=BC=,故选:A.5.解:∵D、E分别是△ABC的边AC、BC的中点,∴DE是△BCD的中线;BD是△ABC的中线;AD=DC,BE=EC;DE是△BCD的中线,不是△ABC的中线.观察选项,只有选项D符合题意;故选:D.6.解:∵点D,E,F分别是边AB,AC,BC的中点,∴DF、EF是△ABC的中位线,∴DF∥AC,EF∥AB,∴四边形ADFE是平行四边形,∴∠DFE=∠A=65°,故选:D.7.解:∵D,E分别是BA,BC的中点,∴DE是△ABC的中位线,∴DE=AC,∵AH⊥BC,F为AC的中点,∴FH=AC,∴DE=FH,故选:C.8.解:∵点D,E分别是边AB,AC的中点,∴DE是△ABC的中位线,∵BC=14,∴DE=BC=7,∵∠AFB=90°,AB=8,∴DF=AB=4,∴EF=DE﹣DF=7﹣4=3,故选:B.9.解:∵BQ平分∠ABC,BQ⊥AE,∴∠ABQ=∠EBQ,∵∠ABQ+∠BAQ=90°,∠EBQ+∠BEQ=90°,∴∠BAQ=∠BEQ,∴AB=BE,同理:CA=CD,∴点Q是AE中点,点P是AD中点(三线合一),∴PQ是△ADE的中位线,∵BE+CD=AB+AC=32﹣BC=32﹣12=20,∴DE=BE+CD﹣BC=8,∴PQ=DE=4.故选:B.10.解:∵AD是∠BAC平分线,∴∠BAD=∠CAD,在△AGF和△ACF中,,∴△AGF≌△ACF(ASA)∴AG=AC=3,GF=FC,∴GB=AB﹣AG=1,∵CF=FG,CE=EB,∴EF是△CGB的中位线,∴EF=GB=,故选:C.二.填空题11.解:∵D,E分别是边AB,AC的中点,∴DE是△ABC的中位线,∴DE=BC=3.5,故答案为:3.5.12.解:如图,连接AD,BC,根据平移的性质知:AD=4,AB=CD且AB∥CD,则四边形ABCD是平行四边形,∴O点是AC的中点,∵E是CD中点,∴OE是△ACD的中位线,∴OE=AD=2.故答案是:2.13.解:在△ADB和△EDB中,,∴△ADB≌△EDB(ASA),∴EB=AB=10,AD=DE,∵BC=24,∴CE=BC﹣BE=14,∵AF=FC,AD=DE,∴DF=CE=7,故答案为:7.14.解:∵点F是CD的中点,∴S△DEF=S△CEF,设S△DEF=S△CEF=x,∵D、E分别是AB、AC的中点,∴S△ADE=S△CDE=2x,S△BDC=S△ADC=4x,S△BDF=2x,∴S四边形BDEF=3x.∵S四边形BDEF=6,∴3x=6,∴x=2,∴S△ABC=2S△BDC=8x=16,故答案为:16.15.解:∵点P是对角线BD的中点,点E、F分别是AB、CD的中点,∴PF=BC,PE=AD,又AD=BC,∴PE=PF,∴∠PFE=∠PEF=30°,∴∠EPF=120°,故答案为:120°.三.解答题16.(1)证明:∵D,E为AB,AC的中点,∴DE为△ABC的中位线,∴DE∥BC,DE=BC,∵CF=BC,∴DE=CF;(2)解:由(1)可知,DE∥BC,DE=CF,∴四边形DCFE为平行四边形,∴EF=DC,在等边△ABC中,D为AB中点,∴CD⊥AB,∴CD=BC•sin60°=2,∴EF=2.17.(1)证明:在△ADB和△ADE中,,∴△ADB≌△ADE(ASA)∴AE=AB,BD=DE,∵BD=DE,BM=MC,∴DM=CE;(2)解:在Rt△ADB中,AB==10,∴AE=10,由(1)得,CE=2DM=4,∴AC=CE+AE=14.18.(1)证明:如图1中,∵AE平分∠BAC,BE⊥AE于点E,∴△ABD是等腰三角形,∴BE=DE,∵BF=FC,∴EF=DC==(AC﹣AB).(2)结论:EF=(AB﹣AC),理由:如图2中,延长AC交BE的延长线于P.∵AE⊥BP,∴∠AEP=∠AEB=90°,∴∠BAE+∠ABE=90°,∠P AE+∠APE=90°,∵∠BAE=∠P AE,∴∠ABE=∠APE,∴AB=AP,∵AE⊥BP,∴E为BP的中点,∴BE=PE,∵点F为BC的中点,∴BF=FC,∴EF=PC=(AP﹣AC)=(AB﹣AC).。
八年级数学北师大版初二下册--第六单元 6.3《三角形的中位线》课件
新课学习 证明:如图,延长DE至F,使EF=DE,连接CF. A ∵ AE=CE,∠AED=∠CEF, ∴△ABC≌△CDA(SAS). D E ∴AD=CF,∠ADE=∠F. ∴BD∥CF. ∵AD=BD, B C ∴BD=CF. ∴四边形ABCD是平行四边形. ∴DF∥BC,DF=BC.
1 1 ∴DE∥BC, DE DF BC . 2 2
作业布置
课本P152习题:6.6
板书设计 三角形中位线 一、三角形中位线的概念:
连接三角形两边的中点的线段叫做三角形的中位线。
二、三角形中位线的性质:
三角形的中位线平行与第三边,并且等于它的一半。
B
D · E · F
·
C
新课学习
(2)将△ADE绕点E按顺时针方向旋转180º到 △CFE 的位置(如图),这样就得到了一个与 △ABC 面积相等的□DBCF. A D
E
F
C 从小明的上述做法中,你能猜想出三角形两 边中点的连线与第三边有怎样的关系?能证明你 的猜想吗?
B
新课学习
三角形中位线的性质
F
新课学习 利用定理“三角形的中位线平行于第三边,且
等于第三边的一半”,可以证明小明分割出的四个
小三角形全等. 已知:如图,D,E,F分别是△ABC各边的中点. 求证: △ADE≌△DBF≌△EFC≌△FED.
A
D B
E C
F
新课学习
分析:利用三角形中位线性质,可转化用(SSS) 来证明三角形全等. 证明: ∵ D,E,F分别是△ABC各边的中点.
A
M
B
N C
C
D
E
F
B
课堂练习
3、已知:如图,A,B两地被池塘隔开,在没有任 何测量工具的情况下,有通过学习方法估测出 了A,B两地之间的距离:先在AB外选一点C,然 后步测出AC,BC的中点M,N,并测出MN的长,由 此他就知道了A,B间的距离.你能说出其中的 A 道理吗? 其中的道理是: M 连结A、B, ∵MN是△ABC的的中位线, C B N ∴AB=2MN.
北师大版八年级下册数学三角形的中位线专项训练(原创)
14.如图, 的周长为26,点 , 都在边 上, 的平分线垂直于 ,垂足为点 , 的平分线垂直于 ,垂足为点 ,若 ,则 的长为______.
三、解答题
15.如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF= BC,连接CD和EF.
10.2
【来源】浙江省温州市瑞安市2017-2018学年八年级下学期期末数学试题
【解析】
【分析】
根据平行四边形的性质求出AD的长,再根据中位线的性质即可求出OE的长.
【详解】
解:∵ ,
∵ ,
∴ .
∵ 为 的中点,
∴ 为 的中位线,
∴ .
故答案为:2.
【点睛】
此题主要考查平行四边形与中位线的性质,解题的关键是熟知平行四边形的对边相等.
2.B
【来源】福建省福州市闽侯县2018-2019学年八年级下学期期末考试数学试题
【解析】
【分析】
根据三角形中位线定理计算即可
【详解】
∵M、N分别是AC、BC中点,
∴NM是△ACB的中位线,
∴AB=2MN=80m,
故选:B.
【点睛】
此题考查三角形中位线定理,解题关键在于掌握运算法则
3.C
【来源】广西梧州藤县2017—2018学年八年级下学期期末数学抽考试题
(1)求证:DE=CF;
(2)求EF的长.
16.如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.
(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.
6.3三角形的中位线-北师大版八年级数学下册课件(共15张PPT)
目录
content
01 学 习 目 标 02 课 堂 学 习 03 课 堂 小 结 04 当 堂 检 测
学习目标 1 经历探索三角形中位线定理的过程,发展合情推理能力。
2
证明三角形中位线定理,发展演绎推理能力;运用三角形中位线 定理解决简单问题
02
1. 如图1所示,在△ABC中,D、E分别是AB、CA的中点,并且 ∠ADE=70°,∠A=80°,则∠C= 30°. 2. 如图2所示,在△ABC中,D、E、F分别是BC、CA 、AB的中 点,△ABC的周长是18cm,则△DEF的周长是 9 cm.
3.如图3,在四边形ABCD中,已知AB=CD,M、N、P分别是AD、BC、BD的中点,
C.3
D.4
感谢聆听!
∠ABD=20°,∠BDC=70°,则∠NMP的度数为 25
.
【例1】如图4,点E、F、G、H分别为四边形ABCD的边AB、BC、CD、AD的中点, 试判断四边形EFGH的形状,并说明理由.
归纳与小结:1.在此四边形问题的解决中,依然运用了
思想,将四边形问题
成三角形问题,具体做法为连接
;
2.本例中点四边形EFG点四边形的形状都是
.
【例2】求证:三角形的一条中位线与第三边上的中线互相平分. 已知:如图,△ABC的中,D、E分别是边AB、AC的中点,AF是BC边上的中线 求证: DE与AF互相平分
03
课堂小结
Life isn't about waiting for the storm to pass. it's about learning to dance
三.课堂小结
1.三角形中位线的定义:连接
[初中数++学]三角形的中位线(课件)+北师大版数学八年级下册
A
B
A
D
F
B
C
B
C
E
A E
直观想象
问题2:连接三角形的每条中位线,看看得到了什么样的图形?
四个小三角形全等。
问题3:如果要四个小朋友所分的蛋糕形状和大小都相同,你 有合理的解决方案吗? 沿着三角形三条中位线切开即可。
把实际问题向数学问题转化——应用意识
动手操作
问题4:你能通过剪拼的方式,将一个三角形拼成一个与其面积相等的平行四边形吗?
例1 已知:如图,在四边形ABCD中, E,F,G,H分别为各边的中点. 求证:四边形EFGH是平行四边形.
转化思想
分析:将四边形ABCD分割为三角形,利用三角形 的中位线可转化一组对边平行且相等或两组对边 分别平行或两组对边分别相等三种方法均可证明.
证明:连接AC.
∵E,F,G,H分别为各边△ABC
的中位线.
1
求证:DE∥BC, DE= 2 BC.
A
A
D
D
E
B
C
B
E
F
C
证明猜想
证明:如图,延长DE至F,使EF=DE,连接CF. ∵ AE=CE, ∠AED=∠CEF, ∴△ADE≌△CFE(SAS), ∴AD=CF,∠A=∠ECF. ∴CF∥AB. ∵AD=BD, ∴BD=CF. ∴四边形DBCF是平行四边形.
北师大版八年级下册
第六章 平行四边形
6.3 三角形的中位线
导入新课
情境引入 如图,有一块三角形的蛋糕,准备平均分给四个小朋友,
要求四个人所分的大小相同,请你设计合理的解决方案。
情境导入
小明的分法是这样的:先做边BC上的中线AF,再分别取 AB、AC边的中点D、E,分别连接DF、EF,则所分四部分蛋 糕的大小相同,你同意吗?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中位线课后练习
题一:已知,以一个三角形各边中点为顶点的三角形的周长为8cm,则原三角形的周长为_______ cm.
题二:已知三角形的各边长分别是8cm、10cm和12cm,则以各边中点为顶点的三角形的周长为
__________ cm.
题三:如图,∠CDA=∠BAD=90°,AB=2CD,M,N分别为AD,BC的中点,连MN交AC、BD于点E、F,
若ME=4,求EF的长.
题四:如图,梯形ABCD中,AD∥BC,中位线EF分别交BD、AC于点M、N.若AD=4cm,EF=6cm,则
EM=______cm,FN=______cm,MN=______cm,BC
=______cm.
题五:如图,在△ABC中,D、E、F分别为BC、AC、AB的中点,AH⊥BC于点H,FD=8cm,求HE的值.
题六: 如图,BD、CE是△ABC的中线,G、H分别是BE、CD的中点,BC=8,求GH的长.
题七:如图,已知四边形ABCD中,R,P分别是BC,CD上的点,E,F分别是AP,RP的中点,当点
P在CD上从C向D移动而点R
不动时,那么下列结论成立的是( )
A.线段EF的长逐渐增大
B.线段EF的长逐渐减少
C.线段EF的长不变
D.线段EF的长与点P的位置有关
题八:下列4个判断:
①当△ABC绕顶点A旋转时,△ABC各内角的大小不变;
②斜边和周长对应相等的两个直角三角形全等;
③有两边及第三边上的高对应相等的两个三角形全等;
④有两边及第三边上的中线对应相等的两个三角形全等;
其中正确判断的编号是 .
中位线
课后练习参考答案
题一:
16.
详解:由中点和中位线定义可得原三角形的各边长分别为新三角形各边长的2倍,所以原三角形的
周长为新三角形的周长的2倍为16,故答案为16.
题二:
15.
详解:如图,D,E,F分别是△ABC的三边的中点,则DE=12AC,DF=12BC,EF=12AB,
∴△DEF的周长为DE+DF+EF=12(AC+BC+AB)=12×(8+10+12)cm=15cm.
题三:
4.
详解:∵∠CDA=∠BAD=90°,M,N分别为AD,BC的中点,
∴四边形ABCD是梯形,MN是梯形的中位线,∴MN=12(AB+CD),
在△ACD中,ME∥CD,且M为AD的中点,
∴E为AC中点,即ME是△ADC的中位线,∴CD=2ME=2×4=8,
又∵AB=2CD,∴AB=2×8=16,MN=12(AB+CD)=12×(8+16)=12,
在△BCD中,NF是中位线,故NF=12CD=12×8= 4,
∴EF=MNMENF=1244= 4.
题四:
2,2,2,8.
详解:∵EF是梯形ABCD的中位线,∴EF∥AD∥BC,EF=12(AD+BC),
∴点M、N分别是BD、AC的中点,
∴EM与FN分别是△ABD与△ACD的中位线,MF是△DBC的中位线,
∵AD=4cm,EF=6cm,∴EM=NF=12AD=2cm,AD+BC=2EF=12cm,
∴BC=8cm,∴MF=12BC=4cm,∴MN=EFEMFN=2cm.
题五:
8cm.
详解:∵D、F是BC、AB的中点,∴AC=2FD=2×8=16cm,
∵E是AC的中点,AH⊥BC于点H,∴EH=12AC=8cm.
题六:
6.
详解:连接DE,∵AE=EB,AD=DC,∴DE∥BC,DE=12BC=12×8=4,
又∵EG=GB,DH=HC,∴GH=12(ED+BC)=12(4+8)=6.
题七:
C.
详解:如图,连接AR,因为AR的长度不变,根据中位线定理可知,EF∥AR,且EF=12AR,所以当点
P在CD上从C向D移动而点R不动时,线段EF
的长不变.
故选C.
题八:
①④.
详解:①当△ABC绕顶点A旋转时,根据旋转变换的性质,△ABC各内角的大小不变,故本小题正确;
②斜边和周长对应相等的两个直角三角形,直角边不一定对应相等,两三角形不一定全等,故本小
题错误;
③有两边及第三边上的高对应相等,这两边的夹角有可能一个是锐角一个是钝角,所以这两个三角
形不一定全等,故本小题错误;
④有两边及第三边上的中线对应相等,可以倍长中线利用三角形全等证明相等两边的夹角相等,所
以这两个三角形全等,故本小题正确.
综上,正确判断的编号是①④.
故答案为:①④.
