高中物理竞赛模拟试题三及答案
高中物理竞赛模拟试题三及答案

1、一条轻绳跨过一轻滑轮(滑轮与轴间摩擦可忽略),在绳的一端挂一质量为m 1的物体,在另一侧有一质量为m 2的环,求当环相对于绳以恒定的加速度a 2′ 沿绳向下滑动时,物体和环相对地面的加速度各是多少?环与绳间的摩擦力多大?2.如图(a )所示,一滑块在光滑曲面轨道上由静止开始下滑h 高度后进入水平传送带,传送带的运行速度大小为v =4m/s ,方向如图。
滑块离开传送带后在离地H 高处水平抛出,空气阻力不计,落地点与抛出点的水平位移为s 。
改变h 的值测出对应的 s 值,得到如图(b )所示h ≥0.8m 范围内的s 2随h 的变化图线,由图线可知,抛出点离地高度为H =__________m ,图中h x =__________m 。
3 (12分)过山车质量均匀分布,从高为h 的平台上无动力冲下倾斜轨道并进入水平轨道,然后进入竖直圆形轨道,如图所示,已知过山车的质量为M ,长为L ,每节车厢长为a ,竖直圆形轨道半径为R, L > 2πR ,且R >>a ,可以认为在圆形轨道最高点的车厢受到前后车厢的拉力沿水平方向,为了不出现脱轨的危险,h 至少为多少?(用R .L 表示,认为运动时各节车厢速度大小相等,且忽略一切摩擦力及空气阻力)4.(20分)如图所示,物块A 的质量为M ,物块B 、C 的质量都是m ,并都可看作质点,且m <M <2m 。
三物块用细线通过滑轮连接,物块B 与物块C 的距离和物块C 到地面的距离都是L 。
现将物块A 下方的细线剪断,若物块A 距滑轮足够远且不计一切阻力,物块C 落地后不影响物块A 、B 的运动。
求: (1)物块A 上升时的最大速度; (2)若B 不能着地,求mM满足的条件;(3)若M =m ,求物块A 上升的最大高度。
5.(12分)如图所示,一平板车以某一速度v 0匀速行驶,某时刻一货箱(可视为质点)无初速度地放置sx (b )于平板车上,货箱离车后端的距离为l =3m ,货箱放入车上的同时,平板车开始刹车,刹车过程可视为做a =4m/s 2的匀减速直线运动。
38届高中物理竞赛试题及答案

38届高中物理竞赛试题及答案在第38届高中物理竞赛中,试题设计旨在考察学生的物理基础知识、分析问题和解决问题的能力。
以下是本次竞赛的试题及答案。
试题一:力学问题题目描述:一个质量为m的物体从高度h处自由下落,忽略空气阻力,求物体落地时的速度。
解答:根据自由落体运动的公式,物体落地时的速度v可以通过公式v = √(2gh)计算得出。
其中,g为重力加速度,取9.8m/s²。
试题二:电磁学问题题目描述:一个长为L的导线,通有电流I,导线与电流方向垂直的磁场强度为B,求导线受到的安培力。
解答:根据安培力公式F = BIL,其中B为磁场强度,I为电流,L为导线长度。
将已知数值代入公式,即可求得导线受到的安培力。
试题三:光学问题题目描述:一束单色光从折射率为n1的介质入射到折射率为n2的介质,入射角为θ1,求折射角θ2。
解答:根据斯涅尔定律,n1 * sin(θ1) = n2 * sin(θ2)。
已知n1、n2和θ1,可以通过公式求得折射角θ2。
试题四:热学问题题目描述:一个理想气体在等压过程中从状态A变化到状态B,已知状态A的温度为T1,体积为V1,求状态B的温度T2。
解答:根据理想气体状态方程PV = nRT,其中P为压强,n为摩尔数,R为气体常数,T为温度,V为体积。
在等压过程中,P和n为常数,因此T1 * V1 = T2 * V2。
已知T1和V1,以及状态B的体积V2,可以求得T2。
试题五:现代物理问题题目描述:一个电子在磁场中做圆周运动,已知电子的电荷量为e,质量为m,磁场强度为B,求电子运动的轨道半径r。
解答:根据洛伦兹力公式F = evB,其中F为洛伦兹力,e为电子电荷量,v为电子速度,B为磁场强度。
由于电子在磁场中做圆周运动,洛伦兹力提供向心力,因此有F = mv²/r。
将两个公式联立,解得r = mv/eB。
以上是第38届高中物理竞赛的部分试题及答案,这些题目覆盖了物理学的多个重要领域,旨在全面考察学生的物理知识和应用能力。
高中物理竞赛初赛模拟试题(有答案)
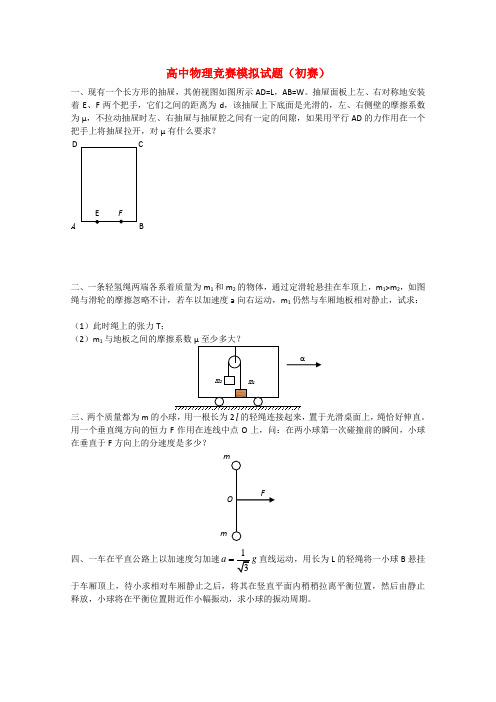
高中物理竞赛模拟试题(初赛)一、现有一个长方形的抽屉,其俯视图如图所示AD=L ,AB=W 。
抽屉面板上左、右对称地安装着E 、F 两个把手,它们之间的距离为d ,该抽屉上下底面是光滑的,左、右侧壁的摩擦系数为μ,不拉动抽屉时左、右抽屉与抽屉腔之间有一定的间隙,如果用平行AD 的力作用在一个把手上将抽屉拉开,对μ有什么要求?二、一条轻氢绳两端各系着质量为m 1和m 2的物体,通过定滑轮悬挂在车顶上,m 1>m 2,如图绳与滑轮的摩擦忽略不计,若车以加速度a 向右运动,m 1仍然与车厢地板相对静止,试求:(1)此时绳上的张力T ;(2)m 1三、两个质量都为m 的小球,用一根长为2l 的轻绳连接起来,置于光滑桌面上,绳恰好伸直。
用一个垂直绳方向的恒力F 作用在连线中点O 上,问:在两小球第一次碰撞前的瞬间,小球在垂直于F 方向上的分速度是多少?四、一车在平直公路上以加速度匀加速a g直线运动,用长为L 的轻绳将一小球B 悬挂于车厢顶上,待小求相对车厢静止之后,将其在竖直平面内稍稍拉离平衡位置,然后由静止释放,小球将在平衡位置附近作小幅振动,求小球的振动周期。
CBAm五、一根一端封闭的均匀玻璃管长96cm ,内有一端长20cm 为的水银柱水银柱下方为一空气柱,当温度为27°时玻璃管开口竖直向上,空气柱长60cm ,此时外界大气压为76cmHg ,试问:为使水银柱不全部从玻璃管中溢出,温度可达到多少度?六、三个相同的金属圈两两相交地焊接成如图所示的形状,若每一金属圈的原长电阻(即它断开时测两端的电阻)为R ,试求图中A 、B 两点之间的电阻。
七、在倾角为30°的斜面上,固定两根足够长的光滑平行导轨,一个匀强磁场垂直斜面竖直向上,磁感强度为B=0.4T ,导轨间距L=0.5m 两根金属棒ab 、cd 水平地放在导轨上,金属棒质量m ab =0.1kg.、m cd =0.2kg 两金属棒总电阻r=0.2Ω,导轨电阻不计,现使金属棒ab 以ν=2.5m/s 的速度沿斜面向上匀速运动,求: (1)金属棒cd 的最大速度;(2)在cd 有最大速度时,作用在ab 的外力的功率。
高中物理竞赛复赛模拟卷(三)参考答案 .doc

高中物理竞赛复赛模拟卷(三)参考答案第一题(18分)如图所示时,设小环与重物的速率分别为v 1和v 2;加速度大小分别为a 1和a 2,则 1.由机械能守恒,可得222121212sin Mv mv MgL +⨯=θ ① 而θθsin cos 21v v =②联立①、②可得(考虑到M=2m ) θ31sin 2gL v =θθ22cos sin 2gL v =2.由牛顿第二定律: 对小环:1cos ma T =θ③ 对重物:Ma T Mg =-θsin 2④小环相对重物与绳的结点作圆周运动,以该结点(即重物)为参照物,则有1sin v v =θ(v 为m 相对M 的速度)⑤212cos sin /a a v L θθ-=⑥并考虑到M=2m ,联立各式得 θsin 3mg T = 第二题(20分)1.'q 是q 的球面镜像电荷。
如图所示,可以肯定镜像电荷'q 一定在对称轴上,设其电量为'q ,距球心O 的间距为r ,则考察对称轴与球面的两交点B 、'B 的电势,可得r R q KR d q KU B -+-='① rR q K R d q K U B +++=''② 而球接触,0'==U U B③联立①、②、③得'Rq q d=-dR r 2=2.要使带电小球d 能在圆周上做匀速圆周运动,必须使轨道上各点的电势相等。
然而由两点电荷(A 与'A 处的)在空间产生的电场中等势面若是1个球面,则该等势面的电势一定为零。
由此可知A 与'A 互为镜像电荷。
由1的结论易得:2',''R R q q r r r =-=(其中''OA r =),解出:q rRq R r q d R r -=-=='','2 第三题(18分)取与金属环上一小段孤长一起做加速运动的坐标系,该坐标系与构成金属晶格的离子相连。
高中的物理竞赛试题及答案

高中的物理竞赛试题及答案高中物理竞赛试题一、选择题(每题3分,共30分)1. 一个物体从静止开始做匀加速直线运动,经过4秒后速度达到4m/s。
求物体的加速度。
A. 0.5 m/s²B. 1 m/s²C. 2 m/s²D. 4 m/s²2. 两个质量分别为m1和m2的物体,通过一根轻绳连接并悬挂在无摩擦的定滑轮上。
如果m1 > m2,系统将如何运动?A. 系统静止不动B. 系统加速下降C. 系统加速上升D. 系统减速上升3. 一个电子在电场中受到的电场力大小为F,如果电场强度增加到原来的两倍,电子受到的电场力将如何变化?A. 保持不变B. 增加到原来的两倍C. 增加到原来的四倍D. 增加到原来的八倍4. 一个物体在水平面上以初速度v0开始滑行,摩擦系数为μ。
求物体停止滑行所需的时间。
A. 无法确定B. \( \frac{v_0}{\mu g} \)C. \( \frac{v_0}{\sqrt{\mu g}} \)D. \( \sqrt{\frac{v_0}{\mu g}} \)5. 一个弹簧振子的振动周期为T,当振幅减半时,振动周期将如何变化?A. 保持不变B. 减半C. 增加到原来的两倍D. 增加到原来的四倍6. 一个点电荷Q产生电场的强度在距离r处为E,当距离增加到2r时,电场强度将如何变化?A. 保持不变B. 减半C. 增加到原来的两倍D. 增加到原来的四倍7. 一个物体在竖直方向上做自由落体运动,忽略空气阻力。
经过时间t后,物体的速度和位移分别是多少?A. 速度v=gt,位移s=1/2gt²B. 速度v=2gt,位移s=gt²C. 速度v=gt,位移s=gt²D. 速度v=2gt,位移s=2gt8. 一个物体从高度h自由落下,不计空气阻力。
求物体落地时的速度。
A. \( \sqrt{2gh} \)B. \( \sqrt{gh} \)C. \( 2\sqrt{gh} \)D. \( \sqrt{h/g} \)9. 一个物体在水平面上以初速度v0开始滑行,经过时间t后,其速度变为v。
高中物理竞赛决赛模拟试题(有答案)
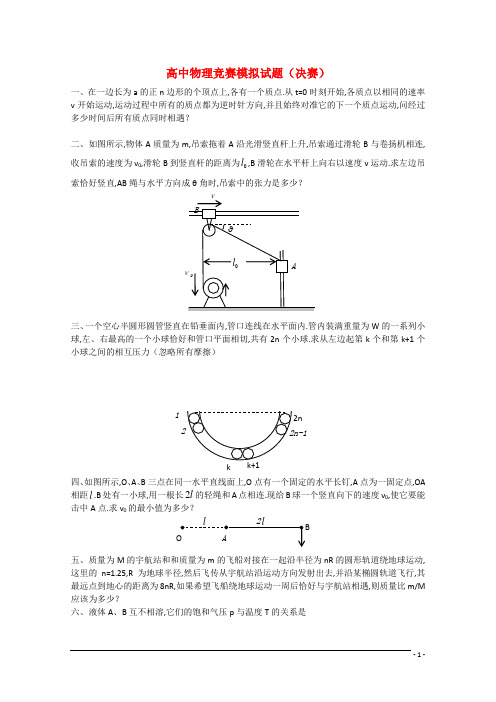
高中物理竞赛模拟试题(决赛)一、在一边长为a 的正n 边形的个顶点上,各有一个质点.从t=0时刻开始,各质点以相同的速率ν开始运动,运动过程中所有的质点都为逆时针方向,并且始终对准它的下一个质点运动,问经过多少时间后所有质点同时相遇?二、如图所示,物体A 质量为m,吊索拖着A 沿光滑竖直杆上升,吊索通过滑轮B 与卷扬机相连,收吊索的速度为ν0,滑轮B 到竖直杆的距离为0l ,B 滑轮在水平杆上向右以速度ν运动.求左边吊索恰好竖直,AB 绳与水平方向成θ角时,吊索中的张力是多少?三、一个空心半圆形圆管竖直在铅垂面内,管口连线在水平面内.管内装满重量为W 的一系列小球,左、右最高的一个小球恰好和管口平面相切,共有2n 个小球.求从左边起第k 个和第k+1个小球之间的相互压力(忽略所有摩擦)四、如图所示,O 、A 、B 三点在同一水平直线面上,O 点有一个固定的水平长钉,A 点为一固定点,OA 相距l .B 处有一小球,用一根长2l 的轻绳和A 点相连.现给B 球一个竖直向下的速度ν0,使它要能击中A 点.求ν0的最小值为多少?五、质量为M 的宇航站和和质量为m 的飞船对接在一起沿半径为nR 的圆形轨道绕地球运动,这里的n=1.25,R 为地球半径,然后飞传从宇航站沿运动方向发射出去,并沿某椭圆轨道飞行,其最远点到地心的距离为8nR,如果希望飞船绕地球运动一周后恰好与宇航站相遇,则质量比m/M 应该为多少?六、液体A 、B 互不相溶,它们的饱和气压p 与温度T 的关系是k0(i n ip a l i A B p T b ==+)(或) 式中p 0为标准大气压,a 、b 为液体本身性质所决定的常量.已测得两个温度点的p i/p 0值如下:(1)在外部压强为p 0时,确定A 、B 的沸点.(2)现将液体A 和B 各100g 注入容器中,并在A 表层覆盖有薄层无挥发性的液体C,C 与A 、B 互不相溶,C 的作用防止A 自由挥发,各液层不厚,液内因重力而形成的附加压均可忽略,A 、B 的摩尔质量比γ=M A /M B =8今对容器缓慢持续加热,液体温度t ℃随时间τ的变化如图所示.请确定图中温度t 1、t 2(精确到1℃)以及在1τ时刻液体A 和液体B 的质量(精确到0.1克)假设A 、B 蒸汽均能作理想气体处理,因此也也服从道尔顿分压定律.七、平行板电容器两极板都是正方形,其面积均为S=1.0×10-2m 2,相距为d=1.0×10-3m,将这个电容器与电源相连接,电源的电动势ε=100,再把厚度为d,长度等于电容器极板长度的电解质板(相对介电常数εr =2)以匀速ν=2.3×10m/S 引入两极板间,问:(1)电路中的电流强度为多少?(2)介质板插入过程中电源的输出能量为多少?(3)电容器中电解质板引入前后所储存的能量有何变化?比较电源输出的能量与电容器中能量的变化是否相同?说明原因.八、图是有24个等值电阻连接而成的网络,图中电源的电动势为ε=3.00V,内阻r 为2.00Ω的电阻与一阻值为28.0Ω的电阻R ′及二极管D 串联后引出两线;二极管的正向伏安曲线如图所示.P 0C BAt 2 t 1τ100400.284,0.0727890 1.476,0.6918A B A B p p C p pC ====0000:p p :p p(1)若将P、Q两端与图中电阻网络E、G两点相接,测得二极管两端的电压为0.86V,求电阻网络两点E与G的电压.(2)若将P、Q两端与图中电阻网络B、D两点相接,求同二极管D的电流I D和网格中E、G间的电压U EG.九、考虑不用发射到绕太阳运动的轨道上的方法,要在太阳系建立一个质量为m静止的太空站.这个太空站有一个面向太阳的大反射面(反射系数为1),来自太阳的辐射功率L产生的辐射压力使太空站受到一个背离太阳的力,此力与质量为M S的太阳对太空站的万有引力方向相反,大小相等,因而太空站处于平衡状态.忽略行星对太空站的作用,求:(1)此太空站的反射面面积A;(2)平衡条件和太阳与太空站之间的距离是否有关?(3)设反射面是边长为d的正方形,空间站的质量为106kg,确定d之值.已知太阳的辐射功率是3.77×1026W.太阳质量为1.99×1030kg.7142122 23 24参考答案一、□解Ⅰ 对一个正n 边形,内角的度数是(2)n nπ-,设每边的长度是a (以五边形为例)A 顶点对着B 质点运动到点F 处,B 质点对着C 顶点运动到了G 处(如图),在△BGF 中用余弦定理FG 2=(a-ν∆t )2+(ν∆t )2-2(ν∆t )(a-ν∆t )cos (2)n nπ- 舍去高阶小量12212222cos()2211cos()n FG a v ta v ta n vt n a a n ππ-⎡⎤=-∆-∆⎢⎥⎣⎦⎧-⎫⎡⎤=-+⎨⎬⎢⎥⎣⎦⎩⎭因为22[1cos()]1v t n a nπ-+<< 所以2{1[1cos()]}2[1cos()]v t n FG a a nn a FG v t n ππ-=-+--=+每边边长的减短率为2[1cos()]n v nπ-+ 相遇时间22[1cos()](1cos )a at n v v n nππ==-+- □解Ⅱ 在整个运动过程中所有质点总是在一个正n 形的顶点上(只是正n 形不断变小),因此α和θ不会变,即α=nπ,θ=2n ππ-.质点向着正n 边形中点O 运动的速度为cos sin /sin 2v v v na l nπθπ⊥===到达中点的时间222sin ()(1cos )l a at v v v n nππ⊥===- 二、□解Ⅰ 这是一个比较复杂的运动,将此运动看成两个运动的合成:一个是B 滑轮不动,卷扬机以速度ν0收吊索;另一个是AB 段吊索长度不变,B 滑块以ν向右运动.第一个运动使A 滑EG ADFCBν块得到了一个速度ν1=sin v θ第二个运动使A 滑块得到另一个速度 ν2=-cot θ·ν A 的真实速度 νA =ν1+ν2=0cos sin v v θθ-将A 的速度分解成沿吊索方向的分量νA Ⅱ和垂直吊索方向的分量A v ⊥'0cos cos sin A v v v θθθ⊥-'=B 速度的垂直于吊索的分量sin B v v θ⊥=所以A 相对于B 垂直于吊索方向的速度0cos sin A B A v v v v v θθ⊥⊥⊥-'=-=A 物体的向心加速度2200cos /cos A A v v a l l θθ⊥⊥==分析A 的受力情况可知sin cos cos T mg N maT Nθθθ--==联立,即可求得T□解Ⅱ 以滑轮B 为参照物,A 物体速度可看成水平方向的速度ν和竖直方向的速度ν′的合成,卷扬机虽然也有向左的速度ν,但不影响吊索的速度,所以物体A 沿吊索方向的速度亦为ν0.即0cos sin v v v θθ'=+得0cos sin v v v θθ-'=A 速度垂直吊索的分量0sin cos cos sin A v v v v v θθθθ⊥'=--=以下同解Ⅰ 三、如图,对第k(k ≥2)个滚珠进行受力分析,它受到左右两侧的压力分别记为N k-1和N K ,还受到管壁的经向弹力P 和重力W.建立如图直角坐标系,只讨论在x 方向上的合力为零的条件则有1cos cos cos 0K K N W N αβα-+-=有图中几何关系可知ν/2/2nαθθπ==所以有α=4nπ同时有(1)24(21)4k n nk nππβπ-=+-=将α,β值代入式可得1(21)cos4[]cos4k k k n N N W n ππ---=即有213213cos4[]cos45cos4[]cos4(21)cos4[]cos4k k n N N W n n N N W nk n N N W nππππππ--=-=--=两边相加后可得13521coscos cos 444{}cos4k k n nn N N W nππππ-+++-=()对第一个钢珠受力分析不难得到1cos 4[]cos4n N W nππ=因此xN k111121[cos ]4cos4[2cos sin ]2144cos 42sin41{[sinsin ]}22sin4sin 22sin4ki k kki i ki i n N Wni i n nn ni i n nk nnππππππππππππ====-=--=--==∑∑∑∑()()()2n ()2n所以sin2()sin2k k n N W nππ=四、如图,小球沿半圆轨道运动到B ′位置时,有机械能受恒定理可知,它应具有向上速度ν0.若ν0足够大,则小球可沿较小半圆轨道击中A 点.若ν0较小,则可能在较小半圆轨道的某C 点脱离半圆轨道改取斜抛轨道,也有可能击中A 点,这种方式对应的ν0即为所求的最小值.为C 点引入方位角.小球在C 点脱离圆轨道故此时绳中张力恰为零.小球速度ν应满足以下关系式2sin /mg F mv l θ==心式中m 为小球质量.l 为半圆轨道半径,又由机械能受恒可得22011sin 22mv mv mgl θ=+ 上述两式可解得20sin 2v glθ=建立如图坐标O-xy 系,小球在点C 时刻定为t=0,则C 点后斜抛运动的x 、y 分运动为2cos (sin )1sin (cos )2x l v t y l v t gt θθθθ=-+⎧⎪⎨=+-⎪⎩ 消去t,可得22222cos (cos )1(cos )sin []sin 2sin 1(cos )cos 2sin (cos )sin sin v x l x l y l g v v x gl x l l l l v θθθθθθθθθθθθ++=+-+=++- 由前面所述,可得2sin v gl θ=代入上式可得23(cos )cos (cos )sin sin 2sin x xyl ll θθθθθθ++=+- 要求小球与A 点相遇,即抛物线轨道需过x=l ,因此23(1cos )cos (1cos )0sin sin 2sin θθθθθθ++=+-可展开并逐渐化简为42222222222322322sin sin cos 2sin cos 12cos cos 02sin (sin cos )2cos (1sin )1cos 02sin 2cos 1cos 022cos 2cos 1cos 0θθθθθθθθθθθθθθθθθθθ++---=+----=---=----=最后得cos θ的三次方程式2313cos 2cos 0θθ--=其解为1cos 2θ=因此3sin θ=与前面的20sin /3v gl θ=联立,即算得最小ν0值为033/2v gl =.五、如图所示,斜线覆盖的内圆是地球,其外为飞船离开后的椭圆轨道,再外面是飞船与宇航站开始的圆轨道,最外面是飞船的新轨道.地球质量记为M e ,飞船被发射前,它与宇航站一起运动的速度为u,则有22()()()eG M m M M m u nR nR ++=得BB′A yCν0xθ O2llu =飞船发射后的瞬间,飞船的速度记为u,宇航站的速度记为V,根据动量受恒有:()M m u MV mv +=+即得所需要的比值为()()V u m M u v -=- 于是问题转化为求v 和V分离后飞船近地点与地心相距nR,速度大小为ν,远地点与地心相距8nR,飞船速度大小记为ν′,则由开普勒第二定律和动能受恒得22811228e e vnR v nR GM m GM m mv mv nR nR '=⎧⎪⎨'-=-⎪⎩ 由此解得43v u ==分离后宇航站远地点与地心间距离设为nR,速度大小记为V.近地点与地心间距r,速度大小为V ℃.同样可列方程组:221122e e V nR V rGMM MV GMM r MV nR ''=⎧⎪'=-⎨-⎪⎩ 可解得V =由可以看出,若求得r 便可算出m/M 值为求r,可利用开普勒第三定律,设飞船新轨道的周期为t,而它的半轴长则为(8)2nR nR +;宇航站新轨道周期设为T,而它的半长轴则为()2nR r +,有 3322(8)()nR nR nR r t T ++=即329()()nR t nR r T ⎡⎤=⎢⎥+⎣⎦飞船运行一周后恰好与宇航站相遇,因此t=Kt k=1、2、3、…… 代入上式后便可得2323(9)k nRr k-=宇航站不能与地球相碰,否则它不可能再与飞船相遇,故要求 r>R代入上式,并考虑到n=1.25,可得 k ≤11现由上式计算m/M 值()()33m V u M u v -==-=-=要求 m/M>0 因此 k 2/3>9/2 即 k ≥10可见k 取值只可为 k=10或k=11 因此0.048mM=或0.153 六、(1)沸点即01i p p =时的温度,由于0()0i n p l p =,可得沸点i i iaT b -=.对于A 0.284[](273.1540)1.476[](273.1590)An AAn Aa lb a l b =++=++解之得3748.49,10.711A A a K b =-=同理得5121.64,13.735B B a K b =-=据此可得液体A 、B 沸点00349.4577372.89100A B T K C T K C===≈(2)系统有两次沸腾现象,t 1、t 2是沸点.第一次应发生在A 、B 交界面处,界面上气泡内压强等于A 、B 的饱和气压之和,其值先达到p 0,此时沸腾温度t 1低于A 、B 各自的沸点.有110()()A B p t p t p +=由于(/)0i ai T b ip e p += 令11001,273.15,T t t t t =+=满足即代入0,,,,A A B B a b a b t 值,采用二分逼近方法取值,可得t 1=67℃ A 、B 交界面一消失,第一次沸腾结束.容器内仅剩一种液体,要加热到t 2该液体的沸点才出现第二次沸腾.T 2必为100℃或者77℃.在温度t 1的沸腾过程中,从交界面出升离的气泡中,A 、B 的饱和气质量比1122()()8()()A A A A AB B B B B m M p t p t m M p t p t ρρ=== 由(2)式可得t 1时,A 、B 的饱和气压:100()0.734,0.267A B p t p p p ==因此22.0ABm m = 这表明A 蒸发质量是B 的22倍,液体A 的100克全部蒸发掉,液体B 仅剩4.5克,可见在t 1时刻容器中,液体A 的质量为0,液体B 的质量为95.5克,因此t 2=100℃ 七、(1)在电介质匀速插入过程中,电容不断增加经过t 之后,电容为00(4r r SvC C Kd Kdt C Kdεεπ=+-=+电容增量之值0(4r tC C C Kdεπ-=-=因Q=C ε,故电容器上电量相应增加之值为(4r tQ C Kdεεεπ-==所以充电电流29(4(21)10210()r Q I t KdA εεπ---==-⨯==⨯(2)电源输出的电能972210100910()2.310W I t J ε---==⨯⨯⨯=⨯⨯ (3)介质未插入时,电容所贮电能为2210229371122411010024 3.14910104.4310()S W C Kd J εεπ---==⨯=⨯⨯⨯⨯⨯⨯=⨯ 插入介质后,电容所贮电能增加22700011() 4.4310()22r W C C C J εεε-=-==⨯所以电源输出能量W>∆W,由题设电源内阻,线路电阻均不计,那么电源多输出的电能W-∆W 到什么地方去了.把介质插入电容器之间时,在介质板上产生极化电荷,极板上自由电贺对极化电荷产生吸引力,在忽略介质板和电容器极板之间的摩擦力时,要使介质板匀速地插入电容器中去,必须在加一个外力与此吸引力相平衡.因此,在介质板匀速插入电容器时,外力做负功,使电源输出的一部分能量W-∆W 变成了其它形式的能量. 八、(1)当引线两端P 、Q 与电阻网格E 、G 两点连接时,二极管两端的电压U D1=0.86V,此时对应的电流从图中查得为25.0mA,则E 、G 两点间的电压为11130.025(28.02)0.861.39()EG D U I R U rI V ε'=---=-⨯+-=考虑到对称性,网格EG 两端的等效电阻R EG 可由图表示,其值 R EG =13R/3而1011118151201055.6()729.9()133()()()()(16/7)2722130.695()14EGEG EG EA U R I R R I II U R R R R I R V ==Ω==Ω=++=+==从图可看出EA EG U U =的一半,即0.695V(2)当引线两端P 、Q 与电阻网格B 、D 两点相接时,由图求得等效电阻R BD 与R 0关系,并代入R 0的阻值05529.97721.4()BD R R ==⨯=Ω 通过二极管D 的电流i D 与二极管两端的电压关系22()D D BD U I R R r ε'=-++代入数据得22351.4D D U I =-这是一条联系U D 与的I D 直线方程,而U D 、I D 同时又满足二极管伏安特性曲线中一直线22351.4D D U I =-与二极管伏安特性曲线的纵坐标即为二极管的电流,由图读出240.5D I mA =R 1 F根据对称性,图中,M 、P 两点等势, N 、Q 两点等势,流过R 18、R 22及R 3、R 7流过电阻的电流均为零,因此E 、G 间的电势差与M 、N 两点之间的电势差相等241112418120()2[]722352()72D EG MN D I R R U U R R R R R R I R V +==+++++==九、(1)设空间站与太阳距离为r,则太阳辐射在空间站反射面单位面积内的功率即为光强Ф=4L rπ,太阳对反射面产生的压强是光子的动量传递给反射面的结果,这一光压为于是反射面受到的辐射压力22LF PA A r cπ==辐射 太阳对太空站的万有引力为2S M mGF r =引力.式中G 为万有引力常数.在太空站处于平衡状态时,F F =辐射引力即222S M mG L A r c rπ= 这就得到,反射面面积2S GM mcA Lπ=(2)有上面的讨论可知,由于辐射压力和太阳引力都与r 2成反比,因而平衡条件与太阳和空间站的距离r 无关.(3)若A=d 2,并以题给数据代入前式得到HR 142.5810d m===⨯。
高中物理竞赛模拟试题
高中物理竞赛模拟试题一、选择题(每题3分,共30分)1. 一个物体从静止开始做匀加速直线运动,经过时间t后,其速度为v。
如果将时间t延长到2t,那么物体的速度将变为:A. 2vB. 3vC. 4vD. 5v2. 以下哪种情况下,物体的动量守恒?A. 物体受到一个恒定的力B. 物体受到一个变化的力C. 物体受到多个力的作用,但合力为零D. 物体受到多个力的作用,且合力不为零3. 根据能量守恒定律,下列哪个陈述是正确的?A. 能量可以在不同形式之间转换,但总量不变B. 能量可以被创造或消失C. 能量转换过程中总量会减少D. 能量转换过程中总量会增加4. 一个理想的弹簧振子做简谐振动,其周期T与以下哪个因素无关?A. 弹簧的劲度系数B. 振子的质量C. 振子的振幅D. 振子的初始速度5. 根据麦克斯韦方程组,以下哪个选项描述了电场与磁场之间的关系?A. 电场可以产生磁场B. 变化的磁场可以产生电场C. 稳定的电场可以产生磁场D. 稳定的磁场可以产生电场6. 一个带正电的粒子在磁场中运动,如果磁场方向与粒子速度方向垂直,那么粒子的运动轨迹将是:A. 直线B. 圆周C. 螺旋D. 抛物线7. 根据热力学第一定律,在一个封闭系统中,能量可以:A. 被创造或消失B. 在不同形式之间转换,但总量不变C. 从低温物体自发地转移到高温物体D. 从高温物体自发地转移到低温物体8. 以下哪个现象与光电效应有关?A. 光的衍射B. 光的干涉C. 光的偏振D. 光的反射9. 根据相对论,当一个物体的速度接近光速时,以下哪个现象会发生?A. 物体的质量将显著增加B. 物体的长度将显著增加C. 物体的时间将显著变慢D. 物体的电荷将显著增加10. 在量子力学中,海森堡不确定性原理表明:A. 粒子的位置和动量可以同时被精确测量B. 粒子的位置和动量不能同时被精确测量C. 粒子的能量和时间可以同时被精确测量D. 粒子的能量和时间不能同时被精确测量二、填空题(每空2分,共20分)11. 一个物体做自由落体运动,下落高度为h,忽略空气阻力,其下落时间为______。
高中物理竞赛题(含答案)
高中物理竞赛题(含答案)一、单项选择题1. 在自由落体过程中,物体的势能增加,动能减小。
A. 正确B. 错误2. 一列火车以$v$速度行驶,它的长度为$L$,宁静的人听到车头发出声音后$T$秒后听到车尾发出的声音。
则$v$为:A. $\frac{L}{2T}$B. $\frac{2L}{T}$C. $\frac{L}{T}$D. $\frac{T}{L}$3. 两个均质、半径相等、长度不同的均匀圆筒A、B,均可在竖直平面内以固定点O为转轴转动,轴线分别与定点OA、OB平行。
当它们同时从静止转动起来时,轮毂周向速度$V_1$比$V_2$:A. $V_1=V_2$B. $V_1>V_2$C. $V_1<V_2$D. 不确定4. 一个长为$L$的导线,施加电流$I$,沿任意方向在匀强磁场中运动,做完一周回路时,会发生电流改变的原因是:A. 因为改变导线的长度B. 因为导线被磁场力拉直了C. 因为导线切割磁力线D. 不确定5. 一根长度为$l$,截面积为$S$,长度均匀分布电荷$q$的细长直线,经过小球$O$($O$到直线距离为$r$)的电场强度$E$是:A. $\frac{1}{4\pi\epsilon_0}\frac{q}{r^2}$B. $\frac{1}{4\pi\epsilon_0}\frac{q}{\sqrt{l^2+r^2}}$C. $\frac{1}{4\pi\epsilon_0}\frac{ql}{\sqrt{l^2+r^2}}$D. $\frac{1}{4\pi\epsilon_0}\frac{q}{l^2+r^2}$答案:1.A 2.B 3.C 4.C 5.A二、填空题1. 一个直导线,垂直于均匀磁场B,长度为$l$,电流为$I$,受到的磁感应强度$B_1$是$______$2. 单色光的波长为500nm,折射率为1.5,其在空气和该介质交界面的发射角是$______°$3. 质量为$m$,长度为$l$,弹性系数为$k$的弹簧在自由状态下的振动周期是$______$4. 质量为$m$的物体在竖直向下的重力作用下自由下落的过程中,重力势能不断$______$,动能不断$______$5. 一列火车以$v$速度行驶,铁轨相对静止。
三模物理试题及答案
三模物理试题及答案一、选择题(每小题3分,共30分)1. 以下关于光的折射现象的描述,正确的是:A. 光从空气斜射入水中时,折射角大于入射角B. 光从水中斜射入空气中时,折射角小于入射角C. 光从空气垂直射入水中时,折射角等于入射角D. 光从水中斜射入空气中时,折射角大于入射角答案:C2. 一个物体在水平面上受到一个斜向上的拉力F,同时受到重力G和支持力N的作用,保持静止。
关于这三个力的关系,以下说法正确的是:A. F和G的合力与N平衡B. F和N的合力与G平衡C. F、G和N三个力相互平衡D. F、G和N三个力中任意两个力的合力与第三个力平衡答案:D3. 以下关于电场的描述,正确的是:A. 电场线是真实存在的B. 电场线越密集的地方,电场强度越大C. 电场线是闭合的D. 电场线的方向与正电荷所受电场力的方向相反答案:B4. 一个带正电的小球靠近一个不带电的金属球时,金属球的感应电荷分布情况是:A. 金属球外表面感应出正电荷B. 金属球外表面感应出负电荷C. 金属球内表面感应出正电荷D. 金属球内表面感应出负电荷答案:D5. 以下关于磁场的描述,正确的是:A. 磁场对静止的电荷没有作用力B. 磁场对运动的电荷没有作用力C. 磁场对运动的电荷一定有作用力D. 磁场对运动的电荷的作用力与电荷的运动方向有关答案:D6. 一个物体在竖直方向上受到重力G和拉力F的作用,保持匀速直线运动。
关于这两个力的关系,以下说法正确的是:A. G和F是一对平衡力B. G和F是一对作用力和反作用力C. G和F的方向相同D. G和F的方向相反答案:A7. 以下关于电磁感应现象的描述,正确的是:A. 只有闭合电路的一部分导体在磁场中运动时才能产生感应电流B. 闭合电路中的导体在磁场中运动时一定能产生感应电流C. 只有当导体切割磁感线时才能产生感应电流D. 只有当导体在磁场中做匀速直线运动时才能产生感应电流答案:C8. 以下关于原子核的描述,正确的是:A. 原子核由质子和中子组成B. 原子核由电子和中子组成C. 原子核由质子和电子组成D. 原子核由质子和电子组成答案:A9. 以下关于相对论的描述,正确的是:A. 相对论认为时间和空间是绝对的B. 相对论认为时间和空间是相对的C. 相对论认为质量和能量是相互独立的D. 相对论认为质量和能量是相互转化的答案:B10. 以下关于热力学的描述,正确的是:A. 热力学第一定律表明能量可以无中生有B. 热力学第二定律表明热量可以自发地从低温物体传到高温物体C. 热力学第三定律表明绝对零度是可以达到的D. 热力学第三定律表明绝对零度是不可能达到的答案:D二、填空题(每空2分,共20分)11. 光在真空中的传播速度是_______m/s。
物理竞赛高中试题及答案
物理竞赛高中试题及答案一、选择题(每题4分,共40分)1. 光在真空中的传播速度是()。
A. 3×10^8 m/sB. 2×10^8 m/sC. 3×10^5 m/sD. 2×10^5 m/s答案:A2. 根据牛顿第二定律,一个物体的加速度与作用力成正比,与物体的质量成反比。
如果一个物体的质量增加一倍,而作用力保持不变,那么它的加速度将()。
A. 增加一倍B. 减少一半C. 保持不变D. 增加两倍答案:B3. 一个物体从静止开始自由下落,不计空气阻力,其下落过程中的加速度是()。
A. 9.8 m/s²B. 10 m/s²C. 9.8 km/h²D. 10 km/h²答案:A4. 以下哪个选项是正确的能量守恒定律的表述?()A. 能量不能被创造或销毁,但可以改变形式。
B. 能量可以被创造或销毁,但不能改变形式。
C. 能量不能被创造或销毁,也不能改变形式。
D. 能量可以被创造或销毁,也可以改变形式。
答案:A5. 一个电子在电场中受到的电场力是()。
A. 与电子的电荷成正比B. 与电子的电荷成反比C. 与电场强度成正比D. 与电场强度成反比答案:A6. 根据热力学第一定律,在一个封闭系统中,能量()。
A. 可以被创造或销毁B. 可以被转移但不能被创造或销毁C. 既不能被创造也不能被销毁D. 可以被创造但不能被销毁答案:C7. 一个物体在水平面上以恒定速度运动,其动能()。
A. 保持不变B. 增加C. 减少D. 先增加后减少答案:A8. 光的折射定律表明,入射角和折射角之间的关系是()。
A. 入射角越大,折射角越大B. 入射角越大,折射角越小C. 入射角和折射角成正比D. 入射角和折射角成反比答案:A9. 根据电磁学理论,一个闭合电路中的感应电动势与()。
A. 磁通量的变化率成正比B. 磁通量的变化率成反比C. 磁通量的大小成正比D. 磁通量的大小成反比答案:A10. 一个物体在竖直方向上受到的重力是50 N,若要使其保持静止状态,需要施加的力是()。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、一条轻绳跨过一轻滑轮(滑轮与轴间摩擦可忽略),在绳的一端挂一质量为m 1的物体,在另一侧有一质量为m 2的环,求当环相对于绳以恒定的加速度a 2′ 沿绳向下滑动时,物体和环相对地面的加速度各是多少?环与绳间的摩擦力多大?2.如图(a )所示,一滑块在光滑曲面轨道上由静止开始下滑h 高度后进入水平传送带,传送带的运行速度大小为v =4m/s ,方向如图。
滑块离开传送带后在离地H 高处水平抛出,空气阻力不计,落地点与抛出点的水平位移为s 。
改变h 的值测出对应的 s 值,得到如图(b )所示h ≥0.8m 范围内的s 2随h 的变化图线,由图线可知,抛出点离地高度为H =__________m ,图中h x =__________m 。
3 (12分)过山车质量均匀分布,从高为h 的平台上无动力冲下倾斜轨道并进入水平轨道,然后进入竖直圆形轨道,如图所示,已知过山车的质量为M ,长为L ,每节车厢长为a ,竖直圆形轨道半径为R, L > 2πR ,且R >>a ,可以认为在圆形轨道最高点的车厢受到前后车厢的拉力沿水平方向,为了不出现脱轨的危险,h 至少为多少?(用R .L 表示,认为运动时各节车厢速度大小相等,且忽略一切摩擦力及空气阻力)4.(20分)如图所示,物块A 的质量为M ,物块B 、C 的质量都是m ,并都可看作质点,且m <M <2m 。
三物块用细线通过滑轮连接,物块B 与物块C 的距离和物块C 到地面的距离都是L 。
现将物块A 下方的细线剪断,若物块A 距滑轮足够远且不计一切阻力,物块C 落地后不影响物块A 、B 的运动。
求: (1)物块A 上升时的最大速度; (2)若B 不能着地,求mM满足的条件;(3)若M =m ,求物块A 上升的最大高度。
5.(12分)如图所示,一平板车以某一速度v 0匀速行驶,某时刻一货箱(可视为质点)无初速度地放置sx (b )于平板车上,货箱离车后端的距离为l =3m ,货箱放入车上的同时,平板车开始刹车,刹车过程可视为做a =4m/s 2的匀减速直线运动。
已知货箱与平板车之间的摩擦因数为μ=0.2,g =10 m/s 2。
求:⑪为使货箱不从平板上掉下来,平板车匀速行驶时的速度v 0应满足什么条件? ⑫如果货箱恰好不掉下,则最终停在离车后端多远处?6.物理学中库仑定律和万有引力定律有相似的表达形式,对带异种电荷的两粒子组成的系统而言,若定义相距无穷远处电势能为零,则相距为r 时系统的电势能可以表示为12p Q Q E kr=-。
(1)若地球质量为1m ,某人造地球卫星质量为2m ,也定义相距无穷远处引力势能为零,写出当地心与卫星相距R 时该系统引力势能表达式。
(地球可看作均匀球体,卫星可看成质点)(2)今有一颗卫星贴着地球表面绕行时速度大小为v =7.90km/s ,当该卫星在离地面高度为h =3R 地处绕行时,绕行速度v '为多大?(R地为地球半径)(3)若在离地面高度为3R 地处绕行的卫星质量为1t ,则至少需要对该卫星补充多大的能量才能使其脱离地球的束缚?7. (12分)如图所示,1和2是放在水平地面上的两个小物块(可视为质点),与地面的滑动摩擦系数相同,两物块间的距离d =170.00m ,它们的质量分别为m 1=2.00kg 、m 2=3.00kg。
现令它们分别以初速度v 1=10.00m/s 和v 2=2.00m/s 迎向运动,经过时间t =20.0s ,两物块相碰,碰撞时间极短,碰后两者粘在一起运动。
求从刚碰后到停止运动过程中损失的机械能。
8.(20分)对于两物体碰撞前后速度在同一直线上,且无机械能损失的碰撞过程,可以简化为如下模型:A 、B 两物体位于光滑水平面上,仅限于沿同一直线运动。
当它们之间的距离大于等于某一定值d 时;相互作用力为零;当它们之间的距离小于d 时,存在大小恒为F 的斥力。
设A 物体质量m 1=1.0kg,开始时静止在直线上某点;B 物体质量m 2=3.0kg,以速度υ0从远处沿该直线向A 运动,如图所示。
若d =0.10m,F =0.60N, υ0=0.20m/s,求:(1) 相互作用过程中A 、B 加速的大小;(2) 从开始相互作用到A 、B 间的距离最小时,系统(物体组)动能的减少量; (3) A 、B 间的最小距离。
9.如图,长木板a b 的b 端固定一档板,木板连同档板的质量为M=4.0kg ,a 、b 间距离s=2.0m 。
木板位于光滑水平面上。
在木板a 端有一小物块,其质量m=1.0kg ,小物块与木板间的动摩擦因数10.0=μ,它们都处于静止状态。
现令小物块以初速s m v /0.40=沿木板向前滑动,直到和档板相撞。
碰撞后,小物块恰好回到a 端而不脱离木板。
求碰撞过程中损失的机械能。
10柴油打桩机的重锤由气缸、活塞等若干部件组成,气缸与活塞间有柴油与空气的混合物。
在重锤与桩碰撞的过程中,通过压缩使混合物燃烧,产生高温高压气体,从而使桩向下运动、锤向上运动。
现把柴油打桩机和打桩过程简化如下:柴油打桩机重锤的质量为m ,锤在桩帽以上高度为h 处(如图1)从静止开始沿竖直轨道自由落下,打在质量为M (包括桩帽)的钢筋混凝土桩子上。
同时,柴油燃烧,产生猛烈推力,锤和桩分离,这一过程的时间极短。
随后,桩在泥土中向下移动一距离l 。
已知锤反跳后到达最高点时,锤与已停下的桩帽之间的距离也为h (如图2)。
已知m=1.0×103 kg ,M=2.0×103 kg ,h=2.0m ,l=0.20m ,重力加速度g=10m/s 2,混合物的质量不计。
设桩向下移动的过程中泥土对桩的作用F 是恒力。
求此力的大小。
1.物体受力如图所示,分别对两个物体列出动力学方程111m g f m a -=(1) 222m g f m a -=(2) 加速度满足关系式212a a a '=+(3) 解方程得:1222112()m m g m a a m m '-+=+(4)2112212()m m g m a a m m '-+=+(5) 12212(2)m m g a f m m '-=+(6)2、10,1.6,3.(12分)取过山车为研究对象,过山车从平台上滑下到车厢占满竖直圆形轨道过程中,由于只有重力做功,故机械能守恒,竖直圆形轨道上的过山车可以把这部分的重心看作在轨道的圆心上,所以有:2122M Mgh=R gR+M L π⋅⋅v ① 在竖直方向受到重力和轨道对它向下的压力,受力分析如图所示,设一节车厢质量为m ,则有:f m 2gfm 1g2mg+N=mRv ②N ≥0 ③联立解得222R R h +L π≥4.(1)A 、B 、C 三物块系统机械能守恒。
B 、C 下降L ,A 上升L 时,A 的速度达最大。
(1分)2)2(212v m M MgL mgL +=- (2分) M2m gL)M 2m (2v +-=(2分)(2)当C 着地后,若B 恰能着地,即B 物块下降L 时速度为零。
(1分)A 、B 两物体系统机械能守恒。
2)(21v m M mgL MgL +=- (2分),将v 代入,整理得:M=2m (2分) 所以2mM>时,B 物块将不会着地。
(2分) (3)由于M =m ,C 物块着地后,A 以速度v 匀速上升直到B 物块落地,此后做竖直上抛运动,设上升的高度为h ,则h=3)M 2m (2L )M 2m (22gv 2Lg =+-=(3分)A 上升的最大高度H =2L +h =37L(3分)5.60≤v m/s ;离车后端0.5 m6.(14分)解析(1)由类比可知,该系统引力势能表达式为:(2)由万有引力提供向心力得,上式中解得km/s(3)卫星在该处的动能:由系统的势能:得系统的机械能:则需要给卫星补充的能量:7. 解:因两物块与地面间的滑动摩擦系数相同,故它们在摩擦力作用下加速度的大小是相同的,以a 表示此加速度的大小。
先假定在时间t 内,两物块始终作减速运动,都未停下。
现分别以s 1和s 2表示它们走的路程,则有21121at t v s -=(1)22221at t v s -=(2) 而s 1+s 2=d (3)解(1)、(2)、(3)三式并代入有关数据得a =0.175m/s 2 (4) 经过时间t ,两物块的速度分别为v'1=v 1−at (5) v'2=v 2−at (6) 代入有关数据得v'1=6.5m/s(7) v'2=−1.5m/s(8)v'2为负值是不合理的,因为物块是在摩擦力作用下作减速运动,当速度减少至零时,摩擦力消失,加速度不复存在,v'2不可为负。
v'2为负,表明物块2经历的时间小于t 时已经停止运动,(2)式从而(4)、(6)、(7)、(8)式都不成立。
在时间t 内,物块2停止运动前滑行的路程应是av s 2222=(9) 解(1)、(9)、(3)式,代入有关数据得a =0.20m/s 2(10)由(5)、(10)式求得刚要发生碰撞时物块1的速度v'1=6.0m/s(11) 而物块2的速度v'2=0(12) 设V 为两物块碰撞后的速度,由动量守恒定律有m 1v'1=(m 1+m 2)V (13) 刚碰后到停止运动过程中损失的机械能221)(21ΔV m m E+=(14)由(13)、(14)得21212121Δm m v'm E +=(15) 代入有关数据得ΔE =14.4J(16)评分标准:本题12分。
通过定量论证得到(9)式共4分,求得(11)式得4分,(13)式1分8.解:(1)a 1=21m/s 60.0=m Fa 2=22m/s 20.0=m F(2)两者速度相同时,距离最近,由动量守恒 m 2υ2=(m 1+m 2)υ υ=m/s 15.0)(2102=+m m m υ|△E k |=J 015.0)(2121221202=+-υυm m m (3)根据匀变速直线运动规律 υ1=a 1t υ2=υ0-a 2t当υ1=υ2时解得A 、B 两者距离最近时所用时间t =0.25ss 1=2121t a s 2=υ0t -2121t a△s =s 1+d -s 2将t =0.25 s 代入,解得A 、B 间的最小距离 △ s min =0.075m 9.解:设木块和物块最后共同的速度为v ,由动量守恒定律v M m mv )(0+= ①设全过程损失的机械能为E ,220)(2121v M m mv E +-=②用s 1表示从物块开始运动到碰撞前瞬间木板的位移,W 1表示在这段时间内摩擦力对木板所做的功。
