新版精选2019高考数学《导数及其应用》专题完整题(含参考答案)

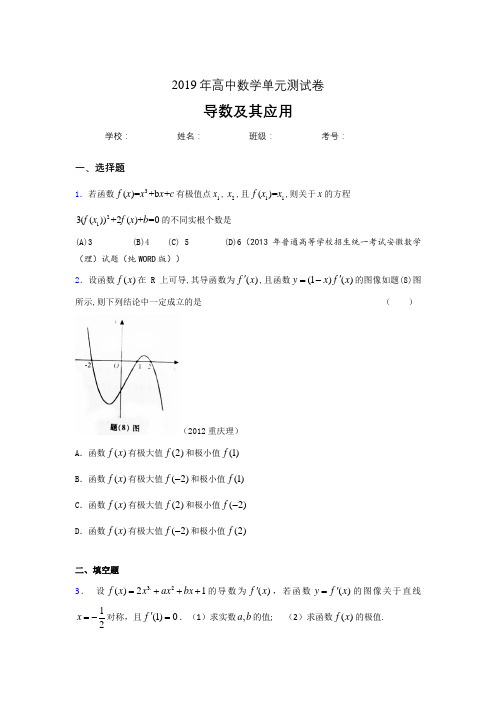
2019年高中数学单元测试卷导数及其应用学校：__________ 姓名：__________ 班级：__________ 考号：__________一、选择题1．已知函数)(()(x f x f x y ''=其中的图象如右图所示))(的导函数是函数x f ，下面四个图象中)(x f y =的图象大致是（ ）(2005江西理)2．设曲线1*()n y x n N +=∈在点（1，1）处的切线与x 轴的交点的横坐标为n x ,则12nx x x ⋅⋅⋅的值为（ ）A.1nB.11n +C. 1nn + D.1答案 B 3．设曲线11x y x +=-在点(32)，处的切线与直线10ax y ++=垂直，则a =（ ） A ．2 B ．12 C ．12- D ．2-(2008全国1理)D.由()3212211,','|,2,21121x x y y y a a x x x =+==+=-=--==---- 4．曲线12e x y =在点2(4e )，处的切线与坐标轴所围三角形的面积为______________5．已知()f x 与()g x 是定义在R 上的连续函数，如果()f x 与()g x 仅当0x =时的函数值为0，且()()f x g x ≥，那么下列情形不可能．．．出现的是 （ ）A ．0是()f x 的极大值，也是()g x 的极大值B ．0是()f x 的极小值，也是()g x 的极小值C ．0是()f x 的极大值，但不是()g x 的极值D ．0是()f x 的极小值，但不是()g x 的极值 答案 C 二、填空题6．设)(x f '和)(x g '分别是()f x 和()g x 的导函数，若()()0f x g x ''≤在区间I 上恒成立，则称)(x f 和)(x g 在区间I 上单调性相反.若函数31()23f x x ax =-与2()2g x x bx =+在开区间(,)a b 上单调性相反（0a >），则b a -的最大值为 ．7．若对任意的x D ∈,均有()()()12f x f x f x ≤≤成立，则称函数()f x 为函数()1f x 到函数()2f x 在区间D 上的“折中函数”．已知函数()()()11,0,f x k x g x =--= ()()1ln h x x x =+，且()f x 是()g x 到()h x 在区间[]1,2e 上的“折中函数”，则实数k 的取值为 ▲8． 已知函数()f x 的导函数()29f x x '=-，且(0)f 的值为整数，当(,1]x n n ∈+*()n N ∈时，()f x 的值为整数的个数有且只有1个，则n = ．49．函数()sin xf x e x =+在区间[0,]π上的最小值为 。

10．设0a >，函数x x x g xax x f ln )(,)(-=+=，若对任意的12,[1,]x x e ∈，都有12()()f x g x ≥成立，则a 的取值范围为 ▲ ．11．如图为函数32()f x ax bx cx d =+++的图象，'()f x 为函数()f x 的导函数，则不等式'()0x f x ⋅<的解集为______12．函数e x y =的图象在点()e k a k a , 处的切线与x 轴的交点的横坐标为1k a +，其中*k ∈N ，10a =，则135a a a ++= ．13．设曲线1*()n y xn N +=∈在点（1，1）处的切线与x 轴的交点的横坐标为n x ,则12n x x x ⋅⋅⋅的值为(A) 1n (B) 11n + (C) 1nn + (D) 1（2009陕西卷文）14．若直线y=kx-3与y=2lnx 曲线相切，则实数K=_________15． 曲边梯形由曲线,0,1,5x y e y x x ====所围成，过曲线,[1,5]x y e x =∈上一点P 作切线，使得此切线从曲边梯形上切出一个面积最大的普通梯形，这时点P 的坐标是____________．三、解答题16．已知函数()2a f x x x=+，()ln g x x x =+，其中0a >．（1）若1x =是函数()()()h x f x g x =+的极值点，求实数a 的值；（2）若对任意的[]12,1x x e ∈，（e 为自然对数的底数）都有()1f x ≥()2g x 成立，求实数a的取值范围．17．已知函数()ln f x x x a x =--.(1)若a =1，求函数()f x 在区间[1,]e 的最大值; (2)求函数()f x 的单调区间；(3)若()0f x >恒成立，求a 的取值范围．18．已知函数，m ∈R ．（1）若，求证：函数f （x ）是R 上的奇函数；（2）若函数f （x ）在区间（1，2）没有零点，求实数m 的取值范围．（14分）19．设函数()3292f x x x px q =-++在2x =处取得极值． 在 ⑵求函数)(x f 的单调区间；⑵ 若方程()0f x =有且仅有三个实根，求实数q 的取值范围. （本小题满分14分）20．已知函数2()ln f x x ax x =--，a ∈R ．⑴若函数()y f x =在其定义域内是单调增函数，求a 的取值范围；⑵设函数()y f x =的图象被点(2,(2))P f 分成的两部分为12,c c （点P 除外），该函数图象在点P 处的切线为l ，且12,c c 分别完全位于直线l 的两侧，试求所有满足条件的a 的值．21．已知f (x )＝ax －ln(－x )，x ∈(－e ,0)，g (x )＝－ln(－x )x ，其中e 是自然常数，a ∈R ． （1）讨论a ＝－1时, f (x )的单调性、极值； （2）求证：在（1）的条件下，|f (x )|＞g (x )＋12；（3）是否存在实数a ，使f (x )的最小值是3，如果存在，求出a 的值；如果不存在，说明理由．22．已知()()ln f x ax x =--，(,0)x e ∈-，ln()()x g x x-=-，其中e 是自然常数，.a R ∈（1）讨论1a =-时， ()f x 的单调性、极值; （2）求证：在（1）的条件下，1|()|().2f xg x >+（3）是否存在实数a ，使()f x 的最小值是3，如果存在，求出a 的值；如果不存在，说明理由。

23．某商店经销一种世博会纪念品，每件产品的成本为30元，并且每卖出一件产品需向税务部门上交a 元（a 为常数，25a ≤≤）的税收.设每件产品的售价为x 元(3541x ≤≤),根据市场调查,日销售量与xe (e 为自然对数的底数)成反比例.已知每件产品的日售价为40元时，日销售量为10件．（1）求该商店的日利润()L x 元与每件产品的日售价x 元的函数关系式；（2）当每件产品的日售价为多少元时，该商品的日利润()L x 最大，并求出()L x 的最大值．24．设0a >，函数2()|ln 1|f x x a x =+-. （Ⅰ）当2a =时，求函数()f x 的单调增区间；（Ⅱ）若[1,)x ∈+∞时，不等式a x f ≥)(恒成立，实数a 的取值范围.关键字：含绝对值；分段函数；求单调区间；恒成立问题；求参数的取值范围；不能参变分离25．已知函数xxx f ln )(=(0,1x x >≠)． （1）求函数)(x f 的极值;（2）若不等式axe x >对任意实数x 恒成立，求实数a 的取值范围．26．设函数0),(,)1(31)(223>∈-++-=m R x x m x x x f 其中 （Ⅰ）当时，1=m 曲线））（，在点（11)(f x f y =处的切线斜率（Ⅱ）求函数的单调区间与极值；（Ⅲ）已知函数)(x f 有三个互不相同的零点0，21,x x ，且21x x <。

若对任意的],[21x x x ∈，)1()(f x f >恒成立，求m 的取值范围。

答案 ：当1)1(,2)(,31)(1'2/23=+=+==f x x x f x x x f m 故时，所以曲线））（，在点（11)(f x f y =处的切线斜率为1.（2）解析 12)(22'-++-=m x x x f ，令0)('=x f ，得到m x m x +=-=1,1因为m m m ->+>11,0所以当x 变化时，)(),('x f x f 的变化情况如下表：)(x f 在)1,(m --∞和),1(+∞+m 内减函数，在)1,1(m m +-内增函数。

函数)(x f 在m x +=1处取得极大值)1(m f +，且)1(m f +=313223-+m m 函数)(x f 在m x -=1处取得极小值)1(m f -，且)1(m f -=313223-+-m m（3）解析 由题设， ))((31)131()(2122x x x x x m x x x x f ---=-++-=所以方程13122-++-m x x =0由两个相异的实根21,x x ，故321=+x x ，且0)1(3412>-+=∆m ，解得21)(21>-<m m ，舍因为123,32,221221>>=+><x x x x x x 故所以若0)1)(1(31)1(,12121≥---=<≤x x f x x 则，而0)(1=x f ，不合题意若,121x x <<则对任意的],[21x x x ∈有,0,021≤-≥-x x x x则0))((31)(21≥---==x x x x x x f 又0)(1=x f ，所以函数)(x f 在],[21x x x ∈的最小值为0，于是对任意的],[21x x x ∈，)1()(f x f >恒成立的充要条件是031)1(2<-=m f ,解得3333<<-m 综上，m 的取值范围是)33,21( 【考点定位】本小题主要考查导数的几何意义，导数的运算，以及函数与方程的根的关系解不等式等基础知识，考查综合分析问题和解决问题的能力。

27．设函数22()f x a x =（0a >），()ln g x b x =．(1) 若函数()y f x =图象上的点到直线30x y --=距离的最小值为，求a 的值；(2) 关于x 的不等式2(1)()x f x ->的解集中的整数恰有3个，求实数a 的取值范围；(3) 对于函数()f x 与()g x 定义域上的任意实数x ，若存在常数,k m ，使得()f x kx m ≥+和()g x kx m ≤+都成立，则称直线y kx m =+为函数()f x 与()g x 的“分界线”．设2a =，b e =，试探究()f x 与()g x 是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．28．某工厂生产某种儿童玩具，每件玩具的成本为30元，并且每件玩具的加工费为t 元（其中t 为常数，且25t ≤≤），设该工厂每件玩具的出厂价为x 元（3541x ≤≤），根据市场调查，日销售量与x e （e 为自然对数的底数）成反比例，当每件玩具的出厂价为40元时，日销售量为10件.(Ⅰ）求该工厂的日利润y (元)与每件玩具的出厂价x 元的函数关系式；(Ⅱ）当每件玩具的日售价为多少元时，该工厂的利润y 最大，并求y 的最大值. 18．29．设函数()|1||1|f x x ax =+++，已知(1)(1)f f -= ，且11()()f f a a -=（a ∈R ，且a ≠0），函数32()g x ax bx cx =++（b ∈R ，c 为正整数）有两个不同的极值点，且该函数图象上取得极值的两点A 、B 与坐标原点O 在同一直线上。