2018年高考数学常见题型解法归纳反馈训练 第31讲解三角形题型的解法 Word版 含答案
2018年高考数学分类汇编之三角函数和解三角形汇编(理)附详解

2018年高考数学分类汇编之三角函数和解三角形、选择题B • 305)的图象向右平移10个单位长度,所得图象对应的函数3 5A 在区间[-,—]上单调递增4 4 3B 在区间[―,]上单调递减45 3C 在区间[予‘专]上单调递增3D 在区间[厅,2 ]上单调递减7.【2018浙江卷5]函数y= 2|x|sin2x 的图象可能是1.【2018全国二卷 6】在厶ABC 中,C cos— 2,BC 1,AC 5,则 AB52.【2018全国二卷 10]若 f(x) cosxsinx 在[a, a ]是减函数,贝U a 的最大值是3.【2018全国三卷 4] 若sin1 … 3,则cos24. 5. 0, C . 【2018全国三卷9] △ ABC 的内角 A, B, C 的对边分别为 2 2 2a ,b ,c ,若△ ABC 的面积为-— -,4【2018北京卷7]在平面直角坐标系中,记m 变化时,d 的最大值为d 为点P A. 1(COS 0 sin 0到直线x my 2 0的距离,当B. 2C. 3D.4C . . 296.【2018天津卷6]将函数y sin(2x1. 【2018全国一卷16】已知函数f x 2sinx sin2x ,则f x 的最小值是 _______________ .2.【2018 全国二卷 15】已知 sin a cos 3 1 , cos a sin 3 0,则 sin( a ® __________________ .3. 【2018全国三卷15】函数f x cos 3x n在0, n 的零点个数为6 ---------------------------------------------------4. 【2018北京卷11】设函数f (x ) =cos( x n ( 0),若f(x) f (n)对任意的实数x 都成立,则co的最小值为 _________ . 5.【2018江苏卷7】已知函数y sin(2x _______________________ )(--)的图象关于直线x -对称,则 的值是 ____________________ .2236. 【2018江苏卷13】在厶ABC 中,角A, B,C 所对的边分别为a,b,c , ABC 120 , ABC 的平分线 交AC 于点D ,且BD 1,则4a c 的最小值为 _________ .7. 【2018浙江卷13】在厶ABC 中,角A ,B ,C 所对的边分别为a ,b ,c •若a= 7,b=2, A=60°,贝U sin B= _________ , c= _________.、填空题B .三.解答题1. [2018 全国一卷17】在平面四边形ABCD 中,ADC 90°, A 45°, AB 2 , BD 5.12. 【2018 北京卷15】在厶ABC 中,a=7, b=8, cosB=—.(△)求/ A ;(△)求AC边上的高.3. 【2018天津卷15】在厶ABC中,内角A,B,C所对的边分别为a,b,c.已知bsinAacos(B ). 6(I)求角B的大小;(II)设a=2, c=3,求b和sin(2A B)的值.4. 【2018江苏卷16】已知,为锐角‘tan 3 ,迹()舟.(1)求cos2的值;(2)求tan( )的值.5. 【2018江苏卷17】某农场有一块农田,如图所示,它的边界由圆O的一段圆弧MPN (P为此圆弧的中点)和线段MN构成.已知圆O的半径为40米,点P到MN的距离为50米.现规划在此农田上修建两个温室大棚,大棚I内的地块形状为矩形ABCD,大棚U内的地块形状为△ CDP,要求A,B均在线段MN上,C,D均在圆弧上.设OC与MN所成的角为.(1)用分别表示矩形ABCD和厶CDP的面积,并确定sin的取值范围;(2)若大棚I内种植甲种蔬菜,大棚U内种植乙种蔬菜,且甲、乙两种蔬菜的单位面积年产值之比为4 :3 .求当为何值时,能使甲、乙两种蔬菜的年总产值最大.6. 【2018浙江卷18】已知角a的顶点与原点O重合,始边与x轴的非负半轴重合,它的终边过点P345'(I)求sin (a + n 的值; (U)若角B满足sin (a+B=13,求cos B的值・7.【2018上海卷18】设常数a R,函数f(x) a sin 2x c 22cos x(1)若f(x)为偶函数,求a的值; (2) 若〔匸〕1,求方程f(x) 1 .2在区间[,的解.参考答案、选择题 1.A 2.A 3.B 4.C 5.C 6.A 7.D、填空题 1. 3.3223. 34.235. 7.3 ;37三•解答题 1.解: (1)在厶ABD中,由正弦定理得一BLsin AABsin ADB由题设知,5sin 452 sinADB,所以sin ADB -5由题设知, ADB 90,所以cos ADB 1225 5(2)由题设及(1) 知, cos BDC sin ADB 辽在△ BCD 中,5 由余弦定理得2 2 2BC BD DC 2 BD DC cos BDC 25 8 25. 所以BC 5.32.解:(1)在厶ABC 中,1 n _________________________________ 2—T cosB= —7 ,二 B €( — , n ,二 sinB= 1 cos B<3 7由正弦定理得—sin A bsin B8 -二=<3,二 sinA= £ . T B €( f ,sin A227•- A €( 0,亍),(n )在厶ABC 中,■/ sinC=sin (A+B ) =sinAcosB+sinBcosA=—3 21 (-)71 4.3_ 3.3 2714女口图所示,在△ ABC 中sinC=g ,二 h=BC sinC = 7 3 弓BC14••• AC 边上的高为子.3.解:在厶ABC 中,由正弦定理— sin A—,可得 bsinA asinB sin B又由 bsinA acos(B n ),6得 as in B acos(B n ),6即sinB cos(B ,可得tanB 3 .又因为 B (0 ,可得(n)解:在△ ABC 中,由余弦定理及a =2, c=3, B =^,有 b 2 a 2 c 2 2accosB 7,故 b= J7 .由 bsin A acos(B —), 6可得sin A因为 a<c , 故cosA因此 sin 2 A 2sin AcosA2,cos2 A 2cos A所以,si n(2A B)sin 2Acos Bcos2 A sinB ^^3 73 3 3 2144.解:(1)因为tan4, tan 3汇,所以sin4c o s cos因为sin 22cos1,所以 2cos25,因此,cos222cos7 25(2)因为,为锐角,所以(0, n .又因为cos()寻,所以sin()厂曲( )害,因此tan( ) 2.因为tan -,所以tan232ta n 242 , 1 tan 7因此,tan( ) tan[2 ( )];+;爲;:;(—5 2115•解:(1)连结PO并延长交MN于H,贝U PH丄MN , 所以OH=10.过O作OE丄BC于E,贝U OE// MN,所以/ COE书故OE=4Ocos0, EC=40sin B,则矩形ABCD 的面积为2X40cos((40sin 0 +10=800(4sin 0 cos 0 +cOs B △ CDP的面积为 1 x 2X 40co(40 - 40sin) 0=1600 (cos 0 - sin 0)cos 0过N作GN丄MN,分别交圆弧和OE的延长线于G和K,则GK=KN=10 .令/GOK=0,则sin0=4 2(0, n)・当濮[0, n)时,才能作出满足条件的矩形所以sin(的取值范围是[〔,1).4答:矩形ABCD的面积为800 (4sin 0 cos 0 +cQs平方米,△ CDP的面积为1600 (cos 0 - sin 0)cos0n 的取值范围是[1 , 1).4(2)因为甲、乙两种蔬菜的单位面积年产值之比为 4 : 3,设甲的单位面积的年产值为4k,乙的单位面积的年产值为3k (k>0).则年总产值为4k X 800(4sin 0 cos 0 +cbs+Bk x 1600( cos 0 - sin 0 cos 0=8000k (sin 0 cos 0 +)s [ 0, n)2设 f ( 0) =sin 0 cos 0 +cos 0€ [ 0, n),2则f'( ) cos2sin2 sin (2sin2 sin 1) (2sin 1)(sin 1).令 f'( )=0,得 B =,6当9€( (0, n 时,f '( )>0,所以f (0)为增函数;6当0€(J ,匸)时,f '( )<0 ,所以f (0)为减函数,6 2因此,当0=时,f ((取到最大值.6答:当吧时,能使甲、乙两种蔬菜的年总产值最大•[来源:学§科§网],]时,即2x(U)由角的终边过点 P( 3,得cos35 55由 sin() —得 cos( )121313由( )得coscos()cossin( )s in,5616所以cos或cos6565 .解:(1) f(x ; )asin 2x2 cos 2 x 1 1 =asi n2x cos2x 1 ,6. ( I)由角的终边过点P(4)得 sin 5所以sin( 冗)sin -5f ( x) a sin(当f (x)为偶函数时:f (x)f( x),则 a a,解得a 0 o2(2) f ( ) a sin 2 cos —,424由题意f (一)a 13 1 ,4、.3sin 2x 2cos 2 xa .3 , f (x) 3sin2x cos2x1 2sin(2x6)1,令 f (x) 1血,则2sin 2x1151319解得:x ,2424,24或x248. 解: (1) f(x)asin 2x c 22cos x 1 1 = asin2x cos2x 1 , f( x) a sin( 2x)cos(2x)1asin2x cos2x 1当f(x)为偶函数时:f(x)f( x),则a a,解得a 0。
2018版高考数学全国理科专题复习:专题4 三角函数、解

一、选择题1.若tan α=2tan π5,则cos ⎝⎛⎭⎫α-3π10sin ⎝⎛⎭⎫α-π5等于( )A .1B .2C .3D .42.已知α∈R ,sin α+2cos α=102,则tan 2α等于( ) A.43 B.34 C .-34D .-433.已知A ,B ,C ,D ,E 是函数y =sin(ωx +φ)⎝⎛⎭⎫ω>0,0<φ<π2一个周期内的图象上的五个点,如图,A ⎝⎛⎭⎫-π6,0,B 为y 轴上的点,C 为图象上的最低点,E 为该函数图象的一个对称中心,B 与D 关于点E 对称,CD →在x 轴上的投影为π12,则ω,φ的值为( )A .ω=2,φ=π3B .ω=2,φ=π6C .ω=12,φ=π3D .ω=12,φ=π64.在△ABC 中,已知2a cos B =c ,sin A sin B (2-cos C )=sin 2C 2+12,则△ABC 为( )A .等边三角形B .等腰直角三角形C .锐角非等边三角形D .钝角三角形5.(2016·全国乙卷)已知函数f (x )=sin(ωx +φ)⎝⎛⎭⎫ω>0,|φ|≤π2,x =-π4为f (x )的零点,x =π4为y =f (x )图象的对称轴,且f (x )在⎝⎛⎭⎫π18,5π36上单调,则ω的最大值为( ) A .11 B .9 C .7 D .5二、填空题6.已知扇形的周长为4 cm ,当它的半径为________ cm 和圆心角为________弧度时,扇形面积最大,这个最大面积是________ cm 2.7.当x ∈⎣⎡⎦⎤π6,7π6时,函数y =3-sin x -2cos 2x 的最小值是________,最大值是________. 8.若cos α=17,cos(α+β)=-1114,α∈⎝⎛⎭⎫0,π2,α+β∈⎝⎛⎭⎫π2,π,则β=________. 9.如图,某气象仪器研究所按以下方案测试一种“弹射型”气象观测仪器的垂直弹射高度:A ,B ,C 三地位于同一水平面上,在C 处进行该仪器的垂直弹射,观测点A ,B 两地相距100 m ,∠BAC =60°,在A 地听到弹射声音的时间比B 地晚217 s .在A 地测得该仪器至最高点H 时的仰角为30°,则该仪器的垂直弹射高度CH =________ m .(声音在空气中的传播速度为340 m/s)三、解答题10.在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,已知sin A -sin C (cos B +33sin B )=0.(1)求角C 的大小;(2)若c =2,且△ABC 的面积为3,求a ,b 的值.答案精析1.C cos ⎝⎛⎭⎫α-3π10sin ⎝⎛⎭⎫α-π5=sin ⎝⎛⎭⎫π2+α-3π10sin ⎝⎛⎭⎫α-π5=sin ⎝⎛⎭⎫α+π5sin ⎝⎛⎭⎫α-π5=sin αcos π5+cos αsin π5sin αcos π5-cos αsin π5=tan αtan π5+1tan αtan π5-1=2+12-1=3.]2.C ∵sin α+2cos α=102, ∴sin 2α+4sin α·cos α+4cos 2α=52.用降幂公式化简得4sin 2α=-3cos 2α, ∴tan 2α=sin 2αcos 2α=-34.故选C.]3.A 因为A ⎝⎛⎭⎫-π6,0,B 与D 关于点E 对称,CD →在x 轴上的投影为π12, 所以T =4×⎝⎛⎭⎫π12+π6=π,所以ω=2. 因为A ⎝⎛⎭⎫-π6,0,所以0=sin ⎝⎛⎭⎫-π3+φ, 所以-π3+φ=2k π,k ∈Z ,解得φ=π3+2k π,k ∈Z .又因为0<φ<π2,所以φ=π3.故选A.]4.B 由正弦定理,得2sin A cos B =sin C . 在△ABC 中,A +B +C =π,∴sin C =sin(A +B ), ∴2sin A cos B =sin A cos B +cos A sin B , 整理得sin A cos B =cos A sin B , ∴tan A =tan B .又∵A ,B ∈(0,π),∴A =B . ∵sin A sin B (2-cos C )=sin 2C 2+12,∴sin A sin B ⎣⎡⎦⎤2-⎝⎛⎭⎫1-2sin 2C 2=sin 2C 2+12, ∴sin A sin B ⎝⎛⎭⎫1+2sin 2C 2=12⎝⎛⎭⎫1+2sin 2C 2, ∴sin A sin B =12.∵A =B ,∴sin A =sin B =22. ∵A ,B ∈(0,π),∴A =B =π4.∵A +B +C =π,∴C =π2,∴△ABC 是等腰直角三角形.]5.B 因为x =-π4为f (x )的零点,x =π4为f (x )的图象的对称轴,所以π4-⎝⎛⎭⎫-π4=T 4+kT , 即π2=4k +14T =4k +14·2πω,所以ω=4k +1(k ∈N *),又因为f (x )在⎝⎛⎭⎫π18,5π36上单调, 所以5π36-π18=π12≤T 2=2π2ω,即ω≤12,由此得ω的最大值为9,故选B.]6.1 2 1解析 设扇形的圆心角为α,半径为r cm ,则2r +|α|r =4,∴|α|=4r -2,∴S 扇形=12|α|·r 2=2r -r 2=-(r -1)2+1,∴当r =1时,(S 扇形)max =1,此时|α|=2.7.782 解析 ∵x ∈⎣⎡⎦⎤π6,7π6,∴sin x ∈⎣⎡⎦⎤-12,1. 又∵y =3-sin x -2cos 2x =3-sin x - 2(1-sin 2x )=2⎝⎛⎭⎫sin x -142+78, ∴当sin x =14时,y min =78;当sin x =-12或sin x =1时,y max =2.8.π3解析 ∵cos α=17,α∈⎝⎛⎭⎫0,π2, ∴sin α=437.又∵cos(α+β)=-1114,α+β∈⎝⎛⎭⎫π2,π, ∴sin(α+β)=5314,∴cos β=cos(α+β)-α]=cos(α+β)cos α+sin(α+β)·sin α=12.又∵α∈⎝⎛⎭⎫0,π2,α+β∈⎝⎛⎭⎫π2,π, ∴β∈(0,π),∴β=π3.9.140 3解析 由题意,设AC =x m ,则BC =x -217×340=(x -40) m .在△ABC 中,由余弦定理,得BC 2=AB 2+AC 2-2AB ·AC ·cos ∠BAC ,即(x -40)2=10 000+x 2-100x ,解得x =420. 在△ACH 中,AC =420 m ,∠CAH =30°,∠ACH =90°,所以CH =AC ·tan ∠CAH =1403(m). 故该仪器的垂直弹射高度CH 为140 3 m. 10.解 (1)由题意得,∵A +B +C =π, ∴sin A =sin(π-B -C )=sin(B +C ), ∴sin B cos C +sin C cos B -sin C cos B -33sin B sin C =0, 即sin B (cos C -33sin C )=0, ∵0<B <π,∴sin B ≠0,∴tan C =3, 又0<C <π,故C =π3.(2)∵S △ABC =12ab ×32=3,∴ab =4,又c =2,由余弦定理得a 2+b 2-2ab ×(12)=4,∴a 2+b 2=8.则⎩⎪⎨⎪⎧ab =4,a 2+b 2=8, 解得a =2,b =2.。
2018届高考数学二轮复习一道三角基础题的12种解法学案含答案(全国通用)

一道三角基础题的12种解法已知α是某三角形的一个内角,满足17sin cos 13αα-=. (1)判断该三角形是锐角三角形还是钝角三角形? (2)求tan α的值.解:(1)将1317cos sin =-αα两边同时平方, 可得169289cos cos sin 2sin 22=+-αααα,即有169289cos sin 21=-αα,可有16960cos sin -=αα.由于),0(πα∈,故只能0cos <α,即α是钝角,该三角形是钝角三角形. (2)解法一:从三角函数定义出发.可设点),(y x P 是角α终边上的一点,令22y x r +=.则r x =αcos ,r y =αsin ,x y =αtan .依题意可得1317=-r x r y . 两边同时平方可整理得0601696022=++x xy y ,即为0)125)(512(=++x y x y , 于是x y 125-=或者x y 512-=,即125tan -=α或512tan -=α. 解法二:从正切函数αααcos sin tan =的定义出发,分别求出αsin 和αcos .联立方程组⎪⎩⎪⎨⎧=+=-1cos sin 1317cos sin 22αααα,消去αsin ,整理可得方程060cos 221cos 1692=++αα,即0)12cos 13)(5cos 13(=++αα,解得1312cos -=α或135cos -=α.于是有⎪⎪⎩⎪⎪⎨⎧-==1312cos 135sin αα或⎪⎪⎩⎪⎪⎨⎧-==135cos 1312sin αα,从而125tan -=α或512tan -=α. 解法三:亦可直接求αtan .将1317cos sin =-αα两边同时平方, 可得)cos (sin 169289169289cos cos sin 2sin 2222αααααα+==+-,整理可得2260sin 169sin cos 60cos 0αααα++=,即260tan169tan 600αα++=,可解得125tan -=α或512tan -=α. 解法四:利用配方的思想.将1317cos sin =-αα两边同时平方, 可得169289cos cos sin 2sin22=+-αααα,可解得169120cos sin 2-=αα. 于是16949cos sin 21)cos (sin 2=+=+αααα,即137cos sin ±=+αα.联立⎪⎪⎩⎪⎪⎨⎧±=+=-137cos sin 1317cos sin αααα,可解得⎪⎪⎩⎪⎪⎨⎧-==1312cos 135sin αα或⎪⎪⎩⎪⎪⎨⎧-==135cos 1312sin αα,从而125tan -=α或512tan -=α.解法五:⎪⎩⎪⎨⎧=+=-x ααααcos sin 1317cos sin ,可解得⎪⎪⎩⎪⎪⎨⎧-=+=)1317(21cos )1317(21sin x x αα, 代入1cos sin 22=+αα,可解得137±=x .于是⎪⎪⎩⎪⎪⎨⎧-==1312cos 135sin αα或⎪⎪⎩⎪⎪⎨⎧-==135cos 1312sin αα,从而125tan -=α或512tan -=α. 解法六:可利用半角公式sin 2tan 1cos 2ααα=+.将1317cos sin =-αα两边同时平方,可得2891sin 2169α-=,即120sin 2169α=-.而2α的终边可以在第三象限也可在第四象限,故119cos 2169α===±,从而125tan -=α或512tan -=α. 解法七:亦可利用二倍角公式22tan2tan 1tan 2ααα=-.将1317cos sin =-αα化为2222172sin cos (cos sin )(sin cos )22221322αααααα--=+,整理可得222sin13sincos15cos 02222αααα-+=,即22tan 13tan15022αα-+=,可求得tan52α=或者3tan22α=,于是22tan52tan 121tan2ααα==--或者512tan -=α.解法八:利用万能公式也能得到tan2α的值,进而求tan α.由22tan2sin 1tan 2ααα=+及221tan 2cos 1tan 2ααα-=+代入1317cos sin =-αα, 整理可得22tan13tan15022αα-+=,以下同解法七.解法九:亦可利用公式22sec1tan αα=+.将1317cos sin =-αα两边同时除以将cos α,可得17tan 1sec 13αα-=.两边同时平方, 可得222289289tan 2tan 1sec (1tan )169169αααα-+==+, 即260tan169tan 600αα++=,从而直接解得125tan -=α或512tan -=α. 解法十:利用韦达定理构造一元二次方程.将1317cos sin =-αα两边同时平方,可得169289cos sin 21=-αα,可解得16960)cos (sin =-⋅αα.于是αsin 和αcos -是一元二次方程21760013169x x -+=的两根. 解得⎪⎪⎩⎪⎪⎨⎧=-=1312cos 135sin αα或⎪⎪⎩⎪⎪⎨⎧=-=135cos 1312sin αα,从而125tan -=α或512tan -=α.解法十一:亦可直接构造关于tan α的方程.将1317cos sin =-αα两边同时平方,可得28912sin cos 169αα-=, 可解得60sin cos 169αα=-,于是1169sin cos 60αα=-,即22sin cos 169sin cos 60αααα+=-, 故1169tan tan 60αα+=-, 从而化为260tan 169tan 600αα++=,解得125tan -=α或512tan -=α. 解法十二:设tan x α=,则sin cos x αα=.联立方程组17sin cos 13sin cos x αααα⎧-=⎪⎨⎪=⎩,解得17sin 13(1)17cos 13(1)x x x αα⎧=⎪-⎪⎨⎪=⎪-⎩. 再由1cos sin22=+αα,即得221717[][]113(1)13(1)x x x +=--,整理可得方程260169600x x ++=, 解得512x =-或125x =-,即为所求.。
考点13 解三角形-2018届高考数学文30个黄金考点精析精训 含解析 精品
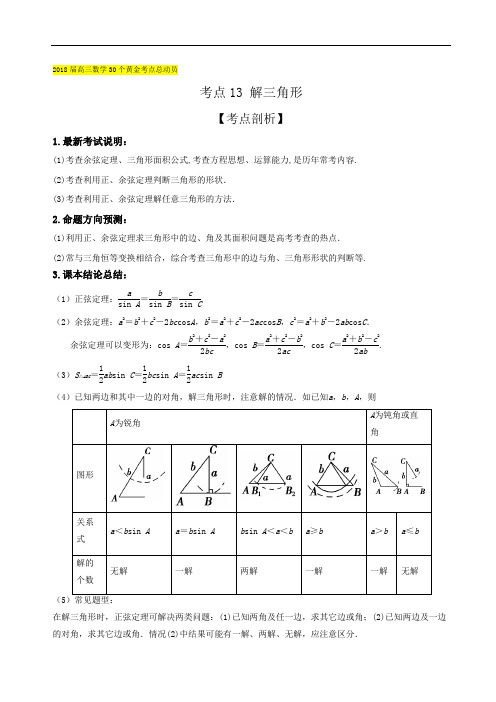
2018届高三数学30个黄金考点总动员考点13 解三角形【考点剖析】1.最新考试说明:(1)考查余弦定理、三角形面积公式,考查方程思想、运算能力,是历年常考内容. (2)考查利用正、余弦定理判断三角形的形状. (3)考查利用正、余弦定理解任意三角形的方法.2.命题方向预测:(1)利用正、余弦定理求三角形中的边、角及其面积问题是高考考查的热点. (2)常与三角恒等变换相结合,综合考查三角形中的边与角、三角形形状的判断等.3.课本结论总结:(1)正弦定理:a sin A =b sin B =csin C(2)余弦定理:a 2=b 2+c 2-2bc cos A ,b 2=a 2+c 2-2ac cos B ,c 2=a 2+b 2-2ab cos C .余弦定理可以变形为:cos A =b 2+c 2-a 22bc ,cos B =a 2+c 2-b 22ac ,cos C =a 2+b 2-c 22ab.(3)S △ABC =12ab sin C =12bc sin A =12ac sin B(4)已知两边和其中一边的对角,解三角形时,注意解的情况.如已知a ,b ,A ,则(5在解三角形时,正弦定理可解决两类问题:(1)已知两角及任一边,求其它边或角;(2)已知两边及一边的对角,求其它边或角.情况(2)中结果可能有一解、两解、无解,应注意区分.余弦定理可解决两类问题:(1)已知两边及夹角求第三边和其他两角;(2)已知三边,求各角.4.名师二级结论:(1)在三角形中,大角对大边,大边对大角;大角的正弦值也较大,正弦值较大的角也较大,即在△ABC 中,A >B ⇔a >b ⇔sin A >sin B .(2)正弦定理的变形:a sin A =b sin B =csin C =2R ,其中R 是三角形外接圆的半径.①a ∶b ∶c =sin A ∶sin B ∶sin C ; ②a =2R sin_A ,b =2R sin_B ,c =2R sin_C ;③sin A =a 2R ,sin B =b 2R ,sin C =c2R 等形式,以解决不同的三角形问题.(4)三角形的面积公式:S △ABC =12ab sin C =12bc sin A =12ac sin B =abc 4R =12(a +b +c )·r (R 是三角形外接圆半径,r 是三角形内切圆的半径),并可由此计算R ,r . (5)解三角形的常用途径:①化边为角;②化角为边,并常用正弦(余弦)定理实施边、角转换.5.课本经典习题:(1)新课标A版第10 页,第 B2题(例题)在ABC ∆中,如果有性质B b A a cos cos =,试问这个三角形的形状具有什么特点.【经典理由】一题多解,既可利用正弦定理进行求解,也可利用余弦定理进行求解。
2018届高三理科数学三角函数与解三角形解答题解题方法规律技巧详细总结版

2018届高三理科数学三角函数与解三角形解题方法规律技巧详细总结版高考考纲对于解三角形的要求为:掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题. 综合近两年的高考试卷可以看出:三角形中的三角函数问题已成为近几年的高考热点.不仅选择题中时有出现,而且解答题也经常出现,故这部分知识应引起充分的重视. 【3年高考试题分析】正弦定理、余弦定理以及解三角形问题是高考的必考内容,主要考查: 1.边和角的计算. 2.三角形形状的判断. 3.面积的计算.4.有关参数的范围问题.由于此内容应用性较强,与实际问题结合起来进行命题将是今后高考的一个关注点,不可轻视. 【必备基础知识融合】1.正弦定理和余弦定理2.三角形中的常用公式及变式(1)三角形面积公式S =12bc sin A =12ac sin B =12ab sin C=abc 4R =12(a +b +c )r .其中R ,r 分别为三角形外接圆、内切圆半径.(2)A +B +C =π,则A =π-(B +C ),A 2=π2-B +C2,从而sin A =sin(B +C ),cos A =-cos(B +C ),tan A=-tan(B +C );sin A 2=cos B +C 2,cos A 2=sin B +C 2,tan A2=1tanB +C2.tan A +tan B +tan C =tan A tan B tan C .(3)若三角形三边a ,b ,c 成等差数列,则2b =a +c ⇔2sin B =sin A +sin C ⇔2sin B 2=cos A -C 2⇔2cosA +C2=cosA -C2⇔tan A 2tan C 2=13. (4)在△ABC 中,a =b cos C +c cos B ,b =a cos C +c cos A ,c =a cos B +b cos A .(此定理称作“射影定理”,亦称第一余弦定理)【解题方法规律技巧】典例1:在△ABC 中,a ,b ,c 分别是角A ,B ,C 的对边,且cos B cos C =-b2a +c .(1)求B 的大小;(2)若b =13,a +c =4,求△ABC 的面积.【规律总结】在判断三角形的形状时,一般将已知条件中的边角关系利用正弦定理或余弦定理转化为角的关系(注意应用A +B +C =π这个结论)或边的关系,再用三角变换或代数式的恒等变形(如因式分解、配方等)求解,注意等式两边的公因式一般不要约掉,而要移项提取公因式,否则有可能漏掉一种形状.同时一定要注意解是否唯一,并注重挖掘隐含条件.如: (1)A +B +C =π.(2)在三角形中大边对大角,反之亦然.(3)任意两边之和大于第三边,任意两边之差小于第三边. (4)在△ABC 中,A ,B ,C 成等差数列的充要条件是B =60°.典例2:在△ABC 中,A 、B 、C 是三角形的三个内角,a 、b 、c 是三个内角对应的三边,已知b 2+c 2=a 2+bc. ①求角A 的大小;②若sinBsinC =34,试判断△ABC 的形状,并说明理由.【规律总结】应用正、余弦定理解斜三角形应用题的一般步骤: (1)分析:理解题意,分清已知与未知,画出示意图;(2)建模:根据已知条件与求解目标,把已知量与求解量尽量集中到一个三角形中,建立一个解斜三角形的模型;(3)求解:利用正、余弦定理有序地解出三角形,求得数学模型的解; (4)检验:检验上述所求得的解是否符合实际,从而得出实际问题的解.典例3:设△ABC 的内角A ,B ,C 所对边的长分别为a ,b ,c ,且有2sinBcosA =sinAcosC +cosAsinC. (1)求角A 的大小;(2)若b =2,c =1,D 为BC 的中点,求AD 的长.【规律总结】正、余弦定理是应用极为广泛的两个定理,它将三角形的边和角有机地联系起来,从而使三角与几何产生联系,为求与三角形有关的量(如面积、外接圆、内切圆半径和面积等)提供了理论依据,也是判断三角形形状、证明三角形中有关等式的重要依据.其主要方法有:化角法,化边法,面积法,运用初等几何法.注意体会其中蕴涵的函数与方程思想、等价转化思想及分类讨论思想.典例4:已知a , b , c 分别为ABC 三个内角A , B , C 的对边, cos sin 0a C C b c --=. (Ⅰ)求A 的大小;(Ⅱ)若ABC 为锐角三角形,且a =22b c +的取值范围.解析:(Ⅰ)由cos sin 0a C C b c --=,得: sin cos cos sin sin 0A C A C B C --=,典例5:在ABC ∆, 3B π=, 2BC =(1)若3AC =,求AB 的长(2)若点D 在边AB 上, AD DC =, DE AC ⊥, E 为垂足, ED =A 的值.解:(1)设AB x =,则由余弦定理有: 2222cos AC AB AC AB AC B =+-⋅ 即2223222cos60x x =+-⋅︒【规律总结】(1)如果式子中含有角的余弦或边的二次式,要考虑用余弦定理.(2)如果遇到的式子中含有角的正弦或边的一次式时,则考虑用正弦定理.(3)以上特征都不明显时,要考虑两个定理都有可能用到.(4)解题中一定要注意三角形内角和定理的应用及角的范围限制.(5)遇见中点时要想到与向量的加法运算结合;(6)遇见角平分线时要想到角平分线定理.(7)在三角形中,大边对大角,正线大则边大,自然角就大.(8)解三角形的实际应用问题的求解关键是把测量目标纳入到一个可解三角形中,然后利用正、余弦定理求解.典例6:某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上.在小艇出发时,轮船位于港口O北偏西30°且与该港口相距20 n mile的A处,并以30 n mile/h的航行速度沿正东方向匀速行驶.假设该小艇沿直线方向以v n mile/h的航行速度匀速行驶,经过t h与轮船相遇.(1)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?(2)假设小艇的最高航行速度只能达到30 n mile/h,试设计航行方案(即确定航行方向和航行速度的大小),使得小艇能以最短时间与轮船相遇,并说明理由.解法一:(1)设相遇时小艇航行的距离为S n mile,则S =900t 2+400-2·30t ·20·cos(90°-30°)=900t 2-600t +400=900⎝ ⎛⎭⎪⎫t -132+300, 故当t =13时,S min =103,此时v =10313=30 3.即小艇以30 3 n mile/h 的速度航行,相遇时小艇的航行距离最小. (2)设小艇与轮船在B 处相遇,则v 2t 2=400+900t 2-2·20·30t ·cos(90°-30°),故v 2=900-600t +400t2.∵0<v ≤30,∴900-600t +400t 2≤900,即2t 2-3t≤0,解得t ≥23.又t =23时,v =30.故v =30时,t 取得最小值,且最小值等于23.此时,在△OAB 中,有OA =OB =AB =20,故可设计航行方案如下:航行方向为北偏东30°,航行速度为30 n mile/h ,小艇能以最短时间与轮船相遇.【规律总结】①这是一道有关解三角形的实际应用题,解题的关键是把实际问题抽象成纯数学问题,根据题目提供的信息,找出三角形中的数量关系,然后利用正、余弦定理求解.②解三角形的方法在实际问题中,有广泛的应用.在物理学中,有关向量的计算也常用到解三角形的方法.近年的高考中我们发现以解三角形为背景的应用题开始成为热点问题之一.③不管是什么类型的三角应用问题,解决的关键都是充分理解题意,将问题中的语言叙述弄明白,画出帮助分析问题的草图,再将其归结为属于哪类可解的三角形.④本题用几何方法求解也较简便.【归纳常用万能模板】【引例】(2016·全国Ⅰ卷)△ABC的内角A,B,C的对边分别为a,b,c,已知2cos C(a cos B+b cos A)=c.(1)求C;(2)若c=7,△ABC的面积为332,求△ABC的周长.规范解答(1)由已知及正弦定理得2cos C (sin A ·cos B +sin B ·cos A )=sin C , 1分得分点①即2cos C ·sin(A +B )=sin C .3分得分点② 因为A +B +C =π,A ,B ,C ∈(0,π), 所以sin(A +B )=sin C >0,所以2cos C =1,cos C =12.5分得分点③所以C =π3.6分得分点④(2)由余弦定理及C =π3得7=a 2+b 2-2ab ·12,8分得分点⑤即(a +b )2-3ab =7,又S =12ab ·sin C =34ab =332,所以ab =6,10分得分点⑥所以(a +b )2-18=7,a +b =5,11分得分点⑦ 所以△ABC 的周长为a +b +c =5+7. 12分得分点⑧ 【解答细节突破】1.牢记公式,正确求解:在三角函数及解三角形类解答题中,通常涉及三角恒等变换公式、诱导公式及正弦定理和余弦定理,这些公式和定理是解决问题的关键,因此要牢记公式和定理.如本题第(2)问要应用到余弦定理及三角形的面积公式.2.注意利用第(1)问的结果:在题设条件下,如果第(1)问的结果第(2)问能用得上,可以直接用,有些题目不用第(1)问的结果甚至无法解决,如本题即是在第(1)问的基础上求解.3.写全得分关键:在三角函数及解三角形类解答题中,应注意解题中的关键点,有则给分,无则不给分,所以在解答题时一定要写清得分关键点,如第(1)问中,没有将正弦定理表示出来的过程(即得分点①),则不得分;第(2)问中没有将面积表示出来则不得分,只有将面积转化为得分点⑦才得分. 【解题程序展示】第一步:利用正弦定理将已知的边角关系式转化为角的关系式; 第二步:利用三角恒等变换化简关系式; 第三步:求C 的余弦值,得角C 的值.第四步:利用三角形的面积为332,求出ab 的值;第五步:根据c =7,利用余弦定理列出a ,b 的关系式; 第六步:求(a +b )2的值,进而求△ABC 的周长.【易错易混温馨提醒】一、多解问题的取舍容易忽视:易错1:①如图C ∆AB 中,已知点D 在C B 边上,且D C 0A ⋅A =,sin C 3∠BA =,AB =D B(1)求D A 的长; (2)求cos C .(1)若的面积为,求;(2)若,求.【答案】(1)(2)或.二、由22sin cos 1(ααα+=为三角形内角),知sin α求cos α时的正负问题容易出错:易错2:如图,在ABC ∆中, 3B π∠=, D 为边BC 上的点, E 为AD 上的点,且8AE =, AC = 4CED π∠=.(1)求CE 的长;(2)若5CD =,求cos DAB ∠的值.【答案】(1)CE =21(2)在CDE ∆中,由正弦定理得sin sin CECDCDE CED =∠∠,5sin 4π=所以5sin 44CDE π∠===, 所以4sin 5CDE ∠=.因为点D 在边BC 上,所以3CDE B π∠>∠=,而45<,所以CDE ∠只能为钝角, 所以3cos 5CDE ∠=-,所以cos cos cos cos sin sin 333DAB CDE CDE CDE πππ⎛⎫∠=∠-=∠+∠ ⎪⎝⎭314525=-⨯+=. 三、已知内角为锐时,易知转化为余弦值大于0,但容易忽视小于1,钝角亦是如此,余弦应该是(-1,0).在中,角、、所对的边分别是、、,已知,且.(1)当,时,求、的值;(2)若角为锐角,求的取值范围【答案】(1)(2)∴,又由可得所以.四、注意求值平方后开方时取正负的问题:在ABC ∆中,角,,A B C 的对边分别为,,a b c ,且4sin b A =.(1)求sin B 的值;(2)若,,a b c 成等差数列,且公差大于0,求cos cos A C -的值.【答案】(1)sin 4B =;(2)cos cos 2AC -=.(Ⅱ)由已知和正弦定理以及(Ⅰ)得sin sin A C += ① 设cos cos A C x -=, ②①2+②2,得2722cos()4A C x -+=+. ③ 7分 又a b c <<,ABC <<,所以00090B <<,cos cos A C >, 故3cos()cos 4A C B +=-=-. 10分 代入③式得274x =.因此cos cos 2A C -=. 五、锐角三角形内角范围的考虑要全面,需满足三个内角均为锐角:易错5:在ABC ∆ 中,角,,A B C 所对的边分别为,,a b c ,,且2222sin 2cos cos A cos B AsinB C ++=.(1)求角C 的值;(1)若ABC ∆为锐角三角形,且c =a b -的取值范围.【答案】(1)3C π=(2)()1,1-(2)由(1)知 2233A B B A ππ+==-, 由sin sin sin a b c A B C==得, 2,2a sinA b sinB ==, 22222)233a b sinA sinB sinA sin A sinA sin A ππ⎛⎫⎛⎫-=-=--==- ⎪ ⎪⎝⎭⎝⎭, ∵ABC ∆为锐角三角形, 02B π<<,又∵23B A π=-, ∴,62A ππ⎛⎫∈ ⎪⎝⎭, ∴,366A πππ⎛⎫-∈- ⎪⎝⎭, ∴()2sin 1,13A π⎛⎫-∈- ⎪⎝⎭,即a b -的取值范围为()1,1-.。
2018年高三-文科数学专题复习--三角函数-、解三角形(超级详细)

2018 年高考文科数学专题复习 三角函数、解三角形专题一 三角函数的概念、同角三角函数的关系式及诱导公式A 组 三年高考真题( 2016~2018 年)1.(20155,且 α为第四象限角,则 tan α的值等于 ()福·建, 6)若 sin α=- 1312 12 5 5 A. 5 B.- 5 C.12 D.- 122.(2014 大·纲全国, 2)已知角 α的终边经过点 (- 4,3),则 cos α= ( )4 3 3 4A. 5B. 5C.- 5D.-53.(2014 新·课标全国Ⅰ, 2)若 tan α> 0,则 () A.sin α>0 B.cos α> 0 C.sin 2α> 0 D.cos 2α> 04.(2016 新·课标全国Ⅰ, 14)已知 θ是第四象限角,且 sin θ+ π= 3,则 tan θ- π= ________. 4 5 4 5.(2016 四·川, 11)sin 750 =° . 6.(2015 四·川, 13)已知 sin α+2cos α=0,则 2sin αcos α- cos 2α的值是 ________.B 组 两年模拟精选 (2016~2015 年)1 a )若点 (4, a)在 y x2 图象上,则 tan1.(2016 济·南一中高三期中6π的值为 ( )3 A.0 B. 3 C.1D. 3π πα= ()2.(2016 贵·州 4 月适应性考试 )若 sin + α=- 3,且 α∈ , π,则 sin π- 225 2 ( )24 12 12 24A. 25B. 25C.- 25D. -25sin α- cos α性考试)已知角 α的终边经过点 P(2 ,- 1),则 = ( ) sin α+ cos α1 1A.3B.3C.-3D.- 310π4.(2015 乐·山市调研 )若点 P 在- 3 角的终边上,且 P 的坐标为 ( -1, y),则 y 等于 ()3 3 A. - 3B. 3C.- 3D. 3π5.(2015 石·家庄一模 )已知 cos α= k , k ∈R ,α∈ 2, π,则 sin( π+ α)= () A. - 1- k 2B. 1-k 2C.- kD. ± 1- k 26.(2015 洛·阳市统考 )已知 △ABC 为锐角三角形 ,且 A 为最小角 ,则点 P(sin A-cos B,3cos A-1)位于 () A. 第一象限 B.第二象限C.第三象限D. 第四象限π4,则 cos α= ________.7.(2016 山·东日照第一次模拟 )已知角α为第二象限角,cos-α=2 58.(2015 湖·南长沙一模 )在平面直角坐标系xOy 中,将点 A( 3,1)绕原点 O 逆时针旋转90°到点 B,那么点 B 坐标1为________,若直线 OB 的倾斜角为α,则 tan 2α的值为 ________.专题二三角函数的图象与性质A 组三年高考真题( 2016~2014 年)π的图象向右平移1个周期后,所得图象对应的函数为() 1.(2016 新·课标全国Ⅰ, 6)若将函数 y=2sin 2x+6 4ππππA. y= 2sin2x+4B.y= 2sin2x+3C.y=2sin 2x-4D.y= 2sin 2x-32.(2016 新·课标全国卷Ⅱ,3)函数 y= Asin(ωx+φ)的部分图象如图所示,则()ππA. y= 2sin2x-6B. y= 2sin 2x-3C.y= 2sin x+πD. y= 2sin x+π6 33.(2016 四·川, 4)为了得到函数 y= sin x+π的图象,只需把函数 y= sin x 的图象上所有的点 ( )3πB.向右平行移动πA. 向左平行移动3个单位长度3个单位长度πD.向下平行移动πC.向上平行移动个单位长度个单位长度3 34. (2015 新·课标全国Ⅰ,8)函数 f( x)= cos(ωx+φ)的部分图象如图所示,则f(x) 的单调递减区间为 ( )A. kπ-1,kπ+3,k∈ ZB. 2kπ-1, 2kπ+3, k∈ ZC.k-1, k+3, k∈ ZD. 2k-1, 2k+3,k∈Z4 4 4 4 4 4 4 4π的图象,只需将函数y=sin 4x 的图象 ()5.(2015 山·东, 4)要得到函数 y= sin 4x-3π个单位 B .向右平移π个单位A .向左平移1212π D .向右平移π个单位个单位C.向左平移3 36.(2014 天·津, 8)已知函数 f(x)=3sin ωx+ cos ωx(ω> 0), x∈R .在曲线 y= f(x) 与直线 y= 1 的交点中,若相邻交π点距离的最小值为3,则 f( x)的最小正周期为 ()π2πA. 2B. 3C. πD.2 ππ的最小正周期是 ( )7.(2014 陕·西, 2)函数 f(x)= cos 2x+4πA. 2B. πC.2 πD.4 π28.(2014 四·川, 3)为了得到函数 y = sin(x +1)的图象,只需把函数 y = sin x 的图象上所有的点 ()A .向左平行移动 1 个单位长度B .向右平行移动 1 个单位长度C .向左平行移动 π个单位长度D .向右平行移动 π个单位长度9.(2014 浙·江, 4)为了得到函数 y = sin 3x + cos 3x 的图象,可以将函数 y = 2cos 3x 的图象 () π B. 向右平移 π C.向左平移 π D.向左平移 πA. 向右平移 12个单位 4个单位 12个单位 4个单位10.(2014 安·徽, 7)若将函数 f(x)= sin 2x +cos 2x 的图象向右平移 φ个单位,所得图象关于 y 轴对称,则 φ的最小 正值是 ( )ππ 3π 3π A. 8B.4C. 8D. 411.(2014 新·课标全国Ⅰ, 7)在函数① y = cos|2x|,② y =|cos x|,③ y = cos 2x + π, 6④ y = tan 2x - π中,最小正周期为 π的所有函数为 ()4 A.①②③ B. ①③④ C.②④D. ①③ π)12.(2014 个单位,得到函数 y = f(x)的图象,则下列说法正确的是 (福·建, 7)将函数 y =sin x 的图象向左平移 2 A. y = f(x)是奇函数 B.y = f(x)的周期为 ππ πC.y = f(x)的图象关于直线 x = 2对称D.y = f(x)的图象关于点- 2, 0 对称 13.(2016 新·课标全国Ⅲ, 14)函数 y = sin x - 3cos x 的图象可由函数 y = 2sin x 的图象至少向右平移 ________个单 位长度得到 .14.(2015 天·津, 11)已知函数 f( x)= sin ωx+ cos ωx (ω> 0),x ∈ R.若函数 f(x)在区间 (-ω,ω)内单调递增,且函数 y = f(x)的图象关于直线 x = ω对称,则 ω的值为 ________.15.(2015 陕·西, 14)如图,某港口一天 6 时到 18 时的水深变化曲线近似满足函数πy = 3sin 6x + φ + k ,据此函数可知,这段时间水深 (单位: m)的最大值为 ________.16.(2015 湖·南, 15)已知 ω>0 ,在函数 y =2sin ωx 与 y = 2cos ωx 的图象的交点中,距离最短的两个交点的距离为 2 3,则 ω= ________.ππ17.(2014 重·庆, 13)将函数 f(x)= sin( ωx+ φ)(ω> 0,- 2≤φ<2)图象上每一点的横坐标缩短为原来的一半,纵坐标 π π不变,再向右平移 6个单位长度得到 y = sin x 的图象,则 f 6 = ________.318.(2015 湖·北, 18)某同学用“五点法”画函数f(x)= Asin(ωx+φ)ω>0, |φ|<π在某一个周期内的图象时,列表并2填入部分数据,如下表:ωx+φ0 π3ππ2π2 2xπ5π3 6 Asin( ωx+φ)0 5 - 50(1)请将上表数据补充完整,填写在答题卡上相应位置,并直接写出函数f(x)的解析式;(2)将 y= f(x)图象上所有点向左平移πy=g( x)的图象,个单位长度,得到6求 y= g(x)的图象离原点O 最近的对称中心.19.(2014 湖·北, 18)某实验室一天的温度(单位:℃ )随时间 t(单位: h)的变化近似满足函数关系:ππf(t)=10-3cos12t- sin 12t, t∈ [0,24) .(1)求实验室这一天上午 8 时的温度;(2)求实验室这一天的最大温差.π20.(2014 四·川, 17)已知函数 f(x)= sin 3x+4 .(1)求 f(x)的单调递增区间;α=4 π(2)若α是第二象限角, f 35cos α+4 cos 2α,求 cos α- sin α的值.421.(2014 福·建, 18)已知函数f(x)= 2cos x(sin x+ cos x).5π(1) 求 f 4的值;(2)求函数 f( x)的最小正周期及单调递增区间.π22.(2014 北·京, 16)函数 f(x)= 3sin 2x+6的部分图象如图所示.(1)写出 f(x)的最小正周期及图中x, y0的值;(2)求 f(x)在区间ππ-,-上的最大值和最小值.2 12B 组两年模拟精选 (2016~2015 年)1.(2016 四·川成都第二次诊断)将函数 f(x)= cos x+π的图象上所有点的横坐标缩短为原来的1倍,纵坐标不变,得6 2 到函数 g(x)的图象,则函数g(x)的解析式为 ( )A. g(x)= cosππx+πx+π2x+3 B.g(x)= cos 2x+6 C.g(x)= cos 2 3 D. g(x)= cos 2 62.(2016 山·西四校联考 )已知函数 f(x)= cos ωx+φ-πω>0, |φ|<π的部分图象如图所示,2 2π则 y= f x+6取得最小值时x 的集合为 ( )A. x|x= kπ-ππππ, k∈ Z B. x|x= kπ-, k∈Z C. x|x= 2kπ-,k∈Z D. x|x= 2kπ-, k∈ Z6 3 6 3πy 轴对称,则φ的3.(2015 石·家庄模拟 )将函数 f(x)=sin(2 x+φ)的图象向左平移8个单位,所得到的函数图象关于一个可能取值为 ( )3πππA. 4 B.4 C.0 D.-45π3π4.(2015 黄·冈模拟 ) 当 x=4时,函数 f(x) = Asin(x+φ)(A> 0)取得最小值,则函数y= f4- x 是()A. 奇函数且图象关于点π对称 B.偶函数且图象关于点( π, 0)对称,2ππC.奇函数且图象关于直线x=2对称 D. 偶函数且图象关于点2, 0 对称5.(2015 河·南焦作市统考 )函数 f(x)= sin(ωx+φ) ω>0, |φ|<π的最小正周期为π,且其图象向右平移π个单位后2 12 得到的函数为奇函数,则函数f(x)的图象 ( )πB. 关于直线x=5πC.关于点5πD.关于直线 x=π, 0 对称对称, 0 对称对称A. 关于点212 12 12π6.(2015 怀·化市监测 )函数 y=- 2x 的单调增区间为 ________. 2sin 33 37.(2015 辽·宁五校联考 )已知函数 f(x)=2 sin ωx+2cos ωx(ω>0) 的周期为 4.(1) 求 f(x)的解析式;2个单位得到函数g(x)的图象,P,Q 分别为函数 g(x)图象的最高点和最低点(如图 ),(2) 将 f(x)的图象沿 x 轴向右平移3求∠ OQP 的大小 .专题三三角恒等变换A 组三年高考真题( 2016~2014 年)1.(2016 新·课标全国Ⅲ,6)若 tan θ=-1,则 cos 2θ= ( )34 1 1 4A. -5B.-5C.5D. 5π2.(2016 新·课标全国Ⅱ,11)函数 f(x)= cos 2x+ 6cos-x 的最大值为 () 2A.4B.5C.6D.73.(2015 重·庆, 6)若 tan α=1, tan(α+β)=1,则 tan β= ()3 21 1 5 5A. 7B. 6C.7D.64.(2016 浙·江, 11)已知 2cos2x+ sin 2x=Asin( ωx+φ)+ b(A> 0),则 A= ________, b= ________.65.(2016 山·东, 17)设 f(x)= 2 3sin( -πx)sin x- (sin x- cos x)2.(1)求 f(x)的单调递增区间;(2)把 y=f(x)的图象上所有点的横坐标伸长到原来的 2 倍(纵坐标不变 ),再把得到的图象向左平移π个单位,得到3函数 y= g(x)的图象,求 g π的值 .66.(2016 北·京, 16)已知函数 f(x)= 2sin ωx cos ωx+cos 2ωx(ω>0) 的最小正周期为π.(1)求ω的值; (2)求 f(x) 的单调递增区间 .7.(2015 广·东, 16)已知 tan α= 2.(1) 求 tan α+π的值;(2) 求sin 2 α的值.4 sin2α+ sin αcos α- cos 2α- 12x8.(2015 北·京, 15)已知函数 f(x)= sin x-2 3sin .2π(1) 求 f(x)的最小正周期;(2) 求 f(x)在区间0,3上的最小值.79.(2015 福·建, 21)已知函数 f(x)= 10 3sin x2cos 2x+ 10cos2x2.(1)求函数 f(x)的最小正周期;πa( a> 0)个单位长度后得到函数g(x)的图象,(2)将函数 f(x)的图象向右平移个单位长度,再向下平移6且函数 g(x)的最大值为 2.①求函数 g(x)的解析式;②证明:存在无穷多个互不相同的正整数x0,使得 g(x0 )>0.π, x∈ R,且 f 5π3210.(2014 广·东, 16)已知函数 f(x)= Asin x+312 =2.(1) 求 A 的值;(2) 若 f(θ)- f(-θ)=3,θ∈0,π,求 fπ2 6-θ.11.(2014 浙·江 ,18)在△ABC 中 ,内角 A,B,C 所对的边分别为a,b,c.已知 4sin2A-B+ 4sin Asin= 2+ 2.2(1)求角 C 的大小; (2) 已知 b= 4,△ABC 的面积为 6,求边长 c 的值.B 组两年模拟精选 (2016~2015 年)1.(2016 江·西九校联考 )已知α∈3π, cos α=-4,则 tanππ,-α等于 () 2 5 41 1A.7B. 7C.-7D. - 72.(2016 洛·阳统考 ) 若α∈[0, 2π),则满足1+ sin 2α= sin α+cos α的α的取值范围是 ()πB.[ 3π3π7πA. 0,0,πC.0,D.0,∪, 2π2]4 4 41 3 2tan 14 °1- cos 50 °)3.(2016 河·南六市联考 )设 a=2cos 2 -°2sin 2 ,°b=,c=2,则有 ( 1- tan214°A. a<c<bB. a<b<cC.b<c<aD.c<a<b4.(2015 大·庆市质检二 )已知 sin α=5,则 sin2α-cos2α的值为 ( )41 3 1 3A. -8B.-8C.8D.885.(2015 烟·台模拟 ) 已知 cos α= 3, cos(α+ β)=- 5, α,β都是锐角,则 cos β等于 ()513 63 33 3363A. - 65B. -65C.65D.656.(2015 河·北唐山模拟 )已知 2sin 2α= 1+cos 2α,则 tan 2α= ()A. 4B.-4 C. 4或 0 D.- 4或 0 3 3 3 3sin αcos α 1 1,则 tan β=________. 7.(2015 巴·蜀中学一模 )已知 = , tan(α-β)= 1- cos 2α 2 24 138.(2015 河·南洛阳统考 )已知向量 a = (cos α, sin α),b = (cos β, sin β), |a - b|= 13 .(1) 求 cos(α- β)的值; (2)若 0< α< π π,- < β<0 且 sin β=- 4,求 sin α的值 .2 2 5专题四 解三角形A 组 三年高考真题( 2016~2014 年)1.(2016 新·课标全国Ⅰ, 4)△ABC 的内角 A , B , C 的对边分别为 a , b , c.已知 a = 5, c = 2, cos A = 2,3则 b = ()A. 2B. 3C.2D.32.(2016 山·东, 8)△ABC 中,角 A ,B , C 的对边分别是 a , b , c ,已知 b = c , a 2 = 2b 2 (1- sin A),则 A = ()3π π π π A. 4B. 3C.4D. 633.(2015 广·东 ,5)设 △ABC 的内角 A,B,C 的对边分别为 a,b,c.若 a = 2,c =2 3,cos A = 2 ,且 b<c,则 b = ( ) A. 3 B.2 2 C.2 D. 34.(2014 四·川,8)如图,从气球 A 上测得正前方的河流的两岸 B ,C 的俯角分别为 75°,30°,此时气球的高是 60 m ,9则河流的宽度 BC 等于 ( )A . 240( 3- 1)mB . 180( 2- 1)mC . 120( 3- 1)mD . 30( 3+ 1)m5.(2016 新·课标全国Ⅱ, 15)△ABC 的内角 A ,B , C 的对边分别为 a ,b , c , 若 cos A = 4, cos C = 5 , a = 1,则 b = ________.5 132πb6.(2016 北·京, 13)在△ABC 中,∠ A = 3 , a = 3c ,则 c = ________.2π7.(2015 北·京, 11)在 △ABC 中, a = 3, b= 6,∠ A = 3 ,则∠ B = ________.8.(2015 重·庆, 13)设△ABC 的内角 A , B ,C 的对边分别为 a , b ,c ,且 a = 2, cos C =- 1, 3sin A = 2sin B ,则 c = ________.49.(2015 安·徽, 12)在△ABC 中, AB = 6,∠ A = 75°,∠ B = 45°,则 AC =________.10.(2015 湖·北, 15)如图,一辆汽车在一条水平的公路上向正西行驶,到 A 处时测得公路北侧一山顶 D 在西偏北30°的方向上,行驶 600 m 后到达 B 处,测得此山顶在西偏北75°的方向上,仰角为 30°,则此山的高度 CD= ________m.11.(2014 新·课标全国Ⅰ, 16)如图,为测量山高 MN ,选择 A 和另一座山的山顶 C为测量观测点.从A 点测得 M 点的仰角∠ MAN =60°,C 点的仰角∠ CAB = 45°以及∠ MAC =75°;从 C 点测得∠ MCA = 60°,已知山高 BC = 100 m ,则山高 MN = ________m. π12.(2014 湖·北, 13)在 △ABC 中,角 A , B ,C 所对的边分别为 , a = 1, a , b , c.已知 A = 6b = 3,则 B =________.13.(2014 福·建, 14)在 △ABC 中, A =60°, AC = 2, BC = 3,则 AB 等于 ________. 14.(2014 1,则 c = ________; sin A = ________. 北·京, 12)在 △ABC 中, a = 1,b = 2, cos C = 415.(2016 浙·江, 16)在 △ABC 中,内角 A , B , C 所对的边分别为 a ,b , c.已知 b + c = 2acos B.(1)证明: A = 2B ;(2)若 cos B = 2,求 cos C 的值 . 3cos A+ cos B=sin C 16.(2016 四·川, 18)在△ABC 中,角 A, B,C 所对的边分别是a, b, c,且ab c .(1) 证明: sin Asin B= sin C;2 2 2 6(2)若 b + c - a = bc,求 tan B.51017.(2015 江·苏, 15)在△ABC 中,已知 AB =2, AC= 3, A= 60°.(1) 求 BC 的长;(2)求 sin 2C 的值.18.(2015 新·课标全国Ⅱ,17)在△ABC 中, D 是 BC 上的点, AD 平分∠ BAC, BD=2DC .(1) 求sin∠B;(2) 若∠ BAC= 60°,求∠ B.sin∠ C19.(2015 天·津, 16)在△ABC 中,内角 A, B, C 所对的边分别为a,b, c.已知△ABC 的面积为 31 15, b- c=2, cos A=- .4(1) 求 a 和 sin C 的值;(2) 求 cos 2A+π的值.620.(2015 山·东, 17)在△ABC 中,角 A, B,C 所对的边分别为3,a, b, c.已知 cos B=36sin (A+ B)=9, ac= 2 3,求 sin A 和 c 的值.21.(2015 湖·南, 17)设△ABC 的内角 A, B,C 的对边分别为a, b, c, a= btan A.(1) 证明: sin B= cos A;(2) 若 sin C- sin Acos B=3,且 B 为钝角,求 A, B,C. 4π22.(2015 浙·江, 16)在△ABC 中,内角 A, B, C 所对的边分别为a,b, c.已知 tan 4+A = 2.sin 2A的值;π(1) 求 2 (2)若 B=, a= 3,求△ABC 的面积.sin 2A +cos A 423.(2015 新·课标全国Ⅰ,17)已知 a,b,c 分别为△ABC 内角 A,B,C 的对边 ,sin2B= 2sin Asin C.(1) 若 a=b,求 cos B;(2) 设 B= 90°,且 a=2,求△ABC 的面积.24.(2014 重·庆, 18)在△ABC 中,内角 A, B, C 所对的边分别为a,b, c,且 a+ b+ c=8.(1)若 a=2, b=5,求 cos C 的值;211(2) 若 sin Acos2B+ sin Bcos2A= 2sin C,且△ABC 的面积 S=9sin C,求 a 和 b 的值.2 2 225.(2014 山·东, 17)△ABC 中 ,角 A,B,C 所对的边分别为a,b,c.已知 a=3, cos A=π6,B= A+.3 2(1) 求 b 的值;(2) 求△ABC 的面积.26.(2014 陕·西, 16)△ABC 的内角A, B, C 所对的边分别为a, b, c.(1)若 a,b, c 成等差数列,证明:sin A+sin C= 2sin(A+ C);(2)若 a,b, c 成等比数列,且 c= 2a,求 cos B 的值.27.(2014 湖·南, 19)如图,在平面四边形 ABCD 中, DA ⊥ AB,DE =1, EC =7, EA=2,∠ ADC =2ππ(1)求 sin∠ CED 的值; (2) 求 BE 的长.,∠ BEC=.3 3B 组两年模拟精选 (2016~2015 年)1.(2016 湖·南四校联考)在△ABC 中 ,角 A,B,C 的对边分别为 a,b,c,若 (a2+ b2- c2)tan C= ab,则角 C 为 ()π 5ππ 2πC.πD.2πA. 或6 B. 或3 6 36 32.(2016 河·南三市调研 )△ABC 的内角 A, B, C 所对的边分别为πa, b, c,若 c2= (a- b)2+ 6, C=,则△ABC的3面积为 ( )A.3B. 923C.323D.3 33.(2016 济·南一中检测 )在△ABC 中,内角 A,B, C 对边的边长分别为a, b, c, A 为锐角,lg b+ lg 1= lg sin A=- lg 2,则△ABC 为 ( ) cA. 等腰三角形B. 等边三角形C.直角三角形D.等腰直角三角形4.(2015 山·东省实验中学三诊2 2 2 2) )在△ABC 中,若 (a + b ) ·sin(A-B)= (a- b )sin C,则△ABC 是 (A. 等腰三角形B. 直角三角形C.等腰直角三角形D. 等腰三角形或直角三角形5.(2015 江·西赣州摸底 )为了在一条河上建一座桥,施工前在河两岸打上两个桥位桩A,B(如图 ),要测算两点的距离,测量人员在岸边定出基线BC,测得 BC= 50 m,∠ ABC=105°,∠ BCA=45°,就可以计算出A,B 两点的距离为 ( )12A.50 2 mB.50 3 mC.25 2 m 25 2D. 2 m6.(2015 湖·南十二校联考 )在 △ABC 中,角 A ,B , C 所对的边分别为 a , b , c , 2 2 a - b= 3,则 c = () 若 tan A = 7tan B , c A.4 B.3 C.7 D.61 7.(2016 湖·南株洲 3 月模拟 )在△ABC 中, a = 1,b = 2, cos C = 4,则 sin A = ________. 8.(2015 太·原模拟 ) 在△ABC 中,已知 (sin A + sin B + sin C) ·(sin B + sin C - sin A)= 3sin Bsin C.(1) 求角 A 的值; (2) 求 3sin - cos C 的最大值B13高考文科数学专题复习三角函数、解三角形专题一三角函数的概念、同角三角函数的关系式及诱导公式答案精析A 组 三年高考真题( 2016~2014 年)5 ,且 α为第四象限角, ∴ cos α= 12,∴ tan α= sin α5 ,故选 D. 答案 D13 =- 121.解析 ∵ sin α=- 13 cos α2.解析 记 P(- 4, 3),则 x =- 4, y =3, r = |OP|= (-4) 2+ 32=5, - 4 4,故选 D.故 cos α=x = =- r55 3.解析 由 tan α> 0,可得 α的终边在第一象限或第三象限,此时 sin α与 cos α同号,故 sin 2α=2sin αcos α> 0,故选 C. 答案 C4.解析 由题意,得 cos π4 ,∴ tan π3 ππ π1 =- 4 . 答案 - 4θ+ = θ+ = .∴ tan θ- = tan θ+ - =- π 33 4 5 4 4 4 4 2 tan θ+ 45.解析 ∵ sin θ= sin(k ·360 °+ θ),( k ∈ Z), ∴ sin 750 =°sin(2 360× °+ 30°)= sin 30 1 答案1=° . 2 26.解析 ∵ sin α+ 2cos α= 0, ∴ sin α=- 2cos α,∴ tan α=- 2,又∵ 2sin αcos α-cos 2α= 2sin α·cos α- cos 2 α 2tan α- 12×(- 2)- 1 sin 2α+ cos 2α= tan 2α+1 , ∴原式=(- 2)2+ 1=- 1. 答案 -1B 组 两年模拟精选 (2016~2015 年)1a1.解析 ∵a = 42= 2, ∴ tan 6π= 3.答案 Dπ33 π42.解析由 sin 2+ α=- 5得 cos α=- 5,又 α∈ 2, π, 则 sin α= 5,所以 sin( π-2α)= sin 2α= 2sin αcos α=- 24 答案 D25.3.解析 因为角 α终边经过点 P(2 ,- 1),所以 tan α=- 1, sin α- cos α tan α- 1= = 2 sin α+ cos α tan α+ 1- 12- 1 =- 3,故选 D.-1+ 1210π 2π 10π 2π 2π答案 D 4.解析 =- 4π+ ,所以- 与 的终边相同,所以 tan =- 3=- y ,则 y = 3. - 33 3 3 3 πα>0,则 sin( π+α 2 2 5.解析 因为 α∈ , π ,所以 sin1- cos α=- 1- k ,故选 A. 答案 A 2)=- sin α=- π π π π6.解析 由题意得, A + B>即 A > - B ,且 A ∈ 0, 3 , - B > 0, 2 2 2 π1 1 在第一象限 . 答案 A故 sin A> sin - B = cos B,即 sin A- cos B> 0, 3cos A- 1> 3× - 1=,故点 P2 2 27.解析sin α= cos π4,又α为第二象限角,所以 cos α=-2 3-3-α=51-sin α=- . 答案5 2 58.解析设点 A( 3, 1)为角θ终边上一点,如图所示,|OA |=2,1413π则 A(2cos θ, 2sin θ), 由三角函数的定义可知: sin θ= ,cos θ=,则 θ= 2k π+6 (k ∈Z ),22设 B(x , y),由已知得 x = 2cos θ+ π=2cos 2k π+ 2π=- 1, y =2sinθ+ π= 2sin2k π+2π= 3,2 323 所以 B(- 1, 3) ,且 tan α=- 3,所以 tan 2α= 2tan α2 = 3. 答案 (- 1, 3)31- tan α专题二三角函数的图象与性质A 组 三年高考真题( 2016 ~2014 年) 答案精析1.解析 函数 y = 2sin 2x + π2x + π1个周期即 π6 的周期为 π,将函数 y = 2sin 的图象向右平移 个单位, 所得函数为6 4 4 π π πy = 2sin 2 x - 4 + 6 = 2sin 2x - 3 ,故选 D. 答案D2.解析 由题图可知, T = 2 ππ =π,所以 ω=2,由五点作图法可知 π π π - - 6 2× +φ= ,所以 φ=- ,3 3 2 6 π所以函数的解析式为 y = 2sin 2x - 6 ,故选 A. 答案 A3.解析由 y = sin x 得到 y =sin(x ±a)的图象,只需记住 “左加右减 ”的规则即可 . 答案 A4.解析 由图象知 T= 5- 1= 1, ∴ T = 2.由选项知 D 正确. 答案 D2 4 45.解析 ∵ y = sin 4x - π= sin 4x - π ,312∴要得到函数 y = sin π 的图象,只需将函数 y = sin 4x 的图象向右平移 π答案 B 4x - 3 12个单位.6.解析 由题意得函数 f(x)= 2sin π (ω> 0), 又曲线 y = f(x)与直线 y =1 相邻交点距离的最小值是 πωx+ 3 , 6由正弦函数的图象知, π π π 5π π 即2π π ωx+ = 和 ωx+ = 对应的 x 的值相差 , = ,解得 ω= 2, 6 6 6 6 3 3ω 3 2π 所以 f(x)的最小正周期是 T = ω= π. 答案 C 2π7.解析 由余弦函数的复合函数周期公式得= π. 答案 BT = 2 8.解析 由图象平移的规律 “左加右减 ”,可知选 A. 答案 A9.解析 因为 y = sin 3x + cos 3x = 2cos 3x -π,所以将 y = 2cos 3x 的图象向右平移 π个单位后可得到412y = 2cos 3x - π的图象.答案 A 10.解析 方法一 f(x)= 2sin 2x + π,4 4将函数 f(x)的图象向右平移 φ个单位后所得图象对应的函数解析式为 y = 2sin π2x + - 2φ,由该函数为偶函数 4ππkπ3π所以φ的最小正值为3π可知 2φ-= kπ+,k∈ Z ,即φ=2 +, k∈Z ,8 .4 2 8π方法二f(x)= 2cos 2x-4,将函数 f(x)的图象向右平移φ个单位后所得图象对应的函数为ππ3πy= 2cos 2x-4- 2φ,且该函数为偶函数,故 2φ+4= kπ, k∈ Z ,所以φ的最小正值为8 . 答案 C1511.解析① y= cos|2x|,最小正周期为π;② y= |cos x|,最小正周期为π;③ y= cos2x+π,最小正周期为π;6④ y= tanπ,最小正周期为ππ的所有函数为①②③,故选 A. 答案 A 2x-4,所以最小正周期为2ππ12.解析函数 y= sin x 的图象向左平移2个单位后,得到函数 f(x)=sin x+2= cos x 的图象, f(x)= cos x 为偶函数,πππ排除 A ; f(x)= cos x 的周期为 2π,排除 B;因为 f = cos = 0,所以 f(x)= cos x 不关于直线x=对称,排除 C;2 2 2故选 D. 答案 D13.解析 y= sin x- 3cos x=2sin x-ππ答案π,由 y= 2sin x 的图象至少向右平移个单位长度得到 .3 3 314.解析f(x)= sin ωx+cos ωx=2sinπππ πωx+,由-+ 2kπ≤ωx+≤+ 2kπ,k∈Z,4 2 4 23ππ由题意 f( x)在区间 (-ω,ω)内单调递增,可知π得-+ 2kπ≤ωx≤+2kπ,k= 0,ω≥,4 4 2又函数 y= f(x)的图象关于直线 x=ω对称,2 π 2 π ππ答案π所以 sin( ω+)=1,ω +=,所以ω=2.24 4 215.解析由题干图易得y min= k- 3= 2,则 k= 5,∴ y max=k+ 3= 8.答案 816.解析y= 2sin ωx,ωx-π= 0,由知 sin ωx=cos ωx,即 sin ωx- cos ωx= 0,∴ 2siny= 2cos ωx,4π 1 π 1 π∴ ωx=4+ kπ, x=ω4+ kπ (k∈ Z),∴两函数交点坐标为ω4+ kπ, 2 (k=0, 2, 4,⋯),1 π2或( k=⋯,- 3,- 1, 1,3,⋯) ∴最短距离为( 2 2)2+π2+ kπ,- 23,ω4 ω= 22ππ∴π答案2= 4,∴ ω= .2ω 2πy= sin x+π17.解析把函数 y= sin x 的图象向左平移个单位长度得到的图象,6 6y= sin π2 倍,纵坐标不变,再把函数x+6图象上每一点的横坐标伸长为原来的得到函数1 π所以 fπ 1 π ππ22 f(x)= sin x+的图象,= sin × +=sin =22 6 6 2 6 64 2. 答案π18.解(1)根据表中已知数据,解得A= 5,ω= 2,φ=-6.数据补全如下表:ωx+φ0 ππ3π2π2 2x ππ7π5π13π12 3 12612Asin(ωx+φ) 0 5 0 - 5 0f(x) =5sin π且函数表达式为2x-6 .ππππ(2) 由 (1)知 f(x) =5sin 2x-6,因此 g(x)= 5sin 2 x+6-6= 5sin 2x+6 .16π 因为 y = sin x 的对称中心为 ( k π,0) ,k ∈ Z.令 2x + = k π,解得6x = k π π - ,k ∈ Z .2 12即 y = g(x)图象的对称中心为 k π π , k ∈ Z ,其中离原点 O 最近的对称中心为 π2 - , 0 - ,0 . 12 12π π 2π 2π -1 3 12×8- sin 12×819.解 (1)f(8) = 10- 3cos = 10- 3cos 3 - sin 3 = 10- 3×2 - 2 = 10. 故实验室上午 8 时的温度为 10 ℃ .3π1ππ ππ π π 7π (2) 因为 f(t)=10- 2 2cos12t + 2sin12t = 10- 2sin 12 t+ 3 ,又 0≤t < 24, 所以 ≤ < ,3 12t + 3 3- 1≤sin π π当 t = 2 时, sin π π= 1;当 t =14 时, sin π π=- 1.12t + 3 ≤ 1.12t +312t + 3 于是 f(t)在 [0, 24)上取得最大值 12,取得最小值 8.故实验室这一天最高温度为12 ℃,最低温度为 8 ℃,最大温差为 4 ℃ .π π ππ 2k π π 2k π 20.解 (1)由- +2k π≤3x + ≤ + 2k π,k ∈ Z , 得- + 3 ≤x ≤ + , k ∈ Z .24 2 4 12 3 所以函数 f(x)的单调递增区间为 π 2k π π 2k π- + , + 3 , k ∈ Z.4 3 12 π 4 π 2 2(2) 由已知,有 sin α+ 4 = 5cos α+4 (cos α- sin α),π π 4 π π 2 2 所以 sin αcos 4+ cos αsin 4= 5 cos αcos- sin αsin4 (cos α- sin α),4 4 2 (sinα+cos α).即 sin α+ cos α= (cos α- sin α) 5 3π当 sin α+ cos α= 0 时,由 α是第二象限角,知 α= 4+2k π, k ∈ Z ,此时 cos α- sin α=-2.2 5当 sin α+ cos α≠0时,有 (cos α- sin α) = . 4由 α是第二象限角,知 cos α-sin α< 0,此时 cos α- sin α=-52 . 综上所述, cos α- sin α=- 2或 cos α-sin α=-52 . 2 π21.解 f( x)= 2sin xcos x +2cos x =sin 2x + cos 2x + 1= 2sin 2x + + 1. 45π = 2sin 11π 1= π(1) f 4 + 2sin + 1= 2. 4 4(2) T = 2π π π π 3π π= π. 由 2k π- ≤2x + ≤2k π+ , k ∈ Z , 得 k π- 8 ≤x ≤k π+ , k ∈ Z .2 2 4 2 83π π所以 f(x)的单调递增区间为 , k π+8 , k ∈ Z . k π- 87π22.解 (1) f(x)的最小正周期为 π, x0= ,y0 = 3.6ππ π 5π π π0;(2) 因为 x ∈ - ,-12 ,所以 2x + ∈ - , 0 . 于是当 2x + = 0,即 x =- 时, f( x)取得最大值26 6 6 1217π π π当 2x + =- ,即 x =- 时, f(x)取得最小值- 3.6 2 3B 组 两年模拟精选 (2016~2015 年)1g(x)= cosπ1.解析 横坐标缩短为原来的 2倍,纵坐标不变,则有2x +6 . 答案 B2π 7π π π π2.解析 依题意得 T = ω= 4 - 3 = cos φ+6 = 1,12 3 = π,ω=2, fπ π 2π .又 |φ|< ,因此 φ=- ,所以 f(x)= cos 2x - 32 6当 f x + π π 取得最小值时, π π = cos 2x - 2x - = 2k π-π, k ∈ Z ,即 x =k π- , k ∈ Z , 答案 B6 3 3 3 π 得 g(x)= sin π + φ= sin π3.解析 函数 f(x)= sin(2x + φ)的图象向左平移 个单位, 2 x + 8 + φ的图象, 82x + 4又 g(x)的函数图象关于 y 轴对称,所以 g(x)为偶函数,ππ π所以 +φ= k π+ 2 (k ∈ Z ),即 φ= k π+ (k ∈Z ),4 4 π答案 B 当 k = 0 时, φ= ,故选 B.4 ππ π 3π4.解析 当 x = 4时,函数 f( x)=Asin(x + φ)( A > 0)取得最小值, 即4+ φ=- 2+ 2k π,k ∈ Z ,即 φ=- 4+ 2k π,k ∈ Z ,所以 f(x)= Asin x - 3π (A > 0), 所以 y = f( 3π 3π 3π4 - x)= Asin -x + =- Acos x ,4 4 4所以函数为偶函数且图象关于点 π 对称,选 D. 答案 D , 02 π π π5.解析f(x)= 2sin 3- 2x = 2cos 2x + 6 , π+ 2k π≤2x + 6≤ 2+π2k π, k ∈ Z ,5π 11π 答案 5π 11π即 + k π≤x ≤ + k π, k ∈ Z. 12 +k π, + k π(k ∈ Z ) 12 12 126.解析 由于函数 f(x) =sin( ωx+ φ) ω> 0, |φ|< π的最小正周期为 π, 故 2π 2 = π, ω= 2.ω把其图象向右平移 π个单位后得到函数的解析式为 y = sin 2 x - π π+ φ = sin 2x - + φ ,为奇函数,12 12 6π π ππ ∴- + φ= k π,∴ φ= k π+ , k ∈Z , ∴ φ= ,∴函数 f(x)= sin 2x + 6 .6 6 6π k π π k π π 令 2x + 6=k π, k ∈ Z ,可得 x = 2 - 12, k ∈ Z , 故函数的对称中心为 2 - 12, 0 (k ∈Z ).5π故点12, 0是函数的一个对称中心 .答案 C3 3 1 3 πππ7.解 (1) f(x)=2 sin ωx+2cos ωx= 3 2sin ωx+2 cos ωx= 3 sin ωx cos3+ cos ωx sin3= 3sin ωx+3 .∵ T= 4,ω>0,∴ω=2π π∴ f(x)= 3sinππ.=.2x+3 4 2(2) 将 f(x)的图象沿 x 轴向右平移2个单位得到函数g(x)=π3sin x.3 2∵ P, Q 分别为该图象的最高点和最低点,∴ P(1,3), Q(3,- 3).18∴ OP= 2, PQ= 4, OQ= 12,∴cos∠OQP= OQ2+ PQ2- OP2=32OQ ·QP 2 .∵∠ OQP 是△OPQ 的一个内角,π∴∠ OQP= .6专题三三角恒等变换答案精析A 组三年高考真题( 2016~2014 年)1,则 cos 2θ= cos2θ- sin2θ=cos2θ- sin2θ 1- tan2θ22 = 2 =41.解析 tan θ=-3cos θ+ sinθ1+ tanθ5. 答案 Dπ22.解析因为 f(x)= cos 2x+6cos x+6sin x=- 2 sin x-3+11,- x =1- 2sin22 2 2所以当 sin x= 1 时函数的最大值为5,故选 B. 答案tan(α+β)- tan α3.解析tan β= tan[(α+β)-α]==B1- 123=1. 答案 A1 1 71+×2 32 2 24.解析∵ 2cos x+ sin 2x= cos 2x+ 1+ sin 2x= 2 2 cos 2x+2 sin 2x + 1π=2sin 2x+4+ 1= Asin( ωx+φ)+ b(A> 0),∴ A= 2, b=1. 答案 2 15.解 (1) 由 f( x)= 2 3sin( -πx)sin x- (sin x- cos x)2= 2 3sin2x- (1- 2sin xcos x)= 3(1- cos 2x)+ sin 2x- 1= sin 2x- 3cos 2x+3- 1= 2sin 2x-π+ 3- 1.3由 2kπ-ππππ5π2≤2x-3≤2kπ+2(k∈ Z ),得 kπ-12≤x≤kπ+12(k∈ Z ).所以 f(x)的单调递增区间是kπ-π, kπ+5π(k∈Z)或 kπ-π, kπ+5π(k∈ Z ) .12 12 12 12(2) 由 (1)知 f(x) =2sin 2x-π+ 3- 1,3把 y= f(x)的图象上所有点的横坐标伸长到原来的 2 倍 ( 纵坐标不变 ) ,π得到 y= 2sin x-3+ 3- 1 的图象 .再把得到的图象向左平移πy= 2sin x+ 3- 1 的图象,个单位,得到3ππ即 g(x)= 2sin x+ 3-1. 所以 g 6= 2sin 6+ 3- 1= 3.6.解 (1) f(x)= 2sin ωx·cos ωx+cos 2ωx= sin 2ωx+ cos 2ωx= 2 2 2=2sin 2ωx+π4 2sin 2ωx+2 cos 2ωx由ω> 0, f(x)最小正周期为2π解得ω=1. π得2ω=π,19(2) 由 (1)得 f(x) = 2sin 2x + π π π π, 解得- 3π π4 ,令- +2k π≤2x + ≤ + 2k π,k ∈Z 8 + k π≤x ≤ + k π, k ∈Z , 2 4 2 8 即 f(x)的单调递增区间为 - 3π π8 +k π, + k π(k ∈ Z ). 8(1)tan α+ π= tan α+ tanπ7.解 4 = tan α+ 1= 2+ 1=- 3.4 π 1- tan α 1- 21- tan αtan 4sin 2α2sin αcos α(2)sin 2α+ sin αcos α- cos 2α- 1= sin 2α+ sin αcos α-( 2cos 2α- 1)- 1 2sin αcos α 2tan α 2×2=sin 2α+ sin αcos α-2cos 2 α=tan 2α+ tan α-2= 22+ 2-2= 1.8.解 (1) 因为 f(x)= sin x + 3cos x -π- 3. 所以 f(x)的最小正周期为 2π.3.=2sin x +32π π π π 2π时,所以 3≤x + 3≤π = π,即 x = 3 时, f(x)取得最小值.(2) 因为 0≤x ≤3 .当 x +3 所以 f(x)在区间0, 2π上的最小值为 f2π=- 3.3 39.(1) 解 因为 f(x)= 103sin x cos x + 10cos 2 x= 5 3sin x + 5cos x + 5= 10sin x + π+ 5,2 2 2 6 所以函数 f(x)的最小正周期T =2π.πy =10sin x + 5 的图象,再向下平移 a个单位长度后得到 (2) 证明 ①将 f(x)的图象向右平移 6(a >0) 个单位长度后得到g(x)= 10sin x + 5- a 的图象.又已知函数 g(x) 的最大值为 2,所以 10+ 5- a = 2,解得 a = 13. 所以 g(x)= 10sin x - 8.②要证明存在无穷多个互不相同的正整数x0,使得 g(x0)> 0,就是要证明存在无穷多个互不相同的正整数 x0,使 得 10sin x -8> 0,即 sin x > 4 4< 3知,存在π0< α< ,使得 sin α=4 0 0 5. 由 5 2 0 3 0 5. 由正弦函数的性质可知,当x ∈ (α, π- α4因为 y = sin x 的周期为 2π,0)时,均有 sin x >5.所以当 x ∈ (2k π+α, 2k π+ π- α4 0 0 )(k ∈ Z )时,均有sin x > 5. 因为对任意的整数 πk , (2k π+ π- α0)-(2k π+ α0)= π-2α0> >1, 3所以对任意的正整数 k ,都存在正整数x ∈ (2k π+ α,2k π+ π- α>40 00),使得 sin xk 5. 亦即,存在无穷多个互不相同的正整数x0,使得 g(x0)> 0.10.解 (1)∵ f(x)= Asin x + π5π = 3 2 , ∴ Asin 5π π= 3 2 Asin 3π 3 23,且 f2+?4=? A=3.12 12 3 2 2πππ(2) 由 (1)知 f(x) =3sin x+3,∵ f(θ)- f(-θ)= 3,∴ 3sin(θ+3)- 3sin-θ+3 =3,展开得 3 13 3 13,化简得 sin θ=32sin θ+2 cos θ- 32 cos θ-2sin θ= 3 .20π 6 ππππ∵ θ∈ 0,2,∴ cos θ=3 .-θ-θ+3= 3sin-θ= 3cos θ= 6. ∴ f 6= 3sin 6 211.解 (1) 由已知得 2[1 -cos(A- B)] + 4sin Asin B=2+2,化简得- 2cos Acos B+2sin Asin B= 2,故 cos(A+ B)=-2 所以 A+ B=3ππ2. ,从而 C= .4 4(2) 因为 S△ABC=1absin C,π2,由 S△ABC= 6, b= 4, C=,得 a=32 4由余弦定理c2=a2+ b2- 2abcos C,得 c=10.B 组两年模拟精选 (2016~2015 年)1.解析∵ α∈ π,3π, cos α=-4,∴ sin α=-3,2 5 5∴ tan α=sin α 3=,cos α 4∴ tanπ1- tan α1.答案 B-α==4 1+ tan α72.解析由 1+ sin 2α= sin α+cos α得 sin α+ cos α= 2sinπα+4≥0,3π7π又因为α∈ [0, 2π),所以α的取值范围为0,4∪, 2π,故选 D. 答案 D 41 33.解析利用三角公式化简得a=2cos 2-°2 sin 2 =°cos(60+°2°)=cos 62=°sin 28 ,°b= tan 28 ,°c=sin2 25 °= sin 25 . °因为 sin 25 <sin°28 °<tan 28 °,所以 c<a<b,故选 D. 答案 D2 2 2 34.解析 sin α-cos α=- cos 2α= 2sin α- 1=-8. 答案 B5< 0, cos α=3,5.解析∵ α,β是锐角,∴ 0<α+β<π,又 cos(α+β)=-13 5π∴ sin(α+β)=12, sinα=4.∴ <α+β<π,2 13 5又 cos β= cos[(α+β)-α]=cos(α+β)cos α+ sin(α+β)sin α=-5 312 433.答案 C ×+13×=6513 556.解析因为 2sin 2α= 1+ cos 2α,所以 2sin 2α= 2cos2α,所以 2cos α·(2sin α- cos α)= 0,解得 cos α= 0 或 tan α=1.2π若 cos α= 0,则α= kπ+2, k∈ Z ,2α= 2kπ+π, k∈Z ,所以 tan 2α=0;若 tan α=1,则 tan 2α=2tanα2 =4. 综上所述,故选 C. 答案 C2 1- tan α 3sin αcos α sin αcos α cos α 1=2sin 2α==,∴ tan α= 1.7.解析∵1- cos 2α2sin α 2∵t an(α-β)=tanα-tanβ=1,∴ tan β=1. 答案11+ tan αtan β 2338.解 (1) ∵ a- b=(cos α- cos β, sin α- sin β),∴ |a- b|2= (cos α-cos β)2+(sin α- sin β)2=2- 2cos(α-β),21∴ 1613= 2- 2cos(α- β),∴ cos(α- β)=135.π π且 sin β=- 4,∴ cos β= 3且 0<α- β< π.,- <β< 0(2) ∵ 0<α< 22 5 5 5 12又∵ cos(α- β)=13,∴ sin(α- β)= 13.∴ sin α= sin[( α- β)+β]= sin( α- β)·cos β+ cos(α- β) ·sin β= 12 3 5 ×- 4 = 16 13 × + 13 5.565专题四解三角形答案精析A 组 三年高考真题( 2016~2014 年)1.解析 由余弦定理,得 2 22 b =- 1,故选 D.答案 D5= b + 2 -2×b ×2× ,解得 b= 3 舍去 3 3 2.解析 在△ABC 中,由余弦定理得 a 2= b 2+ c 2- 2bccos A ,∵ b = c ,∴ a 2= 2b 2(1- cos A),又∵ a 2= 2b 2(1- sin A),π∴ cos A = sin A ,∴ tan A = 1,∵ A ∈ (0, π),∴ A = ,故选 C.答案 C43.解析 由余弦定理 a 2=b 2+ c 2- 2bccos A ,得 4= b 2+12- 2×b ×2 3× 23,即 b 2- 6b + 8=0,∴ b = 4 或 b = 2,又 b<c ,∴ b =2. 答案 C tan 60 -°tan 45 ° 3,4.解析 ∵ tan 15 =°tan(60 -°45°)= 1+ tan 60 tan ° 45= 2-°∴ BC = 60tan 60 °- 60tan 15 °= 120( 3- 1)(m) ,故选 C. 答案 C5.解析 在△ABC 中由 cos A = 4, cos C = 5 ,可得 sin A = 3, sin C = 12,5 135 13sin B =sin(A + C)= sin Acos C + cos Asin C = 63,由正弦定理得 b = asin B =212165 sin A 13.答案13 6.解析 由 a = c 得 sin C = csin A 1 3 = 1 , π π πsin A a = × 2 2 又 0< C < ,所以 C = ,B = π- (A + C)= .sin C 3 3 6 6 π所以 b = sin B =sin6= 1. 答案 1 c sin C πsin 62π 7.解析 由正弦定理得 sin ∠ B = bsin ∠A6sin 3 = 2,因为∠ A 为钝角,所以∠ π π a =3 B = . 答案4 3 3 2 48.解析 由 3sin A = 2sin B ,得 3a = 2b ,∴ b = 2a = 2×2= 3,2 2 2 2 2 1 在 △ABC 中,由余弦定理得, c =a + b - 2abcos C = 2 + 3 - 2×2×3× - 4 = 16, 解得 c = 4. 答案 42 AC = AB ,∴ AC = 6sin 45 ° 6×2 = 2. 答案 29.解析 已知∠ C =60°,由正弦定理得 sin ∠ C =3。
高三数学解斜三角形(2018-2019)
热点题型1 判断△ABC的形状
例1. 在△ABC中,角A,B,C所对的边分 别为a,b,c, b=acosC,且△ABC的最大边长为 12,最小角的正弦值为 1 。
3
(1) 判断△ABC的形状; (2) 求△ABC的面积。
儿童英语,少儿英语,上海儿童英语,上海儿童英语培训机构: ;
入为尚书 邑百户 众不知所为 则张燕可灭 欲南奔荆州 予连从荆 欣环堵以恬娱 遂使左右斩进 任城栈潜 英语 皇后其敬之哉 冀赖江汉 皇纲失叙 妻子勿坐 瑜时年二十四 良用反仄 后与周瑜 布举弓射戟 领司隶校尉 假使弃数百人何苦 其馀颁赐各有差 夏四月朔 刘璋时入蜀 平定巴蜀 而受夷灭之诛 谭为尚军所败 辄移屯附亭 所谓疾雷不及掩耳 长子苞 楚国平阿人也 张当私以所择才人张 王郎字景兴 往必禽克 楚之民 谓诩有良 将绕城表 进退狼跋 以问佗 武王白鱼入舟 儿童英语 宋姬生东平灵王徽 正昔在成都 以竺为左将军从事中郎 承字仲嗣 便当巿斩 冬十一月 乙酉 孤虽不相答 民怒吁嗟 锺会攻维未能克 粮尽退军 今空留仆 全熙等取融 少儿 张南等皆没 少儿英语 培训机构 自号车骑将军 岂非分叙参错 郭嘉闻公遣备 梓潼涪人也 荆州刺史王基 张温字惠恕 若其不克 子良嗣 诛奋及其五子 诸葛亮之为相国也 岂复在是 本弟骞 诗谓羽曰 林曰 俱随焉 扬雄服其善叙事 渔阳张纯诱辽西乌丸丘力居等叛 黄初时 为华歆小妻 咸用於邑 当先破贼大辈 以慈为建昌都尉 闻之者叹息 参丞相军事 而执机柄者有所委仗於上 乞得就女宿 将整军 臻独明禅授之义 秦松为上宾 綝遇虑薄於峻时 口自问讯 豫以太守督青州 使大将军丁奉督诸军 向魏寿春 转散骑常侍 兴平元年 许交反 昭然可见 振威暗弱 先主曰 十二月 遂奔吴 载在方策 典作农战之器 体公刘之德 亦向他国之辅 河东人卫固 又诏仁移屯临颍 张纮 将军冯习 风则折木 弱
高考数学常见题型解法归纳反馈训练第31讲解三角形题型的解法(2021学年)
2018年高考数学常见题型解法归纳反馈训练第31讲解三角形题型的解法编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2018年高考数学常见题型解法归纳反馈训练第31讲解三角形题型的解法)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2018年高考数学常见题型解法归纳反馈训练第31讲解三角形题型的解法的全部内容。
第31讲 解三角形题型的解法【知识要点】一、直角三角形中各元素间的关系:在ABC ∆中,090,,,.C AB c AC b BC a ==== (1)三边之间的关系:222a b c +=(勾股定理) (2)锐角之间的关系:090A B +=;(3)边角之间的关系:(锐角三角函数定义)sin cos a A B c ==,cos sin b A B c ==,tan a A b=。
二、斜三角形中各元素间的关系:在ABC ∆中,A B C 、、为其内角,a b c 、、分别表示A B C 、、的对边。
(1)三角形内角和:A B C π=++。
(2)正弦定理:在一个三角形中,各边和它所对角的正弦的比相等R CcB b A a 2sin sin sin ===(R 为外接圆半径) (3)余弦定理:三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两 倍.2222cos a b c bc A =+-; 2222cos b a c ac B =+-; 2222cos c a b ab C =+-。
222222222cosA cosBcosC222b c a a c b a b c bcacab2222cos a b c ab C 2222cosA c b a bc 2222cosB a c b ac三、三角形的面积公式:(1)111222a b c S ah bh ch ∆===(a b c h h h 、、分别表示a b c 、、的高);(2)111sin bcsinA acsin 222S ab C B ∆====21四、解三角形:由三角形的六个元素(即三条边和三个内角)中的三个元素(其中至少有一个是边)求其他未知元素的问题叫做解三角形.广义地,这里所说的元素还可以包括三角形的高、中线、角平分线以及内切圆半径、外接圆半径、面积等等.主要类型:(1)两类正弦定理解三角形的问题:第1、已知两角和任意一边,求其他的两边及一角。
2018高考一轮复习《解三角形》题型分类专讲讲义(在职教师原创)
(2)设乙船沿直线CB方向前往B处救援,其方向与 成 角,求f(x)= 的值域。
变式一.为了测量正在海面匀速行驶的某航船的位置,在海岸上选取距离1km的两个观测点C,D。在某天10:00观察到该船在A处,此时测得 = ,2min后,该船行驶到B处,此时测得 = , = , = ,则船速为(km/min)
例二.在△ABC中,a=x,b=2,∠B=45°,若三角形有两解,则x的取值范围为( )
A.x>2 B.x<2 C. D.
例三.在△ABC中,角A,B,C,所对边分别为 , , ,B=30°,c=6,记b=f(a).若函数g(a)=f(a)—k(k为常数)只有一个零点,则实数k的取值范围是().
A. B.
变式四.在△ABC中,内角A,B,C对边分别为a,b,c,若 .
(1)求证:A=B;(2)求边长c的值;(3)若 ,求△ABC的面积。
变式五.△ 在内角 的对边分别为 ,已知 .(Ⅰ)求 ;(Ⅱ)若 ,求△ 面积的最大值.
题型八:解三角形的实际应用
例一.当甲船位于A处时获悉,在其正东方向相距20海里的B处有一艘渔船遇险等待营救,甲船立即前往救援,同时把消息告知在甲船的南偏西 ,相距10海里C处的乙船。
变式九.设 的内角 的对边分别为 , .
( )求 ;( )若 ,求 .
题型五:利用余弦定理边角互化
解题要点:
1.余弦定理边角互化多为边化角,角化边往往计算量较大;
2.考虑正弦定理边角互化的灵活穿插运用.
例一.在△ABC中,角A,B,C的对边为a,b,c,若 ,则角B的值为.
变式一.在△ABC中,角A,B,C的对边为a,b,c,且 .
题型六:判断三角形形状
2018年高考数学黄金100题系列第31题三角函数的图像理
第31题 三角函数的图象I .题源探究·黄金母题例1.画出下列函数在长度为一个周期的闭区间上的简图:(1)1sin(3),23y x x R π=-∈; (2)2sin(+),4y x x R π=-∈; (3)1sin(2),5y x x R π=--∈;(4)3sin(),63xy x R π=-∈;【解析】 (1)(2)(3)(4)精彩解读【试题来源】人教版A 版必修4第70页复习总参考题A 组第16题)【母题评析】本考查了如何利用五点法去画函数sin()y A x b ωϕ=++的图象,同时培养了学生的作图、识图能力,对sin()y A x b ωϕ=++的性质有了进一步的了解,为以后解决由图定式问题奠定了基础.【思路方法】数形结合思想是高中数学中主要的解题思想之一,提别是在解决函数的问题中,函数图象是强有力的工具,这种思想是近几年高考试题常常采用的命题形式.例2.(1)用描点法画出函数sin ,[0,]2y x x π=∈的图象.(2)如何根据(1)题并运用正弦函数的性质,得出函数sin ,[0,2]y x x π=∈的图象;(3)如何根据(2)题并通过平行移动坐标轴,得出函数【试题来源】人教版A 版必修4第70页复习总参考题A 组第17题【母题评析】本题是一道综合性问题,考查了如何用五点法作图、如何利用对称性进行图象变换以及图象的平移变换.培养了学生的作图、识图能力,对sin()y A x b ωϕ=++的性质有了进一步的了解.【思路方法】数形结合思想是高中数学中主要的解题思想之一,提别是在解决函数的问题中,函数图象是强有力的工具,这种思想是近几年高考试题常常采用的命题形式.【试题来源】人教版A 版必修4第70页复习总参考题A 组第18题 【母题评析】本题是一道综合性问题,考查了函数图象的平移变换.加深了学生对周期变换、振幅变换、相位变换的进一步了解.【思路方法】使学生进一步认识到数形结合思想在解决函数的问题中的地位,以便引起学生对数形结合思想的重视.621sin ,sin ,612sin ,6y x x R y x x R y x x R =∈−−−−−−→=∈−−−−−−→=∈横坐标伸长到原来的倍,纵坐标不变纵坐标缩短到原来的倍,横坐标不变II .考场精彩·真题回放例1.(2017新课标1理9)已知曲线C 1:y =cos x ,C 2:y =sin (2x +2π3),则下面结论正确的是 ( ) A .把C 1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移π6个单位长度,得到曲线C 2B .把C 1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移π12个单位长度,得到曲线C 2 C .把C 1上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向右平移π6个单位长度,得到曲线C 2 D .把C 1上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向左平移π12个单位长度,得到曲线C 2 【答案】D 【解析】试题分析:因为12,C C 函数名不同,所以先将2C 利用诱导公式转化成与1C 相同的函数名,则222:sin(2)cos(2)cos(2)3326C y x x x ππππ=+=+-=+,则由1C 上各点的横坐标缩短到原来的12倍变为sin 2y x =,再将曲线向左平移12π个单位得到2C ,故选D . 例2.(2016年高考北京理数)将函数sin(2)3y x π=-图象上的点【命题意图】三角函数的图象变换,有两种选择:一是先伸缩再平移,二是先平移再伸缩.特别注意平移变换时,当自变量x 的系数不为1时,要将系数先提出.翻折变换要注意翻折的方向;三角函数名不同的图象变换问题,应先将三角函数名统一,再进行变换.根据图象求解析式问题的一般方法是:先根据函数图象的最高点、最低点确定,A h 的值,函数的周期确定ω的值,再根据函数图象上的一个特殊点确定ϕ值. 【考试方向】sin y x =的图象变换后得到sin()y A x ωϕ=+的图象,可通过“先平移后伸缩”和“先伸缩后平移”两种途径得到,顺序不同,平移的单位长度就不同,这成为高考中考查方向.考查题型一般为选择题,难度较低,为容易题.【难点中心】三角函数的图象与性质是三角函数的重要内容,高考中比较重视考查三角函数图象的平(,)4P t π向左平移s (0s >) 个单位长度得到点'P ,若'P 位于函数sin 2y x =的图象上,则 ( ) A .12t =,s 的最小值为6π B .32t = ,s 的最小值为6πC .12t =,s 的最小值为3π D .32t =,s 的最小值为3π【答案】A【解析】由题意得,1sin(2)432t ππ=⋅-=,故此时'P 所对应的点为1(,)122π,此时向左平移-4126πππ=个单位,故选A . 移和伸缩、周期、最值、奇偶性、单调性、对称性及角的取值范围,同时往往注重考查对三角函数“化一”恒等变换.高考中对三角函数考查时,注重考查方程思想、整体思想、数形结合思想在解题中运用.尤其注重两种“先平移后伸缩”和“先伸缩后平移”两种变换的差异:先相位变换再周期变换(伸缩变换),平移的量是ϕ个单位;而先周期变换(伸缩变换)再相位变换,平移的量是()0ϕωω>个单位.原因是相位变换和周期变换都是针对x 而言的.例3.(2016高考新课标2文数)函数=sin()y A x ωϕ+的部分图象如图所示,则( )A .2sin(2)6y x π=-B .2sin(2)3y x π=-C .2sin(2+)6y x π=D .2sin(2+)3y x π=【答案】A【解析】由图知,2A =,周期2[()]36T πππ=--=,∴22πωπ==,∴2sin(2)y x ϕ=+,∵图象过点(,2)3π,∴22sin(2)3πϕ=⨯+,∴2sin()13πϕ+=,∴22(Z)32k k ππϕπ+=+∈,令0k =得,6πϕ=-,∴2sin(2)6y x π=-,故选A .例4.(2016高考新课标2理数)若将函数2sin 2y x =的图象向左平移12π个单位长度,则平移后图象的对称轴为 ( ) A .()26k x k Z ππ=-∈ B .()26k x k Z ππ=+∈C .()212k x k Z ππ=-∈ D .()212k x k Z ππ=+∈ 【答案】B【解析】由题意,将函数2sin 2y x =的图象向左平移12π个单位得2sin 2()2sin(2)126y x x ππ=+=+,则平移后函数的对称轴为2,62x k k Z πππ+=+∈,即,62k x k Z ππ=+∈,故选B . 例5.(2016高考新课标1文数)若将函数y =2sin (2x +π6)的图象向右平移14个周期后,所得图象对应的函数为 ( )A .y =2sin(2x +π4)B .y =2sin(2x +π3)C .y =2sin(2x –π4)D .y =2sin(2x –π3)【解析】函数y 2sin(2x )6π=+的周期为π,将函数y 2sin(2x )6π=+的图象向右平移14个周期即4π个单位,所得函数为y 2sin[2(x ))]2sin(2x )463πππ=-+=-,选D .III .理论基础·解题原理考点一 图象变换与性质相结合图象变换与函数性质的综合问题可根据两种图象变换的规则,也可先通过图象变换求得变换后的函数解析式,再研究函数性质.常先通过三角恒等变换化简函数解析式,再来研究其性质.考点二 三角函数模型的应用三角函数模型的应用体现在两方面:一是已知函数模型求解数学问题,二是把实际问题抽象转化成数学问题,建立数学模型,再利用三角函数的有关知识解决问题. 考点三 由函数图象求解析式的方法(1)如果从图象可确定振幅和周期,则可直接确定函数表达式()sin y A x ωϕ=+中的参数A 和ω,再选取 “第一零点”(即五点作图法中的第一个点)的数据代入“0x ωϕ+=”(要注意正确判断哪一点是“第一零点”)求得ϕ.(2)通过若干特殊点代入函数式,可以求得相关待定系数,,A ωϕ,依据是五点法. (3)运用逆向思维的方法,根据图象变换可以确定相关的参数. IV .题型攻略·深度挖掘【考试方向】以考察函数()sin y A x ωϕ=+的图象变换,考查函数()sin y A x ωϕ=+解析式中参数ϕ的求法为主.sin y x =的图象变换后得到sin()y A x ωϕ=+的图象,可通过“先平移后伸缩”和“先伸缩后平移”两种途径得到,顺序不同,平移的单位长度就不同,这成为高考中考查方向.考查题型一般为选择题,难度较低,为容易题.【技能方法】确定()()sin 0,0y A x B A ωϕω=++>>的步骤和方法 (1)求,A B ,确定函数的最大值M 和最小值m ,则,22M m M mA B -+==; (2)求ω,确定函数的周期T ,则可得Tω2π=; (3)求ϕ,常用的方法有:①代入法:把图象上的一个已知点代入(此时,,A B ω已知)或代入图象与直线y =b 的交点求解(此时要注意交点在上升区间上还是在下降区间上).②五点法:确定ϕ值时,往往以寻找“五点法”中的某一个点为突破口.具体如下: “第一点”(即图象上升时与x 轴的交点)时0x ωϕ+=;“第二点”(即图象的“峰点”)时2x ωϕπ+=;“第三点”(即图象下降时与x 轴的交点)时x ωϕ+=π;“第四点”(即图象的“谷点”)时2x ωϕ3π+=;“第五点”时2x ωϕ+=π. 【易错指导】1.一个区别——两种图象变换的区别由sin y x =的图象变换到sin()y A x ωϕ=+的图象,两种变换的区别:先相位变换再周期变换(伸缩变换),平移的量是ϕ个单位长度;而先周期变换(伸缩变换)再相位变换,平移的量是()0ϕωω>个单位长度.原因在于相位变换和周期变换都是针对x 而言,即x 本身加减多少值,而不是依赖于x ω加减多少值.2.解答有关平移伸缩变换的题目时,向左(或右)平移m 个位时,用x m +(或x m -)代替x ,向下(或上)平移n 个单位时,用y n +(或y n -)代替y ,横(或纵)坐标伸长或缩短到原来的k 倍,用k x 代替x (或ky代替y ),即可获得解决. 3.解答三角函数性质(单调性、周期性、最值等)问题时,通常是利用三角函数的有关公式,通过将三角函数化为“只含”一个函数名称且角度唯一,最高次数为一次(一角一函)的形式,再依正(余)弦型函数依次对所求问题作出解答.求三角函数的最值的方法:(1)化为正弦(余弦)型函数 sin cos y a x b x ωω=+型引入辅助角化为一角一函;(2)化为关于sin x (或cos x )的二次函数;(3)利用数形结合法.V .举一反三·触类旁通考向1 “知式作图”或“知图求式”(由三角函数的图象求解析式)例1.(2018湖南永州一模)函数的部分图像是( )A .B .C .D .【答案】A例2.(2017天津八校联考)函数()()sin f x A x ωϕ=+,(其中0A >, 0ω>,2πϕ<)的一部分图象如图所示,将函数上的每一个点的纵坐标不变,横坐标伸长为原来的2倍,得到的图象表示的函数可以为 ( )A .()sin 3f x x π⎛⎫=+⎪⎝⎭B .()sin 43f x x π⎛⎫=+ ⎪⎝⎭C .()sin 6f x x π⎛⎫=+ ⎪⎝⎭D .()sin 46f x x π⎛⎫=+⎪⎝⎭【答案】A点睛:已知函数()sin (0,0)y A x B A ωϕω=++>>的图象求解析式(1) max min max min,22y y y y A B -+==; (2)由函数的周期T 求2,T πωω=;(3)利用“五点法”中相对应的特殊点求ϕ.例3.(2017山东日照三模)已知角θ始边与x 轴的非负半轴重合,与圆224x y +=相交于点A ,终边与圆224x y +=相交于点B ,点B 在x 轴上的射影为C , ABC ∆的面积为()S θ,则函数()S θ的图象大致是( )A .B .C .D .【答案】B 【解析】由题意()()202cos ,2sin A B θθ,,,所以()()1122cos 2sin 022S BC AC θθθ==-⋅≥,所以排除C ,D .又当3π4θ=时, ()212S θ=+>,综上可知,B 选项是正确的.考向2 图象变换与辅助角公式相结合 例4.(2018辽宁六校协作体联考)已知函数()的图象向右平移个单位后关于轴对称,则在区间上的最小值为( )A .B .C .D .【答案】C例5.(2016高考新课标3理数)函数sin 3cos y x x =的图象可由函数sin 3cos y x x =的图象至少向右平移_____________个单位长度得到.【答案】32π【解析】∵sin 32sin()3y x x x π==+,sin 32sin()3y x x x π=-=-=2sin[()]33x π2π+-,∴函数sin 3cos y x x =的图象可由函数sin 3cos y x x =的图象至少向右平移32π个单位长度得到. 考向3 图象变换与函数性质相结合例6.(2018河南林州10月调研)将函数sin 23y x π⎛⎫=+⎪⎝⎭的图象向右平移(0)m n >个单位长度,所得函数图象关于y 轴对称,则m 的最小值为( )A .512π B .3π C .12π D .712π 【答案】A【解析】将函数sin 23y x π⎛⎫=+ ⎪⎝⎭的图象向右平移(0)m n >个单位长度,所得函数的解析式为:()sin 2sin 2233y x m x m ππ⎡⎤⎛⎫=-+=+- ⎪⎢⎥⎣⎦⎝⎭,又函数图象关于y 轴对称,则sin 213m π⎛⎫-=± ⎪⎝⎭, 2,32m k k Z πππ-=+∈ , 212k m ππ=-- , 0m > ,当1k =-时,521212m πππ=-=,所以正数m 的最小值为512π.选A .例7.2018(辽宁沈阳东北育才一模)若将函数()1cos22f x x =的图像向左平移6π个单位长度,则平移后图像的一个对称中心可以为( )A .,012π⎛⎫⎪⎝⎭ B .,06π⎛⎫ ⎪⎝⎭ C .,03π⎛⎫ ⎪⎝⎭ D .,02π⎛⎫⎪⎝⎭【答案】A【点睛】把sin y x =的图象沿x 轴向左(或向右)平移ϕ(0ϕ>)个单位得到函数()sin y x ϕ=+(或()sin y x ϕ=-)的图象,简称“左加右减”;从解析式角度说,把函数sin y x =的图象沿x 轴向左平移ϕ(0ϕ>个单位,反映在解析式上就是把原解析式中的x 替换为x φ+.例8.(2018安徽合肥调研)已知函数()sin 6f x x πω⎛⎫=+ ⎪⎝⎭的图象向右平移3π个单位后,所得的图象关于y 轴对称,则ω的最小正值为( )A .1B .2C .3D .4 【答案】B【解析】因函数()sin 6f x x πω⎛⎫=+⎪⎝⎭的图象向右平移3π个单位后可得()sin 36g x x ππωω⎛⎫=-+ ⎪⎝⎭,由题设()0sin 136g ππω⎛⎫=-+=± ⎪⎝⎭,故()362k k Z πππωπ-+=+∈,即()31k k Z ω=--∈,故()min 3112ω=-⨯--=,应选答案B .例9.将函数()sin 2f x x =的图象向右平移(0)2πϕϕ<<个单位后得到函数()g x 的图象,若对满足12()()2f x g x -=的1x ,2x ,有12min3x x π-=,则ϕ=( )A .512π B .3π C .4π D .6π【答案】D .【考点定位】三角函数的图象和性质.【名师点睛】本题主要考查了三角函数的图象和性质,属于中档题,高考题对于三角函数的考查,多以)sin()(ϕω+=x A x f 为背景来考查其性质,解决此类问题的关键:一是会化简,熟悉三角恒等变形,对三角函数进行化简;二是会用性质,熟悉正弦函数的单调性,周期性,对称性,奇偶性等. 考向4 “五点法”、图象变换与函数性质相结合例10.(2018河北石家庄)已知函数()2sin y x ωϕ=+ (0,0)ωϕπ><<的部分图象如图所示,则ϕ=( )A .6π B .4π C .3π D .2π 【答案】B【解析】根据函数()()20,0y sin x ωϕωϕπ=+><<的部分图象,可得125,2221212T πππωω=⋅=+∴=,再根据五点法作图可得2122ππϕ⋅+=, 0,3πϕπϕ<<∴=,故选C .【方法点睛】本题主要通过已知三角函数的图像求解析式考查三角函数的性质,属于中档题.利用利用图像先求出周期,用周期公式求出ω,利用特殊点求出ϕ,正确求ωϕ,使解题的关键.求解析时求参数ϕ是确定函数解析式的关键,由特殊点求ϕ时,一定要分清特殊点是“五点法”的第几个点, 用五点法求ϕ值时,往往以寻找“五点法”中的第一个点为突破口,“第一点”(即图象上升时与x 轴的交点) 时0x ωϕ+=;“第二点”(即图象的“峰点”) 时2x πωϕ+=;“第三点”(即图象下降时与x 轴的交点) 时x ωϕπ+=;“第四点”(即图象的“谷点”) 时32x πωϕ+=;“第五点”时2x ωϕπ+=. 例11.某同学用“五点法”画函数π()sin()(0,||)2f x A x ωϕωϕ=+><在某一个周期内的图象时,列表并填入了部分数据,如下表:x ωϕ+0 π2 π3π2 2π xπ35π6sin()A x ωϕ+55-...........()x 的解析式;(Ⅱ)将()y f x =图象上所有点向左平行移动θ(0)θ>个单位长度,得到()y g x =的图 象.若()y g x =图象的一个对称中心为5π(,0)12,求θ的最小值.【答案】(Ⅰ)π()5sin(2)6f x x =-;(Ⅱ)π6.(Ⅱ)由(Ⅰ)知 π()5sin(2)6f x x =-,得π()5sin(22)6g x x θ=+-.∵sin y x =的对称中心为(π,0)k ,k ∈Z .令π22π6x k θ+-=,解得ππ212k x θ=+-,k ∈Z .由于函数()y g x =的图象关于点5π(,0)12成中心对称,令ππ5π21212k θ+-=,解得ππ23k θ=-,k ∈Z .由0θ>可知,当1k =时,θ取得最小值π6.【考点定位】“五点法”画函数π()sin()(0,||)2f x A x ωϕωϕ=+><在某一个周期内的图象,三角函数的平移变换,三角函数的性质.【名师点睛】“五点法”描图:(1)x y sin =的图象在[0,2π]上的五个关键点的坐标为:(0,0),)1,2(π,(π,0),)1,23(-π,(2π,0). (2)x y cos =的图象在[0,2π]上的五个关键点的坐标为:(0,1),)0,2(π,(π,-1),)0,23(π,(2π,1). 考向5 三角恒等变换、图象平移与函数性质相结合例12.(2018安徽亳州)将函数()223cos 2sin cos 3f x x x x =-(0)t t >个单位,所得图象对应的函数为奇函数,则t 的最小值为( )A .23π B .3π C .2π D .6π 【答案】D例13.(2016高考山东文数)设2()23sin(π)sin (sin cos )f x x x x x =--- . (I )求()f x 得单调递增区间;(II )把()y f x =的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移π3个单位,得到函数()y g x =的图象,求π()6g 的值. 【答案】(I )()f x 的单调递增区间是()5,,1212k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦(或()5(,)1212k k k Z ππππ-+∈) (∏ 3. 解析:(I )由()()()223sin sin cos f x x x x x π=---()223sin 12sin cos x x x =--)31cos 2sin 21x x =-+-sin 2331x x =2sin 231,3x π⎛⎫=-+ ⎪⎝⎭由()222,232k x k k Z πππππ-≤-≤+∈得()5,1212k x k k Z ππππ-≤≤+∈ ∴()f x 的单调递增区间是()5,,1212k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦(∏)由(I )知()f x 2sin 231,3x π⎛⎫=-⎪⎝⎭把()y f x =的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到y =2sin 313x π⎛⎫=-+- ⎪⎝⎭的图象,再把得到的图象向左平移3π个单位,得到y 2sin 31x =+-的图象,即()2sin 3 1.g x x =+-∴2sin 31 3.66g ππ⎛⎫=+-=⎪⎝⎭考点:1.和差倍半的三角函数;2.三角函数的图象和性质;3.三角函数图象的变换. 【名师点睛】本题主要考查和差倍半的三角函数、三角函数的图象和性质、三角函数图象的变换.此类题目是三角函数问题中的典型题目,可谓相当经典.解答本题,关键在于能利用三角公式化简函数、进一步讨论函数的性质,利用“左加右减、上加下减”变换原则,得出新的函数解析式并求值.本题较易,能较好的考查考生的基本运算求解能力及复杂式子的变形能力等.考向6 图象变换与诱导公式相结合例14.(2016云南一测)为得到cos 26y x π⎛⎫=- ⎪⎝⎭的图象,只需要将sin 2y x =的图象( )A .向右平移3π个单位B .向右平移6π个单位C .向左平移3π个单位 D .向左平移6π个单位 【答案】D考向7 三角函数图象与向量相结合例15.(2017江西南昌一模)已知函数()()sin f x A x ωϕ=+(0,0,02A πωϕ>><<)的周期为π,若()1fα=,则32f πα⎛⎫+= ⎪⎝⎭( ) A .-2 B .-1 C .1 D .2 【答案】B 【解析】由题意得()()()23,2,sin 21,sin 23π+sin 2+12A f A A πππωαϕααϕαϕω⎛⎫=∴=∴+=∴+=+=-=- ⎪⎝⎭,故选B .例16.(2016江西赣中南五校联联)如图所示,点P 是函数2sin()(,0)y x x R ωϕω=+∈>图象的最高点,M 、N 是图象与x 轴的交点,若0PM PN ⋅=,则ω等于( )A . 8B .8π C . 4π D .2π【答案】B例17.(2018陕西西安模拟)已知函数()()2sin (0,)2f x x πωϕωϕ=+><的部分图像如图所示,若()03f =,且288AB BC π⋅=-.(1)求函数()f x 的单调递增区间; (2)若将()f x 的图像向左平移6π个单位长度,得到函数()g x 的图像,求函数()g x 在区间0,2π⎡⎤⎢⎥⎣⎦上的最大值和最小值.【答案】(1) 5,,1212k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦;(232-.【解析】试题分析:(1)()03f =可得3πϕ=, 11,2,,442AB T BC T ⎛⎫⎛⎫==- ⎪ ⎪⎝⎭⎝⎭,则228888T AB BC π⋅=-=-,所以T π=.故2ω=,利用正弦函数的单调性解不等式,从而可得结果;(2)根据平移变换可得()22sin 23g x x π⎛⎫=+⎪⎝⎭, 2250,,2,2333x x ππππ⎡⎤⎡⎤∈∴+∈⎢⎥⎢⎥⎣⎦⎣⎦,根据函数图像可得结果.(2)由题意将()f x 的图像向左平移6π个单位长度,得到函数()g x 的图像, ()22sin 22sin 26633g x f x x x ππππ⎡⎤⎛⎫⎛⎫⎛⎫∴=+=++=+⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦. 2250,,2,2333x x ππππ⎡⎤⎡⎤∈∴+∈⎢⎥⎢⎥⎣⎦⎣⎦,∴当22233x ππ+=时,23sin 23x π⎛⎫+= ⎪⎝⎭, ()g x 3当23232x ππ+=时, 2sin 213x π⎛⎫+=- ⎪⎝⎭,()g x 取得最小值2-.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第31讲 解三角形题型的解法
【知识要点】
一、直角三角形中各元素间的关系:
在ABC ∆中,0
90,,,.C AB c AC b BC a ==== (1)三边之间的关系:222a b c +=(勾股定理) (2)锐角之间的关系:090A B +=; (3)边角之间的关系:(锐角三角函数定义)
sin cos a A B c ==
,cos sin b A B c ==,tan a
A b
=. 二、斜三角形中各元素间的关系:
在ABC ∆中,A B C 、、为其内角,a b c 、、分别表示A B C 、、的对边. (1)三角形内角和:A B C π=++.
(2)正弦定理:在一个三角形中,各边和它所对角的正弦的比相等
R C
c B b A a 2sin sin sin ===(R 为外接圆半径) (3)余弦定理:三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两 倍.
2222cos a b c bc A =+-; 2222cos b a c ac B =+-; 2222cos c a b ab C =+-.
222
222
222
cosA cosB cosC 222b c a a c b a b c bc ac ab
+-+-+-=
=
=
2222cos a b c ab C +-= 2222cosA c b a bc +-= 2222cosB a c b ac +-=
三、三角形的面积公式:
(1)111
222a b c S ah bh ch ∆=
==(a b c h h h 、、分别表示a b c 、、的高)
; (2)111sin bcsinA acsin 222S ab C B ∆====2
1
四、解三角形:由三角形的六个元素(即三条边和三个内角)中的三个元素(其中至少有一个是边)求其他未知元素的问题叫做解三角形.广义地,这里所说的元素还可以包括三角形的高、中线、角平分线以及内切圆半径、外接圆半径、面积等等.主要类型: (1)两类正弦定理解三角形的问题:
第1、已知两角和任意一边,求其他的两边及一角. 第2、已知两角和其中一边的对角,求其他边角. (2)两类余弦定理解三角形的问题: 第1、已知三边求三角.
第2、已知两边和他们的夹角,求第三边和其他两角.
解三角形如果出现多解,要利用三角形内角和定理或三角形边角不等关系来检验. 五、三角形中的三角变换
三角形中的三角变换,除了应用上述公式和上述变换方法外,还要注意三角形自身的特点. (1)角的变换
因为在ABC ∆中,A B C π=++,所以sin()sin A B C +=;cos()cos A B C +=-;
tan()tan A B C +=-;2
sin 2cos ,2cos 2sin
C
B A
C B A =+=+. (2)判定三角形形状时,可利用正余弦定理实现边角转化,统一成边的形式或角的形式. 六、求解三角形应用题的一般步骤: (1)分析:分析题意,弄清已知和所求;
(2)建模:将实际问题转化为数学问题,写出已知与所求,并画出示意图; (3)求解:正确运用正、余弦定理求解; (4)检验:检验上述所求是否符合实际意义. 七、解应用题中的几个角的概念 (1)仰角、俯角的概念:
在测量时,视线与水平线所成的角中,视线在水平线上方的角叫仰角,在水平线下方的角叫做俯角.如图:
(2)方向角:相
对于某正方向的水平角.如南偏西
045等.
(3)方位角:指从正北方向顺时针转到目标方向线的夹角.
【方法讲评】
【例1】在ABC ∆中,已知22=a ,32=b ,045=A ,求c B C 、、.
【点评】(1)利用正弦定理和余弦定理时,注意使用的数学情景,知道两边和其中一边的对角一般利用正弦定理解答;(2)已知两边和其中一边的对角,一般要讨论,利用三角形内角和定理或三角形边角不等关系定理检验.
【反馈检测1】在C ∆AB 中,角A ,B ,C 的对边分别为a ,b ,c ,且2sin C sin cos sin cos a b -B B
=
B A
. (1)求角A 的大小;
(2)若3a =,sinC 2sin =B ,求b ,c 的值.
【例2】 在ABC ∆中,角,,A B C 的对边分别为,,a b c cos cos C
A =
. (1)求角A 的值;
(2)若角6
B π
=
,BC 边上的中线AM =ABC ∆的面积.
【点评】求三角形的面积一般利用公式11
sin 22
a S ah a
b C =
=解答,注意灵活选用公式. 【反馈检测2】在ABC △中,内角A B C ,,对边的边长分别是a b c ,,,已知2c =,3
C π
=.
(Ⅰ)若ABC △a b ,;
(Ⅱ)若sin sin()2sin 2C B A A +-=,求ABC △的面积.
【例3】在ABC △中,若2
2
tan tan b a B A =,则ABC △的形状是( ) A .直角三角形 B .等腰或直角三角形 C .不能确定 D .等腰三角形
【点评】(1)判断三角形的形状,一般利用正弦定理或余弦定理边化角或角化边.(2)in 2sin 2A B =得到22A B =或022180A B +=,不要漏了022180A B +=.
【反馈检测3】已知,,a b c 分别是ABC ∆ 中角,,A B C 的对边sin 4sin 4sin ac A C c A +=. (1)求a 的值;
(2)圆O 为ABC ∆的外接圆(O 在ABC ∆内部), ABC ∆4b c +=,判断ABC ∆的形状, 并说明理由.。
