锐角三角函数说课课件
合集下载
锐角三角函数课件PPT
2、在Ｒt△ABC中∠Ｃ＝９００,已知∠A为锐 角，sinA＝ 4 ，求SinB的值。
5
3.已知在RT△ABC中,∠C=900,D是BC中 点,DE⊥AB,垂足为E,sin∠BDE= 4
5 AE=7,求DE的长.
A
E
B
D
C
谢谢！
100倍，sinA的值（ C A.扩大100倍 C.不变
） 1
B.缩小1 0 0 D.不能确定
3.如图 A 300
B
1
3 则 sinA=___2___ .
C 7
练一练
3.如图,在Rt △ABC中,∠C=90°,AB=13,BC=5
求sinA和sinB的值.
B
解:在Rt △ABC中,
13
5
BC 5 sinA= = ,
锐角三角函数课件PPT
意大利的伟大科学家C 伽俐 ．略，曾在斜塔的顶
层做过自由落体运动的实 验.
B
“斜而未倒”
α
A
情
问题 为了绿化荒山，某地打算从位于山脚下的 机井房沿着山坡铺设水管，在山坡上修建一座扬
境 水站，对坡面的绿地进行喷灌．现测得斜坡与水
探 平面所成角的度数是30°，为使出水口的高度为
A
C
AB 13
A= CA2B B2C =1235 2= 1,2
∴sinB=AC=12. AB 13
想一想
C
如图, ∠C=90°CD⊥AB.
sinB可以由哪两条线段之比?
A
若ＡC=5,CD=3,求sinB的值.
┌ DB
解: ∵∠B=∠ACD
∴sinB=sin∠ACD
在Rt△ACD中，AD= A2C － C2D =52－ 32=4
浙教版数学九年级下册1.1《锐角三角函数》说课稿2
浙教版数学九年级下册1.1《锐角三角函数》说课稿2一. 教材分析《锐角三角函数》是浙教版数学九年级下册第一章的第一节内容。
本节课的主要内容有：锐角三角函数的定义，正弦、余弦、正切函数的定义及它们的图象和性质。
这部分内容是中学数学中非常重要的基础知识，是进一步学习中学几何、三角函数和其他数学分支的基础。
在本节课中，学生将掌握锐角三角函数的基本概念，了解它们之间的关系，以及学会用锐角三角函数解决一些实际问题。
二. 学情分析九年级的学生已经学习了初中阶段的数学基础知识，对函数的概念有一定的了解。
但是，对于锐角三角函数的定义和性质，他们可能还比较陌生。
因此，在教学过程中，需要引导学生从已有的知识出发，逐步理解和掌握锐角三角函数的知识。
同时，学生应该具备一定的观察能力、推理能力和解决问题的能力，以便能够更好地学习和理解本节课的内容。
三. 说教学目标1.知识与技能目标：学生能够理解锐角三角函数的定义，掌握正弦、余弦、正切函数的定义及它们的图象和性质。
2.过程与方法目标：学生能够通过观察、实验、推理等方法，探索和发现锐角三角函数之间的关系。
3.情感态度与价值观目标：学生能够积极参与课堂活动，培养对数学的兴趣和自信心，提高合作和交流的能力。
四. 说教学重难点1.教学重点：锐角三角函数的定义，正弦、余弦、正切函数的定义及它们的图象和性质。
2.教学难点：锐角三角函数之间的关系，以及如何运用锐角三角函数解决实际问题。
五. 说教学方法与手段在本节课的教学中，我将采用以下教学方法和手段：1.引导法：通过提问、引导学生观察和思考，激发学生的学习兴趣和主动性。
2.案例分析法：通过具体的案例，让学生更好地理解和掌握锐角三角函数的知识。
3.小组讨论法：学生进行小组讨论，促进学生之间的交流和合作，培养学生的团队精神。
4.多媒体辅助教学：利用多媒体课件，生动形象地展示锐角三角函数的图象和性质，帮助学生更好地理解和记忆。
六. 说教学过程1.导入：通过提问，引导学生回顾已学的函数知识，为新课的学习做好铺垫。
人教版《锐角三角函数》PPT完美课件
正12弦．是一在直直角角三三角角形形的中两定边义长的分，别反为映6和了8直，角求三该角三形角边形与中角较的小关锐系角. 的正弦值． 正由弦勾是 股在定直理角得三AB角2形=A中C定2+义B的C2，=反2B映C了2.直角三角形边与角的关系.
第例2如8，章当锐∠A角＝三3角0°函时数，我们有
行喷灌. 现测得斜坡的坡角(∠A )为 30°，为使出水口的高度 由人勾教股 版定· 数理学得· A九B年2=级A（C2下+）BC2=2BC2.
例现1测得如斜图坡，的在坡R角t△(∠AABC)为中3，0∠°，C=为9使0°出，水求口si的nA高和度为sin3B5的m值，. 需要准备多长的水管？
为 35 m，需要准备多长的水管？ 所正以弦是在直角三角形中定义的，反映了直角三角形边与角的关系.
A例．如s，in当A∠＝A3＝sin30A°′时，B我．们sin有A＝sin A′ 现能测根得 据斜正坡弦的概坡念角正确(∠进A 行)为计3算0°。，为使出水口的高度为 35 m，需要准备多长的水管？
由勾股定理得 AB2=AC2+BC2=2BC2.
在直角三角形中，当锐角 A 的度数一定时， 在 Rt△ABC 中，∠C =90°，AC =5，BC =4，则 sinA =
．
理解并掌握锐角正弦的定义，知道当直角三角形的锐角固定时，它的对边与斜边的比值都固定 (即正弦值不变)。
从上述情境中，你可以发现一个什么数学问题呢？能否结合数学图形把它描述出来？
现测得斜坡的坡角(∠A )为 30°，为使出水口的高度为 35 m，需要准备多长的水管？
A．sin A＝3sin A′ B．sin A＝sin A′
正弦是在直角三角形中定义的，反映了直角三角形边与角的关系.
第例2如8，章当锐∠A角＝三3角0°函时数，我们有
行喷灌. 现测得斜坡的坡角(∠A )为 30°，为使出水口的高度 由人勾教股 版定· 数理学得· A九B年2=级A（C2下+）BC2=2BC2.
例现1测得如斜图坡，的在坡R角t△(∠AABC)为中3，0∠°，C=为9使0°出，水求口si的nA高和度为sin3B5的m值，. 需要准备多长的水管？
为 35 m，需要准备多长的水管？ 所正以弦是在直角三角形中定义的，反映了直角三角形边与角的关系.
A例．如s，in当A∠＝A3＝sin30A°′时，B我．们sin有A＝sin A′ 现能测根得 据斜正坡弦的概坡念角正确(∠进A 行)为计3算0°。，为使出水口的高度为 35 m，需要准备多长的水管？
由勾股定理得 AB2=AC2+BC2=2BC2.
在直角三角形中，当锐角 A 的度数一定时， 在 Rt△ABC 中，∠C =90°，AC =5，BC =4，则 sinA =
．
理解并掌握锐角正弦的定义，知道当直角三角形的锐角固定时，它的对边与斜边的比值都固定 (即正弦值不变)。
从上述情境中，你可以发现一个什么数学问题呢？能否结合数学图形把它描述出来？
现测得斜坡的坡角(∠A )为 30°，为使出水口的高度为 35 m，需要准备多长的水管？
A．sin A＝3sin A′ B．sin A＝sin A′
正弦是在直角三角形中定义的，反映了直角三角形边与角的关系.
锐角三角函数的定义第1课时说课稿
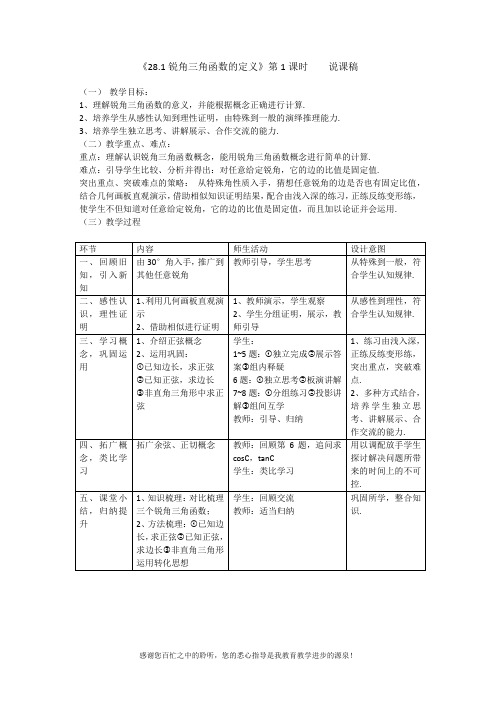
《28.1锐角三角函数的定义》第1课时说课稿
（一）教学目标：
1、理解锐角三角函数的意义，并能根据概念正确进行计算.
2、培养学生从感性认知到理性证明，由特殊到一般的演绎推理能力.
3、培养学生独立思考、讲解展示、合作交流的能力.
（二）教学重点、难点：
重点：理解认识锐角三角函数概念，能用锐角三角函数概念进行简单的计算.
难点：引导学生比较、分析并得出：对任意给定锐角，它的边的比值是固定值.
突出重点、突破难点的策略：从特殊角性质入手，猜想任意锐角的边是否也有固定比值，结合几何画板直观演示，借助相似知识证明结果，配合由浅入深的练习，正练反练变形练，使学生不但知道对任意给定锐角，它的边的比值是固定值，而且加以论证并会运用. （三）教学过程
感谢您百忙之中的聆听，您的悉心指导是我教育教学进步的源泉！。
锐角三角函数PPT优质课市公开课一等奖省优质课获奖课件.pptx
∠A邻边与斜边比叫做余弦。记作cosA
第5页
∠A对边与邻边比叫做正切。记作tanA
第6页
当直角三角形一个锐角 大小确定时，其对边与邻 边比值也是惟一确定吗？
第7页
B
思索：锐角A正切值能够等
于1吗？为何？
A
┌ C
能够大于1吗？
对于锐角A每一个确定值，sinA、cosA、tanA都有唯 一确实定值与它对应，所以把锐角A正弦、余弦、正切叫
做∠A锐角三角函数。
第8页
例2 在Rt △ABC中，∠C＝90°，AB=10,BC=6,
求sinA,cosA,tanA值。
解：由勾股定理得
B
AC AB 2 BC 2 102 62 8
因此sin A BC 6 3 AB 10 5
cos A AC 8 4 AB 10 5
tan A BC 6 3 AC 8 4
3.如图
B
3
A 300
C
7
则 sinA=______ .
第2页
2.在Rt△ABC中，锐角A对边和斜边同时扩大
100倍，sinA值（ ）
A.扩大100倍
B.缩小
C.不变
D.不能确定
第3页
在直角三角形中，一个角邻边比斜边、对边 比邻边又是什么情况呢？
第4页
如图：在Rt △ABC中，∠C＝90°，当∠A确定时， ∠A对边与斜边比随之确定。此时，其它边之间比是 否也随之确定呢？为何？
B
(1) tanA =
(
)
=
CD
AC ( )
D
A
C
(2) tanB=
(
)
=
CD
BC ( )
第5页
∠A对边与邻边比叫做正切。记作tanA
第6页
当直角三角形一个锐角 大小确定时，其对边与邻 边比值也是惟一确定吗？
第7页
B
思索：锐角A正切值能够等
于1吗？为何？
A
┌ C
能够大于1吗？
对于锐角A每一个确定值，sinA、cosA、tanA都有唯 一确实定值与它对应，所以把锐角A正弦、余弦、正切叫
做∠A锐角三角函数。
第8页
例2 在Rt △ABC中，∠C＝90°，AB=10,BC=6,
求sinA,cosA,tanA值。
解：由勾股定理得
B
AC AB 2 BC 2 102 62 8
因此sin A BC 6 3 AB 10 5
cos A AC 8 4 AB 10 5
tan A BC 6 3 AC 8 4
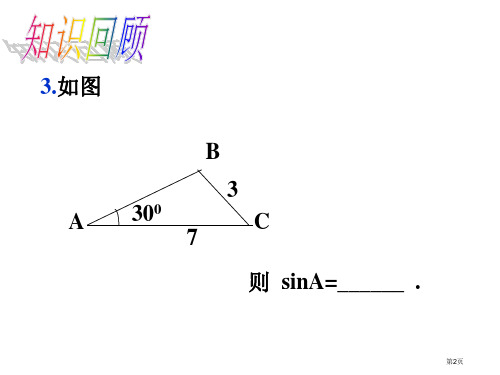
3.如图
B
3
A 300
C
7
则 sinA=______ .
第2页
2.在Rt△ABC中，锐角A对边和斜边同时扩大
100倍，sinA值（ ）
A.扩大100倍
B.缩小
C.不变
D.不能确定
第3页
在直角三角形中，一个角邻边比斜边、对边 比邻边又是什么情况呢？
第4页
如图：在Rt △ABC中，∠C＝90°，当∠A确定时， ∠A对边与斜边比随之确定。此时，其它边之间比是 否也随之确定呢？为何？
B
(1) tanA =
(
)
=
CD
AC ( )
D
A
C
(2) tanB=
(
)
=
CD
BC ( )
人教高中数学必修一A版《三角函数的概念》三角函数说课教学课件复习(三角函数的概念)
课件
课件
课件
课件
课件
课件
课件
课件
课件
②若a<0，则r＝－5a，角α在第四象限， 课件课件
课件 课件
课件 课件
课件 课件
课件
课件
sin α＝－4a5a＝－45，cos α＝－－35aa＝35，
所以2sin α＋cos α＝－85＋35＝－1.
栏目导航
由角 α 终边上任意一点的坐标求其三角函数值的步骤：
3．sin235π＝________.
课件
课件
课件
课件
课件
课件
课件
课件
课件
课件
课件
课件 课件
课件 课件
课件 课件
课件 课件
课件
课件
课件
3 2
[sin235π＝sin8π＋π3＝sinπ3
＝ 23.]
栏目导航
4．角 α 终边与单位圆相交于点
3＋1
3 1
M ， ，则 cos α＋sin α 的值为 2 2
2．借助公式的运算，提升数学
切)在各象限的符号．(易错点)
运算素养.
3．掌握公式——并会应用.
栏目导航
自
主 课件
课件 课件 课件 课件 课件 课件 课件
课件 课件
课件 课件
课件 课件
课件
课件
课件 课件
课件 课件
课件
课件
预
习
探新知
栏目导航
1．单位圆
课件
课件
课件
课件
课件
课件
课件
课件
课件
课件
课件
课件
课件 课件
《锐角三角函数》课件PPT1
新课导入
问题引入
如图，在 Rt△ABC 中，∠C＝90°，当锐角 A 确定时，∠A的对边
与斜边的比就随之确定.
此时，其他边之间的比是否也确定了呢？
B
A
C
新课讲解
知识点1 余弦
合作探究
如图， △ABC 和 △DEF 都是直角三角形， 其中∠A =∠D，
∠C =∠F = 90°，则 AC DF 成立吗？为什么？
( D)
解析：根据锐角三角函数的概念，知 sin70°＜1，cos70°＜1， tan70°＞1. 又∵cos70°＝sin20°，正弦值随着锐角的增大而 增大，∴sin70°＞cos70°＝sin20°. 故选D.
当堂小练
3. 如图，在 Rt△ABC 中，∠C = 90°，cosA = 15 ， 求 sinA、tanA 的值． 17
CD 8 4
拓展与延伸
5. 如图，在△ABC中，AB=AC=4，BC=6. 求cosB 及tanB 的值.
解：过点 A 作 AD⊥BC 于点 D.
A
∵ AB = AC，BC=6，
∴ BD = CD = 3，
∴cos B BD 3 . AB 4
B
D
C
在 Rt△ABD 中，AD AB2 BD2 42 32 7，
当堂小练
4. 如图，在 Rt△ABC 中，∠ACB = 90°，CD⊥AB， 垂足为 D. 若 AD = 6，CD = 8. 求 tanB 的值.
解: ∵ CD⊥AB， ∠ACB＝ ∠ADC =90°，
∴∠B+ ∠A=90°， ∠ACD+ ∠A =90°， ∴∠B = ∠ACD， ∴ tan∠B =tan∠ACD= AD 6 3 .
《锐角三角函数》_完美课件
【获奖课件ppt】《锐角三角函数》_ 完美课 件1-课 件分析 下载 【获奖课件ppt】《锐角三角函数》_ 完美课 件1-课 件分析 下载
D
【获奖课件ppt】《锐角三角函数》_ 完美课 件1-课 件分析 下载 【获奖课件ppt】《锐角三角函数》_ 完美课 件1-课 件分析 下载
【获奖课件ppt】《锐角三角函数》_ 完美课 件1-课 件分析 下载 【获奖课件ppt】《锐角三角函数》_ 完美课 件1-课 件分析 下载
【获奖课件ppt】《锐角三角函数》_ 完美课 件1-课 件分析 下载 【获奖课件ppt】《锐角三角函数》_ 完美课 件1-课 件分析 下载
九年级数学下册（RJ）
【获奖课件ppt】《锐角三角函数》_ 完美课 件1-课 件分析 下载 【获奖课件ppt】《锐角三角函数》_ 完美课 件1-课 件分析 下载
【获奖课件ppt】《锐角三角函数》_ 完美课 件1-课 件分析 下载 【获奖课件ppt】《锐角三角函数》_ 完美课 件1-课 件分析 下载
【获奖课件ppt】《锐角三角函数》_ 完美课 件1-课 件分析 下载 【获奖课件ppt】《锐角三角函数》_ 完美课 件1-课 件》_ 完美课 件1-课 件分析 下载 【获奖课件ppt】《锐角三角函数》_ 完美课 件1-课 件分析 下载
【获奖课件ppt】《锐角三角函数》_ 完美课 件1-课 件分析 下载 【获奖课件ppt】《锐角三角函数》_ 完美课 件1-课 件分析 下载
【获奖课件ppt】《锐角三角函数》_ 完美课 件1-课 件分析 下载 【获奖课件ppt】《锐角三角函数》_ 完美课 件1-课 件分析 下载
【获奖课件ppt】《锐角三角函数》_ 完美课 件1-课 件分析 下载 【获奖课件ppt】《锐角三角函数》_ 完美课 件1-课 件分析 下载
课件《锐角三角函数》优秀课件完美版_人教版1
结论：只要梯子的倾斜角确定，倾斜角的对边与斜边的比值，倾斜角的邻边与斜边的比值随之确定. “一个锐角的正弦等于它余角的余弦”“一个锐角的余弦等于它余角的正弦” （3）SinA、cosA这一个完整的符号，不表示“sin”、“cos”和A相乘。 （3）SinA、cosA这一个完整的符号，不表示“sin”、“cos”和A相乘。 “一个锐角的正弦等于它余角的余弦”“一个锐角的余弦等于它余角的正弦” 如图，（1）Rt△AB2C2和Rt△AB1C1有什么关系？ 结论：只要梯子的倾斜角确定，倾斜角的对边与斜边的比值，倾斜角的邻边与斜边的比值随之确定. 这是一个变化的过程. 如图，（1）Rt△AB2C2和Rt△AB1C1有什么关系？
3、如图，菱形ABCD中，AE⊥BC于E点，EC=1， sinB=5 /13 ，求四边形ABCD的周长和面积。
（3）SinA、cosA这一个完整的符号，不表示“sin”、“cos”和A相乘。 如图，（1）Rt△AB2C2和Rt△AB1C1有什么关系？ 2、 利用勾股定理求出各边的长度。 “一个锐角的正弦等于它余角的余弦”“一个锐角的余弦等于它余角的正弦” （3）SinA、cosA这一个完整的符号，不表示“sin”、“cos”和A相乘。 “一个锐角的正弦等于它余角的余弦”“一个锐角的余弦等于它余角的正弦” [环节四] 一个锐角的正弦与它余角的余弦的关系 结论：sinA值越大，梯子越陡，cosA值越小，梯子越陡。 [环节三] 梯子的倾斜程度与SinA、cosA的关系。 结论：只要梯子的倾斜角确定，倾斜角的对边与斜边的比值，倾斜角的邻边与斜边的比值随之确定. 2、如图，在△ABC中，AD是BC边上的高，tanB=cos∠DAC （1）求证：AC=BD （2）若SinC=，BC=9，求AD。 结论：sinA值越大，梯子越陡，cosA值越小，梯子越陡。 [环节四] 一个锐角的正弦与它余角的余弦的关系 锐角三角函数 ---正弦与余弦 [环节四] 一个锐角的正弦与它余角的余弦的关系 如图，（1）Rt△AB2C2和Rt△AB1C1有什么关系？ （3）SinA、cosA这一个完整的符号，不表示“sin”、“cos”和A相乘。
3、如图，菱形ABCD中，AE⊥BC于E点，EC=1， sinB=5 /13 ，求四边形ABCD的周长和面积。
（3）SinA、cosA这一个完整的符号，不表示“sin”、“cos”和A相乘。 如图，（1）Rt△AB2C2和Rt△AB1C1有什么关系？ 2、 利用勾股定理求出各边的长度。 “一个锐角的正弦等于它余角的余弦”“一个锐角的余弦等于它余角的正弦” （3）SinA、cosA这一个完整的符号，不表示“sin”、“cos”和A相乘。 “一个锐角的正弦等于它余角的余弦”“一个锐角的余弦等于它余角的正弦” [环节四] 一个锐角的正弦与它余角的余弦的关系 结论：sinA值越大，梯子越陡，cosA值越小，梯子越陡。 [环节三] 梯子的倾斜程度与SinA、cosA的关系。 结论：只要梯子的倾斜角确定，倾斜角的对边与斜边的比值，倾斜角的邻边与斜边的比值随之确定. 2、如图，在△ABC中，AD是BC边上的高，tanB=cos∠DAC （1）求证：AC=BD （2）若SinC=，BC=9，求AD。 结论：sinA值越大，梯子越陡，cosA值越小，梯子越陡。 [环节四] 一个锐角的正弦与它余角的余弦的关系 锐角三角函数 ---正弦与余弦 [环节四] 一个锐角的正弦与它余角的余弦的关系 如图，（1）Rt△AB2C2和Rt△AB1C1有什么关系？ （3）SinA、cosA这一个完整的符号，不表示“sin”、“cos”和A相乘。