第02章 电路的基本分析方法
第02章 半导体二极管及基本电路

一、N 型半导体:
N型
电子为多数载流子
+4 +4 +4
空穴为少数载流子
+4 +5 +4 自由电子
磷原子 施主原子
载流子数 电子数
N型杂质半导体的特点:
1、与本征激发不同,施主原子在提供多余电子的同时 并不产生空穴,而成为正离子被束缚在晶格结构 中,不能自由移动,不起导电作用。
2、在室温下,多余电子全部被激发为自由电子,故N
特性 符号及等效模型:
iD
uD
S
S
正向偏置时: 管压降为0,电阻也为0。 反向偏置时: 电流为0,电阻为∞。
正偏导通,uD = 0; 反偏截止, iD = 0 R =
二、二极管的恒压降模型
iD U (BR) URM O IF uD
iD UD(on) uD
uD = UD(on)
0.7 V (Si) 0.2 V (Ge)
iD 急剧上升
死区 电压
UD(on) = (0.6 0.8) V 硅管 0.7 V (0.1 0.3) V 锗管 0.2 V iD = IS < 0.1 A(硅) 几十 A (锗) 反向电流急剧增大 (反向击穿)
U(BR) U 0 U < U(BR)
反向击穿类型: 电击穿 — PN 结未损坏,断电即恢复。 热击穿 — PN 结烧毁。 反向击穿原因: 齐纳击穿: 反向电场太强,将电子强行拉出共价键。 (Zener) (击穿电压 < 6 V) 反向电场使电子加速,动能增大,撞击 雪崩击穿: 使自由电子数突增。 (击穿电压 > 6 V)
t
例: ui = 2 sin t (V),分析二极管的限幅作用。 1、 0.7 V < ui < 0.7 V
电工基础实用教程(机电类) 第2章 电阻电路的分析方法

结点(3):
i4 i5 i6 0 回路(3): R2i2 R4i4 R6i6 0
第2章 22
支路电流法
(1) 选择支路电流i1,..., ib 作为未知量; (2) 根据KCL和KVL以及VCR, 建立电路变量方程; N个结点: (N-1)个独立的KCL方程; b条支路: (b-N+1)个独立回路KVL方程; b个VCR
R2
R4
Req
R2 ( R3 R4 ) Req R1 R2 R3 R4
2.1.1 无源一端口网络的等效变换
一、电阻的串联
i
1
u1 R1
u2 R2
un Rn
u
1' <一> 串联的特点:通过各电阻的电流相同。
<二> 串联的等效电阻 根据KVL可得:
u u1 u2 un
Y形联接与D形联接即非并联又非串联,如:
Req ?R1Βιβλιοθήκη R5R2R4
R3
1
1 i1
i1
R1
R3
3
i3
R31
R12
R2
i2
2 3
i3
R23
2
(a)为Y形或星形联接 <1> 对应电压u12,u23和u31相同;
i2 (b)为D形 或三角 形 。
' ' ' i1 i1 , i2 i2 , i3 i3 <2> 流入对应端的电流相同。即
例 2.1:
Req ?
2W
1W 2W
2W
4W
2W
2W
2W
2W
? ?
?
电路的基本分析方法 练习题及答案第2章

第2章 电路的基本分析方法习题答案2-1 在8个灯泡串联的电路中,除4号灯不亮外其它7个灯都亮。
当把4号灯从灯座上取下后,剩下7个灯仍亮,问电路中有何故障?为什么?解:4号灯灯座短路。
如开路则所有灯泡都不亮。
2-2 额定电压相同、额定功率不等的两个白炽灯能否串联使用,那并联呢? 解:不能串联使用,因其电阻值不同,串联后分压不同,导致白炽灯无法正常工作。
在给定的电压等于额定电压的前提下,可以并联使用。
2-3 如图2-34所示,R 1=1Ω,R 2=5Ω,U =6V ,试求总电流强度I 以及电阻R 1、R 2上的电压。
图2-34 习题2-3图解:A 151621=++=R R U I=,V 551= V 111=2211=⨯==⨯=IR U IR U2-4 如图2-35所示,R 1=3Ω,R 2=6Ω,U =6V ,试求总电流I ;以及电阻R 1,R 2上的电流。
图2-35 习题2-4图解:总电阻为:Ω263632121=+⨯+=R R R R R=A 326=∴=R U I=由分流公式得:A 13633A 2363621122121=⨯++=⨯++I=R R R =I I=R R R =I2-5 电路如图2-36(a)~(f)所示,求各电路中a 、b 间的等效电阻R ab 。
(a) (b) (c)(d) (e) (f)2-36 习题2-5图解:(a) Ω4.3)6//4()2//2(ab =+=R(b) Ω2)33//()66//4ab =++(=R (c)Ω2)]6//3()6//3//[(13ab =++)(=R(d) Ω2)6//1)6//3(ab =+)(=R (e) Ω7)10//10(}6//6//]2)8//8{[(ab =++=R (f) Ω6}6//]64)4//4{[()4//4(ab =+++=R2-6 求图2-37所示电路中的电流I 和电压U 。
图2-37 习题2-6电路图解:图2-37等效变换可得:由上图可得;Ω8)816//)]}99//(6[5.7{=+++(总=RA 5.1812==总I 则根据并联电路分流作用可得:A 5.05.1)816()]99//(6[5.7)]99//(6[5.7=1=⨯++++++I则A 15.05.1=13=-=-I I I 总 I 3再次分流可得:A 75.0169999=4=⨯+++IA 25.016996=2=⨯++I所以I =0.75A ,U = U +-U - =9×I 2-8×I 1 = 9×0.25-8×0. 5=-1.75V2-7 电路如图2-38(a)~(g)所示,请用电源等效变换的方法进行化简。
大学物理学第2章正弦交流电路_02

解法2: 利用相量图分析求解
设 U AB为参考相量,
I1 10A
I2 100 5 5
2 2
j10Ω
I
I1
A
A
I 1 超前 U AB 90
10 2A,
I2
C1
B
5Ω j5Ω
V
画相量图如下:
I 2滞后UAB 45°
由相量图可求得: I =10 A
UL= I XL =100V U L超前I 90°
I1 Z2 j400 I 0.5 33 A Z1 Z 2 100 j200 j400
0.89 - 59.6 A
同理:
I
I2
Z1 I Z1 Z 2
100 j200 0.5 33 A 100 j200 j400 0.5 93.8 A
UL
I1 100 10
U
由相量图可求得: V =141V
45° I 45°
I2
U AB
10 2
2.5 正弦稳态电路的功率
2.5.1 功率
一、瞬时功率
I +
i = Im sinωt U u = Umsin (ωt + ) - p = u i = UmImsin(ωt + ) sinωt = U I cos + U I cos ( 2ωt + )
S =√P2 + Q2 = 190 V· A
例2 如图所示是测量电感线圈参数R和L的实验电路,已知电 压表的读数为50V,电流表的读数为1A,功率表的读数为30W, 电源的频率f=50Hz。试求R和L的值。 ﹡ I 解:根据图中3个仪表的读数, A W ﹡ + 可先求得线圈的阻抗 电 R 感 Z | Z | R jL V U 线 圈 L U | Z | 50 I 功率表读数表示线圈吸收的有功功率,故有 P UI cos 30W 30 arctan( ) 53.130 UI 从而求得
第二章_电路的分析方法
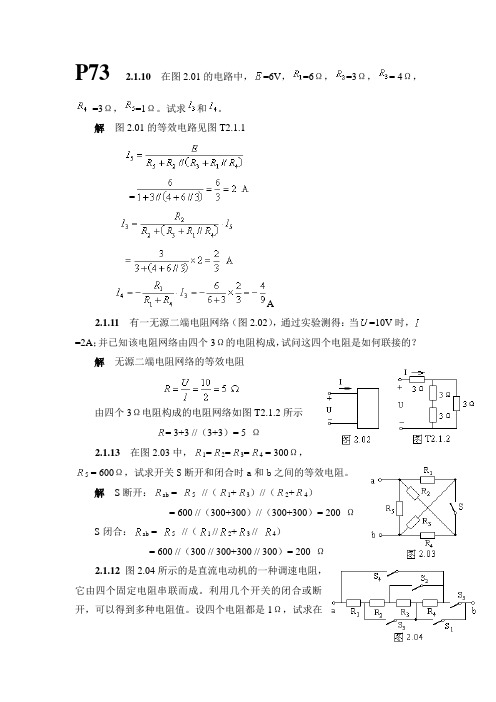
P732.1.10在图2.01的电路中,=6V,=6Ω,=3Ω,= 4Ω,=3Ω,=1Ω。
试求和。
解图2.01的等效电路见图T2.1.1=A2.1.11有一无源二端电阻网络(图2.02),通过实验测得:当=10V时,=2A;并已知该电阻网络由四个3Ω的电阻构成,试问这四个电阻是如何联接的?解无源二端电阻网络的等效电阻由四个3Ω电阻构成的电阻网络如图T2.1.2所示= 3+3 //(3+3)= 5 Ω2.1.13在图2.03中,1=2=3=4 = 300Ω,= 600Ω,试求开关S断开和闭合时a和b之间的等效电阻。
= 5 //(1+3)//(2+4)解S断开:= 600 //(300+300)//(300+300)= 200 ΩS闭合:= 5 //( 1 //2+ 3 // 4)= 600 //(300 // 300+300 // 300)= 200 Ω2.1.12图2.04所示的是直流电动机的一种调速电阻,它由四个固定电阻串联而成。
利用几个开关的闭合或断开,可以得到多种电阻值。
设四个电阻都是1Ω,试求在下列三种情况下a ,b 两点间的电阻值:(1)S 1和S 5闭合,其他断开;(2)S 2,S 3和S 5闭合,其他断开;(3)S 1,S 3和S 4闭合,其他断开。
解 (1)S 1和S 5闭合:ab =1 +2 +3 = 3Ω(2)S2,S 3和S 5闭合: ab = 1 + 2 // 3 // 4 =(3)S1,S 3和S 4闭合:ab =1 //4 = 0.5 Ω2.1.5 图2.05是一衰减电路,共有四档。
当输入电压=16V 时,试计算各档输出电压。
解 a 档输出电压:== 16 Vb 档输出电压:== 5.5 //≈5 Ω同理:,2.1.6 图2.06所示的是由电位器组成的分压电路,电位器的电阻P =270Ω,两边的串联电阻1 =350Ω,2 =550Ω。
设输入电压1=12V ,试求输出电 压2的变化范围。
电路分析基础 张凤霞课件-第02章.电阻电路的等效变换

120 60
ab
20 100 60
40
2020/5/25
返回 上页 下 页
例5 求: Rab
5
15
6
a 20 b
7
6
缩短无 电阻支路
Rab=10
4
ba
15
10
20
5
a
15 b
7 6 6 4 a
b
15 7 3
2020/5/25
返回 上页 下 页
例6 求: Rab
iR
对称电路 c、d等电位
变量之间无控制和被控的关系,则称 N1和 N2为 单口网络(二端网络)。
一个单口网络对电路其余部分的影响,决定于其 端口电流电压关系(VAR)。
2020/5/25
返回 上页 下 页
二. 等效单口网络
a
i +
b u-
N
u f (i)
a
i +
b u-
N'
u f(i)
若网络 N 与 N 的VAR相同,则称该两网络为
等效单口网络。
将电路中一个单口网络用其等效网络代替(称 为等效变换),电路其余部分的工作状态不会 改变。
2020/5/25
返回 上页 下 页
2.1.2 单口网络端口伏安关系(VAR)的求取
将单口网络从电路中分离出来,标 好其端口电流、电压的参考方向;
假定端电流i 已知(相当于在端口 接一电流源),求出 u = f (i) 。或 者,假定端电压 u 已知(相当于在 端口接一电压源),求出 i = g (u) 。
返回 上页 下 页
• 三端网络的端口VAR
端口独立电流(例如 i1、i2 )与端口独立电压(例 如 u13 、u23 )之间的关系。
《电路与电工技术》第2章 电阻电路的基本分析方法和定理
2.1 电阻电路的等效变换
2.1.1 电阻的串联、并联及其等效变换
3、电阻的混联
解 图中,可见R4与R5并联(记R4∥R5),可得
R45=R4∥R5=1Ω
为串联电路简化后如图2.5(b)所示,可见R2 与R45为串
联 R245 R2 R45 (11) 2
电路再简化后如图2.5(c)所示,可见R3 与R245 并联
2.1.1 电阻的串联、并联及其等效变换
2、电阻的串联
应用特点:
(1)分压原理:串联电阻上的电压与电阻阻值的大 小成正比。 (2)限流原理:当负载变化(或电源电压变化)时 ,为了防止电路中的电流过大,可以在电路中串联电 阻来限制电流。
2.1 电阻电路的等效变换
2.1.1 电阻的串联、并联及其等效变换
因此a、b之间ห้องสมุดไป่ตู้等效电阻 Rab为:
Rab
1[(1101)//1211] 2
4
有关等电位点的图 图2-118
2.1 电阻电路的等效变换
2.1.3 电阻的(Y形)/(Δ形)等效变换
电阻之间的联接既不是串联也不是并联,可以运用KCL、 KVL、欧姆定律及电路等效的概念,对它们作彼此之间的互 换,使变换后的电阻联接方式与电路其它部分的电阻构成串 联或并联。这里介绍常见的电阻的Y—Δ变换和Δ—Y变换。
流过的电流之和。
2.1 电阻电路的等效变换
2.1.1 电阻的串联、并联及其等效变换
3、电阻的混联
特点: 电路中有电阻的串联,又有电阻的并联,这种连接方
式称电阻的串并联,又称为电阻的混联。 混联电路可以通过电阻的串联、并联来逐步变换,最
终可简化为一个等效电阻R。
例2.2 如图所示电路是一个电阻混联电 路,试求a、b两端的等效电阻。
电工学-第二章习题答案
第二章 电路的分析方法2.1.1 在图2.01的电路中,V 6=E ,Ω=61R ,Ω=32R ,Ω=43R ,Ω=34R ,Ω=15R 。
试求3I 和4I 。
4I ↓图2.01解:图2.01电路可依次等效为图(a )和图(b )。
R 3R 1R(b)Ω=+×=+×=23636414114R R R R R Ω=+++×=+++×=2243)24(3)(14321432R R R R R R R A 22165=+=+=R R E IA 322363)(214323=×+=++=I R R R R IA 943263631414−=×+−=+−=I R R R I2.3.3 计算图2.12中的电流3I 。
Ω=1R A2S =图2.12解:根据电压源与电流源的等效变换,图2.12所示电路可依次等效为图(a )和图(b ),由图(b )可求得A 2.15.023=+=I由图(a )可求得:A 6.02.121213=×==I IΩ=1R V22=Ω=14R(b)Ω=12R2.6.1 在图2.19中,(1)当将开关S 合在a 点时,求电流1I ,2I 和3I ;(2)当将开关S 合在b 点时,利用(1)的结果,用叠加定理计算电流321,I I I 和 。
I图2.19I (a)I (b)解:(1)当将开关S 合在a 点时,图2.19所示电路即为图(a ),用支路电流法可得:=+=+=+12042130423231321I I I I I I I 解得:===A 25A 10A 15321I I I(2)开关S 合在b 点时,利用叠加原理图2.19所示电路可等效为图(a )和图(b ),其中图(a )电路中130V 和120V 两个电压源共同作用时所产生的电流已在(1)中求得,即:A 151=,I A 102=,I A 253=,I由图3(b )可求得:A 642422202=+×+=,,I A 464241−=×+−=,,IA26422=×+=则:A 11415111=−=+=,,,I I IA 16610,222=+=+=,,I I IA 27225333=+=+=,,,I I I2.6.2 电路如图2.20(a )所示,V 10ab ,,V 124321=====U R R R R E 。
[整理]02第二章 放大电路基础
第二章放大电路基础一、基本要求:1、认识三种组态放大电路,知道其特点及应用;2、知道放大电路基本工作原理,认识单管共发射极放大电路组成并会分析;知道静态工作点、输入电阻和输出电阻的概念及意义;3、会测试和调整静态工作点,知道静态工作点与波形失真的关系4、认识多级放大电路,认识放大电路的频率特性。
二、重难点:1、重点:单管共发射极放大电路组成、分析及特性;2、难点:放大电路原理,放大电路技术指标的理解。
三、例题:例2.1电路如题2.1(a)图所示,图(b)是晶体管的输出特性,静态时V BEQ=0.7V。
利用图解法分别求出R L =∞和R L =3kΩ时的静态工作点和最大不失真输出电压V om (有效值)。
解:空载时:I BQ =20μA ,I CQ =2mA ,V CEQ =6V ;最大不失真输出电压峰值约为6-0.3=5.7V ,有效值约为4.03V 。
带载时:I BQ =20μA ,I CQ =2mA ,V CEQ =3V ;最大不失真输出电压峰值约为 2.7V ,有效值约为1.91V 。
v o+V BB v CE /V题2. 1图(a) (b)v CE /V解题2. 1图v CES例2.2在由NPN 型管组成的共射电路中,由于电路参数不同,在信号源电压为正弦波时,测得输出波形如题2.2图(a )、(b )、(c )所示,试说明电路分别产生了什么失真,如何消除?解:(a)饱和失真,增大R b ,减小R c 。
(b)截止失真,减小R b 。
(c)同时出现饱和失真和截止失真,应增大V CC 。
例2.3若由PNP 型管组成的共射电路中,输出电压波形如题2.2图(a )、(b )、(c )所示,则分别产生了什么失真?题2.2图解:(a )截止失真;(b )饱和失真;(c )同时出现饱和失真和截止失真。
例2.4电路如题2.4图(a)所示, 已知β=50,r be =1kΩ;V CC =12V ,R b1=20kΩ, R b2=10kΩ, R c =3kΩ, R e =2kΩ, R s =1kΩ,R L =3kΩ,(1)计算Q 点;(2)画出小信号等效电路;(3)计算电路的电压增益A v =v o /v i 和源电压增益A vs =v o /v s ;输入电阻R i 、输出电阻R o 。
电工技术--第二章 电路的分析方法
A
R1 Us1 R2
I2
R3 Us2 B
I3
A
I1 '
A
I2' I1"
R1 Us1
R2
R1
R2
I2"
R3
I3'
+
R3 Us2
I3 "
B
B
A
I1
R1 R2
A
I2
R3
A
I2'
R3
I1' I3
R1
R2
I1" I3'
R1
R2
I2"
R3
Us1 Us2
=
Us1
+
Us2
I3"
B
B
B
解: I1
U S1 R 2R 3 R1 + R2 + R3
例1 :
I1 R1 I3
a
I2 R2 R3 2 +
对结点 a: I1+I2–I3=0 对网孔1: I1 R1 +I3 R3=E1 E2 对网孔2: I2 R2+I3 R3=E2
+ E1
-
1
-
b
联立求解各支路电流
例:试求各支路电流。
a
c
支路中含有恒流源 I3 注意:当支路中含有恒流源 时,若在列KVL方程时,所选 回路中不包含恒流源支路
+
U -
I RL
Ro Uo
+
+ _
I RL
网络
U B
B 有源二端网络
戴维南等效电路
任意一个线性有源二端网络对外都可等 效为等效电压源。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
应用欧姆定律消去支路电压得: 3
i3 R3
R2i2 R3i3 R1i1 0
R4i4 R5i5 R3i3 0
R5
i5 i6
R1i1 R5i5 R6i6 uS
电路分析基础
支路电流法求解电路的步骤
对于有n个节点、m条支路的电路,要求解支路电 流,未知量共有m个。只要列出m个独立的电路方程, 便可以求解这m个变量,步骤如下: • 任选n-1个独立节点和m-n+1个独立回路,选择独立回 路的一种简单方法就是直接选网孔,并在电路图上标出 各支路电流的参考方向及独立回路的参考绕行方向; • 应用KCL对独立节点列出n-1个电流方程式。
增补方程:U=7I3
b 注意 有受控源的电路,方程列写分两步: ①先将受控源看作独立源列方程; ②将控制量用未知量表示,并代入①中所列的方 程,消去中间变量。
返节目录
电路分析基础
例4 用支路电流法求电压u1 和u2
a I3
+
I1 + 1V –
1
2 + 2V –
I2 u1 –
2u1
7 + u2 –
• 应用KVL对独立回路列出m-n+1个电压方程式,。 • 代入电路参数,联立求解方程式组,求出m个支路电流, 并进一步计算支路电压和进行其他分析。
返节目录
电路分析基础
支路电流法应用举例
• 举例一 用支路电流法求解下图所求电路中各支路电流,并用 功率平衡校验求解结果。
①
I1
R1=7Ω Ⅰ + US1=70V
+
③
R1
+
US3
-
4个节点、 ②
R6
R3
3个网孔、
R4
R5
④
R2
+
6条支路。 需列KCL方程:4-1=3个 需列KVL方程:6-4+1=3个
7个回路、
US1
-
-
US2
在练习本上列出各方程式
①
返节目录
电路分析基础
例1 求各支路电流及各电压源发出的功率
a I1 + 70V – 7 I2 11 + 1 2 6V – b
电路分析基础
线性电路的一般分析方法
• 普遍性:对任何线性电路都适用。 • 系统性:计算方法有规律可循。
方法的基础
• 电路的连接关系—KCL,KVL定律。 • 元件的电压、电流关系特性。 复杂电路的一般分析法就是根据KCL、KVL及VCR 列独立方程、解方程。根据列方程时所选变量的不同 可分为支路电流法、回路电流法和节点电压法。 中心任务:(1)如何选择分析电路的变量; (2) 如何建 立相应的独立方程.
电路分析基础
第2章 电路的基本分析方法
2.1 支路 电流法 2.5 戴维南 定理
2.2 回路 电流法 2.3 节点 电压法
2.4 叠加 定理
返章目录
电路分析基础
本章的学习目的和要求
熟练掌握支路电流法,因为它是直接应用 基尔霍夫定律求解电路的最基本方法之一;理 解回路电流及节点电压的概念,掌握回路电流 法(网孔电流法)和节点电压法的内容及其正 确运用;深刻理解线性电路的叠加性,了解叠 加定理的适用范围;理解有源二端网络和无源 二端网络的概念及其求解步骤,初步学会应用 戴维南定理分析电路的方法。
u2= –7I3+2I2+2= –2.84V
返节目录Байду номын сангаас
电路分析基础
第2节 回路电流法
• 定义
以假想的回路电流为未知量,根据KVL定律列出必 要的电路方程,进而求解客观存在的各支路电流的方 法,称回路电流法。其基本思想是:为减少未知量(方 程)的个数,假想每个回路中有一个回路电流。各支路 电流可用回路电流的线性组合表示,来求得电路的解。
返节目录
电路分析基础
基本(一般)分析法与等效电路法
一般分析方法 • 可求解任意电路的所有支路电压和电流。 等效电路法
• 只适用于简单电路,且只能分析某些支路的 电压和电流。
一般分析方法可分为: • 传统分析法:支路电流法、网孔电流法、节点电压法 • 拓扑分析法:回路电流法、割集电压法
返节目录
I1 1218 203 6A
I 2 406 203 2A
I 3 I1 I 2 6 2 4A
P 6 70 420 W 70
P 2 6 12 W 6
返节目录
电路分析基础
例2 列写支路电流方程.(电路中含有理想电流源)
解1 (1) n–1=1个KCL方程: 节点a: –I1–I2+I3=0
KCL和KVL的独立方程数
1.KCL的独立方程数
2 1
1 6 4 3 2
1
i1 i4 i6 0
i1 i2 i3 0
2
3 5
3 4
i2 i5 i6 0
i3 i4 i5 0
4
1 + 2 + 3 + 4 =0
结论 n个节点的电路, 独立的KCL方程为n-1个
i1 R i2 R2 1 + il1 + uS1 il2 uS2 – – b
R11=R1+R2
回路1中所有电阻之和, 称回路1的自电阻。
返节目录
电路分析基础
i1 R i2 R2 1 网孔2中所有电阻之和,称 + il1 + uS1 il2 网孔2的自电阻。 uS2 – R12= R21= –R2 – b 网孔1、网孔2之间的互电阻。
返节目录
电路分析基础
第1节 支路电流法
• 定义
以支路电流为未知量,根据基尔霍夫两定律列出必 要的电路方程,进而求解客观存在的各支路电流的方 法,称支路电流法。
• 适用范围
原则上适用于各种复杂电路,但当支路数很多时, 方程数增加,计算量加大。因此,该方法一般适用于 支路数较少的电路。
返节目录
电路分析基础
电路分析基础
方程的列写 回路1: R1 il1+ R2(il1- il2) -uS1+ uS2=0 回路2: R2(il2- il1) + R3 il2 -uS2=0
整理得:
(R1+ R2) il1-R2il2 = uS1-uS2 - R2il1+ (R2 +R3) il2 = uS2
i3 R3 观察可以看出如下规律:
US2=6V
返节目录
电路分析基础
支路电流法应用举例
④⑤代入①可得:10-I3+[(6-7I3) ÷ 11] - I3=0 解得:I3=4A 代入 ④⑤可得:I1=6A,I2=-2A I2得负值,说明它的实际方向与参考方向相反。 求各元件上吸收的功率,进行功率平衡校验 R1上吸收的功率为:PR1=62×7=252W R2上吸收的功率为:PR2=(-2)2×11=44W R3上吸收的功率为:PR3=42×7=112W US1上吸收的功率为:PS1=-(6×70)=-420W 发出功率 US2上吸收的功率为:PS2=-(-2)×6=12W 吸收功率 元件上吸收的总功率:P=252+44+112+12=420W 电路中吸收的功率等于发出的功率,计算结果正确
• 适用范围
原则上适用于各种复杂电路,包括平面电路或非平 面电路。但对于支路数较多、且网孔数较少的电路尤其 适用。如果选择网孔作为独立回路(即网孔电流法), 则仅适用于平面电路。
返节目录
电路分析基础
i1 R i2 R2 1 + il1 + uS1 uS2 il2 – – b 列写的方程 i3 独立回路数为2个。选 图示的两个网孔为独立回 路,支路电流可表示为:
加、减运算可以得到其他回路的KVL方程。
返节目录
电路分析基础
结论
① KVL的独立方程数 = 独立回路数 = m-(n-1) ② n个节点、m条支路的电路,独立的KCL和KVL 方程数为:
(n 1) m (n 1) m
返节目录
电路分析基础
例
R2 i2 1 R1 i3
2 R4 i4 R3 2
① n–1=1个KCL方程: 节点a: I1–I2–I3=0
联立上述四个方程,可解得
u1=2I2+2
I1=0.43A, I2= –0.71A, I3=1.14A, u1=0.57V
返节目录
电路分析基础
求受控源两端得电压u2时,应回到原电路 进行求解。 a I3 + I1 1 2 I2 7 + + + u1 u2 1V 2V 2u1 – – – – b 此时:
节点a: –I1+I3=6 避开电流源支路取回路: 7I1+7I3=70
返节目录
I3 7
电路分析基础
例3 列写支路电流方程(电路中含有受控源)
a
7 + 70V – I1 I2 11 + I3 1 + U 7 2 _ 5U _ 解 节点a:–I1–I2+I3=0
7I1–11I2=70-5U 11I2+7I3= 5U
-
解 图示电路n=2,m=3
I1+I2-I3=0 ①
I3
R3=7Ω Ⅱ
I2
R2=11Ω
+
选取节点①列写KCL方程式
选取两个网孔列写KVL方程 对网孔Ⅰ:7I1+7I3=70 ② - ② 对网孔Ⅱ:11I2+7I3=6 ③ 由方程式②可得:I1=10-I3 ④ 由方程式③可得:I2=(6-7I3) ÷ 11 ⑤
解 I3
7
① n–1=1个KCL方程: 节点a: –I1–I2+I3=0
