高一物理典型例题
高一物理典型例题汇总

高一物理必修1知识集锦及典型例题各部分知识网络 (一)运动的描述:-(D 表示物体位置的变动,可用从起点到终点的有向线段表示,是矢量 1(2》位移的大小小于或等于路程Q )物理意义:表示物休位置变化的快慢[平均速度严巻方向与位移方向相同瞬时速度*当加-0时山二号^方向为那一刻的运动方向 「①速厦是矢童,而逋率是标量 平均速率=遐遅时何艸砲卒时间③瞬时速度的大小等于瞬时速率 [■物理意义:表示物体速度变化的快慢I 加速度峠定小=汪汽速度的变化率人单位m/乳是矢量'〔方向:与速度变化的方向相同■与速度的方向关系不确定[意义:表示位移随时何的变化规律 应用:①判断运动性质〔匀速、变速、静止)俨一E 图象丿 ②判斯运动方向(正方向、负方向) 1 ③比较运动快慢 I ④确定也移或时间等 图象](意义:表示速度随时间的变化规律应用:①确定某时刻的速度②求位移(面积)I 图象]③判斷运匪性质(静止、匀速、匀变速、非匀变速) ④ 判断运动方向(正方向、负方向〉 ⑤ 出较加速度大小等X[根据纸带上点谨的疏密判断运动情况'实验:用打点计时器测速度{求两点间的平均速度卫=善.粗略求瞬时速度’当心取很小的值时,瞬时速度釣等于平均速度x=aT 2 , o (a 6 a 5 a 』(a 3 a ? aJa2(3T)(推述运动的物理量v 速度⑶与速率的区别与联系2②平均速度二运动的描述测匀变速直线运动的加速度:△「物理意义:表不物体速度蛮化的快馒 定义2=耳^(速度的变化率人单位m/d 矢量.其方向与速度变化的方向相同,与速度方向的关系不确定 、速度、速度变化量与加速度的区别'意义;表示位移随时间的变化规律应用:①判斯运动性质(匀速、变速、静止)卩一£图象」②判断运动方向(正方向、负方向)③比较运动快慢 、④确定位務或时间靈臾匸表示速度随时间的变化规律 应用:①确定某时刻的速度 ② 求位移(面积)③ 判断运动性质(静止、匀速、匀变速、非匀变速) ④ 判断运动方向(正方向、负方向) •⑤比较加速度大小等,加速度恒定•速度均匀变化] Vt = v^+at 工=Sf+*亦< —说=2a 工一 询+讪 吟一y-二叫 a 与v 同向,加速运动;a 与v 反向,减速运动。
高一物理经典例题 (115)

高一物理经典例题
40.可爱的企鹅喜欢在冰面上玩游戏。
如图所示,有一只企鹅在倾角为θ=37°的倾斜冰面上先以a=1.0m/s2的加速度从冰面底部由静止开始沿直线向上“奔跑”,t=4s时突然卧倒以肚皮贴着冰面向上滑行,最后退滑到出发点,完成一次游戏(企鹅在滑动过程中姿势保持不变)。
若企鹅肚皮与冰面间的动摩擦因数为μ=0.25,已知sin37°=0.6,不计空气阻力,g=10m/s2,求:
(1)企鹅向上“奔跑”的位移大小;
(2)企鹅在冰面向上滑行的加速度大小;
(3)企鹅退滑到出发点时的速度大小。
解:(1)企鹅向上“奔跑”的位移大小:
x1=1
2at
2=1
2
×1×42m=8m
(2)企鹅在冰面向上滑行过程,由牛顿第二定律得:mgsinθ+μmgcosθ=ma
代入数据解得:a=8m/s2
(3)企鹅开始上滑时的速度:
v=at=1×4m/s=4m/s
企鹅向上滑行的距离:
x2=v2
2a
=4
2
2×8m=1m
企鹅向上运动的总位移大小:
x=x1+x2=8m+1m=9m
企鹅向下滑行过程,由牛顿第二定律得:
mgsinθ﹣μmgcosθ=ma′
代入数据解得:a′=4m/s2
由v2−v02=2ax可知,企鹅下滑回到出发点时的速度大小
v′=√2a′x=√2×4×9m/s=6√2m/s
答:(1)企鹅向上“奔跑”的位移大小是8m;(2)企鹅在冰面向上滑行的加速度大小是8m/s2;(3)企鹅退滑到出发点时的速度大小是6√2m/s。
高一物理经典例题 (454)

高一物理经典例题42.质量为m 的汽车在平直公路上行驶,阻力f 保持不变,当速度达到v 0时,发动机的实际功率正好等于额定功率P 0,此后,汽车在额定功率下继续加速行驶,公路足够长。
(1)求汽车能达到的最大速度v m 。
(2)在图中,定性画出汽车的速度由v 0加速到v m 的过程中,速度v 随时间t 变化关系的图线。
(3)若汽车的速度从v 0增大到v 1,所用时间为t ,求这段时间内汽车的位移x 。
解:(1)当牵引力等于阻力时,速度达到最大,则P =fv m ,解得v m =P 0f(2)由功率公式:P =Fv 可知,汽车的牵引力:F =P 0v , 由牛顿第二定律得:F ﹣f =ma解得:a =P 0mv −f m , 汽车做加速运动,速度v 不断增大,汽车达到额定功率P 0后,其加速度a 逐渐减小, 汽车做加速度逐渐减小的加速运动,v ﹣t 图象如图所示:(3)对汽车,由动能定理得:P 0t ﹣fx =12mv m 2−12mv 02解得:x =2P 0tf 2+mv 02f 2−mP 022f 3答:(1)求汽车能达到的最大速度v m 为P 0f ;(2)在图中,定性画出汽车的速度由v 0加速到v m 的过程中,速度v 随时间t 变化关系的图线如图所示;(3)若汽车的速度从v0增大到v1,所用时间为t,这段时间内汽车的位移x为2P0tf2+mv02f2−mP022f3。
43.一个质量m=2kg的物体从H高处自由落下,经过5s落到地面,取g10m/s2,空气阻力不计,求(1)物体下落高度H;(2)物体落地前1s内的位移△x;(3)物体落地前瞬间重力的功率P。
解:(1)物体做自由落体运动,物体下落高度H=12gt2=12×10×52m=125m(2)物体前4s下落的高度为:H′=12gt′2=12×10×42m=80m物体落地前1s内的位移△x=H﹣H′=125﹣80m=45m(3)物体落地速度为:v=gt=10×5m/s=50m/s物体落地前瞬间重力的功率为:P=mgv=2×10×50W=1000W 答:1)物体下落高度H为125m;(2)物体落地前1s内的位移△x为45m;(3)物体落地前瞬间重力的功率P为1000W。
高一物理弹力典型例题

高一物理弹力典型例题1. 弹力的基本概念弹力,听起来就像是弹簧的舞蹈,是不是?简单来说,弹力是物体因为形变而产生的力。
比如说,你捏一个橡皮泥,它会变形,但当你放开时,它又会恢复原样。
这种“恢复”的力,就是弹力!真是神奇,对吧?想象一下,如果没有弹力,生活会多无趣,连玩具都没办法弹回来,大家岂不是都要愁眉苦脸?1.1 弹力的类型我们常见的弹力主要分为两种:伸长和压缩。
伸长的弹力就像是你拉弹簧的时候,那种“快放手吧,我要回到原来的样子”的感觉。
而压缩的弹力,就像你坐在沙发上,沙发对你的反抗力。
哈哈,感觉好像在和沙发打仗呢!1.2 勒让与胡扯弹力的计算就得提到胡克定律,这个名字一听就很高大上,其实就是告诉我们:弹力和形变成正比。
想象一下,弹簧越拉越长,它的弹力就越大。
这就好比你去健身房,越练越强壮,弹簧也是一样。
记住哦,弹簧的“力量”不容小觑!2. 弹力的应用说到应用,弹力可是无处不在哦!想象一下,你在游乐园玩过山车,那个令人肾上腺素飙升的瞬间,其实就是利用了弹力。
过山车在高空自由落体,突然一抬头,哇,那种“弹起来”的感觉,真是刺激!2.1 日常生活中的弹力在我们的日常生活中,弹力的身影随处可见。
你见过篮球吗?那球一弹,直接就能飞得老高,完全就是在和地球较劲呢!还有那些小孩子玩的蹦床,蹦蹦跳跳,简直乐开了花。
你看,弹力让生活充满乐趣,怎么能不爱呢?2.2 自然界的弹力再说说自然界,弹力同样扮演着重要的角色。
想象一下,树木的枝条在风中摇摆,那是因为有弹力在支撑着它们。
当狂风来袭,树木虽然会弯曲,但弹力会让它们挺直腰杆。
大自然的力量,真是让人叹为观止!3. 弹力的趣味实验说到实验,物理可真是个玩得不亦乐乎的领域。
我们可以做一个简单的实验:拿一根弹簧和一个重物,把重物挂在弹簧上,看看弹簧的长度变化。
哇哦,弹力的奥秘就这样展现在眼前!就像是一场魔术表演,你的眼睛绝对不会眨一下。
3.1 动手动脚你也可以试试用不同的重量,看看弹簧拉伸得有多远,或者用橡皮筋来比较一下。
(完整版)高一物理力学典型例题
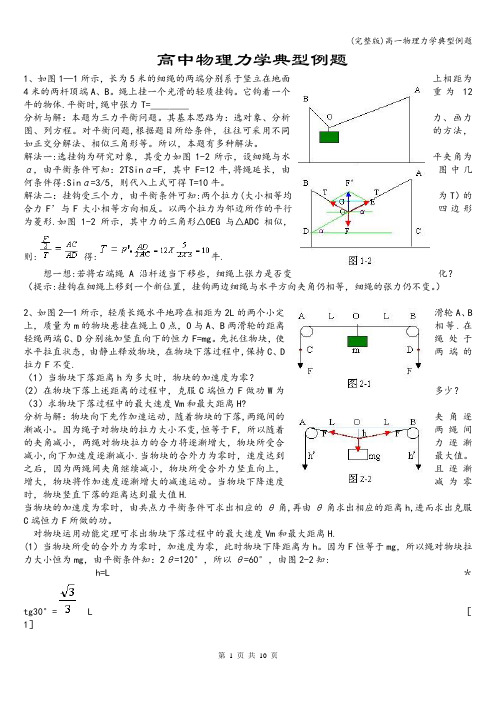
高中物理力学典型例题1、如图1—1所示,长为5米的细绳的两端分别系于竖立在地面上相距为4米的两杆顶端A、B。
绳上挂一个光滑的轻质挂钩。
它钩着一个重为12牛的物体.平衡时,绳中张力T=____分析与解:本题为三力平衡问题。
其基本思路为:选对象、分析力、画力图、列方程。
对平衡问题,根据题目所给条件,往往可采用不同的方法,如正交分解法、相似三角形等。
所以,本题有多种解法。
解法一:选挂钩为研究对象,其受力如图1-2所示,设细绳与水平夹角为α,由平衡条件可知:2TSinα=F,其中F=12牛,将绳延长,由图中几何条件得:Sinα=3/5,则代入上式可得T=10牛。
解法二:挂钩受三个力,由平衡条件可知:两个拉力(大小相等均为T)的合力F’与F大小相等方向相反。
以两个拉力为邻边所作的平行四边形为菱形.如图1-2所示,其中力的三角形△OEG与△ADC相似,则:得:牛.想一想:若将右端绳A 沿杆适当下移些,细绳上张力是否变化?(提示:挂钩在细绳上移到一个新位置,挂钩两边细绳与水平方向夹角仍相等,细绳的张力仍不变。
)2、如图2—1所示,轻质长绳水平地跨在相距为2L的两个小定滑轮A、B 上,质量为m的物块悬挂在绳上O点,O与A、B两滑轮的距离相等.在轻绳两端C、D分别施加竖直向下的恒力F=mg。
先托住物块,使绳处于水平拉直状态,由静止释放物块,在物块下落过程中,保持C、D两端的拉力F不变.(1)当物块下落距离h为多大时,物块的加速度为零?(2)在物块下落上述距离的过程中,克服C端恒力F做功W为多少?(3)求物块下落过程中的最大速度Vm和最大距离H?分析与解:物块向下先作加速运动,随着物块的下落,两绳间的夹角逐渐减小。
因为绳子对物块的拉力大小不变,恒等于F,所以随着两绳间的夹角减小,两绳对物块拉力的合力将逐渐增大,物块所受合力逐渐减小,向下加速度逐渐减小.当物块的合外力为零时,速度达到最大值。
之后,因为两绳间夹角继续减小,物块所受合外力竖直向上,且逐渐增大,物块将作加速度逐渐增大的减速运动。
高一物理运动学经典例题

练习一 运动学经典例题一、匀加速推论1. 一质点做匀加速直线运动,第三秒内的位移2m ,第四秒内的位移是2.5m ,那么以下说法中不正确的是( )A .这两秒内平均速度是2.25m/sB .第三秒末即时速度是2.25m/sC .质点的加速度是0.125m/s2D .质点的加速度是0.5m/s22. ( 多选 ) 一物体以初速度 v 0 做匀减速直线运动,第 1 s 内通过的位移为 x 1 = 3 m ,第 2 s 内通过的位移为 x 2 = 2 m ,又经过位移 x 3 物体的速度减小为 0 ,则下列说法正确的是 ( )A .初速度 v 0 的大小为 2.5 m /sB .加速度 a 的大小为 1 m /s 2C .位移 x 3 的大小为 1.125 mD .位移 x 3 内的平均速度大小为 0.75 m /s二、初速为零的比例式3.一个物体沿着斜面从静止滑下做匀变速直线运动.已知它前2 s 内的位移为3 m ,则它在第四个2 s 内的位移是( )A .14 mB .21 mC .24 mD .48 m4. (多选)物体由静止做匀加速直线运动,第3 s 内通过的位移是3 m ,则( )A .第3 s 内平均速度是1 m/sB .物体的加速度是1.2 m/s2C .前3 s 内的位移是6 mD .3 s 末的速度是3.6 m/s5. 做匀减速直线运动的物体经4 s 后停止,若在第1 s 内的位移是14 m ,则最后1 s 内的位移是( )A .3.5 mB .2 mC .1 mD .06. 一个物体从静止开始做匀加速直线运动,以 T 为时间间隔,在第三个 T 时间内位移是 3 m ,第三个 T 时间末的瞬时速度为 3 m /s ,则 ( )A .物体的加速度是 1 m /s 2B .第一个 T 时间末的瞬时速度为 0.6 m /sC .时间间隔 T = 1 sD .物体在第 1 个 T 时间内的位移为 0.6 m三、平均速度与中间时刻瞬时速度互换7. 一物体做匀加速直线运动,通过一段位移Δx 所用的时间为t1,紧接着通过下一段位移Δx 所用时间为t2.则物体运动的加速度为( ) A.2Δx t1-t2t1t2t1+t2 B.Δx t1-t2t1t2t1+t2 C.2Δx t1+t2t1t2t1-t2 D.Δx t1+t2t1t2t1-t2四、刹车模型8. 某战车在伊位克境内以大小为40 m /s 的速度做匀速直线运动,刹车后获得的加速度大小为10 m/ s 2 ,则刹车后 2 s 内与刹车后5 s 内战车通过的路程之比为( ) A.1∶1 B.3∶1C.4∶3 D.3∶4五、公式对比9. 一辆汽车在平直公路上做刹车实验,若从0 时刻起汽车在运动过程中的位移与速度的关系式为x =(10 -0.1 v 2 )m ,则下列分析正确的是( )A.上述过程的加速度大小为10 m /s 2 B.刹车过程持续的时间为5 s C.0 时刻的初速度为10 m /s D.刹车过程的位移为5 m六、v-t图像解题10. ( 多选) 在一次救灾活动中,一辆救灾汽车由静止开始做匀加速直线运动,刚运动了8 s ,由于前方突然有巨石滚下,堵在路中央,所以又紧急刹车,匀减速运动经4 s 停在巨石前.则关于汽车的运动情况,下列说法正确的是( )A.加速、减速中的加速度大小之比为a 1∶a 2 等于2∶1B.加速、减速中的平均速度大小之比等于1∶1C.加速、减速中的位移大小之比x 1∶x 2 等于2∶1D.加速、减速中的加速度大小之比a 1∶a 2 不等于1∶211.如图所示为A、B两质点在同一直线上运动的位移—时间(x-t)图象,A质点的图像为直线,B质点的图象为过原点的抛物线,两图象交点C、D坐标如图。
高一物理平抛运动的九个典型例题hmh
一、对着斜面的平抛
例题1、如图所示,倾角为37°的斜面长乙L=1.9m,在斜面底 端正上方的O点将一小球以速度v0=3m/s的速度水平抛出,与此 同时静止释放在顶端的滑块,经过一段时间后将小球恰好能够 以垂直斜面的方向击中滑块.(小球和滑块均视为质点,重力加 速度g=10m/s2,sin37°=0.6,cos37°=0.8),求: (1)抛出点O离斜面底端的高度; (2)滑块与斜面间的动摩擦因素μ.
三、对着竖直墙壁的平抛运动 例题3、如图所示,某同学为了找出平抛运动物体的初速度之间 的关系,用一个小球在O点对准前方的一块竖直放置的挡板,O 与A在同一高度,小球的水平初速度分别是v1、v2、v3,打在挡 板上的位置分别是B、C、D,且AB∶BC∶CD=1∶3∶5.则v1、 v2、v3之间的正确关系是 D ( )
A.v1∶v2∶v3=3∶2∶1 C.v1∶v2∶v3=9∶4∶1
B.v1∶v2∶v3=5∶3∶1 D.v1∶v2∶v3=6∶3∶2
四、半圆内的平抛运动 例题4、如图所示,AB为半圆环ACB的水平直径,C为环上的最低点, 环半径为R。一个小球从A点以速度v0水平抛出,不计空气阻力.则 下列判断正确的是 ( D ). A.要使小球掉到环上时的竖直分速度最大,小球应该落在BC之间 B.即使V0取值不同,小球掉到环上时的速度方向和水平方向之间 的夹角也相同 C.若V0取值适当,可以使小球垂直撞击半圆环 D.无论V0取何值,小球都不可能垂直撞击半圆环
(1)1.7m
(2)0.125
二、顺着斜面的平抛运动
例题2、如图所示,从倾角为θ 的足够长斜面上的A点,先后将同一小球以不同 的初速度水平向右抛出.第一次初速度为V1;球落到斜面上瞬时速度方向与斜 面夹角为α 1;第二次初度为V2;球落到斜面上瞬时速度方向与斜面夹角为α 2, 不计空气阻力,若V1>V2,则α 1______ = α 2(填>、=、<)小球离斜面距离的 最大值H1________H > 2(填>、=、<)
高一物理必修一典型例题
高一物理必修一典型例题高一物理必修一典型例题汇总考点:比较x-t图象和v-t图象1.x-t图象和v-t图象的比较图象 x-t图象 v-t图象物体的运动性质表示从正位移处开始一直做反向匀速直线运动表示先正向做匀减速直线运动,再反向做匀速并越过零位移处加速直线运动表示物体静止不动表示物体做正向匀速直线运动表示物体从零位移处开始做正向匀速直线运动表示物体从静止做正向匀加速直线运动表示物体做正向匀加速直线运动表示物体做加速度增大的正向加速运动2.图象中“交点、线、面积、斜率、截矩”分别表示的意义图象中的符号意义交点” x-t图象中表示两物体相遇;v-t图象中表示两物体该时刻速度相等线” x-t图象上表示位移随时间变化的规律;v-t图象上表示速度随时间变化的规律面积” x-t图象上“面积”无实际意义;v-t图象上“面积”表示位移斜率” 表示速度或加速度截矩” 表示初速度或初位移典型例题:1.(多选) 质点做直线运动的位移-时间图象如图所示,该质点()A。
在第1秒末速度方向发生了改变B。
在第2秒和第3秒的速度方向相反C。
在前2秒内发生的位移为零D。
在第3秒末和第5秒末的位置相同答案] AC2.质点做直线运动的速度-时间图象如图所示,该质点()A。
在第1秒末速度方向发生了改变B。
在第2秒末加速度方向发生了改变C。
在前2秒内发生的位移为零D。
第3秒末和第5秒末的位置相同解析] 在2秒内速度都为正,因此第1秒末的速度方向没有发生改变,A错误;图象的斜率表示加速度,1~3秒内图象的斜率一定,加速度不变,因此第2秒末加速度方向没有发生变化,B错误;前2秒内的位移为图线与时间轴所围的面积,即位移x=1/2×2×2 m=2 m,C错误;第3秒末到第5秒末的位移为x=-1/2×2×1+1/2×2×1=0,因此这两个时刻质点处于同一位置,D正确。
3.(多选) 下图所示为甲、乙两个物体做直线运动的运动图象,则下列叙述正确的是()A。
高一物理功和功率典型例题(老师用)
功综合习题:【例1】如图所示,线拴小球在光滑水平面上做匀速圆周运动,圆的半径是1m,球的质量是0.1kg,线速度v=1m/s,小球由A点运动到B点恰好是半个圆周。
那么在这段运动中线的拉力做的功是()A.0 B.0.1J C.0.314J D.无法确定解析:小球做匀速圆周运动,线的拉力为小球做圆周运动的向心力,由于它总是与运动方向垂直,所以,这个力不做功。
故A是正确的。
【例2】下面列举的哪几种情况下所做的功是零()A.卫星做匀速圆周运动,地球引力对卫星做的功B.平抛运动中,重力对物体做的功C.举重运动员,扛着杠铃在头上的上方停留10s,运动员对杠铃做的功D.木块在粗糙水平面上滑动,支持力对木块做的功解析:引力作为卫星做圆周运动的向心力,向心力与卫星运动速度方向垂直,所以,这个力不做功。
杠铃在此时间内位移为零。
支持力与位移方向垂直,所以,支持力不做功。
故A、C、D 是正确的。
【例3】用力将重物竖直提起,先是从静止开始匀加速上升,紧接着匀速上升。
如果前后两过程的运动时间相同,不计空气阻力,则()A.加速过程中拉力做的功比匀速过程中拉力做的功大B.匀速过程中拉力做的功比加速过程中拉力做的功大C.两过程中拉力做的功一样大D.上述三种情况都有可能解析:应先分别求出两过程中拉力做的功,再进行比较。
重物在竖直方向上仅受两个力作用,重力mg、拉力F。
匀加速提升重物时,设拉力为F1,物体向上的加速度为a,根据牛顿第二定律得F1-mg=ma拉力F1所做的功211121)(at a g m s F W ⋅+=⋅=2)(21at a g m += ①匀速提升重物时,设拉力为F 2,根据平衡条件得F 2=mg 匀速运动的位移22at t at vt s =⋅== 所以匀速提升重物时拉力的功2222mgat s F W == ②比较①、②式知:当a>g 时,21W W >;当a=g 时,21W W =;当a<g 时,21W W < 故D 选项正确。
高一物理典型例题
高一物理必修1知识集锦及典型例题一. 各部分知识网络 (一)运动的描述:测匀变速直线运动的加速度:△x=aT 2 ,6543212()()(3)a a a a a a a T ++-++=a与v同向,加速运动;a与v反向,减速运动。
(二)力:实验:探究力的平行四边形定则。
研究弹簧弹力与形变量的关系:F=KX.(三)牛顿运动定律:.改变(四)共点力作用下物体的平衡: 静止 平衡状态匀速运动F x 合=0 力的平衡条件:F 合=0 F y 合=0 合成法 正交分解法常用方法 矢量三角形动态分析法相似三角形法 正、余弦定理法物体的平衡二、典型例题例题 1..某同学利用打点计时器探究小车速度随时间变化的关系,所用交流电的频率为50 Hz,下图为某次实验中得到的一条纸带的一部分,0、1、2、3、4、5、6、7为计数点,相邻两计数点间还有3个打点未画出.从纸带上测出x1=3.20 cm,x2=4.74 cm,x3=6.40 cm,x4=8.02 cm,x5=9.64 cm,x6=11.28 cm,x7=12.84 cm.(1)请通过计算,在下表空格内填入合适的数据(计算结果保留三位有效数字);(2)根据表中数据,在所给的坐标系中作出v-t图象(以0计数点作为计时起点);由图象可得,小车运动的加速度大小为________m /s2例2. 关于加速度,下列说法中正确的是A. 速度变化越大,加速度一定越大B. 速度变化所用时间越短,加速度一定越大C. 速度变化越快,加速度一定越大D. 速度为零,加速度一定为零例3. 一滑块由静止开始,从斜面顶端匀加速下滑,第5s末的速度是6m/s。
求:(1)第4s末的速度;(2)头7s内的位移;(3)第3s内的位移。
例4. 公共汽车由停车站从静止出发以0.5m/s2的加速度作匀加速直线运动,同时一辆汽车以36km/h的不变速度从后面越过公共汽车。
求:(1)经过多长时间公共汽车能追上汽车?(2)后车追上前车之前,经多长时间两车相距最远,最远是多少?例5.静止在光滑水平面上的物体,受到一个水平拉力,在力刚开始作用的瞬间,下列说法中正确的是A. 物体立即获得加速度和速度B. 物体立即获得加速度,但速度仍为零C. 物体立即获得速度,但加速度仍为零D. 物体的速度和加速度均为零例6. 质量m =4kg 的物块,在一个平行于斜面向上的拉力F =40N 作用下,从静止开始沿斜面向上运动,如图所示,已知斜面足够长,倾角θ=37°,物块与斜面间的动摩擦因数µ=0.2,力F 作用了5s ,求物块在5s 内的位移及它在5s 末的速度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
. . 高一物理必修1知识集锦及典型例题 一. 各部分知识网络 (一)运动的描述:
测匀变速直线运动的加速度:△x=aT2 ,6543212()()(3)aaaaaaaT .
. a与v同向,加速运动;a与v反向,减速运动。 .
. (二)力:
实验:探究力的平行四边形定则。 研究弹簧弹力与形变量的关系:F=KX. .
. 作用力与 反作用力
牛顿第一定律 牛顿第二定律 牛顿第三定律
牛顿定律 的应用
两类基本问题
(三)牛顿运动定律:
伽利略的“理想斜面实验”和“科学推理”
内容: 一切物体总保持匀速直线运动状态或静止状态,直到有外力迫 使 它改变这种状态为止. 定义:物体具有保持匀速直线运动状态或静止状态的性质 惯性 量度:质量是物体惯性大小的唯一量度 表现形式:惯性大,物体运动状态难以改变,惯性小,运动状态容易 改变 内容:物体的加速度与所受合外力成正比,与物体的质量成反比,加速度的方 向与合外力的方向相同 公式:F合=ma,此式成立的条件是各物理量的单位均用国际单位
内容:两物体之间的作用力与反作用力总是大小相等,方向相反,而且作用在 同一条直线上 同性:力的性质相同 异体:分别作用在两个不同的物体上 同时产生、同时变化、同时消失 由受力情况确定运动情况 由运动情况确定受力情况 超重和失重 力和加速度的瞬时分析 临界问题和极值问题的分析 整体法与隔离法 实验:用控制变量法探究加速度与力、质量的关
牛顿运动定律及其应用 .
. (四)共点力作用下物体的平衡: 静止 平衡状态 匀速运动
Fx合=0 力的平衡条件:F合=0 Fy合=0 合成法 正交分解法 常用方法 矢量三角形动态分析法 相似三角形法 正、余弦定理法
物体的平衡.
. 二、典型例题 例题1..某同学利用打点计时器探究小车速度随时间变化的关系,所用交流电的频率为50 Hz,下图为某次实验中得到的一条纸带的一部分,0、1、2、3、4、5、6、7为计数点,相邻两计数点间还有3个打点未画出.从纸带上测出x1=3.20 cm,x2=4.74 cm,x3=6.40 cm,x4=8.02 cm,x5=9.64 cm,x6=11.28 cm,x7=12.84 cm.
(1)请通过计算,在下表空格内填入合适的数据(计算结果保留三位有效数字); 计数点 1 2 3 4 5 6 各计数点的速度/(m·s-1) 0.50 0.70 0.90 1.10 1.51
(2)根据表中数据,在所给的坐标系中作出v-t图象(以0计数点作为计时起点);由图象可得,小车运动的加速度大小为________m /s2 例2. 关于加速度,下列说法中正确的是 A. 速度变化越大,加速度一定越大 B. 速度变化所用时间越短,加速度一定越大 C. 速度变化越快,加速度一定越大 D. 速度为零,加速度一定为零 例3. 一滑块由静止开始,从斜面顶端匀加速下滑,第5s末的速度是6m/s。求: (1)第4s末的速度;(2)头7s内的位移;(3)第3s内的位移。
例4. 公共汽车由停车站从静止出发以0.5m/s2的加速度作匀加速直线运动,同时一辆汽车以36km/h的不变速度从后面越过公共汽车。求: (1)经过多长时间公共汽车能追上汽车? (2)后车追上前车之前,经多长时间两车相距最远,最远是多少? 例5.静止在光滑水平面上的物体,受到一个水平拉力,在力刚开始作用的瞬间,下列说法中正确的是 A. 物体立即获得加速度和速度 . . B. 物体立即获得加速度,但速度仍为零 C. 物体立即获得速度,但加速度仍为零 D. 物体的速度和加速度均为零 例6. 质量m=4kg的物块,在一个平行于斜面向上的拉力F=40N作用下,从静止开始沿斜面向上运动,如图所示,已知斜面足够长,倾角θ=37°,物块与斜面间的动摩擦因数µ=0.2,力F作用了5s,求物块在5s内的位移及它在5s末的速度。(g=10m/s2,sin37°=0.6,cos37°=0.8) 例7. 在天花板上用竖直悬绳吊一重为G的小球,小球受几个力?这些力的反作用力是哪些力?这些力的平衡力是哪些力? 例8. 如图所示,质量为m的物块放在倾角为的斜面上,斜面体的质量为M,斜面与物块无摩擦,地面光滑,现对斜面施一个水平推力F,要使物块相对斜面静止,力F应多大?
例9. 如图所示,一质量为m的小球在水平细线和与竖直方向成角的弹簧作用下处于静止状态,试分析剪断细线的瞬间,小球加速度的大小和方向。
例10. 一个人站在体重计的测盘上,在人下蹲的过程中,指针示数变化应是 A. 先减小,后还原 B. 先增加,后还原 C. 始终不变 D. 先减小,后增加,再还原 例11、水平传送带以4m/s的速度匀速运动,传送带两端AB间距为20m,将一质量为2Kg的木块无初速地放在A端,木块与传送带的动摩擦因数为0.2,求木块由A端运动到B端所用的时间。(g=10m/s2)
F θ .
. 例12、木块A、木板B的质量分别为10Kg和20Kg, A、B间的动摩擦因数为0.20,地面光滑。设A、B间的滑动摩擦力与最大静摩擦力大小相等。木板B长2m,木块A静止在木板B的最右端,现用80N的水平拉力将木板B从木块A下抽出来需要多长时间? (木块A可视为质点,g=10m/s2)
例13.如图4所示,在水平地面上有一倾角为θ的斜面体B处于静止状态,其斜面上放有与之保持相对静止的物体A.现对斜面体B施加向左的水平推力,使物体A和斜面体B一起向左做加速运动,加速度从零开始逐渐增加,直到A和B开始发生相对运动,关于这个运动过程中A所受斜面的支持力FN以及摩擦力f的大小变化情况,下列说法中正确的是( ) A.FN增大,f持续增大 B.FN不变,f不变 C.FN减小,f先增大后减小 D.FN增大,f先减小后增大 图4 例14.如图8所示,物体B靠在水平天花板上,在竖直向上的力F作用下,A、B保持静止,A与B间的动摩擦因数为μ1,B与天花板间的动摩擦因数为μ2,则关于μ1、μ2的值下列判断可能正确的是( ) A.μ1=0,μ2≠0 B.μ1≠0,μ2=0 C.μ1=0,μ2=0 D.μ1≠0,μ2≠0 例15.如图2-2-23是用来粉刷墙壁的涂料滚的示意图.使用时,用撑竿推着涂料滚沿墙壁上下滚动,把涂料均匀地粉刷到墙壁上.撑竿的重量和墙壁的摩擦均不计,而且撑竿足够长.粉刷工人站在离墙壁某一距离处缓缓上推涂料滚,使撑竿与墙壁间的夹角越来越小.该过程中撑竿对涂料滚的推力为F1,涂料滚对墙壁的压力为F2,下列说法中正确的是( ) A.F1增大 B.F1减小 C.F2增大 D.F2减小 16.下图是某些同学根据实验数据画出的图象,下列说法中正确的是( ) 图2-2-23 . . A.形成图(甲)的原因是平衡摩擦力时长木板倾角过大 B.形成图(乙)的原因是平衡摩擦力时长木板倾角过小 C.形成图(丙)的原因是平衡摩擦力时长木板倾角过大 D.形成图(丁)的原因是平衡摩擦力时长木板倾角过小 17.如图所示是某同学做“探究加速度与力、质量的关系”实验时已接通电源正要释放纸带时的情况,请你指出该同学的四个错误. 例题1 答案: (1)v5=1.31 (2)2.5
例题2解析:由加速度的定义式vat可知,加速度与速度的变化量和速度变化所用的时间两个因素有关。速度变化越大,加速度不一定越大;速度变化所用时间越短,若速度变化量没有确定,也不能确定加速度一定越大。加速度是描述速度变化快慢的物理量,速度变化越快,加速度一定越大;速度为零,并不是速度的变化量为零,故加速度不一定为零。 答案:C
例题3解析:根据初速度为零的匀变速直线运动的比例关系求解。 (1)因为123:::vvv……=1:2:3:…… 所以45:4:5vv 第4s末的速度为
45446/4.8/55vvmsms
(2)由tvx得前5s内的位移为: mmtvx155262 因为123:::xxx……2231:2:3…… 所以2257:5:7xx . . 前7s内的位移为:2752771529.455xxmm (3)由(2)可得2215:1:5xx
1522
1150.655xxmm
因为13:xx……=1:5:…… 所以13:xx=1:5 第3s内的位移31550.63xxmm 例题4解析:(1)追上即同一时刻二者处于同一位置,由于它们出发点相同,所以相遇时位移相同,即 x汽=x公 at2/2=v汽t t=2v公/a=210/0.5=40s (2)在汽车速度大于公共汽车速度过程中,二者距离逐渐增大,速度相等时距离最大,之后公共汽车速度将大于汽车速度,二者距离就会减小,所以速度相等时相距最远。 则 v汽=v公 at= v汽 t= v汽/a=10/0.5=20s 最远距离x= v汽t- at2/2=1020-0.5202/2=100m 例题5 解析 由牛顿第二定律的瞬时性可知,力作用的瞬时即可获得加速度,但无速度。 答案 B 说明 力是加速度产生的原因,加速度是力作用的结果,加速度和力之间,具有因果性、瞬时性、矢量性。 例题6解析:如图,建立直角坐标系,把重力mg沿x轴和y轴的方向分解 Gx=mgsinθ Gy=mgcosθ y轴 FN=mgcosθ Fµ=µFn=µmgcosθ x轴 由牛顿第二定律得 F-Fµ-GX=ma 即 F-µmgcosθ-mgsinθ=ma
a=mmgmgFsincos =46.01048.01042.040
F θ G GY
GX
FN
F
