反比例函数经典例题
中考数学压轴题----《反比例函数综合》例题讲解
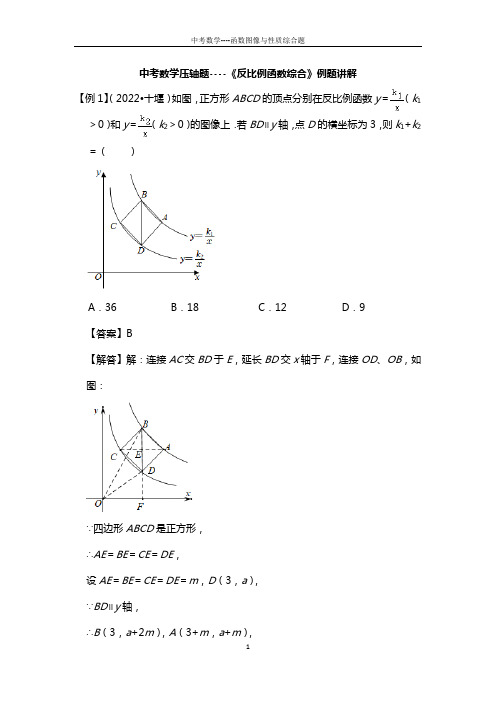
中考数学压轴题----《反比例函数综合》例题讲解【例1】(2022•十堰)如图,正方形ABCD的顶点分别在反比例函数y=(k1>0)和y=(k2>0)的图像上.若BD∥y轴,点D的横坐标为3,则k1+k2=()A.36B.18C.12D.9【答案】B【解答】解:连接AC交BD于E,延长BD交x轴于F,连接OD、OB,如图:∵四边形ABCD是正方形,∴AE=BE=CE=DE,设AE=BE=CE=DE=m,D(3,a),∵BD∥y轴,∴B(3,a+2m),A(3+m,a+m),∵A,B都在反比例函数y=(k1>0)的图像上,∴k1=3(a+2m)=(3+m)(a+m),∵m≠0,∴m=3﹣a,∴B(3,6﹣a),∵B(3,6﹣a)在反比例函数y=(k1>0)的图像上,D(3,a)在y=(k2>0)的图像上,∴k1=3(6﹣a)=18﹣3a,k2=3a,∴k1+k2=18﹣3a+3a=18;故选:B【变式1-1】(2021•鄂州)如图,点A是反比例函数y=(x>0)的图像上一点,过点A作AC⊥x轴于点C,AC交反比例函数y=(x>0)的图像于点B,点P是y轴正半轴上一点.若△PAB的面积为2,则k的值为.【答案】8【解答】解:连接OA、OB,∵AC⊥x轴,∴AC∥y轴,∴S△AOB=S△APB,∵S△APB=2,∴S△AOB=2,由反比例函数系数k的几何意义可得:S△AOC=6,S△BOC=,∴6﹣=2,解得:k=8,故答案为8.【变式2-2】(2021•荆州)如图,过反比例函数y=(k>0,x>0)图像上的四点P1,P2,P3,P4分别作x轴的垂线,垂足分别为A1,A2,A3,A4,再过P1,P2,P3,P4分别作y轴,P1A1,P2A2,P3A3的垂线,构造了四个相邻的矩形.若这四个矩形的面积从左到右依次为S1,S2,S3,S4,OA1=A1A2=A2A3=A3A4,则S1与S4的数量关系为.【答案】S1=4S4【解答】解:∵过双曲线上任意一点、向坐标轴作垂线所围成的矩形面积S是个定值,OA1=A1A2=A2A3=A3A4,∴S1=k,S2=k,S3=k,S4=k,∴S1=4S4.故答案为:S1=4S4.【变式1-3】(2022•毕节市)如图,在平面直角坐标系中,正方形ABCD的顶点A,B分别在x轴、y轴上,对角线交于点E,反比例函数y=(x>0,k >0)的图像经过点C,E.若点A(3,0),则k的值是.【答案】4【解答】解:设C(m,),∵四边形ABCD是正方形,∴点E为AC的中点,∴E(,),∵点E在反比例函数y=上,∴,∴m=1,作CH⊥y轴于H,∴CH=1,∵四边形ABCD是正方形,∴BA=BC,∠ABC=90°,∴∠OBA=∠HCB,∵∠AOB=∠BHC,∴△AOB≌△BHC(AAS),∴BH=OA=3,OB=CH=1,∴C(1,4),∴k=4,故答案为:4.【变式1-4】(2022•雁塔区校级模拟)如图,正方形ACBE的边长是,点B,C分别在x轴和y轴正半轴上,BO=2,ED⊥x轴于点D,ED的中点F在反比例函数y=(x>0)的图像上,则k=.【答案】3【解答】解:∵正方形ACBE的边长是,BO=2,∴BC=BE=,∴OC===1,∵∠ABC=90°,∴∠OBC+∠EBD=90°,∵∠OBC+∠OCB=90°,∴∠OCB=∠EBD,在△OBC和△DEB中,,∴△OBC≌△DEB(AAS),∴BD=OC=1,DE=OB=2,∴OD=3,∴E(3,2),∵点F是ED的中点,∴F(3,1),∵点F在反比例函数y=(x>0)的图像上,∴k=3×1=3,故答案为3.【变式1-5】(2021•广元)如图,点A(﹣2,2)在反比例函数y=的图像上,点M在x轴的正半轴上,点N在y轴的负半轴上,且OM=ON=5.点P (x,y)是线段MN上一动点,过点A和P分别作x轴的垂线,垂足为点D 和E,连接OA、OP.当S△OAD<S△OPE时,x的取值范围是.【答案】1<x<4【解答】解:过点B作BF⊥ON于F,连接OB,过点C作CG⊥OM于点G,连接OC,如图,∵点A(﹣2,2)在反比例函数y=的图像上,∴k=﹣4.∴y=.∵点A(﹣2,2),∴AD=OD=2.∴.设B(a,b),则ab=﹣4,OF=﹣b,BF=a.∴==2.同理:S△OCG=2.从图中可以看出当点P在线段BC上时,S△OPE>S△OBF,即当点P在线段BC上时,满足S△OAD<S△OPE.∵OM=ON=5,∴N(0,﹣5),M(5,0).设直线MN的解析式为y=mx+n,则:,解得:.∴直线MN的解析式为y=x﹣5.∴,解得:,.∴B(1,﹣4),C(4,﹣1).∴x的取值范围为1<x<4.【变式1-6】(2021•荆门)如图,在平面直角坐标系中,Rt△OAB斜边上的高为1,∠AOB=30°,将Rt△OAB绕原点顺时针旋转90°得到Rt△OCD,点A 的对应点C恰好在函数y=(k≠0)的图像上,若在y=的图像上另有一点M使得∠MOC=30°,则点M的坐标为.【答案】(,1)【解答】解:作AE⊥OB于E,MF⊥x轴于F,则AE=1,∵∠AOB=30°,∴OE=AE=,将Rt△OAB绕原点顺时针旋转90°得到Rt△OCD,点A的对应点C为(1,),∵点C在函数y=(k≠0)的图像上,∴k=1×=,∴y=,∵∠COD=∠AOB=30°,∠MOC=30°,∴∠DOM=60°,∴∠MOF=30°,∴OF=MF,设MF=n,则OF=n,∴M(n,n),∵点M在函数y=的图像上,∴n=,∴n=1(负数舍去),∴M(,1),故答案为(,1).【变式1-7】(2021•达州)如图,将一把矩形直尺ABCD和一块等腰直角三角板EFG摆放在平面直角坐标系中,AB在x轴上,点G与点A重合,点F在AD上,EF交BC于点M,反比例函数y=(x<0)的图像恰好经过点F,M,若直尺的宽CD=1,三角板的斜边FG=4,则k=.【答案】﹣12【解答】解:过点M作MN⊥AD,垂足为N,则MN=CD=1,在Rt△FMN中,∠MFN=45°,∴FN=MN=1又∵FG=4,∴NA=MB=FG﹣FN=4﹣1=3,设OA=a,则OB=a+1,∴点F(﹣a,4),M(﹣a﹣1,3),又∵反比例函数y=(x<0)的图像恰好经过点F,M,∴k=﹣4a=3(﹣a﹣1),解得,a=3,∴k=﹣4a=﹣12,故答案为:﹣12.a11。
反比例函数_经典例题

二、经典例题(一)考察概念例1 已知函数 y = (5m — 3)x n -2 + (n+m )(1)当m ,n 为何值时,是一次函数?(2)当m ,n 为何值时,为正比例函数?(3)当m ,n 为何值时,为反比例函数?例2 已知y=y 1+y 2 ,y 1与x +1成正比例,y2与x +1成反比例,当x =0时,y=-5;当x =2时,y=-7。
(1)求y与x 的函数关系式;(2)当y=5时,求x 的值(二)考察函数图象和性质例3 在反比例函数y = x k 3-的图象上,当x >0时,y 随x 的增大而增大,则k 的取值范围为 。
例4 反比例函数y = x6的图象上有三点(x 1,y 1)、(x 2,y 2)、(x 3,y 3),其中x 1<x 2<0<x 3,则y 1,y 2,y 3用“<”连接 。
(三)考察反比例函数y =xk (k 为常数,且0k ≠) 中k 的几何意义例5 点A 是反比例函数图象上的一点,过A 作AB ⊥y 轴于B 点,若△ABO 面积为2,则反比例函数解析式为 。
变形1:点A 是反比例函数图象上的一点,过A作AB⊥y轴于B点,点P在x轴上,△ABP的面积为2,则反比例函数解析式为。
变形2:如图,点D、C为反比例函数上两点,DF⊥x轴于点F,CE⊥y轴于E,则△DEF与△CEF面积的大小关系为。
例6如图,正比例函数y=kx(k>0)与反比例函数1yx=的图象交于A,C两点,过A点作x轴的垂线,交x轴于B,过C点作y轴的垂线交y轴于D,连结AB,BC,CD,AD,则ABCD的面积为。
(四)综合问题例7 如图,在直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数myx=的图象交于A(-2,1)、B(1,n)两点。
(1) 求上述反比例函数和一次函数的表达式;(2) 观察图象,写出一次函数值小于反比例函数值的x的取值范围?(3) 连接AO,BO,求△AOB的面积。
反比例函数经典例题

A. + =0B. · <0C. · >0D. =
4.反比例函数y=的图象过点P(-1.5,2),则k=________.
5.点P(2m-3,1)在反比例函数y=的图象上,则m=__________.
6.已知反比例函数的图象经过点(m,2)和(-2,3)则m的值为__________.
求:(1)一次函数和反比例函数的解析式;(2)两函数图象的另一个交点B的坐标;
(3)△AOB的面积.
7.如图所示,一次函数y=ax+b的图象与反比例函数y=的图象交于A、B两点,与x轴交于点C.已知点A的坐标为(-2,1),点B的坐标为(,m).
(1)求反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值小于反比例函数的值的x的取值范围.
A、不小于 m3B、小于 m3C、不小于 m3D、小于 m3
5.如图,A、C是函数 的图象上的任意两点,过A作 轴的垂线,垂足为B,过C作y轴的垂线,垂足为D,记RtΔAOB的面积为S1,RtΔCOD的面积为S2则()
A.S1>S2B.S1<S2
C.S1=S2D.S1与S2的大小关系不能确定
6.关于x的一次函数y=-2x+m和反比例函数y= 的图象都经过点A(-2,1).
反比例函数经典例题
【例1】如果函数 的图像是双曲线,且在第二,四象限内,那么的值是多少?
【解析】有函数图像为双曲线则此函数为反比例函数 ,( )即 ( )又在第二,四象限内,则 可以求出, , , 。若 则下列各式正确的是()
A. B. C. D.
【解析】可直接以数的角度比较大小,也可用图像法,还可取特殊值法。
反比例函数经典例题

反比例函数经典例题:
反比例函数是一种常见的数学函数,其数学表达式为 y = k/x,其中 k 是常数。
下面是一个经典的反比例函数例题:
问题:如果两个变量 x 和 y 成反比例关系,并且当 x = 4 时,y = 10。
求当x = 5 时,y 的值是多少?
解答:根据反比例函数的定义,我们知道 y = k/x,其中 k 是常数。
将已知条件代入方程,我们得到 10 = k/4。
通过求解这个方程,我们可以计算出 k 的值。
10 = k/4
k = 10 * 4
k = 40
现在我们已经确定了常数 k 的值为 40。
接下来,我们可以使用这个 k 值来计算当 x = 5 时,y 的值。
y = k/x
y = 40/5
y = 8
所以,当 x = 5 时,y 的值为 8。
这是一个经典的反比例函数的例题,通过理解反比例函数的概念和运用相关公式,我们可以解决类似的问题。
反比例函数实际问题例题

1、某工厂生产一种零件,如果每天生产x个零件,那么需要y天完成全部生产任务。
已知当每天生产100个零件时,需要20天完成。
如果生产效率不变,当每天生产200个零件时,需要的天数是?A. 40天B. 20天C. 10天D. 5天(答案)C2、一个水池,如果用x台抽水机同时抽水,需要y小时才能抽干。
现在知道用3台抽水机需要8小时才能抽干。
如果增加抽水机的数量到6台,那么需要的小时数是?A. 16小时B. 8小时C. 4小时D. 2小时(答案)C3、某公司计划招聘x名新员工,如果每名员工的工作效率相同,那么完成一项任务需要y 天。
已知如果招聘10名员工,需要20天完成任务。
如果公司想要在10天内完成任务,那么需要招聘的员工数量是?A. 5名B. 10名C. 20名D. 40名(答案)C4、一个果园,如果每天摘x筐苹果,那么需要y天才能摘完。
现在知道如果每天摘10筐,需要20天才能摘完。
如果果园主想要在10天内摘完所有的苹果,那么每天需要摘的筐数是?A. 5筐B. 10筐C. 20筐D. 40筐(答案)C5、某城市的水费是按照用水量来计算的,如果每月用水x吨,那么需要支付y元的水费。
已知如果每月用水5吨,需要支付100元。
如果某月想要支付50元的水费,那么可以用的水量是?A. 1吨B. 2.5吨C. 5吨D. 10吨(答案)B6、一个工人如果每天工作x小时,那么可以完成y个零件。
现在知道如果每天工作8小时,可以完成16个零件。
如果工人想要在一天内完成32个零件,那么需要工作的小时数是?A. 4小时B. 8小时C. 12小时D. 16小时(答案)D7、某公司投资了一个项目,如果每年投资x万元,那么需要y年才能收回成本。
已知如果每年投资100万元,需要5年才能收回成本。
如果公司想要在3年内收回成本,那么每年需要投资的金额是?A. 50万元B. 100万元C. 150万元D. 约166.67万元(答案)D8、一个学生如果每天学习x小时,那么需要y天才能掌握一项技能。
反比例函数经典例题

反比例函数经典例题【一】考察概念例1 已知函数 y = (5m — 3)xn-2+ (n+m )(1)当m ,n 为何值时,是一次函数?(2)当m ,n 为何值时,为正比例函数? (3)当m ,n 为何值时,为反比例函数?例2 已知y=y 1+y 2 ,y 1与x +1成正比例,y2与x +1成反比例,当x =0时,y=-5;当x =2时,y=-7。
(1)求y与x 的函数关系式; (2)当y=5时,求x 的值 【二】察函数图象和性质 例3 在反比例函数y =xk 3-的图象上,当x >0时,y 随x 的增大而增大,则k 的取值范围为 。
例4 反比例函数y =x6的图象上有三点(x 1,y 1)、(x 2,y 2)、(x 3,y 3),其中x 1<x 2<0<x 3,则y 1,y 2,y 3用“<”连接 。
【三】考察反比例函数y =xk(0k ≠)中k 的几何意义 例5 点A 是反比例函数图象上的一点,过A 作AB ⊥y 轴于B 点,若△ABO 面积为2,则反比例函数解析式为 。
变形1:点A 是反比例函数图象上的一点,过A 作AB ⊥y 轴于B 点,点P 在x 轴上,△ABP 的面积为2,则反比例函数解析式为 。
变形2:如图,点D 、C 为反比例函数上两点,DF ⊥x 轴于点F ,CE ⊥y 轴于E ,则△DEF 与△CEF 面积的大小关系为 。
例6 如图,正比例函数y =kx (k>0)与反比例函数1yx=的图象交于A ,C 两点,过A 点作x 轴的垂线,交x 轴于B ,过C 点作y 轴的垂线交y 轴于D ,连结AB ,BC ,CD ,AD ,则ABCD 的面积为。
【四】综合问题例7 如图,在直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数m yx =的图象交于A(-2,1)、B(1,n)两点。
(1) 求上述反比例函数和一次函数的表达式;(2) 观察图象,写出一次函数值小于反比例函数值的x的取值范围?(3) 连接AO,BO,求△AOB的面积。
反比例函数好题精选20题
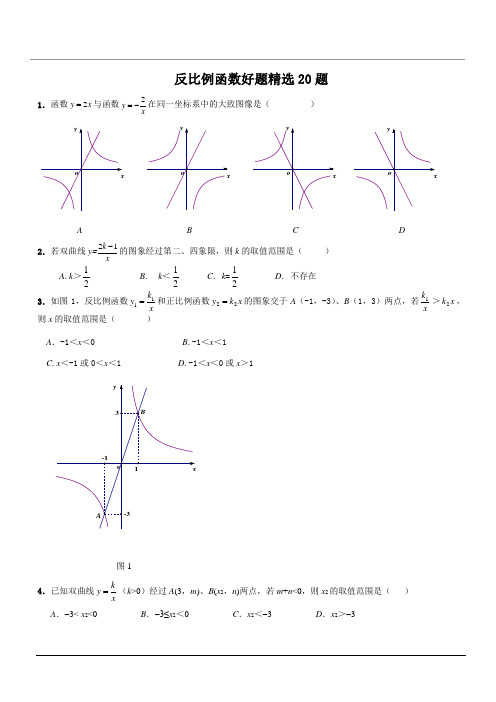
反比例函数好题精选20题1.函数2y x=与函数2yx=-在同一坐标系中的大致图像是()A B C D2.若双曲线y=21kx-的图象经过第二、四象限,则k的取值范围是()A.k>21B. k<21C. k=21D. 不存在3.如图1,反比例函数xky11=和正比例函数xky22=的图象交于A(-1,-3)、B(1,3)两点,若xk1>xk2,则x的取值范围是()A.-1<x<0 B.-1<x<1C.x<-1或0<x<1D.-1<x<0或x>1图14.已知双曲线kyx=(k>0)经过A(3,m)、B(x2,n)两点,若m+n<0,则x2的取值范围是()A.-3< x2<0 B.-3≤x2<0 C.x2<-3 D.x2>-35.函数1(0)y x x =≥ , xy 92=(0)x >的图象如图2所示,则结论: ① 两函数图象的交点A 的坐标为(3 ,3 ) ② 当3x >时,21y y > ③ 当 1x =时, BC = 8 ④当 x 逐渐增大时,1y 随着x 的增大而增大,2y 随着x 的增大而减小.其中正确结论的序号是____________.图图4 6. 如图3,点A 在双曲线1y x =上,点B 在双曲线3y x=上,且AB ∥x 轴,C 、D 在x 轴上,若四边形ABCD 为矩形,则它的面积为 .图5 图6 图77.如图4,点A 在双曲线2(0)y x x =>上,点B 在双曲线4(0)y x x=>上,且AB //y 轴,点P 是y 轴上的任意一点,则△P AB 的面积为 .8. 如图5,已知双曲线)0k (xk y >=经过直角三角形OAB 斜边OB 的中点D ,与直角边AB 相交于点C .若△OBC 的面积为3,则k =____________.9. 如图6,A 、M 是反比例函数图像上的两点,过点M 作直线MB ∥x 轴,交y 轴于点B ;过点A 作直线AC y ∥轴交x 轴于点C ,交直线MB 于点D .BM :DM =8:9,当四边形OADM 的面积为427时,k = . 10.如图7,已知双曲线(0)ky x x=>经过矩形OABC 的边AB ,BC 的中点F ,E ,且四边形OEBF 的面积为2,则k = .y=1x11.两个反比例函数k y x =和1y x=在第一象限内的图象如图8所示,点P 在ky x =的图象上,PC ⊥x 轴于点C ,交1y x =的图象于点A ,PD ⊥y 轴于点D ,交1y x=的图象于点B ,当点P 在ky x =的图象上运动时,以下结论: ①△ODB 与△OCA 的面积相等; ②四边形P AOB 的面积不会发生变化; ③P A 与PB 始终相等;④当点A 是PC 的中点时,点B 一定是PD 的中点.其中一定正确的是 .图812. 如图9,将—矩形OABC 放在直角坐际系中,O 为坐标原点.点A 在x 轴正半轴上.点E 是边AB 上的—个动点(不与点A 、N 重合),过点E 的反比例函数(0)ky x x=>的图象与边BC 交于点F 。
专题13 反比例函数的图象和性质压轴题八种模型全攻略(解析版)

专题13反比例函数的图象和性质压轴题八种模型全攻略【考点导航】目录【典型例题】 (1)【考点一根据反比例函数的定义求参数】 (1)【考点二已知反比例函数的定义求函数的解析式】 (3)【考点三判断(画)反比例函数图象】 (5)【考点四由反比例函数图象的对称性求点的坐标】 (7)【考点五已知反比例函数分布的象限求参数范围】 (9)【考点六已知反比例函数的增减性求参数】 (10)【考点七比较反比例函数值或自变量的大小】 (11)【考点八已知反比例函数的解析式求图象和性质】 (13)【过关检测】 (15)【典型例题】【考点一根据反比例函数的定义求参数】∴10m +≠,251m -=-,∴2m =±,故答案为:2±【点睛】本题主要考查反比例函数的定义,熟练掌握反比例函数的定义是解题的关键.【考点二已知反比例函数的定义求函数的解析式】【考点三判断(画)反比例函数图象】.B.C.D.....【答案】C【分析】根据反比例函数的图象和性质进行判断即可..B.C.D.【答案】C【分析】根据反比例函数的性质,0k>时,图象在一、三象限,进行判断即可.【详解】解:∵反比例函数6yx=,60k=>,∴图象分布在第一、三象限,即:故选C.【点睛】本题考查反比例函数的图象.熟练掌握反比例函数的性质,是解题的关键.3.(2023·宁夏银川的大致图像可能是(A.B.C.D.【详解】A .由图象可知:0,0a b >>,故A 错误;B .由图象可知:0,0a b <>,故B 正确;C .由图象可知:0,0a b ><,但正比例函数图象未过原点,故C 错误;D .由图象可知:0,0a b <<,故D 错误;故选:B .【点睛】本题考查了根据已知参数的取值范围确定函数的大致图象的问题,熟知参数对于函数图象的影响是解题的关键.【考点四由反比例函数图象的对称性求点的坐标】A .(2,3)--B .【答案】B【分析】反比例函数的图象是中心对称图形,则经过原点的直线的两个交点一定关于原点对称.【详解】解: 点A 与B A ∴点的坐标为(2,3).故选:B .【点睛】本题主要考查了反比例函数图象的中心对称性,解题的关键是熟练掌握横纵坐标分别互为相反数.【变式训练】1.(2023春·江苏·八年级专题练习)已知正比例函数的一个交点坐标为()1,m ,则另一个交点的坐标为【考点五已知反比例函数分布的象限求参数范围】【考点六已知反比例函数的增减性求参数】【考点七比较反比例函数值或自变量的大小】【考点八已知反比例函数的解析式求图象和性质】【变式训练】【过关检测】一、单选题....【答案】A【分析】本题主要考查了一次函数与反比例函数图像的性质,根据题意分以下两种情况讨论,a<0时,利用一次函数与反比例函数图象的性质进行分析判断即可解题.【详解】解:当0a >时,y =过一、三象限,且y ax a =-过一、三、四象限,故二、填空题三、解答题x<-时,对于x∵当1n≥.∴216.(2024上·福建·九年级统考期末)已知点(3)若点(,)A a b 与点(1,)B a c +是该函数图象上的两点,试比较【答案】(1)6y x=(2)2,画图见解析(3)b c>【分析】本题主要考查反比例函数的解析式,图象的画法以及性质,解决本题的关键是熟练掌握这些知识(3)由图象可知,在第一象限内y随着x的增大而减小, ,+>a a1b c∴>.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
反比例函数经典例题
反比例函数
一、基础知识
1. 定义:一般地,形如xky(k为常数,ok)的函数称为反比例函数.xky还可以写成kxy1
2. 反比例函数解析式的特征:
⑴等号左边是函数y,等号右边是一个分式.分子是不为零的常数k(也叫做比例系数k),分
母中含有自变量x,且指数为1。
⑵比例系数
0k
⑶自变量x的取值为一切非零实数。
⑷函数y的取值是一切非零实数。
3. 反比例函数的图像
⑴图像的画法:描点法
① 列表(应以O为中心,沿O的两边分别取三对或以上互为相反的数)
② 描点(有小到大的顺序)
③ 连线(从左到右光滑的曲线)
⑵反比例函数的图像是双曲线,xky(k为常数,0k)中自变量0x,函数值0y,所以双
曲线是不经过原点,断开的两个分支,延伸部分逐渐靠近坐标轴,但是永远不与坐标轴相
交。
⑶反比例函数的图像是是轴对称图形(对称轴是xy或xy)。
⑷反比例函数xky(0k)中比例系数k的几何意义是:过双曲线xky (0k)上任意引x轴
y
轴的垂线,所得矩形面积为k。
4.反比例函数性质如下表:
k
的取值 图像所在象限 函数的增减性
ok
一、三象限
在每个象限内,y值随x的增大而减小
ok
二、四象限
在每个象限内,y值随x的增大而增大
反比例函数经典例题
5. 反比例函数解析式的确定:利用待定系数法(只需一对对应值或图像上一个点的坐标即可求
出k)
6.“反比例关系"与“反比例函数":成反比例的关系式不一定是反比例函数,但是反比例函数
x
k
y
中的两个变量必成反比例关系.
7. 反比例函数的应用
二、例题
【例1】如果函数222kkkxy的图像是双曲线,且在第二,四象限内,那么的值是多少?
【解析】有函数图像为双曲线则此函数为反比例函数xky,(0k)即kxy1(0k)又在第
二,四象限内,则0k可以求出的值
【答案】由反比例函数的定义,得:
01222k
kk
解得
0211k
kk或
1k
1k
时函数222kkkxy为
x
y1
【例2】在反比例函数xy1的图像上有三点1x,1y,2x,2y,3x,3y 。若
321
0xxx
则下列各式正确的是( )
A.213yyy B.123yyy C.321yyy D.231yyy
【解析】可直接以数的角度比较大小,也可用图像法,还可取特殊值法.
解法一:由题意得111xy,221xy,
3
3
1
x
y
3210xxx,213
yyy
所以选A
解法二:用图像法,在直角坐标系中作出xy1的图像
描出三个点,满足3210xxx观察图像直接得到213yyy选A
解法三:用特殊值法
213321321321
,1,1,211,1,2,0yyyyyyxxxxxx令
反比例函数经典例题
【例3】如果一次函数的图像与反比例函数xmnymnmxy30相交于点(221,),那么该直
线与双曲线的另一个交点为( )
【解析】
12132212213nmmn
nm
xxmnynmxy解得,,相交于与双曲线直线
221111121,122211y
x
y
x
x
y
xy
x
yxy得解方程组双曲线为直线为
11,另一个点为
【例4】 如图,在AOBRt中,点A是直线mxy与双曲线xmy在第一象限的交点,且2AOBS,
则m的值是_____.
图
解:因为直线mxy与双曲线xmy过点A,设A点的坐标为AAyx,.
则有AAAAxmymxy,.所以AAyxm。
又点A在第一象限,所以AAAAyyABxxOB,.
所以myxABOBSAAAOB212121•.而已知2AOBS。
所以4m.
三、练习题
1。反比例函数xy2的图像位于( )
A.第一、二象限 B.第一、三象限 C.第二、三象限 D.第二、四象限
反比例函数经典例题
o y x y x o y x o y x o
A B C D
2.若y与x成反比例,x与z成正比例,则y是z的( )
A、正比例函数 B、反比例函数 C、一次函数 D、不能确定
3.如果矩形的面积为6cm2,那么它的长ycm与宽xcm之间的函数图象大致为( )
4.某气球内充满了一定质量的气体,当温度不变时,
气球内气体的气压P ( kPa ) 是气体体积V ( m3 )
的反比例函数,其图象如图所示.当气球内气压大于120 kPa时,气
球将爆炸.为了安全起见,气球的体积应( )
A、不小于54m3 B、小于54m3 C、不小于45m3 D、小于45m
3
作x轴的垂线,垂足5.如图 ,A、C是函数xy1的图象上的任意两点,过A
为B,过C作y轴的垂线,垂足为D,记RtΔAOB的面积为S1,RtΔCOD的面
积为S2则 ( )
A. S1 >S2 B. S1 〈S2
C. S1=S2 D. S1与S2的大小关系不能确定
6.关于x的一次函数y=—2x+m和反比例函数y=1nx的图象都经过点A(-2,1)。
求:(1)一次函数和反比例函数的解析式;(2)两函数图象的另一个交点B的坐标;
(3)△AOB的面积.
7。 如图所示,一次函数y=ax+b的图象与反比例函数y=错误!的图象交于A、B两点,与
x
轴交于点C.已知点A的坐标为(-2,1),点B的坐标为(错误!,m).
(1)求反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值小于反比例函数的值的x的取值范围.
O
y
x
A
B
C
D
反比例函数经典例题
O
C
A
B
8. 某蓄水池的排水管每小时排水8m3,6小时可将满池水全部排空.
(1)蓄水池的容积是多少?
(2)如果增加排水管,使每小时的排水量达到Q(m3),那么将满池水排空所需的时间t(h)
将如何变化?
(3)写出t与Q的关系式.
(4)如果准备在5小时内将满池水排空,那么每小时的排水量至少为多少?
(5)已知排水管的最大排水量为每小时12m3,那么最少需多长时间可将满池水全部排空?
.9.某商场出售一批名牌衬衣,衬衣进价为60元,在营销中发现,该衬衣的日销售量y(件)是日
销售价x元的反比例函数,且当售价定为100元/件时,每日可售出30件.
(1)请写出y关于x的函数关系式;
(2)该商场计划经营此种衬衣的日销售利润为1800元,则其售价应为多少元?
10.如图,在直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数myx的图象交于A
(-2,1)、B(1,n)两点.
(1)求上述反比例函数和一次函数的表达式;
(2)求△AOB的面积。
反比例函数经典例题
四、课后作业
1.对与反比例函数xy2,下列说法不正确的是( )
A.点(1,2)在它的图像上
B.它的图像在第一、三象限
C.当0x时,
的增大而增大随xy
D.当0x时,
的增大而减小随xy
2.已知反比例函数0kykx的图象经过点(1,-2),则这个函数的图象一定经过( )
A、(2,1) B、(2,—1) C、(2,4) D、(-1,—2)
3.在同一直角坐标平面内,如果直线xky1与双曲线xky2没有交点,那么1k和2k的关系一定
是( )
A。 1k+2k=0 B. 1k·2k<0 C。 1k·2k〉0 D。1k=
2
k
4. 反比例函数y=kx的图象过点P(-1.5,2),则k=________.
5. 点P(2m-3,1)在反比例函数y=错误!的图象上,则m=__________.
6。 已知反比例函数的图象经过点(m,2)和(-2,3)则m的值为__________.
7. 已知反比例函数xmy21的图象上两点2211,,,yxByxA,当210xx时,有21yy,则m的
取值范围是?
8.已知y与x-1成反比例,并且x=—2时y=7,求:
(1)求y和x之间的函数关系式; (2)当x=8时,求y的值;
(3)y=-2时,x的值。
9. 已知3b,且反比例函数xby1的图象在每个象限内,y随x的增大而增大,如果点3,a在
