2022年河南省新乡市长垣县中考数学一模试题及答案解析
2024年河南省中考数学试卷正式版含答案解析

绝密★启用前2024年河南省中考数学试卷学校:___________姓名:___________班级:___________考号:___________注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上,写在试卷上无效。
3.考试结束后,本试卷和答题卡一并交回。
第I卷(选择题)一、选择题:本题共10小题,每小题3分,共30分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.如图,数轴上点P表示的数是( )A. −1B. 0C. 1D. 22.据统计,2023年我国人工智能核心产业规模达5784亿元.数据“5784亿”用科学记数法表示为( )A. 5784×108B. 5.784×1010C. 5.784×1011D. 0.5784×10123.如图,乙地在甲地的北偏东50°方向上,则∠1的度数为( )A. 60°B. 50°C. 40°D. 30°4.信阳毛尖是中国十大名茶之一.如图是信阳毛尖茶叶的包装盒,它的主视图为( )A.B.C.D.5.下列不等式中,与−x>1组成的不等式组无解的是( )A. x>2B. x<0C. x<−2D. x>−36.如图,在▱ABCD中,对角线AC,BD相交于点O,点E为OC的中点,EF//AB 交BC于点F.若AB=4,则EF的长为( )A. 12B. 1 C. 43D. 27.计算(a·a···a⏟a个)3的结果是( )A. a5B. a6C. a a+3D. a3a8.豫剧是国家级非物质文化遗产,因其雅俗共赏,深受大众喜爱.正面印有豫剧经典剧目人物的三张卡片如图所示,它们除正面外完全相同.把这三张卡片背面朝上洗匀,从中随机抽取一张,放回洗匀后,再从中随机抽取一张,两次抽取的卡片正面相同的概率为( )A. 19B. 16C. 15D. 13⏜的中点,连接BD,CD.以点D为圆心,BD的长为半径在⊙O内画弧,则阴影部分的面积为( )A. 8π3B. 4πC. 16π3D. 16π10.把多个用电器连接在同一个插线板上,同时使用一段时间后,插线板的电源线会明显发热,存在安全隐患.数学兴趣小组对这种现象进行研究,得到时长一定时,插线板电源线中的电流I与使用电器的总功率P的函数图象(如图1),插线板电源线产生的热量Q与I的函数图象(如图2).下列结论中错误的是( )A. 当P=440W时,I=2AB. Q随I的增大而增大C. I每增加1A,Q的增加量相同D. P越大,插线板电源线产生的热量Q越多第II卷(非选择题)二、填空题:本题共5小题,每小题3分,共15分。
河南省实验中学2022年九年级下学期一模数学试题(含答案与解析)

【8题答案】
【答案】A
【解析】
【分析】画出树状图,共有6个等可能的结果,小明同学抽出的两张卡片都是冰墩墩卡片的结果有2个,再由概率公式求解即可.
【详解】解:两张正面印有冰墩墩图案的卡片分别记为A1、A2,正面印有雪容融图案的卡片记为B,
根据题意画树状图如下:
共有6个等可能的结果,小明同学抽出的两张卡片都是冰墩墩卡片的结果有2个,
成绩得分用x表示,共分成四组:A. ,B. ,C. ,D. .
七年级10名学生的成绩是:96,80,96,86,99,96,90,100,89,82.
八年级10名学生的成绩在C组中的数据是:94,90,92.
七、八年级抽取的学生成绩统计表
年级
平均数
中位数
众数
方差
七年级
92
52
八年级
92
93
100
50.4
【初步运用】
(1)如图3,已知线段 和直线l,用直尺和圆规在l上作出所有的点P,使得 (不写作法,保留作图痕迹,你作图过程中用到哪些数学原理?请写出一条.
【问题拓展】
(2)如图4,已知矩形 , , ,M为边 上的点.若满足 的点M恰好有两个,则m的取值范围为_________.
24.如图,已知二次函数 图象经过点 .
A. B. C. D.
9.已知点 , , 都在直线 上,则 , , 的大小关系是()
A. B. C. D.
10.如图,已知菱形OABC的顶点O(0,0),B(2,2),菱形的对角线的交于点D;若将菱形OABC绕点O逆时针旋转,每秒旋转45°,从如图所示位置起,经过60秒时,菱形的对角线的交点D的坐标为()
【1题答案】
2020届河南省新乡市中考数学一模试卷(有答案)(加精)

河南省新乡市中考数学一模试卷一、选择题(每小题3分,共30分)1.下列各数中,最小的数是()A.﹣ B.﹣1 C.﹣|﹣| D.3﹣22.大量事实证明,环境污染治理刻不容缓.据统计,全球每秒钟约有14.2万吨污水排入江河湖海.把14.2万用科学记数法表示为()A.1.42×105B.1.42×104C.142×103D.0.142×1063.如图所示是8个完全相同的小正方体组成的几何体,则该几何体的左视图是()A.B.C.D.4.某同学做了四道题:①3m+4n=7mn;②(﹣2a2)3=﹣8a6;③6x6÷2x2=3x3;④y3•xy2=xy5,其中正确的题号是()A.②④ B.①③ C.①② D.③④5.有15位同学参加一个知识竞赛活动,若他们比赛得分互不相同,且该竞赛共设8分获奖名额,甲同学知道自己的分数后,若要判断自己能否获奖,那么在15位同学成绩统计数据中,只要知道这组数据的()A.平均数B.中位数C.众数 D.方差6.如图,AB是⊙O的直径,OD垂直弦AC于点E,且交⊙O于点D,过点D作⊙O的切线与BA的延长线相交于点F,下列结论不一定正确的是()A.∠CDB=∠BFD B.△BAC∽△OFD C.DF∥AC D.OD=BC7.如图,双曲线y=(x>0)经过线段AB的中点M,则△AOB的面积为()A.18 B.24 C.6 D.128.如图是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c>0的解集是()A.﹣1<x<5 B.x>5 C.x<﹣1 D.x<﹣1或x>59.如图,△ABC中,∠C=90°,∠A=30°,BC=2,按照如下步骤作图:①分别以点A,B为圆心,大于线段AB长度的一半为半径画弧,两弧分别相交于点M,N;②作直线MN分别交AB,AC于点D,E,连结BE,则BE的长是()A.B.3 C.D.10.如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B、C重合),现将△PCD沿直线PD折叠,使点C落到点C′处;作∠BPC′的角平分线交AB于点E.设BP=x,BE=y,则下列图象中,能表示y与x的函数关系的图象大致是()A.B.C.D.二、填空题(每小题3分,共15分)11.|﹣3|0+= .12.写一个你喜欢的整数m的值,使关于x的一元二次方程x2﹣3x+2m=0有两个不相等的实数根,m= .13.用m、n、p、q四把钥匙去开A、B两把锁,其中仅有钥匙m能打开锁A,仅有钥匙n能打开锁B,则“取一把钥匙恰能打开一把锁”的概率是.14.如图,菱形ABCD,∠A=60°,AB=4,以点B为圆心的扇形与边CD相切于点E,扇形的圆心角为60°,点E是CD的中点,图中两块阴影部分的面积分别为S1,S2,则S2﹣S1= .15.如图,矩形ABCD中,AB=8,AD=6,将矩形ABCD折叠,使得点B落在边AD上,记为点G,BC的对应边GI与边CD交于点H,折痕为EF,则AE= 时,△EGH为等腰三角形.三、解答题(本题共8小题,满分75分)16.先化简(﹣)÷然后代入合适的x值求值,整数x满足﹣.17.截止2016年第一季度末,微信每月活跃用户已达到5.49亿,用户覆盖200多个国家,超过20种语言,个品牌的微信公众号总数已经超过800万个,微信已成为中国电子革命的代表,并成为人们生活中不可或缺的日常使用工具,某评测中心进行了抽样调查,统计出如下两个统计图表:(1)在条形统计图中,“转发内容”的人数占到样本容量的15%,则样本容量是;(2)补全条形统计图;(3)扇形统计图中“学生”所占比例是,所对应的圆心角是度;(4)某市约有20万微信用户,请你估计其中喜欢“给别人点赞”的学生有多少人?18.如图,以Rt△ABC的直角边AB为直径作⊙O与斜边AC交于点D,E为BC边的中点,连接DE,OE.(1)求证:DE是⊙O的切线.(2)填空:①当∠CAB= 时,四边形AOED是平行四边形;②连接OD,在①的条件下探索四边形OBED的形状为.19.数学兴趣小组想利用所学的知识了解某广告牌的高度(图中GH的长),经测量知CD=2m,在B处测得点D的仰角为60°,在A处测得点C的仰角为30°,AB=10m,且A、B、H三点共线,请根据以上数据计算GH 的长(,要求结果精确得到0.1m)20.在平面直角坐标系内,双曲线:y=(x>0)分别与直线OA:y=x和直线AB:y=﹣x+10,交于C,D两点,并且OC=3BD.(1)求出双曲线的解析式;(2)连结CD,求四边形OCDB的面积.21.2016年11月13日巴基斯坦瓜达尔港正式开港,此港成为我国“一带一路”必展战略上的一颗璀璨的明星,某大型远洋运输集团有三种型号的远洋货轮,每种型号的货轮载重量和盈利情况如下表所示:甲乙丙平均货轮载重的吨数(万吨)10 5 7.5平均每吨货物可获例如(百元) 5 3.6 4(1)若用乙、丙两种型号的货轮共8艘,将55万吨的货物运送到瓜达尔港,问乙、丙两种型号的货轮各多少艘?(2)集团计划未来用三种型号的货轮共20艘装运180万吨的货物到国内,并且乙、丙两种型号的货轮数量之和不超过甲型货轮的数量,如果设丙型货轮有m艘,则甲型货轮有艘,乙型货轮有艘(用含有m的式子表示),那么如何安排装运,可使集团获得最大利润?最大利润的多少?22.如图1,过等边三角形ABC边AB上一点D作DE∥BC交边AC于点E,分别取BC,DE的中点M,N,连接MN.(1)发现:在图1中, = ;(2)应用:如图2,将△ADE绕点A旋转,请求出的值;(3)拓展:如图3,△ABC和△ADE是等腰三角形,且∠BAC=∠DAE,M,N分别是底边BC,DE的中点,若BD⊥CE,请直接写出的值.23.如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为Q(2,﹣1),且与y轴交于点C(0,3),与x轴交于A,B两点(点A在点B的右侧),点P是该抛物线上的一动点,从点C沿抛物线向点A运动(点P与A 不重合),过点P作PD∥y轴,交AC于点D.(1)求该抛物线的函数关系式;(2)当△ADP是直角三角形时,求点P的坐标;(3)在题(2)的结论下,若点E在x轴上,点F在抛物线上,问是否存在以A、P、E、F为顶点的平行四边形?若存在,求点F的坐标;若不存在,请说明理由.河南省新乡市中考数学一模试卷参考答案与试题解析一、选择题(每小题3分,共30分)1.下列各数中,最小的数是()A.﹣ B.﹣1 C.﹣|﹣| D.3﹣2【考点】2A:实数大小比较.【分析】正实数都大于0,负实数都小于0,正实数大于一切负实数,两个负实数绝对值大的反而小,据此判断即可.【解答】解:根据实数比较大小的方法,可得﹣|﹣|<﹣1<﹣<3﹣2,∴各数中,最小的数是﹣|﹣|.故选:C.2.大量事实证明,环境污染治理刻不容缓.据统计,全球每秒钟约有14.2万吨污水排入江河湖海.把14.2万用科学记数法表示为()A.1.42×105B.1.42×104C.142×103D.0.142×106【考点】1I:科学记数法—表示较大的数.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【解答】解:14.2万=142000=1.42×105.故选:A.3.如图所示是8个完全相同的小正方体组成的几何体,则该几何体的左视图是()A.B.C.D.【考点】U2:简单组合体的三视图.【分析】根据主视图、左视图、俯视图是分别从物体正面、侧面和上面看所得到的图形,从而得出该几何体的左视图.【解答】解:该几何体的左视图是:故选B.4.某同学做了四道题:①3m+4n=7mn;②(﹣2a2)3=﹣8a6;③6x6÷2x2=3x3;④y3•xy2=xy5,其中正确的题号是()A.②④ B.①③ C.①② D.③④【考点】4I:整式的混合运算.【分析】各项计算得到结果,即可作出判断.【解答】解:①原式不能合并,不符合题意;②原式=﹣8a6,符合题意;③原式=3x4,不符合题意;④原式=xy5,符合题意,故选A5.有15位同学参加一个知识竞赛活动,若他们比赛得分互不相同,且该竞赛共设8分获奖名额,甲同学知道自己的分数后,若要判断自己能否获奖,那么在15位同学成绩统计数据中,只要知道这组数据的()A.平均数B.中位数C.众数 D.方差【考点】WA:统计量的选择.【分析】由于比赛设置了8个获奖名额,共有15名选手参加,故应根据中位数的意义分析.【解答】解:因为8位获奖者的分数肯定是15名参赛选手中最高的,而且15个不同的分数按从小到大排序后,中位数及中位数之后的共有8个数,故只要知道自己的分数和中位数就可以知道是否获奖了.故选:B.6.如图,AB是⊙O的直径,OD垂直弦AC于点E,且交⊙O于点D,过点D作⊙O的切线与BA的延长线相交于点F,下列结论不一定正确的是()A.∠CDB=∠BFD B.△BAC∽△OFD C.DF∥AC D.OD=BC【考点】S8:相似三角形的判定;MC:切线的性质.【分析】根据切线的性质、直径的性质、相似三角形的判定和性质等知识,一一判断即可.【解答】解:∵AD是切线,∴OD⊥DF,∵AC⊥OD,∴DF∥AC,故C正确,∴∠F=∠CAB,∵∠CDB=∠CBA,∴∠CDB=∠BFD,故A正确,∵AB是直径,∴∠AEO=∠ACB=90°,∴OE∥BC,∴△BAC∽△OAE,∵△OAE∽△OFD,∴△BAC∽△OFD,故B正确,无法证明OD=BC,故选D.7.如图,双曲线y=(x>0)经过线段AB的中点M,则△AOB的面积为()A.18 B.24 C.6 D.12【考点】G6:反比例函数图象上点的坐标特征;G5:反比例函数系数k的几何意义.【分析】设点M的坐标为(m,n),由点M为线段AB的中点即可得知点A(2m,0)、点B(0,2n),再根据反比例函数图象上点的坐标特征结合三角形的面积即可求出S△AOB的值.【解答】解:设点M的坐标为(m,n),则点A(2m,0),点B(0,2n),∵点M在双曲线y=(x>0)上,∴mn=6,∴S△AOB=OA•OB=2mn=12.故选D.8.如图是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c>0的解集是()A.﹣1<x<5 B.x>5 C.x<﹣1 D.x<﹣1或x>5【考点】HC:二次函数与不等式(组).【分析】根据二次函数的对称性求出与x轴的另一个交点坐标,然后根据函数图象写出x轴上方部分的x 的取值范围即可.【解答】解:由图可知,对称轴为直线x=2,∵抛物线与x轴的一个交点坐标为(5,0),∴抛物线与x轴的另一个交点坐标为(﹣1,0),又∵抛物线开口向下,∴不等式ax2+bx+c>0的解集是﹣1<x<5.故选A.9.如图,△ABC中,∠C=90°,∠A=30°,BC=2,按照如下步骤作图:①分别以点A,B为圆心,大于线段AB长度的一半为半径画弧,两弧分别相交于点M,N;②作直线MN分别交AB,AC于点D,E,连结BE,则BE的长是()A.B.3 C.D.【考点】N2:作图—基本作图;KG:线段垂直平分线的性质;KO:含30度角的直角三角形.【分析】先根据直角三角形的性质求出AB的长,再由作法可知DE是线段AB的垂直平分线,故可得出BD=AD,BE=AE,再由直角三角形的性质即可得出结论.【解答】解:∵△ABC中,∠C=90°,∠A=30°,BC=2,∴AB=2BC=4.∵DE是线段AB的垂直平分线,∴BD=AD=AB=2,BE=AE,∴∠ABE=∠A=30°,∴BE===.故选A.10.如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B、C重合),现将△PCD沿直线PD折叠,使点C落到点C′处;作∠BPC′的角平分线交AB于点E.设BP=x,BE=y,则下列图象中,能表示y与x的函数关系的图象大致是()A.B.C.D.【考点】E7:动点问题的函数图象.【分析】连接DE,根据折叠的性质可得∠CPD=∠C′PD,再根据角平分线的定义可得∠BPE=∠C′PE,然后证明∠DPE=90°,从而得到△DPE是直角三角形,再分别表示出AE、CP的长度,然后利用勾股定理进行列式整理即可得到y与x的函数关系式,根据函数所对应的图象即可得解.【解答】解:如图,连接DE,∵△PC′D是△PCD沿PD折叠得到,∴∠CPD=∠C′PD,∵PE平分∠BPC′,∴∠BPE=∠C′PE,∴∠EPC′+∠DPC′=×180°=90°,∴△DPE是直角三角形,∵BP=x,BE=y,AB=3,BC=5,∴AE=AB﹣BE=3﹣y,CP=BC﹣BP=5﹣x,在Rt△BEP中,PE2=BP2+BE2=x2+y2,在Rt△ADE中,DE2=AE2+AD2=(3﹣y)2+52,在Rt△PCD中,PD2=PC2+CD2=(5﹣x)2+32,在Rt△PDE中,DE2=PE2+PD2,则(3﹣y)2+52=x2+y2+(5﹣x)2+32,整理得,﹣6y=2x2﹣10x,所以y=﹣x2+x(0<x<5),纵观各选项,只有D选项符合.故选:D.二、填空题(每小题3分,共15分)11.|﹣3|0+= ﹣1 .【考点】24:立方根;6E:零指数幂.【分析】根据题目中的式子,可以计算出正确的结果,从而可以解答本题.【解答】解:|﹣3|0+=1+(﹣2)=﹣1,故答案为:﹣1.12.写一个你喜欢的整数m的值,使关于x的一元二次方程x2﹣3x+2m=0有两个不相等的实数根,m= 1 .【考点】AA:根的判别式.【分析】根据根的判别式求出m<,答案不唯一,只要取小于的整数就可以.【解答】解:∵关于x的一元二次方程x2﹣3x+2m=0有两个不相等的实数根,∴△=(﹣3)2﹣4×1×2m=9﹣8m>0,解得:m<,取m=1,故答案为:1.13.用m、n、p、q四把钥匙去开A、B两把锁,其中仅有钥匙m能打开锁A,仅有钥匙n能打开锁B,则“取一把钥匙恰能打开一把锁”的概率是.【考点】X6:列表法与树状图法.【分析】画树状图展示所有8种等可能的结果数,再找出取一把钥匙恰能打开一把锁”的结果数,然后根据概率公式求解.【解答】解:画树状图为:共有8种等可能的结果数,其中取一把钥匙恰能打开一把锁”的结果数为2,所以取一把钥匙恰能打开一把锁”的概率==,故答案为:.14.如图,菱形ABCD,∠A=60°,AB=4,以点B为圆心的扇形与边CD相切于点E,扇形的圆心角为60°,点E是CD的中点,图中两块阴影部分的面积分别为S1,S2,则S2﹣S1= 2﹣π.【考点】MC:切线的性质;L8:菱形的性质;MO:扇形面积的计算.【分析】连接BE,由以点B为圆心的扇形与边CD相切于点E,得到在菱形ABCD中,∠A=60°,AB=4,求得BE⊥CD,由点E是CD的中点,得到CE=CD=2,BE=2,∠EBC=30°,于是得到结论.【解答】解:连接BE,∵以点B为圆心的扇形与边CD相切于点E,∵在菱形ABCD中,∠A=60°,AB=4,∴BE⊥CD,∵点E是CD的中点,∴CE=CD=2,BE=2,∠EBC=30°,∵扇形的圆心角为60°,∴S2﹣S1=×CE•BE﹣=2×2﹣π=2﹣π.故答案为:2﹣π.15.如图,矩形ABCD中,AB=8,AD=6,将矩形ABCD折叠,使得点B落在边AD上,记为点G,BC的对应边GI与边CD交于点H,折痕为EF,则AE= 4﹣2 时,△EGH为等腰三角形.【考点】PB:翻折变换(折叠问题);KI:等腰三角形的判定;LB:矩形的性质.【分析】根据余角的性质得到∠AEG=∠DGH,根据全等三角形的性质得到DG=AE,由折叠的性质得到BE=GE,根据勾股定理列方程即可得到结论.【解答】解:∵在矩形ABCD中,∠A=∠D=∠B=∠EGH=90°,∴∠AGE+∠AEG=∠AGE+∠DGH=90°,∴∠AEG=∠DGH,∵△EGH为等腰三角形,∴EG=GH,在△AEG与△DGH中,,∴△AEG≌△DGH,∴DG=AE,∵AB=8,AD=6,将矩形ABCD折叠,使得点B落在边AD上,∴BE=GE,∴BE=8﹣AE,∴AG=AE+2,∵AG2+AE2=GE2,∴(AE+2)2+AE2=(8﹣AE)2,∴AE=4﹣2,∴AE=4﹣2时,△EGH为等腰三角形.故答案为:4﹣2.三、解答题(本题共8小题,满分75分)16.先化简(﹣)÷然后代入合适的x值求值,整数x满足﹣.【考点】6D:分式的化简求值;2B:估算无理数的大小.【分析】根据分式的减法和除法可以化简题目中的式子,然后选取一个使得原分式有意义的x的值代入求值即可,注意整数x满足﹣.【解答】解:(﹣)÷==2(x﹣2)﹣(x+2)=2x﹣4﹣x﹣2=x﹣6,∵x满足﹣,∴当x=1时,原式=1﹣6=﹣5.17.截止2016年第一季度末,微信每月活跃用户已达到5.49亿,用户覆盖200多个国家,超过20种语言,个品牌的微信公众号总数已经超过800万个,微信已成为中国电子革命的代表,并成为人们生活中不可或缺的日常使用工具,某评测中心进行了抽样调查,统计出如下两个统计图表:(1)在条形统计图中,“转发内容”的人数占到样本容量的15%,则样本容量是200 ;(2)补全条形统计图;(3)扇形统计图中“学生”所占比例是15% ,所对应的圆心角是54 度;(4)某市约有20万微信用户,请你估计其中喜欢“给别人点赞”的学生有多少人?【考点】VC:条形统计图;V2:全面调查与抽样调查;V3:总体、个体、样本、样本容量;V5:用样本估计总体;VB:扇形统计图.【分析】(1)由30除以其所占的比例,即可求出样本容量;(2)用样本容量减去A、C、D、E的数据,即可求出喜欢给别人评论的人数,再补全条形统计图即可;(3)观察扇形统计图,用1减去其它各部分所占比例,即可求出“学生”所占比例,再用其乘360°即可得出结论;(4)利用总体×学生所占比例×喜欢给别人评论的人数÷样本容量,即可求出结论.【解答】解:(1)由题意可得:30÷15%=200.故答案为:200;(2)200﹣70﹣40﹣10=50(人),补全条形统计图,如图所示.(3)1﹣40%﹣32%﹣13%=15%,15%×360°=54°.故答案为:15%;54.(4)200000×15%×=10500(人).答:其中喜欢“给别人点赞”的学生大约有10500人.18.如图,以Rt△ABC的直角边AB为直径作⊙O与斜边AC交于点D,E为BC边的中点,连接DE,OE.(1)求证:DE是⊙O的切线.(2)填空:①当∠CAB= 45°时,四边形AOED是平行四边形;②连接OD,在①的条件下探索四边形OBED的形状为正方形.【考点】MR:圆的综合题.【分析】(1)连接OD后,证明△DOE≌△BOE后,可得∠OBE=∠ODE=90°,所以DE是⊙O的切线;(2)①由(1)可知:∠ODE=90°,要使四边形AOED是平行四边形,即需要DE∥AO,所以需要∠AOD=90°,又因为OA=OD,所以∠CA B=45°;②由①可知:四边形OBED是矩形,又因为OD=OB,所以四边形OBED是正方形.【解答】解:(1)连接OD,∵E是BC的中点,O是AB的中点,∴OE是△ABC的中位线,∴OE∥AC,∠BOE=∠BAC,∠DOE=∠ADO,∵OD=OA,∴∠BAC=∠ADO,∴∠BOE=∠DOE,在△DOE与△BOE中,,∴△DOE≌△BOE,∴∠OBE=∠ODE=90°,∴DE是⊙O的切线;(2)①当∠CAB=45°时,∴∠ADO=45°,∴∠AOD=90°,又∵∠EDO=90°,∴DE∥AB,∵OE∥AC,∴四边形AOED是平行四边形;②由①可知:∠EDO=∠DOB=∠ABC=90°,∴四边形OBED是矩形,∵OD=OB,∴矩形OBED是正方形.故答案为:①45°;②正方形.19.数学兴趣小组想利用所学的知识了解某广告牌的高度(图中GH的长),经测量知CD=2m,在B处测得点D的仰角为60°,在A处测得点C的仰角为30°,AB=10m,且A、B、H三点共线,请根据以上数据计算GH 的长(,要求结果精确得到0.1m)【考点】TA:解直角三角形的应用﹣仰角俯角问题.【分析】首先过点D作DE⊥AH于点E,设DE=xm,则CE=(x+2)m,解Rt△AEC和Rt△BED,得出AE=(x+2),BE=x,根据AE﹣BE=10列出方程(x+2)﹣x=10,解方程求出x的值,进而得出GH的长.【解答】解:如图,过点D作DE⊥AH于点E,设DE=xm,则CE=(x+2)m.在Rt△AEC和Rt△BED中,有tan30°=,tan60°=,∴AE=(x+2),BE=x,∵AE﹣BE=AB=10,∴(x+2)﹣x=10,∴x=5﹣3,∴GH=CD+DE=2+5﹣3=5﹣1≈7.7(m).答:GH的长约为7.7m.20.在平面直角坐标系内,双曲线:y=(x>0)分别与直线OA:y=x和直线AB:y=﹣x+10,交于C,D两点,并且OC=3BD.(1)求出双曲线的解析式;(2)连结CD,求四边形OCDB的面积.【考点】G8:反比例函数与一次函数的交点问题.【分析】(1)过点A、C、D作x轴的垂线,垂足分别是M、E、F,由直线y=x和y=﹣x+10可知∠AOB=∠ABO=45°,证明△CEO∽△DEB,从而可知==3,然后设设D(10﹣m,m),其中m>0,从而可知C的坐标为(3m,3m),利用C、D在反比例函数图象上列出方程即可求出m的值.(2)求分别求出△OCE、△DFB△、梯形CDFE的面积即可求出答案.【解答】解:(1)过点A、C、D作x轴的垂线,垂足分别是M、E、F,∴∠AMO=∠CEO=∠DFB=90°,∵直线OA:y=x和直线AB:y=﹣x+10,∴∠AOB=∠ABO=45°,∴△CEO∽△DEB∴==3,设D(10﹣m,m),其中m>0,∴C(3m,3m),∵点C、D在双曲线上,∴9m2=m(10﹣m),解得:m=1或m=0(舍去)∴C(3,3),∴k=9,∴双曲线y=(x>0)(2)由(1)可知D(9,1),C(3,3),B(10,0),∴OE=3,EF=6,DF=1,BF=1,∴S四边形OCDB=S△OCE+S梯形CDFE+S△DFB=×3×3+×(1+3)×6+×1×1=17,∴四边形OCDB的面积是1721.2016年11月13日巴基斯坦瓜达尔港正式开港,此港成为我国“一带一路”必展战略上的一颗璀璨的明星,某大型远洋运输集团有三种型号的远洋货轮,每种型号的货轮载重量和盈利情况如下表所示:甲乙丙平均货轮载重的吨数(万吨)10 5 7.5平均每吨货物可获例如(百元) 5 3.6 4(1)若用乙、丙两种型号的货轮共8艘,将55万吨的货物运送到瓜达尔港,问乙、丙两种型号的货轮各多少艘?(2)集团计划未来用三种型号的货轮共20艘装运180万吨的货物到国内,并且乙、丙两种型号的货轮数量之和不超过甲型货轮的数量,如果设丙型货轮有m艘,则甲型货轮有16﹣0.5m 艘,乙型货轮有4﹣0.5m 艘(用含有m的式子表示),那么如何安排装运,可使集团获得最大利润?最大利润的多少?【考点】FH:一次函数的应用;9A:二元一次方程组的应用.【分析】(1)设用乙、丙两种型号的货轮分别为x艘,y艘,根据题意列方程组即可得到结论;(2)甲型货轮有(16﹣0.5m)艘,乙型货轮有(4﹣0.5m)艘,根据题意列不等式得到m=2,4,6,设集团的总利润为w,于是得到结论.【解答】解:(1)设用乙、丙两种型号的货轮分别为x艘,y艘,则,解得:,答:用2艘乙种型号的货轮,6艘丙种型号的货轮;(2)甲型货轮有(16﹣0.5m)艘,乙型货轮有(4﹣0.5m)艘,则4﹣0.5m+m≤16﹣0.5m,解得:m≤12,∵m为正整数,(16﹣0.5m)与94﹣0.5m)均为正整数,∴m=2,4,6,设集团的总利润为w,则w=10×5(16﹣0.5m)+5×3.6(4﹣0.5m)+7.5×4m=﹣4m+872,当m=2时,集团获得最大利润,最大利润为8.64亿元.故答案为:16﹣0.5m,4﹣0.5m.22.如图1,过等边三角形ABC边AB上一点D作DE∥BC交边AC于点E,分别取BC,DE的中点M,N,连接MN.(1)发现:在图1中, = ;(2)应用:如图2,将△ADE绕点A旋转,请求出的值;(3)拓展:如图3,△ABC和△ADE是等腰三角形,且∠BAC=∠DAE,M,N分别是底边BC,DE的中点,若BD⊥CE,请直接写出的值.【考点】SO:相似形综合题.【分析】(1)如图1中,作DH⊥BC于H,连接AM.只要证明四边形MNDH时矩形,即可解决问题.(2)如图2中,连接AM、AN.只要证明△BAD∽△MAN,利用相似比为即可解决问题.(3)如图3中,连接AM、AN,延长AD交CE于H,交AC于O.由△BAD∽△MAN,推出==sin∠ABC,只要证明△ABC时等腰直角三角形即可解决问题.【解答】解:(1)如图1中,作DH⊥BC于H,连接AM.∵AB=AC,BM=CM,∴AM⊥BC,∵△ADE时等边三角形,∴∠ADE=60°=∠B,∴DE∥BC,∵AM⊥BC,∴AM⊥DE,∴AM平分线段DE,∵DN=NE,∴A、N、M共线,∴∠NMH=∠MND=∠DHM=90°,∴四边形MNDH时矩形,∴MN=DH,∴==sin60°=,故答案为.(2)如图2中,连接AM、AN.∵△ABC,△ADE都是等边三角形,BM=MC,DN=NE,∴AM⊥BC,AN⊥DE,∴=sin60°,=sin60°,∴=,∵∠MAB=∠DAN=30°,∴∠BAD=∠MAN,∴△BAD∽△MAN,∴==sin60°=.(3)如图3中,连接AM、AN,延长AD交CE于H,交AC于O.∵AB=AC,AD=AE,BM=CM,DN=NE,∴AM⊥BC,AN⊥DE,∵∠BAC=∠DAE,∴∠ABC=∠ADE,∴sin∠ABM=sin∠ADN,∴=,∵∠BAM=BAC,∠DAN=∠DAE,∴∠BAM=∠DAN,∴∠BAD=∠MAN.∴△BAD∽△MAN,∴==sin∠ABC,∵∠BAC=∠DAE,∴∠BAD=∠CAE,∵AB=AC,AD=AE,∴△BAD≌△CAE,∴∠ABD=∠ACE,∵BD⊥CE,∴∠BHC=90°,∴∠ACE+∠COH=90°,∵∠AOB=∠COH,∴∠ABD+∠AOB=90°,∴∠BAO=90°,∵AB=AC,∴∠ABC=45°,∴=sin45°=.23.如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为Q(2,﹣1),且与y轴交于点C(0,3),与x轴交于A,B两点(点A在点B的右侧),点P是该抛物线上的一动点,从点C沿抛物线向点A运动(点P与A不重合),过点P作PD∥y轴,交AC于点D.(1)求该抛物线的函数关系式;(2)当△ADP是直角三角形时,求点P的坐标;(3)在题(2)的结论下,若点E在x轴上,点F在抛物线上,问是否存在以A、P、E、F为顶点的平行四边形?若存在,求点F的坐标;若不存在,请说明理由.【考点】HF:二次函数综合题.【分析】(1)已知了抛物线的顶点坐标,可将抛物线的解析式设为顶点式,然后将函数图象经过的C点坐标代入上式中,即可求出抛物线的解析式;(2)由于PD∥y轴,所以∠ADP≠90°,若△ADP是直角三角形,可考虑两种情况:①以点P为直角顶点,此时AP⊥DP,此时P点位于x轴上(即与B点重合),由此可求出P点的坐标;②以点A为直角顶点,易知OA=OC,则∠OAC=45°,所以OA平分∠CAP,那么此时D、P关于x轴对称,可求出直线AC的解析式,然后设D、P的横坐标,根据抛物线和直线AC的解析式表示出D、P的纵坐标,由于两点关于x轴对称,则纵坐标互为相反数,可据此求出P点的坐标;(3)P、B重合,E点在x轴上,这样A、P、E三点在x轴上,所以A、P、E、F为顶点不可能构成平行四边形,所以只有(2)②的一种情况符合题意,由②知此时P、Q重合;假设存在符合条件的平行四边形,那么根据平行四边形的性质知:P、F的纵坐标互为相反数,可据此求出F点的纵坐标,代入抛物线的解析式中即可求出F点的坐标.【解答】解:(1)∵抛物线的顶点为Q(2,﹣1),∴设抛物线的解析式为y=a(x﹣2)2﹣1,将C(0,3)代入上式,得:3=a(0﹣2)2﹣1,a=1;∴y=(x﹣2)2﹣1,即y=x2﹣4x+3;(2)分两种情况:①当点P1为直角顶点时,点P1与点B重合;令y=0,得x2﹣4x+3=0,解得x1=1,x2=3;∵点A在点B的右边,∴B(1,0),A(3,0);∴P1(1,0);②当点A为△AP2D2的直角顶点时;∵OA=OC,∠AOC=90°,∴∠OAD2=45°;当∠D2AP2=90°时,∠OAP2=45°,∴AO平分∠D2AP2;又∵P2D2∥y轴,∴P2D2⊥AO,∴P2、D2关于x轴对称;设直线AC的函数关系式为y=kx+b(k≠0).将A(3,0),C(0,3)代入上式得:,解得;∴y=﹣x+3;设D2(x,﹣x+3),P2(x,x2﹣4x+3),则有:(﹣x+3)+(x2﹣4x+3)=0,即x2﹣5x+6=0;解得x1=2,x2=3(舍去);∴当x=2时,y=x2﹣4x+3=22﹣4×2+3=﹣1;∴P2的坐标为P2(2,﹣1)(即为抛物线顶点).∴P点坐标为P1(1,0),P2(2,﹣1);(3)由(2)知,当P点的坐标为P1(1,0)时,不能构成平行四边形;当点P的坐标为P2(2,﹣1)(即顶点Q)时,平移直线AP交x轴于点E,交抛物线于F;∵P(2,﹣1),∴可设F(x,1);∴x2﹣4x+3=1,解得x1=2﹣,x2=2+;∴符合条件的F点有两个,即F1(2﹣,1),F2(2+,1).。
新乡市长垣县2022年八年级下学期《数学》期中试题与参考答案

新乡市长垣县2022年八年级下学期《数学》期中试题与参考答案一、选择题每小题3分,共30分。
1.下列二次根式中,属于最简二次根式的是( )A.B.C.D.【分析】根据最简二次根式的概念判断即可.解:A、==,被开方数不含分母,不是最简二次根式;B、,是最简二次根式;C、=2,被开方数中不含能开得尽方的因数,不是最简二次根式;,不是最简二次根式;D、=2,被开方数中不含能开得尽方的因数,不是最简二次根式;故选:B.2.下列计算正确的是( )A.=﹣3B.=3C.=D.﹣=【分析】利用二次根式化简的法则,二次根式的减法的法则对各项进行运算即可.解:A、,故A不符合题意;B、,故B不符合题意;C、,故C符合题意;D、与不属于同类二次根式,不能运算,故D不符合题意;故选:C.3.下列不能判定△ABC是直角三角形的是( )A.a=2,b=3,c=B.a:b:c=3:4:5C.∠A:∠B:∠C=3:4:5D.∠A=40°,∠B=50°【分析】根据勾股定理的逆定理可以判断选项A和B中的三条线段能否够构成直角三角形,根据三角形内角和可以判断C和D,从而可以判断哪个选项符合题意.解:A、因为()2=22+32,故选项A中的三条线段能构成直角三角形,不符合题意;B、因为32+42=52,故选项B中的三条线段能构成直角三角形,不符合题意;C、因为∠A:∠B:∠C=3:4:5,所以最大的角∠C=180°×=75°,故选项C中的三角形不能构成直角三角形,符合题意;D、因为∠A=40°,∠B=50°,∠A+∠C+∠B=180°,所以∠C=180°﹣40°﹣50°=90°,故选项C中的三角形是直角三角形,不符合题意.故选:C.4.若式子在实数范围内有意义,则x的取值范围是( )A.x≥1且x≠2B.x≤1C.x>1且x≠2D.x<1【分析】分式有意义,分母不等于零;二次根式的被开方数是非负数.解:依题意,得x﹣1≥0且x﹣2≠0,解得x≥1且x≠2.故选:A.5.下列条件中,不能判定四边形ABCD是平行四边形的是( )A.AB∥CD,AB=CD B.AB=CD,AD=BCC.AB∥CD,∠B=∠D D.AB∥CD,AD=BC【分析】根据平行四边形的判定定理分别进行分析即可.解:A、因为AB∥CD,AB=CD,所以四边形ABCD是平行四边形,故此选项不合题意;B、因为AB=CD,AD=BC,所以四边形ABCD是平行四边形,故此选项不合题意;C、因为AB∥CD,∠B=∠D,所以四边形ABCD是平行四边形,故此选项不合题意;D、因为AB∥CD,AD=BC,不能得出四边形ABCD是平行四边形,故此选项符合题意;故选:D.6.在菱形ABCD中,∠ABC=80°,BA=BE,则∠BAE=( )A.70°B.40°C.75°D.30°【分析】利用菱形的性质和等腰三角形的性质即可求解.解:在菱形ABCD因为∠ABC=80°,所以∠ABD=40°.因为BA=BE,所以∠BAE==70°.故选:A.7.如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开,若测得AB的长为3.6千米,则M,C两点间的距离为( )千米.A.7.2B.1.2C.1.8D.3.6【分析】根据题意可得∠ACB=90°,然后利用直角三角形斜边上的中线性质,进行计算即可解答.解:由题意得:AC⊥BC,所以∠ACB=90°,因为AB=3.6千米,点M是AB的中点,所以CM=AB=1.8(千米),故选:C.8.如图,为了测算出学校旗杆的高度,小明将升旗的绳子拉到旗杆底端,并在与旗杆等长的地方打了一个结,然后将绳子底端拉到离旗杆底端5米的地面某处,发现此时绳子底端距离打结处约1米,则旗杆的高度是( )A.12B.13C.15D.24【分析】设旗杆的高度为xm,则AC=xm,AB=(x+1)m,BC=5m,利用勾股定理得到52+x2=(x+1)2,然后解方程求出x即可.解:如图,设旗杆的高度为xm,则AC=xm,AB=(x+1)m,BC=5m,在Rt△ABC中,52+x2=(x+1)2,解得x=12,答:旗杆的高度是12m.故选:A.9.如图,在矩形OABC中,点B的坐标是(1,3),则AC的长是( )A.3B.2C.D.4【分析】根据勾股定理求出OB,根据矩形的性质得出AC=OB,即可得出答案.解:连接OB,过B作BM⊥x轴于M,因为点B的坐标是(1,3),所以OM=1,BM=3,由勾股定理得:OB==,因为四边形OABC是矩形,所以AC=OB,所以AC=,故选:C.10.如图,点E,F,G,H ABCD的边AB,BC,CD,DA的中点.下列三种说法:①四边形EFGH一定是平行四边形;②若AC=BD,则四边形EFGH是菱形;③若AC⊥BD,则四边形EFGH是矩形.其中正确的是( )A.①B.①②C.①③D.①②③【分析】根据三角形中位线定理得到EH∥BD,GF∥BD,EF∥AC,EH=BD,EF=AC,根据平行四边形、菱形、矩形的判定定理判断即可.解:因为点E,F,G,H分别为四边形ABCD的边AB,BC,CD,DA的中点,所以EH∥BD,GF∥BD,EF∥AC,EH=BD,EF=AC,所以四边形EHGF是平行四边形,故①符合题意;若AC=BD,则EF=EH,所以平行四边形EHGF是菱形,故②符合题意;若AC⊥BD,则EF⊥EH,所以平行四边形EHGF是矩形,故③符合题意;故选:D.二、填空题(每小题3分,共15分)11.如图,点A表示的实数是 .【分析】利用勾股定理,求得OA的长度即可.解:根据勾股定理可知,OA==,所以A点表示的数是.故答案为:.12.如图是一株美丽的勾股树,所有四边形都是正方形,所有三角形是直角三角形,若正方形A、B、C面积为2、8、5,则正方形D的面积为 15 .【分析】根据勾股定理和正方形的性质即可得到结论.解:由勾股定理得,正方形D的面积=正方形A的面积+正方形B的面积+正方形C面积=2+8+5=15,故答案为:15.13.甲船以24km/h的速度离开港口O向北偏东40°方向航行,乙船同时离开港口O以10km/h的速度沿一定方向航行,半小时后分别到达A、B两点,且相距13km,则乙船沿 南偏东50° 方向航行.【分析】根据已知可得出△AOB是直角三角形,进而结合方向角得出答案.解:因为甲船以24km/h的速度、乙船以10km/h的速度航行了半小时,所以OA=24×0.5=12(km),AO=5km,因为AB=13km,所以52+122=132,则OB2+AO2=AB2,所以△AOB是直角三角形,所以∠3+∠2=90°,因为∠1+∠2=90°,所以∠1=∠3=40°,所以乙船沿南偏东50°方向航行.故答案为:南偏东50°.14.如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD,已知AB=6cm,BC=8cm,则四边形ODEC的周长为 20 cm.【分析】根据矩形的性质得出∠ABC=90°,AD=BC=8cm,CD=AB=6cm,OA=OC=AC,OB=OD=BD,AC=BD,求出OC=OD,根据菱形的判定得出四边形OCED是菱形,根据菱形的性质得出OD=OC=DE=CE,根据勾股定理求出AC,再求出OC即可.解:因为四边形ABCD是矩形,AB=6cm,BC=8cm,所以∠ABC=90°,AD=BC=8cm,CD=AB=6cm,OA=OC=AC,OB=OD=BD ,AC=BD,所以OC=OD,因为DE∥AC,CE∥BD,所以四边形OCED是平行四边形,又因为OC=OD所以四边形OCED是菱形,所以OD=OC=DE=CE,由勾股定理得:AC===10(cm),所以AO=OC=5cm,所以OC=CE=DE=OD=5cm,即四边形ODEC的周长为5+5+5+5+5=20(cm),故答案为:20.15.我们知道,四边形具有不稳定性.如图,在平面直角坐标系中,边长为2的正方形ABCD 的边AB在x轴上,AB的中点是坐标原点O,固定点A,B,把正方形沿箭头方向推,使点D 落在y轴正半轴上点D'处,则点C的对应点C'的坐标为 (2,) .【分析】由已知条件得到AD′=AD=2,AO=AB=1,根据勾股定理得到OD′==,于是得到结论.解:因为AD′=AD=2,AO=AB=1,所以OD′==,因为C′D′=2,C′D′∥AB,所以C′(2,),故答案为(2,).三、解答题(共75分)16.计算:(1)﹣6+;(2)(3﹣)2+×.【分析】(1)先把每一个二次根式化成最简二次根式,然后再进行计算即可解答;(2)先算乘法,再算加减,进行计算即可解答.解:(1)﹣6+=4﹣2+3=5;(2)(3﹣)2+×=9﹣6+5+2=14﹣4.17.如图,平行四边形ABCD的对角线AC,BD相交于点O,AC⊥AB,点E是CD的中点,若AB=6,OE=5.(1)求BC的长;(2)求平行四边形ABCD的面积.【分析】(1)根据平行四边形可得O为BD中点,进而根据中位线定理可得BC的长;(2)根据勾股定理可得AC=8,然后根据平行四边形ABCD的面积=2S△ABC,即可解决问题.解:(1)因为四边形ABCD为平行四边形,所以DO=BO,因为E是CD的中点,所以BC=2OE=10;(2)因为AC⊥AB,所以∠BAC=90°,在Rt△ABC中,AB=6,BC=10,所以AC==8,所以平行四边形ABCD的面积=2S△ABC=2×AB•AC=6×8=48.18.一住宅楼发生火灾,消防车立即赶到,准备在距大楼9米的C处升起云梯到火灾窗口展开营救,已知云梯AB长15m,云梯底部B距离地面2米,此时消防队员能否救下等候在距离地面约13米窗口的受困群众?说说你的理由.【分析】先根据题意建立直角三角形,然后利用勾股定理求出AB的长度,最后与云梯的长度比较即可得出答案.解:能救下.理由如下:如图所示:由题意得,BD=9米,AD=13﹣2=11米,在RT△ABD中,AB2=AD2+BD2,所以AB2=(13﹣2)2+92=121+81=202,而152=225>202,故能救下.19.如图,在▱ABCD中,以点B为圆心,BA长为半径画弧,交BC于点E,在AD上截取AF =BE.连接EF.(1)求证:四边形ABEF是菱形;(2)请用无刻度的直尺在▱ABCD内找一点P,使∠APB=90°.(标出点P的位置,保留作图痕迹,不写作法)【分析】(1)根据平行四边形的性质和判定,菱形的判定即可证明;(2)连接AE,BF,根据菱形的性质可得AE和BF的交点即为点P.【解答】(1)证明:因为四边形ABCD是平行四边形,所以AF∥BE,因为AF=BE,所以四边形ABEF是平行四边形,因为BA=BE,所以四边形ABEF是菱形;(2)如图所示:点P即为所求:20.如图:正方形网格中每个小方格的边长为1,且点A、B、C均为格点.(1)求△ABC的面积;(2)通过计算判断△ABC的形状;.(3)求AB边上的高.【分析】(1)由矩形的面积减去三个直角三角形的面积即可;(2)由勾股定理和勾股定理的逆定理即可得出结论;(3)由三角形的面积即可得出结果.解:(1)△ABC的面积=4×4﹣×4×2﹣×2×1﹣×3×4=5;(2)由勾股定理得:AC2=42+22=20,BC2=22+12=5,AB2=32+42=25,所以AC2+BC2=AB2,所以△ABC是直角三角形,∠ACB=90°;(3)因为AC==2,BC=,△ABC是直角三角形,所以AB边上的高===2.21.平行四边形ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.(1)求证:四边形BFDE(2)若AF平分∠BAD,且AE=6,DE=8,求矩形BFDE的面积.【分析】(1)根据有一个角是90度的平行四边形是矩形即可判定.(2)首先证明AD=DF,求出AD即可解决问题.【解答】(1)证明:因为四边形ABCD是平行四边形,所以AB=CD,AB∥CD,所以DF∥BE,因为CF=AE,所以DF=BE,所以四边形BFDE是平行四边形,因为DE⊥AB,所以∠DEB=90°,所以四边形BFDE是矩形.(2)解:因为AB∥CD,所以∠BAF=∠AFD,因为AF平分∠BAD,所以∠DAF=∠AFD,所以AD=DF,在Rt△ADE中,因为AE=6,DE=8,所以AD==10,所以矩形的面积为8×10=80.22.【教材呈现】人教八年级下册数学教材第59页的部分内容.如图1,把一张矩形纸片按如图那样折一下,就可以裁出正方形纸片,为什么?【问题解决】如图1,已知矩形纸片ABCD(AD>AB),将矩形纸片沿过点A的直线折叠,使点B落在边AD上,点B的对应点为F,折痕为AE,点E在BC上.求证:四边形ABEF是正方形.(请完成以下填空)证明:因为四边形ABCD是矩形,所以∠BAD=∠B=90°,因为折叠,所以∠AFE=∠B=90°,所以四边形ABEF是矩形,( 有三个角是直角的四边形为矩形 )因为折叠,所以AB= AF ,所以四边形ABEF是正方形.( 有一组邻边相等的矩形是正方形 )【问题拓展】如图2,已知平行四边形纸片ABCD(AD>AB),将平行四边形纸片沿过点A 的直线折叠,使点B落在边AD上,点B的对应点为F,折痕为AE,点E在边BC上.(1)求证:四边形ABEF是菱形.(2)连结BF,若AE=5,BF=10,则菱形ABEF的面积为 25 .【分析】【问题解决】由矩形的性质得∠BAD=∠B=90°,再由折叠的性质得:∠AFE=∠B =90°,AB=AF,则四边形ABEF是矩形,然后由AB=AF,即可得出结论;【问题拓展】(1)由平行四边形的性质得AD∥BC,则∠FAE=∠BEA,再证AB=BE,则AF =BE,得四边形ABEF是平行四边形,然后由AF=AB即可得出结论;(2)由菱形面积公式得S菱形ABEF=AE•BF,即可得出答案.【解答】【问题解决】解:因为四边形ABCD是矩形,所以∠BAD=∠B=90°,由折叠的性质得:∠AFE=∠B=90°,所以四边形ABEF是矩形(有三个角是直角的四边形为矩形),由折叠的性质得:AB=AF,所以四边形ABEF是正方形(有一组邻边相等的矩形是正方形),故答案为:有三个角是直角的四边形为矩形,AF,有一组邻边相等的矩形是正方形;【问题拓展】(1)证明:因为四边形ABCD是平行四边形,所以AD∥BC,所以∠FAE=∠BEA,由折叠的性质得:AF=AB,∠BAE=∠FAE,所以∠BEA=∠BAE,所以AB=BE,所以AF=BE,所以四边形ABEF是平行四边形,又因为AF=AB,所以平行四边形ABEF是菱形;(2)解:如图2,因为四边形ABEF是菱形,AE=5,BF=10,所以S菱形ABEF=AE•BF=×5×10=25,故答案为:25.23.下面是张华设计的尺规作图.已知:矩形ABCD.作法:①分别以A,B为圆心,以大于AB长为半径,在AB两侧作弧,分别交于点E,F;②作直线EF;③以点A为圆心,AB为半径作弧,交直线EF于点G,连接AG,BG;根据张华设计的尺规作图,解决下列问题:(1)求∠BAG的度数;(2)过点D作DH∥AG,交直线EF于点H.①求证:四边形AGHD为平行四边形.②用等式表示平行四边形AGHD的面积S1和矩形ABCD的面积S2的数量关系为 S2=2S1 .【分析】(1)连接BG,由作图知,EF是线段AB的垂直平分线,得到AG=BG,推出△ABG 是等边三角形,于是得到结论;(2)①根据矩形的性质得到∠BAD=90°,推出GH∥AD,得到四边形AGHD是平行四边形;②设EF与AB交于M,根据矩形和平行四边形的面积公式即可得到结论.【解答】(1)解:连接BG,由作图知,EF是线段AB的垂直平分线,所以AG=BG,因为AB=AG,所以AB=AG=BG,所以△ABG是等边三角形,所以∠BAG=60°;故答案为:60°;(2)①证明:因为四边形ABCD是矩形,所以∠BAD=90°,因为EF⊥AB,所以GH∥AD,因为GH=AD,所以四边形AGHD是平行四边形;③解:设EF与AB交于M,因为S2=AD•AB,S1=HG•AM=AD•AB=AD•AB,所以S2=2S1,故答案为:S2=2S1.。
2022年河南省中考数学模拟试卷(一)

(满分120分,建议用时100分钟)一、选择题(每小题3分,共30分)1. (2021长沙)下列四个实数中,最大的数是( )A .4B .πC .-1D .-3 2. 据国家卫健委统计,截至2021年12月25日,我国已完成新冠疫苗病毒全程接种人数超过12亿.数据“12亿”用科学记数法表示为( )A .1.2×108B .1.2×109C .0.12×109D .0.12×10103. (2021郴州)由5个相同的小立方体搭成的物体如图所示,则它的俯视图为( )A .B .C .D . 4. (2021广州)下列运算正确的是( ) A .|-(-2)|=-2B.3+= C .(a 2b 3)2=a 4b 6 D .(a -2)2=a 2-4 5. 如图,AE ∥BD ,∠1=120°,∠2=40°,则∠C 的度数是( )A .10°B .20°C .30°D .40° 6. (2021河池)已知□ABCD ,下列条件中,不能判定这个平行四边形为矩形的是( )A .∠A =∠B B .∠A =∠CC .AC =BD D .AB ⊥BC 7. 若使关于x 的一元二次方程ax 2-2x +2=0有两个不相等实数根,则a 的值可以为( ) A .1 B .12 C .0 D .-18. (2021阜新)小颖有两顶帽子,分别为红色和黑色,有三条围巾,分别为红色、黑色和白色,她随机拿出一顶帽子和一条围巾戴上,恰好为红色帽子和红色围巾的概率是( )A .16B .23C .12D .569. 如图,在△ABC 中,∠ABC =90°.AB ∥x 轴,已知点C 的纵坐标是6,将△ABC 绕点A 旋转90°得到△ADE ,使C 恰好落在y 轴的负半轴E 点处,若点C 和点D 关于原点成中心对称,则点A 的坐标为( )A .(-3,2)B .(-4,1)C .(-4,2)D .(-3,1)21E DCBA2022年河南中考数学模拟试卷(一)10. 如图1,在正方形ABCD 中,点P 从点D 出发,沿着D -A 方向匀速运动,到达点A 后停止运动,点Q 从点D 出发,沿着D -C -B -A 的方向匀速运动,到达点A 后停止运动.已知点P 的运动速度为4.图2表示P ,Q 两点同时出发x 秒后,△APQ 的面积y 与x 的函数关系,则点Q 的运动速度可能是( )A .2B .3C .8D .12二、填空题(每小题3分,共15分)11. 若分式293x x--的值为0,则实数x 的值为__________. 12. 请写出一个图象与直线y =x 无交点的反比例函数的表达式:___________.13. 2022年在北京—张家口举办冬季奥运会,北京成为世界上第一个既举办夏季奥运会,又举办冬季奥运会的城市.某队要从两名选手中选取一名参加比赛,为此对这两名队员进行了五次测试,测试成绩如图所示,我们可以判断_______选手的成绩更稳定.(填A 或B ).14. 如图,点C 在AB ︵上,若AB=1+,ACBAC =45°,则BC ︵的长度为___________.第14题图 第15题图 15. (2021盐城)如图,在矩形ABCD 中,AB =3,AD =4,E ,F 分别是边BC ,CD 上一点,EF ⊥AE ,将△ECF 沿EF 翻折得△EC ′F ,连接AC ′,当BE =___________时,△AEC ′是以AE 为腰的等腰三角形.三、解答题(本大题共8个小题,满分75分)16. (10分)(2021德州)(1)计算:101(π4)4cos603-⎛⎫--︒ ⎪⎝⎭; (2)化简:11a b b a a b ⎛⎫⎛⎫-÷- ⎪ ⎪⎝⎭⎝⎭.图1Q A B C次序CBA C′FE DC B A17. (9分)某校七、八年级各有300名学生,近期对他们“新型冠状病毒”防治知识进行了线上测试,为了了解他们的掌握情况,从七、八年级各随机抽取了50名学生的成绩(百分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息:a .七年级的频数分布直方图如下(数据分为5组:50≤x <60,60≤x <70,70≤x <80,80≤x <90,90≤x ≤100):b .七年级学生成绩在80≤x <90的这一组是:80 80.5 81 82 82 83 83.5 84 84 85 86 86.5 87 88 89 89c .七、八年级学生成绩的平均数、中位数、众数如下:(1)表中m 的值为_____________;(2)在随机抽样的学生中,防治知识成绩为84分的学生,在________年级排名更靠前,理由是_____________________________________________;(3)若各年级防治知识的前90名将参加线上防治知识竞赛,预估七年级分数至少达到________分的学生才能入选.18. (9分)如图,A ,B 两点在双曲线k y x(x >0)的图象上,已知点A (1,4),B (52,m ),分别经过A ,B 两点向坐标轴作垂线段,得到三个矩形:记阴影部分矩形面积为S ,另两个矩形面积分别记为S 1,S 2.(1)求反比例函数解析式及m 的值;(2)求S 1+S 2的值./分19. (9分)(2021成都)越来越多太阳能路灯的使用,既点亮了城市的风景,也是我市积极落实节能环保的举措.某校学生开展综合实践活动,测量太阳能路灯电池板离地面的高度.如图,已知测倾器的高度为1.6米,在测点A 处安置测倾器,测得点M 的仰角∠MBC =33°,在与点A 相距3.5米的测点D 处安置测倾器,测得点M 的仰角∠MEC =45°(点A ,D 与N 在一条直线上),求电池板离地面的高度MN 的长.(结果精确到1米;参考数据:sin33°≈0.54,cos33°≈0.84,tan33°≈0.65)20. (9分)(2020德州)如图,点C 在以AB 为直径的⊙O 上,点D 是半圆AB 的中点,连接AC ,BC ,AD ,BD ,过点D 作DH ∥AB 交CB 的延长线于点H .(1)求证:直线DH 是⊙O 的切线;(2)若AB =10,BC =6,求AD ,BH 的长.E D CBA N M33°45°D21.(9分)某电器超市销售每台进价分别为200元,170元的A,B两种型号的电风扇,表中是近两周的销售情况:(1)求A,B两种型号的电风扇的销售单价;(2)若超市准备用不多于5 400元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1 400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.22.(10分)已知抛物线y=ax2-2ax-8(a≠0)经过点(4,0).(1)求抛物线的函数表达式和顶点坐标.(2)直线l交抛物线于点A(-2,m),B(n,-5),n为正数.①若点P在抛物线上且在直线l下方(不与点A,B重合),求点P纵坐标y P的取值范围;②平移抛物线y=ax2-2ax-8,使其顶点在直线l上,求平移后所得抛物线与y轴交点纵坐标的最小值.23. (10分)综合与实践数学活动课上,老师让同学们结合下述情境,提出一个数学问题:如图1,四边形ABCD 是正方形,四边形BEDF 是矩形.探究展示:“兴趣小组”提出的问题是:“如图2,连接CE .求证:AE ⊥CE .”并展示了如下的证明方法: 证明:如图3,分别连接AC ,BD ,EF ,AF .设AC 与BD 相交于点O .∵四边形ABCD 是正方形,∴OA =OC =12AC ,OB =OD =12BD ,且AC =BD . 又∵四边形BEDF 是矩形.∴EF 经过点O ,∴OE =OF =12EF ,且EF =BD . ∴OE =OF ,OA =OC .∴四边形AECF 是平行四边形.(依据1)∵AC =BD ,EF =BD ,∴AC =EF .∴四边形AECF 是矩形.(依据2)∴∠CEA =90°,即AE ⊥CE .反思交流:(1)上述证明过程中“依据1”,“依据2”分别是什么?拓展再探:(2)“创新小组”受到“兴趣小组”的启发,提出的问题是:“如图4,分别延长AE ,FB 交于点P ,求证:EB =PB .”请你帮助他们写出该问题的证明过程.(3)“智慧小组”提出的问题是:若∠BAP =30°,AE1,求正方形ABCD 的面积.请你解决“智慧小组”提出的问题.图1FED C B A图2F E D C B A 图3O F E DC B A P图4FED C BA。
河南省新乡市中考数学一模试卷
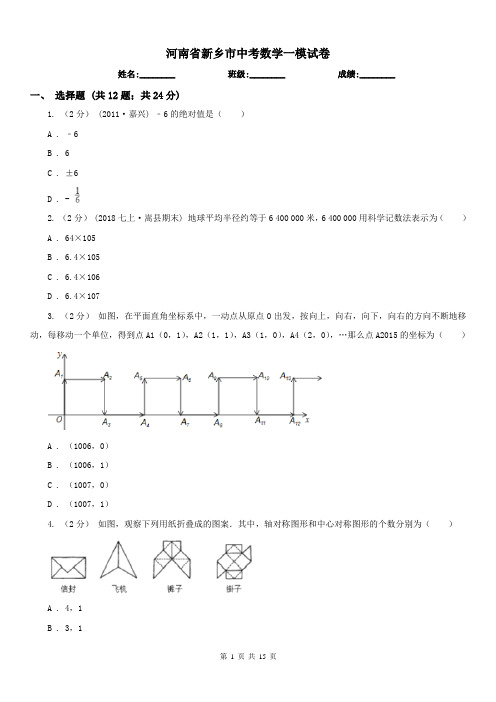
河南省新乡市中考数学一模试卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分)(2011·嘉兴) ﹣6的绝对值是()A . ﹣6B . 6C . ±6D . -2. (2分) (2018七上·嵩县期末) 地球平均半径约等于6 400 000米,6 400 000用科学记数法表示为()A . 64×105B . 6.4×105C . 6.4×106D . 6.4×1073. (2分)如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…那么点A2015的坐标为()A . (1006,0)B . (1006,1)C . (1007,0)D . (1007,1)4. (2分)如图,观察下列用纸折叠成的图案.其中,轴对称图形和中心对称图形的个数分别为()A . 4,1B . 3,1C . 2,2D . 1,35. (2分)(2018·丹棱模拟) 下列说法正确的是()A . 打开电视,它正在播放广告是必然事件B . 要考察一个班级中的学生某天完成家庭作业的情况适合抽样调查C . 甲、乙两人射中环数的方差分别为,说明乙的射击成绩比甲稳定D . 在抽样调查中,样本容量越大,对总体的估计就越准确6. (2分)如图,△ABC中,P为AB上一点,在下列四个条件中:①∠ACP=∠B;②∠APC=∠ACB;③AC2=AP•AB;④AB•CP=AP•CB,能满足△APC与△ACB相似的条件是()A . ①②④B . ①③④C . ②③④D . ①②③7. (2分)关于x的方程组的解是,则的值是()A . 5B . 3C . 2D . 18. (2分)如图所示的几何体是由六个相同的小正方体组合而成的,它的俯视图是()A .B .C .D .9. (2分)(2016·海拉尔模拟) 一组数据:2,4,5,6,x的平均数是4,则这组数的方差是()A .B . 2C . 10D .10. (2分)在平面直角坐标系中,已知线段AB的两个端点分别是A(4 ,-1),B(1,1),线段AB平移后得到线段A 'B',若点A'的坐标为 (-2 ,2 ) ,则点 B'的坐标为()A . (-5 ,4 )B . (4 ,3 )C . (-1 ,-2 )D . (-2,-1)11. (2分)如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①a>0 ②2a+b=0③a+b+c>0 ④当﹣1<x<3时,y>0其中正确的个数为()A . 1B . 2C . 3D . 412. (2分)(2016·济宁) 如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,sin∠AOB= ,反比例函数y= 在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于()A . 60B . 80C . 30D . 40二、填空题 (共6题;共6分)13. (1分)边长为1的正六边形的外接圆半径是________.14. (1分)(2016·南岗模拟) 把多项式a3b﹣6a2b+9ab因式分解,最后结果等于________.15. (1分)(2018·濠江模拟) 已知关于x的方程有两个相等的实数根,那么m = ________16. (1分) (2018九下·湛江月考) 圆锥底面圆的半径为2,侧面展开图的半径为5,则侧面展开图的圆心角是________.17. (1分)若函数y=(m+2)x|m|﹣3是反比例函数,则m的值为________ .18. (1分)一家医院某天出生了3个婴儿,假设生男生女的机会相同,那么这3个婴儿中,出现2个男婴、1个女婴的概率是________三、计算题 (共9题;共81分)19. (5分)(2019·潮南模拟) 计算: +(π﹣2019)0﹣(﹣)﹣2﹣4cos30°20. (5分)计算:+﹣2sin60°+|tan60°﹣2|21. (10分)(2016·鄞州模拟) 如图,在平行四边形ABCD中,对角线AC,BD并于点O,经过点O的直线交AB于E,交CD于F.(1)求证:OE=OF.(2)连接DE,BF,则EF与BD满足什么条件时,四边形DEBF是矩形?请说明理由.22. (15分)已知:一次函数y=﹣2x+10的图象与反比例函数(k>0)的图象相交于A,B两点(A在B 的右侧).(1)当A(4,2)时,求反比例函数的解析式及B点的坐标;(2)在1的条件下,反比例函数图象的另一支上是否存在一点P,使△PAB是以AB为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.(3)当A(a,﹣2a+10),B(b,﹣2b+10)时,直线OA与此反比例函数图象的另一支交于另一点C,连接BC交y 轴于点D.若,求△ABC的面积.23. (11分)某校为了解学生孝敬父母的情况,在全校范围内随机抽取了若干名学生进行调查,调查的内容包括:A.帮父母做家务;B.给父母买礼物;C.陪父母聊天、散步;D.其他.调查结果如图:根据以上信息解答下列问题:(1)该校共调查了________ 名学生;(2)请把条形统计图补充完整;(3)若该校有2000名学生,估计该校全体学生中选择C选项的有多少人?24. (5分)根据下列语句,画出图形.(1)已知如图1,四点A,B,C,D.①画直线AB;②连接AC、BD,相交于点O;③画射线AD,BC,交于点P.(2)如图2,已知线段a,b,画一条线段,使它等于2a﹣b(不要求写画法).25. (5分)某市为了改善市区交通状况,计划修建一座新大桥,如图,新大桥的两端位于A、B两点,小张为了测量A、B之间的河宽,在垂直与新大桥AB的直线型道路l上测得如下数据:∠BDA=76.1°,∠BCA=68.2°,CD=82米.求AB的长(精确到0.1米,sin76.1°≈0.97,cos76.1°≈0.24,tan76.1°≈4.0;sin68.2°≈0.93,cos68.2°≈0.37,tan68.2°≈2.5.)26. (10分)(2016·鄞州模拟) 如图,已知边长为6的等边△ABC内接于⊙O.(1)求⊙O半径;(2)求的长和弓形BC的面积.27. (15分)(2017·兴庆模拟) 如图,BD是正方形ABCD的对角线,BC=2,边BC在其所在的直线上平移,将通过平移得到的线段记为PQ,连接PA、QD,并过点Q作QO⊥BD,垂足为O,连接OA、OP.(1)请直接写出线段BC在平移过程中,四边形APQD是什么四边形?(2)请判断OA、OP之间的数量关系和位置关系,并加以证明;(3)在平移变换过程中,设y=S△OPB,BP=x(0≤x≤2),求y与x之间的函数关系式,并求出y的最大值.参考答案一、选择题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共6题;共6分)13-1、14-1、15-1、16-1、17-1、18-1、三、计算题 (共9题;共81分)19-1、20-1、21-1、21-2、22-1、23-1、23-2、23-3、24-1、25-1、26-1、26-2、27-1、27-2、27-3、。
2022年河南省中考数学模拟调研试卷(附答案详解)

2022年河南省中考数学模拟调研试卷一、选择题(本大题共10小题,共30.0分)1.√(−3)2的化简结果为()A. 3B. −3C. ±3D. 92.已知点A(m−1,3)与点B(2,n+1)关于x轴对称,则m+n的值为()A. −1B. −7C. 1D. 73.一个不透明的袋子中有黄色和若干个白色的两种小球,这些球除颜色外其他完全相同,已知黄球有9个,每次摸球前先将袋子中的球摇匀,任意摸出一个球记下颜色后,放回袋中,再摇匀,再摸,通过大量重复摸球后发现,摸到黄球的频率稳定在30%,估计袋子中白球的个数是()A. 15B. 18C. 20D. 214.如图,一艘轮船在A处测得灯塔P位于其北偏东60°方向上,轮船沿正东方向航行30海里到达B处后,此时测得灯塔P位于其北偏东30°方向上,此时轮船与灯塔P的距离是()A. 15√3海里B. 30海里C. 45海里D. 30√3海里5.将抛物线y=12x2−6x+21向左平移2个单位后,得到新抛物线的解析式为()A. y=12(x−8)2+5 B. y=12(x−4)2+5C. y=12(x−8)2+3 D. y=12(x−4)2+36.如图,△ABC内接于⊙O,∠B=65°,∠C=70°.若BC=2√2,则BC⏜的长为()A. πB. √2πC. 2πD. 2√2π7.以x为自变量的二次函数y=x2−2(b−2)x+b2−1的图象不经过第三象限,则实数b的取值范围是()A. b ≥54B. b ≥1或b ≤−1C. b ≥2D. 1≤b ≤28. 二次函数y =−(x −1)2+5,当m ≤x ≤n 且mn <0时,y 的最小值为2m ,最大值为2n ,则m +n 的值为( )A. 52B. 2C. 32D. 12 9. 如图▱ABCD ,F 为BC 中点,延长AD 至E ,使DE :AD =1:3,连结EF 交DC 于点G ,则S △DEG :S △CFG =( )A. 2:3B. 3:2C. 9:4D. 4:910. 如图,在菱形ABCD 中,∠ABC =60°,AB =4,点E 是AB边上的动点,过点B 作直线CE 的垂线,垂足为F ,当点E 从点A 运动到点B 时,点F 的运动路径长为( )A. √3B. 2√3C. 23πD. 43π二、填空题(本大题共5小题,共15.0分)11. 从2,3,4,6中随机选取两个数记作a 和b(a <b),那么点(a,b)在直线y =2x 上的概率是______.12. 如图,在△ABC 中,sinB =13,tanC =√22,AB =3,则AC 的长为______.13. 若关于x 的一元二次方程ax 2+2x −1=0无解,则a 的取值范围是______ .14. 如图,△ABC 是等腰直角三角形,∠ACB =90°,AC =BC =2,把△ABC 绕点A 按顺时针方向旋转45°后得到△AB′C′,则线段BC 在上述旋转过程中所扫过部分(阴影部分)的面积是______.15.如图,二次函数解析式为y=Ax2+Bx+C(A≠0),则下列命题中正确的有______(填序号).①ABC>0;②B2<4AC;③4A−2B+C>0;④2A+B>C.三、解答题(本大题共8小题,共75.0分)16.解方程:(1)x2−2x−3=0;(2)3x2−2√3x=−1.17.某市对当年初中升高中数学考试成绩进行抽样分析,试题满分100分,将所得成绩(均为整数)整理后,绘制了如图所示的统计图,根据图中所提供的信息,回答下列问题:(1)共抽取了多少名学生的数学成绩进行分析;(2)如果80分以上(包括80分)为优生,估计该年的优生率为多少?(3)该年全市共有22000人参加初中升高中数学考试,请你估计及格(60分及60分以上)人数大约为多少?18.某数学兴趣小组去测量一座小山的高度,在小山顶上有一高度为20米的发射塔AB,如图所示.在山脚平地上的D处测得塔底B的仰角为30°,向小山前进80米到达点E处,测得塔顶A的仰角为60°,求小山BC的高度.19.已知关于x的一元二次方程x2+2x−k=0有两个不相等的实数根.(1)求k的取值范围;(2)若方程的两个不相等的实数根是a,b,求aa+1−1b+1的值.20.如图,AB是⊙O的直径,C为⊙O上一点,PC切⊙O于C,AE⊥PC交PC的延长线于E,AE交⊙O于D,PC与AB的延长线相交于点P,连接AC、BC.(1)求证:AC平分∠BAD;(2)若PB:PC=1:2,PB=4,求AB的长.21.毕业季即将到来,某礼品店购进了一批适合大学生的毕业纪念品,该礼品店用4000元购进A种礼品若干件,用8400元购进B种礼品若干件,所购B种礼品的数量比A种礼品的数量多10件,且B种礼品每件的进价是A种礼品每件进价的1.4倍.(1)A、B两种礼品每件的进价分别为多少元?(2)礼品店第一次所购礼品全部售完后,再次购进A、B两种礼品(进价不变),其中A种礼品购进的数量在第一次的基础上增加了2a%,售价在进价的基础上提高了0.9a%;B种礼品购进的数量在第一次的基础上增加了2a%,售价在进价的基础上提高了a%.全部售出后,第二次所购礼品的利润为12000元(不考虑其他因素),求第二次购进A、B两种礼品各多少件?22.如图,已知锐角三角形ABC内接于圆O,OD⊥BC于点D,连接OA.(1)若∠BAC=60°,OA.①求证:OD=12②当OA=1时,求△ABC面积的最大值.(2)点E在线段OA上,OE=OD,连接DE,设∠ABC=m∠OED,∠ACB=n∠OED(m,n是正数),若∠ABC<∠ACB,求证:m−n+2=0.23.如图,二次函数y=x2+bx+c的图象与x轴交于A,B两点,与y轴交于点C,且关于直线x=1对称,点A的坐标为(−1,0).(1)求二次函数的表达式;(2)连接BC,若点P在y轴上时,BP和BC的夹角为15°,求线段CP的长度;(3)当a≤x≤a+1时,二次函数y=x2+bx+c的最小值为2a,求a的值.答案和解析1.【答案】A【解析】解:原式=|−3|=3.故选:A.直接根据√a2=|a|进行计算即可.本题考查了二次根式的计算与化简:√a2=|a|.2.【答案】A【解析】【分析】本题比较容易,考查平面直角坐标系中两个关于坐标轴成轴对称的点的坐标特点:关于x轴对称的点,横坐标相同,纵坐标互为相反数.本题考查了对称点的坐标规律:(1)关于x轴对称的点,横坐标相同,纵坐标互为相反数;(2)关于y轴对称的点,纵坐标相同,横坐标互为相反数;(3)关于原点对称的点,横坐标与纵坐标都互为相反数.【解答】解:∵点A(m−1,3)与点B(2,n+1)关于x轴对称,∴{m−1=2n+1+3=0,∴{m=3n=−4,∴m+n=3+(−4)=−1.故选A.3.【答案】D【解析】【分析】根据概率的求法,找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率即可.此题考查了利用概率的求法估计总体个数,利用如果一个事件有n种可能,而且这些事是解题关键.件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=mn【解答】解:∵通过大量重复摸球实验后发现,摸到黄球的频率稳定在30%,∴根据题意任意摸出1个,摸到黄色乒乓球的概率是:30%,设袋中白色乒乓球的个数为a个,.则30%=9a+9解得:a=21,∴白色乒乓球的个数为:21个.故选D.4.【答案】B【解析】【分析】本题考查了方位角和等腰三角形的性质,属于基础题.易得∠APB=180°−30°−120°=30°=∠BAP,根据等腰三角形的性质可得BP= AB=30;【解答】解:由图可知∠BAP=30°,∠ABP=90°+30°=120°所以∠APB=180°−30°−120°=30°=∠BAP,所以BP=AB=30(海里),故选:B.5.【答案】D【解析】解:y=12x2−6x+21=12(x2−12x)+21=12[(x−6)2−36]+21=12(x−6)2+3,故y=12(x−6)2+3,向左平移2个单位后,得到新抛物线的解析式为:y=12(x−4)2+3.故选:D.直接利用配方法将原式变形,进而利用平移规律得出答案.此题主要考查了二次函数图象与几何变换,正确配方将原式变形是解题关键.6.【答案】A【解析】【分析】本题考查圆周角定理,弧长公式,等腰直角三角形的性质的等知识,解题的关键是熟练掌握基本知识,属于常考题.连接OB,OC,首先证明△OBC是等腰直角三角形,求出OB即可解决问题.【解答】解:连接OB,OC.∵∠A=180°−∠ABC−∠ACB=180°−65°−70°=45°,∴∠BOC=90°,∵BC=2√2,∴OB=OC=2,=π,∴BC⏜的长为90×π×2180故选:A.7.【答案】A【解析】【分析】此题主要考查了二次函数的图象和性质,解题的关键是会根据图象的位置得到关于b的不等式组解决问题.由于二次函数y=x2−2(b−2)x+b2−1的图象不经过第三象限,所以抛物线的顶点在x轴的上方或在x轴的下方经过一、二、四象限,根据二次项系数知道抛物线开口方向向上,由此可以确定抛物线与x轴有无交点,抛物线与y轴的交点的位置,由此即可得出关于b的不等式组,解不等式组即可求解.【解答】解:∵二次函数y=x2−2(b−2)x+b2−1的图象不经过第三象限,∵二次项系数a=1,∴抛物线开口方向向上,当抛物线的顶点在x轴上方时,则b2−1≥0,△=[2(b−2)]2−4(b2−1)≤0,解得b≥5;4当抛物线的顶点在x轴的下方时,设抛物线与x轴的交点的横坐标分别为x1,x2,∴x1+x2=2(b−2)>0,b2−1>0,∴△=[2(b−2)]2−4(b2−1)>0,①b−2>0,②b2−1≥0,③由①得b<5,由②得b>2,4∴此种情况不存在,∴b≥5,4故选:A.8.【答案】D【解析】解:二次函数y=−(x−1)2+5的大致图象如下:.①当m≤0≤x≤n<1时,当x=m时y取最小值,即2m=−(m−1)2+5,解得:m=−2.当x=n时y取最大值,即2n=−(n−1)2+5,解得:n=2或n=−2(均不合题意,舍去);②当m≤0≤x≤1≤n时,当x=m时y取最小值,即2m=−(m−1)2+5,解得:m=−2.当x=1时y取最大值,即2n=−(1−1)2+5,解得:n=52,或x=n时y取最小值,x=1时y取最大值,2m=−(n−1)2+5,n=52,∴m=118,∵m<0,∴此种情形不合题意,所以m+n=−2+52=12.故选:D.条件m≤x≤n和mn<0可得m<0,n>0所以y的最小值为2m为负数,最大值为2n为正数.最大值为2n分两种情况,(1)结合抛物线顶点纵坐标的取值范围,求出n=2.5,结合图象最小值只能由x=m时求出.(2)结合抛物线顶点纵坐标的取值范围,图象最大值只能由x=n求出,最小值只能由x= m求出.本题考查了二次函数的最值问题,二次函数的增减性,根据函数解析式求出对称轴解析式是解题的关键.9.【答案】D【解析】【分析】本题主要考查了相似三角形的判定和性质,平行四边形的性质,中点的定义.表示出CF是解题的关键.先设出DE=x,进而得出AD=3x,再用平行四边形的性质得出BC=3x,进而求出CF,最后用相似三角形的性质即可得出结论.【解答】解:设DE=x,∵DE:AD=1:3,∴AD=3x,∵四边形ABCD是平行四边形,∴AD//BC,BC=AD=3x,∵点F是BC的中点,∴CF=12BC=32x,∵AD//BC,∴△DEG∽△CFG,∴S△DEGS△CFG =(DECF)2=(x32x)2=49,故选:D.10.【答案】D【解析】解:如图,连接AC、BD交于点G,连接OG.∵BF⊥CE,∴∠BFC=90°,∴点F的运动轨迹在以边长BC为直径的⊙O上,当点E从点A运动到点B时,点F的运动路径长为BG⏜,∵四边形ABCD是菱形,∴AB=BC=CD=AD=4,∵∠ABC=60°,∴∠BCG=60°,∴∠BOG=120°,∴BG⏜的长=120⋅π⋅2180=43π,故选:D.如图,连接AC、BD交于点G,连接OG.首先说明点E从点A运动到点B时,点F的运动路径长为BG⏜,求出圆心角,半径即可解决问题.本题考查菱形的性质、弧长公式、轨迹等知识,解题的关键是正确寻找点F的运动轨迹,属于中考常考题型.11.【答案】13【解析】解:画树状图如图所示,一共有6种情况,b=2a的有(2,4)和(3,6)两种,所以点(a,b)在直线y=2x上的概率是26=13,故答案为:13.画出树状图,找到b=2a的结果数,再根据概率公式解答本题考查了一次函数图象上点的坐标特征,列表法与树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.12.【答案】√3【解析】【分析】此题考查了解直角三角形,涉及的知识有:锐角三角函数定义,以及勾股定理,熟练掌握各自的性质是解本题的关键.过A作AD垂直于BC,在直角三角形ABD中,利用锐角三角函数定义求出AD的长,在直角三角形ACD中,利用锐角三角函数定义求出CD的长,再利用勾股定理求出AC的长即可.【解答】解:过A作AD⊥BC,在Rt△ABD中,sinB=13,AB=3,∴AD=AB⋅sinB=1,在Rt△ACD中,tanC=√22,∴ADCD =√22,即CD=√2,根据勾股定理得:AC=√AD2+CD2=√1+2=√3,故答案为√3.13.【答案】a<−1【解析】解:∵关于x的一元二次方程ax2+2x−1=0无解,∴a≠0且△=22−4×a×(−1)<0,解得a<−1,∴a的取值范围是a<−1.故答案为:a<−1.根据一元二次方程的定义和根的判别式的意义得到a≠0且△=22−4×a×(−1)<0,然后求出a的取值范围.本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2−4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了一元二次方程的定义.14.【答案】12π【解析】【分析】本题考查了扇形面积的计算:阴影面积的主要思路是将不规则图形面积转化为规则图形的面积.也考查了等腰直角三角形的性质和旋转的性质.先根据等腰直角三角形的性质得到∠BAC=45°,AB=√2AC=2√2,再根据旋转的性质得∠BAB′=∠CAC′=45°,则点B′、C、A共线,然后根据扇形门口计算,利用线段BC 在上述旋转过程中所扫过部分(阴影部分)的面积=S扇形BAB′−S扇形CAC′进行计算即可.【解答】解:∵△ABC是等腰直角三角形,∴∠BAC=45°,AB=√2AC=2√2,∵△ABC绕点A按顺时针方向旋转45°后得到△AB′C,∴∠BAB′=∠CAC′=45°,∴点B′、C、A共线,∴线段BC在上述旋转过程中所扫过部分(阴影部分)的面积=S扇形BAB′+S△AB′C−S扇形CAC′−S△ABC=S扇形BAB′−S扇形CAC′=45⋅π⋅(2√2)2360−45⋅π⋅22360=1 2π.故答案为12π.15.【答案】①③④【解析】解:∵抛物线开口向上,∴A>0,∵对称轴x=−B2A>0,∴B<0,∵抛物线与y轴交于负半轴,∴C<0,∴ABC>0,①命题正确;∵抛物线与x轴有两个交点,∴B2−4AC>0,∴B2>4AC,②命题不正确;∵当x=−2时,y>0,∴4A−2B+C>0,③命题正确;由图可知A−B+C<0,故C<B−A<B+2A,④命题正确.故答案为:①③④.根据二次函数对称轴、开口方向、与y轴的交点,可以判定A、B、C的符号;根据图象与x轴交点情况可以判断B2−4AC的符号;根据特殊点的位置再判断剩下两个式子的符号.本题考查命题和二次函数的图象的性质.解决本题的关键在于根据图象开口方向、对称轴、与坐标轴交点、图像上特殊点的的位置,列出关系式来判定各命题是否正确.16.【答案】解:(1)(x−3)(x+1)=0,x−3=0或x+1=0,所以x1=3,x2=−1;(2)3x2−2√3x+1=0,Δ=(−2√3)2−4×3×1=0,x=−b±√b2−4ac2a =2√3±02×3=√33,所以x1=x2=√33.【解析】(1)利用因式分解法解方程;(2)先把方程化为一般式,然后利用求根公式解方程.本题考查了解一元二次方程−因式分解法:因式分解法就是利用因式分解求出方程的解的方法,这种方法简便易用,是解一元二次方程最常用的方法.也考查了公式法.17.【答案】解:(1)根据题意有30+35+45+60×2+70=300;答:共抽取了300名学生的数学成绩进行分析;(2)从表中可以看出80分以上(包括80分)的人数有35+70=105,共300人;所以优生率是105÷300=35%;答:该年的优生率为35%.(3)从表中可以看出及格人数为300−30−60=210人,则及格率=210÷300=70%,所以22000人中的及格人数是22000×70%=15400(名);答:全市及格的人数有15400人.【解析】本题是一道利用统计知识解答实际问题的重点考题,计算量略大,难度中等.主要考查利用统计图表,处理数据的能力和利用样本估计总体的思想.解答这类题目,观察图表要细致,对应的图例及其关系不能错位,计算要认真准确.(1)从表中读出学生数,相加可得学生总数;(2)从表中成绩这一坐标中先找到80分以上(包括80分)的人数,再除以总数,得出优生率.(3)先从表中查出及格率,再计算全市共有22000人的及格人数.18.【答案】解:设BC为x米,则AC=(20+x)米,由条件知:∠DBC=∠AEC=60°,DE=80米.在直角△DBC中,tan60°=DCBC=DCx,则DC=√3x米.∴CE=(√3x−80)米.在直角△ACE中,tan60°=ACCE =20+x√3x−80=√3.解得x=10+40√3.答:小山BC的高度为(10+40√3)米.【解析】设BC为x米,则AC=(20+x)米,通过解直角△DBC和直角△ACE列出关于x的方程,利用方程求得结果.本题考查的是解直角三角形的应用−仰角俯角问题,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.19.【答案】解:(1)∵方程有两个不相等的实数根,∴△=b2−4ac=4+4k>0,解得k>−1.∴k的取值范围为k>−1;(2)由根与系数关系得a+b=−2,a⋅b=k,a a+1−1b+1=ab−1ab+a+b+1=k−1k−2+1=1.【解析】(1)根据方程有两个不相等的实数根可得△=4+4k>0,解不等式求出k的取值范围;(2)由根与系数的关系可得a+b=−2,a⋅b=k,代入整理后的代数式,计算即可.此题考查了一元二次方程ax2+bx+c=0根的判别式和根与系数的关系的应用,(1)△>0时,方程有两个不相等的实数根;(2)△=0时,方程有两个相等的实数根;(3)△<0时,方程没有实数根;(4)x1+x2=−ba ,x1⋅x2=ca.20.【答案】解:(1)如图所示:连接OC.∵PC是⊙O的切线,∴OC⊥EP.又∵AE⊥PC,∴AE//OC.∴∠EAC=∠ACO.又∵∠ACO=∠OAC,∴∠EAC=∠OAC.∴AC平分∠BAD;(2)∵AB是⊙O的直径,∴∠ACB=90°,∴∠BAC+∠ABC=90°.∵OB=OC,∴∠OCB=∠ABC.∵∠PCB+∠OCB=90°,∴∠PCB=∠PAC.∵∠P=∠P,∴△PCA∽△PBC,∴PCPB =PAPC,∴PA=PC2PB=16.∴AB=PA−PB=16−4=12.【解析】(1)先AE//OC,然后依据平行线的性质可得到∠EAC=∠ACO.,接下来由∠ACO=∠AOC,可证明∠EAC=∠OAC;(2)先证明∠PCB=∠PAC,从而可证明△PCA∽△PBC,依据相似三角形的性质可求得PA 的长,最后依据AB=PA−PB求解即可.本题主要考查的是相似三角形的性质和判定、切线的性质、圆周角定理的应用,熟练掌握相关定理是解题的关键.21.【答案】解:(1)设A种礼品每件的进价为x元,则B种礼品每件的进价为1.4x元,依题意得:84001.4x −4000x=10,解得:x=200,经检验,x=200是原方程的解,且符合题意,∴1.4x=280(元).答:A种礼品每件的进价为200元,B种礼品每件的进价为280元.(2)第一次购进A种礼品的数量为4000÷200=20(件),第一次购进B种礼品的数量为8400÷280=30(件).依题意得:200×0.9a%×20(1+2a%)+280×a%×30(1+2a%)=12000,整理得:a2+50a−5000=0,解得:a1=−100(不合题意,舍去),a2=50,∴20(1+2a%)=40(件),30(1+2a%)=60(件).答:第二次购进A种礼品40件,B种礼品60件.【解析】(1)设A种礼品每件的进价为x元,则B种礼品每件的进价为1.4x元,根据数量=总价÷单价,结合所购B种礼品的数量比A种礼品的数量多10件,即可得出关于x的分式方程,解之经检验后即可得出结论;(2)利用数量=总价÷单价,可分别求出第一次购进A,B两种礼品的数量,利用总利润=每件礼品的利润×销售数量,即可得出关于a的一元二次方程,解之即可得出a的值,将其正值分别代入20(1+2a%)和30(1+2a%)中即可求出结论.本题考查了分式方程的应用以及一元二次方程的应用,解题的关键是:(1)找准等量关系,正确列出分式方程;(2)找准等量关系,正确列出一元二次方程.22.【答案】解:(1)①连接OB、OC,则∠BOD=12∠BOC=∠BAC=60°,∴∠OBC=30°,∴OD=12OB=12OA;②∵BC长度为定值,∴求△ABC面积的最大值,要求BC边上的高最大,当AD过点O时,AD最大,即:AD=AO+OD=32,根据勾股定理求出BD=√32,△ABC面积的最大值=12×BC×AD=12×2BD×32=3√34;(2)如图2,连接OC,设:∠OED =x ,则∠ABC =mx ,∠ACB =nx ,则∠BAC =180°−∠ABC −∠ACB =180°−mx −nx =12∠BOC =∠DOC , ∵∠AOC =2∠ABC =2mx ,∴∠AOD =∠COD +∠AOC =180°−mx −nx +2mx =180°+mx −nx , ∵OE =OD ,∴∠AOD =180°−2x ,即:180°+mx −nx =180°−2x ,化简得:m −n +2=0.【解析】(1)①连接OB 、OC ,则∠BOD =12∠BOC =∠BAC =60°,即可求解;②BC 长度为定值,△ABC 面积的最大值,要求BC 边上的高最大,即可求解;(2)∠BAC =180°−∠ABC −∠ACB =180°−mx −nx =12∠BOC =∠DOC ,而∠AOD =∠COD +∠AOC =180°−mx −nx +2mx =180°+mx −nx ,即可求解.本题为圆的综合运用题,涉及到30°直角三角形的性质、三角形内角和公式,其中(2)∠AOD =∠COD +∠AOC 是本题容易忽视的地方.23.【答案】解:(1)∵点A(−1,0)与点B 关于直线x =1对称,∴点B 的坐标为(3,0),代入y =x 2+bx +c ,得:{1−b +c =09+3b +c =0, 解得{b =−2c =−3, 所以二次函数的表达式为y =x 2−2x −3;(2)如图所示:由抛物线解析式知C(0,−3),则OB=OC=3,∴∠OBC=45°,若点P在点C上方,则∠OBP=∠OBC−∠PBC=30°,∴OP=√33OB=3×√33=√3,∴CP=3−√3;若点P在点C下方,则∠OBP′=∠OBC+∠P′BC=60°,∴OP’=√3OB=3√3,∴CP=3√3−3;综上,CP的长为;(3)若a+1<1,即a<0,则函数的最小值为(a+1)2−2(a+1)−3=2a,解得a=1−√5(正值舍去);若a<1<a+1,即0<a<1,则函数的最小值为1−2−3=2a,解得:a=−2(舍去);若a>1,则函数的最小值为a2−2a−3=2a,解得a=2+√7(负值舍去);综上,a的值为1−√5或2+√7.【解析】(1)先根据题意得出点B的坐标,再利用待定系数法求解可得;(2)分点P在点C上方和下方两种情况,先求出∠OBP的度数,再利用三角函数求出OP的长,从而得出答案;(3)分对称轴x=1在a到a+1范围的右侧、中间和左侧三种情况,结合二次函数的性质求解可得.本题是二次函数的综合问题,解题的关键是掌握待定系数法求函数解析式、三角函数的运用、二次函数的图象与性质及分类讨论思想的运用.。
河南省新乡市中考数学一模试卷

河南省新乡市中考数学一模试卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分) (2019八上·海港期中) 下列几种说法正确的有()①无理数都是无限小数;②带根号的数是无理数;③实数分为正实数和负实数;④无理数包括正无理数、0和负无理数。
A . ①②③④B . ②③C . ①④D . ①2. (2分)(2017·延边模拟) 2016年10月17日,神州十一号飞船成功发射升空.发射当天约有161000个相关精彩栏目的热门视频在网络上热播.将数据161000用科学记数法表示为()A . 1.61×103B . 0.161×105C . 1.61×105D . 16.1×1043. (2分)如图,AB∥CD,FE⊥DB,垂足为E,∠1=50°,则∠2的度数是()A . 60°B . 50°C . 40°D . 30°4. (2分)如图,10×2网格中有一个△ABC,图中与△ABC相似的三角形的个数有()A . 1个B . 2个C . 3个5. (2分)(2016·河池) 下列四个几何体中,主视图为圆的是()A .B .C .D .6. (2分)下列二次根式中,与的乘积为有理数的是()A .B .C .D .7. (2分) (2020九上·南宁期末) 如图,是矩形内的任意一点,连接、、、, 得到 , , , ,设它们的面积分别是,,,,给出如下结论:①② ③若,则④若,则点在矩形的对角线上.其中正确的结论的序号是()A . ①②B . ②③8. (2分)下列说法中,正确的说法有()①对角线互相平分且相等的四边形是菱形;②一元二次方程x2﹣3x﹣4=0的根是x1=4,x2=﹣1;③依次连结任意四边形各边中点所得的四边形是平行四边形;④一元一次不等式2x+5≤11的整数解有3个;⑤某班演讲比赛,共有甲、乙、丙三位选手,班主任让三位选手抽签决定演讲先后顺序,从先到后恰好是甲、乙、丙的概率是.A . 1个B . 2个C . 3个D . 4个9. (2分) (2019九上·沙坪坝月考) 如图,平行四边形AOBC中,对角线交于点E,双曲线经过A、E两点,若平行四边形AOBC的面积为12,则k()A . 2B . 4C .D . 810. (2分)有下列说法:①一元二次方程x2+px-1=0不论p为何值必定有两个不相同的实数根;②若,则一元二次方程ax2+bx+c=0必有一根为-2;③代数式有最小值1;④有两边和第三边上的高对应相等的两个三角形全等;其中正确的是()A . ①④D . ①②③④11. (2分)(2017·濮阳模拟) 一个不透明的袋中,装有2个黄球、3个红球和5个白球,它们除颜色外都相同.从袋中任意摸出一个球,是白球的概率是()A .B .C .D .12. (2分) (2017七下·晋中期末) 下列各式不能成立的是()A . (x2)3=x6B . x2•x3=x5C . (x﹣y)2=(x+y)2﹣4xyD . x2÷(﹣x)2=﹣1二、填空题 (共6题;共6分)13. (1分)(2017·静安模拟) 在实数范围内分解因式:2x2﹣6=________14. (1分)(2012·连云港) 我市某超市五月份的第一周鸡蛋价格分别为7.2,7.2,6.8,7.2,7.0,7.0,6.6(单位:元/kg),则该超市这一周鸡蛋价格的众数为________(元/kg).15. (1分)如图,点A、B、C都在⊙O上,OC⊥OB,点A在劣弧BC上,且OA=AB,则∠ABC=________.16. (1分) (2016九上·海淀期末) 如图,在平面直角坐标系xOy中,△ABC与△ 顶点的横、纵坐标都是整数.若△ABC与△ 是位似图形,则位似中心的坐标是________.17. (1分) (2019八上·深圳开学考) 如图,∠D=∠C=90°,E是DC的中点,AE平分∠DAB,∠DEA=28°,18. (1分) (2019九上·磴口期中) 抛物线y=x2﹣mx﹣m2+1的图象过原点,则m为________.三、解答题 (共8题;共83分)19. (5分)(2018·兰州) 计算:20. (10分) (2020八下·西安期中)(1)解不等式,并把它的解集写在数轴上.(2)解不等式组并写出它的所有整数解.21. (15分) (2017九上·盂县期末) 如图,△ABC在方格纸中(1)请在方格纸上建立平面直角坐标系,使A(2,3),C(6,2),并求出B点坐标;(2)以原点O为位似中心,相似比为2,在第一象限内将△ABC放大,画出放大后的图形△A′B′C′;(3)计算△A′B′C′的面积S.22. (13分) (2020八下·房县期末) 某校初三进行了第三次模拟考试,该校领导为了了解学生的数学考试情况,抽样调查部分学生的数学成绩,并将抽样的数据进行了如下整理:①如下分数段整理样本;等级等级分数段各组总分人数A110<X≤120P4B100<X≤110843nC90<X≤100574mD80<X≤901712②根据左表绘制扇形统计图.(1)填空m=________,n=________,数学成绩的中位数所在的等级________;(2)如果该校有1200名学生参加了本次模拟测,估计D等级的人数;(3)已知抽样调查学生的数学成绩平均分为102分,求A等级学生的数学成绩的平均分数.23. (10分) (2020九上·吴兴期中) 如图,圆内接四边形ABCD,AB是⊙O的直径,OD∥AC交BC于点E.(1)求证:△BCD为等腰三角形;(2)若BE=4,AC=6,求DE.24. (5分)(2020·开远模拟) (列方程解应用题)为提高学生的阅读兴趣,某学校建立了共享书架,并购买了一批书籍.其中购买A种图书花费了3000元,购买B种图书花费了1600元,A种图书的单价是B种图书的1.5倍,购买A种图书的数量比B种图书多20本,求A和B两种图书的单价分别为多少元?25. (10分)如图(1)在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.(1)求证:DE=AD+BE.(2)当直线MN绕点C旋转到图2的位置时,DE、AD、BE又怎样的关系?请直接写出你的结论,不必说明理由.26. (15分)(2016·南充) 如图,抛物线与x轴交于点A(﹣5,0)和点B(3,0).与y轴交于点C(0,5).有一宽度为1,长度足够的矩形(阴影部分)沿x轴方向平移,与y轴平行的一组对边交抛物线于点P和Q,交直线AC于点M和N.交x轴于点E和F.(1)求抛物线的解析式;(2)当点M和N都在线段AC上时,连接MF,如果sin∠AMF= ,求点Q的坐标;(3)在矩形的平移过程中,当以点P,Q,M,N为顶点的四边形是平行四边形时,求点M的坐标.参考答案一、选择题 (共12题;共24分)答案:1-1、考点:解析:答案:2-1、考点:解析:答案:3-1、考点:解析:答案:4-1、考点:解析:答案:5-1、考点:解析:答案:6-1、考点:解析:答案:7-1、考点:解析:答案:8-1、考点:解析:答案:9-1、考点:解析:答案:10-1、考点:解析:答案:11-1、考点:解析:答案:12-1、考点:解析:二、填空题 (共6题;共6分)答案:13-1、考点:解析:答案:14-1、考点:解析:答案:15-1、考点:解析:答案:16-1、考点:解析:答案:17-1、考点:解析:答案:18-1、考点:解析:三、解答题 (共8题;共83分)答案:19-1、考点:解析:答案:20-1、答案:20-2、考点:解析:答案:21-1、答案:21-2、答案:21-3、考点:解析:答案:22-1、答案:22-2、答案:22-3、考点:解析:答案:23-1、答案:23-2、考点:解析:答案:24-1、考点:解析:答案:25-1、答案:25-2、考点:解析:答案:26-1、答案:26-2、答案:26-3、考点:解析:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1页,共28页 2022年河南省新乡市长垣县中考数学一模试卷
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项) 1. 下列各数中,比−2小的数是( )
A. −3 B. −1 C. 0 D. 2
2. 天问一号是我国首个软着陆火星的探测器,它承载着中国人对火星探索的期望.截至2021
年8月19日晚23时20分,天问一号火星探测器距离地球约8230000公里.8230000用科学记数法表示为( ) A. 0.823×10
7 B. 8.23×104 C. 8.23×106 D. 823×104
3. 下列几何体是由4个相同的小正方体搭成的,其中主视图和左视图相同的是( )
A. B. C. D. 4. 下列运算正确的是( )
A. (−𝑎)
2=−𝑎2 B. 2𝑎2−𝑎2=2
C. 𝑎
2⋅𝑎=𝑎3 D. (𝑎−1)2=𝑎2−1
5. 如图,𝐴𝐵//𝐶𝐷,∠𝐴=45°,∠𝐶=30°,则∠𝐸的度数是( )
A. 10°
B. 15°
C. 20°
D. 25°
6. 某校七年级开展“阳光体育”活动,对喜欢乒乓球、足球、篮球、羽毛球的学生人数进
行统计(每人只能选择其中一项),得到如图所示的扇形统计图.若喜欢羽毛球的人数是喜欢足球的人数的4倍,喜欢乒乓球的人数是21人,则下列说法正确的是( ) 第2页,共28页
A. 被调查的学生人数为80人 B. 喜欢篮球的人数为16人
C. 喜欢足球的扇形的圆心角为36° D. 喜欢羽毛球的人数占被调查人数的35%
7. 不等式组{
12𝑥−2≥−3
2(4−𝑥)>4的解集在数轴上表示为( )
A. B. C. D. 8. 将4个数𝑎、𝑏、𝑐、𝑑排成2行、2列,两边各加一条竖直线记成
∣∣∣𝑎𝑏𝑐𝑑∣∣∣,定义∣∣∣𝑎𝑏𝑐𝑑∣∣
∣=𝑎𝑑−𝑏𝑐.
则方程∣∣∣𝑥16𝑥𝑥∣
∣∣=−8的根的情况为( )
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 没有实数根 D. 只有一个实数根
9. 如图,在菱形𝐴𝐵𝐶𝐷中,∠𝐵𝐴𝐷=60°,𝐴𝐵=√3,点𝐴,𝐶在直线𝑦=𝑥上,且点𝐴的坐标
为(
√22,√2
2).将菱形𝐴𝐵𝐶𝐷绕原点𝑂逆时针旋转,每次旋转45°,则第85次旋转结束时,点𝐶的坐
标为( ) 第3页,共28页
A. (√2,0) B. (0,2)
C. (0,−2) D. (√2−1,√2−1)
10. 如图①,在𝑅𝑡△𝐴𝐵𝐶中,∠𝐴𝐶𝐵=90°,∠𝐴=30°,动点𝐷从点𝐴出发,沿𝐴→𝐶→𝐵以
1𝑐𝑚/𝑠的速度匀速运动到点𝐵,过点𝐷作𝐷𝐸⊥𝐴𝐵于点𝐸,图②是点𝐷运动时,△𝐴𝐷𝐸的面积
𝑦(𝑐𝑚2)随时间𝑥(𝑠)变化的关系图象,则𝐴𝐵的长为( )
A. 4𝑐𝑚 B. 6𝑐𝑚 C. 8𝑐𝑚 D. 10𝑐𝑚
二、填空题(本大题共5小题,共15.0分) 11. 若代数式
𝑥
𝑥−2有意义,则实数𝑥的取值范围是______.
12. 请写出一个图象经过(2,1)的函数解析式______.
13. 为了深化落实“双减”工作,促进中小学生健康成长,教育部门加大了实地督查的力度,
对我校学生的作业、睡眠、手机、读物、体质“五项管理”要求的落实情况进行抽样调查,计划从“五项管理”中随机抽取两项进行问卷调查,则抽到“作业”和“手机”的概率为______.
14. 如图,已知点𝐶、𝐷是以𝐴𝐵为直径的半圆的三等分点,𝐶𝐷
⏜的长为2𝜋3,连接𝑂𝐶、𝐴𝐷,则
图中阴影部分的面积为______. 第4页,共28页
15. 如图,在矩形𝐴𝐵𝐶𝐷中,𝐴𝐵=4,𝐵𝐶=6,𝐸是𝐵𝐶的中点,连接𝐴𝐸,𝑃是边𝐴𝐷上一动点,
沿过点𝑃的直线将矩形折叠,使点𝐷落在𝐴𝐸上的点𝐷′处,当△𝐴𝑃𝐷′是直角三角形时,𝑃𝐷=______.
三、解答题(本大题共8小题,共75.0分。解答应写出文字说明,证明过程或演算步骤) 16. (本小题10.0分)
(1)计算:
2−1−√14+𝜋0−|−3|;
(2)化简:𝑥2−1𝑥2+𝑥÷(𝑥−2𝑥−1𝑥).
17. (本小题9.0分) 为庆祝中国共产党建党100周年,讴歌中华民族实现伟大复兴的奋斗历程,继承革命先烈的优良传统,某中学开展了建党100周年知识测试该校七、八年级各有300名学生参加,从中各随机抽取了50名学生的成绩(百分制),并对数据(成绩)进行整理,描述和分析,下面给出了部分信息: 𝑎.八年级的频数分布直方图如下(数据分为5组:50≤𝑥<60,60≤𝑥<70,70≤𝑥<80,
80≤𝑥<90,90≤𝑥≤100);
𝑏.八年级学生成绩在80≤𝑥<90的这一组是:
80 81 82 83 83 83.5 83.5 84 84 85 86 86.5 87 88 89 89 𝑐.七、八年级学生成绩的平均数、中位数、众数如下:
年级 平均数 中位数 众数 七年级 87.2 85 91 八年级 85.3 𝑚 90 根据以上信息,回答下列问题: (1)表中𝑚的值为______ ; 第5页,共28页
(2)在随机抽样的学生中,建党知识成绩为84分的学生,在______ 年级排名更靠前,理由是
______ ;
(3)若各年级建党知识测试成绩前60名将参加线上建党知识竞赛,预估八年级分数至少达到
______ 分的学生才能入选;
(4)若成绩85分及以上为“优秀”,请估计八年级达到“优秀”的人数.
18. (本小题9.0分) 如图,在平面直角坐标系中,直线𝑦=𝑥与反比例函数𝑦=
1
𝑥(𝑥>0)的图象交于点𝐴,将直线
𝑦=𝑥沿𝑦轴向上平移𝑘个单位长度,交𝑦轴于点𝐵,交反比例函数图象于点𝐶,且
𝐵𝐶𝑂𝐴=1
3.𝐴𝐷⊥𝑦
轴于点𝐷、𝐶𝐸⊥𝑦于点𝐸. (1)求证:△𝐵𝐶𝐸∽△𝑂𝐴𝐷;
(2)求点𝐴和点𝐶的坐标;
(3)求𝑘值.
19. (本小题9.0分) 如图,𝐶𝐵是⊙𝑂的直径,𝐶𝐹是⊙𝑂的切线,切点为𝐶,点𝐷为直径𝐶𝐵右侧⊙𝑂上一点,连接𝐵𝐷 第6页,共28页
并延长𝐵𝐷,交直线𝐶𝐹于点𝐴,连接𝑂𝐷. (1)尺规作图:作出∠𝐶𝑂𝐷的角平分线,交𝐶𝐴于点𝐸,连接𝐷𝐸(保留作图痕迹,不写作法);
(2)在(1)的条件下,
①求证:𝐷𝐸=𝐴𝐸. ②若⊙𝑂半径为2,当𝐵𝐷
⏜
的长为______ 时,四边形𝑂𝐶𝐸𝐷是正方形.
20. (本小题9.0分) 如图,为了测量山坡上竖直旗杆𝐶𝐷的高度,小明在点𝐴处利用测角仪测得旗杆顶端𝐷的仰角为37°,然后他沿着正对旗杆𝐶𝐷的方向前进10𝑚到达𝐵点处,此时测得旗杆顶部𝐷和底端𝐶的仰角分别为45°和30°,求旗杆𝐶𝐷的高度.(结果精确到0.1𝑚.参考数据:𝑠𝑖𝑛37°≈35,𝑐𝑜𝑠37°≈45,𝑡𝑎𝑛37°≈34,√
3≈1.732)
21. (本小题9.0分) 书法是中华民族的文化瑰宝,是人类文明的宝贵财富,是我国基础教育的重要内容.某学校准备为学生的书法课购买一批毛笔和宣纸,已知购买40支毛笔和100张宣纸需要280元;购买30支毛笔和200张宣纸需要260元. (1)求毛笔和宣纸的单价;
(2)某超市给出以下两种优惠方案:
方案𝐴:购买一支毛笔,赠送一张宣纸; 第7页,共28页
方案𝐵:购买200张宣纸以上,超出的部分按原价打八折,毛笔不打折. 学校准备购买毛笔50支,宣纸若干张(超过200张).选择哪种方案更划算?请说明理由. 22. (本小题10.0分) 如图,直线𝑦=−2𝑥+8与𝑥轴交于点𝐴,与𝑦轴交于点𝐵,抛物线𝑦=𝑥2+𝑏𝑥+𝑐经过点𝐴和点
𝐵.
(1)求抛物线的解析式;
(2)结合图象直接写出不等式𝑥2+𝑏𝑥+𝑐>−2𝑥+8的解集;
(3)若点𝐶(1,𝑦1),𝐷(𝑚,𝑦2)都在抛物线上,当𝑦2>𝑦1时,求𝑚的取值范围.
23. (本小题10.0分) 在△𝐴𝐵𝐶中,𝐴𝐵=𝐴𝐶,点𝐷为𝐴𝐵边上一动点,∠𝐶𝐷𝐸=∠𝐵𝐴𝐶=𝛼,𝐶𝐷=𝐸𝐷,连接𝐵𝐸,𝐸𝐶. (1)问题发现:
如图①,若𝛼=60°,则∠𝐸𝐵𝐴=______,𝐴𝐷与𝐸𝐵的数量关系是______; (2)类比探究:
如图②,当𝛼=90°时,请写出∠𝐸𝐵𝐴的度数及𝐴𝐷与𝐸𝐵的数量关系并说明理由;
(3)拓展应用:
