考研数学旋转体表面积公式
旋转体的表面积与体积

思考:边长为1的正方形以其一边所在直线旋转 一周,所得几何体的表面积和体积?
圆锥的表面积和体积
圆锥的侧面展开图是扇形
S圆锥表面积 S底 S侧 r rl r (r l )
2
V圆锥 1 1 Sh r 2 h 3 3
O
思考:边长为2的正方形以其一对角线所在直 线旋转一周,所得
(r上l r下l )
O’
V圆台
1 (S上 3
S上S下 S下)h
O
思考:已知如图所示圆台的 三视图,求其表面积和体积。
圆柱、圆台、圆锥的侧面积和体积的内在联系
S圆台侧面积 (r上l r下l )
r上 0
r上 r下
S圆柱侧面积 2r下l
圆台的表面积和体积
参照圆柱和圆锥的侧面展开图,试想象圆台的侧 面展开图是什么 . 圆台的侧面展开图是扇环
O’
S圆台表面积 S上 S下 S侧
2 2
O
r上 r下 (r上l r下l )
V圆台 1 (S上 3 S上S下 S下)h
圆台的表面积和体积
S圆台表面积 r上 r
组合体:多面体和旋转 体
棱柱、棱锥、棱台的表面积和体积
h'
h'
表面积就是各侧面面积和底面面积之和.
V柱体 Sh
V台体
V锥体
1 Sh 3
1 (S上 3
S上S下 S下)h
圆柱的表面积和体积
r O
O 圆柱的侧面展开图是矩形
S圆柱表面积 S上 S下 S侧
V圆柱
2r 2rl 2r (r l ) 2 Sh r h
《运动会素描》
考研数学-专题11 平面域的面积与旋转体的体积

_______ .
[ 3 − ln 2] 2
∫x
【例 2】设 f (x) = t t d t, 则曲线 y = f (x) 与 x 轴所围成封闭图形的面积 −1 为 _________ . x
∫ 【解】 由于 t t 为奇函数,则 f (x) = t t d t 为偶函数, −1 而 f ′(x) = x x < 0, (x < 0), f (−1) = 0,
0
0
D y≥0
∫ = 2π π (1+ cosθ )3 sinθdθ = 8π
30
3
【例
10】已知曲线
L
:
⎧x
⎨ ⎩
y
= =
f (t), (0
cos t
≤
t
<
π) 2
,其中函数
f
(t) 具有连续导数,且
f (0) = 0, f ′(t) > 0(0 < t < π ). 若曲线 L 的切线与 x 轴的交点到切点的距离恒为 1. 2
∫ = 4π
2
[(x −1) +1]
1− (x −1)2 dx
0
∫ = 4π 2 1− (x −1)2 dx 0
= 4π ⋅ π 2
(奇偶性平移) (定积分几何意义)
= 2π 2
方法二 Vy = 2π ∫∫ r(x, y)dσ = 2π ∫∫ xdσ
D
D
3
= 2π ∫∫[(x −1) +1]dσ D
(B)
【例 4】 设平面图形 A 由 x 2 + y 2 ≤ 2x 所确定,试求
(Ⅰ)图形 A 绕 y 旋转一周所得旋转体的体积;
曲线绕x轴旋转所得几何体的 表面积

曲线绕x轴旋转所得几何体的表面积
曲线绕x轴旋转所得几何体的表面积的概念是一个值得探讨的话题。
在几何学中,表面积可以定义为某个物体表面上所有点的距离之和,这一概念可以帮助我们理解曲线绕x轴旋转所得几何体的表面积。
首先,我们要弄清楚曲线绕x轴旋转所得几何体的几何形状。
这种几何体通常是一个圆柱体,它由一个圆,一个圆锥和一个圆台组成。
圆的表面积可以用公式πr²计算,而圆锥和圆
台的表面积则可以用πr1 × (r2 + h)和πr1 × (r2 + h)计算。
接下来,我们要计算曲线绕x轴旋转所得几何体的表面积。
我们需要先用公式计算出每个部分的表面积,然后将它们加起来,就可以得出曲线绕x轴旋转所得几何体的表面积。
最后,我们要考虑曲线绕x轴旋转所得几何体的表面积的应用。
这种几何体的表面积可以用来计算物体的体积,这在结构工程、航天科学和流体力学等领域都有着重要的应用。
总而言之,曲线绕x轴旋转所得几何体的表面积是一个有趣的话题,通过计算可以得出它的表面积,这种几何体的表面积可以用来计算物体的体积,在工程、航天科学和流体力学等领域有着重要的应用。
9.4.5旋转体的表面积

360
nπl l扇= 180
r
2
l
求多面体的表面积可以通过求各 个平面多边形的面积和得到,那么 旋转体的表面积该如何求呢?
思考:把圆锥的侧面分别沿着一条母线 展开,分别得到什么图形?展开的图形与原图 有什么关系?
扇形
nπl l扇= 180
nπl 1 S圆锥侧=S扇= = l扇l = πrl 360 2
2
R扇=l
l
r
r O
l
O
圆柱的侧面展开图是矩形
2 r
S 2 r 2 rl 2 r ( r l )
2
例1.一个圆柱形的锅炉,底面半径 r=1m, 高h=2.3m。求锅炉的表面积(保留2位有效数 字)。 注意:表面积=全面积= 侧面积+底面积.
O`
O
解:锅炉的侧面积:
S1=2πrl=4.6πm2,
隆德职中 2017
一、知识回顾
1、棱柱: 侧面积公式: 表面积公式: 2、棱锥: 侧面积公式: 表面积公式:
忆一忆
1.已知圆的半径为r,则圆的面积为
r
r2
2
2.如图③ 扇形的半径为 r, 圆心角 ,
弧长是
S
l , 则扇形的面积是
r2
也可表示成 —————— , 1 S lr 2 ——————。弧长是
作业:
s = 4πR
2
154页练习1、2、3
17
开,得到什么图形?
2r
S r rl r (r l )
2
S圆锥侧=πrl
l
r
O
圆锥的侧面展开图是扇形
例2:已知圆锥的底面半径为2,母线长
旋转体测面积公式

旋转体测面积公式旋转体是我们生活中常见的几何体之一,它具有独特的形状和特点。
在数学中,我们可以通过旋转体的面积公式来计算其表面积。
本文将以人类的视角,生动地描述旋转体的面积公式及其相关知识。
让我们来了解一下什么是旋转体。
旋转体是由一个平面图形绕着一个轴旋转而成的立体图形。
常见的旋转体包括圆台、圆柱和圆锥等。
这些旋转体在我们的日常生活中无处不在,如酒杯、水杯和灯罩等。
对于圆柱体而言,它的面积公式非常简单。
我们只需要知道圆柱的底面半径和高度,就可以计算出它的表面积。
圆柱的表面积公式为:S = 2πr(r + h),其中π为圆周率,r为底面半径,h为高度。
通过这个公式,我们可以轻松计算出圆柱的表面积,从而了解它的大小和形状。
接下来,让我们来看一下圆锥体的面积公式。
与圆柱体类似,圆锥体的表面积也可以通过一定的公式来计算。
圆锥的表面积公式为:S = πr(r + l),其中l为斜高,r为底面半径。
通过这个公式,我们可以计算出圆锥的表面积,进而了解它的特点和形态。
当然,除了圆柱和圆锥,还有其他类型的旋转体,如圆台体等。
这些旋转体的面积公式也各不相同,但都可以通过一定的计算方法来求解。
我们可以通过数学知识和公式,准确地计算出旋转体的表面积,进一步了解它们的形态和特点。
旋转体的面积公式是我们研究旋转体的重要工具。
通过这些公式,我们可以计算出旋转体的表面积,从而深入了解它们的形态和特点。
无论是圆柱、圆锥还是其他类型的旋转体,它们都有着独特的形状和特征,通过面积公式,我们可以更好地理解和掌握它们。
希望通过这篇文章,读者能够对旋转体的面积公式有更深入的了解,并能够应用到实际生活中。
4.立体图形的体积、表面积、侧面积几何重心与转动惯量计算公式
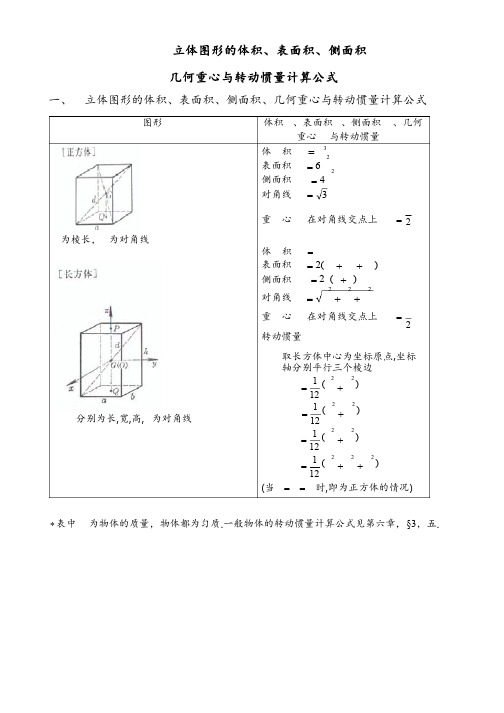
立体图形的体积、表面积、侧面积几何重心与转动惯量计算公式一、 立体图形的体积、表面积、侧面积、几何重心与转动惯量计算公式图形 体积、表面积、侧面积、几何重心与转动惯量为棱长,为对角线分别为长,宽,高,为对角线体 积 3=表面积26=侧面积24=对角线 3=重 心 在对角线交点上2=体 积 =表面积 )(2++=侧面积 )(2+=对角线222++=重 心 在对角线交点上2= 转动惯量取长方体中心为坐标原点,坐标轴分别平行三个棱边)(12122+=)(12122+=)(12122+=)(121222++= (当==时,即为正方体的情况)*表中为物体的质量,物体都为匀质.一般物体的转动惯量计算公式见第六章,§3,五.图形 体积、表面积、侧面积、几何重心与转动惯量为边长,为高为底边长,为高,为对角线为棱数,为底边长,为高,为斜高 体 积 =表面积 +=2侧面积 )(++=式中为底面积重 心2=(、分别为上下底重心)转动惯量对于正三棱柱()取为坐标原点,轴与棱平行1248324==体 积 225981.2233»=表面积61962.563322+»+= 侧面积 6=对角线224+=重 心2=(、分别为上下底重心)转动惯量取为坐标原点,轴与棱平行12583524==体 积 31=表面积 +=侧面积2'==式中为底面积,'为一侧三角形面重 心4h GQ = (Q 为底面的重心)图形体积V 、表面积S 、侧面积M 、几何重心G 与转动惯量Ja,b,c,p,q,r 为棱长h 为高体积 011111010101028812222222222222c b ac p qb p r a q r V = 重心PQ GQ 41= (P 为顶点,Q 为底面的重心)体积)''(3FF F F h V ++=式中F F ,'分别为上下底面积重心 '''3'24FF F F F FF F PQ GQ ++++=(P ,Q 分别为上下底重心)分别为上下底边长,为棱数,为高,为斜高体 积÷÷øöççèæ÷øöçèæ++=2''13表面积 ++='侧面积 )'(2+=式中,'分别为上下底面积重 心2222'''3'24++++= (、分别为上下底重心)图形 体积、表面积、侧面积、几何重心与转动惯量两底为矩形,分别为上下底边长,为高,1为截头棱长体积]'')')('([6++++= '''1--=重心''2''2''3''2++++++= (分别为上下底重心)底为矩形,a,b为其边长,h为高,a’为上棱长r为半径 重心'2'2aaaaPQGQ++=(P为上棱中点,Q为下底面重心)体 积33352360.0634ddrV»==pp 表面积24rS p=重 心 G与球心O重合转动惯量取球心O为坐标原点mrJJJzyx252===mrJo253=图形 体积V、表面积S、侧面积M、几何重心G与转动惯量J[半球体]r为半径,O为球心r为球半径,a为弓形底圆半径,h为拱高,a为锥角(弧度)r为球半径,a为拱底圆半径,h为拱高 体 积 331232drVpp==表面积23rS p=侧面积22rM p=重 心 rGO83=转动惯量取球心O为坐标原点,z轴与GO重合 mrJJJzyx252===mrJo253=体 积 hrhrV220944.232»=p表面积 )2(ahrS+=p侧面积 (锥面部分) rM pa=重 心 )2(83hrGO-=转动惯量z轴与GO重合úûùêëé-÷øöçèæ-=2sin2cos2cos1215225aaap rJz÷øöçèæ+-=2cos2cos32533aahmr体 积)3(3)3(6222hrhhahV-=+=pp表面积 )2()2(222aharhS+=+=pp 侧面积(球面部分))(222harhM+==pp重 心)3()2(432hrhrGO--=图形 体积V、表面积S、侧面积M、几何重心G与转动惯量J[球台]r为球半径,a¢,a分别为上下底圆的半径,h为高R为中心半径,D为中心直径,r为圆截面半径,d为圆截面直径体 积 )'33(6222haahV++=p表面积 )'2(22aarhS++=p侧面积 rhM p2=2222222'÷÷øöççèæ--+=hhaaar重 心22244'33'23haaaahGO++-=222222'33'422haahaahGQ++++=(Q为下底圆心)体 积 222242DdRrVpp==表面积 DdRrS224pp==重 心 G在圆环的中心上转动惯量取圆环的中心为坐标原点,z轴垂直于圆环所在平面mRrJJyx÷÷øöççèæ+==28522mRrJz÷øöçèæ+=2243图形体积V 、表面积S 、侧面积M 、几何重心G 与转动惯量J [圆柱体]r 为底面半径,h 为高R 为外半径,r 为内半径,h 为高r 为底圆半径,h,H 分别为最小,最大高度,a 为截角,D 为截头椭圆轴体 积h r V 2p = 表面积)(2h r r S +=p 侧面积rh M p 2= 重 心 2hGQ =(P ,Q 分别为上下底圆心) 转动惯量 取重心G 为坐标原点,z 轴垂直底面m h r J J y x ÷øöçèæ+==34122m r J z 22=体 积th R r R h V p p 2)(22=-= 表面积 )(222r R M S -+=p侧面积 R h r R h M p p 4)(2=+= 式中t 为管壁厚,R 为平均半径重 心2h GQ = 转动惯量 取z 轴与GQ 重合 m r R J z 2)(22+=体 积 )(22h H r V +=p 表面积 ÷øöçèæ++=a p cos 112r M S ÷øöçèæ+++=2D h H r r p 侧面积 )(h H r M +=p 截头椭圆轴22)(4h H r D -+= 重 心tan 22r h H +a)(2tan 2h H r GK +=a (GQ 为重心到底面距离,GK 为重心到轴线O O ¢的距离)图形体积V 、表面积S 、侧面积M 、几何重心G 与转动惯量Jh 为截段最大高度,b 为底面拱高,2a 为底面弦长,r 为底面半径,a 2为弧所对圆心角(弧度)体 积])(3)3([3222a r b r a r a bh V -+-=÷øöçèæ--=a a a cos sin 31sin 33a b hr侧面积(柱面部分)])[(2a r b b rhM +-=a体 积abc abc V 1888.434»=p 重 心G 在椭球中心O 上 转动惯量 取椭球中心为坐标原点,z 轴与c 轴重合m c b J x )(5122+=m a c J y)(5122+= m b a J z)(122+=a,b,c 为半轴图形体积V 、表面积S 、侧面积M 、几何重心G 与转动惯量J体 积h r V 23p= 表面积 )(l r r S +=p 侧面积 rl M p = 母 线 22h r l +=重 心4h GQ = (Q 为底圆中心,O 为圆锥顶r为底圆半径,h为高,l为母线r,R分别为上,下底圆半径,h为高,l为母线上下底平行,F¢,F分别为上,下底面积,F为中截面面积,h为高取圆锥顶点为坐标原点,z轴与GQ 重合mhrJJyx÷÷øöççèæ+==22453mrJz2103=体 积 )(322RrrRhV++=p表面积 )(22rRMS++=p侧面积 )(rRlM+=p母 线22)(hrRl+-=圆锥高(母线交点到底圆的距离)rRhrhH-+=重 心2222324rRrRrRrRhGQ++++=(P,Q分别为上下底圆心)体 积 )4'(60FFFhV++»[注] 棱台、圆台、球台、圆锥、棱柱、圆柱等都是拟棱台的特例图形 体积V、表面积S、侧面积M、几何重心G与转动惯量Jd 为上,下底圆直径,D 为中截面直径,h 为高母线为圆弧时: 体积)2(26180.0)2(122222d D h d D hhV +»+=p2)2(08727.0d D h +»母线为抛物线时: 体积 ÷øöçèæ++=2243215d Dd D h V p )348(05236.022d Dd D h ++» 重心2h GQ = (P ,Q 分别为上下底圆心)二、 多面体[正四面体] [正八面体] [正十二面体] [正二十面体]图形面数f4 8 12 20 棱数k 6 12 30 30 顶点数e 462012体积V 31179.0a34714.0a36631.7a31817.2a表面积S27321.1a24641.3a26457.20a26603.8a表中a 为棱长.[欧拉公式] 一个多面体的面数为f ,棱数为k ,顶点数为e ,它们之间满足 2=+-f k e。
绕y轴旋转得到的旋转体表面积

绕y轴旋转得到的旋转体表面积
绕y轴旋转得到的旋转体表面积是一个重要且复杂的课题,其计算方
法又是多样的。
它包括曲线积分、平面图形积分和旋转体积计算等。
1.曲面积分法
曲面积分可以确定一条曲线的弧长,包括椭圆和圆柱面积等。
曲线积
分是求积分的一个常用方法,有无穷多种方法采用此方法进行积分,
从简单易解的牛顿-拉夫逊积分到复杂但收敛快的复化积分法,再到准
实数计算的显式积分, 曲面积分通常用于求取旋转体表面积。
2.平面图形积分法
这种方法是用平面图形的面积来计算所需的旋转体表面积。
可以通过
计算椭圆形、矩形、正方形的面积,再结合这些图形的旋转,来计算
所需的旋转体表面积,这样可以比较快地求得正确的表面积。
3.旋转体积计算法
这种方法是根据旋转体的中心坐标和半径,通过计算椭球体积的公式
来求得。
旋转体的体积公式可以表示为:V = 4/3πr^3,根据这个公式,只需要计算出半径,就可以求出旋转体的体积。
然后根据体积可以求
出表面积。
绕y轴旋转得到的旋转体表面积,可以用这些方法进行精准计算,但
应当根据实际情况和具体要求来进行选择。
此外,实用性和准确性也影响着最终的计算结果。
古尔丁定理求旋转体表面积

古尔丁定理求旋转体表面积古尔丁定理求旋转体表面积一、引言在数学中,旋转体是一个非常重要的概念,它是由一个平面图形绕着某个轴线旋转而成的立体图形。
旋转体广泛应用于各种领域,比如建筑设计、机械制造、航空航天等。
在计算旋转体表面积时,古尔丁定理是一个非常有用的工具。
二、古尔丁定理的定义古尔丁定理是指,在平面上存在一条曲线,将其绕某个轴线旋转一周所得到的旋转体表面积等于该曲线沿轴线方向上的长度与该曲线绕轴线旋转一周所得到的螺旋线长度之积。
三、古尔丁定理的证明为了证明古尔丁定理,我们需要从几何和微积分两个角度进行分析。
1. 几何分析设平面上存在一条曲线L,并以y轴为轴将L绕x轴逆时针旋转一周所得到的立体图形为S。
我们可以将S划分成无数个小块,每个小块都可以看作一个圆台。
设第i个小块半径为ri,高为hi,底面圆周长为Li,则该小块的表面积为:Si = πri^2 + πriLi将该小块绕x轴旋转一周所得到的螺旋线长度为:di = 2πrihi则整个立体图形S的表面积为:S = ∑Si = ∑(πri^2 + πriLi) = π∑(ri^2 + riLi)将该曲线L沿y轴方向上的长度表示为L,则有:L = ∫[a,b]√(1+(dy/dx)^2)dx其中a和b分别表示曲线L在x轴上的两个交点。
我们可以通过微积分方法求出该曲线绕y轴旋转一周所得到的螺旋线长度,即:d = 2π∫[a,b]√(1+(dy/dx)^2)dx因此,根据古尔丁定理可得:S = Ld即旋转体表面积等于曲线沿轴线方向上的长度与曲线绕轴线旋转一周所得到的螺旋线长度之积。
2. 微积分分析古尔丁定理还可以通过微积分方法进行证明。
设平面上存在一条曲线L,并以y轴为轴将L绕x轴逆时针旋转一周所得到的立体图形为S。
我们可以将该曲线表示为y=f(x),则有:S = 2π∫[a,b]f(x)√(1+(dy/dx)^2)dx其中a和b分别表示曲线L在x轴上的两个交点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
考研数学旋转体表面积公式
旋转体是指一个平面图形绕着某条轴线旋转一周形成的立体图形。
求解旋转体的表面积需要根据具体的旋转体形状来选择相应的公式。
常见的旋转体包括圆锥、圆柱和圆盘等。
下面分别介绍它们的表面积公式:
1. 圆锥的表面积公式:
圆锥的侧面积为 L = πrl,其中 r 为底面半径,l 为母线长度。
圆锥的底面积为 B = πr²,其中 r 为底面半径。
圆锥的总表面积为 S = L + B = πrl + πr²。
2. 圆柱的表面积公式:
圆柱的侧面积为 L = 2πrh,其中 r 为底面半径,h 为高度。
圆柱的底面积为 B = πr²。
圆柱的总表面积为 S = L + 2B = 2πrh + 2πr²。
3. 圆盘的表面积公式:
圆盘的侧面积为 L = 2πrh,其中 r 为半径,h 为高度。
圆盘的底面积为 B = πr²。
圆盘的总表面积为 S = L + B = 2πrh + πr²。
需要注意的是,以上公式中的 r 和 h 分别表示旋转体的半径和高度,具体应根据题目给出的条件进行替换计算。
另外,如
果旋转体的形状与以上所列的不同,可能需要其他相关公式来计算表面积。
