定积分的应用(体积、旋转体的侧面积)演示模板.ppt
合集下载
第六节-定积分的应用PPT课件

A(y)2xytan
2tan yR2y2
V 2tan
R
y
R2y2dy
0
y
o
R (x, y) x
-
练习题
1.求ysix,n y0,0x绕 x 轴和 y 轴旋转一周的旋转体 的体积. 解:由公式有 V x 0 si2x nd 2 x 0 (1 co 2 x)d s x 2 2
-
例20. 求由星形线xaco 3t,syasi3tn0t
垂直于x 轴 的截面是直角三角形, 其面积为
A(x)1(R2x2)tan(RxR)
2 利用对称性
V20 R1 2(R 2x2)tan dx
2tanR2x1x3R 2R3 tan
3 03
y
ox
R x
-
机动 目录 上页 下页 返回 结束
思考: 可否选择 y 作积分变量 ? 此时截面面积函数是什么 ?
如何用定积分表示体积 ? 提示:
方法2 利用椭圆参数方程
x a cost
y
b sin
t
则
V2 a y2dx 2
2
ab2sin3tdt
0
0
2ab2 2 1
3
4 ab2
3
特别当b =
a
时,
就得半径为a
的球体的体积
4 3
a3 .
-
机动 目录 上页 下页 返回 结束
例2. 求由曲线 y , 直x 线 及 x轴 所1 围x成的平面图形 绕 轴旋转x一周所生成的旋转体的体积.
例1 由曲线
x2 a2
y2 b2
1
所围图形绕
x
轴旋转而
转而成的椭球体的体积.
y
2tan yR2y2
V 2tan
R
y
R2y2dy
0
y
o
R (x, y) x
-
练习题
1.求ysix,n y0,0x绕 x 轴和 y 轴旋转一周的旋转体 的体积. 解:由公式有 V x 0 si2x nd 2 x 0 (1 co 2 x)d s x 2 2
-
例20. 求由星形线xaco 3t,syasi3tn0t
垂直于x 轴 的截面是直角三角形, 其面积为
A(x)1(R2x2)tan(RxR)
2 利用对称性
V20 R1 2(R 2x2)tan dx
2tanR2x1x3R 2R3 tan
3 03
y
ox
R x
-
机动 目录 上页 下页 返回 结束
思考: 可否选择 y 作积分变量 ? 此时截面面积函数是什么 ?
如何用定积分表示体积 ? 提示:
方法2 利用椭圆参数方程
x a cost
y
b sin
t
则
V2 a y2dx 2
2
ab2sin3tdt
0
0
2ab2 2 1
3
4 ab2
3
特别当b =
a
时,
就得半径为a
的球体的体积
4 3
a3 .
-
机动 目录 上页 下页 返回 结束
例2. 求由曲线 y , 直x 线 及 x轴 所1 围x成的平面图形 绕 轴旋转x一周所生成的旋转体的体积.
例1 由曲线
x2 a2
y2 b2
1
所围图形绕
x
轴旋转而
转而成的椭球体的体积.
y
定积分的几何应用体积ppt正式完整版

V2 1u[4(u3)2]du 令ux3 5
2 2(x3)(4x2)dx 2
2 2(3x)(4x2)dx (※) 2
补充 2. 如果旋转体是由连续曲线 y f ( x)、直 线 x a、 x b(0ab)及 x轴所围成的曲边梯
形绕 x = m (>b) 旋转一周而成的立体,体积为
V2b(mx)| f(x)|dx (※)——柱壳法 a
3
[ ( 3 4 y ) 2 ( 3 4 y ) 2 ] dy
1 24yd,y
4
V1 20 4ydy6 4.
v
(二)利用坐标平移:
x u 3
y
v
P
3u
在 u o v 坐 标 系 下 旋 转 体 即 为 即 抛 物 线 v 4 (u 3 )2
与 v = 0 所 围 成 的 图 形 绕 v 轴 旋 转 所 得 。
二、平行截面面积为已知的立体的体积
如果一个立体不是旋转体,但却知道该立体上垂直 于一定轴的各个截面面积,那么,这个立体的体积也可 用定积分来计算.
x[a,b]
在[a,b]上任取小区 o
x x dx
x
间[x,xdx],
取以dx 为底的窄边梯形绕 x轴旋转而成的薄
片的体积为体积元素, dV [f(x)2 ]dx
旋转体的体积为 V b[f(x)]2dx a
2
2
2
例 1 求星形线 x 3 y 3 a 3 (a 0)绕 x轴旋转
构成旋转体的体积.
线 x a、 x b(0ab)及 x轴所围成的曲边梯
形绕 y轴旋转一周而成的立体,体积为
b
Vy2ax| f(x)|dx(※)——柱壳法
利用这个公式,可知上例中
定积分的应用(体积、旋转体的侧面积) ppt课件

d S 2 y ds 2 y dx
因为2 y dx 不是薄片侧面积△S 的
的线性主部 . 若光滑曲线由参数方程
y y f (x)
oa x b x ds dx
给出, 则它绕 x 轴旋转一周所得旋转体的 侧面积为
S 2 (t) 2 (t) 2 (t) d t
例1. 求由摆线
的一拱与 x 轴所围平面图形的面积 .
解:
2
AdA0 a (1 cost) a (1 cost) d t
a2 2 (1 cos t)2 d t 0
y
4a2 2 sin4 t d t
0
2
8a2 sin4 u d u 0
16 a2 2 sin4 u d u 0
解:解方程组
x2 y x
y
2
2
2
y
y x2
得交点(1, 1) ,(1, 1) 。
1 o 1 x
Vx 1 (2 x2 )dx 1 x4dx
x2 y22
1
2
1
(2
x
2
1
x4 )dx
2(2 x
x3
x5
)
1
0
3 50
2(2 1 1) 44. 3 5 15
y b
o x ax
则 V 2 a y2 dx 0
(利用对称性)
2
b2 a2
a
(a
2
x2
)
dx
0
2
b2 a2
a2 x
1 3
x3
a 0
4 ab2
因为2 y dx 不是薄片侧面积△S 的
的线性主部 . 若光滑曲线由参数方程
y y f (x)
oa x b x ds dx
给出, 则它绕 x 轴旋转一周所得旋转体的 侧面积为
S 2 (t) 2 (t) 2 (t) d t
例1. 求由摆线
的一拱与 x 轴所围平面图形的面积 .
解:
2
AdA0 a (1 cost) a (1 cost) d t
a2 2 (1 cos t)2 d t 0
y
4a2 2 sin4 t d t
0
2
8a2 sin4 u d u 0
16 a2 2 sin4 u d u 0
解:解方程组
x2 y x
y
2
2
2
y
y x2
得交点(1, 1) ,(1, 1) 。
1 o 1 x
Vx 1 (2 x2 )dx 1 x4dx
x2 y22
1
2
1
(2
x
2
1
x4 )dx
2(2 x
x3
x5
)
1
0
3 50
2(2 1 1) 44. 3 5 15
y b
o x ax
则 V 2 a y2 dx 0
(利用对称性)
2
b2 a2
a
(a
2
x2
)
dx
0
2
b2 a2
a2 x
1 3
x3
a 0
4 ab2
定积分的几何应用课件

电场中的电势
总结词
定积分可计算电场中的电势
详细描述
在静电场中,电势差与电场强度成正比。通过定积分可以计算出 某一点处的电势,即对电场强度进行积分。
公式表示
电势 = ∫E·dl
05
定积分的近似计算
方法
矩形法
总结词
矩形法是一种简单直观的定积分近似计算方法,通过将积分 区间划分为若干个小的矩形,然后求和来逼近定积分。
详细描述
辛普森法则是梯形法的一种改进,它考虑了函数在积分区间的整体变化趋势,将 积分区间分成若干个小的子区间,然后在每个子区间上应用梯形法来逼近定积分 。辛普森法则的精度比矩形法和梯形法更高,但计算量也相对较大。
THANKS
感谢您的观看
3
曲边三角形面积的近似计算
在无法直接计算定积分的情况下,可以使用近似 方法计算曲边三角形的面积,如矩形法、梯形法 等。
任意图形的面积
任意图形面积的计算
01
通过定积分计算任意图形的面积,首先需要找到图形的边界曲
线表达式,然后确定上下限,最后计算定积分。
任意图形面积的几何意义
02
任意图形面积表示的是边界曲线围成的平面区域面积。
详细描述
矩形法的基本思想是将积分区间分成若干个小的矩形,每个 矩形的宽度为小区间的宽度,高度为函数在相应小区间的平 均值。然后,将这些矩形的面积加起来,得到的就是定积分 的近似值。
梯形法
总结词
梯形法是一种基于几何直观的定积分近似计算方法,通过将积分区间划分为若干个小的梯形,然后求 和来逼近定积分。
围绕旋转轴旋转的平面图形被称为 旋转面。
旋转体的体积公式
圆柱的体积公式
V = πr²h,其中r是底面半径,h是高。
高等数学-定积分及其应用ppt课件.ppt
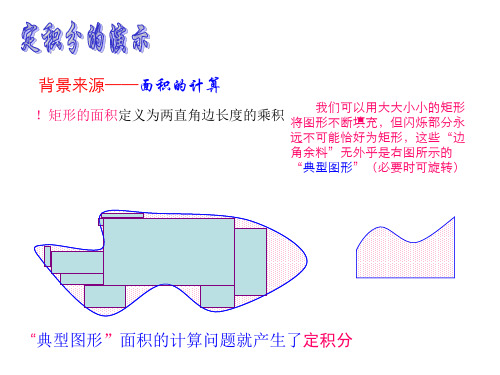
一、引例
在变速直线运动中, 已知位置函数
与速度函数
之间有关系:
物体在时间间隔
内经过的路程为
这种积分与原函数的关系在一定条件下具有普遍性 .
5.3 定积分的计算
则积分上限函数
证:
则有
定理1. 若
5.3.1 牛顿 – 莱布尼兹公式
说明:
1) 定理 1 证明了连续函数的原函数是存在的.
2) 变限积分求导:
5.6.1 广义积分
引例. 曲线
和直线
及 x 轴所围成的开口曲
边梯形的面积
可记作
其含义可理解为
1 连续函数在无限区间上的积分
定义1. 设
若
存在 ,
则称此极限为 f (x) 在区间 的广义积分,
记作
这时称广义积分
收敛 ;
如果上述极限不存在,
就称广义积分
发散 .
类似地 , 若
公式, 复化求积公式等,
并有现成的数学软件可供调用.
性质1 常数因子可提到积分号外 性质2 函数代数和的积分等于它们积分的代数和。
5.2 定积分的简单性质
性质3 若在区间 [ a , b ]上 f (x)≡K,则 性质4 定积分的区间可加性 若 c 是 [ a , b ] 内的任一点,则
的面积 .
解:
例3. 汽车以每小时 36 km 的速度行驶 ,
速停车,
解: 设开始刹车时刻为
则此时刻汽车速度
刹车后汽车减速行驶 , 其速度为
当汽车停住时,
即
得
故在这段时间内汽车所走的距离为
刹车,
问从开始刹
到某处需要减
设汽车以等加速度
车到停车走了多少距离?
在变速直线运动中, 已知位置函数
与速度函数
之间有关系:
物体在时间间隔
内经过的路程为
这种积分与原函数的关系在一定条件下具有普遍性 .
5.3 定积分的计算
则积分上限函数
证:
则有
定理1. 若
5.3.1 牛顿 – 莱布尼兹公式
说明:
1) 定理 1 证明了连续函数的原函数是存在的.
2) 变限积分求导:
5.6.1 广义积分
引例. 曲线
和直线
及 x 轴所围成的开口曲
边梯形的面积
可记作
其含义可理解为
1 连续函数在无限区间上的积分
定义1. 设
若
存在 ,
则称此极限为 f (x) 在区间 的广义积分,
记作
这时称广义积分
收敛 ;
如果上述极限不存在,
就称广义积分
发散 .
类似地 , 若
公式, 复化求积公式等,
并有现成的数学软件可供调用.
性质1 常数因子可提到积分号外 性质2 函数代数和的积分等于它们积分的代数和。
5.2 定积分的简单性质
性质3 若在区间 [ a , b ]上 f (x)≡K,则 性质4 定积分的区间可加性 若 c 是 [ a , b ] 内的任一点,则
的面积 .
解:
例3. 汽车以每小时 36 km 的速度行驶 ,
速停车,
解: 设开始刹车时刻为
则此时刻汽车速度
刹车后汽车减速行驶 , 其速度为
当汽车停住时,
即
得
故在这段时间内汽车所走的距离为
刹车,
问从开始刹
到某处需要减
设汽车以等加速度
车到停车走了多少距离?
定积分的几何应用体积精选幻灯片

y
2 3 2 3 2 3
2 3
2 3
2 3
解 y a x ,
y a x
2 2 3 2 3
3
x [ a , a ]
a
o
a x
旋转体的体积
a V a x dx 2 a x dx a 0 a 2 3 2 3 2 3 2 3 3 3
奇函数
偶函数
11
例 3 求由曲线 y 4 x 2 及 y 0 所围成的图形 绕直线 x 3旋转构成旋转体的体积.
解(一) 取积分变量为y , y [0,4]
体积元素为
dV [ PM QM ]dy
2 2
P
dyQM来自3 [( 3 4 y )2 ( 3 4 y )2 ]dy
的曲边梯形绕 y 轴旋转一周而成的立体,体 y 积为
V
d
d
2 [ ( y )] dy
c
x ( y)
c
o
x
6
例2. 计算摆线
的一拱与 y=0
所围成的图形分别绕 x 轴 , y 轴旋转而成的立体体积 . 解: 绕 x 轴旋转而成的体积为
y
y πa
Vx
2π a
5 3 1 π 32 π a sin u d u 32 π a 0 6 4 2 2 5 π2 a3
2 a
0
x | f ( x ) | dx
2 a( t sin t ) a(1 cos t )d[a( t sin t )]
0
2
2 a
3
0
2
( t sin t )(1 cos t ) dt 6 3 a 3 .
2 3 2 3 2 3
2 3
2 3
2 3
解 y a x ,
y a x
2 2 3 2 3
3
x [ a , a ]
a
o
a x
旋转体的体积
a V a x dx 2 a x dx a 0 a 2 3 2 3 2 3 2 3 3 3
奇函数
偶函数
11
例 3 求由曲线 y 4 x 2 及 y 0 所围成的图形 绕直线 x 3旋转构成旋转体的体积.
解(一) 取积分变量为y , y [0,4]
体积元素为
dV [ PM QM ]dy
2 2
P
dyQM来自3 [( 3 4 y )2 ( 3 4 y )2 ]dy
的曲边梯形绕 y 轴旋转一周而成的立体,体 y 积为
V
d
d
2 [ ( y )] dy
c
x ( y)
c
o
x
6
例2. 计算摆线
的一拱与 y=0
所围成的图形分别绕 x 轴 , y 轴旋转而成的立体体积 . 解: 绕 x 轴旋转而成的体积为
y
y πa
Vx
2π a
5 3 1 π 32 π a sin u d u 32 π a 0 6 4 2 2 5 π2 a3
2 a
0
x | f ( x ) | dx
2 a( t sin t ) a(1 cos t )d[a( t sin t )]
0
2
2 a
3
0
2
( t sin t )(1 cos t ) dt 6 3 a 3 .
第四节定积分的应用0882428页PPT
m 1inaxi
3
一、微元法(曲边梯形的面积A)
由连续曲线y=f(x)≥0与直线 x=a、x=b、y=0
围成的平面图形,称为曲边梯形.
y f (x)
面积微元 dAf(x)dx
o a xxdx b x
x
b
A a f (x)dx
微元法
4
二、平面图形的面积
由曲线 y f 1 ( x ) , y f 2 ( x ) f 1 ( x ) ( f 2 ( x ) ) 和直线
解:(1)求交点作图
y
yx4
y22x y2,x2 yx4y4,x8
(2)求面积
4 (2,2) 2
o2
2 (2,2)
(8,4)
8x
y2 2x
2
8
A0[ 2x( 2x)]dx 2[ 2x(x4)]dx
或A
4
[(
y
4)
1
y2]dy
2
2
9
以 dx为高的小圆柱体的体积,故所求体积微元为
dx V y2d xf2(x)dx
10
三、旋转体的体积
同理,由曲线 x(y)和直线 yc, yd( cd)
及直线 x0围成的平面图形绕 y 轴旋转一周而成
的旋转体的体积为
y
Vycdx2dy cd2 (y)dy
d
y dy
422 22 dy
0
4
((
0
yy))22dy 4(4y)dy8. 0
13
三、旋转体的体积(例题)
例3.由曲线 x2(yb)2a2( 0ab) 围成的图形
绕 x 轴旋转一周所得体积.
D5-4定积分的应用.ppt
解:因为总收益是边际收益函数在[0,x]上的定积分, 所以生产 x 单位时的总收益和平均单位收益为:
t R x 200 dt 0 50
x
§5.4
x
定积分的应用
t R x 200 dt 0 50
t2 200t 100
轴旋转一周围成的立体体积时, 有
V a π[ f ( x )] dx
b 2
yy O
当考虑连续曲线段
aa x
y
bb xx
绕 y 轴旋转一周围成的立体体积时,
有
d
y
V c π[ ( y )] d y
d 2
x ( y)
c O
x
§5.4
定积分的应用
§5.4
例4. 计算由曲面
定积分的为
L 40 0.2 40 16 40 20 300 元
2
§5.4
定积分的应用
例9、已知生产某商品 x 单位时,边际收益函数为
R x 以及平均单位收益 R x .
x R x 200 (元/单位),试求生产x单位时总收益 50
0
q
其中 C0 为固定成本 .
§5.4
定积分的应用
例7、设某产品在时刻 t 总产量的变化率为: 2 f t 100 12t 0.6t (单位/小时) 求从 t =2到 t =4这两小时的总产量 解 因为总产量是它的变化率的原函数,所以从 t =2到 t =4这两小时的总产量为:
4
x 0
x2 200 x 100
R x x R x 200 x 100
定积分的分部积分法和应用(面积、体积).ppt
2 2
π
π
∫
a +T
a
f (x ) dx =
∫
T
0
f (x ) dx .
以T为周期的周期函数 为周期的 在任一长度为T的区间上的定积分值相等 在任一长度为 的区间上的
例
∫π
∫
0
100π
|sinx | dx = ,
∫π
4
9π 4
|sinx | dx = .
2π
sin n x dx = ,
∫
10π n
30π n
(3) 极坐标系下 极坐标系下
极点在区域内部 ① 极点在区域内部 A = 2 π 1 r 2 (θ ) d θ (3) 极坐标系下 坐标系 ∫0 2 θ θ 设 r = r (θ) (α ≤ θ ≤ β ) ,求由 r = r (θ) , θ = α , θ = β 极点在区域外 ② 极点在区域外部 所围图形的图形的面积. 所围图形的图形的面积 = β 1 r 2 (θ ) − r 2 (θ ) d θ A ∫ 2 α 2 1 [ 求曲边扇形的 面积 A ,积分 变 是θ , θ∈ α, β]. 量
解: 10 作草图
(0,2),(12,4). , , , . 30 确定“横分”还是“竖分”y 型区域, 右减左 确定“横分”还是“竖分” 型区域, 为积分变量) (以 y 为积分变量还是以 x 为积分变量)
20 求交点
法一: 横分” “ ( 为积分变量) 法一: 横分” 以 y 为积分变量)
A= ∫
f ( x) ∈ C ,
求
∫
1
x 0
1 tf (2 x − t )dt = arctan x 2 , f (1) = 1 , 2
π
π
∫
a +T
a
f (x ) dx =
∫
T
0
f (x ) dx .
以T为周期的周期函数 为周期的 在任一长度为T的区间上的定积分值相等 在任一长度为 的区间上的
例
∫π
∫
0
100π
|sinx | dx = ,
∫π
4
9π 4
|sinx | dx = .
2π
sin n x dx = ,
∫
10π n
30π n
(3) 极坐标系下 极坐标系下
极点在区域内部 ① 极点在区域内部 A = 2 π 1 r 2 (θ ) d θ (3) 极坐标系下 坐标系 ∫0 2 θ θ 设 r = r (θ) (α ≤ θ ≤ β ) ,求由 r = r (θ) , θ = α , θ = β 极点在区域外 ② 极点在区域外部 所围图形的图形的面积. 所围图形的图形的面积 = β 1 r 2 (θ ) − r 2 (θ ) d θ A ∫ 2 α 2 1 [ 求曲边扇形的 面积 A ,积分 变 是θ , θ∈ α, β]. 量
解: 10 作草图
(0,2),(12,4). , , , . 30 确定“横分”还是“竖分”y 型区域, 右减左 确定“横分”还是“竖分” 型区域, 为积分变量) (以 y 为积分变量还是以 x 为积分变量)
20 求交点
法一: 横分” “ ( 为积分变量) 法一: 横分” 以 y 为积分变量)
A= ∫
f ( x) ∈ C ,
求
∫
1
x 0
1 tf (2 x − t )dt = arctan x 2 , f (1) = 1 , 2
定积分的应用9411954页PPT
0
0
2 02
3) 旋转体体积
定义:旋转体就是由一个平面图形绕这平面内一 条直线(轴)旋转一周而形成的立体图形。
这直线叫做旋转轴。如圆柱、圆锥体,球体等。 特点:与旋转轴垂直的横截面都是圆
圆柱
圆锥
圆台
1):体积元素为小圆柱体:dV=底面积×高
取积分变量为x, y
yf(x)
x[a,b]
在[a,b]上任取小区 o
(2)A=
d
[g(y)f(y)]dy
c
例 3 计 算 由 曲 线 y22x和 直 线 yx4所 围
成 的 图 形 的 面 积 .
解 两曲线的交点
yx4
y2 2x
y x4
y2 2x
(2 , 2 )(,8 ,4 ).
如选x为积分变量,图形需分成两块。
选 y为积分变量 y[2,4]
S022sin 2tdt8
(极坐标)
曲线弧为 rr() ()
其 中 ()在 [, ]上 具 有 连 续 导 数 .
xyrr(())scions ()
d s (d)x 2(d)y 2r2()r2()d,
弧长
s
x2y2dt4023asintcotds t
y
6a.
a o
ax
例 求摆线 x 1 cost
y
t
sint
一拱(0≤t≤2π)的弧长S。
解 dxsitn, dy1cots
dt
dt
d S s2 t i ( n 1 ct) o 2 d s t 2 ( 1 ct) d o 2 圆的参数方程
x y
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
。
例 1.设有半径为R 的正圆柱体,被通过其底的直径 而与底面交成 的 平 面所截,求截得的圆柱楔的体积。
解:如图建立坐标系,
ytan
R
则底圆的方程为 x2 y2 R2 。 x
x[ R,R] ,用过点 x且垂直于x轴
y
o
y
的平面去截楔形,截得的截面是直角三角形,R x
故截面积为 A( x) 1 y ytan 1(R2 x2 )tan ,
则 V 20a y2 dx 2 ab2 sin3t d t
2 ab2 2 1
3
4 ab2
3
特别当b
=
a
时,
就得半径为a
的球体的体积
4
3
a3
.
9
例 3.已知圆台的上底 半径为r1 ,下底半径为r2 , 高为 h ,求它的体积。
解:如图选择坐标系,母线 AB 的方程为
y
0
r1
h r2
(
x
2
2
V
R
A( x)dx
R
1 (
R2
x2 )tandx
2 R3tan.
R
R2
3
(二)旋转体的体积
特别 , 当考虑连续曲线段
轴旋转一周围成的立体体积时, 有
V b [ f (x)]2 dx a
y
y f (x)
当考虑连续曲线段
o ax b x
绕 y 轴旋转一周围成的立体体积时,
有
V d [( y)]2dy c
2
例3. 求双纽线
所围图形面积 .
解: 利用对称性 , 则所求面积为
1 a2 cos2 d
2
y
4
a2 4 cos 2 d (2 ) 0
o
ax
a2sin 2 a2
4
思考: 用定积分表示该双纽线与圆 r a 2 sin
所围公共部分的面积 .
答案:
A 2
6 a2 sin2 d
0
4 6
2
3 a2
2 a x
例2. 计算心形线
与圆
所围图形的面积 .
1 2cos cos 2
解: 利用对称性 , 所求面积
A
1a2 2
2
1 a2 (1 cos )2 d
2
1 2
(1
cos
2
)
1 a2 a2 (3 2cos 1 cos 2 )d
2
2
2y
1 a2 a2 (3 2)
2
4
o
a 2a x
ax
bx
A(x)
ax
bx
取 x 为积分变量,积分区间为[a,b] 。在[a,b] 上任取一
代表小区间[ x, x dx ] ,对应的立体中一薄片的 体积 V
近似等于底面积为 A( x) ,高为dx 的柱体的体积 A( x)dx ,
即体积微元 所求体积为
dV A( x)dx ,
V
b a
A(
x )dx
r2
)
y
h
x
r1
r2 h
y r2
o
V
hx2dy
0
h
(
0
r1 r2 h
yr2 )2dy
h
r1 r2
h
(
r1
r2
0h
yr2 )2 d (
r1 r2 h
yr2 )
A(r1,h)
B(r2 ,0)
x
h ( r1 r2 3(r1 r2 ) h
yr2 )3
h 0
h 3(r1 r2
)
(r13
r23
)
1 o 1 x
Vx 1 (2 x2 )dx 1 x4dx
x2 y22
1
2
1
1
(2
x2
x4
)dx
2(2 x
x3
x5
)
1
0
3 50
2(2 1 1) 44. 3 5 15
1
Vy ydy
2 (2 y2 )dy
0
1
1 y2 1 (2 y 1 y3 ) 2
20
31
[(2 2 2 2 )(2 1 )]
y
d y x (y) c
ox
例2计算由椭圆
所围图形绕 x 轴旋转而
转而成的椭球体的体积. 解: 方法1 利用直角坐标方程
y b
o x ax
则 V 2 a y2 dx 0
(利用对称性)
2
b2 a2
a
(a
2
x2
)
dx
0
2
b2 a2
a2 x
1 3
x3
a 0
4 ab2
3
8
方法2 利用椭圆参数方程
利用对称性
2
a3 0
(1 cos t)3 d t
16
a3 sin6 0
t 2
dt
(令 u
t) 2
32
a3
2
0
sin 6
u
du
32
a3
5 6
3 4
1 2
2
5 2a3
14
绕 y 轴旋转而成的体积为
y
2a
x x2 ( y)
o
a 2 a x
x x1( y)
2a
2
(t
sin t)2 a sin
2
3
3
( 4 2 7 ). 36
y
2
y x2
1
o
x
x2 y成的图形分别绕 x 轴 , y 轴旋转而成的立体体积 .
解: 绕 x 轴旋转而成的体积为
y
Vx
2 a y2 dx
0
y
o
a 2 a x
2 a2 (1 cos t)2 a(1 cost) d t 0
1 2
a
2
cos 2
d
3
二、体积
(一)平行截面面积为已知的立体的体积
设有一立 体 位于平面 xa, xb (ab) 之间,已知它被
过点 ( x, 0, 0) (a xb) 且垂直于 x 轴 的平面所截得的截面面
积为 A( x) ,假定 A( x)是 x 的连续函数,求 立 体 的 体积V 。
A(x)
3h(r12
r1r2
r22
)
当上底半径 r1 0 ,下底半径r2 r 时,
则得圆锥的体积为V 1r 2h 。 3
例 4.求由 x2 y2 2 和 y x2 所围成的图形分别
绕 x 轴 、 y 轴 旋转而成的旋转体的体积。
解:解方程组
x2 y x
y
2
2
2
y
y x2
得交点(1, 1) ,(1, 1) 。
1
例1. 求由摆线
的一拱与 x 轴所围平面图形的面积 .
解:
2
AdA0 a (1 cost) a (1 cost) d t
a2 2 (1 cos t)2 d t 0
y
4a2 2 sin4 t d t
0
2
8a2 sin4 u d u 0
16 a2 2 sin4 u d u 0
o (令u t )
0
2
令u t 2
16
a
3
0
(2u
sin
2u)
sin
4
u
d
u
令v u
2
16
a3
2
2
(2v
sin 2v) cos4 v d v
偶函数
奇函数
18
例 6.证明:由 0a xb, 0 y f ( x) 所围成的图形
绕
y 轴 旋转所成的旋转体的体积为:Vy 2
bx f ( x)dx 。
a
证明:以 x 为 积分变量,把在[a,b] 上的任意子区间
0
a
2
(t
tdt sin t)2
a
sin
注意上下限
tdt
!
a3 2 (t sin t)2 sin td t 0
注
15
说明:
y
x xdx
柱面面积
柱壳体积
2 a(t sin t) a (1 cost)
17
2
2
0
a(t
sin
t)
a2
(1
cos
t)2
d
t
8 a3 2 (t sin t)sin4 t d t
