定性数据分析第二章课后答案
统计学第五版课后习题答案(完整版)

统计学(第五版)课后习题答案(完整版)第一章思考题1.1什么是统计学统计学是关于数据的一门学科,它收集,处理,分析,解释来自各个领域的数据并从中得出结论。
1.2解释描述统计和推断统计描述统计;它研究的是数据收集,处理,汇总,图表描述,概括与分析等统计方法。
推断统计;它是研究如何利用样本数据来推断总体特征的统计方法。
1.3统计学的类型和不同类型的特点统计数据;按所采用的计量尺度不同分;(定性数据)分类数据:只能归于某一类别的非数字型数据,它是对事物进行分类的结果,数据表现为类别,用文字来表述;(定性数据)顺序数据:只能归于某一有序类别的非数字型数据。
它也是有类别的,但这些类别是有序的。
(定量数据)数值型数据:按数字尺度测量的观察值,其结果表现为具体的数值。
统计数据;按统计数据都收集方法分;观测数据:是通过调查或观测而收集到的数据,这类数据是在没有对事物人为控制的条件下得到的。
实验数据:在实验中控制实验对象而收集到的数据。
统计数据;按被描述的现象与实践的关系分;截面数据:在相同或相似的时间点收集到的数据,也叫静态数据。
时间序列数据:按时间顺序收集到的,用于描述现象随时间变化的情况,也叫动态数据。
1.4解释分类数据,顺序数据和数值型数据答案同1.31.5举例说明总体,样本,参数,统计量,变量这几个概念对一千灯泡进行寿命测试,那么这千个灯泡就是总体,从中抽取一百个进行检测,这一百个灯泡的集合就是样本,这一千个灯泡的寿命的平均值和标准差还有合格率等描述特征的数值就是参数,这一百个灯泡的寿命的平均值和标准差还有合格率等描述特征的数值就是统计量,变量就是说明现象某种特征的概念,比如说灯泡的寿命。
1.6变量的分类变量可以分为分类变量,顺序变量,数值型变量。
变量也可以分为随机变量和非随机变量。
经验变量和理论变量。
1.7举例说明离散型变量和连续性变量离散型变量,只能取有限个值,取值以整数位断开,比如“企业数”连续型变量,取之连续不断,不能一一列举,比如“温度”。
第2章 数据分析(梅长林)习题题答案
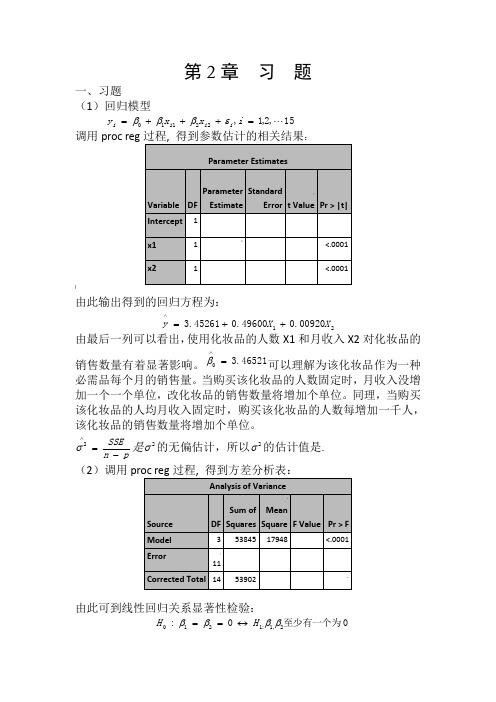
第2章 习 题一、习题(1)回归模型15,2,1,22110 =+++=i x x y i i i i εβββ调用proc reg:]由此输出得到的回归方程为:2100920.049600.045261.3X X y ++=∧由最后一列可以看出,使用化妆品的人数X1和月收入X2对化妆品的销售数量有着显著影响。
46521.30=∧β可以理解为该化妆品作为一种必需品每个月的销售量。
当购买该化妆品的人数固定时,月收入没增加一个一个单位,改化妆品的销售数量将增加个单位。
同理,当购买该化妆品的人均月收入固定时,购买该化妆品的人数每增加一千人,该化妆品的销售数量将增加个单位。
pn SSE-=∧2σ是2σ的无偏估计,所以2σ的估计值是. (2)调用由此可到线性回归关系显著性检验:0至少有一个为0:2,1:1210ββββH H ↔==的统计量/(1)/()SSR p MSRF SSE n p MSE-==-的观测值47.56790=F ,检验的p 值0001.0)(000<>==F F p p H另外9989.053902538452===SST SSR R ,2R 描述了由自由变量的线性关系函数值所能反映的Y 的总变化量的比例。
2R 越大,表明线性关系越明显。
这些结果均表明Y 与X1,X2之间的回归关系高度显著。
(3)若置信水平05.0=α,由17881.2)12(975.0=t ,利用参数估计值得到21,0,βββ的置信区间分别为:对,0β2942.54516.343065.21781.245216.3±=⨯±,即)7458.8,8426.1(-) 对1β:01318.049600.000605.01781.249600.0±=⨯±,即)50198.0,48282.0( )2β:0021.000920.00009681.01781.200920.0±=⨯±,即)00113.0,0071.0(-(4)首先检验X1对Y 是否有显著性影:假设其约简模型为:15,2,1,220 =++=i x y i i i εββ 由观测数据并利用proc reg 过程拟合此模型求得:88137.484)(=R SSE 13215=-=R f 88357.56)(=F SSE 12315=-=R f由[()()]()()/R F FSSE R SSE F f f F SSE F f --=求得检验统计量的值为:3.9012/88357.5688357.5688137.4840=-=F05.0))13,1(()(0000<>==>==F F P F F p p H由此拒绝原假设,所以x2对Y 有显著影响。
统计学贾俊平-课后思考题和练习题答案

统计学(第五版)贾俊平课后思考题和练习题答案(最终完整版)第一部分思考题第一章思考题什么是统计学统计学是关于数据的一门学科,它收集,处理,分析,解释来自各个领域的数据并从中得出结论。
解释描述统计和推断统计描述统计;它研究的是数据收集,处理,汇总,图表描述,概括与分析等统计方法。
推断统计;它是研究如何利用样本数据来推断总体特征的统计方法。
统计学的类型和不同类型的特点统计数据;按所采用的计量尺度不同分;(定性数据)分类数据:只能归于某一类别的非数字型数据,它是对事物进行分类的结果,数据表现为类别,用文字来表述;(定性数据)顺序数据:只能归于某一有序类别的非数字型数据。
它也是有类别的,但这些类别是有序的。
(定量数据)数值型数据:按数字尺度测量的观察值,其结果表现为具体的数值。
统计数据;按统计数据都收集方法分;观测数据:是通过调查或观测而收集到的数据,这类数据是在没有对事物人为控制的条件下得到的。
实验数据:在实验中控制实验对象而收集到的数据。
统计数据;按被描述的现象与实践的关系分;截面数据:在相同或相似的时间点收集到的数据,也叫静态数据。
时间序列数据:按时间顺序收集到的,用于描述现象随时间变化的情况,也叫动态数据。
解释分类数据,顺序数据和数值型数据答案同举例说明总体,样本,参数,统计量,变量这几个概念对一千灯泡进行寿命测试,那么这千个灯泡就是总体,从中抽取一百个进行检测,这一百个灯泡的集合就是样本,这一千个灯泡的寿命的平均值和标准差还有合格率等描述特征的数值就是参数,这一百个灯泡的寿命的平均值和标准差还有合格率等描述特征的数值就是统计量,变量就是说明现象某种特征的概念,比如说灯泡的寿命。
变量的分类变量可以分为分类变量,顺序变量,数值型变量。
变量也可以分为随机变量和非随机变量。
经验变量和理论变量。
举例说明离散型变量和连续性变量离散型变量,只能取有限个值,取值以整数位断开,比如“企业数”连续型变量,取之连续不断,不能一一列举,比如“温度”。
数据分析方法课后答案

数据分析方法课后答案【篇一:数据的分析练习题及答案】、选择题:(每题3分,共15分)1.小明家要买台电脑,下面是甲、乙、丙三种电脑近几年来的销量,如果小明想买一台近期比较流行的电脑,他应买()a.甲b.乙c.丙2.小李是个彩票迷,为了能得奖,他特意询问了前15天的中奖号码分别是:519、、706、328、556、768、215、435、741、624、307、821、696、741、471、285. 你认为这样的观点是否合理()a.不合理b.合理3.小靖想买双好的运动鞋,于是她上网查找有关资料,得到下表:她想买一双价格在300-600元之间,且她喜欢白色、红白相间、浅绿或淡黄色, 并且防水性能很好,那么她应选()a.甲b.乙c.丙d.丁4.为了计算植树节时本班同学所种植的30棵树苗的平均高度, 三位同学先将所有树苗的然后,他们分别这样计算这30棵树苗的平均高度:130130列式正确的是()a.(1)b.(1)和(2);c.(1)和(3)d.(2)和(3)5.某班在一次物理测试中的成绩为:100分7人,90分14人,80分17人,70分8人, 60分2人,50分2人.则该班此次测试的平均成绩为() a.82分b.62分c.64分d.75分二、填空题:(每题4分,共20分)6.一次知识竞赛中,36名参赛选手的得分情况为:5人得75分,8人得80分,6 人得85分,8人得90分,7人得95 分, 2 人得100 分, 要计算他们的平均得分, 可列算式:_____________.(1)7.某校九年级6个班级的学生的人数和平均体重如下表:要计算全校学生的平均体重,可列算式________,平均体重约为__________.8.某家庭搬进新居后,又添置了新的家用电器,为了了解用电量的大小, 该家庭在6月初连续几天观察电表的度数,如下表所示:9.为了解我国14岁男孩的平均身高,从北方抽取了300个男孩,平均身高1.60m; 从南方抽取了200个男孩,平均身高为1.50m;若北方14岁男孩数与南方14岁男孩数的比为3:2,由此可推断我国14岁男孩的平均身高约为______m.10.小明先用5千米/时的速度行驶3小时后,又用4千米/时的速度行驶5小时到达目的地,则小明的平均速度为________. 三、解答题:(每题9分,共54分)11.某同学对他在本学期的自我检测成绩进行了统计:95分的有12次,90 分的有10次,85分的有15次,80分的有3次,75分的有1次,65分的有3次.试计算该同学本学期自我检测的平均成绩..12.超市里要举行转盘摇奖活动,转盘如图所示,买满100元可摇奖一次,有人说:如果大家都摇到自行车,那么超市岂不是亏本了?如果你是超市决策者,会不会因此而改变有奖销售的方案呢?说说你的理由?自行车300元洗洁精2.80元酱油5.0元西红柿2.00元墨水3.50元13.请你根据上表比较这两个国家的数据,你能得出什么结论?14.由于水资源贫乏,节约用水非常重要,请你调查一下,本班每位学生所在家庭的月人均用水量,并据此制作频数分布图,同时估计一下当地家庭的月人均用水量.15.爸爸给小明一串钥匙,共有4把,小明决定先试试哪把是防盗门的钥匙. 请你用模拟实验方法估计一下,他第1次试开就成功的机会有多大?16.转动如图所示的转盘两次,每次指针都指向一个数字. 如果两次所指的数字之积是质数,游戏者a得10分;乘积不是质数,游戏者b得10分.你认为这个游戏公平吗?如果你认为这个游戏不公平,你愿意做游戏者a还是游戏者b?为什么?31246517.有人对记忆和遗忘的规律进行研究,人在记忆过某些知识后, 在不同时间段对其进行测试,结果如下表:分析测试结果,在图中绘制曲线图,并回答遗忘在数量上的变化规律.记忆效果1%记忆的保持曲线图答案:一、1.b 2.a 3.d 4.d 5.a148?50?49.8?46?50.2?55?49.5?48?51?52?50.3?547., 49.8kg50?46?55?48?52?54358.387.75 9.1.56 10.千米/时8三、144所以,美国的吸烟总人数和每天吸烟的总数都大于日本,但吸烟人口占总人口的比例小于日本.14.列出调查表,对本班学生实事求是地进行调查以获得真实的信息.15.可用4个相同的球,1个白的,3个黑的,每次抽1个,则第1次抽到白球的概率为所求概率,1为. 41516.不公平,愿做b 解:乘积是质数的概率是,乘积不是质数的概率是, 游戏不公平,故66愿做b.17.遗忘曲线表明了遗忘在数量上的变化规律,遗忘的数量随时间的前进而递增;这种递增先快后慢,在识记后的短时间内特别迅速,然后逐渐缓慢下来.二、6.记忆效果1%/d记忆的保持曲线图【篇二:定性数据分析第三章课后答案】9、对72个可疑患者用两种不同的方法进行检测,检测结果如下:问:检测方法1阳性和阴性的比例是否与检测方法2阳性和阴性的比例相同?解:(1)提出原假设根据题意,我们假设检测方法1阳性和阴性的比例与检测方法2阳性和阴性的比例是相同。
最新第2章 数据分析(梅长林)习题题答案
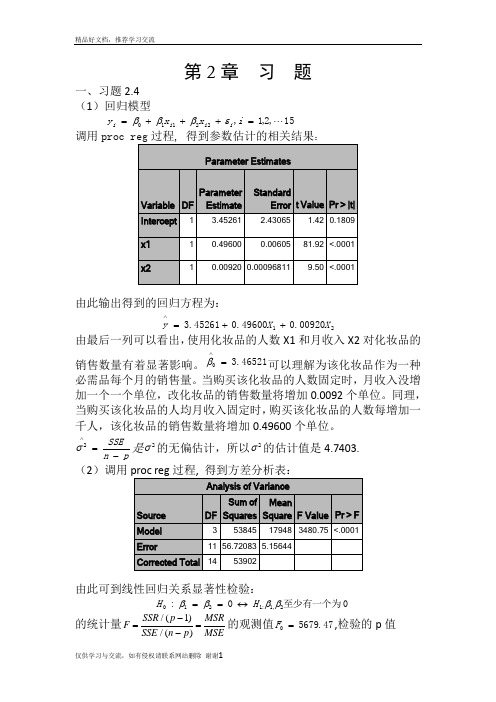
第2章 习 题一、习题2.4 (1)回归模型15,2,1,22110 =+++=i x x y i i i i εβββ调用:由此输出得到的回归方程为:2100920.049600.045261.3X X y ++=∧由最后一列可以看出,使用化妆品的人数X1和月收入X2对化妆品的销售数量有着显著影响。
46521.30=∧β可以理解为该化妆品作为一种必需品每个月的销售量。
当购买该化妆品的人数固定时,月收入没增加一个一个单位,改化妆品的销售数量将增加0.0092个单位。
同理,当购买该化妆品的人均月收入固定时,购买该化妆品的人数每增加一千人,该化妆品的销售数量将增加0.49600个单位。
pn SSE-=∧2σ是2σ的无偏估计,所以2σ的估计值是4.7403. (2)调用由此可到线性回归关系显著性检验:0至少有一个为0:2,1:1210ββββH H ↔== 的统计量/(1)/()SSR p MSRF SSE n p MSE-==-的观测值47.56790=F ,检验的p 值0001.0)(000<>==F F p p H另外9989.053902538452===SST SSR R ,2R 描述了由自由变量的线性关系函数值所能反映的Y 的总变化量的比例。
2R 越大,表明线性关系越明显。
这些结果均表明Y 与X1,X2之间的回归关系高度显著。
(3)若置信水平05.0=α,由17881.2)12(975.0=t ,利用参数估计值得到21,0,βββ的置信区间分别为:对,0β2942.54516.343065.21781.245216.3±=⨯±,即)7458.8,8426.1(-) 对1β:01318.049600.000605.01781.249600.0±=⨯±,即)50198.0,48282.0( 2β:0021.000920.00009681.01781.200920.0±=⨯±,即)00113.0,0071.0(-(4)首先检验X1对Y 是否有显著性影:假设其约简模型为:15,2,1,220 =++=i x y i i i εββ 由观测数据并利用proc reg 过程拟合此模型求得:88137.484)(=R SSE 13215=-=R f 88357.56)(=F SSE 12315=-=R f由[()()]()()/R F FSSE R SSE F f f F SSE F f --=求得检验统计量的值为:3.9012/88357.5688357.5688137.4840=-=F05.0))13,1(()(0000<>==>==F F P F F p p H由此拒绝原假设,所以x2对Y 有显著影响。
定性数据研究方法chap2

服从自由度为
的 chi方分布
chi方独立性检验
例:
chi方独立性检验
Pearson 和似然比检验统计量分别为
和 自由度:
拒绝零假设
chi方独立性检验 data Survey; input Gender Party count @@; cards; 1 1 279 1 2 73 1 3 225 2 1 165 2 2 47 2 3 191 ; run; proc format; value gender 1='female' 2='Male'; value party 1='Democrat' 2='Independent‘ 3='Republican'; run; proc freq data=survey order=data; format gender gender. party party.; weight count; tables gender*party / chisq expected nopercent norow nocol; run;
边际分布 (marginal distribution)
1 2 … J Total
1 2 … I Total 其中:
…
…
… … … … …
…
… 1
列联表的概率结构
条件分布(conditional distribution)
相信死后再生
性别 女 男
是 0.81 0.79
否或不确定 0.19 0.21
第二章 列联表(Contingency Tables)
2.1 列联表的概率结构 2.2 两个比例的比较
2.3 胜算比
统计学(贾俊平第八版)课后思考题及答案

统计学(贾俊平第八版)课后思考题及答案第一章:统计学基本概念和方法思考题1:什么是统计学?统计学的研究对象是什么?统计学是从观察数据的现象和规律出发,运用数理统计方法进行概括、分析和推断的科学。
统计学研究的对象是数据的概括和整体行为特征,即基本统计量和统计分布。
答案:统计学是一门应用数学的学科,其研究范围包括数据的收集、整理、描述、分析和推断等方面。
统计学通过运用数理统计方法,帮助我们从观察到的数据中发现其中的规律和趋势,从而对现象和问题作出合理的判断和推断。
统计学的研究对象主要包括两个方面。
一方面,统计学关注数据的概括和整体行为特征,例如对数据集的中心趋势(平均数、中位数)和离散程度(标准差、方差)进行描述和分析,这些统计量可以帮助我们对数据进行概括和比较。
另一方面,统计学研究数据的统计分布,即数据的分布形状和特征,例如正态分布、偏态分布等,这些分布有助于我们根据数据的特点进行进一步的推断和推测。
第二章:统计学的数据描述思考题2:试举例说明数据分为哪些类型?数据分为定性数据和定量数据两种类型。
答案:数据可以分为定性数据和定量数据两种类型。
定性数据是指不能用数字表示的数据,其特征主要是描述性的,例如性别、喜好等。
定性数据通常采用文字或符号进行记录和表达。
定量数据是指可以用数字表示的数据,其特征主要是数量性的,例如身高、体重等。
定量数据可以进行数学运算和统计分析。
举例来说,一个学生调查问卷中的“性别”以及“对某个电影的评价(好、中、差)”是属于定性数据;而问卷中的“年龄”和“观看该电影的次数”则是属于定量数据。
第三章:概率与概率分布思考题3:什么是概率?请以一个例子来解释。
概率是指某个事件发生的可能性。
它在统计学中用于描述随机现象的规律性和不确定性。
答案:概率是描述某个事件发生的可能性的数值。
概率可以从0到1之间的任何一个数值,其中0表示不可能发生,1表示肯定会发生。
举个例子来说明,假设有一个标准的骰子,每个面上有1到6的数字。
定性数据的统计分析

混合方法研究是一种将定量和定性研究相结合的方法,这种方法可以综
合利用定量和定性的优势,提高研究的全面性和准确性。
感谢您的观看
THANKS
新闻报道内容分析是对新闻
总
报道中的文本内容进行深入
结
分析和解读,以了解新闻事 件的发展趋势和影响。
词
对新闻报道进行分类、
数 据
筛选和整理,确保数据
收
质量。
集
将内容分析结果以图表、 数
报告等形式展示,为企
据 预
业或政府机构提供决策处Fra bibliotek支持。
理
从新闻网站、媒体平台
内 容
等途径收集相关新闻报
分
道。
析
利用文本挖掘技术对新闻报
指非数值型数据,如文字、符号、图片等
分类
按照数据的性质和用途,将定性数据分为类别、顺序、等级和符号等类型
02
定性数据收集方法
访谈法
总结词
通过与研究对象进行面对面的交流,深入了解其观点、态度和经历。
详细描述
访谈法是一种常用的定性数据收集方法,通过与研究对象进行面对面的交流,可以深入了解其观点、态度和经历。 访谈可以采用开放式或半开放式的问题形式,以便获取更具体的信息。访谈过程中应注意建立互信关系,并尊重 被访谈者的隐私和意愿。
03
定性数据分析方法
内容分析法
总结词
内容分析法是一种对文本内容进行客观、系统和定量描述的技术。
详细描述
内容分析法通过对文本内容进行编码、分类和统计,以揭示文本中隐含的意义、 趋势和模式。它广泛应用于新闻媒体、社交媒体、学术文献等领域,帮助研究者 深入了解文本信息的内涵和影响。
主题分析法
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
. 页脚 第二章课后作业 【第1题】 解:由题可知消费者对糖果颜色的偏好情况(即糖果颜色的概率分布),调查者
取500块糖果作为研究对象,则以消费者对糖果颜色的偏好作为依据,500块糖果的颜色分布如下表1.1所示: 表1.1 理论上糖果的各颜色数 橙色 黄色 红色 棕色 绿色 蓝色 150 100 100 50 50 50
由题知r=6,n=500,我们假设这些数据与消费者对糖果颜色的偏好分布是相符,所以我们进行以下假设: 原假设::0H类iA所占的比例为)6,...,1(0ippii
其中iA为对应的糖果颜色,)6,...,1(0ipi已知,1610iip 则2检验的计算过程如下表所示: 颜色类别 i
n
0inp
020)(iiinpnpn
1A 172 150 3.2267
2A 124 100 5.7600
3A 85 100 2.2500
4A 41 50 1.6200
5A 36 50 3.9200
6A 42 50 1.2800
合计 500 500 0567.182
在这里6r。检验的p值等于自由度为5的2变量大于等于18.0567的概率。在Excel中输入“)5,0567.18(chidist”,得出对应的p值为05.00028762.0p,故拒绝原假设,即这些数据与消费者对糖果颜色的偏好分布不相符。 . 页脚 【第2题】 解:由题可知 ,r=3,n=200,假设顾客对这三种肉食的喜好程度相同,即顾客
选择这三种肉食的概率是相同的。所以我们可以进行以下假设: 原假设 )3,2,1(31:0ipHi
则2检验的计算过程如下表所示: 肉食种类 i
n
inp
iiinpnpn2)(
猪肉 85 66.67 5.03958 牛肉 41 66.67 9.88374 羊肉 74 66.67 0.80589
合计 200 200 72921.152
在这里3r。检验的p值等于自由度为2的2变量大于等于15.72921的概率。在Excel中输入“)2,72921.15(chidist”,得出对应的p值为05.00003841.0p,故拒绝原假设,即认为顾客对这三种肉食的喜好程度是不相同的。
【第3题】 解:由题可知 ,r=10,n=800,假设学生对这些课程的选择没有倾向性,即选
各门课的人数的比例相同,则十门课程每门课程被选择的概率都相等。所以我们可以进行以下假设: 原假设)10,...,2,1(1.0:0ipHi
则2检验的计算过程如下表所示: 类别(课程) in 0inp
020)(iiinpnpn
1 74 80 0.4500 2 92 80 1.8000 3 83 80 0.1125 4 79 80 0.0125 5 80 80 0.0000 6 73 80 0.6125 . 页脚 7 77 80 0.1125 8 75 80 0.3125 9 76 80 0.2000 10 91 80 1.5125 合计 800 800 125.52
在这里10r。检验的p值等于自由度为9的2变量大于等于5.125的概率。在Excel中输入“)9,125.5(chidist”,得出对应的p值为05.0823278349.0p,故接受原假设,即学生对这些课程的选择没有倾向性,各门课选课人数的频率为0.1。
【第4题】 解:(1)由题可知,r=3,n=5606,假设1997年8月中国股民投资状况的调查
数据和比较流行的说法是相符合。所以我们可以进行以下假设: 原假设::0H类iA所占的比例为)3,2,1(0ippii
其中)3,2,1(iAi为股票投资中对应的赢、持平和亏,)3,2,1(0ipi已知,1310iip 则2检验的计算过程如下表所示: 股票投资状况 i
n
0inp
020)(iiinpnpn
1A 1697 560.6 2303.61213
2A 1780 1121.2 387.10082
3A 2129 3924.2 821.24842
合计 5606 5606 96137.35112 在这里3r。检验的p值等于自由度为2的2变量大于等于3511.96137的概率。在Excel中输入“)2,72921.15(chidist”,得出对应的p值为05.00p,故拒绝原假设,即认为1997年8月中国股民投资状况的调查数据和比较流行的说法是不相符合的。 (2)解:由题知股票投资中,赢包括盈利10%及以上、盈利10%以下,符合条件 . 页脚 的股民共有151+122=273人;持平可以指基本持平,符合条件的股民共有240人;亏包括亏损不足10%和亏损10%及以上,符合条件的股民共有517+240=757人。 由题可知,r=3,n=1270,假设2003年2月青年报上的调查数据和比较流行的说法是相符合。所以我们可以进行以下假设: 原假设::0H类iA所占的比例为)3,2,1(0ippii
其中)3,2,1(iAi为股票投资中对应的赢、持平和亏,)3,2,1(0ipi已知,1310iip 则2检验的计算过程如下表所示: 股票投资状况 in 0inp
020)(iiinpnpn
1A 273 127 167.84252
2A 240 254 0.77165
3A 757 889 19.59955
合计 1270 1270 21372.1882
在这里3r。检验的p值等于自由度为2的2变量大于等于188.21372的概率。在Excel中输入“)2,21372.188(chidist”,得出对应的p值为05.00p,故拒绝原假设,即认为2003年2月青年报上的调查数据和比较流行的说法是不相符合的。
【第5题】 解:由题意,我们将“开红花”、“开白花”和“开粉红色花”分别记为321,,AAA,
并记iA所占的比例为)3,2,1(ipi,本题所要检验的原假设为: pqpqpH2 ,p ,p :322210 其中1qp,这些ip都依赖一个未知参数p。在原假设0H成立时的似然函数为 . 页脚 13210860362242)1()2()()()(pppqqppL
则对L(p)取对数得 )1ln(132ln108)(lnpppL 从而有对数似然方程 01132108)(lnppp
pL
即pp132)1(108。据此求得p的极大似然估计45.0ˆp,从而得到ip的极大似然估计 3,2,1),ˆ(ˆipppii。它们分别为0.2025、0.3025和0.495。由此得各类的期望频数的估计值3,2,1,ˆipni。它们分别为24.3、36.3、132.20和59.4。所以2统计量的值为 0.012244.59)4.5960(3.36)3.3636(3.24)3.2424(2222 这里r=3,m=1,r-m-1=1。检验的p值等于自由度为1的2变量。利用Excel可以算出p值05.0911893.0)1,01224.0(chidistp,故接受原假设,即我们认为以上数据在0.05的水平下与遗传学理论是相符的。
【第6题】 解:由题意,我们可以得到以下信息:
① 遗传因子的分布律为:(其中p+q+r=1)
遗传因子 A B
O
概率 p q
r
②血型的分布律为: 血型 O A B AB
概率 2
r
prp22 qrq22
pq2
将“O”血型、“A”血型、“B”血型和“AB”血型这四类血型分别记为41A......, ,A,并记iA所占的比例为)4,......,1( ipi,本题所要检验的原假设为: . 页脚 pqpqrqpprprH2 ,2 ,2p ,p :42322210 这些ip都依赖两个未知参数qp,。在原假设0H成立时的似然函数为
5813213243643674858132243623742)2()22()22()1( )2()2()2()(),(pqpqqqppqppqqrqprprqpL
则对L(p,q)求对数得 pqpqqqppqpqpL2ln58)22ln(132ln132)22ln(436ln436)1ln(748),(ln对),(lnqpL求偏导数得
058221321322287201748ln058222640224364361748lnqpqqqpqpq
L
ppqqppqppL
利用Mathematica软件求解(程序编码及运行结果见附录) 解得p和q的极大似然估计为100.0ˆ89,2.0ˆqp,从而得ip的极大似然估
计4,....,1 ),ˆ,ˆ(ˆiqpppii。它们分别为0.37332、0.43668、0.13220和0.05780。由此得各类的期望频数的估计值1,....,4i ,ˆipn。它们分别为373.32、436.68、132.20和57.80。所以2统计量的值为
003292.0 80.57)80.5758(20.132)20.132132(68.436)68.436436(32.373)32.373374(22222
这里r=4,m=2,r-m-1=1。检验的p值等于自由度为1的2变量。有Excel可以算出p值为05.0 954245.0)1 ,003292.0(chidistp,故接受0H,我们认为以上数据与遗传学理论是相符的。
附录 ①程序代码: NSolve[{(-748)/(1-p-q)+436/p+(-436)/(2-p-2*q)+0+(-264)/(2-q-2*p)+58/p==0,(-748)/(1-p-q)+0+(-872)/(2-p-2*q)+132/q+(-132)/(2-q-2*p)+58/q==0},{p,q}]//MatrixForm
