非参数回归模型及半参数回归模型
【国家社会科学基金】_非参数回归模型_基金支持热词逐年推荐_【万方软件创新助手】_20140806
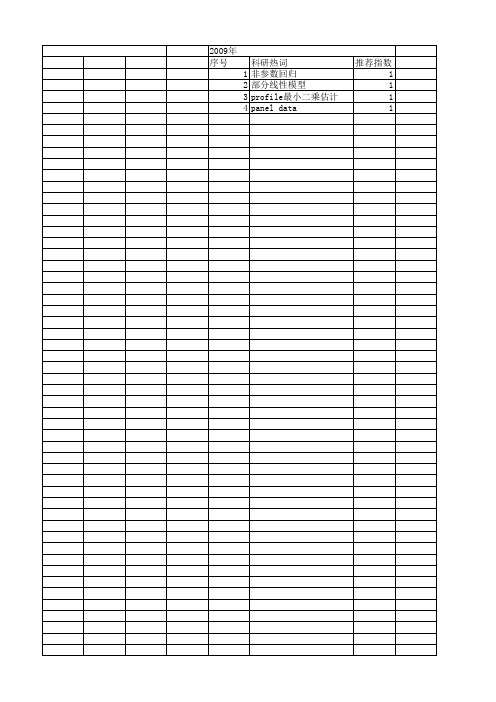
科研热词 推荐指数 非参数随机森林法 1 非参数密度 1 随机右删失 1 门槛面板回归 1 部分线性变系数模型 1 违约风险 1 自组织神经网络 1 缺失数据 1 统计诊断 1 渐近正态 1 波动性 1 汇率 1 惩罚样条 1 局部建模 1 基尼系数 1 变量含误差 1 压缩gibbs抽样 1 半参数再生散度模型 1 创新收敛 1 光滑样条 1 人力资本门槛 1 个人住房按揭贷款 1 不可忽略缺失数据 1 profile最小二乘 1 m-h算法 1 logistic回归模型 1 kaplan-meier乘积限估计 1
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
科研热词 非参数回归 高频流动性指标 非参数面板模型 非参数立方样条回归 非参数估计 通用模型 逐点回归估计 线性回归 相关系数 物种相互作用 漂移向量 混沌震荡 扩散矩阵 局部多项武估计 密度依赖性 城乡收入差距 变系数分析 不确定相互关系 gmalss模型 gaic准则 bct分布
推荐指数 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2012年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
2013年 科研热词 面板固定效应模型 面板回归 面板分位数回归 非参数模型 非参数可加模型 逐点回归 经济增长 消费结构 服务业fdi 政府消费 收入分配 技术溢出 居民消费 局部线性回归 城乡消费差异 城乡收入差距 全要素生产率 人均实际gdp 人口结构 malmquist指数 推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
半参数模型中有偏估计的进一步研究

乘估计是在1806年和1809年分别被Gauss和Lengedre[1,2]提出来的,自从被提出来以后,在统计学领域就成为了研究的焦点,特别是在1900年,Markov-Gauss定理[1,2]被Markov证明了以后,就得出了最小二乘估计具有很好的统计性质,最小二乘估计就一直都被认为是最好的估计方法,而被得到广泛的应用。
再到1971年,Rao[1,2]对最小二乘估计进行深入的研究得出了统一的最小二乘估计理论,就进一步牢固了最小二乘理论地位。
然而,随着研究的深入,新的评价准则的引入,特别变量个数的增加,在1955年,Stein[1]发现了在变量个数大于2时,最小二乘估计拟合效果不够理想,存在许多比最小二乘估计好的估计,这就是非常著名的Stein现象。
后来研究者发现造成这个现象的原因,是因为随着参数变量个数的增加,参数之间就很可能会存在多重共线性的情况(又叫复共线性),这个时候,变量之间存在近似的线性关系,就是设计矩阵的最大特征值和最小特征值之间的比值非常大或者设计矩阵的某个特征值趋近于0。
对于如何去克服改进这个现象造成的不良影响,就成为了统计学一个热门的话题,许多学者对其做了研究[14],提出了许多估计方法,其中最重要的估计方法就是对最小二乘估计进行改进提出新的估计方法,但是这些估计方法都有一个共同的特点,它们都是让估计方法以偏离真实值为代价,来得到的新的估计。
因此这些估计就叫做有偏估计。
其中比较重要的有:Stein[15]提出的Stein估计(SLSE),Massy[16]提出了主成分估计(PCE),Hoerl和kenard[17,18]提出了岭估计(RE),杨虎[10]提出了泛岭估计(即是统一有偏估计),Liu[19]对岭估计进行改进提出了Liu估计(LR)。
在这些估计基础上,又有很多的学者对他们进行了改进提出了新的估计方法,例如:王松桂[1]提出了广义主成分估计,黎雅莲,杨虎[6]考虑在线性模型受到约束条件下提出了统一有偏估计并研究了它们的性质,Liu[20]对Liu估计进行进一步改进得得到了Liu型估计。
Cox比例风险模型

Cox比例风险模型——Hazard model(一)方法简介1概念界定COX回归模型,全称Cox 比例风险回归模型(Cox’s proportional hazards regression model),简称Cox 回归模型。
是由英国统计学家D.R.Cox(1972)年提出的一种半参数回归模型。
该模型以生存结局和生存时间为因变量,可同时分析众多因素对生存期的影响,能分析带有截尾生存时间的资料,且不要求估计资料的生存分布类型。
由于上述优良性质,该模型自问世以来,在医学随访研究中得到广泛的应用,是迄今生存分析中应用最多的多因素分析方法。
(绕绍奇,徐天和,2013)与参数模型相比,该模型不能给出各时点的风险率,但对生存时间分布无要求,可估计出各研究因素对风险率的影响,因而应用范围更广。
2 方法创始人:Cox (1972) proportional (成比例的)hazard regression model.详细介绍了该方法的具体推演过程以及相关的实例。
参考文献:Cox, D. R. (1992). Regression models and life-tables. Journal of the Royal Statistical Society, 34(2), 187-220.3 基础知识h(X,t)由两部分组成:h0(t)不要求特定的形式,具有非参数方法的特点,而exp(…) 部分的自变量效应具有参数模型的形式,所以Cox 回归属于半参数模型。
等比例风险假设是最为关键的适用条件,类似于线性回归模型中的线性相关假设。
比例风险( PH) 假定的检验方法目前,检验Cox 回归模型PH 假定的方法主要有图示法和假设检验法[6]两种。
图示法包括: ( 1)Cox &K-M 比较法,( 2 ) 累积风险函数法,( 3 )Schoenfeld 残差图法; 假设检验法包括: ( 1) 时协变量法,( 2) 线性相关检验法,( 3) 加权残差Score 法; ( 4) Omnibus 检验法。
马尔卡夫链的介绍

非线性时间序列与马尔可夫链第一章.非线性时间序列浅释 (2)1.从线性到非线性自回归模型的差异2.线性时间序列定义的多样性第二章. 非线性时间序列模型 (6)1. 概述2. 非线性自回归模型3. 带条件异方差的自回归模型第三章. 马尔可夫链---描述AR模型的特性 (12)1.马尔可夫链2. AR模型所确定的马尔可夫链3.若干例子第四章. 统计建模方法 (29)1. 概论2. 线性性检验3. AR模型参数估计4.AR模型阶数估计第五章. 实例和展望 (46)1. 实例2.展望参考文献 (50)第一章.非线性时间序列浅释1. 从线性到非线性自回归模型的差异时间序列{x t}是一串随机变量序列, 它有广泛的实际背景, 特别是在经济与金融领域中尤其显著. 关于它们的线性与非线性概念, 可用以下的例子作些简单的解释.考察一阶线性自回归模型---LAR(1):x t=αx t-1+e t, t=1,2,…(1.1) 其中{e t}为i.i.d.序列,且Ee t=0, Ee t=σ2<∞, e t与{x t-1,x t-2,…}独立. 使用(1.1)式, 递推可得x t=αx t-1+e t= e t + αx t-1= e t + α{ e t-1 + αx t-2}= e t + αe t-1 + α2 x t-2 =…=e t+αe t-1+α2e t-2+…+αn-1e t-n+1+αn x t-n. (1.2) 当|α|<1时, 不难论证αn x t-n→ 0, (1.3) {e t+αe t-1+α2e t-2+…+αn-1e t-n+1}→∑j=0∞αj e t-j. (1.4) 于是模型LAR(1)有平稳解, 且可表达为x t=∑j=0∞αj e t-j. (1.5) 可见, 求LAR(1)模型解的方法是很简便的. 而且, 还容易推广到p 阶LAR(p)模型. 为此考察如下的p阶线性自回归模型LAR(p):x t =α1x t-1+α2x t-2+...+αp x t-p +e t , t=1,2,… (1.6) 其中{e t }为i.i.d.序列,且Ee t =0, Ee t =σ2<∞, e t 与{x t-1, x t-2,…}独立. 虽然, 反复使用(1.6)式, 仍然可得到(1.2)式的类似结果, 但是, 用扩张后的多元AR(1)模型求解时, 则显示出与LAR(1)模型求解的步骤完全相似. 为此记X t =⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+--11p t t t x x x ,U=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛001 , A=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛000.........00121 p ααα, (1.7)于是(1.6)式可写成如下的等价形式:X t =A X t-1+ e t U. (1.8) 仿照(1.2)式, 反复使用此式, 递推可得X t =AX t-1+e t U= e t U+ e t-1AU+A 2x t-2=⋯=e t U+e t-1AU+e t-2A 2U+…+e t-n+1A n-1U+A n x t-n . (1.9) 如果矩阵A 的谱半径(A 的特征值的最大模)λ(A), 满足λ(A)<1, 上式启发我们, (1.8)式有如下的解:X t =∑k=0∞A k Ue t-k . (1.10) 其中向量X t 的第一分量x t 形成的序列{x t }, 就是模型(1.6)式的解. 由此不难看出, 它有以下表达方式x t =∑k=0∞ϕk e t-k . (1.11)其中系数ϕk 由(1.6)式的α1,α2, ... ,αp 确定, 细节从略,此外, (1.11)式给了人们一点启发, 即考虑形如x t=∑k=0∞ψk e t-k, ∑k=0∞ψk2<∞, (1.12)的时间序列, 其中系数ψk能保证(1.12)式中的x t有定义. 在文献中, 这样的{x t}被称为线性时间序列.虽然这里给出了线性时间序列的定义, 但是, 我们暂时不去定义非线性时间序列, 先讨论一阶非线性自回归模型---NLAR(1), 并与线性LAR(1)模型进行比较. 首先写出NLAR(1)模型如下x t=ϕ(x t-1)+e t,t=1,2,…(1.13)其中{e t}为i.i.d.序列,且Ee t=0, Ee t=σ2<∞, e t与{x t-1, x t-2,…}独立, 这些假定与LAR(1)模型相同, 但是, ϕ(x t-1)是x t-1非线性函数, 比如ϕ(x t-1)=x t-1/{a+bx t-12}. 此时虽然仍可反复使用(1.13)式, 进行递推, 但是所得结果是x t=ϕ (x t-1) +e t= e t+ ϕ (x t-1)= e t+ ϕ ( e t-1+ ϕ (x t-2))= e t+ ϕ ( e t-1+ ϕ ( e t-2+ ϕ (x t-3)))=…=e t+ ϕ ( e t-1+ ϕ ( e t-2+ …+ϕ (x t-n))…). (1.14) 根据此式, 我们既不能轻易判断ϕ(x t-1)函数满足怎样的条件时, 上式会有极限, 也不能猜测其极限有怎样的形式.对于p阶非线性自回归模型x t =ϕ(x t-1,x t-2,…,x t-p )+e t , t=1,2,… (1.15) 仿照(1.6)至(1.9)式的扩张的方法, 引入记号 Φ( x t-1,x t-2,…,x t-p )≡⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+-----1121),...,,(p t t p t t t x x x x x ϕ, (1.16)得到与(1.15)式等价的模型X t =Φ(X t-1) +e t U, t=1,2,… (1.17)但是, 却得不出(1.9)至(1.11)式的结果.至此可看出, 从线性到非线性自回归模型有实质性差异, 要说清楚它们, 并不太简单. 从数学理论而言, 讨论线性自回归模型可借用泛函分析方法, 讨论非线性自回归模型则要借用马尔可夫链的理论和方法. 这也正是本讲座要介绍的主要内容.2. 线性时间序列定义的多样性现在简单叙述一下非线性时间序列定义的复杂性, 它与线性时间序列的定义有关. 前一小节中(1.12)式的线性时间序列, 只是一种定义方式. 如果改变对系数ψk 的限制条件, 就会给出不同的定义. 在近代研究中, (1.12)式的序列{e t }又被放宽为平稳鞅差序列, 这又引出另一种线性时间序列. 这在预报理论中有重要背景.无论对哪种线性时间序列, 都要研究它们的概率特性. 这已有丰富的成果载入文献. 可是, 非线性时间序列与此情况不同, 几乎没有文章研究它们的一般特性. 我们将要介绍的马尔可夫链, 也只是用来讨论满足非线性自回归模型的时间序列的特性问题.第二章. 非线性时间序列模型1. 概论从(1.12)式可见,线性时间序列{x t}, 被{e t}的分布和全部系数ψi 所决定. 在此有无穷多个自由参数,这对统计不方便,因此人们关心依赖有限参数的线性时间序列,即满足有限参数模型. 常用的如ARMA模型. 同样, 讨论非线性时间序列, 参数模型也更普遍. 不过, 由于非线性函数的多样性, 使得非线性时序模型更复杂. 在介绍此类模型之前, 我们先对非线性时序模型的分类作一概述.通用假定: {εt}为i.i.d.序列,且Eεt=0, 而且εt与{x t-1, x t-2,…}独立. (这是受研究方法所限)可加噪声模型:x t=ϕ(x t-1,x t-2,…,x t-p)+εt,(2.1)其中ϕ(…)是p元函数. 当它仅依赖于有限个未知参数时, 记此参数向量为α, 其相应的(2.1)模型常写成x t=ϕ(x t-1,x t-2,…,x t-p;α)+εt,(2.2)否则, 称(2.1)式称为非参数模型.带条件异方差的模型:x t=ϕ(x t-1,x t-2,…,x t-p)+S(x t-1,x t-2,…,x t-q)εt,(2.3) 其中ϕ(…)是p元函数, S(…)是q元函数. 它们也有参数与非参数的区分. 显然(2.3)式不是可加噪声模型.一般非线性时序模型:x t=ψ(x t-1,x t-2,…,x t-p; εt,εt-1,…,εt-q),t=1,2,… (2.4) 其中ψ(…)是p+q元函数. 显然, (2.4)式是最广义的非线性ARMA模型, 但是, 无论理论研究, 还是统计建模, 都难于进行, 所以在文献中很少见此模型. 只有双线性模型作为它的一种特殊情况, 有些应用和研究结果出现. 现写出一般双线性模型x t=∑j=1pαj x t-j+∑j=0qβjεt-j+∑i=1P∑j=1Qθijεt-i x t-j. (2.5)其中β0=1. 一种简单情况如x t=αx t-1+ θεt-1x t-1+εt. (2.6) 2. 非线性自回归模型前面的(2.1)和(2.2)式是非线性自回归模型, 而且属于可加噪声模型类. 现介绍几种(2.2)式的常见形式.函数后的线性自回归模型:f(x t)=α1f(x t-1)+α2f(x t-2)+...+αp f(x t-p)+εt,(2.7)其中f(.)是一元函数, 它有已知和未知的不同情况, 不过总考虑单调增函数的情况, α=(α1,α2,…,αp)τ是未知参数. 在实际应用中, {x t}是可获得量测的序列.当f(.)是已知函数时, {f(x t)}也是可获得量测的序列, 于是只需考虑y t=f(x t)满足的线性AR模型y t=α1y t-1+α2y t-2+...+αp y t-p+εt,(2.8)这是线性自回归模型. 在宏观计量经济分析中, 常常对原始数据先取对数后, 再作线性自回归模型统计分析, 就属于此种情况. 这种先取对数的方法, 不仅简单, 而且有经济背景的合理解释,它反应了经济增长幅度的量化规律. 虽然在统计学中还有更多的变换可使用, 比如Box-Cox变换, 但是, 由于缺少经济背景的合理解释,很少被使用. 由此看来, 当f(.)有实际背景依据时, 可以考虑使用(2.7)式的模型.当f(.)是未知函数时, {f(x t)}不是可量测的序列, 于是只能考虑(2.7)模型. 注意f(.)是单调函数, 记它的逆变换函数为f-1(.), 由(2.7)式可得x t=f-1(α1f(x t-1)+α2f(x t-2)+...+αp f(x t-p)+εt),(2.9) 此式是(2.4)式的特殊情况, 此类模型很少被使用. 取而代之是考虑如下的模型x t=α1f(x t-1)+α2f(x t-2)+...+αp f(x t-p)+εt, (2.10) 其中f(.)是一元函数, 也有已知和未知之分, 可不限于单调增函数. 此式属于(2.2)式的特殊情况, 有一定的使用价值. 例如x t =α1I(x t-1<0)x t-1+α2I(x t-1≥0)x t-1+εt , (2.11) 其中I(.)是示性函数. 此模型是分段线性的, 是著名的TAR 模型的特殊情况(详见后文). 其分段形式如下:x t =⎩⎨⎧≥+<+----.0,,0,112111t t t t t t x x x x εαεα t=1,2,… (2.12)请注意, (2.10)和(2.11)式有一个共同的特征, 就是未知参数都以线性形式出现在模型中. 这一特点在统计建模时带来极大的方便. 此类模型便于实际应用. 但是, 对于{x t }而言不具有线性特性, 所以, 讨论它们的平稳解, 以及建模理论等问题, 都需要借助于马尔可夫链的工具.参数型的非线性自回归模型: 即(2.2)式,x t =ϕ(x t-1,x t-2,…,x t-p ;α)+εt , (2.13)其中ϕ(…)是p 元已知函数, 但是其中含有未知参数α=(α1,α2,…,αp )τ. 一般说来, α在一定范围内取值.例如,x t =212111--+t t x x αα+εt , (2.14)其中α=(α1,α2)τ是未知参数, 它们的取值范围是: -∞<α1<∞, 0≤α2<∞.这里需要指出, 使用(2.13)式的模型, 不仅要借助马尔可夫链的工具, 而且在统计建模时遇到两种麻烦, 其一是参数估计的计算麻烦, 二是确定ϕ(…)函数的麻烦. 一般来说, 只有根据应用背景能确定ϕ(…)函数形式时, 才会考虑使用此类模型.除了以上两类模型外, 还有(2.1)式的非参数自回归模型, 以及从统计学中引入的半参数自回归模型. 对它们的统计建模更困难. 本讲座主旨在于介绍如何用马尔可夫链的工具, 描述非线性自回归模型的基本特性, 对这类模型不再仔细讨论.3. 带条件异方差的自回归模型前面的(2.3)式就是带条件异方差的自回归模型. 在这一小节里, 将介绍几种(2.3)式的常见形式.函数型条件异方差的自回归模型:x t=ϕ(x t-1,x t-2,…,x t-p)+S(x t-1,x t-2,…,x t-q)εt,(2.15)其中ϕ(…)是p元函数, S(…)是q元函数. 它们也有参数型和非参数型之分别, 这里不再赘述. 有两点必须指出: 为保证(2.15)式中S(…)被唯一确定, 还要限定Eεt2=1; 另外, 为(2.15)式建模时, 需要对ϕ(…)和S(…)都作估计.带ARCH模型的自回归模型:x t=ϕ(x t-1,x t-2,…,x t-p)+e t, (2.16)其中e t=S(e t-1,e t-2,…,e t-q)εt,S(e t-1,e t-2,…,e t-q)={α0+α1e t-12+…+αp e t-p2}1/2. (2.17)带ARCH 模型的自回归模型, 与函数型条件异方差的自回归模型, 都可借助马尔可夫链的工具加以研究. 研究带GARCH 模型的自回归模型, 仍有困难. 现在回顾(2.12)式的一般形式:x t =⎩⎨⎧≥++++<++++------,,...,,...22121201111110c x x x c x x x d t t q t q t d t t p t p t εαααεααα (2.18)其中{ε1t }和{ε2t }为相互独立的i.i.d.序列, 且ε1t ~N(0,σ12), ε2t ~N(0,σ22), 此外, 在(2.18)式中, d ≥1可能是未知的, c 被称为门限值, 一般也是未知的, 这些未知信息都会带来统计的麻烦. 现在我们讨论它的类型问题. 为此先改写它的形式如下:x t ={α10+α11x t-1+…+α1p x t-p +ε1t }I(x t-d <c)+{α20+α21x t-1+…+α2q x t-q +ε2t }I(x t-d ≥c)={α10+α11x t-1+…+α1p x t-p }I(x t-d <c)+{α20+α21x t-1+…+α2q x t-q }{I(x t-d ≥c)+{ε1t I(x t-d <c)+ε2t I(x t-d ≥c)}. (2.19) 由此可见, 当{ε1t }={ε2t }={εt }时, 上式变成x t ={α10+α11x t-1+…+α1p x t-p }I(x t-d <c)+{α20+α21x t-1+…+α2q x t-q }{I(x t-d ≥c) +εt , (2.20) 此式表明, 它属于(2.10)式的自回归模型. 由(2.20)式, 不难写出(2.10)式中的f k (.)函数(k=1,2,…,p+q+2), 注意它们都不是连续函数. 在实际应用中发现, (2.19)式中的两个残差项很少相同. 在此情况下, (2.19)式属于上述提到的哪一类呢? 易见, 它有条件异方差特性, 但是, 它又不像(2.15)或(2.16)式的任何一类. 它属于下面的多噪声驱动的自回归模型.两噪声驱动的自回归模型:x t=ϕ(x t-1,x t-2,…,x t-p)+S1(x t-1,x t-2,…,x t-q)ε1t,+ S2(x t-1,x t-2,…,x t-q)ε2t,(2.21) 其中{ε1t}和{ε2t}为相互独立的i.i.d.序列, Eε1t=Eε1t=0, Eε1t2=1 Eε2t2=1. 为了统计建模方便, 常假定它们有正态分布. 读者不难看出(2.19)式中的ϕ(x t-1,x t-2,…,x t-p), S1(x t-1,x t-2,…,x t-q)和S2(x t-1,x t-2,…,x t-q)的具体表达式.顺便指出, 称{ε1t}和{ε2t}为驱动噪声, 因为它们都是白噪声序列, 而且是不可观测的. 这样的模型可称为自激系统. 此类模型亦可借助于马尔可夫链的工具加以研究. 读者不难想到多噪声驱动的自回归模型, 这里从略.第三章. 马尔可夫链---描述AR模型的特性1.马尔可夫链时间序列{x t; t=1,2,…}, 是一个随机变量序列, 也简称随机序列. 与随机过程{x(t); t=∈(0,∞)}相比, 它只在离散时间取随机变量值的过程, 故此得名. 随机过程的类型很多, 研究的方法很多, 取得的成果也很多. 其中最重要的是马尔可夫过程, 当它是随机序列时, 称为马尔可夫链. 初次接触此类过程时, 先了解马尔可夫链为宜, 即{x t; t=1,2,…}为一马尔可夫链. 为易于理解概念的实质, 不妨考虑x t只取两个可能值的最简单情况. 以下就从一个示意性的例子说起.一个例子: 甲乙二人进行赌博, 每局分主(庄家)客方, 第一局的主客方由二人协商确定, 以后各局, 由前一局的取胜者担任(每局必分胜负)主方. 记x t=1表示在第t局时由甲任主方; x t=2表示在第t局时由乙任主方. 那么{x1, x2, …}是一个时间序列. 虽然它们只取1和2两个可能值, 但是不能预先知道它们的确切取值, 所以这它是随机序列.我们先用直观分析方法考察此例的特征. 如果此赌博含有技巧因素, 那么他们坐庄的多少与他们的水平有关. 以t表示当前局, 那末, x t的取值已定. 比如x t=1时, 意味着甲坐庄, 此时不能预知x t+1=1还是2. 如果x t+1=1意味着甲继续坐庄, 如果x t+1=2意味着甲丢掉庄家. 虽然不能预知x t+1的取值, 但是我们关心甲有多大把握继续坐庄. 重复上面的叙述, 当x t=2时, 我们关心甲有多大把握上庄. 在以上分析中, 我们忽略了x1, x2, …, x t-1的已知取值信息, 在已知x1,x 2, …, x t-1 , x t 时, 回答前面的两个问题, 只与x t 的取值有关. 此特征是被马尔可夫首先注意到的(1906年).现在将以上问题给出概率描述如下:P(x t+1=1⎜x t =1)=? P(x t+1=1⎜x t =2)=?被马尔可夫注意到的特征的概率论描述如下:P(x t+1=k ⎜x t =j,x t-1=j t-1,…,x 1=j 1)=P(x t+1=k ⎜x t =j), (3.1)如果上式的P(x t+1=k ⎜x t =j)与t 无关(详见后文), 可记P(x t+1=k ⎜x t =j)=p jk , j, k=1,2. (3.2)称p jk 为从状态j 向状态k 的转移概率. 注意, 此时只有两个可能状态(对应于x t =1或2), 于是易见p j1+p j2=1, 即p j2=1- p j1, j=1,2. (3.3)再将这些记号概括到如下的矩阵中, 即P=⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎭⎫ ⎝⎛q q p p p p p p 1122211211, (3.4)称P 为马尔可夫链{x t }的一步转移概率矩阵, 也简称为转移矩阵. 又因(3.3)式成立, 故可简化记为p 11= p, p 22=q. p 11恰好表示甲继续坐庄的概率(相当于把握的大小), p 22恰好表示甲继续不坐庄的概率. 经马尔可夫和后来人的不断研究表明, 在以上例子中, 转移矩阵P 能刻画出马尔可夫链{x t }的全部概率特征. 对更广泛的马尔可夫过程也有类似结论. 在随机过程中有关马尔可夫过程的内容非常丰富. 在本讲义中, 只介绍某些马尔可夫链的知识, 又尽可能少地涉及深层理论内容. 为此, 我们先将马尔可夫过程理论分为四大类, 概括在如下的一拦表中, 据此可明确我们将关心哪一类. 当然, 也只关心此类中的局部内容(见后文便知). 为列此表, 首先注意, 在马尔可夫过程{x t}中, 时间t 有连续和离散的区分; x t的取值(又称为状态)也有连续和离散的区分. 上述例子就是离散型, 而且是两状态的, 这是有限状态马尔可夫链的最简单的情况. 依此划分可列出下表:马尔可夫过程分类表有趣的是, 这四类的研究历程有如下的先后次序: 离散状态马尔可夫链, 20年代---马尔可夫过程, 50年代---马尔可夫跳过程, 60年代---连续状态马尔可夫链, 70年代---我们关心连续状态马尔可夫链, 这是较近代的内容(1975年以后). 此内容恰好是近代非线性时间序列分析盼望已久的理论基础. 以下的各节将介绍连续状态马尔可夫链的定义和特性.马尔可夫链的定义: 若随机序列{x t}具有以下性质, 则称它为马尔可夫链,P(x t+1<x⎜x t, x t-1, …, x1)=P(x t+1<x⎜x t). (3.5)上式表明: 在给定x t, x t-1, …, x1时, x t+1的条件分布, 与给定x t时x t+1的条件分布相等, 记它为F t(x|x t). 在给定x t时, F t(x|x t)是一个分布函数, 它会随着x t的取值不同而不同. 易见, 此定义对离散和连续状态的马尔可夫链都适用.在非线性时间序列模型讨论中, 还须要用到多元马尔可夫链, 即{X t}中的X t=( X t1, X t2,…, X tm)τ是随机向量. 以上定义不难推广到向量的情况.向量马尔可夫链的定义: 若随机序列{X t}具有以下性质, X t=( X t1, X t2,…, X tm)τ是随机向量, 而且P(X t+1∈A ⎜X t, X t-1, …,X1)=P(X t+1∈A ⎜X t). (3.6) 在(3.6)式中的A, 是m维欧氏空间的可测集合. 特别取A={Y: Y =(Y1, Y2,…, Y m)τ , Y i<x i, i=1,2,…,m}, 便得到X t+1的多元分布函数.其实, 向量马尔可夫链的定义蕴涵了马尔可夫链的定义. 在后文中不再区分向量与非向量, 一律用马尔可夫链称之, 或者简称马氏链. 它们的维数会不言自明. 有了上述定义, 我们的目的是介绍马尔可夫链的平稳性条件. 为此, 还有几个概念不可缺少. 严格地说, 这几个概念和上面的定义, 都要用到测度论的术语. 这里回避了它们, 因为我们只是为了使用这些概念, 而不是研究它们. 在后文中将看到, 这并不影响使用这些概念来解决非线性自回归模型的平稳性等问题.齐时马尔可夫链: 如果马尔可夫链{x t}(一元的或多元的)满足P(x, A)=P(x t+1∈A⎜x t=x), t=1,2,…(3.7)与时刻t无关, 称{x t}为齐时马尔可夫链. 再记P k(x, A)=P(x t+k∈A⎜x t=x), k=1,2,…(3.8) 表示在当前时刻t处在x t=x, 经过k步后的x t+k落入A 的概率, 简称为k步转移概率. 显然, 依(3.7)式知P1(x, A)=P(x t+1∈A⎜x t=x)= P(x, A).又易见P2(x, A)=P(x2∈A⎜x0=x)=⎰P(y, A)P(x, dy). (3.9)此式表明, 两步转移概率P2(x, A), 可写成从x0=x先用一步转移到y, 再从x1=y转移到A的概率的平均. 其平均是指按一步转移概率分布完成, 以一元为例, P1(x, (-∞,y))= P(x, (-∞,y)), P(x, dy)=dP(x, (-∞,y)). 重复上面的推理可得P k(x, A)=P(x k∈A⎜x0=x)=⎰P k-1(y, A)P(x, dy),k=2,3,…(3.10) 马尔可夫链的不可约性: 如果马尔可夫链{x t}满足∑k=1∞ P k(x, A)>0, (3.11)其中x是m(≥1)维欧氏空间R m的任意一点, A是m(≥1)维欧氏空间的任意一个有正测度的可测集合, 这里的测度不妨用Lebesgue测度, 在本讲义中已是够用了.现在对不可约概念作些直观解释. 先从(3.11)式的定义可看出, 从R m中的任何一点出发, 对任何指定的正测度集合A, 用有限步转移到A的概率是正的. 换句话说, 不存在那样的点x和正测度集合A, 从x出发永远不能到达A. 更直观解释可用类似于前边的例子. 考察甲对乙, 丙对丁同来赌博, 并争用同一赌具的例子. 因为只有一个台面可用, 于是, 要用抽签决定哪一对进行赌博. 我们记x t=1表示在第t局时由甲坐庄; x t=2表示由乙坐庄; x t=3表示由丙坐庄; x t=4表示由丁坐庄. 于是{x1, x2, …}是一个时间序列. 不难验证这是一个马尔可夫链. 但是, 当x1=1或2时, 此后的x t, 只能x t=1或2, 不可能取3或4; 反之, 如果x1=3或4时, 此后也只能x t=3或4, 不可能取1或2. 这就是说, 在(3.11)式中取x=1, A={3,4}时, (3.11)式等于0值. 所以此马尔可夫链不是不可约的. 此例显然是编撰的, 通过它可说明, 对于可约的马尔可夫链, 可以分解成子序列分别去研究. 也就是说, 我们应当对甲--乙和丙--丁的博弈分别进行考察, 没有必要放在一个马尔可夫链中来讨论.马尔可夫链的周期性: 如果存在互不相交的正测度可测集合A1,A2,…,A d, 使得马尔可夫链{x t}满足P(x, A k)=1, 当x∈A k-1, k=2,3,…,d,P(x, A1)=1, 当x∈A d.则称{x t}为具有周期长度为d的周期马尔可夫链.此定义表明, 周期马尔可夫链, 必然从A1转移到A2, 再从A2转移到A3,…, 最后, 又从A d转移到A1, 形成周期性的转移规律. 须注意, 从A k-1转移到A k时, 具体转移到A k中哪一点, 仍然是随机的, 否则不是随机序列了. 虽然如此, 对周期马尔可夫链, 只需要研究其等间隔的子链{x td}即可, 因为其它子链{x td+k}(k=1,2,…,d-1)与{x td}的概率结构相同. 所以, 我们也只需考察非周期马尔可夫链, 即d=1的情况. 对此概念不在作直观解释了.马尔可夫链的小集合: 对于马尔可夫链{x t}, 如果存在非空的可测集合C∈R m, 一个正整数q, 一个正常数λ, 和某个概率测度ν, 使得P q(x, A) ≥λν(A), 对于任何x∈C, A∈R m, (3.12)则称C是马尔可夫链{x t}的小集合.以上小集合是一个重要的概念, 它是从一般离散状态马尔可夫链中的相应概念演化而来的. 对它要作直观解释比较困难, 将涉及太多的其它相关知识, 这里只得放弃了. 好在, 在下一节的应用时只用此定义而已, 在很宽松的条件下, 又是通过很容易的论证, 即可得知怎样的马尔可夫链会有怎样的小集合.以上叙述了马尔可夫链的转移概率. 现在考虑它的分布. 首先考察x0的分布, 它是初始的随机变量, 可以有其自己的分布, 也称为此马尔可夫链的初始分布, 不妨记为F0. 欲考察x1的分布F1, 根据齐时马尔可夫链的性质, 利用条件分布公式可得(当m=1时) F1(x)=P(x1<x)=⎰P(y, (-∞,x))dF0(y).当x1的维数m>1时, 将上面的分布F0和分布F1, 改用概率测度记号P0和P1更方便, 即有P1(A)=P(x1∈A)=⎰P(y, A)P0(dy). (3.13)仿此式可得P t(A)=P(x t∈A)=⎰P(y, A)P t-1(dy), t=1,2,… (3.14) 依此式和x0的概率测度P0, 就能确定马尔可夫链的全部概率分布. 在初始概率测度中, 如果存在这样的P, 能保证(3.13)式成为P1(A)=P(x1∈A)=⎰P(y,A)P(dy)=P(A)=P(x0∈A), (3.15) 此式意味着, 初始概率测度P经过一步转移后得到x1的概率测度P1, 与P相同, 或者说, 此概率测度P经过一步转移后不变, 称这样的P为不变概率测度. 将(3.15)式代入(3.14)式, 并反复迭代可得P t(A)=P(x t∈A)=⎰P(y, A)P t-1(dy)=⎰P(y, A)P(dy). t=1,2,…(3.16) 可见, 若以不变概率测度作为初始概率测度时, 则x t 都有相同的分布.马尔可夫链的平稳性: 考察齐时马尔可夫链{x t; t=0,1,2,…}, 若它有不变概率分布, 则称它为马尔可夫链的平稳分布, 当以此作为初始概率测度时, 则称这样的马尔可夫链为平稳的, 或者说它具有平稳性.须注意, 不是任何马尔可夫链都有平稳分布. 人们自然关心怎样的马尔可夫链有平稳分布, 如何获得其平稳分布的问题. 稍后将讨论此类问题.马尔可夫链的遍历性: 如果马尔可夫链{x t}有不变概率测度P, 对任意x∈R m, 取(3.13)式中的P0(x0=x)=1, 即取初始概率测度为在点x处的点分布, 记P n x为由(3.14)式确定的x n的概率测度, 如果有lim n→∞||P n x-P||=0, (3.17)称此马尔可夫链{x t}为遍历的; 如果存在ν>1使得lim n→∞νn||P n x-P||=0, (3.18)称此马尔可夫链{x t}为几何速度遍历, 又简称几何遍历性. 在(3.18)式中的||P n x-P||表示(P n x-P)的模数, 即两个概率测度P n x和P之差的距离的度量. 我们这里采用(P n x-P)的全变差作为度量模数. 粗略地说, 就是||P n x-P||=⎰|P n x(dy)-P(dy)|.注意, 上式右边的积分, 如果放弃取绝对值的记号, 上式=1-1=0; 加上绝对值记号, 称为全变差. 显然, 上式>0, 除非P n x=P.根据上述定义, 如果一个马尔可夫链有遍历性, 那么, 从任何一点x出发, 经过n步转移后得到x n的概率测度P n x, 都会收敛到它的不变概率测度P, 甚至于会有几何速度收敛. 具有遍历本必有不变概率测度, 可见这是重要的性质. 至于如何判断马尔可夫链是否有遍历性, 请看以下的定理.飘移定理: 如果马尔可夫链{x t}是齐时的, 不可约的, 非周期的, 还存在小集合C, 此外还有一非负(m 元)可测函数g, 和常数c 1>0, c 2>0, 使得(i) E{g(x n )| x n-1 =x}≤g(x)-c 1, 当x ∉C,(ii) E{g(x n )| x n-1 =x}≤c 2, 当x ∈C,那么, 此马尔可夫链为遍历的. 如果还存在0<ρ<1, 使得以上(i)被如下的(i)’代替, (ii)仍保持, 即(i)’ E{g(x n )| x n-1 =x}≤ρg(x)-c 1, 当x ∉C,那么, 此马尔可夫链为几何遍历的.此定理是下一节定理的基基础. 在实际应用时, 既可直接使用此定理, 也可以使用下一节的定理. 而且, 下一节的定理是针对NLAR(p)模型的, 更实用.2. AR 模型所确定的马尔可夫链对于p 阶非线性自回归模型x t =ϕ(x t-1,x t-2,…,x t-p )+εt , t=1,2,… (3.19)仿照(1.6)至(1.9)式的扩张的方法, 引入记号 Φ(x t-1,x t-2,…,x t-p )≡⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+-----1121),...,,(p t t p t t t x x x x x ϕ, U=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛001 , (3.20)得到与(3.19)式等价的模型X t =Φ(X t-1) +εt U, t=1,2,… (3.21)当p=1时, (3.19)式为x t =ϕ(x t-1)+εt , t=1,2,…于是P(x t <x|x t-1,x t-2,…,x 1)=P(ϕ(x t-1)+εt <x|x t-1,x t-2,…,x 1)=P(ϕ(x t-1)+εt<x|x t-1)=P(x t<x| x t-1),由此可知, 满足NLAR(1)模型的序列{x t}是马尔可夫链. 但是, 满足NLAR(p)模型(3.19)式的序列{x t}不是马尔可夫链. 幸运的是, 仿照推论NLAR(1)序列{x t}是马氏链的步骤, 容易得知, 满足p元NLAR(1)模型(3.21)式的多元序列{x t}是多元马氏链, 因为P( X t∈A| X t-1,X t-2,…,X1)= P( X t∈A| X t-1).在后文中, 常用多元马氏链, 为了节省符号, 一般不用大小写字母来区分一元与多元x t, 在讨论中, 它的维数是不言自明的.引理3.1. 在模型(3.19)式中, 如果εt和ϕ(…)满足(i) i.i.d.序列{εt}中的εt有处处为正的密度函数,(ii) 对任何K<∞, 可测函数ϕ满足sup||x||<K|ϕ(x)| <∞那么, 满足(3.21)式的{X t}是一马尔科夫链, 而且它是: 齐时性的; 不可约性的; 非周期性的;而且任何有界可测集是小集.此结果的证明并不难, 不过, 还是有太多的数学推演内容, 这里从略. 有兴趣者可参见安和陈的书(第4章,1998). 由此引理可见, 尽管在前一小节中叙述了较多的概念, 有的还难于理解, 但是, 当讨论在时序模型中的应用时, 竟如此简单, 并不涉及对诸多概念的太深理解. 由此引理和飘移定理又可得如下定理.定理3.2. 在模型(3.19)式中, 如果εt和ϕ(…)满足(i) εt有处处为正的密度函数, Eεt=0, Eεt2<∞,(ii) 存在0≤ρ<1, c≥0, 和加权模数||.||w , 使得||ϕ(x)||w≤ρ||x||w +c, (3.22) 或者|ϕ(x)|=|ϕ(x1, x2,…, x p)|≤ρmax{|x1|, |x2|,…, |x p|}+c, (3.23)那么, 满足(3.21)式的{X t; t≥1}是几何遍历的马尔科夫链. 其中加权模数是指:||x||w2=∑k=1m w jk x j x k=xτWx, W=(w jk)>0.这里使用加权模数, 是为了放宽(3.22)式的约束性.由此可知, 在时序模型中应用马氏链, 主要归于验证前一引理和此定理的条件.此定理的证明有太多数学推演, 这里从略. 此定理是比较重要的一个. 还有其它的定理讨论自回归模型有遍历性条件, 在此不逐一介绍, 有兴趣者可参见安和陈的书(第4章,1998). 以下再叙述一个有关带条件异方差自回归模型的遍历性定理.定理3.3. 考察带条件异方差的模型:x t=ϕ(x t-1,x t-2,…,x t-p)+S(x t-1,x t-2,…,x t-q)εt,(3.24) 如果εt,ϕ(…)和S(…)满足(i) εt 有处处为正的密度函数, E εt =0, E εt 2=1,(ii) 存在一种加权模数||.||w 和0<ρ<1, c ≥0, 使得(3.22)式成立,(iii) S(…)是正的连续函数, 而且lim ||x||→∞ S(x)/||x||=0, (3.25) 那么, 满足(3.24)式的{X t }是几何遍历的马尔科夫链.3.若干例子以下总假定{εt }满足定理3.2中的条件(i).例3.1. 有界自回归模型. 若非线性AR(p)模型 x t =ϕ(x t-1,x t-2,…,x t-p )+εt , 中的ϕ(…)是有界函数, 即存在K<∞, 使得|ϕ(x)| <K.取ρ=0, c=K, W=I(单位方阵), 则(3.22)式成立, 模型有几何遍历性. 如(2.14)式, ϕ(x t-1)=212111--+t t x x αα是有界函数.例3.2. 衰减型自回归模型. 若非线性AR(p)模型 x t =ϕ(x t-1,x t-2,…,x t-p )+εt , 中的ϕ(…)有以下的衰减性质, 即lim ||x||→∞||ϕ(x)||/||x||=0, (3.26) 任取0<ρ<1, c>0, W=I, 易见(3.22)式成立, 模型有几何遍历性.例3.3. 线性自回归模型. 若线性AR(p)模型 x t =α1x t-1+α2x t-2+…+αp x t-p +εt ,其中系数满足平稳性条件, 即1-α1u-α2u 2-…-αp u p ≠0, |u|≤1. (3.27)回顾(1.6)(1.7)和(1.8)式, 上式可写成等价模型X t =A X t-1+ e t U.依(1.7)式关于A 的定义, 以及(3.27)式, 必存在加权模数 ||.||w 使得(3.22)式成立, 其中0<λ(A)<ρ<1, 这里λ(A)是A 的谱半径. 所以此模型有几何遍历性.例3.4. 半参数自回归模型.x t =α1x t-1+α2x t-2+…+αp x t-p +f(x t-1,x t-2,…,x t-q )+εt , 其中系数满足平稳性条件(3.27)式, 连续函数f(…)满足(3.26)式, 所以此模型有几何遍历性. 论证从略.例3.5. 门限自回归模型.(Threshold AR---TAR) 考察(2.12)和(2.18)式的一般形式, 即x t =⎪⎪⎩⎪⎪⎨⎧∞<<++++≤<++++≤<∞-++++----------,,...,,...,,...1110212121201111110d t s t p t sp t s s d t t p t p t d t t p t p t x c if x x c x c if x x c x if x x εαααεαααεααα (3.28)其中在各段的{εt }亦可互不相同, 且互相独立, 这里讨论相同情况. 如果(3.28)式的系数满足ρ=max 1≤k ≤s ∑j=1p |αkj |<1, (3.29)不难验证(3.23)式成立, 于是此模型有几何遍历性. 例3.6. β-ARCH 模型:x t =h t 1/2εt , t=1,2,… (3.30)。
27_有限样本情况下的计量经济模型

有限样本情况下的计量经济模型第一部分有限样本的定义与特性 (2)第二部分计量经济模型介绍 (4)第三部分有限样本对模型的影响 (7)第四部分模型稳健性检验方法 (11)第五部分估计方法的选择与比较 (15)第六部分有限样本下的假设检验 (18)第七部分实证研究案例分析 (20)第八部分改进模型与未来展望 (23)第一部分有限样本的定义与特性有限样本情况下的计量经济模型是一种广泛应用在实际经济问题研究中的工具。
当数据集的规模受到限制时,这些模型能够帮助我们从理论上和实践上对经济现象进行更深入的分析。
首先,我们要了解什么是有限样本。
在统计学中,样本是指从总体中抽取的一小部分观察值,用来代表整个总体的特性。
而在实际应用中,由于资源、时间或成本的限制,我们通常只能获取到一个有限的样本。
这个样本可能是包含数百个观察值的小型数据集,也可能是包含数千甚至数万观察值的大型数据集。
然而,无论样本大小如何,只要它不是包含了所有可能的观察值的总体,我们就将其称为有限样本。
那么,在有限样本情况下,计量经济模型有哪些特性呢?下面我们将从几个方面来探讨这个问题。
1.估计误差:由于我们只拥有关于总体的一部分信息,因此使用有限样本构建的模型会产生估计误差。
这种误差可以通过增加样本容量来减小,但是无法完全消除。
2.模型偏差:有限样本可能会导致模型参数的偏误。
例如,在线性回归模型中,如果存在异方差性或者多重共线性等问题,就可能导致参数估计结果偏离真实值。
3.假设检验:在有限样本情况下,我们需要对模型的假设进行谨慎的检验。
因为样本量较小,一些假设(如正态性、独立性等)可能并不成立。
如果不加以处理,这些假设不满足的情况将会影响模型的可靠性。
4.预测能力:对于有限样本的模型来说,其预测能力往往会受到限制。
特别是在样本容量较小的情况下,模型的预测性能往往不稳定,容易受到异常值的影响。
为了应对有限样本带来的挑战,我们需要采取一些策略来提高模型的质量。
Lecture4-非参数+空间计量经济学模型概述

• 半参数模型
Yi βZi g (Xi ) i , i 1, 2,, n
模型假定一部分解释变量与被解释变量的关系为线性关 系,这部分解释变量为参数部分的解释变量;其它解释 变量与被解释变量的关系未知,这部分解释变量为非参 数部分的解释变量;
回归函数为参数部分的线性关系加非参数部分的未知函 数关系。
三、空间计量经济学模型的发展
1、概述
• 空间计量经济学(Spatial Econometrics)是在 20世纪70、80年代开始出现的一个计量经济学分 支学科。
– Anselin(1988)给出的定义:其基本内容是在计量经 济学模型中考虑经济变量的空间效应,并进行一系列 的模型设定、估计、检验以及预测的计量经济学模型 方法。
2、从计量经济学模型的角度提出问题
• 截面数据计量经济学模型
– 被解释变量存在一定的相关性 • 用解释变量构造矩条件的矩估计不是无偏估计量。 • 工具变量估计量虽然满足无偏性,但是在估计的过 程中损失了空间相关性的信息。 – 随机误差项存在一定的相关性 • LLN和CLT便不再成立。 • 采用经典模型的方法很难消除。
– 空间依赖性打破了大多数传统经典统计学和计量经济 学中相互独立的基本假设,是对传统方法的继承和发 展。
• 空间效应
– 空间相关性(spatial dependence) – 空间异质性(spatial heterogeneity)
• 将空间效应纳入计量模型分析的框架下,便面临 着两方面的问题。
– 一是如何正确的将空间效应引入既有的模型,或者根 据空间效应的特殊性构造新的计量经济学模型; – 二是对于新的模型,如何进行估计和检验。
Y Xβ ε ε Wμ + μ, μ N[0, I]
基于半参数Hedonic模型的新楼盘房价研究

研究探索
文的目的主要在于分析新开楼盘的显著影响特征因素,并试图 通过半参数方法解决非线性特征变量CBD与房价的函数关系问 题,有利于对房价指数编制的进一步研究提供科学依据。 量。
《统计科学与实践》2012年12期
其中, 为包括常数项在内的显著变量个数, 为样本
三、新开楼盘价格研究方法
(一)半参数方法 半参数回归模型是介于参数回归模型和非参数回归模型之 间。在应用上,模型较单纯的参数模型或非参数模型有更大的 适应性。因而,它是一个在实用上有重要意义且在理论上富有 挑战的领域 。在建立半参数模型之前,首先将新开楼盘的属 性特征变量分成两组:一组用向量 表示,即与价格呈线性关 系的显著特征变量;另一组特征变量由向量 表示,即与房价 呈非线性关系的特征变量,本文针对楼盘CBD,构建对数半参 数回归模型为: (1) 式(1)中, 是楼盘属性特征矩阵, 反映楼盘属性特 征对楼盘价格 变化产生的影响。 是楼盘特征线性主部, 可以把握大势走向,适于外延预测; 是楼盘非线性特征 的非参数部分,可以作局部调整,使数据较精确地拟合。模型 的任务主要是以楼盘价格 ,以及楼盘属性特征包( , ) 出发,估计未知函数 和未知参数 以及方差 。根据权函数法得出未知函数 的估计:
[8]
四、以杭州市场为例新楼盘价格显著属性 特征分析
(一)数据来源及特征变量选取 本文收集的是杭州市首次开盘的均价数据,不考虑二次开 盘或交易的价格。目的是为了避免某楼盘因多次开盘而出现数 据重复的现象。通过杭州楼盘信息快房网、新房搜房网、楼市 以及搜狐焦点网杭州站这四个杭州房地产权威网站,获得 2009年10月至2011年3月杭州新楼盘交易的第一手数据。新 开楼盘的样本量为102个,其中2009年第4季度16个,2010年 第1季度7个,2010年第2季度16个,2010年第3季度20个, 2010年第4季度31个,2011年第1季度12个。对各地的经济发 展、文化氛围、自然环境等条件的差异,比较分析了文献资料 中几种特征变量的优点和局限性,借鉴国内外已有HPM,并 结合杭州市场的特点,选取了建筑特征、区位特征、邻里特征 三大类共21个楼盘特征变量。 (二)特征变量的说明 1.变量符号说明。被解释变量为首次开盘均价 ,属性特 征分别为容积率 、绿化率 、物业费 、CBD 、占地面 积 、建筑面积 、户型面积 、上城区 、下城区 、西 湖区 、拱墅区 、江干区 、滨江区 、下沙区 、萧山
基于半参数方法的车险保费收入实证

基于半参数方法的车险保费收入实证本文利用半参数分析的原理与方法,结合我国车险市场的特点,建立车险价格指数的半参数回归模型。
通过实例分析,对保费收入的实证处理,半参数回归分析的效果优于普通最小二乘法。
又因为半参数回归模型不依赖于模型设定的形式,比线性回归模型具有更大的适用性。
关键词:半参数车险保费收入机动车辆保险在我国财产保险业务中有着举足轻重的地位。
目前我国的车险保险需求正处于不断上升的时期,随着我国经济的不断发展,人民收入水平的不断提高,车险规模将日益扩大。
2003年开始,保险监管部门对车险进行了具有深远意义的改革,各公司有权自行制定车险条款和费率,车险费率和条款开始逐步走向市场化。
因此,我国目前的车险市场还处在逐步完善的过程中,各保险公司还面临着诸多不稳定的影响因素。
所以,分析这些因素的变化情况与车险需求的关系,无论是对于保险公司抓住机遇,还是对于政府部门进行宏观调控和管理,都具有重要意义。
本文将结合我国的实际情况,从微观层面分析影响我国车险市场的一系列因素,在前人已用研究方法的基础上,通过引入半参数的分析方法,定量的研究这些因素与车险需求之间的相关关系。
保险市场相关理论研究保险商品作为一种特殊的商品,保费收入可看作是这种特殊商品的价格,它会随着不同保险公司制定的不同政策,市场计划及汽车销售市场的淡旺季在不同的时期呈现出不同的差异。
国内很多学者都对我国保险市场进行过实证研究,林宝清(1992—1993)将保费收入作为被解释变量,引入国民生产总值(或国内生产总值)、物价指数(全国零售物价指数)和虚拟变量,作为影响保费收入的主要解释变量,建立线性回归模型。
其中,在虚拟变量的选择上,对几个关键性的经济体制变革进行了考虑,肖文及谢文武(2001)、徐爱华(2002)将1992年保险市场对外开放作为一个重要的影响保费收入的虚拟变量。
吴江鸣、林宝清(2003)则将1989年保险市场转型(由垄断转向竞争)设置为虚拟变量,并引入保险险种创新这一虚拟变量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七章 非参数回归模型与半参数回归模型第一节 非参数回归与权函数法一、非参数回归概念前面介绍的回归模型,无论是线性回归还是非线性回归,其回归函数形式都是已知的,只是其中参数待定,所以可称为参数回归。
参数回归的最大优点是回归结果可以外延,但其缺点也不可忽视,就是回归形式一旦固定,就比较呆板,往往拟合效果较差。
另一类回归,非参数回归,则与参数回归正好相反。
它的回归函数形式是不确定的,其结果外延困难,但拟合效果却比较好。
设Y 是一维观测随机向量,X 是m 维随机自变量。
在第四章我们曾引进过条件期望作回归函数,即称g (X ) = E (Y |X ) (7.1.1)为Y 对X 的回归函数。
我们证明了这样的回归函数可使误差平方和最小,即22)]([min )]|([X L Y E X Y E Y E L-=-(7.1.2)这里L 是关于X 的一切函数类。
当然,如果限定L 是线性函数类,那么g (X )就是线性回归函数了。
细心的读者会在这里立即提出一个问题。
既然对拟合函数类L (X )没有任何限制,那么可以使误差平方和等于0。
实际上,你只要作一条折线(曲面)通过所有观测点(Y i ,X i )就可以了是的,对拟合函数类不作任何限制是完全没有意义的。
正象世界上没有绝对的自由一样,我们实际上从来就没有说放弃对L(X)的一切限制。
在下面要研究的具体非参数回归方法,不管是核函数法,最近邻法,样条法,小波法,实际都有参数选择问题(比如窗宽选择,平滑参数选择)。
所以我们知道,参数回归与非参数回归的区分是相对的。
用一个多项式去拟合(Y i ,X i ),属于参数回归;用多个低次多项式去分段拟合(Y i ,X i ),叫样条回归,属于非参数回归。
二、权函数方法非参数回归的基本方法有核函数法,最近邻函数法,样条函数法,小波函数法。
这些方法尽管起源不一样,数学形式相距甚远,但都可以视为关于Y i 的线性组合的某种权函数。
也就是说,回归函数g (X )的估计g n (X )总可以表为下述形式:∑==ni i i n Y X W X g 1)()((7.1.3)其中{W i (X )}称为权函数。
这个表达式表明,g n (X )总是Y i 的线性组合,一个Y i 对应个W i 。
不过W i 与X i 倒没有对应关系,W i 如何生成,也许不仅与X i 有关,而且可能与全体的{X i }或部分的{X i }有关,要视具体函数而定,所以W i (X )写得更仔细一点应该是W i (X ;X 1,…,X n )。
这个权函数形式实际也包括了线性回归。
如果i i i X Y εβ+'=,则Y X X X X X ii '''='-1)(ˆβ,也是Y i 的线性组合。
在一般实际问题中,权函数都满足下述条件:1),,;(,0),,;(111=≥∑=n ni i n i X X X W X X X W(7.1.4)如果考虑在第五章介绍的配方回归与评估模型曾有类似条件,不妨称之为配方条件,并称满足配方条件的权函数为概率权。
下面我们结合具体回归函数看权函数的具体形式。
1.核函数法选定R m 空间上的核函数K ,一般取概率密度。
如果取正交多项式则可能不满足配方条件。
然后令∑=⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛-=n i n in in i a X X aX X K X X X W 11/),,;( (7.1.5)显然∑==ni iW11。
此时回归函数就是i ni nj n i n i n i i i Y a X X K a X X K Y X W X g Y ∑∑∑===⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫⎝⎛-===111)()((7.1.6)2.最近邻函数法首先引进一个距离函数,用来衡量R m 空间中两点u = (u 1,…,u m ) 和v = (v 1,…,v m ) 的距离‖u -v ‖。
可以选欧氏距离∑=-=-ni i iuu 122)(||||υυ,也可以选||||max ||||1i i ni u u υυ-=-≤≤。
为了反映各分量的重要程度,可以引进权因子C 1,…,C n ,使{C i }也满足配方条件。
然后将距离函数改进为∑=-=-ni i i i u C u 122)(||||υυ(7.1.7)||max |||12i i i ni u C u υυ-=-≤≤(7.1.8)现在设有了样本(Y i ,X i ),i =1,…,n ,并指定空间中之任一点X ,我们来估计回归函数在该点的值g (X )。
将X 1,…,X n 按在所选距离‖·‖意义下与X 接近的程度排序:||||||||||||21X X X X X X n k k k -<<-<-(7.1.9)这表示点1k X 与X 距离最近,就赋以权函数k 1;与X 距离次近的2k X 就赋予权函数k 2。
…,等等。
这里的n 个权函数k 1,…,k n 也满足配方条件,并且按从大到小排序,即∑==>≥≥≥ni i n k k k k 1211 ,0(7.1.10)就是n i k X X X W i n k i ,,1 ,),,;(1 ==(7.1.11)若在{‖X i -X ‖, i =1,…,n }中有相等的,可将这n 个相等的应该赋有的权取平均。
比如若前两名相等,‖X 1-X ‖=‖X 2-X ‖, 就令W 1 = W 2=)(2121k k +。
这样最近邻回归函数就是∑∑∑=======ni ni ni i i i i i n i Y X k Y k Y X X X W X g Y 1111)(),,;()((7.1.12)k i 尽管是n 个常数,事先已选好,但到底排列次序如何与X 有关,故可记为k i (X )。
三、权函数估计的矩相合性首先解释矩相合性的概念。
如果对样本 (Y i ,X i ),i =1,…,n 构造了权函数W i = W i (X )=W I (X ;X 1,…,X n ),有了回归函数g (X )的权函数估计∑==ni ii n YW X g 1)(,当Y 的r 阶矩存在(E |Y |r <∞)时,若0|)()(|lim =-∞→r n n X g X g E(7.1.13)则称这样的权函数为矩相合的权函数。
在什么样的条件下构造的权函数是矩相合的呢? Stone(1977)提出了很一般的,几乎是充分必要的条件。
下面我们考虑其充分性条件,并限于考虑概率权。
定理7.1.1 设概率权{W i }满足下述条件: (1)存在有限常数C ,使对R m 上任何非负可测函数(连续函数与分段连续函数是最常见的可测函数)f , 必有)()(1X CEf X f W E n i i i ≤⎪⎭⎫⎝⎛∑= (7.1.14)(2)∀ε>0, 当n →∞时,01)||(||−→−∑=≥-Pni X X i i IW ε(7.1.15)(3)当n →∞时,0max 1−→−≤≤Pi ni W (7.1.16)则{W i }是矩相合的权函数。
定理条件可以作一些直观解释。
条件(1)可以作如下理解,因为权函数是概率权,必有|W i |<1,i =1,…,n 。
于是∑∑∑∑=====≤≤⎪⎭⎫⎝⎛n i n i ni i i i i n i i i X f E X f E X f W E X f W E 1111)()()()((7.1.17)这里取的是C =1。
因此条件(1)可以说不叫做一个条件。
条件(2)是说,与X 的距离超过一定值的那些X i ,对应算出来的权函数之和很小,也就是说,权函数的值主要取决于那些与X 邻近的X i 的值。
这个条件合理。
条件(3)是说,当n 越来越大时,各个权系数将越来越小,这也是合理的要求。
在证明本定理之前,先证两个引理。
引理7.1.1 设概率权函数{W i }适合定理7.1.1的条件(1)及(2),又对某个r , E |f (X )|r <∞,则0)()()(lim 1=⎪⎭⎫⎝⎛-∑=∞→r i n i i n X f X f X W E (7.1.18)证明 先设f 在R m 上有界且一致连续,则任给η>0,存在ε>0,当‖u -v ‖≤ε时,|f (u )-f (v )|≤(η/2)1/r 。
于是εη>-==∑∑+≤-)(||11)()2(2)()()(X X ni irrini ii IX W M X f Xf X W (7.1.19)其中)(sup X f M X=,此处X 表示具体取值。
由条件(2),上式右边第二项依概率收敛于0且不大于1。
依控制收敛定理有0)(lim 1)(||=⎪⎭⎫⎝⎛∑=>-∞→n i X X i n i I X W E ε (7.1.20)故存在n 0,使当n ≥n 0时,有2)(1)(||ηε≤⎪⎭⎫ ⎝⎛∑=>-n i X X i i I X W E(7.1.21)因此当n ≥n 0时,有η≤⎪⎭⎫⎝⎛-∑=n i r i i X f X f X W E 1|)()(|)((7.1.22)于是对这种一致连续的f ,引理得证。
证毕对一般的函数f ,取一个在R m 上连续,且在一有界域之外为0的函数f ~,使∞<2)(~X f E ,且η<-r X f X f E )(~)(,这里η是事先指定的。
因为⎭⎬⎫⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+⎩⎨⎧⎪⎭⎫ ⎝⎛-≤⎪⎭⎫ ⎝⎛-∑∑∑∑===-=r ni i r i i ni i r i ni i r r i n i i X f X f X W E X f X f X W E X f X f X W X f X f X W E |)()(~|)(|)()(~|)( |)(~)(|)(3)()()(11111 (7.1.23)右边括号里第三项等于η<-r X f X f E )()(~;第一项根据条件(1)不超过ηC X f X f CE r <-)()(~;因为f ~在R m 上有界且一致连续,由前面已证结果知当n →∞时,第二项将趋于0。
因此η)1(3|)()(|)(lim 11+≤⎪⎭⎫⎝⎛--=∞→∑C X f X f X W E r r i n i i n (7.1.24) η是任意的,故引理得证。
证毕引理7.1.2 设{W i }为满足定理7.1.1三个条件的概率权,函数f 非负且∞<)(X Ef ,则0)()(lim 12=⎪⎭⎫⎝⎛∑=∞→i n i i n X f X W E (7.1.25)证明 定义一组新的概率权函数2i i W W =',由于0≤W i ≤1, 故0≤i W '≤1。
