三棱锥的外接球问题公开课优质课件
合集下载
(word完整版)三棱锥外接球半径常见解法(含解析),文档
特别三棱锥外接球半径的常有求法【方法介绍】
【法一：补形法】
外接球半径等于长方体体对角线的一半
R
6
，S 4 R26 2
注意：图中三棱锥的外接球与长方体外接球是同一个球。
【法二：轴截面法】
1、搜寻底面△ PBC的外心；
2、过底面的外心作底面的垂线；
3、外接球的球心必在该垂线上，利用轴截面计算出球心的地址。
【法三：向量法】
设外接球的球心坐标为：O ( x, y, z) .由 OP OA OB OC 可得：
【方法总结】
三棱锥外接球半径的常见解法：
1、补形法；
2、轴截面法；
3、向量法 .
【练习坚固】
【参照答案】
练习 1【补形法】【轴截面法】
练习 2【补形法】【轴截面法】
练习 3【补形法】
练习 4【轴截面法】。
外接球与内切球问题课件-高一下学期数学人教A版
三棱锥P − ABC的底面 ABC在圆锥的底上，顶点P点也是圆锥的顶点
P
P
P
P
O
O
O
O
C
C
C
C
A
O1
D
A
O1
B
A
O1
A
O1
B
B
B
P
P
P
图6
图7-1
图7-2
图8
A
O2 B
B C
D
O
A O2 O
A C
O2 D
B O
图8-1
图8-2
图8-3
题设：如图 6,7,8,P的射影是 ABC的外心 三棱锥P−ABC的三条侧棱相等 三棱锥P − ABC的底面 ABC在圆锥的底上，顶点P点也是圆锥的顶点
立体几何的内切球问题
类型一、椎体的内切球
即：
分割法 （等体积法）
1.分割法（等体积法）：若棱锥的体积为V，表面积为S，则内切球的半径为
R
3V S
.
1.分割法（等体积法）：若棱锥的体积为V，表面积为S，则内切球的半径为
R
3V S
.
PS
O
A
E B
H 图8-2
G
D
FM
C
1.分割法（等体积法）：若棱锥的体积为V，表面积为S，则内切球的半径为
R
3V S
.
方法：
R 3V
即：分割法（等体积法）：若棱锥的体积为V，表面积为S，则内切球的半径为 S .
2.截面法：构造三角形利用相似比和勾股定理
• 椎体的内切球
有关内切球的计算，往往可以做出球的一个大圆，化“球” 为“圆”来解决问 题，把空间问题转化为平面问题。对于一般棱锥，内切球的半径往往用等体积 法来确定。类似求三角形内接圆的半径问题（等面积法）。
三棱锥外接球问题
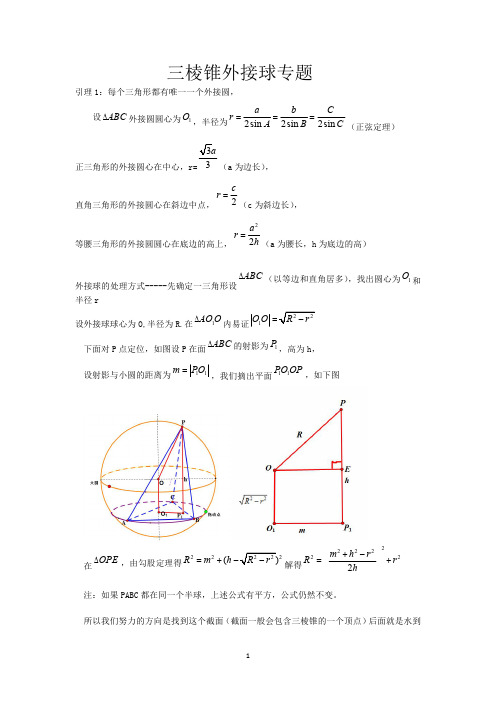
三棱锥外接球专题引理1：每个三角形都有唯一一个外接圆，设ABC D 外接圆圆心为1O ，半径为2sin 2sin 2sin a b Cr A B C ===（正弦定理）正三角形的外接圆心在中心，r=3（a 为边长），直角三角形的外接圆心在斜边中点，2cr =（c 为斜边长），等腰三角形的外接圆圆心在底边的高上，22a r h =（a 为腰长，h 为底边的高）外接球的处理方式-----先确定一三角形设ABC D （以等边和直角居多），找出圆心为1O 和半径r设外接球球心为O,半径为R.在1AO O D内易证1O O =下面对P 点定位，如图设P 在面ABC D 的射影为1P ，高为h，设射影与小圆的距离为11m PO =，我们摘出平面11PO OP，如下图在OPE D，由勾股定理得222(R m h =+-解得2222222m h r R r h+-=+注：如果PABC 都在同一个半球，上述公式有平方，公式仍然不变。
所以我们努力的方向是找到这个截面（截面一般会包含三棱锥的一个顶点）后面就是水到成渠。
如果非要记公式的话可以努力找到h，m 套公式即可。
高中阶段都会有特殊的三角形特殊位置下面简单归类第一类;有线面垂直的---如图PA ABC^面此时m=r，h=PA.22222222h+r 22m h r R r h+-=+=，由此引出补形法，有线面垂直即可补成直三棱柱求解如上右图。
三棱柱不熟也可以用补成长方体（不过要求底面有直角）1.已知ABC △中，90,B DC ∠=︒⊥平面,4,5,3ABC AB BC CD ===，则三棱锥D ABC -的外接球表面积为()A.50π3B.25πC.50πD.1252π3解析：由已知条件可构造一个长方体，长方体的外接球过,,,A B C D 四点，所以长方体的外接球即三棱锥D ABC -的外接球，得外接球直径250R AD ==,外接球表面积为24π50πR =，故选：C.法二：三棱柱中，22222114522350()24r AC R r ==+=+=2.在四面体S ABC -中,SA ⊥平面,120,4,ABC BAC BC SA ∠=︒==则该四面体的外接球的表面积为.(底面无直角补成三棱柱)3.在三棱锥ABC P -中，222==AB AC ，10=BC ，90=∠APC ，平面⊥ABC 平面PAC ，则三棱锥ABC P -外接球的表面积为()找线面垂直补形即可，跟上面一样A.4πB.5πC.8πD.10π3.所以PC ⊥平面PAB ,所以90CPB ∠=︒，故该外接球的半径等于||22BC =，所以球的表面积为224πR 4π(10π2S ==⋅=，故选D。
2024年高考数学一轮复习课件(新高考版) 第7章 §7.2 球的切、接问题[培优课]
![2024年高考数学一轮复习课件(新高考版) 第7章 §7.2 球的切、接问题[培优课]](https://img.taocdn.com/s3/m/bd31667dfd4ffe4733687e21af45b307e871f9ec.png)
思维升华
(1)与球截面有关的解题策略 ①定球心：如果是内切球，球心到切点的距离相等且为半径；如果 是外接球，球心到接点的距离相等且为半径； ②作截面：选准最佳角度作出截面，达到空间问题平面化的目的. (2)正四面体的外接球的半径 R＝ 46a，内切球的半径 r＝126a，其半径 之比 R∶r＝3∶1(a 为该正四面体的棱长).
题型二 补形法
例2 (1)(2023·大庆模拟)在正方形ABCD中，E，F分别为线段AB，BC的
中点，连接DE，DF，EF，将△ADE，△CDF，△BEF分别沿DE，DF，
EF折起，使A，B，C三点重合，得到三棱锥O－DEF，则该三棱锥的外
接球半径R与内切球半径r的比值为
A.2 3
√C.2 6
B.4 3 D. 6
跟踪训练 2 (1)在三棱锥 A－BCD 中，侧棱 AB，AC，AD 两两垂直，△ABC，
△ACD，△ADB 的面积分别为 22， 23， 26，则三棱锥 A－BCD 的外接球
的体积为
√A. 6π
B.2 6π
C.3 6π
D.4 6π
在三棱锥A－BCD中，侧棱AB，AC，AD两两垂直，将其补成长方体， 两者的外接球是同一个，长方体的体对角线就是球的直径. 设长方体同一顶点处的三条棱长分别为a，b，c， 由题意得 ab＝ 6，ac＝ 3，bc＝ 2， 解得 a＝ 3，b＝ 2，c＝1， 所以球的直径为 32＋ 22＋1＝ 6， 它的半径为 26，球的体积为43π× 263＝ 6π.
3 3和 4 3 ，其顶点都在同一球面上，则该球的表面积为
√A.100π
B.128π
C.144π
D.192π
由题意，得正三棱台上、下底面的外接圆的半径分别为
直三棱柱外接球半径 PPT
棱 （3）底面△ABC中，∠ACB=120°,AC=BC=2。 柱
的 外
解：O1是三角形ABC外心，在△ABC中，
接
∠ACB=120°， AC=BC=2，
球 半
由余弦定理得AB= 2 3
径
由正弦定理得△ABC的外接圆半径
O1C=2 在RT△OO1C中，
O1C= 2 ， OO1=2
∴R=OC= 2 2
的
外
接
球
半
径
直 三 棱 柱 的 外 接 球 半 径
直三棱住外接球半径
如图：直三棱柱ABC-A1B1C1中，棱柱高为4，
直 在如下情况求该三棱柱外接球半径。
三 棱
（1）底面△ABC中，AC⊥BC，边长AC=4,BC=2；
柱
的
外
解：在RT△ABC中，AC=4，
接
球
BC=2
半 径
∴AB= 2 5，O1C= 5
在RT△OO1C中，O1C= 5 ，
OO1=2 ∴R=OC=3
如图：直三棱柱ABC-A1B1C1中，棱柱高为4，
直 在如下情况求该三棱柱外接球半径。 三 棱 （2）底面△ABC是正三角形，边长为2；
柱
的
外
解：O1是正三角形ABC中心，
接
球 半 径
边长为2，O1C=
23 3
在RT△OO1C中，O1C=
2
3 3
，
OO1=2 ∴R=OC= 4 3
3
直 三
如图：直三棱柱ABC-A1B1C1中，棱柱高为4， 在如下情况求该三棱柱外接球半径。
直
三
棱 直三棱住外接球半径求解的一般步骤：
柱 的
（1）求上下底面外接圆的圆心
巧解外接球问题-长方体性质的应用课件-高三数学一轮复习(课件共20张PPT)
所以球的半径为 2 ，
因此球的体积为 9 。 2
A
O
C
P
B
例4
一个四面体的所有棱长都为 2 ，四个顶点在
？ 同一球面上，则此球的表面积为（ ）
例4：一个四面体的所有棱长都为 2 ，四个顶点在
同一球面上，则此球的表面积为（ A）
A. 3 B. 4 C. 3 3 D. 6
A B
O D
C
解析： 以四面体的棱为面对角线构，造正方体， 则正方体棱长为 1，外接球半径为 3 ，
.
例3、若三棱锥的三条侧棱两两垂直，且侧棱长分别为
2 、 3 、2 ，则其外接球的体积是
.
这个三棱锥可看成由长方体切割而得， A
故可把这个三棱锥补形成长方体，
O
这样求解就简便得多了。
C
P
B
例3、若三棱锥的三条侧棱两两垂直，且侧棱长分别为 9
2 、 3 、2 ，则其外接球的体积是 2 .
易得长方体对角线长为 3 ， 3
2
表面积为 3
归纳提升:
1 长方体的对角线是它的外接球的直径，因此有 (2R)2a2b2c2
其中 a、b、c 分别为长方体的长、宽、高。
2 棱长为 a 的正方体的外接球半径 R 3 a
2
3 三条侧棱两两垂直的三棱锥的外接球问题可构造长方体来快速解决。
4 正四面体的外接球问题可构造正方体来快速解决。
高三备考专题复习之
巧解外接球问题
——长方体性质的应用
多面体的外接球问题，是高考考查的一个热点， 长方体的外接球问题，更是高考的一个高频考点。 这节课我们就来学习如何快速解决这类问题。
01
长方体外接球
关键是找出球的半径与长方体的长、宽、高的关系
因此球的体积为 9 。 2
A
O
C
P
B
例4
一个四面体的所有棱长都为 2 ，四个顶点在
？ 同一球面上，则此球的表面积为（ ）
例4：一个四面体的所有棱长都为 2 ，四个顶点在
同一球面上，则此球的表面积为（ A）
A. 3 B. 4 C. 3 3 D. 6
A B
O D
C
解析： 以四面体的棱为面对角线构，造正方体， 则正方体棱长为 1，外接球半径为 3 ，
.
例3、若三棱锥的三条侧棱两两垂直，且侧棱长分别为
2 、 3 、2 ，则其外接球的体积是
.
这个三棱锥可看成由长方体切割而得， A
故可把这个三棱锥补形成长方体，
O
这样求解就简便得多了。
C
P
B
例3、若三棱锥的三条侧棱两两垂直，且侧棱长分别为 9
2 、 3 、2 ，则其外接球的体积是 2 .
易得长方体对角线长为 3 ， 3
2
表面积为 3
归纳提升:
1 长方体的对角线是它的外接球的直径，因此有 (2R)2a2b2c2
其中 a、b、c 分别为长方体的长、宽、高。
2 棱长为 a 的正方体的外接球半径 R 3 a
2
3 三条侧棱两两垂直的三棱锥的外接球问题可构造长方体来快速解决。
4 正四面体的外接球问题可构造正方体来快速解决。
高三备考专题复习之
巧解外接球问题
——长方体性质的应用
多面体的外接球问题，是高考考查的一个热点， 长方体的外接球问题，更是高考的一个高频考点。 这节课我们就来学习如何快速解决这类问题。
01
长方体外接球
关键是找出球的半径与长方体的长、宽、高的关系
外接球问题课件——高一下学期数学人教A版
外接球问题
类型一：简单几何体 类型三：线面垂直 类型五：折叠问题
目录
类型二：三条线两两垂直 类型四：面面垂直
简单的几何体
正方体或长方体的外接球的球心是其体对角线的 中点，即外接球的球半径是体对角线的二分之一 正棱柱外接球的球心是上下底面中心连线的中点 直三棱柱的外接球的球心是上下底面三角形外心 连线的中点
根据外接球的球心到各个顶点的距离均 为球半径，构造直角三角形，借助勾股 定理，求出外接球半径
如果底面图形恰好为三角形，则
确定几何体的一个面，找出这个面的外接圆圆心位置，可以利用正弦定理或是三角形外
求外接圆的半径
心的定义（各边中垂线的交点）
假设外接球的球心位置，注意球心与圆心的连线会 求得底面外接圆半径
目录
2.
棱锥的体积公式
补形
特点：一条棱垂直于一个平面，平面有直角
目录
3.
直角三角形的外接圆圆心是斜边的中点 球心与截面圆心的连线垂直于截面
外接球球心到各个顶点的距离为球半径 勾股定理
目录
v v v
确定几何体的一个面，找出这 个面的外接圆圆心位置
假设外接球的球心位置，注意 球心与圆心的连线会垂直于圆 心所在平面（即第一步中确定 的面）
垂直于圆心所在平面（即第一步中确定的面）
根据外接球的球心到各个顶点的距离均为球半径， 构造直角三角形，借助勾股定理，求出外接球半径
数形结合
把立体几何问题转化成平面几何问题
把三维空间问题转化成二维空间问题
目录
4.
等边三角形的外心为重心（中线的交点）
1、找底面的外心位置，求外接圆半径 正弦定理
2、将三维转化成二维 D
3、构造直角三角形，求球半径
类型一：简单几何体 类型三：线面垂直 类型五：折叠问题
目录
类型二：三条线两两垂直 类型四：面面垂直
简单的几何体
正方体或长方体的外接球的球心是其体对角线的 中点，即外接球的球半径是体对角线的二分之一 正棱柱外接球的球心是上下底面中心连线的中点 直三棱柱的外接球的球心是上下底面三角形外心 连线的中点
根据外接球的球心到各个顶点的距离均 为球半径，构造直角三角形，借助勾股 定理，求出外接球半径
如果底面图形恰好为三角形，则
确定几何体的一个面，找出这个面的外接圆圆心位置，可以利用正弦定理或是三角形外
求外接圆的半径
心的定义（各边中垂线的交点）
假设外接球的球心位置，注意球心与圆心的连线会 求得底面外接圆半径
目录
2.
棱锥的体积公式
补形
特点：一条棱垂直于一个平面，平面有直角
目录
3.
直角三角形的外接圆圆心是斜边的中点 球心与截面圆心的连线垂直于截面
外接球球心到各个顶点的距离为球半径 勾股定理
目录
v v v
确定几何体的一个面，找出这 个面的外接圆圆心位置
假设外接球的球心位置，注意 球心与圆心的连线会垂直于圆 心所在平面（即第一步中确定 的面）
垂直于圆心所在平面（即第一步中确定的面）
根据外接球的球心到各个顶点的距离均为球半径， 构造直角三角形，借助勾股定理，求出外接球半径
数形结合
把立体几何问题转化成平面几何问题
把三维空间问题转化成二维空间问题
目录
4.
等边三角形的外心为重心（中线的交点）
1、找底面的外心位置，求外接圆半径 正弦定理
2、将三维转化成二维 D
3、构造直角三角形，求球半径
空间几何体的外接球问题ppt课件
∵AB＝2 3，∴S△ABC＝3 3，DE＝1，PE＝ 2. ∴S 表＝3×12×2 3× 2＋3 3＝3 6＋3 3.
∵PD＝1，∴三棱锥的体积 V＝13×3 3×1＝ 3. 设球的半径为 r，以球心 O 为顶点，三棱锥的四个面为底面把正三棱锥分割为四个小棱
锥，则 r＝ 3
33 6＋3
＝ 3
2－1.
识梳理 相关知识：
1、相关公式：
2、用一个平面去截球，截面是__圆_面____ ； 3、球心和截面圆心的连线_垂__直_于截面；
4、球心到截面的距离d与球 的半径R及 截面的半径r 有下面的关系:
这个直角三角形我们称之为 “特征三角形”．
球与空间几何体的接、切问题（一）
以正方体的外接球为例：
D A
易得球半径 故此球的表面积为4πR2=20π
A1
B1
训练：已知正三棱锥的高为1，底面边长为2，内有一个球 与四个面都相切，则棱锥的内切球的半径为( D )
如图，过点 P 作 PD⊥平面 ABC 于点 D，连接 AD 并延长交 BC 于点 E， 连接 PE，
∵△ABC 是正三角形，∴AE 是 BC 边上的高和中线，D 为△ABC 的中心．
A
解析：ΔABC为等边三角形，PA=PB=PC=3，
所以ΔPAB≅ ΔPBC≅ ΔPAC。
C
P
以PA，B PB，PC为过同一顶点的三条棱作正方体，
则正方体的外接球即为三棱锥P-ABC的外接球。
A
C
P
B
考点一 空间几何体的外接球
3、构造法
变式训练 某几何体的三视图如图所示，则该 1
几何体的外接球的球面面积为_6__π__.
球与空间几何体的接、切问题（一）
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
你更喜欢侧面垂直底面的锥， 每当面面垂直出现， 两个外心就彼此致意， 它们伸长臂膀架起爱的天梯， 迎接你的到来；
你如此神秘，又让我们如此痴迷，请在高考 的路上助我们披荆斩棘，赢一个美好的明天！
课 堂 小 结 致球心
A B
我知道，
你喜欢对棱相等的锥，
体对角线的中点就是你坚持的位置；
D
C
你也喜欢侧棱垂直底面的锥， 因为补形能增加你的高度， 衬托你的威仪；
你还喜欢紧紧依偎的直角三角 形， 因为你像痴情的鸟儿， 总在他们公共斜边的中点上停 留；
你也喜欢侧棱都相等的锥， 因为你像攀援的凌霄花， 借他们的高枝展示自我；
D
sin BAC 3 7 8
2r 2AE BC 9 8 24 7 sin BAC 3 7 7
O
R A
C
rE
B
AE 12 7 DE 62 - AE 2 6 21
7
7
在RtAOE中AO2 AE 2 OE 2
也即R 2
12 7
7
2
6
21 7
2 R
可得R 21, S 4R2 84
V 4 R3 20 5
3
3
C
B
课堂练 习
1、已知在三棱锥 P ABC 中，侧面 PAC 底面 ABC ， AB BC , AB BC 2, AP PC 5 ,求三棱锥 P ABC 的外接球表面积. 2、已知 P, A, B,C 四点均在表面积为 36 的球面上，其中 PA 平面 ABC , BAC 30, AB 6 , AC 3 2 ,求三棱锥 P ABC 的体积.
问题2：边长为2的正方体的外接球的表面积为多少？
解：体对角线l 3a2 12 2 3 则外接球的半径r 3 所以，外接球的表面积为S 4r 2 12
课堂探 究
问题3：假如一个正方体的8个顶点都在同一个球的球面上，那么 任意选出4个顶点，这4个顶点还在该球的球面上吗？
A D
答： 在
B C
课堂探 究
方法：确定球心位置法
类型5 侧面垂直于底面的三棱锥
【例 5】已知三棱锥 P ABC 的所有顶点都在球 O 的球面上， PAB与 ABC 都是边 长为 2 3 的正三角形， 平面PAB 平面ABC ，求球 O 的体积.
P
23
O O2
A
D
O1
解析：作出辅助线，确定球心的位置 由条件可知OO1 O2D 1, O1C 2 在RtOO1C中，OC 2 OO12 O1C 2 也即R2 12 22 5, R 5
BC 2 , BAC 30 ,求球 O 的半径.
S
O
h
R
A
2
O
r
B2
解析：由正弦定理可得
2r a 2 4 sin A sin 30
r 2 又h 3
R r2 h2 7
C
课堂探 究
方法：直接法
类型3 有公共斜边的两个直角三角形组成的三棱锥
. 【例 3】(2017 年全国卷Ｉ)已知三棱锥 S ABC 的所有顶点都在球 O 的球面上，SC 是球 O 的直径，若平面 SCA 平面 SCB , SA AC , SB BC ,三棱锥 S ABC 的体积为 9，则球 O 的表面积为_______.
高考微 专题
高考专题复习
三棱锥的外接球问题
顾‘’
知识梳 理 1.球的定义 2.球的表面积和体积公式 3.求多面体外接球半径的方法 4. 简单多面体外接球相关结论
①直接法 ②构造一法① ③确定球心位置法
球的截面圆性质
课堂探 究
问题1：长方体或正方体的体对角线和体心与它的外接球有什么关 系？
答：（1）体对角线等于外接球的直径； （2）体心和球心重合.
解析：设长方体的长宽高分别为x、y、z,
A
由条件可得
x2 z2 4 x 1
2D
x
2
y2
4
y
3
6
6 z y2 z2 6 z 3
22
2R
x2 y2 z 2 12
2
3
2
3
7
2
C S 4R2 7
y
B
x
课堂探 究
方法：构造法补形
类型2 侧棱垂直底面的三棱锥
.【例 2】 已知三棱锥 S ABC 的所有顶点都在球 O 的球面上, SA 平面ABC , SA 2 3 ,
S O
C
A B
答案： 36
课堂探 究
方法：确定球心位置法
类型4 侧棱相等的三棱锥
. 【例 4】已知三棱锥 D ABC 中， AB AC AD BD CD 6 , BC 9 ,则三棱锥 D ABC 的外接球的表面积是______.
解析：由条件可知E为ABC外接圆圆心
由余弦定理得 cos BAC 62 62 - 92 - 1， 266 8
问题4：棱长为 1的正四面体的外接球的表面积为多少？
A D
B C
解：把正四面体补充成一个正体，如图所示，
正方体的棱长为 2 ， 外接球的半径r 2 3a2 6 ，
24 所以，外接球的表面积为S 4r 2 3 .
2
课堂探 究
方法：构造法补形
类型1 对棱相等的三棱锥
.
【例 1】 已知四面体 ABCD满足 AB CD 6 ， AC AD BC BD 2 ，则四 面体 ABCD的外接球的表面积是_______.
你如此神秘，又让我们如此痴迷，请在高考 的路上助我们披荆斩棘，赢一个美好的明天！
课 堂 小 结 致球心
A B
我知道，
你喜欢对棱相等的锥，
体对角线的中点就是你坚持的位置；
D
C
你也喜欢侧棱垂直底面的锥， 因为补形能增加你的高度， 衬托你的威仪；
你还喜欢紧紧依偎的直角三角 形， 因为你像痴情的鸟儿， 总在他们公共斜边的中点上停 留；
你也喜欢侧棱都相等的锥， 因为你像攀援的凌霄花， 借他们的高枝展示自我；
D
sin BAC 3 7 8
2r 2AE BC 9 8 24 7 sin BAC 3 7 7
O
R A
C
rE
B
AE 12 7 DE 62 - AE 2 6 21
7
7
在RtAOE中AO2 AE 2 OE 2
也即R 2
12 7
7
2
6
21 7
2 R
可得R 21, S 4R2 84
V 4 R3 20 5
3
3
C
B
课堂练 习
1、已知在三棱锥 P ABC 中，侧面 PAC 底面 ABC ， AB BC , AB BC 2, AP PC 5 ,求三棱锥 P ABC 的外接球表面积. 2、已知 P, A, B,C 四点均在表面积为 36 的球面上，其中 PA 平面 ABC , BAC 30, AB 6 , AC 3 2 ,求三棱锥 P ABC 的体积.
问题2：边长为2的正方体的外接球的表面积为多少？
解：体对角线l 3a2 12 2 3 则外接球的半径r 3 所以，外接球的表面积为S 4r 2 12
课堂探 究
问题3：假如一个正方体的8个顶点都在同一个球的球面上，那么 任意选出4个顶点，这4个顶点还在该球的球面上吗？
A D
答： 在
B C
课堂探 究
方法：确定球心位置法
类型5 侧面垂直于底面的三棱锥
【例 5】已知三棱锥 P ABC 的所有顶点都在球 O 的球面上， PAB与 ABC 都是边 长为 2 3 的正三角形， 平面PAB 平面ABC ，求球 O 的体积.
P
23
O O2
A
D
O1
解析：作出辅助线，确定球心的位置 由条件可知OO1 O2D 1, O1C 2 在RtOO1C中，OC 2 OO12 O1C 2 也即R2 12 22 5, R 5
BC 2 , BAC 30 ,求球 O 的半径.
S
O
h
R
A
2
O
r
B2
解析：由正弦定理可得
2r a 2 4 sin A sin 30
r 2 又h 3
R r2 h2 7
C
课堂探 究
方法：直接法
类型3 有公共斜边的两个直角三角形组成的三棱锥
. 【例 3】(2017 年全国卷Ｉ)已知三棱锥 S ABC 的所有顶点都在球 O 的球面上，SC 是球 O 的直径，若平面 SCA 平面 SCB , SA AC , SB BC ,三棱锥 S ABC 的体积为 9，则球 O 的表面积为_______.
高考微 专题
高考专题复习
三棱锥的外接球问题
顾‘’
知识梳 理 1.球的定义 2.球的表面积和体积公式 3.求多面体外接球半径的方法 4. 简单多面体外接球相关结论
①直接法 ②构造一法① ③确定球心位置法
球的截面圆性质
课堂探 究
问题1：长方体或正方体的体对角线和体心与它的外接球有什么关 系？
答：（1）体对角线等于外接球的直径； （2）体心和球心重合.
解析：设长方体的长宽高分别为x、y、z,
A
由条件可得
x2 z2 4 x 1
2D
x
2
y2
4
y
3
6
6 z y2 z2 6 z 3
22
2R
x2 y2 z 2 12
2
3
2
3
7
2
C S 4R2 7
y
B
x
课堂探 究
方法：构造法补形
类型2 侧棱垂直底面的三棱锥
.【例 2】 已知三棱锥 S ABC 的所有顶点都在球 O 的球面上, SA 平面ABC , SA 2 3 ,
S O
C
A B
答案： 36
课堂探 究
方法：确定球心位置法
类型4 侧棱相等的三棱锥
. 【例 4】已知三棱锥 D ABC 中， AB AC AD BD CD 6 , BC 9 ,则三棱锥 D ABC 的外接球的表面积是______.
解析：由条件可知E为ABC外接圆圆心
由余弦定理得 cos BAC 62 62 - 92 - 1， 266 8
问题4：棱长为 1的正四面体的外接球的表面积为多少？
A D
B C
解：把正四面体补充成一个正体，如图所示，
正方体的棱长为 2 ， 外接球的半径r 2 3a2 6 ，
24 所以，外接球的表面积为S 4r 2 3 .
2
课堂探 究
方法：构造法补形
类型1 对棱相等的三棱锥
.
【例 1】 已知四面体 ABCD满足 AB CD 6 ， AC AD BC BD 2 ，则四 面体 ABCD的外接球的表面积是_______.