第三章线性控制系统的数学模型
控制工程数学模型

控制⼯程数学模型1 控制系统的数学模型数学模型是描述系统输⼊量、输出量以及内部各变量之间关系的数学表达式,揭⽰了系统结构及其参数与其性能之间的内在关系。
静态数学模型:静态条件(变量各阶导数为零)下描述变量之间关系的代数⽅程。
反映系统处于稳态时,系统状态有关属性变量之间关系的数学模型。
动态数学模型:描述变量各阶导数之间关系的微分⽅程,描述动态系统瞬态与过渡态特性的模型。
也可定义为描述实际系统各物理量随时间演化的数学表达式。
微分⽅程或差分⽅程常⽤作动态数学模型。
对于给定动态系统,数学模型表达不唯⼀。
⼯程上常⽤的有:微分⽅程,传递函数和状态⽅程。
不过对于线性系统,它们之间是等价的。
2 建⽴数学模型的⽅法1. 解析法依据系统及元件各变量之间所遵循的物理规律写出相应的数学关系式,建⽴模型。
2. 实验法⼈为地对系统施加某种测试信号,记录其输出响应,并⽤适当的数学模型进⾏逼近,这种⽅法也称为系统辨识。
3 数学模型的形式1. 时间域微分⽅程差分⽅程状态⽅程(⼀阶微分⽅程组)2. 复数域传递函数结构图3. 频率域频率域4 建⽴数学模型的⼀般步骤⽤解析法列写系统或元件微分⽅程的⼀般步骤是:1. 分析系统⼯作原理和信号传递变换过程,确定系统和各元件的输⼊、输出量。
2. 从系统输⼊端开始,按照信号传递变换过程,依据各变量所遵循的物理学定律,依次列写各元件、部件的动态微分⽅程。
3. 消去中间变量,得到⼀个描述元件或系统输⼊、输出变量之间关系的微分⽅程。
4. 写成标准化形式。
与输⼊有关项放在等式右侧,与输出有关项放在等式左侧,且各阶导数项按降幂排列。
5 控制系统微分⽅程的列写5.1 机械系统在机械系统中,有些构件惯性和刚度较⼤,有些构件惯性较⼩、柔度较⼤。
我们将前者的弹性忽略视其为质量块,将后者的惯性忽略视其为⽆质量弹簧。
这样,机械系统便可以抽象为质量-弹簧-阻尼系统。
1. 质量2. 弹簧3. 阻尼5.1.1 机械平移系统列出各元件的动态微分⽅程:消去中间变量并写成标准形式:式中,m、D、k通常均为常数,故机械平移系统可以由⼆阶常系数微分⽅程描述。
线性系统的数学模型

描述控制系统输入、输出变量及内部变量之间关 系的数学表达式称为系统的数学模型。
★ 描述控制系统的输入-输出变量数学模型:
微分方程、传递函数、方框图、频率特性
★ 描述控制系统的内部变量数学模型: 状态空间
说明 ◆ 要分析自动控制系统的性能,必须先建立该系统 的数学模型; ◆ 一个物理系统,要处理的问题或要达到的精度不 同,得到的数学模型也不同。
3.反馈
R(S) E(S) + B(S) H(S) C(S)
G(S)
负反馈 正反馈 单位反馈:H(S)=1
主 要 内 容
§2-1 微分方程 §2-2 传递函数
§2-3 典型环节的传递函数及动态响应
§2-4 电气网络的运算阻抗与传递函数 §2-5 方框图 §2-5 反馈控制系统的传递函数
§2-1
微分方程
对于线性定常系统, 可以用线性常系数微分方程 作为其数学模型,如 a 0dnc (t)/dtn +a1dn-1c (t) /dtn-1+…+anc (t) =b0dmr(t)/dtm +b1dm-1r(t)/dtm-1+…+bmr(t) c(t): 系统的输出; r(t): 系统的输入; a0……an ; b0……bm 均为实数,均由系统本身的结
对电气网络,可以不列微分方程,仅利用运算电 路,经过简单的代数运算,就可以求得传递函数!
§2-5 控制系统的方框图
方框图是以图形表示系统的数学模型;
通过方框图,能够非常清楚地表示出信号在系统各
环节之间的传递过程;
方框图可以方便地求出复杂系统的传递函数; 方框图是分析控制系统的一个简明而有效的工具。
八.二阶振荡环节 1、传递函数
自动控制原理第3章

arctan 9 3
1.25rad
则响应为 y(t) 1 2 e 3t 0.95e j1.25e (1 j)t 0.95e j1.25e (1 j)t 5
1 2 e 3t 0.95e t e j(t1.25) e j(t1.25) 5 1 2 e 3t 1.9e t cos(t 1.25)
平衡位置:力学系统中,当系统外的作 D
用力为零时,位移保持不变的位置。
此时位移对时间的各阶导数为零。 A点和D点是平衡位置, B点和C点不是平衡位置。
O
B
C
A
稳定的平衡位置:若在外力作用下,系统偏离了平衡位置,但 当外力去掉后,系统仍能回到原来的平衡位置,则称这一个平 衡位置是稳定的平衡位置。
所以A点是稳定的平衡位置,而D点不是稳定的平衡位置。
注意:输入信号为非单位阶跃信号时,依齐次性,响应 只是沿纵轴拉伸或压缩,基本形状不变。所以ts 、 tr、 tp 、 σ并不发生变化。
当t < ts时,称系统处于动态;当t > ts时,称系统处于稳态。
3.2 一阶系统的单位阶跃响应
一阶系统(惯性环节)
G(s) 1 Ts 1
单位阶跃响应为
t
y(t) 1 e T
设零初始状态,y(0)=0 r (t)=1(t)时,y(t)的响应曲线为
y(t)
1.05 y(∞)
ym
y(∞)
0.95 y(∞)
tr tp
ts
ym:单位阶跃响应的最大偏离量。 y(∞):单位阶跃响应的稳态值。并非期望值。 ts:调节时间。y(t)进入0.5*y(∞)或0.2* y(∞)构成的误差带 后不再超出的时间。 tr:上升时间。 y(t) 第一次达到 y(∞)的时间。
2.12.2线性系统的微分方程

上式中各量纲是:[La]=亨,[Ra]=欧,[Kb]=伏/ 弧度/秒,
[ω]=弧度/秒,[Ua]=伏,[ia]=安,[ML]公斤⋅ 米,[Cm]=公斤米/安,[f]=公斤⋅米/弧度/秒, [J]=公斤⋅米⋅秒 以上二式分别是以转角和转速为输出量的电 动机的动态方程。
23
考虑到电机中的La一般较小,可以忽略不计,上两式 可简化为
6
7
线性元件的微分方程
列写线性元件微分方程的基本步骤
确定输入 根据机理 列写相应微
输出量
分方程
消去中间变量
标准形式 整理 微分方程
8
标准形式
输出量 及其各阶导数列写在方程式左 端;输出项的系数为1;
输入项及其各阶导数项列写在方程式右 端;
一阶导数前面的系数为时间; 二阶导数前面的系数为时间的平方; 三阶导数前面的系数为时间的立方;
28
消去中间变量 Q2 ,则有:
C dh + k dt
h = Q1
上式为一个一阶非线性微分方程。
29
2.2.2 非线性数学模型的线性化
在一定的条件下或在一定 范围内把非线性的数学模型化 为线性模型的处理方法称为非 线性数学模型的线性化。
线性化的方法有很多种, 例如图所示的具有饱和特性的 放大器,在小信号输入时,输 入与输出的关系是线性的,可 视为线性元件。
u r = R 1 i1 + u c 1
du c 1 dt
=
1 C1
( i1
−
u c1 = R 2 i2 + u c
du c dt
=
1 C2
i2
i2 )
16
由所得方程组消去中间变量得:
第三章(第四节) 系统框图及简化
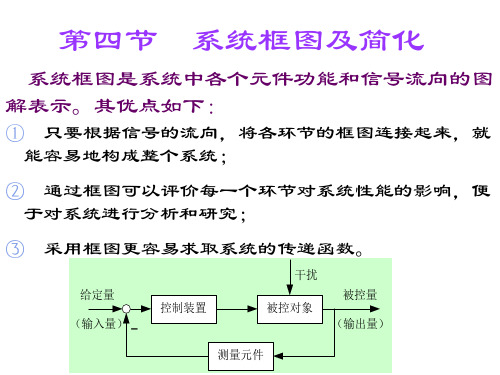
X o (s)
X i (s)
G1 ( s) G2 ( s )
X o (s)G2(s) 来自)X 2 (s)b)
X 0 ( s ) X 1 ( s ) X 2 ( s ) G1 ( s ) X i ( s ) G 2 ( s ) X i ( s ) (G1 ( s ) G2 ( s )) X i ( s ) X 0 (s) G1 ( s ) G2 ( s ) X i (s)
X i (s)
G (s) 1 G (s) H (s)
X o (s)
H(s) a)
b)
闭环传递函数 X 0 ( s ) = G ( s) E ( s)
E ( s ) = X i ( s) B ( s)
消去E (s) (s)得 ﹑B X 0 (s )= G (s ) 轾i (s ) ± H (s ) X 0 (s ) X 臌 轾 G (s ) H (s ) X 0 (s )=G (s ) X i (s ) 1 臌
Y ( s) YN ( s) YX ( s)
G2 (s) G1 (s) X (s) N ( s) 1 G1 (s)G2 (s) H (s)
若设计控制系统时,使
G1 ( s) H ( s) 1,且 G1 ( s)G2 ( s) H ( s) 1
1 则:Y ( s) G1 (s) X (s) N (s) G1 ( s) H ( s)
为便于绘制框图,将上式表示为 1轾 I(s) = 犏 i ( s)- U 0 ( s) U R臌 1 U0 (s ) = I ( s) Cs
U i (s)
1轾 I(s) = 犏 i (s)- U 0 (s) U 臌 R
1 U 0 (s ) = I (s ) Cs
自动控制原理例题与习题范文
自动控制原理例题与习题第一章自动控制的一般概念【例1】试述开环控制系统的主要优缺点。
【答】开环控制系统的优点有:1. 1.构造简单,维护容易。
2. 2.成本比相应的死循环系统低。
3. 3.不存在稳定性问题。
4. 4.当输出量难以测量,或者要测量输出量在经济上不允许时,采用开环系统比较合适(例如在洗衣机系统中,要提供一个测量洗衣机输出品质,即衣服的清洁程度的装置,必须花费很大)。
开环控制系统的缺点有:1. 1.扰动和标定尺度的变化将引起误差,从而使系统的输出量偏离希望的数值。
2. 2.为了保持必要的输出品质,需要对标定尺度随时修正。
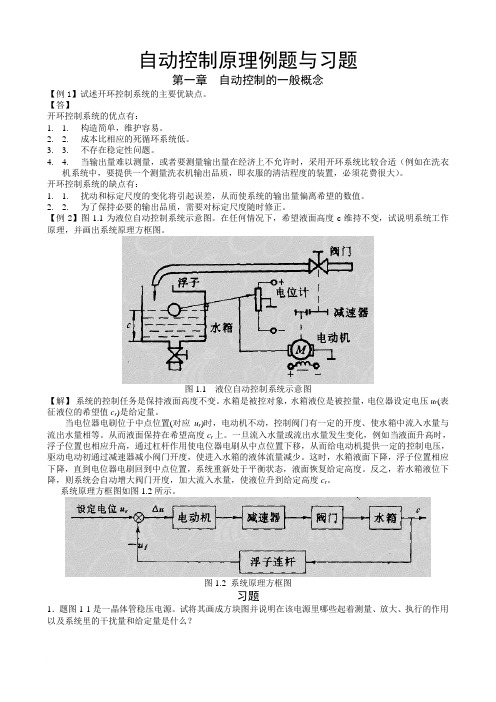
【例2】图1.1为液位自动控制系统示意图。
在任何情况下,希望液面高度c维持不变,试说明系统工作原理,并画出系统原理方框图。
图1.1 液位自动控制系统示意图【解】系统的控制任务是保持液面高度不变。
水箱是被控对象,水箱液位是被控量,电位器设定电压u r(表征液位的希望值c r)是给定量。
当电位器电刷位于中点位置(对应u r)时,电动机不动,控制阀门有一定的开度、使水箱中流入水量与流出水量相等。
从而液面保持在希望高度c r上。
一旦流入水量或流出水量发生变化,例如当液面升高时,浮子位置也相应升高,通过杠杆作用使电位器电刷从中点位置下移,从而给电动机提供一定的控制电压,驱动电动初通过减速器减小阀门开度,使进入水箱的液体流量减少。
这时,水箱液面下降,浮子位置相应下降,直到电位器电刷回到中点位置,系统重新处于平衡状态,液面恢复给定高度。
反之,若水箱液位下降,则系统会自动增大阀门开度,加大流入水量,使液位升到给定高度c r。
系统原理方框图如图1.2所示。
图1.2 系统原理方框图习题1.题图1-1是一晶体管稳压电源。
试将其画成方块图并说明在该电源里哪些起着测量、放大、执行的作用以及系统里的干扰量和给定量是什么?题图1-12.如题图1-2(a)、(b)所示两水位控制系统,要求(1)画出方块图(包括给定输入量和扰动输入量);(2)分析工作原理,讨论误差和扰动的关系。
控制理论中的数学模型
控制理论中的数学模型在现代科学技术中,控制理论对于各种工程问题的解决起着至关重要的作用。
无论是机器人、飞行器、汽车,还是工业化生产过程中的控制,都需要利用数学模型来实现。
在数学模型中,控制理论是其中的一个重要领域。
控制理论的数学模型是一种用数学方法描述系统行为和运动规律的理论。
它的主要内容包括系统建模、控制器设计和系统性能评估等方面。
在控制理论中,系统建模是最基础的环节。
在控制系统中,被控制的对象称为系统,例如机器人运动的轨迹、飞行器的高度和速度、汽车的转向等。
系统建模就是通过数学方法将系统的行为和规律用一组公式或方程表示出来,以便进行控制器的设计和系统性能的评估。
控制理论中的数学模型主要分为线性模型和非线性模型两种类型,它们在应用场景和建模方法上均存在不同之处。
线性模型是控制理论中最常见的一种模型。
它的主要特点是系统的变量之间呈线性关系,即系统对某个输入变量的响应与这个变量的大小是成比例的。
常见的线性模型包括线性微分方程、状态方程和传递函数等。
非线性模型则是指系统中存在非线性关系的模型,如系统中变量的幂次项、三角函数项、指数项、对数项等。
非线性模型的建模更加复杂,但能更好地反映真实系统的动态行为,因此在实际应用中也有很大的用武之地。
控制器设计是指通过控制器控制系统的输出来达到系统最优控制的目的。
控制器又分为各种形态,如比例控制、积分控制、微分控制,以及它们的组合控制等等。
控制器的设计需要根据被控制对象的特点和实际需要,选择合适的控制算法来实现系统的稳定控制和优化控制。
系统性能评估是指通过各种评估方法评估系统的控制效果和性能,以便进行调整和优化。
评估方法包括计算机模拟、实验测量等方法。
评估结果可以用来进一步提高系统的控制性能和工作效率。
在实际应用中,控制理论的数学模型可以应用于各种控制系统,如机器人、飞行器、汽车、电子设备等。
其中最典型的应用是自动控制系统。
例如,自动驾驶汽车就是利用控制理论中的数学模型来实现的。
传递函数
-
-
第二节 传递函数
解:由图列微分方程
2u R L d du ur 解: 输入量: c c + u = u 得 c r RC dt + LC + 2 dt i uc 输出量: C 拉氏变换: ur
+ uc -
RCsUc(s) + LCs2 Uc (s) + U c (s ) 根据基尔霍夫定律:
第二节 传递函数
式中: K 0 — 为放大系数 传递函数性质: S = S1 , S2 · · · , Sn — 传递函数的极点 ( 4 )传递函数是在零初始条件下定义的, (1)传递函数只适用于线性定常系统。 S = 不能反映非零初始条件下系统的运 Z1 , Z2 · · · , Zm — 传递函数的零点 动过程。 传递函数分母多项式就是相应微分方 (2)传递函数取决于系统的结构和参数, 将传递函数中的分子与分母多项式分 程的特征多项式,传递函数的极点就是微 与外施信号的大小和形式无关。 别用因式连乘的形式来表示,即 分方程的特征根。 (3)传递函数一般为复变量S 的有理分式。 K0 (s –z1 ) (s –z2 ) · · · (s – z m ) G (s ) = (s – s 1 ) ( s – s 2 பைடு நூலகம் · · · (s –sn ) n>=m
根据传递函数的定义有
C ( s) bm s m bm1s m1 b1s b0 G( s ) R( s) an s n an1s n1 a1s a0
第二节 传递函数
二、传递函数的求取 传递函数以般有三种方法求取:1、直接计算法, 2、阻抗法,3、动态结构图法(下一节在讲)。 1、2两种一起讲 例题1、求图示RLC电路的传递函数。
控制系统的数学模型
/view/4306d34ef7ec4afe04a1dfc0.html第二章控制系统的数学模型本章目录2.1 列写系统微分方程式的一般方法2.2 非线性数学模型的线性化2.3 传递函数2.4 框图和系统的传递函数2.5 信号流程图与梅逊公式2.6 状态空间模型简介2.7 数学模型的MATLAB描述小结本章简介概述:1. 数学模型 ------描述系统变量之间关系的数学表达式2. 建模的基本方法: (1) 机理建模法(解析法)(2) 实验辩识法3. 控制系统数学模型的主要形式:(1) 外部描述法: 输入--输出描述(2) 内部描述法:状态变量描述系统是指相互联系又相互作用着的对象之间的有机组合。
许多控制系统,不管它们是机械的、电气的、热力的、液压的,还是经济学的、生物学的等等,都可以用微分方程加以描述。
如果对这些微分方程求解,就可以获得控制系统对输入量(或称作用函数)的响应。
系统的微分方程,可以通过支配着具体系统的物理学定律,例如机械系统中的牛顿定律,电系统中的克希霍夫定律等获得。
为了设计(或者分析)一个控制系统,首先需要建立它的数学模型,即描述这一系统运动规律的数学表达式。
有三种比较常用的描述方法:一、是把系统的输出量与输入量之间的关系用数学方式表达出来,称之为输入--输出描述,或端部(外部)描述,例如微分方程式、传递函数和差分方程。
第二种不仅可以描述系统的输入、输出间关系,而且还可以描述系统的内部特性,称之为状态变量描述,或内部描述,它特别适用于多输入、多输出系统,也适用于时变系统、非线性系统和随机控制系统。
另一种方式是用比较直观的方块图模型来进行描述。
同一控制系统的数学模型可以表示为不同的形式,需要根据不同情况对这些模型进行取舍,以利于对控制系统进行有效的分析。
建立系统数学模型的方法有:解析法和实验法。
本章所讨论的数学模型以传递函数和方块图为主,有关状态空间模型的说明本书仅进行简单介绍。
2.1 列写系统微分方程式的一般方法回目录本节应用解析法来建立系统的数学模型。
第三章线性系统的时域分析
系统已达到稳态,系统达到稳态的时间称为系统的响应时 间,对于一阶系统,响应时间为 (3 ~ 4) 。
2013年6月8日星期六 第3章第10页共97页
误差:
t
e(t ) r (t ) c(t ) 1 (1 e ) e
t
当t 时,e(t ) 0
所以,一阶系统能准确跟踪单位阶跃输入。
d n 1 2
C(t)
d 称为阻尼自然振荡频率。
C(∞)
2013年6月8日星期六
0
t
第3章第26页共97页
1 2 c(t ) 1 e nt sin( 1 2 nt arctan ), t 0 1 2 1
当 0时,可得系统的无阻尼响应为:
在工程上,当 1.5 时,使用上述近似关系已 有足够的准确度了.
2013年6月8日星期六 第3章第23页共97页
2013年6月8日星期六
第3章第24页共97页
j
2.欠阻尼 0 1 的情况 §3-3二阶系统的时域响应
×
j n 1
2
系统的闭环极点为:
2
n
s1 ( j 1 ) n s 2 ( j 1 2 ) n
第3章第7页共97页
§3-2 一阶系统的时域响应
一阶系统的框图如下: 系统的传函为:
R(s)
1 s
C (s)
C ( s) 1 R( s ) s 1
分析系统在零初始条件下对典型输入信号的响应
2013年6月8日星期六
第3章第8页共97页
1.单位阶跃响应
C(t)
1 R( s) s 1 1 C (s) s (s 1) s s 1 1 1 s s 1
