计算机仿真试题及答案
仿真考试题及答案

仿真考试题及答案一、单项选择题1. 计算机系统由哪两部分组成?A. 硬件系统和软件系统B. 操作系统和应用程序C. 输入设备和输出设备D. 主机和外设答案:A2. 以下哪个不是计算机硬件的组成部分?A. 中央处理器(CPU)B. 内存C. 操作系统D. 硬盘答案:C3. 在计算机中,1KB等于多少字节?A. 512字节B. 1024字节C. 1000字节D. 2048字节答案:B二、多项选择题1. 以下哪些是计算机病毒的特点?A. 破坏性B. 传染性C. 潜伏性D. 可逆性答案:ABC2. 计算机软件可以分为哪几类?A. 系统软件B. 应用软件C. 硬件软件D. 网络软件答案:ABD三、判断题1. 计算机的内存是临时存储设备,断电后数据会丢失。
答案:正确2. 计算机的硬盘是永久存储设备,数据不会因为断电而丢失。
答案:正确3. 计算机的CPU是中央处理器,负责解释和执行程序指令。
答案:正确四、填空题1. 计算机的存储单位从大到小依次为:____、____、____、____。
答案:TB、GB、MB、KB2. 计算机的二进制数只有两个数字,分别是0和____。
答案:13. 计算机的操作系统主要负责____、____、____和____。
答案:进程管理、存储管理、设备管理、文件管理五、简答题1. 简述计算机硬件和软件的区别。
答案:硬件是指计算机系统中的物理设备,如CPU、内存、硬盘等,它们是计算机运行的基础。
软件则是指计算机系统中的程序和数据,包括操作系统、应用程序等,它们是计算机执行任务的指令和规则。
2. 描述计算机病毒的危害。
答案:计算机病毒可以破坏计算机系统的正常运行,导致数据丢失或损坏,影响计算机性能,甚至造成网络瘫痪。
它们还可以通过自我复制和传播,感染其他计算机,造成更广泛的损害。
六、计算题1. 如果一个计算机的内存为8GB,那么它的内存容量是多少字节?答案:8GB = 8 1024MB = 8 1024 1024KB = 8 1024 1024 1024字节2. 计算一个文件大小为1.5GB的文件占用多少KB。
计算机仿真试题和答案

控制系统计算机辅助设计综合实验指导实验名称:连续与离散系统校正实验,系统可控性与可观性实验,系统的simulink仿真实验陈茜编实验人:苏建聪学号:200830810122班级:08电气工程及其自动化1班信息工程系实验任务书1. 有一个单位负反馈控制系统,如果控制对象的传递函数为设计要求:① 相角裕度≥45°;② 当系统的输入信号是单位斜坡信号时,稳态误差ess ≤0.04。
③ 要求绘制出校正后系统和未校正系统的Bode 图及其闭环系统的单位阶跃响应曲线,并进行对比。
2. 有一个单位负反馈控制系统,如果控制对象的传递函数为:试设计一个串联滞后校正装置。
设计要求:①相角裕度≥45°;② 当系统的输入信号是单位斜坡信号时,稳态误差ess ≤0.04。
③ 要求绘制出校正后系统和未校正系统的Bode 图及其闭环系统的单位阶跃响应曲线,并进行对比。
3. 有一个单位负反馈控制系统,如果控制对象的传递函数为 ()()4+=s s k s G p试设计一个串联超前滞后校正装置,设计要求: ①相角裕度≥45°;② 当系统的输入信号是单位斜坡信号时,稳态误差ess ≤0.04。
③ 要求绘制出校正后系统和未校正系统的Bode 图及其闭环系统的单位阶跃响应曲线,并进行对比。
4. 系统结构图如图所示,其中,采样周期Ts=0.01s ,被控对象()()110+=s s s G ,()s G h 为零阶保持器。
用W 变换法设计一超前校正装置D(z),使系统相位裕度γ≥50°,校验设计后系统的性能指标。
5. 系统结构图如图所示,其中,采样周期Ts=0.01s ,被控对象1)s(0.2s k )(+=s G ο,()s G h 为零阶保持器。
用对数频率法设计D(z),使系统开环增益k ≥30(1/s),截止频率ωc ≥15(1/s),相位裕度γ≥50 °1使 s 11se -1(s)-Tsh T G +≈=,求出未校正系统的开环系统的开环传递函数(s)(s)G G (s)0s =G ,的传递函数模型参数。
计算机仿真习题及答案
计算机仿真试题1.编写一个函数,使其能够产生如下的分段函数:错误!未找到引用源。
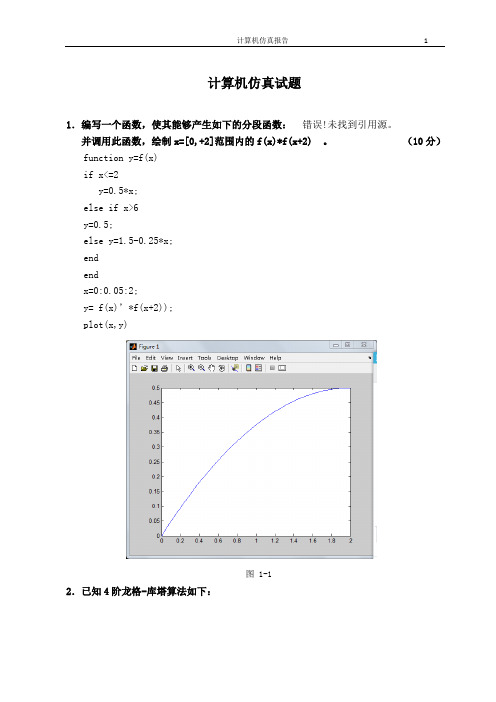
并调用此函数,绘制x=[0,+2]范围内的f(x)*f(x+2) 。
(10分)function y=f(x)if x<=2y=0.5*x;else if x>6y=0.5;else y=1.5-0.25*x;endendx=0:0.05:2;y= f(x)’*f(x+2));plot(x,y)图 1-12.已知4阶龙格-库塔算法如下:试利用该算法求解以下微分方程:(15分)本题可以调用MATLAB函数中龙格-库塔算法函数ode45,首先编写m文件:function dy=func(x,y)dy=-y+1;end再在主窗口调用此文件:[x,y]=ode45('func',[0,5],0)%这里的[0,5]为任取区间,表示方程在此范围的解。
运行结果如下:x =0.00010.00010.00020.00020.00050.00070.00100.00120.00250.00370.00500.00620.01250.01880.02510.0313 0.06270.09410.12550.15690.28190.40690.53190.65690.78190.90691.03191.15691.28191.40691.53191.65691.78191.90692.03192.15692.28192.40692.53192.65692.78192.90693.03193.15693.28193.40693.53193.65693.78193.90694.03194.15694.28194.40694.53194.65694.74274.82854.91425.0000y =0.00010.00010.00020.00020.00050.00070.00100.00120.0025 0.0037 0.0050 0.0062 0.0124 0.0186 0.0248 0.0309 0.0608 0.0898 0.1180 0.1452 0.2457 0.33430.41250.48160.54250.59630.64370.68550.72250.75510.78390.80930.83170.85150.86890.88430.89790.90990.92050.92980.93810.94540.95180.95740.96240.96690.97080.97420.97720.97990.98230.98430.98620.98780.98920.99050.99130.99200.99270.9933为只管起见,我们使用函数命令画出x-y(plot(x,y))的关系如下图:图1-23.用matlab语言求下列系统的状态方程、传递函数、零极点增益、和部分分式形式的模型参数,并分别写出其相应的数学模型表达式:(15分)(1)G(s)=324327242410355024s s ss s s s+++++++(2).X=2.25 -5 -1.25 -0.542.25 -4.25 -1.25 -0.2520.25 -0.5 -1.25 -121.25 -1.75 -0.25 -0.75 0X⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥+⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦uy= [0 2 0 2] X解:(1)a)求对应状态方程参数:num=[1 07 24 24]; den=[1 10 35 50 24]; [A,B,C,D]=tf2ss(num,den) 运行结果:A =-10 -35 -50 -241 0 0 00 1 0 00 0 1 0B =1C =1 7 24 24D =故,状态方程为:.X = x+ uY=[1 7 24 24]xb)求对应零极点增益模型参数:num=[1 07 24 24]; den=[1 10 35 50 24]; [Z,P,K]=tf2zp(num,den) 运行结果如下: Z =-2.7306 + 2.8531i -2.7306 - 2.8531i -1.5388P = -4.0000 -3.0000 -2.0000 -1.0000K = 1故变换后的零极点模型为: G(s)=c)求对应部分分式型:num=[1 07 24 24]; den=[1 10 35 50 24]; [R,P,H]=residue(num,den) 运行结果如下: R =4.0000 -6.0000 2.0000 1.0000P =-4.0000 -3.0000 -2.0000 -1.0000H = []故变换后的部分分式模型为:11223644)(+++++-+=s s s s s G(2)由题给条件,知:A=[2.25 -5 -1.25 -0.5; 2.25 -4.25 -1.25 -0.25;0.25 -0.5 -1.25 -1;1.25 -1.75-10 -35 -50 -24 1 0 0 0 0 1 0 0 0 0 1 010 0 0-0.25 -0.75] B=[4;2;2;0] C=[0 2 0 2],D=0 a)求传递函数矩阵: [num,den]=ss2tf(A,B,C,D) 运行结果为: num =0 4.0000 14.0000 22.0000 15.0000 den =1.0000 4.0000 6.2500 5.25002.2500 故,所对应传递函数模型为:25.225.525.641522144)(23423+++++++=s s s s s s s s Gb)求零极点模型:num=[0 4 14 22 15];en=[1 4 6.25 5.25 2.25]; [Z,P,K]=tf2zp(num,den) 运行结果为: Z =-1.0000 + 1.2247i -1.0000 - 1.2247i -1.5000 P =-1.5000 -1.5000 -0.5000 + 0.8660i -0.5000 - 0.8660iK =4.0000故,零极点模型为:)866.05.0()5.1()2247.11)(5.1(4)(2i s s i s s s G ±++±++=c)求对应部分分式模型: [R,P,H]=residue(num,den) 运行结果为: R =4.0000 -0.0000-0.0000 - 2.3094i -0.0000 + 2.3094iP =-1.5000 -1.5000 -0.5000 + 0.8660i -0.5000 - 0.8660iH = []故变换后的部分分式模型为:i s ii s i s s G 866.05.03094.2866.05.03094.25.14)(+++-+-++=4.已知一单位反馈系统开环传递函数为:,试绘制系统Nyquist图,判断闭环系统的稳定性,并求其单位阶跃响应。
智慧树答案计算机仿真技术知到课后答案章节测试2022年

第一章1.计算机仿真系统的三要素()答案:计算机、模型、系统2.系统研究一般有哪些方法()答案:仿真实验法;理论解析法;直接实验法3.哪些是以硬件为基础的仿真软件( )答案:Proteus4.欠实时仿真,仿真时钟比实际时钟慢。
例如烟火爆炸的仿真分析。
答案:对5.计算机仿真算法的误差主要有()答案:截断误差;舍入误差第二章1.MATLAB软件中,下面哪个命令是用来显示当前文件夹中文件名字的()答案:what2.下面这些哪个是属于元素群运算(点运算)()答案:exp(x)3.哪个是以硬件为基础的仿真软件( )答案:Proteus4.MATLAB是(矩阵实验室),其基本变量是矩阵,其数值元素的格式只有双精度(double)这种形式存在于MATLAB的workpace空间中。
答案:错5.在MATLAB中,运行以下代码,b的结果是()a=[1,0;1,0];b=all(a)答案:[1,0]第三章1.MATLAB中代码文件中边表明文件为函数文件的关键字是()答案:function2.在MATLAB的命令窗口中,运行以下代码,b的结果是()a=[1,0,1,0];forn=ax=n(1)&n(2);end答案:出现错误提示3.在MATLAB的fig窗口中,可以直接打开以下()格式的图形文件答案:fig4.在MATLAB中,对于m函数文件,下面的描述不正确的是()答案:m函数文件是不能够被simulink来调用的5.全局变量是共有变量,在函数文件中不能够直接访问,需要设置一个输入参数才能访问。
答案:错第四章1.以下说法不正确的是()答案:不同幂次的两个多项式不能进行乘法运算2.当实验或测试所获得的样本数据有误差时,适合用来估算数据的方法是()答案:曲线拟合3.若在MATLAB中已有语句a=sym(1); b=1; x=sym('b'),则以下叙述正确的是()答案:a是符号常量,x是符号变量4.若使用命令taylor(f,x,1,'Order',6)对f进行泰勒展开,则展开式的最高阶为()答案:55.在命令行窗口输入下列命令,则命令执行后的输出结果是()>>f=sym(1);>> eval(int(f,1,4))答案:3第五章1.启动Simulink的方法有()答案:在命令行窗口中输入simulink命令;在“主页”选项卡中单击“文件”命令组中的“新建”命令按钮;在“主页”选项卡中单击SIMULINK命令组中的“Simulink”命令按钮2.在一个模型窗口上按住一个模块并同时按Shift键移动到另一个模型窗口,则()答案:在两个模型窗口都有这个模块3.为子系统定制参数设置对话框和图标,使子系统本身有一个独立的操作界面,这种操作称为子系统的()答案:封装4.已知仿真模型如图所示,各模块参数均采用默认设置,则示波器的输出波形是()答案:5.以下关于S函数的描述中,正确的有()答案:S函数有现成的模板程序;S函数模块能够被封装;利用S函数可以对Simulink模块库进行扩充第六章1.下列对象中,哪一个不属于MATLAB控制系统工具箱中规定的LTI对象?()答案:极点留数对象2.tf2zpk函数的作用是?()答案:零极点增益模型转换为状态空间模型3.在MATLAB命令窗口运行如下代码,返回结果为:()>>sys = drss(3,4);isct(sys)答案:14.求系统sys的阶跃相应,返回系统的输出和状态,step函数的调用格式为:()答案:[y,t,x]=step(sys)5.给定开环系统模型作波特图,频率向量w自动给出,作波特图,并在图上标注幅值裕度Gm和对应的频率wg,相位裕度Pm和对应的频率wp,所用函数及调用格式为:()答案:margin(sys)第七章1.在MATLAB的m文件中,可以将滞后环节转化为有理数形式的函数是?()答案:pade2.在simulink中,有多种PID模块,其中下面哪一个是离散的PID模块()答案:;3.在MATLAB的m文件中,LTI对象中属于滞后特征的属性是( )答案:Outputdelay;IOdelay;Inputdelay4.simulink中,PID模块中的只有Kp,Ki,Kd三个参数可以设置。
《计算机仿真技术》试题(含完整答案)

一、数值计算,编程完成以下各题〔共20分,每题5分〕1、脉冲宽度为d ,周期为T 的矩形脉冲的傅里叶级数如下式描述:)2cos(/)/sin(21[)(1τπππτn T d n T d n T d f n ∑∞=+=当150=n ,41=T d ,2/12/1<<-τ,绘制出函数)(τf 的图形。
解: syms n t;f=((sin(n*pi/4))/(n*pi/4))*cos(2*pi*n*t); s=symsum(f,n,1,150); y=(1+2*s)/4; x=-0.5:0.01:0.5; Y=subs(y,'t',x); plot(x,Y)2、画出函数5505.025.55.15.1cos 5)5(sin )(2x x x x ex x f x +++-=在区间[3,5]的图形,求出该函数在区间[3, 5]中的最小值点m in x 和函数的最小值m in f .解:程序如下 x=3:0.05:5;y=(sin(5*x).^2).*exp(0.05*x.^2)-5*(x.^5).*cos(1.5*x)+1.5*abs(x+5.5)+x.^2.5; mix_where=find(y==min(y)); xmin=x(mix_where); hold on; plot(x,y);plot(xmin,min(y),'go','linewidth',5);str=strcat('(',num2str(xmin),',',num2str(min(y)),')'); text(xmin,min(y),str); Xlabel('x')Ylabel('f(x)')经过运行后得到的图像截图如下:运行后的最小值点m in x =4.6,m in f = -8337.86253、画出函数xe x xf x 5.2cos )(3.02-⋅=-在[1,3]区间的图形,并用编程求解该非线性方程0)(=x f 的一个根,设初始点为20=x .解: x=1:0.02:3; x0=2;y=@(x)(cos(x).^2).*exp(-0.3*x)-2.5*abs(x); fplot(y,[1,3]); Xlabel('x') Ylabel('f(x)')X1=fzero('(cos(x).^2).*exp(-0.3*x)-2.5*abs(x)',x0)运行后求得该方程的一个根为z=0.3256。
《计算机仿真技术》试卷B(含答案)

《计算机仿真技术》考试试卷(B 卷)班级 姓名 学号一.填空题。
(每空1分,共20分)1、计算机仿真技术三要素是_______________、_________________、________________。
2、计算机仿真中模型能够代表系统来进行研究,模型主要有________________、________________、________________、________________等几类模型。
3、叙述simulink 中常见的固定步长的仿真算法有:________________、________________、________________、________________。
(任举四种)4、MATALB 主要相似性主要包含以下几种相似_________________、________________、___________________。
5、Simulink 中主要包含_________________、________________、_______________等几种模块。
6、符号运算中,泰勒级数计算的函数是________________,拉普拉斯变换的函数________________,傅里叶级数的计算函数是________________。
二.简答题。
(本题5小题,每题8分,共40分)1、简述根据信号类型分类,计算机仿真主要包含哪几种类型。
2、简述蒙特卡洛法建模的步骤。
3、m 函数文件和m 文本文件之间的区别。
4、叙述三维立体绘图常用的几个绘图指令及其功能。
5、简述matlab 软件的基本组成三.编程题 (本题6小题、共40分)根据下面要求,只需写出程序代码,不需计算结果和图形。
1、(5分)写出右面的矩阵D ,求出其大于4的元素有几个,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=059123107D并通过变量列出其在矩阵的位置和序号2、(5分)求解下面矩阵A 的行列式和逆矩阵,并利用命令取出系数矩阵的逆矩阵的第二行的数据,以小数点后面两位数值的形式显示出来。
计算机仿真与建模技术考核试卷
10.哪些因素可能导致仿真结果的误差?()
A.模型简化的假设
B.数值计算方法的选择
C.输入数据的准确性
D.计算机硬件的限制
11.以下哪些属于系统动力学模型的基本元素?()
A.状态变量
B.流率变量
C.辅助变量
D.常量
12.在仿真项目中,以下哪些步骤是必要的?()
A.明确仿真目标
B.设计仿真实验
C.编写仿真程序
D.分析仿真结果
13.以下哪些软件可以用于复杂系统仿真?()
A. AnyLogic
B. Simulink
C. LabVIEW
D. ProModel
14.哪些方法可以用来提高仿真模型的效率?()
A.简化模型结构
B.优化算法
C.并行计算
D.减少仿真时间
15.在仿真模型的灵敏度分析中,以下哪些是常用的方法?()
D.主成分分析
11.关于计算机仿真与建模,以下哪个说法是正确的?()
A.计算机仿真可以完全替代实验研究
B.建模过程中,模型越复杂越好
C.计算机仿真可以节省实验成本和时间
D.计算机仿真与建模适用于所有领域
12.以下哪个软件主要用于过程建模和仿真?()
A. Arena
B. CAD
C. MATLAB
D. Microsoft Visio
五、主观题(本题共4小题,每题5分,共20分)
1.请简述计算机仿真的基本步骤,并说明每个步骤的重要性。
2.描述连续系统仿真与离散事件仿真的区别,并给出各自适用的场景。
3.什么是敏感性分析?它在计算机仿真中的作用是什么?
4.解释面向对象建模中的“封装”、“继承”和“多态”的概念,并给出实际应用中的例子。
仿真模拟考试题及答案
仿真模拟考试题及答案# 仿真模拟考试题及答案一、选择题1. 以下哪个选项是计算机科学领域的基础概念?A. 量子物理B. 相对论C. 算法D. 遗传学答案:C2. 在编程中,以下哪个关键字用于定义一个类?A. functionB. classC. methodD. variable答案:B3. 数据库管理系统(DBMS)的主要功能是什么?A. 存储数据B. 处理数据C. 管理数据D. 所有选项答案:D二、填空题4. 在HTML中,用来定义文档类型声明的标签是______。
答案:<!DOCTYPE>5. 在Python中,用于实现循环结构的关键字是______。
答案:for 或 while三、简答题6. 请简述什么是面向对象编程(OOP)?答案:面向对象编程(OOP)是一种编程范式,它使用“对象”来设计软件。
对象可以包含数据(属性)和代码(方法),它们可以相互交互以实现特定的功能。
OOP的主要概念包括封装、继承和多态。
7. 什么是云计算,它有哪些主要优势?答案:云计算是一种通过互联网提供计算资源和服务的模式。
它允许用户通过Web访问和使用存储在远程服务器上的数据和应用程序。
云计算的主要优势包括成本效益、可扩展性、灵活性和高可用性。
四、计算题8. 假设你有一个数组 [1, 2, 3, 4, 5],请计算数组中所有元素的总和。
答案:159. 如果一个圆的半径是7,计算它的面积。
答案:3.14159 × 7² = 153.93649五、论述题10. 论述软件开发生命周期的主要阶段,并解释每个阶段的重要性。
答案:软件开发生命周期(SDLC)包括需求分析、设计、实现、测试、部署和维护等阶段。
需求分析阶段确定软件需要满足的功能和性能要求。
设计阶段将需求转化为软件架构和详细设计。
实现阶段是编码过程,将设计转化为可执行代码。
测试阶段确保软件满足需求并且没有缺陷。
部署阶段是将软件发布到生产环境。
计算机仿真题库
25. 请比较数值积分法与离散相似法的区别。 数值积分法比较成熟,精度较高,但计算公式复杂,计算量大,适合离线仿真;而离散 相似法计算公式简单,计算量小,速度快,但精度较低,适合在线仿真。 26. 物理仿真 以真实系统的物理性质和几何形状相似为基础而其他性质不变来构造系统的物理模型, 并在物理模型上进行实验的过程称为物理仿真,也称为实体仿真。其优点在于直观、形象; 缺点在于模型改变困难,实验限制较多,投资较大。 27. 虚拟现实 虚拟现实是用高科技手段构造出来的一种人工环境,它具有模仿人的视觉、听觉、触觉 等感知功能的能力,具有使人可以亲身体验沉浸在这种虚拟环境并与之相互作用的能力。 28. 多媒体仿真 将数字、文字、声音、图形、图像和动画等各种媒体有机组合,并与先进的计算机通信 和广播电视技术相结合,形成一个可组织、存储、操纵和控制多媒体信息的集成环境和交互 系统的仿真技术。 29. 根据系统的动态特性,一般可以将系统做哪些分类? 根据系统的动态特性,可以将系统分为: (1)连续系统和离散系统。时间和各个组成部 分的变量都具有连续形式的系统称为连续系统; 全部或一些组成部分的变量具有离散信号形 式的系统称为离散系统。 (2)线性或非线性系统。如果微分方程的系数是常数或者仅仅是自 变量的函数, 则为线性微分方程, 其符合叠加性原理, 可分为线性定常系统, 线性时变系统; 非线性系统用非线性微分方程表示,其不符合叠加原理。 (3)确定系统和随机系统。确定系 统可以用确定的数学模型进行描述, 输出和输入变量之间有完全确定的函数关系; 随即系统 则指系统内部或环境变量发生不确定变动, 会影响输出变量。 (4) 单变量系统和多变量系统。 这是对输入输出变量个数而言的。 30. 在连续系统的数字仿真中, 仿真算法的选择一般为考虑什么?常用的仿真算法有哪些? 在连续系统的数字仿真中,选择仿真算法一般会考虑求解精度、速度、数值稳定性、自 启动能力、步长等。常用的仿真方法有:欧拉法、四阶龙格-库塔法、离散相似法等。欧拉 法属于自启动算法,适用于线性系统和非线性系统,方法简单,但误差的积累导致求解精度 降低。四阶龙格库塔法也属于自启动算法,适用于线性和非线性系统,支持单步长和可变步 长,求解速度和精度较高,但仿真时间较长。离散相似法一般用于状态方程,按环节离散相 似法可用于非线性系统,按系统离散相似法仅限于线性系统。 31. 什么是实时仿真?什么情况下需要进行实时仿真?它在算法上有什么要求? 实时仿真是指仿真模型的时间比例尺等于系统原模型的时间比例尺的一类仿真,对系统 进行仿真试验时,如果仿真系统有实物,由于实物和人是按真实时间变化和运动的,因此就 需要进行实时仿真。实时仿真要求仿真系统接收实时动态输入,并产生实时动态输出,输入 和输出通常为固定采样时间间隔的数列。 32. 什么是数值稳定性问题?如何保证计算中的数值稳定性? 所谓的数值稳定性问题,是指在扰动影响下,其计算过程中误差的积累是否受到控制的 问题。要保证数值稳定性,应遵循两条原则: (1)保证计算稳定; (2)有一定的计算精度来 选择合理的计算步长。
计算机仿真课后答案
第二章2.1x=[15 22 33 94 85 77 60]x(6)x([1 3 5])x(4:end)x(find(x>70))2.2T=[1 -2 3 -4 2 -3] ;n=length(T);TT=T';for k=n-1:-1:0B(:,n-k)=TT.^k;endBtest=vander(T)2.3A=zeros(2,5);A(:)=-4:5L=abs(A)>3islogical(L)X=A(L)2.4A=[4,15,-45,10,6;56,0,17,-45,0]find(A>=10&A<=20)2.5p1=conv([1,0,2],conv([1,4],[1,1]));p2=[1 0 1 1];[q,r]=deconv(p1,p2);cq='商多项式为'; cr='余多项式为';disp([cq,poly2str(q,'s')]),disp([cr,poly2str(r,'s')])2.6A=[11 12 13;14 15 16;17 18 19];PA=poly(A)PPA=poly2str(PA,'s')第三章3.1n=(-10:10)';y=abs(n);plot(n,y,'r.','MarkerSize',20)axis equalgrid onxlabel('n')3.2x=0:pi/100:2*pi;y=2*exp(-0.5*x).*sin(2*pi*x);plot(x,y),grid on;3.3t=0:pi/50:2*pi;x=8*cos(t);y=4*sqrt(2)*sin(t);z=-4*sqrt(2)*sin(t);plot3(x,y,z,'p');title('Line in 3-D Space');text(0,0,0,'origin');xlabel('X'),ylable('Y'),zlable('Z');grid;3.4theta=0:0.01:2*pi;rho=sin(2*theta).*cos(2*theta); polar(theta,rho,'k');3.5[x,y,z]=sphere(20);z1=z;z1(:,1:4)=NaN;c1=ones(size(z1));surf(3*x,3*y,3*z1,c1);hold onz2=z;c2=2*ones(size(z2));c2(:,1:4)=3*ones(size(c2(:,1:4))); surf(1.5*x,1.5*y,1.5*z2,c2); colormap([0,1,0;0.5,0,0;1,0,0]);grid onhold off第四章4.1for m=100:999m1=fix(m/100);m2=rem(fix(m/10),10);m3=rem(m,10);if m==m1*m1*m1+m2*m2*m2+m3*m3*m3 disp(m)endend4.2function[s,p]=fcircle(r)s=pi*r*r;p=2*pi*r;4.3y=0;n=100;for i=1:ny=y+1/i/i;endy4.4s=0;for i=1:5s=s+factor(i);ends4.5sum=0;i=1;while sum<2000sum=sum+i;i=i+1;end;n=i-24.6function k=jcsum(n)k=0;for i=0:nk=k+2^i;end或function k=jcsum1(n)k=0;i=0;while i<=nk=k+2^i;i=i+1;end第五章5.1A=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-4];b=[13,-9,6,0]';x=A\b5.2[U,fmin]=fminsearch('fxyz',[0.5,0.5,0.5])function f=fxyz(u)x=u(1);y=u(2);z=u(3);f=x+y.^2./x/4+z.^2./y+2./z;5.3X=linspace(0,2*pi,50);Y=sin(X);P=polyfit(X,Y,3)AX=linspace(0,2*pi,50);Y=sin(X);Y1=polyval(P,X)plot(X,Y,':O',X,Y1,'-*')5.4x=0:2.5:10;h=[0:30:60]';T=[95,14,0,0,0;88,48,32,12,6;67,64,54,48,41];xi=[0:0.5:10];hi=[0:10:60]';temps=interp2(x,h,T,xi,hi,'cubic');mesh(xi,hi,temps);第六章6.1syms xy=finverse(1/tan(x))6.2syms x yf=1/(1+x^2); g=sin(y);fg=compose(f,g)6.3syms xg=(exp(x)+x*sin(x))^(1/2);dg=diff(g)6.4F=int(int('x*exp(-x*y)','x'),'y')6.5syms xF=ztrans(x*exp(-x*10))6.6a=[0 1;-2 -3];syms sinv(s*eye(2)-a);6.7f=solve('a*x^2+b*x+c')6.8f=solve('x+y+z=1','x-y+z=2','2*x-y-z=1')6.9y=dsolve('D2y+2*Dy+2*y=0','y(0)=1','Dy(0)=0') ezplot(y),grid on6.10a=maple('simplify(sin(x)^2+cos(x)^2);')6.11f=maple('laplace(exp(-3*t)*sin(t),t,s);')6.12syms t xF=sin(x*t+2*t);L=laplace(F)第七章7.17.27.37.47.57.67.7第八章8.1(1)num=[5]; den=[1,2,2];sys=tf(num,den)(2)s = tf('s');H = [5/(s^2+2*s+2) ];H.inputdelay =2(3)h=tf([0.5,0],[1,-0.5,0.5],0.1)8.2num=2*[1,0.5];den=[1,0.2,1.01];sys=tf(num,den)[z,p,k]=tf2zp(num,den);zpk(z,p,k)[A,B,C,D]=tf2ss(num,den);ss(A,B,C,D)8.3num=[1,5]; den=[1,6,5,1]; ts=0.1;sysc=tf(num,den);sysd=c2d(sysc,ts,'tustin')8.4r1=1;r2=2;c1=3;c2=4;[A,B,C,D]=linmod('x84');[num,den]=ss2tf(A,B,C,D);sys=tf(num,den)8.5A=[1,1,0;0,1,0;0,0,2];B=[0,0;1,0;0,-2];n=size(A)Tc=ctrb(A,B);if n==rank(Tc)disp('系统完全能控');elsedisp('系统不完全能控');end第九章9.1num=[2,5,1];den=[1,2,3];bode(num,den);grid on ;figure;nyquist(num,den);9.2num=5*[1,5,6];den=[1,6,10,8];step(num,den);grid on ;figure;impulse(num,den);grid on ;9.3kosi=0.7;wn=6;num=wn^2;den=[1,2*kosi*wn,wn^2];step(num,den);grid on ;figure;impulse(num,den);grid on ;9.4den=[1,2,8,12,20,16,16];[rtab,info]=routh(den)a=rtab(:,1)if all(a>0)disp('系统是稳定的');elsedisp('系统是不稳定的');end9.5num=7*[1,5];den=conv([1,0,0],conv([1,10],[1,1]));[gm,pm,wg,wc]=margin(num,den)第十章10.1ng0=[1]; dg0=10000*[1 0 -1.1772];g0=tf(ng0,dg0); %满足开环增益的为校正系统的传递函数s=kw2s(0.7,0.5) %期望的闭环主导极点ngc=rg_lead(ng0,dg0,s);gc=tf(ngc,1)g0c=tf(g0*gc);rlocus(g0,g0c);b1=feedback(g0,1); %未校正系统的闭环传递函数b2=feedback(g0c,1); %校正后系统的闭环传递函数figure,step(b1,'r--',b2,'b'); grid on %绘制校正前后系统的单位阶跃响应曲线10.2KK=20;s1=-2+i*sqrt(6);a=1ng0=[10];dg0=conv([1,0],[1,4]);g0=tf(ng0,dg0);[ngc,dgc,k]=rg_lag(ng0,dg0,KK,s1,a);gc=tf(ngc,dgc)g0c=tf(KK*g0*gc);b1=feedback(k*g0,1);b2=feedback(g0c,1);step(b1,'r--',b2,'b');grid on10.3KK=128;s1=-2+i*2*sqrt(3);a=2ng0=[10];dg0=conv([1,0],conv([1,2],[1,8]));g0=tf(ng0,dg0);[ngc,dgc,k]=rg_lag(ng0,dg0,KK,s1,a);gc=tf(ngc,dgc)g0c=tf(KK*g0*gc);rlocus(g0,g0c);b1=feedback(k*g0,1);b2=feedback(g0c,1);figure,step(b1,'r--',b2,'b');grid on10.4ng0=[1];dg0=conv([1,0,0],[1,5]);g0=tf(ng0,dg0);w=logspace(-3,3);KK=1;Pm=50;[ngc,dgc]=lead4(ng0,dg0,KK,Pm,w);gc=tf(ngc,dgc);g0c=tf(KK*g0*gc);bode(KK*g0,w);hold on,bode(g0c,w);grid on,hold off [gm,pm,wcg,wcp]=margin(g0c)Kg=20*log10(gm)g1=feedback(g0c,1);bode(g1),grid on,[mag,phase,w]=bode(g1);a=find(mag<=0.707*mag(1));wb=w(a(1))max(mag)b=find(mag==max(mag))wr=w(b)10.5KK=40; Pm=50;ng0= KK *[1]; dg0=conv([1,0],conv([1,1],[1,4]));g0=tf(ng0,dg0) ;w=logspace(-2,4);[ngc,dgc]=fg_lead_pm(ng0,dg0,Pm,w)gc=tf(ngc,dgc),g0c=tf(g0*gc);b1=feedback(g0,1); b2=feedback(g0c,1);step(b1,'r--', b2,'b'); grid onfigure, bode(g0,'r--',g0c,'b',w), grid on,[gm,pm,wcg,wcp]=margin(g0c), Km=20*log10(gm)10.6KK=200; bp=0.3; ts=0.7; delta=0.05;ng0=[1];dg0=conv([1,0],conv([0.1,1],conv([0.02 1],conv([0.01,1],[0.005 1]))));g0=tf(ng0,dg0);w=logspace(-4,3);t=[0:0.1:3];[mag,phase]=bode(KK*g0,w);[gm0,pm0,wg0,wc0]=margin(mag,phase,w),gm0=20*log10(gm0)%gm0 = -15.6769%2、确定期望的开环传递函数mr=0.6+2.5*bp;wc=ceil((2+1.5*(mr-1)+2.5*(mr-1)^2)*pi/ts), h=(mr+1)/(mr-1)w1=2*wc/(h+1), w2=h*w1w1=wc/10; w2=25;ng1=[1/w1,1]; dg1=conv([1/w2,1],conv([1,0],[1,0]));g1=tf(ng1,dg1);g=polyval(ng1,j*wc)/polyval(dg1,j*wc); K=abs(1/g); %剪切频率处幅值为1,求K值g1=tf(K*g1)%3、确定反馈环节传递函数h=tf(dg1,ng1); Kh=1/K;h=tf(Kh*h) %期望频率特性的倒特性%4、验算性能指标g2=feedback(KK*g0,h); %校正后,系统的开环传递函数b1=feedback(KK*g0,1); b2=feedback(g2,1);bode(KK*g0,'r--',g2,'b',h,'g',w);grid onfigure,step(b1, 'r--',b2, 'b',t); grid on,[pos,tr,ts,tp]=stepchar(b2,delta)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
南京林业大学研究生试卷课程号 33351 课程名称 计算机仿真 20 16 ~20 17 学年第 1 学期 一、(20分)某系统的传递函数为)4)(3)(2)(14(143)(2++++++=S S S S S S S G 试用级联法、串联法和并联法中的两种画出系统模拟结构图,并列出相应的状态方程和输出方程。
自拟仿真,比较两者结果。
答:选用级联法和并联法写出传递函数,公式如下:)4(1)3(43)2()31()41()1(/6/4122/4113/4371/41/1/43)4)(3)(2)(14(143)(4324322+∙+∙++∙++=++++++=++++++=s s s s s s s s s s s s s s s s s s s s G分别画出级联法、并联法的系统模拟结构图及其状态方程和输出方程,图式如下:432342312432114143'''641224113437'x x x y x x x x x x x x x x u x ++====----=4434321321211443'33543'243'41'x y x x x x x x u x x x u x x u x =-=--+=-+=-=使用龙格—库塔法程序进行仿真,令u=1,系统在t=0-2s 之间(仿真步长0.1s )则输出y截图如下:比较后发现两者仿真结果接近。
二、(20分)已知系统的状态方程及输出方程 11231021232031233012332022022022x x x x x xx x x x x x x x x y x x x =+-=⎧⎪=-+=⎪⎨=+-+=⎪⎪=+-⎩拟用四阶龙格-库塔法求系统在t=0-2s 之间的输出值(仿真步长取0.01s 或0.1s ),试编写仿真程序,对仿真结果截图。
(单号C++,双号VB )答:用c++进行四阶龙格-库塔法,系统在t=0-2s间的(仿真步长0.01)编程:#include<iostream>#include<cstring>using namespace std;float x1;float x2;float x3;float x4;float t;float f1(float x1,float x2,float x3,float x4,float t){float f1;return f1=3*x1+2*x2-x3;}float f2(float x1,float x2,float x3,float x4,float t){float f2;return f2=2*x1-x2+2*x3;}float f3(float x1,float x2,float x3,float x4,float t){float f3;return f3=x1+2*x2-x3+2;}float f4(float x1,float x2,float x3,float x4,float t){float f4;return f4=0;}int main(){float k11,k12,k13,k14,k21,k22,k23,k24,k31,k32,k33,k34,k41,k42,k43,k44;float t=0,h=0.01;double y;float x1=0,x2=0,x3=0,x4=0;for(int i=1;i<200;i++){t=t+h;k11 = h * f1(x1, x2, x3, x4, t);k21 = h * f2(x1, x2, x3, x4, t);k31 = h * f3(x1, x2, x3, x4, t);k41 = h * f4(x1, x2, x3, x4, t);k12 = h * f1(x1 + k11 / 2, x2 + k21 / 2, x3 + k31 / 2, x4 + k41 / 2, t + h / 2);k22 = h * f2(x1 + k11 / 2, x2 + k21 / 2, x3 + k31 / 2, x4 + k41 / 2, t + h / 2);k32 = h * f3(x1 + k11 / 2, x2 + k21 / 2, x3 + k31 / 2, x4 + k41 / 2, t + h / 2);k42 = h * f4(x1 + k11 / 2, x2 + k21 / 2, x3 + k31 / 2, x4 + k41 / 2, t + h / 2);k13 = h * f1(x1 + k12 / 2, x2 + k22 / 2, x3 + k32 / 2, x4 + k42 / 2, t + h / 2);k23 = h * f2(x1 + k12 / 2, x2 + k22 / 2, x3 + k32 / 2, x4 + k42 / 2, t + h / 2);k33 = h * f3(x1 + k12 / 2, x2 + k22 / 2, x3 + k32 / 2, x4 + k42 / 2, t + h / 2);k43 = h * f4(x1 + k12 / 2, x2 + k22 / 2, x3 + k32 / 2, x4 + k42 / 2, t + h / 2);k14 = h * f1(x1 + k13, x2 + k23, x3 + k33, x4 + k43, t + h);k24 = h * f2(x1 + k13, x2 + k23, x3 + k33, x4 + k43, t + h);k34 = h * f3(x1 + k13, x2 + k23, x3 + k33, x4 + k43, t + h);k44 = h * f4(x1 + k13, x2 + k23, x3 + k33, x4 + k43, t + h);x1 = x1 + (k11 + 2 * k12 + 2 * k13 + k14) / 6;x2 = x2 + (k21 + 2 * k22 + 2 * k23 + k24) / 6;x3 = x3 + (k31 + 2 * k32 + 2 * k33 + k34) / 6;}y=x1+2*x2-2*x3;cout<<"y="<<y<<endl;return 0;}仿真结果截图如下:三、(20分)已知单位反馈系统的开环传递函数为()()()()34150+++=sssss G试用Z 域离散相似法和时域离散相似法进行仿真,编写仿真程序,对仿真结果截图。
(输出初态为0,输入为3,仿真步长为0.02S,100-200个周期)(单号VB ,双号C++)答:先将函数()()()()34150+++=s s s s s G 化成为:50(1)1+150()(4)(3)s+4s+3s s G s s s s s +==∙∙++ 画出系统结构图:使用z 域离散相似法计算得:3/))*3exp(1(*50*)()*3exp(*)()1(4/))*4exp(3(*)()1()*4exp(*)()1(*3)()1(t n x t n y n y t n w n w t n x n x tn w n w --+-=+-+-++-=++=+ 仿真程序如下:Private Sub Command1_Click() Dim n As Single Dim t As SingleDim w(200) As Single Dim x(200) As Single Dim z(200) As Single Dim y(200) As Single Dim u(200) As Single t = 0.02 y(0) = 0For n = 0 To 199w(n + 1) = w(n) + t * 3x(n + 1) = x(n) * Exp(-4 * t) + w(n + 1) - w(n) * (3 + Exp(-4 * t)) / 4 y(n + 1) = y(n) * Exp(-3 * t) + x(n) * 50 * (1 - Exp(-3 * t)) / 3 NextText1.Text = y(200) End Sub仿真结果截图如下:使用时域相似法计算得:3/))*3exp(1(*)(*50)(*)*3exp()1())*4exp(*25.025.0(*)3)(()*4exp(*)()1(3*)()1(T n x n y T n y T n w T n x n x T n w n w --+-=+--++-=++=+ 仿真程序如下:Private Sub Command1_Click() Dim w(2000) As Single Dim x(2000) As Single Dim y(2000) As Single Dim T As Single Dim n As SingleT = 0.02y(0) = 0For n = 0 To 199w(n + 1) = w(n) + T * 3x(n + 1) = x(n) * Exp(-4 * T) + (w(n) + 3) * (0.25 - 0.25 * Exp(-4 * T))y(n + 1) = Exp(-3 * T) * y(n) + 50 * x(n) * (1 - Exp(-3 * T)) / 3NextText1.Text = y(200)End Sub仿真结果截图如下:四、(20分)投掷硬币实验,至少投掷多少次,才能使正面朝上的频率在0.4-0.6之间的概率不小于0.9 ?试编写仿真程序,对仿真结果截图。
(仿真8000-12000次)答:(仿真12000次)程序如下:Private Sub Command1_Click()Dim a As SingleDim i As IntegerDim j As IntegerDim t As IntegerDim s As SingleFor j = 1 To 12000n = 0For i = 1 To 25r = Rnd()If r >= 0.5 Thenn = n + 1End IfNextIf 0.4 <= n / 25 <= 0.6 Thenm = m + 1End IfIf m / 25 >= 0.9 Thens = s + 1End IfNextText1.Text = sEnd Sub仿真结果截图如下:五、(20分)某自选市场,平均每分钟有6位顾客到来,每位顾客购物时间服从(4.2,7.2)分钟均布(不包括交费时间)。
