免疫算法的matlab代码
蚁群算法
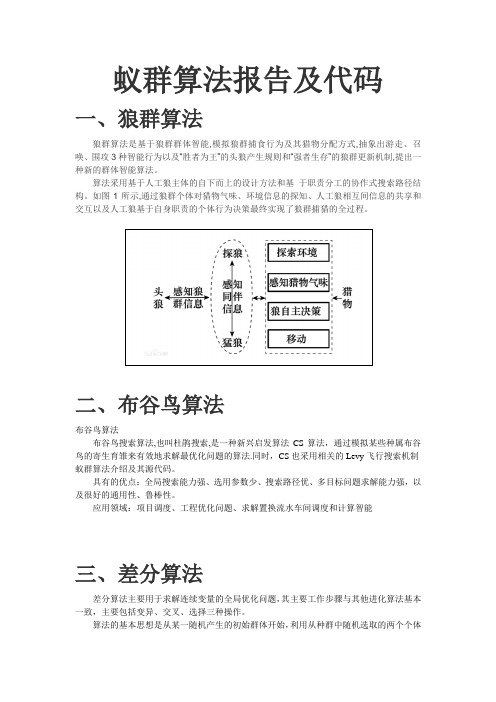
蚁群算法报告及代码一、狼群算法狼群算法是基于狼群群体智能,模拟狼群捕食行为及其猎物分配方式,抽象出游走、召唤、围攻3种智能行为以及“胜者为王”的头狼产生规则和“强者生存”的狼群更新机制,提出一种新的群体智能算法。
算法采用基于人工狼主体的自下而上的设计方法和基于职责分工的协作式搜索路径结构。
如图1所示,通过狼群个体对猎物气味、环境信息的探知、人工狼相互间信息的共享和交互以及人工狼基于自身职责的个体行为决策最终实现了狼群捕猎的全过程。
二、布谷鸟算法布谷鸟算法布谷鸟搜索算法,也叫杜鹃搜索,是一种新兴启发算法CS算法,通过模拟某些种属布谷鸟的寄生育雏来有效地求解最优化问题的算法.同时,CS也采用相关的Levy飞行搜索机制蚁群算法介绍及其源代码。
具有的优点:全局搜索能力强、选用参数少、搜索路径优、多目标问题求解能力强,以及很好的通用性、鲁棒性。
应用领域:项目调度、工程优化问题、求解置换流水车间调度和计算智能三、差分算法差分算法主要用于求解连续变量的全局优化问题,其主要工作步骤与其他进化算法基本一致,主要包括变异、交叉、选择三种操作。
算法的基本思想是从某一随机产生的初始群体开始,利用从种群中随机选取的两个个体的差向量作为第三个个体的随机变化源,将差向量加权后按照一定的规则与第三个个体求和而产生变异个体,该操作称为变异。
然后,变异个体与某个预先决定的目标个体进行参数混合,生成试验个体,这一过程称之为交叉。
如果试验个体的适应度值优于目标个体的适应度值,则在下一代中试验个体取代目标个体,否则目标个体仍保存下来,该操作称为选择。
在每一代的进化过程中,每一个体矢量作为目标个体一次,算法通过不断地迭代计算,保留优良个体,淘汰劣质个体,引导搜索过程向全局最优解逼近。
四、免疫算法免疫算法是一种具有生成+检测的迭代过程的搜索算法。
从理论上分析,迭代过程中,在保留上一代最佳个体的前提下,遗传算法是全局收敛的。
五、人工蜂群算法人工蜂群算法是模仿蜜蜂行为提出的一种优化方法,是集群智能思想的一个具体应用,它的主要特点是不需要了解问题的特殊信息,只需要对问题进行优劣的比较,通过各人工蜂个体的局部寻优行为,最终在群体中使全局最优值突现出来,有着较快的收敛速度。
免疫算法——精选推荐

免疫算法⽬录1选题依据和意义 (2)1.1研究背景及意义 (2)1.2免疫算法的概述 (2)1.3免疫算法的研究现状 (3)1.4物流配送中⼼选址的概述 (4)1.5物流配送中⼼的研究现状: (4)1.6论⽂组织结构 (5)2基本的免疫算法 (5)2.1免疫算法的相关概念介绍: (6)2.2免疫算法的步骤 (7)2.3免疫算法流程图: (8)2.4选择参数 (11)2.5免疫算法与遗传算法的⽐较: (12)3物流配送中⼼选址的数学模型的建⽴ (13)4免疫算法物流配送中⼼选址中的应⽤: (14)5实验: (15)5.1⼩结 (18)6总结与展望 (18)1选题依据和意义1.1研究背景及意义科技⽇新⽉异的发展的21世纪,学科之间的融合成为了各学者的研究新⽅向,各学科之间相互渗透、相互影响、相互作⽤成为了新世纪科技发展的新特征。
其中,由计算机科学与⽣命学科相互结合⽽产⽣的新型智能算法——免疫算法就是其中的代表之⼀。
近年来,随着我国经济的快速发展并逐渐⾛向全球化的道路,物流已成为了经济发展的重要产业之⼀,现如今各⼤城市都建设有⾃⼰的物流配送⽹络,这对于城市的招商引资,资源的优化配置,经济产业的运⾏效率都有着促进作⽤。
物流配送中⼼作为物流业重要的环节,其选址问题吸引着专家学者投⾝研究当中。
由于物流配送中⼼⼀旦选定并进⾏建设,其位置是固定的,所以在地址的选定上尤为重要。
相⽐较于传统的选址⽅法,免疫算法以其收敛速度快,鲁棒性强等特点,得到专家学者们的青睐。
免疫算法是模仿⽣物免疫机制,结合基因的进化机理,⼈⼯地构造出的⼀种新型智能搜索算法。
免疫算法具有⼀般免疫系统的特征,免疫算法采⽤群体搜索策略,⼀般遵循⼏个步骤”产⽣初始化种群→适应度的计算评价→种群间个体的选择、交叉、变异→产⽣新种群”。
通过这样的迭代计算,最终以较⼤的概率得到问题的最优解。
相⽐较于其他算法,免疫算法利⽤⾃⾝产⽣多样性和维持机制,保证了种群的多样性,克服了⼀般寻优过程中特别是多峰值的寻优过程中不可避免的“早熟”问题,求得全局最优解。
30个智能算法matlab代码

30个智能算法matlab代码以下是30个使用MATLAB编写的智能算法的示例代码: 1. 线性回归算法:matlab.x = [1, 2, 3, 4, 5];y = [2, 4, 6, 8, 10];coefficients = polyfit(x, y, 1);predicted_y = polyval(coefficients, x);2. 逻辑回归算法:matlab.x = [1, 2, 3, 4, 5];y = [0, 0, 1, 1, 1];model = fitglm(x, y, 'Distribution', 'binomial'); predicted_y = predict(model, x);3. 支持向量机算法:matlab.x = [1, 2, 3, 4, 5; 1, 2, 2, 3, 3];y = [1, 1, -1, -1, -1];model = fitcsvm(x', y');predicted_y = predict(model, x');4. 决策树算法:matlab.x = [1, 2, 3, 4, 5; 1, 2, 2, 3, 3]; y = [0, 0, 1, 1, 1];model = fitctree(x', y');predicted_y = predict(model, x');5. 随机森林算法:matlab.x = [1, 2, 3, 4, 5; 1, 2, 2, 3, 3]; y = [0, 0, 1, 1, 1];model = TreeBagger(50, x', y');predicted_y = predict(model, x');6. K均值聚类算法:matlab.x = [1, 2, 3, 10, 11, 12]; y = [1, 2, 3, 10, 11, 12]; data = [x', y'];idx = kmeans(data, 2);7. DBSCAN聚类算法:matlab.x = [1, 2, 3, 10, 11, 12]; y = [1, 2, 3, 10, 11, 12]; data = [x', y'];epsilon = 2;minPts = 2;[idx, corePoints] = dbscan(data, epsilon, minPts);8. 神经网络算法:matlab.x = [1, 2, 3, 4, 5];y = [0, 0, 1, 1, 1];net = feedforwardnet(10);net = train(net, x', y');predicted_y = net(x');9. 遗传算法:matlab.fitnessFunction = @(x) x^2 4x + 4;nvars = 1;lb = 0;ub = 5;options = gaoptimset('PlotFcns', @gaplotbestf);[x, fval] = ga(fitnessFunction, nvars, [], [], [], [], lb, ub, [], options);10. 粒子群优化算法:matlab.fitnessFunction = @(x) x^2 4x + 4;nvars = 1;lb = 0;ub = 5;options = optimoptions('particleswarm', 'PlotFcn',@pswplotbestf);[x, fval] = particleswarm(fitnessFunction, nvars, lb, ub, options);11. 蚁群算法:matlab.distanceMatrix = [0, 2, 3; 2, 0, 4; 3, 4, 0];pheromoneMatrix = ones(3, 3);alpha = 1;beta = 1;iterations = 10;bestPath = antColonyOptimization(distanceMatrix, pheromoneMatrix, alpha, beta, iterations);12. 粒子群-蚁群混合算法:matlab.distanceMatrix = [0, 2, 3; 2, 0, 4; 3, 4, 0];pheromoneMatrix = ones(3, 3);alpha = 1;beta = 1;iterations = 10;bestPath = particleAntHybrid(distanceMatrix, pheromoneMatrix, alpha, beta, iterations);13. 遗传算法-粒子群混合算法:matlab.fitnessFunction = @(x) x^2 4x + 4;nvars = 1;lb = 0;ub = 5;gaOptions = gaoptimset('PlotFcns', @gaplotbestf);psOptions = optimoptions('particleswarm', 'PlotFcn',@pswplotbestf);[x, fval] = gaParticleHybrid(fitnessFunction, nvars, lb, ub, gaOptions, psOptions);14. K近邻算法:matlab.x = [1, 2, 3, 4, 5; 1, 2, 2, 3, 3]; y = [0, 0, 1, 1, 1];model = fitcknn(x', y');predicted_y = predict(model, x');15. 朴素贝叶斯算法:matlab.x = [1, 2, 3, 4, 5; 1, 2, 2, 3, 3]; y = [0, 0, 1, 1, 1];model = fitcnb(x', y');predicted_y = predict(model, x');16. AdaBoost算法:matlab.x = [1, 2, 3, 4, 5; 1, 2, 2, 3, 3];y = [0, 0, 1, 1, 1];model = fitensemble(x', y', 'AdaBoostM1', 100, 'Tree'); predicted_y = predict(model, x');17. 高斯混合模型算法:matlab.x = [1, 2, 3, 4, 5]';y = [0, 0, 1, 1, 1]';data = [x, y];model = fitgmdist(data, 2);idx = cluster(model, data);18. 主成分分析算法:matlab.x = [1, 2, 3, 4, 5; 1, 2, 2, 3, 3]; coefficients = pca(x');transformed_x = x' coefficients;19. 独立成分分析算法:matlab.x = [1, 2, 3, 4, 5; 1, 2, 2, 3, 3]; coefficients = fastica(x');transformed_x = x' coefficients;20. 模糊C均值聚类算法:matlab.x = [1, 2, 3, 4, 5; 1, 2, 2, 3, 3]; options = [2, 100, 1e-5, 0];[centers, U] = fcm(x', 2, options);21. 遗传规划算法:matlab.fitnessFunction = @(x) x^2 4x + 4; nvars = 1;lb = 0;ub = 5;options = optimoptions('ga', 'PlotFcn', @gaplotbestf);[x, fval] = ga(fitnessFunction, nvars, [], [], [], [], lb, ub, [], options);22. 线性规划算法:matlab.f = [-5; -4];A = [1, 2; 3, 1];b = [8; 6];lb = [0; 0];ub = [];[x, fval] = linprog(f, A, b, [], [], lb, ub);23. 整数规划算法:matlab.f = [-5; -4];A = [1, 2; 3, 1];b = [8; 6];intcon = [1, 2];[x, fval] = intlinprog(f, intcon, A, b);24. 图像分割算法:matlab.image = imread('image.jpg');grayImage = rgb2gray(image);binaryImage = imbinarize(grayImage);segmented = medfilt2(binaryImage);25. 文本分类算法:matlab.documents = ["This is a document.", "Another document.", "Yet another document."];labels = categorical(["Class 1", "Class 2", "Class 1"]);model = trainTextClassifier(documents, labels);newDocuments = ["A new document.", "Another new document."];predictedLabels = classifyText(model, newDocuments);26. 图像识别算法:matlab.image = imread('image.jpg');features = extractFeatures(image);model = trainImageClassifier(features, labels);newImage = imread('new_image.jpg');newFeatures = extractFeatures(newImage);predictedLabel = classifyImage(model, newFeatures);27. 时间序列预测算法:matlab.data = [1, 2, 3, 4, 5];model = arima(2, 1, 1);model = estimate(model, data);forecastedData = forecast(model, 5);28. 关联规则挖掘算法:matlab.data = readtable('data.csv');rules = associationRules(data, 'Support', 0.1);29. 增强学习算法:matlab.environment = rlPredefinedEnv('Pendulum');agent = rlDDPGAgent(environment);train(agent);30. 马尔可夫决策过程算法:matlab.states = [1, 2, 3];actions = [1, 2];transitionMatrix = [0.8, 0.1, 0.1; 0.2, 0.6, 0.2; 0.3, 0.3, 0.4];rewardMatrix = [1, 0, -1; -1, 1, 0; 0, -1, 1];policy = mdpPolicyIteration(transitionMatrix, rewardMatrix);以上是30个使用MATLAB编写的智能算法的示例代码,每个算法都可以根据具体的问题和数据进行相应的调整和优化。
免疫算法matlab程序解析

免疫算法matlab程序这是免疫算法。
这个算法几乎与遗传算法一样,只是多用了一个免疫函数免疫算法是遗传算法的变体,它不用杂交,而是采用注入疫苗的方法。
疫苗是优秀染色体中的一段基因,把疫苗接种到其它染色体中。
注意:标准遗传算法的一个重要概念是,染色体是可能解的2进制顺序号,由这个序号在可能解的集合(解空间中找到可能解。
这是免疫算法的主程序,它需要调用的函数如下。
接种疫苗函数:%fun cti onino culateChromosome=im mun ity(chromosomeGroup,bacteri nChromosome,paramet er%parameter:1随机制取染色体接种。
2,每个染色体都接种。
3,每个染色体都接种,但接种的位置是随机的%这个函数实现对染色体的疫苗接种%由染色体(可能解的2进制顺序号找到可能解:%x=chromosome_x(fatherChromosomeGroup, on eDime nsion Set,soluti on Sum;把解代入非线性方程组计算误差函数:fun ctio nError= non Li nearSumError1(x;判定程是否得解函数:[solution,isTrue]=isSolution(x,funtionError,solutionSumError; % 选择最优染色体函数:%[bestChromosome,leastF un cti on Error]=best_worstChromosome(fatherChromoso m eGroup,fu nctio nError;%误差比较函数:从两个染色体中,选出误差较小的染色体%[holdBestChromosome,holdLeastF un ctio nError]...% =compareBestChromosome(holdBestChromosome,holdLeastF un ctio nError,... %bestChromosome,leastFuntion Error%为染色体定义概率函数,好的染色体概率高,坏染色体概率低%p=chromosomeProbability(fu nctio nError;%按概率选择染色体函数:%slecteChromosomeGroup=selecteChromome(fatherChromosomeGroup,p;%父代染色体杂交产生子代染色体函数%son ChrmosomeGroup=crossChromosome(slecteChromosomeGroup,2;%防止染色体超出解空间的函数%chromosomeGroup=checkSeque nce(chromosomeGroup,soluti on Sum%变异函数%fatherChromosomeGroup=varia nceCh(s on ChromosomeGroup,0.8,solutio nN;通过实验有如下结果:%1。
应用CUDA加速免疫算法——Jacket与Matlab实现

/■■■聚 f 斓 蝴 )
■_ ■、 嘲 瞬
\~——/
\0— — /
图 1 NVl A Dl CUDA 系 统 框 架
④ 计算③ 中所抽取 的子集每个 个体 与抗 原之间的相似程度 , 算 硬 件 引擎 意 外 , 包 含 了 一 个 C A 集 成 开 发 环 境 , 许 程 序 员 即 还 UD 允 抗 原 亲 和 度 。根 据 抗 原 模 式 的 数 目返 回③ 循 环 。 使 用 C语 言 进 行 基 于 GP 的 通 用 运 算 目的 程 序开 发 , 化 G U编 U 简 P ⑤ 根据预 先设定 的亲和度阀值和④计算所得结果选取最佳亲和 程 难 度 , 高 开 发 效 率 。 提 度 子集 。 3 使 用 J C E 加 速 免疫 算 法 在 MA L B 中 的运 行 A K T TA ⑥调整⑤ 所得到的子集 ,主要依据为④ 的结果或者子集之间的
应用 CU A加速免疫算法——J c e 与 Mal D a kt t b实现 a
覃 涛 ( 贵州大学电气 工程学 院’
摘 要 : 为 继 遗 传 算 法 后 新兴 的一 种 人 工 智 能 算 法— — 免疫 算 法 最 近 几 的 一种 并 行 计 算 通 用 设备 架构 。 与 以往 数据 必须 打 包 成 矢量 才能 处 作
关键 词 : 疫 算 法 C A GUP MAT AB i k t 的形 式 将 数据 宽度 隐藏 起 来 。 支 持数 以千 计 的 线程 同时
运行 , 时 , 这 内存 延 迟 对性 能 的影 响 就 不 再那 么 明显 了 。CU A极 大 D
境 下 的 问题 , 就 是 人 工 免疫 系统 。 这
基于人工免疫克隆选择算法的调度优化MATLAB源码

基于人工免疫克隆选择算法的调度优化MATLAB源码人工免疫克隆选择算法是一种比较新型的智能算法,其基本算法结构与遗传算法是类似的,以下源码是为网络节点分组调度问题而设计的算法。
function[BestX,BestY,AllABfarm,LC1,LC2]=AIA2(M,N,Ns,Ncm,Nr,Pd,alpha,beta,K,Cx,Cy,r,Sx,S y)%% 网络节点分组调度的人工免疫优化算法通用Matlab程序%% 输入参数列表% M------------人工免疫优化算法迭代次数% N------------抗体群的规模% Ns-----------免疫选择算子中选中的抗体个数% Ncm----------克隆变异算子中产生的新抗体的个数% Nr-----------抑制操作中保留下来的抗体个数% Pd-----------变异程度控制参数,取值0~1,越大变异越厉害% alpha--------亲和度加权系数,用于激励度的计算% beta---------浓度加权系数,用于激励度的计算% K------------调度分组的个数% Cx-----------节点的横坐标,1×n的向量% Cy-----------节点的纵坐标,1×n的向量% r------------节点的感知半径,1×n的向量% Sx-----------质点的横坐标,1×m的向量% Sy-----------质点的纵坐标,1×m的向量%% 输出参数列表% BestX--------最优调度方案% BestY--------最优调度对应的平均覆盖率% AllABfarm----历史上所有抗体群的集合,M×1的细胞结构% LC1----------最优抗体亲和度的收敛曲线,M×1% LC2----------抗体群平均亲和度的收敛曲线,M×1%% -----------------------初始化----------------------------------n=length(Cx);LC1=zeros(M,1);LC2=zeros(M,1);AllABfarm=cell(M,1);%控制参数初始化mm=1;%迭代计数器%调用子函数,抗体群初始化ABfarm=AntiBodyInitial(N,n,K);%% -----------------------迭代过程--------------------------------- while mm<=M%设置停止条件%调用子函数,计算抗体群亲和度aff=Affinity(ABfarm,K,Cx,Cy,r,Sx,Sy);%记录收敛曲线maxaff=max(aff);meanaff=mean(aff);LC1(mm)=maxaff;LC2(mm)=meanaff;pos=find(aff==maxaff);BestPos=pos(1);BestX=ABfarm(BestPos,:);BestY=maxaff;AllABfarm{mm}=ABfarm;%调用子函数,计算抗体浓度den=Density(ABfarm);%调用子函数,计算抗体激励度sim=SumUp(aff,den,alpha,beta);%调用子函数,免疫选择算子ABfarmS=Select(ABfarm,sim,Ns);%精英抗体保护ABfarmS(1,:)=BestX;%调用子函数,克隆变异算子ABfarmCM=CloneMutation(ABfarmS,Ncm,Pd,K);%调用子函数,抑制刷新算子ABfarm=RepresRenewal(ABfarmS,ABfarmCM,Nr,N,K,Cx,Cy,r,Sx,Sy);disp(mm);mm=mm+1;end。
免疫算法基本流程 -回复

免疫算法基本流程 -回复免疫算法(Immune Algorithm,IA)是仿生学领域的一种元启发式算法,它模仿人类免疫系统的功能,用于解决复杂问题的优化问题。
其基本流程包括问题建模、个体编码、种群初始化、克隆操作、变异操作、选择操作等,接下来本文将从这些方面进一步展开详细描述。
一、问题建模在使用免疫算法解决优化问题之前,需要将问题进行合理的建模。
建模过程主要涉及问题的因素、目标和约束条件等问题,例如在TSP(Traveling Salesman Problem)中,需要定义地图中所有城市之间的距离以及行走路线的长度等因素。
建模完成后,将其转化为适合于免疫算法处理的数学表示形式,这有助于优化算法的精度和效率。
二、个体编码从问题建模后,需要将问题的变量转化为适合免疫算法处理的个体编码,即将问题的解转化成一些序列或数值,这样才能进行算法的操作。
对于不同的问题,需要设计合适的编码方式,例如对于TSP问题,可以将城市序列编码成01字符串等。
三、种群初始化在免疫算法中,需要构建一个种群,种群中的每个个体代表了问题的一个解。
种群初始化是在搜索空间中随机生成一组解,并且保证这些解满足约束条件。
种群大小需要根据问题规模和计算能力来合理安排,一般情况下,种群大小越大,搜索空间越大,但是计算成本也越高。
四、克隆操作在免疫算法中,克隆操作是其中一个重要的基因变异操作。
该操作的目的是产生大量近似于当前最优的个体,增加搜索空间的多样性。
克隆操作的流程如下:1.计算适应度函数值,根据适应度函数值进行排序。
2.选择适应度函数值最优的一部分个体进行克隆操作。
3.对克隆个体进行加密操作,增加其多样性。
5、变异操作变异操作是免疫算法中的一个基本操作,其目的是使部分克隆个体产生和原个体不同的搜索方向,增加搜索空间的变异性。
在变异操作中,采用随机、局部搜索或任意搜索等方法来对某些个体进行改变其参数或某些属性,以期望产生一些新的解。
变异操作的流程如下:1.从克隆群体中随机选择一定数量的个体进行变异操作。
免疫算法公式

免疫算法公式免疫算法是一种新型的优化算法,其基本思想是模拟生物体免疫系统对外界刺激的反应过程,以实现优化问题的求解。
免疫算法涉及到一些基本的公式,包括:1. 抗体与抗原的亲和度计算公式亲和度是指抗体与抗原之间相互作用的强度,通常使用欧几里得距离或哈密顿距离来计算。
欧几里得距离公式如下:$d(x,y)=sqrt{(x_1-y_1)^2+(x_2-y_2)^2+...+(x_n-y_n)^2}$ 其中,$x$和$y$代表两个向量,$n$代表向量维数。
2. 抗体的亲和力更新公式抗体的亲和力可以通过适当的更新策略来调整,以达到最优解。
典型的更新公式包括:$aff_j=aff_j+alphacdot(aff_i-aff_j)$其中,$aff_i$和$aff_j$分别代表两个抗体的亲和力值,$alpha$是调整因子。
3. 克隆选择算子公式克隆选择算子是免疫算法中的核心操作,它通过复制和选择策略来增加优秀抗体的数量。
克隆选择算子的基本公式如下:$n_i=frac{p_i}{sum_{j=1}^Np_j}$其中,$n_i$代表第$i$个抗体的克隆数量,$p_i$代表抗体$i$的适应度值,$N$代表总抗体数量。
4. 基因重组算子公式基因重组算子是免疫算法的另一个重要操作,它通过随机交换抗体基因的方式来产生新的解。
基因重组算子的公式如下:$x_k=left{begin{aligned}&x_{i,k},&rand()<p_c&x_{j,k},&rand( )>=p_cend{aligned}right.$其中,$x_{i,k}$和$x_{j,k}$分别代表两个抗体在第$k$个基因位置的取值,$p_c$是交叉概率,$rand()$是一个均匀分布的随机数。
以上是免疫算法中一些常用的公式,它们在免疫算法的求解过程中起到非常重要的作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
免疫算法的matlab代码
免疫算法是一种受到生物免疫系统启发的优化算法。
它模拟了生物免疫系统中的免疫记忆、克隆和选择等机制,用于解决各种优化问题。
本文将介绍免疫算法的基本原理和在优化问题中的应用。
免疫系统是人体内的一种重要防御系统,能够识别和消灭入侵的病原体。
免疫系统通过记忆机制来不断学习和适应外界环境,以更好地应对未来的攻击。
免疫算法的设计思想就是基于这种免疫系统的工作原理。
免疫算法的基本流程如下:
1. 初始化种群:随机生成一定数量的个体作为初始解。
2. 免疫选择:根据个体适应度函数,选择一部分表现优秀的个体作为免疫细胞。
3. 免疫记忆:根据免疫细胞的特征,生成一定数量的克隆个体,并引入变异操作增加种群的多样性。
4. 竞争选择:根据克隆个体的适应度函数,选择一部分表现优秀的个体作为下一代种群。
5. 终止条件判断:判断是否满足终止条件,如达到最大迭代次数或找到满意的解。
6. 输出结果:输出最优解或近似最优解。
免疫算法在优化问题中的应用非常广泛。
例如,在函数优化问题中,免疫算法可以用于寻找全局最优解;在组合优化问题中,免疫算法
可以用于求解旅行商问题和背包问题等;在机器学习中,免疫算法可以用于特征选择和模型优化等。
免疫算法是一种有效的优化算法,通过模拟生物免疫系统的工作原理,能够在解决各种优化问题时发挥重要作用。
未来,随着对免疫系统的更深入研究,免疫算法还将不断发展和改进,为各行各业的优化问题提供更好的解决方案。
