(苏明义)高考易错题解析1-2
江苏省常州市高考数学易错解答题含解析

江苏省常州市高考数学易错解答题解答题含答案有解析 1.选修4-5:不等式选讲 已知函数11()22f x x x =-++,M 为不等式()2f x <的解集. (Ⅰ)求M ;(Ⅱ)证明:当a ,b M ∈时,1a b ab +<+.2.如图,在四棱锥 P ABCD -中,底面ABCD 是矩形,PA ⊥底面ABCD ,E 是PC 的中点, 已知2AB =, 22AD =,2PA =,求:(1)直线PC 与平面 PAD 所成角的正切值; (2)三棱锥 P ABE -的体积.3.眉山市位于四川西南,有“千载诗书城,人文第一州”的美誉,这里是大文豪苏轼、苏洵、苏辙的故乡,也是人们旅游的好地方.在今年的国庆黄金周,为了丰富游客的文化生活,每天在东坡故里三苏祠举行“三苏文化”知识竞赛.已知甲、乙两队参赛,每队3人,每人回答一个问题,答对者为本队赢得一分,答错得零分.假设甲队中每人答对的概率均为23,乙队中3人答对的概率分别为23,23,12,且各人回答正确与否相互之间没有影响.(1)分别求甲队总得分为0分;2分的概率; (2)求甲队得2分乙队得1分的概率.4.已知圆C 过点(1,4),(3,2)P Q ,且圆心C 在直线30x y +-=上. (1)求圆C 的标准方程;(2)若过点(2,3)的直线l 被圆C 所截得的弦MN 的长是23l 的方程. 5.已知等差数列{}n a 的前n 项和为n S ,且246a a +=,63a S =. (1)求{}n a 的通项公式;(2)若*k N ∈,且k a ,3k a ,2k S 成等比数列,求k 的值.6.从半径为1的半圆出发,以此向内、向外连续作半圆,且后一个半圆的直径为前一个半圆的半径,如此下去,可得到无数个半圆.(1)求出所有这些半圆围城的封闭图形的周长; (2)求出所有这些半圆围城的封闭图形的面积.7.已知数列{}n a 的前n 项和为n S ,且20S =,()*2n n S n na n N +=∈.(1)试写出数列{}n a 的任意前后两项(即n a 、1n a +)构成的等式; (2)用数学归纳法证明:()*23n a n n N=-∈.8.已知数列{}n a 为递增的等差数列,11a =,且2381a a a +,,成等比数列.数列{}nb 的前n 项和为n S ,且满足21n n S b =-.(1)求{}n a ,{}n b 的通项公式;(2)令2n n n c a b =,求{}n c 的前n 项和n T . 9.数列{}n a 满足:11232n n a a a +==+,. (1)求证:{}1n a +为等比数列; (2)求{}n a 的通项公式.10.如图,ABCD 是正方形,O 是正方形的中心,PO ⊥底面,ABCD E 是PC 的中点.(1)求证:BD ⊥平面PAC ; (2)若2,6AB PB ==求三棱锥B CDE -的体积.11.已知向量5cos ,5a θ⎛⎫= ⎪⎝⎭,25sin ,5b θ⎛⎫= ⎪⎝⎭ (1)若//a b ,求sin cos sin cos θθθθ+-;(2)若a b ⊥,求tan θ.12.近年来,我国自主研发的长征系列火箭的频频发射成功,标志着我国在该领域已逐步达到世界一流水平.火箭推进剂的质量为M ,去除推进剂后的火箭有效载荷质量为m ,火箭的飞行速度为v ,初始速度为0v ,已知其关系式为齐奥尔科夫斯基公式:0ln 1M v v w m ⎛⎫=+⋅+ ⎪⎝⎭,其中w 是火箭发动机喷流相对火箭的速度,假设00v =,3(/)w km s =,25()m t =,ln x 是以e 为底的自然对数, 2.71828e ≈,7.911.216.733313.916,41.82,261.56eee≈≈≈.(1)如果希望火箭飞行速度v 分别达到第一宇宙速度()7.9/km s 、第二宇宙速度()11.2/km s 、第三宇宙速度()16.7/km s 时,求M 的值(精确到小数点后面1位).(2)如果希望v 达到()16.7/km s ,但火箭起飞质量最大值为()2000t ,请问w 的最小值为多少(精确到小数点后面1位)?由此指出其实际意义.13.某网站推出了关于扫黑除恶情况的调查,调查数据表明,扫黑除恶仍是百姓最为关心的热点,参与调查者中关注此问题的约占80%.现从参与关注扫黑除恶的人群中随机选出200人,并将这200人按年龄分组:第1组[)15,25,第2组[)25,35,第3组[)35,45,第4组[)45,55,第5组[)55,65,得到的频率分布直方图如图所示.(1)求出a 的值;(2)求这200人年龄的样本平均数(同一组数据用该区间的中点值作代表)和中位数(精确到小数点后一位). 14.某班在一次个人投篮比赛中,记录了在规定时间内投进n 个球的人数分布情况: 进球数n (个)1 2 3 4 5 投进n 个球的人数(人)1 272其中3n =和4n =对应的数据不小心丢失了,已知进球3个或3个以上,人均投进4个球;进球5个或5个以下,人均投进2.5个球.(1)投进3个球和4个球的分别有多少人?(2)从进球数为3,4,5的所有人中任取2人,求这2人进球数之和为8的概率.15.已知两个不共线的向量a ,b 满足a =,(cos ,sin )b =θθ,R θ∈.(1)若//a b ,求角θ的值;(2)若2a b -与7a b -垂直,求||a b +的值;(3)当0,2π⎡⎤θ∈⎢⎥⎣⎦时,存在两个不同的θ使得||||a ma +=成立,求正数m 的取值范围.16.已知3sin 5θ=,02πθ<<. (1)求tan θ的值; (2)求2sin cos sin 2cos θθθθ-+的值.17.锐角ABC ∆的内角A 、B 、C 所对的边分别为a 、b 、c ,若cos cos sin 3b Cc B a A +=. (1)求A ;(2)若ABC S ∆=a =ABC 的周长.18.已知圆C 的半径是2,圆心为()3,3. (1)求圆C 的方程;(2)若点P 是圆C 上的动点,点Q 在x 轴上,PQ 的最大值等于7,求点Q 的坐标. 19.(6分)已知(1,3),(3,),(1,),//AB BC m CD n AD BC =-==. (1)求实数n 的值;(2)若AC BD ⊥,求实数m 的值.20.(6分)正方体1111ABCD A B C D -的棱长为,a 点,E F 分别是棱1111,B C C D 的中点 (1)证明:四边形BDFE 是一个梯形: (2)求几何体1BCD EC F -的表面积和体积21.(6分)已知数列{}n a 的前n 项和为n S ,满足21n n S a =-,*n N ∈,数列{}n b 满足1(1)(1)n n nb n b n n +-+=+,*n N ∈,且11b =.(1)求数列{}n a 的通项公式; (2)求证:数列n b n ⎧⎫⎨⎬⎩⎭是等差数列,求数列{}n b 的通项公式;(3)若n n n c a b =⋅,数列{}n c 的前n项和为n T ,对任意的*n N ∈,都有2n n T nS a a ≤++,求实数a的取值范围.22.(8分)已知,a b 夹角为,且4a =,2b =,求:(1)a b +; (2)a 与a b +的夹角.23.(8分)在△ABC 中,内角A 、B 、C 所对的边分别为a 、b 、c ,1b =,sin sin sin sin a b c Cb A B C-+=+-. (1)若2A B =,求△ABC 的周长; (2)若CD 为AB 边上的中线,且3CD =,求△ABC 的面积.24.(10分)已知数列{}n a 前n 项和为n S , 12a =-,且满足1112n n S a n +=++(*n N ∈). (Ⅰ)求数列{}n a 的通项公式;(Ⅱ)若()3log 1n n b a =-+,设数列21n n b b +⎧⎫⎨⎬⎩⎭前n 项和为n T ,求证: 34n T <.25.(10分)已知三棱柱111A B C ABC -中,三个侧面均为矩形,底面ABC 为等腰直角三角形,12C C CA CB ===,点D 为棱1CC 的中点,点E 在棱11B C 上运动.(1)求证1A C ⊥AE ;(2)当点E 运动到某一位置时,恰好使二面角1E A D B --6E 到平面1A BD 的距离;(3)在(2)的条件下,试确定线段AC 上是否存在一点F ,使得EF ⊥平面1A DB ?若存在,确定其位置;若不存在,说明理由.26.(12分)在三棱柱111ABC A B C -中,1CC ⊥平面ABC ,AC BC ⊥,AC BC =,D ,E 分别为AB ,11A B 中点.(Ⅰ)求证:AC ⊥平面11BB C C ; (Ⅱ)求证:四边形1CC ED 为平行四边形; (Ⅲ)求证:平面1ABC ⊥平面1CC ED .27.(12分)已知函数2()(2cos )cos(2)f x a x x θ=++为奇函数,且()04f π=,其中a R ∈,(0,)θπ∈.(1)求a ,θ的值. (2)若2()45f α=-,(,)2παπ∈,求sin()3πα+的值.28.某工厂新研发了一种产品,该产品每件成本为5元,将该产品按事先拟定的价格进行销售,得到如下数据:单价x (元) 8 8.2 8.4 8.6 8.8 9 销量y (件)90 8483807568(1)求销量y (件)关于单价x (元)的线性回归方程y bx a =+; (2)若单价定为10元,估计销量为多少件;(3)根据销量y 关于单价x 的线性回归方程,要使利润P 最大,应将价格定为多少?参考公式:1221ni ii ni i x y nx yb x nx==-=-∑∑,a y bx =-.参考数据:614066i ii x y==∑,621434.2i i x ==∑29.设向量()()()sin ,2cos 2sin cos 2cos sin a b c ααββββ===-,,,,. (Ⅰ)若a 与2b c -垂直,求()tan αβ-的值; (Ⅱ)求b c -的最小值.30.如右图,某货轮在A 处看灯塔B 在货轮的北偏东75°,距离为126,在A 处看灯塔C 在货轮的北偏西30°,距离为83,货轮由A 处向正北航行到D 处时,再看灯塔B 在北偏东120°,求:(1)A 处与D 处的距离; (2)灯塔C 与D 处的距离.参考答案解答题含答案有解析1.(Ⅰ){|11}M x x =-<<;(Ⅱ)详见解析. 【解析】试题分析:(I )先去掉绝对值,再分12x ≤-,1122x -<<和12x ≥三种情况解不等式,即可得M ;(II )采用平方作差法,再进行因式分解,进而可证当a ,b ∈M 时,1a b ab +<+.试题解析:(I )12,,211(){1,,2212,.2x x f x x x x -≤-=-<<≥当12x ≤-时,由()2f x <得22,x -<解得1x >-; 当1122x -<<时,()2f x <;当12x ≥时,由()2f x <得22,x <解得1x <.所以()2f x <的解集{|11}M x x =-<<.(Ⅱ)由(Ⅰ)知,当,a b M ∈时,11,11a b -<<-<<,从而22222222()(1)1(1)(1)0a b ab a b a b a b +-+=+--=--<,因此1.a b ab +<+【考点】绝对值不等式,不等式的证明.【名师点睛】形如x a x b c -+-≥(或c ≤)型的不等式主要有两种解法:(1)分段讨论法:利用绝对值号内式子对应的方程的根,将数轴分为(,]a -∞,(,]a b ,(,)b +∞(此处设a b <)三个部分,在每个部分去掉绝对值号并分别列出对应的不等式进行求解,然后取各个不等式解集的并集.(2)图象法:作出函数1y x a x b =-+-和2y c =的图象,结合图象求解. 2.(1)33;(2)22 【解析】 【分析】(1)要求直线PC 与平面PAD 所成角的正切值,先要找到直线PC 在平面PAD 上的射影,即在直线PC 上找一点作平面PAD 的垂线,结合已知与图形,转化为证明CD ⊥平面PAD 再求解;(2)三棱锥的体积计算在于选取合适的底和高,此题以PAB 为底,E 与PB 的中点H 的连线HE 为高计算更为快速,从而转化为证明EH ⊥平面PAB 再求解. 【详解】(1)PA ⊥平面ABCD ,CD ⊥平面ABCD CD PA ∴⊥ 又CD AD ⊥,PA AD A ⋂=,PA ⊂平面PAD ,AD ⊂平面PAD 所以CD ⊥平面PAD ,所以CPD ∠为直线PC 与平面PAD 所成角。
(易错题)高中数学选修1-2第三章《推理与证明》检测(答案解析)(1)

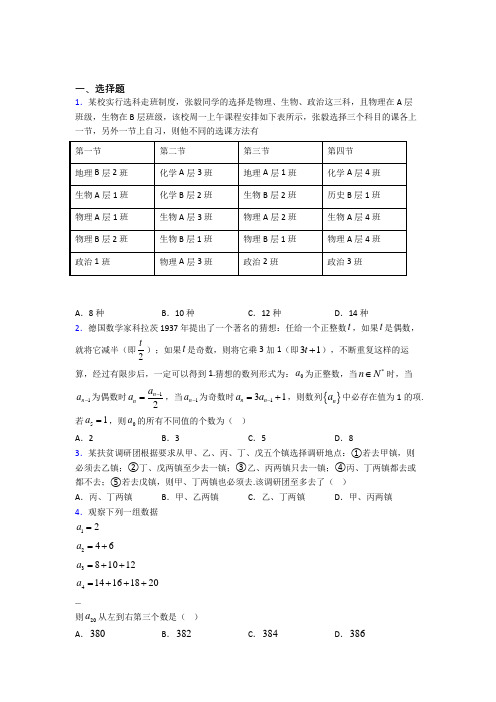
一、选择题1.某校实行选科走班制度,张毅同学的选择是物理、生物、政治这三科,且物理在A 层班级,生物在B 层班级,该校周一上午课程安排如下表所示,张毅选择三个科目的课各上一节,另外一节上自习,则他不同的选课方法有A .8种B .10种C .12种D .14种2.我国古代数学名著《九章算术》的论割圆术中有:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周盒体而无所失矣.”它体现了一种无限与有限的转化过程.比如在表达式11+11+1+...中“…”即代表无限次重复,但原式却是个定值,它可以通过方程11x x +=,求得12x +==( )A .2B .1C .2-D .1-3.天干地支纪年法源于中国,包含十天干与十二地支,十天干即甲、乙、丙、丁、戊、己、庚、辛、壬、癸,十二地支即子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥天干地支纪年法是按顺序以一个天干和一个地支相配,排列起来,天干在前,地支在后,天干由“甲”起,地支由“子”起,比如说第一年为“甲子”,第二年为“乙丑”,第三年为“丙寅”……依此类推,排列到“癸酉”后,天干回到“甲”重新开始,即“甲戌”,“乙亥”,……依此类推.已知一个“甲子”为60年,即天干地支纪年法的一个周期,1949年为“己丑”年,那么到新中国成立80周年时,即2029年为( ) A .己申年B .己酉年C .庚酉年D .庚申年4.观察下列一组数据12a = 246a =+ 381012a =++414161820a =+++…则20a 从左到右第三个数是( ) A .380B .382C .384D .3865.学生的语文、数学成绩均被评定为三个等级,依次为“优秀”“合格”“不合格”.若学生甲的语文、数学成绩都不低于学生乙,且其中至少有一门成绩高于乙,则称“学生甲比学生乙成绩好”.如果一组学生中没有哪位学生比另一位学生成绩好,并且不存在语文成绩相同、数学成绩也相同的两位学生,那么这组学生最多有( ) A .2人B .3人C .4人D .5人6.“克拉茨猜想”又称“31n +猜想”,是德国数学家洛萨·克拉茨在1950年世界数学家大会上公布的一个猜想:任给一个正整数n ,如果n 是偶数,就将它减半;如果n 为奇数就将它乘3加1,不断重复这样的运算,经过有限步后,最终都能够得到1,已知正整数m 经过6次运算后才得到1,则m 的值为( ) A .5或32B .10C .64D .10或647.在等差数列{}n a 中,若0n a >,公差0d ≠,则有2415a a a a >.类比上述性质,在等比数列{}n b 中,若0n b >,公比1q ≠,则关于3b ,5b ,2b ,6b 的一个不等关系正确的是( ) A .3526b b b b > B .5623b b b b > C .3526b b b b +<+D .5623b b b b +<+8.观察下列各式:5678953125,515625,578125,5390625,51953125,=====,则20205的末四位数字为( ) A .3125B .5625C .0625D .81259.祖暅(公元前5~6世纪)是我国齐梁时代的数学家,是祖冲之的儿子,他提出了一条原原理:“幂势既同,则积不容异.”这里的“幂”指水平截面的面积,“势”指高.这句话的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体体积相等.设由椭圆22221(0)x y a b a b+=>> 所围成的平面图形绕y 轴旋转一周后,得一橄榄状的几何体(称为椭球体),课本中介绍了应用祖暅原理求球体体积公式的做法,请类比此法,求出椭球体体积,其体积等于( ) A .243a b π B .243ab π C .22a b πD .22ab π10.已知平面直角坐标系内曲线()1:,0C F x y =,曲线()200:(,),0C F x y F x y -=,若点()00,P x y 不在曲线1C 上,则下列说法正确的是( ) A .曲线1C 与2C 无公共点 B .曲线1C 与2C 至少有一个公共点 C .曲线1C 与2C 至多有一个公共点D .曲线1C 与2C 的公共点的个数无法确定11.设x 、y 、0z >,1a x y =+,1b y z =+,1c z x=+,则a 、b 、c 三数( ) A .都小于2 B .至少有一个不大于2 C .都大于2D .至少有一个不小于212.已知在正三角形ABC 中,若D 是BC 边的中点,G 是三角形ABC 的重心,则2AGGD=.若把该结论推广到空间,则有:在棱长都相等的四面体ABCD 中,若三角形BCD 的重心为M ,四面体内部一点O 到四面体各面的距离都相等,则AOOM 等于( ) A .4B .3C .2D .1二、填空题13.关于圆周率π,祖冲之的贡献有二:①3.1415926 3.1415927π<<;②用227作为约率,355113作为密率,其中约率与密率提出了用有理数最佳逼近实数的问题.约率可通过用连分数近似表示的方法得到,如:111223.14159265333170.0625135770.14159265=+≈+≈+=+,舍去0.0625135,得到逼近π的一个有理数为122377+=化为连分数形式:1111m n k r++++(m ,n ,k 为正整数,r 为0到1之间的无理数),舍去r的一个有理数为__________.14.某大学宿舍三名同学A ,B ,C ,他们来自北京、天津、上海三个不同的城市,已知C 同学身高比来自上海的同学高;A 同学和来自天津的同学身高不同;B 同学比来自天津的同学高,则来自上海的是________同学. 15.观察下列等式: 11=,3211= 123+=,332123+=1236++=,33321236++=……可以推测3333123n +++⋅⋅⋅+=____(*n N ∈,用含有n 的代数式表示). 16.在Rt ABC ∆中,若90,,C AC b BC a ∠=︒==,斜边AB 上的高位h ,则有结论22222a b h a b=+,运用此类比的方法,若三棱锥的三条侧棱两两相互垂直且长度分别为,,a b c 且三棱锥的直角顶点到底面的高为h ,则有结论__________.17.已知111()123f n n=++++.经计算(4)2f >,5(8)2f >,(16)3f >,7(32)2f >,则根据以上式子得到第n 个式子为______. 18.设等差数列{}n a 的前n 项和为n S ,则4S ,84S S -,128S S -,1612S S -成等差数列.类比以上结论有:设等比数列{}n b 的前n 项积为n T ,则4T ,____________,1612T T 成等比数列. 19.学校艺术节对同一类的A ,B ,C ,D 四件参赛作品,只评一件一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下: 甲说:“C 或D 作品获得一等奖”; 乙说:“B 作品获得一等奖”; 丙说:“A ,D 两项作品未获得一等奖”; 丁说:“C 作品获得一等奖”. 若这四位同学中有且只有两位说的话是对的,则获得一等奖的作品是______.20.某种型号的机器人组装由,,,A B C D 四道工序,完成它们需要的时间依次为5,3,3x ,小时,已知完成这四道工序先后顺序及相互关系是:①,A B 可以同时开工;②只有在B 完成后C 才能开工;③只有在,A C 都完成后D 才能开工.若完成该型号的机器人组装总时间为9小时,则完成工序B 需要的时间的最大值为__________.三、解答题21.若0<<3a ,03b <<,03c <<,求证:()3a b -,()3b c -,()3c a -不可能同时大于94. 22.(1)求证:cot tan 2cot 2ααα=+(2)请利用(1)的结论证明:cot tan 2tan24cot 4αααα=++(3)请你把(2)的结论推到更一般的情形,使之成为推广后的特例,并加以证明: (4)化简:tan52tan104tan208tan50︒+︒+︒+︒.23.某同学在一次研究性学习中,发现以下五个式子的值都等于同一个常数. (1)202000sin 10sin 70sin10sin 70+- (2)202000sin 15sin 75sin15sin 75+- (3)202000sin 20sin 80sin 20sin80+-(4)202000sin (13)sin 47sin(13)sin 47-+-- (5)202000sin (78)sin (18)sin(78)sin(18)-+----(1)试从上述五个式子中选择一个,求出这个常数;(2)根据(1)的计算结果,将该同学的发现推广为三角恒等式,并证明该结论. 24.如图1,已知PAB ∆中,PA PB ⊥,点P 在斜边AB 上的射影为点H .(Ⅰ)求证:222111PH PA PB =+; (Ⅱ)如图2,已知三棱锥P ABC -中,侧棱PA ,PB ,PC 两两互相垂直,点P 在底面ABC 内的射影为点H .类比(Ⅰ)中的结论,猜想三棱锥P ABC -中PH 与PA ,PB ,PC 的关系,并证明.25.已知数列{}n a 前n 项和为n S ,且22n a n n=+. (1)试求出1S , 2S , 3S , 4S ,并猜想n S 的表达式. (2)用数学归纳法证明你的猜想.26.在数列{}n a 中,11a =,()1121n n n a ca c n ++=++()n *∈N ,其中实数0c ≠.(1)求23,a a ,并由此归纳出{}n a 的通项公式; (2) 用数学归纳法证明(Ⅰ)的结论.【参考答案】***试卷处理标记,请不要删除一、选择题 1.B 解析:B 【分析】根据表格进行逻辑推理即可得到结果. 【详解】张毅不同的选课方法如下:(1)生物B 层1班,政治1班,物理A 层2班; (2)生物B 层1班,政治1班,物理A 层4班; (3)生物B 层1班,政治2班,物理A 层1班; (4)生物B 层1班,政治2班,物理A 层4班; (5)生物B 层1班,政治3班,物理A 层1班; (6)生物B 层1班,政治3班,物理A 层2班; (7)生物B 层2班,政治1班,物理A 层3班;(8)生物B 层2班,政治1班,物理A 层4班; (9)生物B 层2班,政治3班,物理A 层1班; (10)生物B 层2班,政治3班,物理A 层3班; 共10种,故选B. 【点睛】本题以实际生活为背景,考查了逻辑推理能力与分类讨论思想,属于中档题.2.A解析:A 【分析】根据类比,列方程求解结果. 【详解】2x x =∴=,选A. 【点睛】本题考查利用类比方法列方程求解数学问题,考查基本分析求解能力,属基础题.3.B解析:B 【分析】由题意可得数列天干是以10为等差的等差数列,地支是以12为公差的等差数列,以1949年的天干和地支分别为首项,即可求出答案. 【详解】解:天干是以10为公差构成的等差数列,地支是以12为公差的等差数列,从1949年到2029年经过80年,且1949年为“己丑”年,以1949年的天干和地支分别为首项,则80108÷=,则2029的天干为己, 80126÷=余8,则2029的地支为酉,故选:B . 【点睛】本题考查了学生合情推理的能力,涉及等差数列在实际生活中的应用,属于中档题.4.D解析:D 【分析】先计算前19行数字的个数,进而可得20a 从左到右第三个数. 【详解】由题意可知,n a 可表示为n 个连续的偶数相加,从1a 到19a 共有()119191902+⨯=个偶数,所以20a 从左到右第一个数是第191个偶数,第n 个偶数为2n , 所以第191个偶数为2191382⨯=,20a 从左到右第三个数为386.故选:D. 【点睛】本小题主要考查归纳推理、等差数列求和公式等基础知识,考查运算求解能力,属于中档题.5.B解析:B 【解析】试题分析:用,,A B C 分别表示优秀、及格和不及格,显然语文成绩得A 的学生最多只有1个,语文成绩得B 也最多只有1个,得C 的最多只有1个,因此人数最多只有3人,显然(),(),()AC BB CA 满足条件,故选B .考点:合情推理的应用.6.D解析:D 【分析】通过运算结果逐步倒推出m 的值即可. 【详解】根据题意,正整数m 经过6次运算后得到1,利用倒推思想推理如下:乘以2得2,减1再除以3得0(不符合题意),故正整数m 经过5次运算后得到2; 经同理推算,过4次运算后得到4;经过3次运算后得到8或1(不符合题意,舍去); 经过2次运算后得到16; 经过1次运算后得到32或5; 所以正整数m 的值为64或10. 故选:D. 【点睛】本题考查了归纳推理的应用,进行逆向推理验证是解题关键,属于中档题.7.C解析:C 【分析】利用等差数列和等比数列的通项公式及性质逐一计算判断即可. 【详解】在等比数列{}n b 中,0n b >,公比1q ≠,0q ∴>,即01q <<或1q >, 在A 中,3526b b b b =,故A 错误;在B 中,29561b b b q =,23231b b b q =,故当01q <<时,5623b b b b <,当1q >时5623b b b b >,故B 错误;在C 中,()3351b b b q q q+=+,()42611bb b q q +=+,而()()()()()()243332111110q q q q q q q q q +-+=---=-++>,得431q q q +>+,故3526b b b b +<+,故C 正确;在D 中,()45611b b b q q +=+,()2311b b b q q +=+,故当01q <<时,5623b b b b +<+,当1q >时5623b b b b +>+,故D 错误.故选:C. 【点睛】本题考查了等差数列和等比数列的综合应用,属于中档题.8.C解析:C 【分析】根据5678953125,515625,578125,5390625,51953125,=====,分析次数与末四位数字的关系,归纳其变化规律求解. 【详解】因为5678953125,515625,578125,5390625,51953125,=====,观察可知415k +的末四位数字3125,425k +的末四位数字5625, 435k +的末四位数字8125,445k +的末四位数字0625,又202045044=⨯+,则20205的末四位数字为0625. 故选:C 【点睛】本题主要考查数列中的归纳推理,还考查了理解辨析推理的能力,属于中档题.9.A解析:A 【分析】先构造两个底面半径为a ,高为b 的圆柱,然后在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥,根据祖暅原理得出椭球的体积. 【详解】椭圆的长半轴长为a ,短半轴长为b ,先构造两个底面半径为a ,高为b 的圆柱,然后在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥,根据祖暅原理得出椭球的体积为:()222142233V V V a b a b a b πππ⎛⎫=-=⨯⨯-⨯⨯= ⎪⎝⎭圆柱圆锥,故选:A.【点睛】本题考查了类比推理的问题,类比推理过程中要注重方法的类比,属基础题.10.A解析:A 【分析】利用反证法,假设曲线1C 与2C 有公共点()11,Q x y ,推出矛盾,即可得到结论. 【详解】假设曲线1C 与2C 有公共点()11,Q x y ,则()11,0F x y =和()1100(,),0F x y F x y -=同时成立,()00,0F x y ∴=,∴点()00,P x y 在曲线1C 上,这与已知条件点()00,P x y 不在曲线1C 上矛盾. ∴假设不成立,所以曲线1C 与2C 无公共点. 故选:A . 【点睛】本题考查反证法,关键是理解掌握反证法的定义.11.D解析:D 【分析】利用基本不等式计算出6a b c ++≥,于此可得出结论. 【详解】由基本不等式得111111a b c x y z x y z y z x x y z ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫++=+++++=+++++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭6≥=,当且仅当1x y z ===时,等号成立,因此,若a 、b 、c 三数都小于2,则6a b c ++<与6a b c ++≥矛盾,即a 、b 、c 三数至少有一个不小于2, 故选D. 【点睛】本题考查了基本不等式的应用,考查反证法的基本概念,解题的关键就是利用基本不等式求最值,考查分析问题和解决问题的能力,属于中等题.12.B解析:B 【分析】利用类比推理把平面几何的结论推广到空间中. 【详解】因为O 到四面体各面的距离都相等,所以O 为四面体内切球的球心, 设四面体的内切球半径为r ,则43V Sr =,其中V 表示四面体的体积,S 表示一个面的面积; 所以1433V S AM Sr =⋅=,即14r AM =, 所以34314AMAO OM AM==.故选B. 【点睛】本题主要考查类比推理,平面性质类比到空间时注意度量关系的变化.二、填空题13.【分析】利用题中的定义以及类比推理直接进行求解即可【详解】舍去得到逼近的一个有理数为故答案为:【点睛】本题考查了类比推理解题的关键是理解题中的定义属于基础题解析:1712. 【分析】利用题中的定义以及类比推理直接进行求解即可. 【详解】1111)11111122=+=+=+=+=+++1的一个有理数为11711122122+=++.故答案为:1712【点睛】本题考查了类比推理,解题的关键是理解题中的定义,属于基础题.14.A 【分析】根据题意确定天津的同学再确定上海的同学即可【详解】由于同学同学都与同学比较故同学来自天津;同学比来自天津的同学高即比同学高;而同学身高比来自上海的同学高故来自上海的是同学【点睛】本题考查三解析:A 【分析】根据题意确定天津的同学,再确定上海的同学即可 【详解】由于A 同学,B 同学都与C 同学比较,故C 同学来自天津;B 同学比来自天津的同学高,即比C 同学高;而C 同学身高比来自上海的同学高,故来自上海的是A 同学 【点睛】本题考查三者身份推理问题,总会出现和两个人都有关系的第三方,确定其身份是解题关键15.或或【解析】【分析】观察找到规律由等差数列求和可得【详解】由观察找到规律可得:故可得解【点睛】本题考查观察能力和等差数列求和属于中档题解析:()212n n +⎡⎤⎢⎥⎣⎦或()2214n n +或()2123n +++⋅⋅⋅+ 【解析】 【分析】观察找到规律由等差数列求和可得. 【详解】由观察找到规律可得:()223333(1)123123,2n n n n +⎡⎤+++⋅⋅⋅+=+++⋅⋅⋅+=⎢⎥⎣⎦故可得解. 【点睛】本题考查观察能力和等差数列求和,属于中档题.16.;【解析】【分析】由平面上的直角三角形中的边与高的关系式类比立体中两两垂直的棱的三棱锥中边与高的关系即可【详解】如图设为三棱锥的三条两两互相垂直的侧棱三棱锥的高为连接交于两两互相垂直平面平面故答案为解析:2222222222ab cha b b c c a=++;【解析】【分析】由平面上的直角三角形Rt ABC∆中的边与高的关系式,类比立体中两两垂直的棱的三棱锥中边与高的关系即可.【详解】如图,设PA、PB、PC为三棱锥的三条两两互相垂直的侧棱,三棱锥P ABC-的高为PD h=,连接AD交BC于E,PA、PB、PC两两互相垂直,PA∴⊥平面PBC,PE⊂平面PBC,PA PE∴⊥,PA BC⊥,AE BC∴⊥,PE BC⊥22222b cPEb c∴=+,∴222222PA PEh PDPA PE==+2222222222b cab cb cab c+=++222222222a b ca b b c c a=++.故答案为2222222222a b cha b b c c a=++.【点睛】本题主要考查了类比推理的思想和方法,考查运算求解能力,解答此类问题的关键是根据所给的定理类比出立体中两两垂直的棱的三棱锥中边与高的关系.17.【分析】我们分析等式左边数的变化规律及等式两边数的关系归纳推断后即可得到答案【详解】观察已知中等式:…则故答案为【点睛】归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相解析:()()1*322n n f n N ++>∈ 【分析】我们分析等式左边数的变化规律及等式两边数的关系,归纳推断后,即可得到答案. 【详解】观察已知中等式:()()2134222f f +=>=, ()()35238222f f +=>=, ()()43316232f f +=>=, ()()574332222f f +=>=,…, 则()()1*322n n f n N ++>∈, 故答案为()()1*322n n f n N ++>∈. 【点睛】归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想),属于中档题.18.【解析】对于等比数列通过类比有等比数列的前项积为则成等比数列解析:81248,T T T T 【解析】对于等比数列,通过类比,有等比数列{}n b 的前n 项积为n T ,则4T ,81248,T T T T ,1612T T 成等比数列.19.B 【分析】首先根据学校艺术节对四件参赛作品只评一件一等奖故假设分别为一等奖然后判断甲乙丙丁四位同学的说法的正确性即可得出结果【详解】若A 为一等奖则甲丙丁的说法均错误不满足题意;若B 为一等奖则乙丙的说解析:B 【分析】首先根据“学校艺术节对A B C D 、、、四件参赛作品只评一件一等奖”,故假设A B C D 、、、分别为一等奖,然后判断甲、乙、丙、丁四位同学的说法的正确性,即可得出结果. 【详解】若A 为一等奖,则甲、丙、丁的说法均错误,不满足题意;若B 为一等奖,则乙、丙的说法正确,甲、丁的说法错误,满足题意; 若C 为一等奖,则甲、丙、丁的说法均正确,不满足题意; 若D 为一等奖,则乙、丙、丁的说法均错误,不满足题意; 综上所述,故B 获得一等奖. 【点睛】本题属于信息题,可根据题目所给信息来找出解题所需要的条件并得出答案,在做本题的时候,可以采用依次假设A B C D 、、、为一等奖并通过是否满足题目条件来判断其是否正确.20.3【解析】分析:这是一个简单的合情推理问题我们可以根据四道工序的先后顺序及相互关系计算出完成整个工序需要的最少工作时间再结合该工程总时数为9小时构造方程易得到完成工序需要的天数的最大值详解:因为完成解析:3 【解析】分析:这是一个简单的合情推理问题,我们可以根据四道工序的先后顺序及相互关系,计算出完成整个工序需要的最少工作时间,再结合该工程总时数为9小时构造方程,易得到完成工序B 需要的天数x 的最大值. 详解:因为B 完成后,C 才可以开工,C 完成后,D 才可以开工,完成B C D 、、需用时间依次为,3,3x 小时, 且A ,B 可以同时开工, 该工程总时数为9小时, 则339max x ++= , 所以3max x := ,点睛:本题考查的知识要点:这是一道新运算类的题目,其特点一般是“新”而不“难”,处理的方法一般为:根据新运算的定义,将已知中的数据代入进行运算,易得最终结果,属于基础题型.三、解答题21.见解析 【分析】利用反证法,先假设(3)a b -,(3)b c -,(3)c a -同时大于94,得39(3)(3)(3)()4a b b c c a -⋅-⋅->,再利用基本不等式得出矛盾,即可得证.【详解】证明:假设(3)a b -,(3)b c -,(3)c a -同时大于94.则由9(3)49(3)49(3)4a b b c c a ⎧->⎪⎪⎪->⎨⎪⎪->⎪⎩得39(3)(3)(3)()4a b b c c a -⋅-⋅->,因为0<<3a ,03b <<,03c <<,所以(3)(3)(3)(3)(3)(3)a b b c c a a a b b c c -⋅-⋅-=-⋅-⋅-22233339()()()()2224a ab bc c -+-+-+≤⋅⋅= 这与39(3)(3)(3)()4a b b c c a -⋅-⋅->矛盾,所以假设不成立, 故(3)a b -,(3)b c -,(3)c a -不可能同时大于94. 【点睛】本题考查了反证法证明不等式成立的应用,考查了基本不等式的应用,属于中档题. 22.(1)证明见解析,(2)证明见解析,(3)2211*cot tan 2tan 22tan 22tan 22cot 2,n n n n n N αααααα--=+++++∈,证明见解析(4)cot 5 【分析】(1)右边余切化正切后,利用二倍角的正切公式变形可证;(2)将(1)的结果变形为tan cot 2cot 2ααα=-,然后将所证等式的右边的正切化为余切即可得证;(3)根据(1)(2)的规律可得结果; (4)由(3)的结果可得. 【详解】(1)证明:因为2tan 2cot 2tan tan 2αααα+=+21tan tan 22tan ααα-=+⨯1tan tan tan ααα=+- cot α=,所以cot tan 2cot 2ααα=+ (2)因为cot tan 2cot 2ααα=+,所以tan 2tan 24cot 4ααα++cot 2cot 2αα=-+2(cot 22cot 4)4cot 4)ααα-+cot α=,所以cot tan 2tan24cot 4αααα=++ (3)一般地:2211*cot tan 2tan 22tan 22tan 22cot 2,n n n n n N αααααα--=+++++∈,证明:因为cot tan 2cot 2,ααα=+cot 2tan 22cot 4,ααα=+所以22cot tan 2tan 24cot 4tan 2tan 22cot 2ααααααα=++=++, 以此类推得2211*cot tan 2tan 22tan 22tan 22cot 2,n n n n n N αααααα--=+++++∈(4)tan52tan104tan208tan50︒+︒+︒+︒2233tan 52tan(25)2tan(25)2cot(25)=+⨯+⨯+⨯ cot 5=.【点睛】本题考查了归纳推理,考查了同角公式,考查了二倍角的正切公式,属于中档题.23.(1)34;(2)答案见解析. 【解析】分析:(1)选择(2)计算可得223157515754sin sin sin sin +-=.即该常数为34. (2)根据(1)的计算结果,猜想()()220360604sin sin sin sin αααα++-+=.结合两角和差正余弦公式整理计算即可证得题中的结论. 详解: (1)选择(2)∵20200015751575sin sin sin sin +-= 20200015151515sin cos sin cos +-01313024sin =-=.∴该常数为34.(2)根据(1)的计算结果,推广出的三角恒等式为:()()2200360604sin sin sin sin αααα++-+=. 证明如下:左边()()226060sin sin sin sin αααα=++--()()26060sin sin sin sin αααα⎡⎤=+++-⎣⎦21122sin sin sin sin αααααα⎛⎫⎛⎫=+++- ⎪⎪ ⎪⎪⎝⎭⎝⎭2223144sin cos sin ααα=+-223344sin cos αα=+ 34==右边 所以等式成立.点睛:归纳推理是由部分到整体、由特殊到一般的推理,由归纳推理所得的结论不一定正确,通常归纳的个体数目越多,越具有代表性,那么推广的一般性命题也会越可靠,它是一种发现一般性规律的重要方法. 24.(Ⅰ)证明见解析;(Ⅱ)答案见解析. 【解析】分析:(Ⅰ)先分析得到PA PB AB PH ⋅=,再由勾股定理得到22222PA PB PA PB PH⋅+=,再化简即得222111PH PA PB =+.( Ⅱ)先类比猜想得到猜想:22221111PH PA PB PC=++.再利用(Ⅰ)的结论证明22221111PH PA PB PC=++. 详解:(Ⅰ)由条件得,1122PA PB AB PH ⋅=⋅,所以PA PB AB PH⋅=, 由勾股定理,222PA PB AB +=,所以22222PA PB PA PB PH ⋅+=, 所以 2222222111PA PB PH PA PB PA PB+==+⋅. (Ⅱ)猜想:22221111PH PA PB PC=++. 证明如下:连接AH 延长交BC 于M 点,连接PM , 因为PA PB ⊥,PA PC ⊥,PB PC P ⋂=点,所以PA ⊥平面PBC ,又PM ⊂平面PBC ,得PA PM ⊥,PH ⊥平面ABC ,AM ⊂平面ABC ,则PH AM ⊥.在直角三角形APM 中,由(Ⅰ)中结论,222111PH PA PM =+. PA ⊥平面PBC ,则PA BC ⊥,又PH ⊥平面ABC ,所以PH BC ⊥, 而PH PA P ⋂=点,PH ⊂平面PAM ,所以BC ⊥平面APM ,BC PM ⊥.又PB PC ⊥,由(Ⅰ)中结论,得222111PM PC PB=+.所以22221111PH PA PB PC =++.点睛:(1)本题主要考查几何证明和类比推理及其证明,意在考查学生对这些知识的掌握水平和分析推理能力.(2)解答第2问的关键有两个,其一是连接AH 延长交BC 于M 点,连接PM ,证明222111PH PA PM =+,其二是证明222111,PM PC PB =+都用到第1问的结论.25.(1) 11S =,243S =,332S =,485S =,21n n S n =+. (2)证明见解析. 【解析】试题分析:(1)根据22n a n n=+,求出1234,,,,a a a a ,从而可求出1S ,2S ,3S ,4S ,观察规律,可猜测21n n S n =+;(2)首先验证当1n =时,121111S ⨯==+,等式成立,然后假设当n k =时,等式成立,即21k kS k =+,只需证明当1n k =+时,()()112111k k k k S S a k +++=+=++即可.试题 (1)11212S a ===, 21224163S S a =+=+=, 323413362S S a =+=+=, 4343282105S S a =+=+=, 猜测21n nS n =+.(2)证明:当1n =时,121111S ⨯==+,等式成立, 假设当n k =时,等式成立,即21k kS k =+, 则当1n k =+时,11k k k S S a ++=+()()222111k k k k =+++++ ()()22112k k k k =++++ 222112k k k k =+-+++ 222222k k k +=-=++ ()()2111k k +=++,即当1n k =+时,等式也成立, 故对一切*n N ∈,21n nS n =+. 26.(1) 21(1)n n n a n c c -=-+()n *∈N (2)见解析【解析】试题分析:(1)()2101111a c c ==-+,()22221a c c =-+,()232331a c c =-+ 可归纳猜测()211n n n a n c c-=-+;(2)根据数学归纳法证明原理,01当1n =时,由()2111111a c c -==-+显然结论成立.02假设n k =时结论成立,即()211k k k a k c c -=-+只需证明当1n k =+时,()21111k k k a k cc ++⎡⎤=+-+⎣⎦即可.. 试题(1) 由11a =,及()1121n n n a ca c n ++=++ ()*n N ∈得()22221321a ca c c c =+⋅=-+,()332221a ca c =+⨯+= ()()22321221c c c c ⎡⎤-++⨯+⎣⎦()23231c c =-+ 于是猜测: ()211n n n a n c c-=-+ ()*n N∈(2)下面用数学归纳法予以证明:01当1n =时,由()2111111a c c -==-+显然结论成立.02假设n k =时结论成立,即()211k k k a k c c -=-+那么,当1n k =+时, 由()1121k k k a ca ck ++=++ ()211k k c k c c -⎡⎤=-+⎣⎦()121k c k +++ ()212k k k k c c +=++ ()2111k k k c c +⎡⎤=+-+⎣⎦显然结论成立.由01、02知,对任何*n N ∈都有()211n n n a n c c-=-+ ()*n N∈。
江苏省苏州市高考数学易错解答题含解析

江苏省苏州市高考数学易错解答题解答题含答案有解析1.已知首项为32的等比数列{}n a不是递减数列,其前n项和为n S,且335544,,S a S a S a+++成等差数列.(1)求数列{}n a的通项公式;(2)设1()n nnT S n NS+=-∈,求数列{}n T的最大项的值与最小项的值.2.为推动文明城市创建,提升城市整体形象,2018年12月30日盐城市人民政府出台了《盐城市停车管理办法》,2019年3月1日起施行.这项工作有利于市民养成良好的停车习惯,帮助他们树立绿色出行的意识,受到了广大市民的一致好评.现从某单位随机抽取80名职工,统计了他们一周内路边停车的时间t(单位:小时),整理得到数据分组及频率分布直方图如下:(1)从该单位随机选取一名职工,试估计这名职工一周内路边停车的时间少于8小时的概率;(2)求频率分布直方图中a,b的值.3.在一次人才招聘会上,有A、B两家公司分别开出了它们的工资标准:A公司允诺第一年月工资数为1500元,以后每年月工资比上一年月工资增加230元;B公司允诺第一年月工资数为2000元,以后每年月工资在上一年的月工资增加基础上递增5%,设某人年初被A、B两家公司同时录取,试问:(1)若该人分别在A公司或B公司连续工作n年,则他在第n年的月工资收入分别是多少?(2)该人打算连续在一家公司工作10年,仅从工资收入总量较多作为应聘的标准(不计其它因素),该人应该选择哪家公司,为什么?(3)在A公司工作比在B公司工作的月工资收入最多可以多多少元(精确到1元),并说明理由.4.已知函数f (x)=(1+1tan x )sin 2x -2sin(x +4π)sin(x -4π). (1)若tanα=2,求f(α); (2)若x ∈[12π,2π],求f(x)的取值范围 5.已知函数()4cos sin()16f x x x π=+-.(Ⅰ)求函数()f x 的最小正周期; (Ⅱ)求函数()f x 在区间,64ππ⎡⎤-⎢⎥⎣⎦上的最值以及相应的x 的取值. 6.已知平面向量a ,b ,c ,其中(3,4)a =, (1)若c 为单位向量,且//a c ,求c 的坐标;(2)若||5b =且2a b -与2a b -垂直,求向量a ,b 夹角的余弦值.7.在锐角ABC ∆中,角A ,B ,C 所对的边分别为a ,b ,c ,且cos 3sin a C c A =. (1)求C ;(2)若ABC ∆的面积为8,4a =,求b 的值.8.已知函数()22cos 12f x x πω⎛⎫=+ ⎪⎝⎭(其中0>ω,x ∈R )的最小正周期为2π. (1)求ω的值;(2)如果0,2απ⎡∈⎤⎢⎥⎣⎦,且()85fα=,求cos α的值. 9.某种汽车的购车费用是10万元,每年使用的保险费、养路费、汽油费约为万元,年维修费用第一年是万元,第二年是万元,第三年是万元,…,以后逐年递增万元汽车的购车费用、每年使用的保险费、养路费、汽油费、维修费用的和平均摊到每一年的费用叫做年平均费用.设这种汽车使用年的维修费用的和为,年平均费用为.(1)求出函数,的解析式;(2)这种汽车使用多少年时,它的年平均费用最小?最小值是多少?10.已知函数()()()sin 0,0f x x ωϕωϕπ=+><<的最小正周期为π,且直线2x π=-是其图象的一条对称轴.(1)求函数()f x 的解析式;(2)在ABC ∆中,角A 、B 、C 所对的边分别为a 、b 、c ,且A B C <<,cos a B =,若C 角满足()1f C =-,求a b c ++的取值范围;(3)将函数()y f x =的图象向右平移4π个单位,再将所得的图象上每一点的纵坐标不变,横坐标伸长为原来的2倍后所得到的图象对应的函数记作()y g x =,已知常数R λ∈,*n N ∈,且函数()()()F x f x g x λ=+在(0,)n π内恰有2021个零点,求常数λ与n 的值.11.若2sin()3, 且(,0)2απ∈-, 求tan α的值.12.在ABC ∆中,内角A 、B 、C 的对边分别为a 、b 、c ,且22cos b c a C -=.(1)求角A 的大小; (2)若2a =,求2b c +的最大值及相应的角B 的余弦值.13.已知函数()2sin()f x x ω=,其中常数0>ω; (1)令1ω=,判定函数()()()2F x f x f x π=++的奇偶性,并说明理由;(2)令2ω=,将函数()y f x =图像向右平移6π个单位,再向上平移1个单位,得到函数()y g x =的图像,对任意a R ∈,求()y g x =在区间],10[a a π+上零点个数的所有可能值;14.已知{}n a 是递增数列,其前n 项和为n S ,11a >,且10(21)(2)n n n S a a =++,*n ∈N . (Ⅰ)求数列{}n a 的通项n a ;(Ⅱ)是否存在*,,m n k N ∈使得2()m n k a a a +=成立?若存在,写出一组符合条件的,,m n k 的值;若不存在,请说明理由; (Ⅲ)设32n n n b a -=-,若对于任意的*n N ∈,不等式 125111(1)(1)(1)23n m b b b n ≤+++⋅+恒成立,求正整数m 的最大值. 15.在三棱锥V ABC -中,平面VAB ⊥平面ABC ,CA CB =,O ,M 分别是棱AB ,AV 上的点(1)O 为AB 的中点,求证:平面MOC ⊥平面VAB .(2)若:2:3AO BO =,VB 平面MOC ,求:AM AV 的值.16.已知()cos ,sin a αα=,()cos ,sin b ββ=-,α,β均为锐角,且105ab -=. (1)求()cos αβ+的值; (2)若3cos 5α=,求cos β的值. 17.已知圆C 过点(1,4),(3,2)M N ,且圆心在直线430x y -=上. (1)求圆C 的方程;(2)平面上有两点(2,0),(2,0)A B -,点P 是圆C 上的动点,求22||||AP BP +的最小值;(3)若Q 是x 轴上的动点,,QR QS 分别切圆C 于,R S 两点,试问:直线RS 是否恒过定点?若是,求出定点坐标,若不是,说明理由.18.已知菱形ABCD 的边长为2,M 为BD 上靠近D 的三等分点,且线段27AM =. (1)求DAB ∠的值;(2)点P 为对角线BD 上的任意一点,求()PA PC PD ⋅+的最小值. 19.(6分)已知数列{}n a 满足11a =,121n n a a +=+,*n N ∈. (1)求数列{}n a 的通项公式; (2)设()221log 1n n b a +=+,求数列11n n b b +⎧⎫⎨⎬⎩⎭的前n 项和n T . 20.(6分)如图,三棱柱111ABC A B C -的侧面11BB C C 是边长为2的菱形,160B BC ∠=︒,且1AB B C ⊥.(1)求证: 1ABB ABC ∠=∠;(2)若AB AC =,当二面角1B AB C --为直二面角时,求三棱锥1A BB C -的体积.21.(6分)在ABC ∆中,角A 、B 、C 的对边分别为a 、b 、c ,已知()2cos cos 0a c B b C ++=. (1)求角B 的大小;(2)若3a =,点D 在AC 边上,且BD AC ⊥,15314BD =,求c 边的长.22.(8分)设数列{}n a 是等差数列,其前n 项和为()*n S n ∈N ;数列{}nb 是等比数列,公比大于0,其前n 项和为()*n T n ∈N.已知11b=,322b b =+,424b a a =+,5162b a a =+.(1)求数列{}n a 和数列{}n b 的通项公式; (2)设数列1n n a b ⎧⎫⎨⎩-⎬⎭的前n 项和为n K ,若n K m <对任意的n *∈N 恒成立,求实数m 的取值范围.23.(8分)已知数列{}n a 前n 项和n S 满足()2*n S n n N =∈(1)求数列{}n a 的通项公式; (2)求数列11n n a a +⎧⎫⎨⎬⎩⎭的前n 项和n T .24.(10分)已知海岛在海岛北偏东,,相距20海里,物体甲从海岛以海里/小时的速度沿直线向海岛移动,同时物体乙从海岛沿着海岛北偏西方向以海里/小时的速度移动.(1)问经过多长时间,物体甲在物体乙的正东方向; (2)求甲从海岛到达海岛的过程中,甲、乙两物体的最短距离.25.(10分)已知函数()()sin ,f x A x x R ωϕ=+∈(其中0,0,02A πωϕ>><<)的图象如图所示:(1)求函数()f x 的解析式及其对称轴的方程; (2)当0,2x π⎡⎤∈⎢⎥⎣⎦时,方程()23f x a =-有两个不等的实根12,x x ,求实数a 的取值范围,并求此时12x x +的值.26.(12分)如图1,ABCD 为菱形,∠ABC =60°,△PAB 是边长为2的等边三角形,点M 为AB 的中点,将△PAB 沿AB 边折起,使平面PAB ⊥平面ABCD ,连接PC 、PD ,如图2,(1)证明:AB ⊥PC ;(2)求PD 与平面ABCD 所成角的正弦值(3)在线段PD 上是否存在点N ,使得PB ∥平面MC ?若存在,请找出N 点的位置;若不存在,请说明理由27.(12分)若()()()()sin sin 2cos tan x x f x x x ππππ⎛⎫+- ⎪⎝⎭=--- (1)化简()f x ;(2)求函数()f x 的单调递增区间.28.设数列{}n a 满足12nn n a ka --=(*n N ∈,2n ≥),且28a =,324a =.(1)求1a 和k 的值;(2)求数列 {}n a 的前n 项和n S .29.在ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,1a =,且(1)(sin sin )()sin b A B c b C +-=-. (1)求A ;(2)求ABC 面积的最大值.30.在ABC 中,角,,A B C 所对的边分别为,,a b c ,满足cos cos cos 22cos C A B A B += (1)求cos B 的值;(2)若4a c +=,求b 的取值范围.参考答案解答题含答案有解析1.(1)()131?2n n n a -=-;(2)最大项的值为56,最小项的值为712- 【解析】 试题分析: (1)根据335544,,S a S a S a +++成等差数列,利用等比数列通项公式和前项和公式,展开.利用等比数列{}n a 不是递减数列,可得值,进而求通项. (2)首先根据(1)得到,进而得到,但是等比数列的公比是负数,所以分两种情况:当的当n 为奇数时,n S 随n 的增大而减小,所以1312n S S <≤=;当n 为偶数时,n S 随n 的增大而增大,所以2314n S S =≤<,然后可判断最值. 试题解析:(1)设{}n a 的公比为q .由335544,,S a S a S a +++成等差数列,得55334455S a S a S a S a +--=+--.即534a a =,则25314a q a ==. 又{}n a 不是递减数列且132a =,所以12q =-.故11313(1)222n n n na --⎛⎫=⨯-=-⋅⎪⎝⎭. (2)由(1)利用等比数列的前项和公式,可得得11,121{121,.2nn n n n S n +⎛⎫=--= ⎪⎝⎭-为奇数,为偶数 当n 为奇数时,n S 随n 的增大而减小,所以1312n S S <≤=, 故11113250236n n S S S S <-≤-=-=. 当n 为偶数时,n S 随n 的增大而增大,所以2314n S S =≤<, 故221134704312n n S S S S >-≥-=-=-. 综上,对于n N +∈,总有715126n n S S -≤-≤, 所以数列{}n T 最大项的值为56,最小值的值为712-. 考点:等差中项,等比通项公式;数列增减性的讨论求最值.2.(1)920;(2)120a =,340b =. 【解析】 【分析】(1)由频率分布表即可得解;(2)由频率分布直方图中小矩形的高为频率与组距的比值,观察频率分布表的数据即可得解.【详解】解:(1)记“从该单位随机选取一名职工,这名职工该周路边停车的时间少于8小时”为事件A ,则()6820369808020P A ++===;(2)由频率分布表可得:区间[)4,6的频数为8, 则8180220a ==, 区间[)4,6的频数为12,则12380240b ==. 【点睛】本题考查了频率分布表及频率分布直方图,属基础题.3.(1)在A 公司第n 年收入为2301270n +;在B 公司连续工作n 年收入为12000(15%)-⋅+n ;(2)应选择A 公司,理由见详解;(3)827;理由见详解. 【解析】 【分析】(1)先分别记该人在A 公司第n 年收入为n a ,在B 公司连续工作n 年收入为n b , 根据题中条件,即可直接得出结果;(2)根据等差数列与等比数列的求和公式,分别计算前10的和,即可得出结果;(3)先令123012702000(1.05)-=-=+-⨯n n n n c a b n ,将原问题转化为求n c 的最大值,进而可求出结果. 【详解】(1)记该人在A 公司第n 年收入为n a ,在B 公司连续工作n 年收入为n b , 由题意可得:1500(1)2302301270=+-⋅=+n a n n ,*n N ∈,12000(15%)-=⋅+n n b ,*n N ∈;(2)由(1),当10n =时, 该人在A 公司工资收入的总量为:()110121010()12...1260(15003570)3042002++++=⨯=⨯+=a a a a a (元);该人在B 公司工资收入的总量为:()10121020001(15%)12...123018691(15%)⎡⎤⨯-+⎣⎦+++=⨯≈-+b b b (元)显然A 公司工资总量高,所以应选择A 公司;(3)令123012702000(1.05)-=-=+-⨯n n n n c a b n ,则原问题即等价于求n c 的最大值; 当2n ≥时,12123012702000(1.05)230(1)12702000(1.05)---⎡⎤⎡⎤-=+-⨯--+-⨯⎣⎦⎣⎦n n n n c c n n2230100(1.05)-=-⨯n ,若10-->n n c c ,则2230100(1.05)0--⨯>n ,即2(1.05) 2.3-<n ,解得 1.052log 2.3<+n ; 又 1.0517log 2.318<<,所以1920<<n ,因此,当219≤≤n 时,1n n c c ->;当20n ≥时,1-≤n n c c . 所以19c 是数列{}n c 的最大项,191919827=-≈c a b (元), 即在A 公司工作比在B 公司工作的月工资收入最多可以多827元. 【点睛】本题主要考查数列的应用,熟记等差数列与等比数列的通项公式与求和公式即可,属于常考题型. 4.(1)35;(2)[0,12]. 【解析】 【分析】 【详解】 (1)f(x)=sin cos sin x x x +·sin 2x -sinxsinxcosx)=sin 2x +cosxsinx -sin 2x +cos 2x =sinxcosx +cos 2x ,∴f(α)=2cos sin cos 1a a a+=222cos sin cos sin cos a a aa a++=21tan tan 1a a ++=35. (2)由(1)知,f(x)=cos 2x +sinxcosx=1cos22x ++sin 22x =2sin(2x +4π)+12,∵12π≤x≤2π,512π≤2x +4π≤54π,-2≤sin(2x +4π)≤1,0≤f(x)≤12,∴f(x)∈[0,12]. 本试题组要是考查了三角函数的运用. 5.(Ⅰ)π;(Ⅱ)6x π=时,()f x 取得最大值2;6x π=-时,()f x 取得最小值1-.【解析】 【分析】(Ⅰ)利用二倍角和两角和与差以及辅助角公式将函数化为y =Asin (ωx+φ)的形式,利用三角函数的周期公式求函数的最小正周期. (Ⅱ)利用x ∈[6π-,4π]上时,求出内层函数的取值范围,结合三角函数的图象和性质,求出f (x )的最大值和最小值. 【详解】(Ⅰ)因为函数f (x )=4cosxsin (x 6π+)-1.化简可得:f (x )=4cosxsinxcos 6π+4cos 2xsin 6π-1=2x -1==2sin (2x 6π+) 所以()f x 的最小正周期为π. (Ⅱ)因为64x ππ-≤≤,所以22663x πππ-≤+≤. 当262x ππ+=,即6x π=时,f (x )取得最大值2;当266x ππ+=-,即6x π=时,f (x )取得最小值-1.【点睛】本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用,利用三角函数公式将函数进行化简是解决本题的关键,属于基础题.6.(1)34,55⎛⎫ ⎪⎝⎭或34,55⎛⎫-- ⎪⎝⎭;(2)25. 【解析】 【分析】(1)设(, )c x y =,根据//a c 和||1c =列出关于, x y 的方程求解即可.(2)根据垂直数量积为0,代入,a b 的模长,求解得12a b ⋅=.再根据夹角公式求解即可. 【详解】(1)设(, )c x y =,由//a c 和||1c =可得:223401y x x y -=⎧⎨+=⎩ ∴3545x y ⎧=⎪⎪⎨⎪=⎪⎩或3545x y ⎧=-⎪⎪⎨⎪=-⎪⎩, ∴34,55c ⎛⎫= ⎪⎝⎭或34,55c ⎛⎫=--⎪⎝⎭(2)∵(2)(2)0a b a b -⋅-=, 即222||52||0a a b b -⋅+=, 又||5a =,||5b =, ∴12a b ⋅=,∴向量a ,b 夹角的余弦值125cos ,||||a b a b a b ⋅<>==【点睛】本题主要考查了向量平行的性质与单位向量的求解.同时也考查了根据数量积与模长求解向量夹角的方法等.属于中档题. 7.(1)6C π=(2)8b=【解析】 【分析】(1csinA =acosC sinAcosC =,可得3tanC =,从而可得角C 的大小;(2)利用面积公式直接求解b 即可 【详解】(1sinAcosC =, 因为02Aπ<<所以sinA >0cosC =,即3tanC =,又02C π<<,所以6C π=;(2)由1sin 82S ab C == 得b=8本题考查三角函数中的恒等变换应用,考查正弦定理的应用,面积公式的应用,考查化归思想属于中档题. 8.(1)12ω=(2)334cos α+=【解析】 【分析】(1)先根据二倍角余弦公式化简,再根据余弦函数性质求解(2)先求得3cos 65πα⎛⎫+= ⎪⎝⎭,再根据两角差余弦公式求解 【详解】解:(1)因为()22cos cos 21126f x x x ππωω⎛⎫⎛⎫=+=++ ⎪ ⎪⎝⎭⎝⎭. 所以222T ππω==, 因为0>ω,所以12ω=. (2)由(1)可知()8cos 165f παα⎛⎫=++= ⎪⎝⎭, 所以3cos 65πα⎛⎫+= ⎪⎝⎭,因为0,2απ⎡∈⎤⎢⎥⎣⎦, 所以2,663πππα⎡⎤+∈⎢⎥⎣⎦,所以4sin 65πα⎛⎫+= ⎪⎝⎭.因为cos cos 66ππαα⎡⎤⎛⎫=+- ⎪⎢⎥⎝⎭⎣⎦ cos cos sin sin 6666ππππαα⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭3341334552+=⨯+⨯=. 所以334cos α+=. 【点睛】本题考查二倍角余弦公式、两角差余弦公式以及余弦函数性质,考查基本分析求解能力,属基础题 9.(1),;(2)时,年平均费用最小,最小值为3万元.试题分析:根据题意可知,汽车使用年的维修费用的和为,而第一年的维修费用是万元,以后逐年递增万元,每一年的维修费用形成以为首项,为公差的等差数列,根据等差数列的前项和即可求出的解析式;将购车费、每年使用的保险费、养路费、汽油费以及维修费用之和除以即可得到年平均费用,根据基本不等式即可求出平均费用的最小值.试题解析:(1)根据题意可知,汽车使用年的维修费用的和为,而第一年的维修费用是万元,以后逐年递增万元,每一年的维修费用形成以为首项,为公差的等差数列,根据等差数列的前项和公式可得:因为购车费、每年使用的保险费、养路费、汽油费以及维修费用之和为,所以年平均费用为;(2)因为所以当且仅当即时,年平均费用最小,最小值为3万元.考点:本题考查了等差数列的前项和公式以的掌握,以及基本不等式的应用,同时考查了学生解决实际应用题的能力.10.(1)()cos2f x x =;(2)()21+;(3)1λ=-,1347n =. 【解析】 【分析】(1)由函数的周期公式可求出ω的值,求出函数()y f x =的对称轴方程,结合直线2x π=-为一条对称轴结合ϕ的范围可得出ϕ的值,于此得出函数()y f x =的解析式; (2)由()1f C =-得出2C π=,再由cos a B =结合锐角三角函数得出1c =,利用正弦定理以及内角和定理得出214a b c A π⎛⎫++=++ ⎪⎝⎭,由条件得出04A π<<,于此可计算出a b c ++的取值范围;(3)令()0F x =,得22sin sin 10x x λ--=,换元得出[]sin 1,1t x =∈-,得出方程2210t t λ--=,设该方程的两根为1t 、2t ,由韦达定理得出1212t t =-,分(ii )101t <<、202t <<;(ii )11t =,2102t -<<;(iii )11t =-,2102t <<三种情况讨论,计算出关于x 的方程22sin sin 10x x λ--=在一个周期区间()0,2π上的实根个数,结合已知条件得出λ与n 的值.(1)由三角函数的周期公式可得22πωπ==,()()sin 2f x x ϕ∴=+,令()22x k k Z πϕπ+=+∈,得()422k x k Z πϕπ=-+∈, 由于直线2x π=-为函数()y f x =的一条对称轴,所以,()2422k k Z ππϕπ-=-+∈, 得()32k k Z πϕπ=+∈,由于0ϕπ<<,1k ∴=-,则2ϕπ=, 因此,()sin 2cos 22f x x x π⎛⎫=+= ⎪⎝⎭; (2)A B C <<,由三角形的内角和定理得3A B C C π=++<,3C ππ∴<<.()cos21f C C ==-,且2223C ππ<<,2C π∴=,2C π∴=. cos cos sin 2B A A π⎛⎫∴=-= ⎪⎝⎭,由cos a B =,得sin a A =,由锐角三角函数的定义得sin a A c =,1sin ac A∴==, 由正弦定理得1sin sin b a B A ==,sin sin cos 2b B A A π⎛⎫∴==-= ⎪⎝⎭,sin cos 114a b c A A A π⎛⎫∴++=++=++ ⎪⎝⎭,2C π=,且22A B A π+=>,04A π∴<<,442A πππ∴<+<,sin 14A π⎛⎫<+< ⎪⎝⎭.21a b c ∴<++<,因此,a b c ++的取值范围是()1;(3)将函数()y f x =的图象向右平移4π个单位, 得到函数cos 2cos 2sin 242y x x x ππ⎡⎤⎛⎫⎛⎫=-=-= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦, 再将所得的图象上每一点的纵坐标不变,横坐标伸长为原来的2倍后所得到的图象对应的函数为()sin g x x =,()()()2cos2sin 2sin sin 1F x f x g x x x x x λλλ=+=+=-++,令()0F x =,可得22sin sin 10x x λ--=,令[]sin 1,1t x =∈-,得2210t t λ--=,280λ∆=+>,则关于t 的二次方程2210t t λ--=必有两不等实根1t 、2t ,则1212t t =-,则1t 、2t 异号,(i )当101t <<且201t <<时,则方程1sin x t =和2sin x t =在区间()()0,n n N π*∈均有偶数个根,从而方程22sin sin 10x x λ--=在()()0,n n N π*∈也有偶数个根,不合乎题意;(ii )当11t =,则2102t -<<,当()0,2x π∈时,1sin x t =只有一根,2sin x t =有两根,所以,关于x 的方程22sin sin 10x x λ--=在()0,2π上有三个根,由于202136732=⨯+,则方程22sin sin 10x x λ--=在()0,1346π上有36732019⨯=个根,由于方程1sin x t =在区间()1346,1367ππ上只有一个根,在区间()1367,1368ππ上无实解,方程2sin x t =在区间()1346,1367ππ上无实数解,在区间()1367,1368ππ上有两个根,因此,关于x 的方程22sin sin 10x x λ--=在区间()0,1347π上有2020个根,在区间()0,1348π上有2022个根,不合乎题意; (iii )当11t =-时,则2102t <<,当()0,2x π∈时,1sin x t =只有一根,2sin x t =有两根, 所以,关于x 的方程22sin sin 10x x λ--=在()0,2π上有三个根,由于202136732=⨯+,则方程22sin sin 10x x λ--=在()0,1346π上有36732019⨯=个根,由于方程1sin x t =在区间()1346,1367ππ上无实数根,在区间()1367,1368ππ上只有一个实数根, 方程2sin x t =在区间()1346,1367ππ上有两个实数解,在区间()1367,1368ππ上无实数解, 因此,关于x 的方程22sin sin 10x x λ--=在区间()0,1347π上有2021个根,在区间()0,1348π上有2022个根,此时,()()2211110λλ⨯--⨯--=+=,得1λ=-.综上所述:1λ=-,1347n =. 【点睛】本题考查利用三角函数的性质求三角函数的解析式,以及三角形中的取值范围问题,以及三角函数零点个数问题,同时也涉及了复合函数方程解的个数问题,考查分类讨论思想的应用,综合性较强,属于难题.11.tan α=【解析】 【分析】本题首先可根据2sin()3以及诱导公式得出2sin 3,然后根据(,0)2απ∈-以及同角三角函数关系计算出5cos α3,最后根据sin tan cos ααα=即可得出结果.【详解】 因为2sin()3,所以2sin 3, 因为(,0)2απ∈-,所以cos 0α>, 因为22sin cos 1αα+=,所以解得5cos α3,sin 25tan cos .【点睛】本题考查同角三角函数关系的应用,考查的公式有22sin cos 1αα+=、sin tan cos ααα=以及sin()sin ,考查计算能力,是简单题.12.(1)4A π=(2)b 的最大值为cos 5B =【解析】 【分析】(1)由正弦定理边角互化思想结合内角和定理、诱导公式可得出cos A 的值,结合角A 的取值范围可得出角A 的大小;(2)由正弦定理得出2sin b B =,()2sin 2sin c C A B ==+,然后利用三角恒等变换思想将b 转化为关于角B 的三角函数,可得出b +的值,并求出cos B 的值. 【详解】(1sin cos B C A C -=,()sin cos A C C A C +-=,cos sin sin cos A C A C C A C +-=,sin sin 0A C C -=,由sin 0C >得cos A = 因为0A π<<,所以4A π=;(2)由正弦定理可知,2sin sin sin a b cA B C===, 则有2sin b B =,2sin 2sin 4c C B π⎛⎫==+⎪⎝⎭,2sin 2sin 4b B B B B B π⎫⎛⎫=++=++⎪ ⎪⎪⎝⎭⎭()4sin 2cos B B B θ=+=+,其中sin cos θθ==因为304B π<<,所以34B πθθθ<+<+,所以当2B πθ+=时,b +取得最大值此时cos cos sin 2B πθθ⎛⎫=-==⎪⎝⎭,所以,b +的最大值为cos 5B =. 【点睛】本题考查正弦定理边角互化思想的应用,考查内角和定理、诱导公式,以及三角形中最值的求解,求解时常利用正弦定理将边转化为角的三角函数来求解,解题时要充分利用三角恒等变换思想将三角函数解析式化简,考查运算求解能力,属于中等题.13.(1)非奇非偶,理由见解析;(2)21或20个. 【解析】 【分析】(1)先利用辅助角公式化简()F x ,再利用(0)0F ≠和44F F ππ⎛⎫⎛⎫-≠ ⎪ ⎪⎝⎭⎝⎭可判断()F x 为非奇非偶函数. (2)求出()g x 的解析式后结合函数的图像、周期及给定区间的特点可判断在给定的范围上的零点的个数. 【详解】(1)()2sin 2sin())24F x x x x =++=+ππ,则(0)20F =≠,故()F x 不是奇函数,又0,44F F ππ⎛⎫⎛⎫-== ⎪ ⎪⎝⎭⎝⎭44F F ππ⎛⎫⎛⎫-≠ ⎪ ⎪⎝⎭⎝⎭,故()F x 不是偶函数. 综上,()F x 为非奇非偶函数.(2)()2sin(2),()2sin(2)1,3f x xg x x T ==-+=ππ,()g x 的图象如图所示:令()0g x =,则1sin(2)32x π-=-, 则72236x k πππ-=+或2236x k πππ-=-,k Z ∈, 也就是23x k ππ=+或者12x k ππ=+,k Z ∈,所以()g x 在形如[),m m π+的区间上恰有两个不同零点. 把区间],10[a a π+分成10个小区间,它们分别为:())1,a i a i ππ+-+⎡⎣,1,2,9i =及[]9,10a a ππ++,根据函数的图像可知:前9个区间的长度恰为一个周期且左闭右开,故每个区间恰有两个不同的零点,最后一个区间的长度恰为一个周期且为闭区间,故该区间上可能有两个不同的零点或3个不同的零点. 故在区间],10[a a π+上()g x 可有21个或者20个零点. 【点睛】本题考查正弦型函数的奇偶性、正弦型函数在给定范围上的零点个数,注意说明一个函数不是奇函数或不是偶函数,可通过反例来说明,而零点个数的判断则需综合考虑给定区间的长度、开闭情况及函数的周期. 14.(1)1(51)2n -(2)不存在(3)1 【解析】 【分析】 【详解】(Ⅰ)11110(21)(2)a a a =++,得2112520a a -+=,解得12a =,或112a =. 由于11a >,所以12a =.因为10(21)(3)n n n S a a =++,所以210252n n n S a a =++.故221111101010252252n n n n n n n a S S a a a a ++++=-=++---,整理,得22112()5()0n n n n a a a a ++--+=,即11()[2()5]0n n n n a a a a +++--=.因为{}n a 是递增数列,且12a =,故10n n a a ++≠,因此152n n a a +-=. 则数列{}n a 是以2为首项,52为公差的等差数列. 所以512(1)(51)22n a n n =+-=-.………………………………………………5分 (Ⅱ)满足条件的正整数,,m n k 不存在,证明如下:假设存在*,,m n k N ∈,使得2()m n k a a a +=,则15151(51)2m n k -+-=-. 整理,得3225m n k +-=, ①显然,左边为整数,所以①式不成立.故满足条件的正整数,,m n k 不存在. ……………………1分 (Ⅲ)313(51)21222n n n n b a n n --=-=--=+,12111(1)(1)(1)n b b b ≤+++可转化为 ≤3121231111n n b b b b bb b b ++++⋅⋅⋅4682235721nn +=⋅⋅⋅⋅⋅+. 设46822()35721n f n n +=⋅⋅⋅⋅⋅+则(1)21()35721f n n f n n ⋅⋅⋅++=⋅⋅⋅⋅⋅+2423n n +==+ 24124n n +=>===+.所以(1)()f n f n +>,即当n 增大时,()f n 也增大.12111(1)(1)(1)nb b b ≤+++*n N ∈恒成立,只需min()31f n ≤即可.因为min 4()(1)3f n f ===≤. 即43112448151515m ⨯≤==. 所以,正整数m 的最大值为1. ………………………………………14分15.(1)证明见解析;(2):2:5AM AV = 【解析】 【分析】(1)根据等腰三角形的性质,证得OC AB ⊥,由面面垂直的性质定理,证得OC ⊥平面VAB ,进而证得平面MOC ⊥平面VAB .(2)根据线面平行的性质定理,证得//VB MO ,平行线分线段成比例,由此求得:AM AV 的值. 【详解】(1)AC BC =,O 为AB 的中点,所以OC AB ⊥. 又因为平面VAB ⊥平面ABC ,平面VAB 平面ABC AB =,且OC ⊂平面ABC ,所以OC ⊥平面VAB ,又OC ⊂平面MOC ,所以平面MOC ⊥平面VAB . (2)∵VB平面MOC ,VB ⊂面VAB ,面VAB面MOC MO =∴VB MO ∥,∴::2:5AM AV AO AB ==. 【点睛】本小题主要考查面面垂直的判定定理和性质定理,考查线面平行的性质定理,考查空间想象能力和逻辑推理能力,属于中档题. 16.(1)45;(2)2425【解析】 【分析】(1)计算表达出a b -,再根据105a b -=,两边平方求化简即可求得()cos αβ+. (2)根据()cos cos βαβα=+-⎡⎤⎣⎦,再利用余弦的差角公式展开后分别计算()sin ,sin αβα+求解即可. 【详解】(1)由题意,得()cos cos ,sin sin a b a βαβ-=-+,105a b -=,==()222cos 5αβ∴-+=,()4cos 5αβ∴+=.(2)()4cos 05αβ+=>,α,β均为锐角,αβ∴+仍为锐角,()3sin 5αβ+== 3cos 5α=,4sin 5α∴==,()()433424cos cos cos()cos sin sin 555525βαβααβααβα∴=+-=+++=⨯+⨯=⎡⎤⎣⎦. 【点睛】本题主要考查了根据向量的数量积列出关于三角函数的等式,再利用三角函数中的和差角以及凑角求解的方法.属于中档题.17.(1)22(3)(4)4x y -+-=;(2)26;(3)直线RS 恒过定点()3,3.证明见解析【解析】 【分析】 (1)设圆心4(,)3C a a ,根据则CM CN =,求得3a =和圆的半径,即可得到圆的方程; (2)设(,)P x y ,化简得22AP BP +22||8PO =+,根据圆的性质,即可求解;(3)设(,0)Q t ,圆D 方程22(3)430x y t x y t +-+-+=,根据两圆相交弦的性质,求得相交弦的方程,进而可判定直线RS 恒过定点. 【详解】(1)由题意知,圆心C 在直线430x y -=上,设圆心为4(,)3C a a , 又因为圆C 过点(1,4),(3,2)M N ,则CM CN ==3a =,所以圆心C 为(3,4),半径2r CM ==, 所以圆C 方程为22(3)(4)4x y -+-=.(2)设(,)P x y ,则()22222222()8AP BP x y x y +=++=++22||8PO =+,又由222min||()(52)9PO OC r =-=-=, 所以22min (||)18826AP BP +=+=,即22||||AP BP +的最小值为26.(3)设(,0)Q t ,则以CQ 为直径的圆圆心为3(,2)2t D +,半径为2(3)1612t CQ -+=, 则圆D 方程为2223(3)16()(2)24t t x y +-+-+-=, 整理得22(3)430x y t x y t +-+-+=,直线RS 为圆C 与圆D 的相交弦2222(3)430(3)(4)4x y t x y t x y ⎧+-+-+=⎨-+-=⎩, 两式相减,可得得RS 直线方程(3)43210t x y t -++-=, 即(3)34210x t x y -++-=,令3034210x x y -=⎧⎨+-=⎩,解得33x y =⎧⎨=⎩,即直线RS 恒过定点()3,3.【点睛】本题主要考查了圆的综合应用,其中解答中涉及到圆的标准方程的求解,圆的最值问题的求解,以及两圆的相交弦方程的求解及应用,着重考查了分析问题和解答问题的能力,属于中档试题. 18.(1)60︒,(2)258- 【解析】 【分析】(1)由cos cos ADM ABM ∠=∠结合2BM DM =, 272,AB AD AM ===可求出2BD =,从而得到60DAB ∠=︒(2)建立直角坐标系,设(,323)P m m -+,可得到()282212PA PC PD m m ⋅+=-+,然后利用二次函数的知识求出最小值 【详解】(1)如图,四边形ABCD 为菱形,所以cos cos ADM ABM ∠=∠所以22222222AD DM AM AB BM AM AD DM AB BM+-+-=⋅⋅因为2BM DM =, 272,3AB AD AM === 所以可解得24,33DM BM ==,所以2BD = 所以ABD △是等边三角形,故60DAB ∠=︒(2)以A 为原点,AB 所在直线为x 轴建立如图所示坐标系:则有()0,0A ,()((2,0,3,3B C D 所以线段BD :33(12y x x =+≤≤) 设(,323)P m m +,则有(323PA m m =--(333PC m m =-,(133PD m m =--所以()((32342323PA PC PD m m m m ⋅+=--⋅--282212m m =-+因为12m ≤≤,所以当118m =时取得最小值258-【点睛】本题考查平面向量数量积及其运算,涉及余弦定理,二次函数等基本知识,属于中档题. 19. (1) ()*21nn a n N =-∈ ;(2) ()*11646nTn N n -∈=+ 【解析】 【分析】(1)由121n n a a +=+,构造{}1n a +是以2为首项,2为公比等比数列,利用等比数列的通项公式可得结果; (2)由(1)得()()111111212322123n n b b n n n n +⎛⎫==- ⎪++++⎝⎭,利用裂项相消可求n T . 【详解】(1)由121n n a a +=+得:()1121n n a a ++=+,即1121n n a a ++=+,且112a +=∴数列{}1n a +是以2为首项,2为公比的等比数列11222n n n a -∴+=⨯= ∴数列{}n a 的通项公式为:()*21n n a n N =-∈(2)由(1)得:()()212212log 1log 21121n n n b a n ++=+=-+=+()()111111212322123n n b b n n n n +⎛⎫∴==- ⎪++++⎝⎭()*111111123557211164623n n n T n N n ⎡⎤⎛⎫⎛⎫⎛⎫=-+-+⋅⋅⋅+- ⎪ ⎪ ⎪⎢⎥++⎝⎭⎝⎭⎝⎣-+⎭∴=∈⎦ 【点睛】 关系式1n n a pa q +=+可构造为1+()11n n q q a p a p p +=+--,中档题。
2019高中数学 四大高频考点例析学案 苏教版选修1-2

四大高频考点例析[考题印证][例1] (陕西高考)观察下列等式 12=1 12-22=-3 12-22+32=6 12-22+32-42=-10 ……照此规律,第n 个等式可为____________________________________. [解析] 观察规律可知,第n 个式子为12-22+32-42+…+(-1)n +1n 2=(-1)n +1n (n +1)2.[答案] 12-22+32-42+…+(-1)n +1n 2=(-1)n +1n (n +1)2[例2] (全国甲卷)有三张卡片,分别写有1和2,1和3,2和3.甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是________.[解析] 法一:由题意得丙的卡片上的数字不是2和3.若丙的卡片上的数字是1和2,则由乙的说法知乙的卡片上的数字是2和3,则甲的卡片上的数字是1和3,满足题意;若丙的卡片上的数字是1和3,则由乙的说法知乙的卡片上的数字是2和3,则甲的卡片上的数字是1和2,不满足甲的说法.故甲的卡片上的数字是1和3.法二:因为甲与乙的卡片上相同的数字不是2,所以丙的卡片上必有数字2.又丙的卡片上的数字之和不是5,所以丙的卡片上的数字是1和2.因为乙与丙的卡片上相同的数字不是1,所以乙的卡片上的数字是2和3,所以甲的卡片上的数字是1和3.[答案] 1和3[跟踪演练]1.观察下列等式:13+23=32,13+23+33=62,13+23+33+43=102,…,根据上述规律,第五个等式为________________________________________________________________________.解析:由所给等式可得:等式两边的幂式指数规律明显,底数关系如下: 1+2=3,1+2+3=6,1+2+3+4=10,即左边底数的和等于右边的底数.故第五个等式为: 13+23+33+43+53+63=(1+2+3+4+5+6)2=212. 答案:13+23+33+43+53+63=2122.先阅读下面的文字:“求1+1+1+…的值时,采用了如下的方法:令 1+1+1+…=x ,则有x =1+x ,两边同时平方,得1+x =x 2,解得x =1+52(负值已舍去)”.可以用类比的方法,求得1+12+11+12+…的值为________.解析:由1+12+11+12+…=1+12+1x ,得2x 2-2x -1=0,于是x =1+32(负值已舍去),故所求值为1+32.答案:1+323.下面的数组均由三个数组成:(1,2,3),(2,4,6),(3,8,11),(4,16,20),(5,32,37),…,(a n ,b n ,c n ).(1)请写出c n 的一个表达式,c n =______________________________; (2)若数列{c n }的前n 项和为M n ,则M 10=________.(用数字作答) 解析:(1)通过观察归纳,得a n =n ,b n =2n,c n =a n +b n =n +2n.(2)M10=(1+2+…+10)+(2+22+…+210)=2 101.答案:n+2n2 101[考题印证][例3] (北京高考)设数列A:a1,a2,…,a N(N≥2).如果对小于n(2≤n≤N)的每个正整数k都有a k<a n,则称n是数列A的一个“G时刻”.记G(A)是数列A的所有“G时刻”组成的集合.(1)对数列A:-2,2,-1,1,3,写出G(A)的所有元素;(2)证明:若数列A中存在a n使得a n>a1,则G(A)≠∅;(3)证明:若数列A满足a n-a n-1≤1(n=2,3,…,N),则G(A)的元素个数不小于a N-a1.[解] (1)G(A)的元素为2和5.(2)证明:因为存在a n使得a n>a1,所以{i∈N*|2≤i≤N,a i>a1}≠∅.记m=min{i∈N*|2≤i≤N,a i>a1},则m≥2,且对任意正整数k<m,a k≤a1<a m.因此m∈G(A).从而G(A)≠∅.(3)证明:当a N≤a1时,结论成立.以下设a N>a1.由(2)知G(A)≠∅.设G(A)={n1,n2,…,n p},n1<n2<…<n p.记n0=1,则an0<an1<an2<…<an p.对i=0,1,…,p,记G i={k∈N*|n i<k≤N,a k>an i}.如果G i≠∅,取m i=min G i,则对任何1≤k<m i,a k≤an i<am i.从而m i ∈G (A )且m i =n i +1,又因为n p 是G (A )中的最大元素,所以G p =∅. 从而对任意n p ≤k ≤N ,a k ≤an p ,特别地,a N ≤an p . 对i =0,1,…,p -1,an i +1-1≤an i .因此an i +1=an i +1-1+(an i +1-an i +1-1)≤an i +1.所以a N -a 1≤an p -a 1= i =1p(an i -an i -1)≤p .因此G (A )的元素个数p 不小于a N -a 1.[跟踪演练]4.(北京高考)给定数列a 1,a 2,…,a n ,对i =1,2,3,…,n -1,该数列前i 项的最大值记为A i ,后n -i 项a i +1,a i +2,…,a n 的最小值记为B i ,d i =A i -B i .(1)设数列{a n }为3,4,7,1,写出d 1,d 2,d 3的值;(2)设a 1,a 2,…,a n (n ≥4)是公比大于1的等比数列,且a 1>0,证明:d 1,d 2,…,d n -1是等比数列; (3)设d 1,d 2,…,d n -1是公差大于0的等差数列,且d 1>0,证明a 1,a 2,…,a n -1是等差数列. 解:(1)d 1=2,d 2=3,d 3=6. (2)证明:因为a 1>0,公比q >1, 所以a 1,a 2,…,a n 是递增数列.因此,对i =1,2,…,n -1,A i =a i ,B i =a i +1. 于是对i =1,2,…,n -1,d i =A i -B i =a i -a i +1=a 1(1-q )q i -1.因此d i ≠0且d i +1d i=q (i =1,2,…,n -2), 即d 1,d 2,…,d n -1是等比数列.(3)证明:设d 为d 1,d 2,…,d n -1的公差. 对1≤i ≤n -2,因为B i ≤B i +1,d >0, 所以A i +1=B i +1+d i +1≥B i +d i +d >B i +d i =A i . 又因为A i +1=max{A i ,a i +1}, 所以a i +1=A i +1>A i ≥a i .从而a 1,a 2,…,a n -1是递增数列. 因此A i =a i (i =1,2,…,n -1).又因为B1=A1-d1=a1-d1<a1,所以B1<a1<a2<…<a n-1.因此a n=B1.所以B1=B2=…=B n-1=a n.所以a i=A i=B i+d i=a n+d i.因此对i=1,2,…,n-2都有a i+1-a i=d i+1-d i=d,即a1,a2,…,a n-1是等差数列.5.如图1,等腰梯形ABCD中,AD∥BC,AB=AD,∠ABC=60°,E是BC的中点.如图2,将△ABE沿AE折起,使二面角B-AE-C成直二面角,连结BC,BD.(1)求证:AE⊥BD;(2)判断DE能否垂直于平面ABC.并说明理由.解:(1)证明:取AE中点M,连结BM,DM.∵在等腰梯形ABCD中,AD∥BC,AB=AD,∠ABC=60°,E是BC的中点,∴△ABE与△ADE都是等边三角形,∴BM⊥AE,DM⊥AE,∵BM∩DM=M,BM、DM⊂平面BDM,∴AE⊥平面BDM.∵BD⊂平面BDM,∴AE⊥BD.(2)DE与平面ABC不垂直.证明:假设DE⊥平面ABC,则DE⊥AB.∵BM⊥平面AECD,∴BM⊥DE.∵AB∩BM=B,AB、BM⊂平面ABE,∴DE ⊥平面ABE .∴DE ⊥AE ,这与∠AED =60°矛盾, ∴DE 与平面ABC 不垂直.[考题印证][例4] (北京高考)设a ∈R ,若复数(1+i)(a +i)在复平面内对应的点位于实轴上,则a =________. [解析] (1+i)(a +i)=a -1+(a +1)i. ∵其对应点在实轴上, ∴a +1=0,即a =-1. [答案] -1[例5] (江苏高考)复数z =(1+2i)(3-i),其中i 为虚数单位,则z 的实部是________. [解析] 因为z =(1+2i)(3-i)=3-i +6i -2i 2=5+5i ,所以z 的实部是5. [答案] 5[跟踪演练]6.(安徽高考改编)设i 是虚数单位,z 表示复数z 的共轭复数.若z =1+i ,则zi+i ·z =________.解析:∴z i +i ·z =1+ii+i(1-i)=-i +1+i +1=2.答案:27.(湖南高考)复数 3+ii 2( i 为虚数单位)的实部等于________.解析:直接运算得3+ii2=-(3+i )=-3-i ,故实部为-3.答案:-38.(湖南高考改编)复数z =i ·(1+i)(i 为虚数单位)在复平面上对应点位于第________象限. 解析:z =i(1+i)=-1+i ,在复平面上对应点的坐标为(-1,1),其在第二象限. 答案:二9.设i 是虚数单位,复数1+a i2-i 为纯虚数,则实数a 的值为________.解析:复数1+a i 2-i =(1+a i )(2+i )(2-i )(2+i )=2-a +(2a +1)i5,依题意得⎩⎪⎨⎪⎧2-a =0,2a +1≠0,∴a =2.答案:2[考题印证][例6] (江苏高考)如图是一个算法的流程图,则输出的a 的值是________.[解析] 由a =1,b =9,知a <b , 所以a =1+4=5,b =9-2=7,a <b . 所以a =5+4=9,b =7-2=5,满足a >b . 所以输出的a =9. [答案] 9[例7] (湖北高考改编)阅读如图所示的流程图,运行相应的程序,若输入n 的值为9,则输出S 的值为________.[解析] S=(21+22+…+29)+(1+2+…+9)=210-2+45=1 024+43=1 067.[答案] 1 067[跟踪演练]10.(山东高考改编)执行如图所示的算法流程图,若输入的x的值为1,则输出的n的值为________.解析:12-4×1+3≤0,x=2,n=1;22-4×2+3≤0,x=3,n=2;32-4×3+3≤0,x=4,n=3;42-4×4+3>0,跳出循环,此时输出n值,故输出的n值为3.答案:311.(天津高考改编)阅读如图所示的算法流程图,运行相应的程序,输出S的值为________.解析:S =0,n =3,第1次运行,S =0+(-2)3=-8,n =2,不满足条件;第2次运行,S =-8+(-2)2=-8+4=-4,n =1,满足条件,跳出循环,输出S 的值为-4.答案:-4 12.下面的程序流程图,如果输入三个实数a ,b ,c 要求输出这三个数中最大的数,那么在空白的判断框中,应该填入________.解析:由题意输出的应为x 与c 中较大者,输出的是x , ∴应填c >x . 答案:c >x模块综合检测(考试时间:120分钟 试卷总分:160分)一、填空题(本大题共14小题,每小题5分,共70分) 1.(四川高考)复数2-2i1+i=________.解析:2-2i 1+i =2(1-i )2(1+i )(1-i )=(1-i)2=-2i.答案:-2i2.在某个三段论的推理过程中,若小前提是:2100+1是奇数;结论是:2100+1不能被2整除.则该演绎推理的大前提是_____________________________________.答案:一切奇数都不能被2整除(答案不惟一)3.已知数列{a n }的前n 项和S n =n 2·a n (n ≥2),且a 1=1.通过计算a 2,a 3,a 4,猜想a n =________. 解析:a 2=13=22×3,a 3=16=23×4,a 4=110=24×5,因此a n =2n (n +1).答案:2n (n +1)4.用反证法证明命题“a ,b ∈N ,ab 可被5整除,那么a 、b 中至少有一个能被5整除”时,假设的内容应为___________________.解析:“a ,b 中至少有一个能被5整除”的否定是“a ,b 都不能被5整除”. 答案:a ,b 都不能被5整除 5.①正方形的对角线互相平分; ②平行四边形的对角线互相平分; ③正方形是平行四边形.根据“三段论”推理推出一个结论,则这个结论是________(填序号).解析:根据三段论的一般形式,可以得到大前提是②,小前提为③,故得到结论为①. 答案:①6.(浙江高考改编)若某算法流程框图如图所示,当输入50时,则该程序运行后输出的结果是________.解析:S =0,i =1;S =1,i =2;S =4,i =3;S =11,i =4;S =26,i =5;S =57,i =6,此时S >n ,所以i =6.答案:67.如果复数z =3+a i 满足条件|z -2|<2,那么实数a 的取值范围是___________________. 解析:∵|z -2|<2,∴ 1+a 2<2. ∴-3<a < 3. 答案:(-3,3)8.设a ,b ,c ∈(-∞,0),则a +1b +b +1c +c +1a的取值范围是____________________.解析:a +1b +b +1c +c +1a=-⎣⎢⎡⎦⎥⎤(-a )+1-a -⎣⎢⎡⎦⎥⎤(-b )+1-b -⎣⎢⎡⎦⎥⎤(-c )+1-c ≤-6.答案:(-∞,-6]9.已知a ∈R ,复数z =1+a i1-a i 在复平面内对应的点位于y 轴的负半轴上,那么实数a 的值是________.解析:∵z =(1+a i )2(1-a i )(1+a i )=1-a 2+2a i 1+a 2=1-a 21+a 2+2a1+a 2i ,∴⎩⎪⎨⎪⎧1-a21+a 2=0,2a1+a2<0,解得a =-1.答案:-110.下表是关于出生男婴与女婴调查的列联表,那么A =________,B =________,C =________,D =________.解析:45+A =98⇒A =98-45=53, 98+D =180⇒D =180-98=82,B +47=D ⇒B =82-47=35,C =A +47⇒C =53+47=100.答案:53 35 100 8211.2014年元旦来临之际,某服装商场为了了解大衣的月销售量y (件)与月平均气温x (℃)之间的关系,随机统计了某四个月的月销售量与当月平均气温,其数据如下表:由表中的数据算出线性回归方程y ^=b ^x +a ^中的b ^≈-2.气象部门预测下个月的平均气温约为7 ℃,据此估计该商场下个月大衣的销售量约为________件.解析:x -=10,y -=38,又∵b ^≈-2,∴a ^=y --b ^x -≈38+20=58,∴线性回归方程y ^=-2x +58,把x =7代入y ^=-2x +58,得y ^=-14+58=44,∴该商场下个月大衣的销售量约为44件.答案:4412.下图中还有“哺乳动物”“地龟”“长尾雀”三项未填,请补充完整这一结构图.①________________; ②________________; ③________________.解析:根据结构图及动物间的从属关系,可知①为“哺乳动物”,②为“地龟”,③为“长尾雀”. 答案:①哺乳动物 ②地龟 ③长尾雀13.凸函数的性质定理为:如果函数f (x )在区间D 上是凸函数,则对于区间D 内的任意x 1,x 2,…,x n ,有f (x 1)+f (x 2)+…+f (x n )n ≤f ⎝ ⎛⎭⎪⎫x 1+x 2+…+x n n ,已知函数y =sin x 在区间(0,π)上是凸函数,则在△ABC 中,sin A +sin B +sin C 的最大值为________.解析:∵f (x )=sin x 在区间(0,π)上是凸函数, 且A ,B ,C ∈(0,π), ∴f (A )+f (B )+f (C )3≤f ⎝⎛⎭⎪⎫A +B +C 3=f ⎝ ⎛⎭⎪⎫π3,即sin A +sin B +sin C ≤3sin π3=332,所以sin A +sin B +sin C 的最大值为332.答案:33214.我们用记号e i θ来表示复数cos θ+isin θ,即e i θ=cos θ+isin θ(其中e =2.718…是自然对数的底数,θ的单位是弧度),则①2ei π2=2i ;②e i θ+e -i θ2=sin θ;③e i π+1=0.其中正确的式子代号是________.解析:2ei π2=2⎝⎛⎭⎪⎫cos π2+isin π2=2i ,∴①正确.e-i θ=cos(-θ)+isin(-θ)=cos θ-isin θ,∴e i θ+e-i θ2=cos θ.∴②错.e i π=cos π+isin π=-1,∴③正确. 答案:①③二、解答题(本大题共6小题,共90分)15.(本小题满分14分)已知复数z 1、z 2满足(1+i)z 1=-1+5i ,z 2=a -2-i ,a ∈R .若|z 1-z -2|<|z 1|,求a 的取值范围.解:z 1=-1+5i1+i =2+3i ,z -2=a -2+i ,z 1-z -2=2+3i -a +2-i =4-a +2i.∵|z 1-z -2|<|z 1|, ∴(4-a )2+4<4+9. ∴1<a <7.16.(本小题满分14分)已知a ,b ∈R ,求证:|a |+|b |1+|a |+|b |≥|a +b |1+|a +b |.证明:要证|a |+|b |1+|a |+|b |≥|a +b |1+|a +b |成立,即证|a |+|b |1+|a |+|b |-1≥|a +b |1+|a +b |-1,只需证-11+|a |+|b |≥-11+|a +b |成立.也就是11+|a |+|b |≤11+|a +b |成立.即1+|a |+|b |≥1+|a +b |成立. 因为|a |+|b |≥|a +b |显然成立, 所以原不等式成立.17.(本小题满分14分)已知a ,b ,c ∈R ,且a =x 2-2y +π2,b =y 2-2z +π3,c =z 2-2x +π6.求证:a ,b ,c 中至少有一个大于0. 证明:假设a ,b ,c ,都不大于0, 即a ≤0,b ≤0,c ≤0,那么a +b +c ≤0,而a +b +c =(x -1)2+(y -1)2+(z -1)2+π-3≥π-3>0, 即a +b +c >0,与a +b +c ≤0矛盾. ∴a ,b ,c 中至少有一个大于0.18.(本小题满分16分)对一批货物征收税金:价格在10 000元以上的征税5%;在5 000元以上,10 000元以下(含10 000元)的征税3%;在1 000元以上,5 000元以下(含5 000元)的征税2%;1 000元以下(含1 000元)的货物免税.请设计一个根据货物价格输出税金的流程图.解:程序框图如下图:19.(本小题满分16分)(新课标Ⅱ)某地区2007年至2013年农村居民家庭纯收入y (单位:千元)的数据如下表:(1)求y 关于t 的线性回归方程;(2)利用(1)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.解:(1)由所给数据计算得t =17(1+2+3+4+5+6+7)=4,y =17(2.9+3.3+3.6+4.4+4.8+5.2+5.9)=4.3,∑i =17(t i -t )2=9+4+1+0+1+4+9=28,∑i =17(t i -t)(y i -y )=(-3)×(-1.4)+(-2)×(-1)+(-1)×(-0.7)+0×0.1+1×0.5+2×0.9+3×1.6=14,b ^=∑i =17t i -ty i -y∑i =17t i -t2=1428=0.5, a ^=y -b ^t =4.3-0.5×4=2.3, 所求回归方程为y ^=0.5t +2.3.(2)由(1)知,b ^=0.5>0,故2007年至2013年该地区农村居民家庭人均纯收入逐年增加,平均每年增加0.5千元.将2015年的年份代号t =9代入(1)中的回归方程,得y ^=0.5×9+2.3=6.8, 故预测该地区2015年农村居民家庭人均纯收入为6.8千元.20.(本小题满分16分)(辽宁高考)某大学餐饮中心为了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查结果如下表所示:(1)根据表中数据,问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”; (2)已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品.现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率.解:(1)将2×2列联表中的数据代入公式计算,得 χ2=100×(60×10-20×10)270×30×80×20=10021≈4.762.由于4.762>3.841,所以有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”. (2)从5名数学系学生中任取3人的一切可能结果所组成的基本事件空间Ω={(a 1,a 2,b 1),(a 1,a 2,b 2),(a 1,a 2,b 3),(a 1,b 1,b 2),(a 1,b 2,b 3),(a 1,b 1,b 3),(a 2,b 1,b 2),(a 2,b 2,b 3),(a 2,b 1,b 3),(b 1,b 2,b 3)}.其中a i 表示喜欢甜品的学生,i =1,2.b j 表示不喜欢甜品的学生,j =1,2,3.Ω由10个基本事件组成,且这些基本事件的出现是等可能的.用A 表示“3人中至多有1人喜欢甜品”这一事件,则A={(a1,b1,b2),(a1,b2,b3),(a1,b1,b3),(a2,b1,b2),(a2,b2,b3),(a2,b1,b3),(b1,b2,b3)}.事件A是由7个基本事件组成,因而P(A)=710 .。
(易错题)高中数学选修1-2第三章《推理与证明》测试卷(有答案解析)(2)
一、选择题1.某校实行选科走班制度,张毅同学的选择是物理、生物、政治这三科,且物理在A 层班级,生物在B 层班级,该校周一上午课程安排如下表所示,张毅选择三个科目的课各上一节,另外一节上自习,则他不同的选课方法有A .8种B .10种C .12种D .14种2.德国数学家科拉茨1937年提出了一个著名的猜想:任给一个正整数t ,如果t 是偶数,就将它减半(即2t);如果t 是奇数,则将它乘3加1(即31t +),不断重复这样的运算,经过有限步后,一定可以得到1.猜想的数列形式为:0a 为正整数,当*n N ∈时,当1n a -为偶数时12n n a a -=,当1n a -为奇数时131n n a a -=+,则数列{}n a 中必存在值为1的项.若51a =,则0a 的所有不同值的个数为( ) A .2B .3C .5D .83.某扶贫调研团根据要求从甲、乙、丙、丁、戊五个镇选择调研地点:①若去甲镇,则必须去乙镇;②丁、戊两镇至少去一镇;③乙、丙两镇只去一镇;④丙、丁两镇都去或都不去;⑤若去戊镇,则甲、丁两镇也必须去.该调研团至多去了( ) A .丙、丁两镇 B .甲、乙两镇C .乙、丁两镇D .甲、丙两镇4.观察下列一组数据12a = 246a =+ 381012a =++ 414161820a =+++…则20a 从左到右第三个数是( ) A .380B .382C .384D .3865.学校艺术节对同一类的A 、B 、C 、D 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下: 甲说:“是C 或D 作品获得一等奖” 乙说:“B 作品获得一等奖” 丙说:“A 、D 两项作品未获得一等奖” 丁说:“是C 作品获得一等奖” 若这四位同学中只有两位说的话是对的,则获得一等奖的作品为( ) A .C 作品B .D 作品C .B 作品D .A 作品6.我们知道,在边长为a 的正三角形内任一点到三边的距离之和为定值3a ,类比上述结论,在棱长为a 的正四面体内任一点到其四个面的距离之和为定值,此定值为( ) A .aB .52a C .223a D .63a 7.将正整数1,2,3,4,按如图所示的方式排成三角形数组,则第20行从左往右数第1个数是( )A .381B .361C .362D .4008.杨辉三角,又称帕斯卡三角,是二项式系数在三角形中的一种几何排列,在我国南宋数学家杨辉所著的《评解九章算法》(1261年)一书中用如图所示的三角形解释二项式乘方展开式的系数规律,现把杨辉三角中的数从上到下,从左到右依次排列,得数列:1,1,1,1,2,1,1,3,3,1,1,4,6,4,1…….记作数列{}n a ,若数列{}n a 的前n 项和为n S ,则57S =( )A .265B .521C .1034D .20599.分析法又称执果索因法,若用分析法证明:“设a >b >c ,且a +b +c =0,求证23b ac a -<”索的因应是( )A .0a b ->B .0a c ->C .()>0)(a b a c --D .()<0)(a b a c --10.运用祖暅原理计算球的体积时,构造一个底面半径和高都与球半径相等的圆柱,与半球(如图一)放置在同一平面上,然后在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥(如图二),用任何一个平行与底面的平面去截它们时,可证得所截得的两个截面面积相等,由此证明该几何体与半球体积相等.现将椭圆22149x y +=绕y 轴旋转一周后得一橄榄状的几何体(如图三),类比上述方法,运用祖暅原理可求得其体积等于( )A .4πB .8πC .16πD .32π11.现有甲、乙、丙、丁四人参加数学竞赛,其中只有一位获奖. 有人走访了四人,甲说:“乙、丁都未获奖”,乙说:“是甲或丙获奖”,丙说:“是甲获奖”,丁说:“是乙获奖”,四人所说话中只有一位是真话,则获奖的人是( ) A .甲B .乙C .丙D .丁12.英国数学家布鲁克泰勒(Taylor Brook ,1685~1731)建立了如下正、余弦公式( )()()357211sin 13!5!7!21!n n x x x x x x n --=-+-++-+-()()2462cos 112!4!6!2!nnx x x x x n -=-+-++-+其中*x R n N ∈∈,,!1234n n =⨯⨯⨯⨯⨯,例如:1!12!23!6===,,.试用上述公式估计cos0.2的近似值为(精确到0.01) A .0.99B .0.98C .0.97D .0.96二、填空题13.已知函数1y x =的图象的对称中心为()0,0,函数111y x x =++的图象的对称中心为1,02⎛⎫- ⎪⎝⎭,函数11112y x x x =++++的图象的对称中心为()1,0-.由此推测,函数12202012019x x x y x x x +++=+++++的图象的对称中心为________. 14.设,a b 是两个实数,给出下列条件:①1a b +>;②2a b +=;③2a b +>;④222a b +>;⑤1ab >. 其中能推出:“,a b 中至少有一个大于1”的条件是____________.15.将正偶数按下表排列成5列,每行有4个偶数的蛇形数列(规律如表中所示),则数字2018所在的行数与列数分别是_______________.第1列 第2列 第3列 第4列 第5列第1行2 46 8 第2行 16141210第3行 18 202224 第4行 3232 28 26 ……16.观察下列等式:11234934567254567891049=++=++++=++++++=照此规律,则第五个等式应为________________.17.我国南宋数学家杨辉所著的《详解九章算术》一书中,用图①的数表列出了一些正整数在三角形中的一种几何排列,俗称“杨辉三角形”,该数表的规律是每行首尾数字均为1,从第三行开始,其余的数字是它“上方”左右两个数字之和.现将杨辉三角形中的奇数换成1,偶数换成0,得到图②所示的由数字0和1组成的三角形数表,由上往下数,记第n 行各数字的和为n S ,如123451,2,2,4,2,S S S S S =====⋯⋯,则33S =____________① ②18.我国古代数学名著《九章算术》中割圆术有:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣.”其体现的是一种无限与有限的转化过程,比如在“”即代表无限次重复,但原式却是个定值x . 这可以x =确定x =2,则11111+=++_______.19.设等差数列{}n a 的前n 项和为n S ,则4S ,84S S -,128S S -,1612S S -成等差数列.类比以上结论有:设等比数列{}n b 的前n 项积为n T ,则4T ,____________,1612T T 成等比数列. 20.已知数列:21,12,31,22,13,41,32,23,14,…根据它的前9项的规律,这个数列的第30项为__________.三、解答题21.观察下列各等式:tan10tan 20tan 20tan60tan60tan101︒︒+︒︒+︒︒=tan 20tan30tan30tan 40tan 40tan 201︒︒+︒︒+︒︒= tan33tan 44tan 44tan13tan33tan131︒︒+︒︒+︒︒= (1)尝试再写出一个相同规律的式子;(2)写出能反映以上式子一般规律的恒等式; (3)并对你写出的(2)恒等式进行证明.22.已知函数()3211333f x x x x =-+-.(1)计算()()02f f +、()()13f f -+、1322f f ⎛⎫⎛⎫+⎪ ⎪⎝⎭⎝⎭的值; (2)结合(1)的结果,试从中归纳出函数()f x 的一般结论,并证明这个结论; (3)若实数0x 满足()()0ff x x =,求证:()00f x x=.23.已知两个正数x y ,,证明:这两个正数的算术平均数不小于这两个正数的几何平均数,并指出何时相等.24.(1)在平面上,若两个正方形的边长的比为1:3,则它们的面积比为1:9.类似地,在空间中,对应的结论是什么? (2)已知数列{}n a 满足11212,4n n n a a a a +-==+,求2345,,,a a a a ,并由此归纳得出{}n a 的通项公式(无需证明). 25.观察下列三角形数表记第n 行的第m 个数为(),(,)n m a n N m N +∈∈.(Ⅰ)分别写出()()4,23,2a a -,()()5,24,2a a -,()()6,25,2a a -值的大小;(Ⅱ)归纳出()(),21,2(2)n n a a n --≥的关系式,并求出(),2(1)n a n ≥关于n 的函数表达式. 26.观察下列等式:11-=-;132-+=;1353-+-=-; 13574-+-+=; ………(1)照此规律,归纳猜想出第n 个等式; (2)用数学归纳法证明(1)中的猜想.【参考答案】***试卷处理标记,请不要删除一、选择题 1.B 解析:B 【分析】根据表格进行逻辑推理即可得到结果. 【详解】张毅不同的选课方法如下:(1)生物B 层1班,政治1班,物理A 层2班; (2)生物B 层1班,政治1班,物理A 层4班; (3)生物B 层1班,政治2班,物理A 层1班; (4)生物B 层1班,政治2班,物理A 层4班; (5)生物B 层1班,政治3班,物理A 层1班; (6)生物B 层1班,政治3班,物理A 层2班; (7)生物B 层2班,政治1班,物理A 层3班; (8)生物B 层2班,政治1班,物理A 层4班;(9)生物B 层2班,政治3班,物理A 层1班; (10)生物B 层2班,政治3班,物理A 层3班; 共10种,故选B. 【点睛】本题以实际生活为背景,考查了逻辑推理能力与分类讨论思想,属于中档题.2.B解析:B 【分析】利用51a =出发,按照规则,逆向逐项即可求解0a 的所有可能的取值. 【详解】如果按照规则施行变换后51a =, 则变换中的4=2a ,若变换中的4=2a ,则变换中的3=4a , 若变换中的3=4a ,则变换中的2a 是1或8, 若变换中的2=8a ,则1=16a ,0=32a 或者0=5a ; 若变换中的2=1a ,则1=2a ,则04a =, 则0a 的所有可能的取值为4,5,32共3个, 故选:B. 【点睛】本题主要考查了归纳推理的应用,其中解答中正确理解题意,利用变换规则,进行逆向逐项推理、验证是解答的关键,着重考查了推理与论证能力,试题有一定的难度,属于中档试题.3.A解析:A 【分析】根据条件假设去甲镇,则可找到矛盾,排除两个答案,再假设不去甲镇,去乙镇同样可得到矛盾,进而可得到答案 【详解】解:假设去甲镇,则必去乙镇,但去乙镇则不能去丙镇,不去丙镇则也不能去丁镇, 不去丁镇则也不能去戊镇,而丁、戊都不去则不符合条件.矛盾,则可淘汰选项B 、D , 若不去甲镇去乙镇,同样无法完成参观; 故甲、乙两镇都不能去,则一定不能去戊镇,∴能去的地方只有丙、丁两镇.故选:A . 【点睛】本题考查学生合情推理的能力,也运用假设法是关键,属于中档题,4.D解析:D 【分析】先计算前19行数字的个数,进而可得20a 从左到右第三个数. 【详解】由题意可知,n a 可表示为n 个连续的偶数相加,从1a 到19a 共有()119191902+⨯=个偶数,所以20a 从左到右第一个数是第191个偶数,第n 个偶数为2n , 所以第191个偶数为2191382⨯=,20a 从左到右第三个数为386. 故选:D. 【点睛】本小题主要考查归纳推理、等差数列求和公式等基础知识,考查运算求解能力,属于中档题.5.C解析:C 【解析】分析:根据学校艺术节对同一类的A ,B ,C ,D 四项参赛作品,只评一项一等奖,故假设A ,B ,C ,D 分别为一等奖,判断甲、乙、丙、丁的说法的正确性,即可判断. 详解:若A 为一等奖,则甲,丙,丁的说法均错误,故不满足题意, 若B 为一等奖,则乙,丙说法正确,甲,丁的说法错误,故满足题意, 若C 为一等奖,则甲,丙,丁的说法均正确,故不满足题意, 若D 为一等奖,则只有甲的说法正确,故不合题意,故若这四位同学中只有两位说的话是对的,则获得一等奖的作品是B 故答案为C.点睛:本题考查推理的应用,意在考查学生的分析、推理能力.这类题的特点是:通过几组命题来创设问题情景,依据题目提供的信息,联系所学的知识和方法,实现信息的迁移,达到灵活解题的目的.对于逻辑推理问题,应耐心读题,找准突破点,一般可以通过假设前提依次验证即可.6.D解析:D 【解析】试题分析:类比在边长为a 的正三角形内任一点到三边的距离之和为定值2a , 在一个正四面体中,计算一下棱长为a 的三棱锥内任一点到各个面的距离之和, 如图:由棱长为a 可以得到36,23BF a BO AO a OE ===-, 在直角三角形中,根据勾股定理可以得到222BO BE OE =+, 把数据代入得到6OE a =∴棱长为a 的三棱锥内任一点到各个面的距离之和664123a a ⨯=, 故选D.考点:类比推理.【方法点晴】由平面图形的性质向空间物体的性质进行类比时,常用的思路有:由平面图形中点的性质类比推理出空间里的线的性质,由平面图形中线的性质类比推理出空间中面的性质,由平面图形中面的性质类比推理出空间中体的性质.固我们可以根据已知中平面几何中,关于线的性质“正三角形内任意一点到三边距离之和是一个定值”,推断出一个空间几何中一个关于面的性质.7.C解析:C 【分析】本题可根据图中数字的排列规律来思考,先观察每行数字的个数的规律,然后找到每行第一个数之间的规律,然后根据规律得出第20行的第1项的数字. 【详解】解:由图中数字排列规律可知:∵第1行有1个数,第2行有3个数,第3行有5个数,第4行有7个数,… ∴第i 行有(21)i -个数.可设第i 行第j 个数字为.i j a ,其中121j i ≤≤-.观察每行的第1项,可得: 1.11a =, 2.12a =, 3.15a =, 4.110a =,… ∴ 1.11a =,2.1 1.11a a -=,3.1 2.13a a -=,4.1 3.15a a -=,….1 1.123i i a a i ---=.以上各项相加,可得:.1113523i a i =++++⋅⋅⋅+-()(1)(123)12i i -+-=+2(1)1i =-+.∴220.1(201)1362a =-+=. 故选:C . 【点睛】本题主要考查数列排列规律,等差数列的特点及求通项和求和.属于中档题.8.C解析:C 【分析】由归纳推理及等比数列前n 项和可得:即57a 在第11组中且为第11组中的第2个数,则01901571010222()1034S C C =++⋯+++=,得解.【详解】解:将1,1,1,1,2,1,1,3,3,1,1,4,6,4,1,⋯. 分组为(1),(1,1),(1,2,1),(1,3,3,1),(1,4,6,4,1)⋯ 则第n 组n 个数且第n 组n 个数之和为12n -, 设57a 在第n 组中, 则(1)(1)5722n n n n -+, 解得:11n =,即57a 在第11组中且为第11组中的第2个数,即为110C ,则01901571010222()1034S C C =++⋯+++=, 故选:C . 【点睛】本题考查了归纳推理及等比数列前n 项和,属于中档题.9.C解析:C 【分析】根据分析法的步骤以及不等式的性质求解即可. 【详解】由a >b >c ,且a +b +c =0得b =-a -c ,a >0,c <0.< 只要证22()3a c ac a ---< 即证2220a ac a c -+-> 即证()()()0a a c a c a c -++-> 即证()()0a a c b a c ---> 即证()()0a c a b -->故求证”索的因应是()()0a c a b -->. 故选:C . 【点睛】本题主要考查了分析法,属于中档题.10.C解析:C 【分析】根据椭圆方程,构造一个底面半径为2,高为3的圆柱,通过计算可知高相等时截面面积相等,因而由祖暅原理可得橄榄球几何体的体积的一半等于圆柱的体积减去圆锥的体积. 【详解】由椭圆方程22149x y +=,构造一个底面半径为2,高为3的圆柱在圆柱中挖去一个以圆柱下底面圆心为顶点、上底面为底面的圆锥 当截面与底面距离为()03h h ≤≤时,截圆锥得到的截面小圆半径为r 则132h r =,即23h r = 所以截面面积为224449h r ππππ-=-把y h =代入椭圆方程22149x y +=,可求得3x =±所以橄榄球形状几何体的截面面积为22449h x πππ=-由祖暅原理可得橄榄球几何体的体积为()12=24343=163V V V πππ⎛⎫=-⨯-⨯⨯ ⎪⎝⎭圆柱圆锥 故选:C 【点睛】本题考查了类比推理的综合应用,空间几何体体积的求法,属于中档题.11.B解析:B 【分析】结合题意分类讨论甲乙丙丁获奖的情况,然后考查说真话的人的个数即可确定获奖的人. 【详解】结合题意分类讨论:若甲获奖,则说真话的人为:甲乙丙,说假话的人为:丁,不合题意; 若乙获奖,则说真话的人为:丁,说假话的人为:甲乙丙,符合题意; 若丙获奖,则说真话的人为:甲乙,说假话的人为:丙丁,不合题意; 若丁获奖,则说假话的人为:甲乙丙丁,不合题意; 综上可得,获奖人为乙. 故选B. 【点睛】本题主要考查数学推理的方法,分类讨论的数学思想,属于中等题.12.B解析:B 【分析】利用题设中给出的公式进行化简,即可估算,得到答案. 【详解】由题设中的余弦公式得()()24620.20.20.20.2cos0.2112!4!6!2!nnn =-+-++-+0.040.00160.00006410.98224720=-+-+≈,故答案为B 【点睛】 本题主要考查了新信息试题的应用,其中解答中理解题意,利用题设中的公式,准确计算是解答的关键,着重考查了推理与运算能力,属于基础题.二、填空题13.【分析】由已知可归纳推测出的对称中心为再由函数平移可得的对称中心【详解】由题意题中所涉及的函数的对称中心的横坐标依次为即由此推测的对称中心为又所以其对称中心为故答案为:【点睛】本题考查归纳与推理涉及解析:2019,20202⎛⎫- ⎪⎝⎭【分析】由已知可归纳推测出1111y x x x n =+++++的对称中心为(,0)2n-,再由函数平移可得12202011120201201912019x x x y x x x x x x +++=+++=++++++++的对称中心.【详解】由题意,题中所涉及的函数的对称中心的横坐标依次为10,,1,2--,即120,,,22--由此推测1111y x x x n =+++++的对称中心为(,0)2n-.又12202011120201201912019x x x y x x x x x x +++=+++=++++++++所以其对称中心为2019,20202⎛⎫-⎪⎝⎭. 故答案为:2019,20202⎛⎫- ⎪⎝⎭【点睛】本题考查归纳与推理,涉及到函数的对称中心的问题,是一道中档题.14.③【分析】对于①②④⑤分别用举例的方法进行判断对③用反证法进行证明并判断【详解】若则但故①推不出;若则故②推不出;若则故④推不出;若则故⑤推不出;对于③即则中至少有一个大于1反证法:假设且则与矛盾因解析:③. 【分析】对于①②④⑤分别用举例的方法进行判断,对③用反证法进行证明并判断. 【详解】 若12,23a b ==,则1a b +>,但1,1a b <<,故①推不出; 若1a b ==,则2a b +=,故②推不出; 若2,3a b =-=-,则222a b +>,故④推不出; 若2,3a b =-=-,则1ab >,故⑤推不出; 对于③,即2a b +>,则,a b 中至少有一个大于1, 反证法:假设1a ≤且1b ≤, 则2a b +≤与2a b +>矛盾,因此假设不成立,,a b 中至少有一个大于1. 故答案为:③. 【点睛】本题考查用反证法、举例判断的方法判断命题是否成立,难度一般.反证法的证明步骤:先假设结论不成立,然后利用假设的结论推导出与题意矛盾的条件,即可完成证明.15.行列【分析】设位于第行第列观察表格中数据的规律可得出由此可求出的值再观察奇数行和偶数行最小数的排列可得出的值由此可得出结果【详解】设位于第行第列由表格中的数据可知第行最大的数为则解得由于第行最大的数解析:253行2列【分析】设2018位于第m 行第n 列,观察表格中数据的规律,可得出()8120188m m -<≤,由此可求出m 的值,再观察奇数行和偶数行最小数的排列,可得出n 的值,由此可得出结果. 【详解】设2018位于第m 行第n 列(),,15m n N n *∈≤≤,由表格中的数据可知,第()k k N *∈行最大的数为8k ,则()8120188m m -<≤,解得253m =,由于第252行最大的数为25282016⨯=,所以,2018是表格中第253行最小的数, 由表格中的规律可知,奇数行最小的数放在第2列,那么2n =. 因此,2018位于表格中第253行第2列. 故答案为:253行2列. 【点睛】本题考查归纳推理,解题的关键就是要结合表格中数据所呈现的规律来进行推理,考查推理能力,属于中等题.16.【解析】【分析】左边根据首数字和数字个数找规律右边为平方数得到答案【详解】等式左边:第排首字母为数字个数为等式右边:第五个等式应为:故答案为:【点睛】本题考查了找规律意在考查学生的应用能力 解析:567891011121381++++++++=【解析】 【分析】左边根据首数字和数字个数找规律,右边为平方数,得到答案. 【详解】等式左边:第n 排首字母为n ,数字个数为21n - 等式右边:2(21)n -第五个等式应为:567891011121381++++++++= 故答案为:567891011121381++++++++= 【点睛】本题考查了找规律,意在考查学生的应用能力.17.【分析】首先确定全部是1的行在此基础上确定33行和【详解】由题得全行的数都为 1 的分别是:第1行第2行第4行第8行第16行第32行又因为数 1281632… 的通项为所以第5次全行的数都为1的是第 解析:2【分析】首先确定全部是1的行,在此基础上确定33行和. 【详解】由题得,全行的数都为 1 的分别是:第1行,第2行,第4行,第8行,第16行,第32行, 又因为数 1,2,8,16,32,… 的通项为12n - , 所以第5次全行的数都为1的是第32行, 则第33行为除了首尾为1,其余都为0, ∴332S = 故答案为2 【点睛】本题考查了归纳推理的能力,意在考查学生的逻辑推理能力.18.【分析】根据题目已知的例子令即求得结果【详解】由题意可令即即x2x1=0解得故【点睛】本题主要考查的是类比推理读懂题目中整体代换的方法理解其解答过程是解题的关键属于基础题【分析】根据题目已知的例子,令11111x+=++,即11x x+=,求得结果. 【详解】 由题意,可令11111x+=++,即11x x+=,即x 2-x -1=0,解得12x +=,故11111+=++12. 【点睛】本题主要考查的是类比推理,读懂题目中整体代换的方法,理解其解答过程是解题的关键,属于基础题.19.【解析】对于等比数列通过类比有等比数列的前项积为则成等比数列解析:81248,T T T T 【解析】对于等比数列,通过类比,有等比数列{}n b 的前n 项积为n T ,则4T ,81248,T T T T ,1612T T 成等比数列.20.【解析】分析:观察数列的规律:第大项为由此能够找到这个数列的第30项详解:数列可看成……以此类推第大项为完整前大项和为当时共27项故这个数列的第30项为第8大项中的第3项即为故答案为点睛:本题考查归解析:【解析】分析:观察数列的规律:第N 大项为1N ,-12N 1N,2,N N Z ≥∈(),由此能够找到这个数列的第30项. 详解:数列可看成21,12, 31,22,13, 41,32,23,14, ……以此类推,第N 大项为1N ,-12N 1N2,N N Z ≥∈(), 完整前N 大项和为222+3++=2N N N +- 当=7N 时,共27项,故这个数列的第30项为第8大项中的第3项,即为6=23. 故答案为2.点睛:本题考查归纳推理,解题时要合理分组,探索规律并仔细验证,由特殊到一般推断出数列的规律三、解答题21.(1)tan10tan30tan30tan50tan50tan101︒︒+︒︒+︒︒=;(2)若2παβγ++=,则tan tan tan tan tan tan 1αββγγα++=;(3)证明略.【分析】找到其规律,可以发现三个角相加为90︒时,其值为1,写出对应的数学表达式证明即可. 【详解】(1)例如:tan10tan30tan30tan50tan50tan101︒︒+︒︒+︒︒=. (2)若2παβγ++=,则tan tan tan tan tan tan 1αββγγα++=.(3)证明:sin cos 12tan 2sin tan cos 2πγπγγπγγγ⎛⎫- ⎪⎛⎫⎝⎭-=== ⎪⎛⎫⎝⎭- ⎪⎝⎭又因为1tan()tan 2tan παβγγ⎛⎫+=-=⎪⎝⎭tan tan tan()tan tan 11tan tan αβαβγγαβ+∴+⋅=⋅=-化简即可得tan tan tan tan tan tan 1αββγγα++=. 【点睛】本题考查了学生发现问题,解决问题的能力,能够找到根据所给式子找到三个角的和这一规律是解决问题的关键.22.(1)()()024f f +=,()()134f f -+=,13422f f ⎛⎫⎛⎫+=⎪ ⎪⎝⎭⎝⎭.(2)一般结论为:对任意实数x 都有()()24f x f x +-=,证明见解析(3)证明见解析 【分析】()1代入计算可得所求和为定值;()2可得()()24f x f x +-=,代入计算,化简可得所求结论;()3求得()f x 的导数,判断单调性,根据单调性利用反证法可得证明.【详解】(1)()()18102464333f f +=-+-+-=, ()()111131********f f -+=----+-+-=,1311319991422244238423f f ⎛⎫⎛⎫+=--+-+-+-= ⎪ ⎪⎝⎭⎝⎭.(2)对任意实数x 都有()()24f x f x +-=. 证明:()()32112333f x f x x x x +-=-+-()()()3211223233x x x +---+-- ()()()22212222244633x x x x x x x x ⎡⎤=+-+----+-+-⎣⎦ ()222236424233x x x x =-+-++- 4=. (3)由()()22'23120f x x x x =-+=-+>知,()f x 为R 上的单调增函数.假设()00f x x ≠,则()00f x x >或()00f x x <,若()00f x x >,由()f x 为R 上的单调增函数知,()()()000ff x f x x >>;若()0f x x <,由()f x 为R 上的单调增函数知,()()()000f f x f x x <<, 则()()00f f x x ≠,与条件()()00f f x x =矛盾,故假设不成立.原命题()00f x x =成立. 【点睛】本题主要考查三次函数的图象和性质,主要是单调性的应用,反证法,考查化简运算能力,属于中档题. 23.见详解 【分析】把语言文字转化为数学表达式:2x y+≥()0,0x y >>,利用分析法进行证明,最后得到一个显然成立的不等式,证明其成立即可. 【详解】证明:正数x y ,的算术平均数为2x y+,正数x y ,∴只需证2x y+≥()0,0x y >>即可,即证x y +≥()1成立,要证()1,只需证0x y +-≥ ()2 成立即可, 要证()2,只需证20≥ ()3 成立即可,显然()3是成立的,当且仅当x y =时()3中的等号成立. 【点睛】本题考查了算数平均数和几何平均数的概念,利用分析法证明不等式是解答本题的关键;重在考查学生的逻辑推理能力和逆向思维能力;属于发散思维型试题. 24.(1)见解析;(2)见解析. 【解析】分析:(1)利用类比推理得到若两正方体的棱长的比为1:3,则它们的体积之比为1:27. (2)先根据递推式得到2345,,,a a a a 的值,再归纳出31n a n=-. 详解:(1)对应的结论为:若两正方体的棱长的比为1:3,则它们的体积之比为1:27. (2)由1121321,14n n n a a a a +-==-=+, 得23453313031132321,01,1,191562234445524a a a a --===-===-==-=-==-=-, 由此可归纳得到31n a n=-.点睛:(1)本题主要考查类比推理和不完全归纳法,意在考查学生对这些知识的掌握水平.(2)在平面中类比时,长度的比与面积的比一般类比为空间长度的比与体积的比.25.(1)见解析;(2)2(,2)21n a n n n N =+≥∈(且).【解析】分析:(Ⅰ)直接根据三角形数表中的数值求解即可;(Ⅱ)根据(Ⅰ)观察共同规律,可得()(),21,221n n a a n --=-,利用累加法可得结果.详解:(Ⅰ)观察以上三角形数表可得:()4,2a - ()3,2a =7,()5,2a - ()4,2a =9,()6,2a -()5,2a =11.(Ⅱ)依题意()()(),21,2212n n a a n n --=-≥,()1,23a =,当2n ≥时,()()()()()()()()()()(),21,22,21,23,22,2,21,2...n n n a a a a a a a a -=+-+-++- ,()()()23213357 (213122)n n n n +-=+++++-=+-=+,当1n =时,()1,23a =符合上式所求()2,221n a n n n N (且)=+≥∈. 点睛:本题主要考查归纳推理以及“累加法”的应用,属于中档题.归纳推理的一般步骤: 一、通过观察个别情况发现某些相同的性质. 二、从已知的相同性质中推出一个明确表述的一般性命题(猜想). 常见的归纳推理分为数的归纳和形的归纳两类:(1) 数的归纳包括数的归纳和式子的归纳,解决此类问题时,需要细心观察,寻求相邻项及项与序号之间的关系,同时还要联系相关的知识,如等差数列、等比数列等;(2) 形的归纳主要包括图形数目的归纳和图形变化规律的归纳. 26.(1)135+-++()()()1211n nn n --=-(*N n ∈);(2)见解析.【解析】 试题分析:(1)结合所给的规律可猜想第n 个等式为135=+-++ ()()()1211n nn n--=-(*N n ∈);(2)首先说明n=1等式成立,然后假设当n k =(*N k ∈)时,等式成立,证明当1n k =+时等式成立即可. 试题(1)第n 个等式为135=+-++ ()()()1211n nn n --=-(*N n ∈);(2)用数学归纳法证明: ①当1n =时,等式显然成立;②假设当n k =(*N k ∈)时,等式成立, 即135-+-++ ()()()1211k kk k --=-则当1n k =+时,135-+-++ ()()()()1121121k k k k +--+-+()()()11121k k k k +=-+-+= ()()1121k k k +--++()()111k k +=-+所以当1n k =+时,等式成立. 由①②知,135-+-++ ()()()1211nnn --=-(*N n ∈)。
辅导专家卷苏明义解读2008年高考试题1

辅导专家苏明义解读2008年高考大纲物理来源:学科网点击数:45时间:2008-3-13录入:lipstickxin【字体:】主持人:中国教育新闻网的各位网友好,今天我们有幸邀请到北京新干线学校高考专家组的苏明义老师为我们解读2008年高考物理大纲的变化。
苏老师,向我们网友打个招呼吧。
苏明义:各位网友好,同学们大家好。
主持人:苏老师,请给我们讲一下2008年高考大纲和去年有什么变化好吗?苏明义:大家关心的是考试内容和要求,还有试卷的结构,题的难度,在这些方面实际上没有太大的变化。
高考需要不断的改革,不可能有明显的太大的变化。
马上要进行新课,各省在进入课改以后的高考,旧大纲的考试模式变化就不是很大了,从我们拿到的大纲情况看,变化的部分主要是在题型示例方面的变化,2008年考纲里面把2008年的题型示例选了进来,反映最近一个时期的形式,这样的命题代表了一些想法,题的变化值得我们关注。
主持人:今年题型方面有没有什么变化?苏明义:题目的内容,角度的变化是值得考生注意的,但07年和08年基本没有什么变化。
主持人:前几天我们收到一位网友的提问,问理综类08年是否会出现生物、化学、物理三科结合的考题,即完整意义上的理科综合题?苏明义:不能绝对肯定的说不会出现,但是可能性是非常小的,有两个原因,这个学科的知识本身主干知识不搭界,可能与一个素材结合在一起,化学和物理并不占很大的命题,物理是主要的学科,生物和化学并不是这样,这几年主要是体现在学科内容。
主持人:苏老师,您对2008年物理新课标是否有所涉猎?如果有,您认为新大纲和普通的大纲有什么区别?苏明义:从知识内容和要求来说没有什么明显的变化,无论是新旧大纲,是理综的,还是单科物理的,凡是这样不同的模式,不同的版本,应该都统一在高考模式下面进行的,是不同的形式在考,从具体知识内容和要求上没有太大的变化,由于新课标版的大纲由于各省的方案是不一样的,所以这里面的变化是不同省之间差异是比较大的,有的省是很明确,在三系列的三到一到五之间删除哪些内容不作为高考内容,有些省可能就不这样的规定,可能都任选。
(易错题)高中数学选修1-2第一章《统计案例》测试(含答案解析)
一、选择题1.在一个质地均匀的小正方体的六个面中,三个面标0,两个面标1,一个面标2,将这个小正方体连续抛掷两次,若向上的数字的乘积为偶数,则该乘积为非零偶数的概率为( ) A .14 B .89 C .116D .5322.下列说法:①对于独立性检验,2χ的值越大,说明两事件相关程度越大;②以模型kx y ce =去拟合一组数据时,为了求出回归方程,设ln z y =,将其变换后得到线性方程0.34z x =+,则c ,k 的值分别是4e 和0.3;③根据具有线性相关关系的两个变量的统计数据所得的回归直线方程y a bx =+中,2b =,1x =,3y =,则1a =;④通过回归直线y bx a =+及回归系数b ,可以精确反映变量的取值和变化趋势,其中正确的个数是( ) A .1B .2C .3D .43.甲、乙、丙、丁4个人进行网球比赛,首先甲、乙一组,丙、丁一组进行比赛,两组的胜者进入决赛,决赛的胜者为冠军、败者为亚军.4个人相互比赛的胜率如右表所示,表中的数字表示所在行选手击败其所在列选手的概率.那么甲得冠军且丙得亚军的概率是( ) A .0.15 B .0.105 C .0.045 D .0.214.某研究性学习小组调查研究学生玩手机对学习的影响,部分统计数据如表经计算2K的值,则有()的把握认为玩手机对学习有影响.A.95%B.99%C.99.5%D.99.9%5.从345678910,1112,,,,,,,,中不放回地依次取2个数,事件A=“第一次取到的数可以被3整除”,B=“第二次取到的数可以被3整除”,则()P B|?A=( )A.59B.23C.13D.296.若对于变量x的取值为3,4,5,6,7时,变量y对应的值依次分别为4.0,2.5,-0.5,-1,-2;若对于变量u的取值为1,2,3,4时,变量v对应的值依次分别为2,3,4,6,则变量x和y,变量u和v的相关关系是()A.变量x和y是正相关,变量u和v是正相关B.变量x和y是正相关,变量u和v是负相关C.变量x和y是负相关,变量u和v是负相关D.变量x和y是负相关,变量u和v是正相关7.下面是22⨯列联表:则表中a b,的值分别为()A.84,60 B.42,64 C.42, 74 D.74, 428.下列结论中正确的是()A.若两个变量的线性关系性越强,则相关系数的绝对值越接近于0B.回归直线至少经过样本数据中的一个点C.独立性检验得到的结论一定正确D.利用随机变量2x来判断“两个独立事件,X Y的关系”时,算出的2x值越大,判断“,X Y 有关”的把握越大9.两个变量y与x的回归模型中,分别选择了4个不同模型,对于样本点()11,x y,()22,x y ,…,(),n n x y ,可以用()()22121ˆ1ni i i n ii y yR y y ==-=--∑∑来刻画回归的效果,已知模型1中20.96R =,模型2中23{5x yy x -==-,模型3中20.55R =,模型4中20.41R =,其中拟合效果最好的模型是( ) A .模型1 B .模型2C .模型3D .模型410.工人月工资(元)关于劳动生产率x(千元)的回归方程为,下列说法中正确的个数是( )①劳动生产率为1000元时,工资为730元; ②劳动生产率提高1000元,则工资提高80元; ③劳动生产率提高1000元,则工资提高730元; ④当月工资为810元时,劳动生产率约为2000元. A .1B .2C .3D .411.袋中有6个黄色、4个白色的乒乓球,做不放回抽样,每次任取1个球,取2次,则关于事件“直到第二次才取到黄色球”与事件“第一次取到白球的情况下,第二次恰好取得黄球”的概率说法正确的是( )A .事件“直到第二次才取到黄色球”与事件“第一次取得白球的情况下,第二次恰好取得黄球”的概率都等于23 B .事件“直到第二次才取到黄色球”与事件“第一次取得白球的情况下,第二次恰好取得黄球”的概率都等于415C .事件“直到第二次才取到黄色球”的概率等于23,事件“第一次取得白球的情况下,第二次恰好取得黄球”的概率等于415D .事件“直到第二次才取到黄色球”的概率等于415,事件“第一次取得白球的情况下,第二次恰好取得黄球”的概率等于2312.抛掷一枚质地均匀的骰子两次,记事件{两次的点数均为奇数},{两次的点数之和小于},则( ) A .B .C .D .二、填空题13.甲、乙两位同学进行篮球三分球投篮比赛,甲每次投中的概率为13,乙每次投中的概率为12,每人分别进行三次投篮.乙恰好比甲多投进2次的概率是______. 14.已知如下四个命题:①在线性回归模型中,相关指数2R 表示解释变量x 对于预报变量y 的贡献率,2R 越接近于0,表示回归效果越好;②在回归直线方程ˆ0.812yx =-中,当解释变量x 每增加一个单位时,预报变量ˆy平均增加0.8个单位;③两个变量相关性越强,则相关系数的绝对值就越接近于1;④对分类变量X 与Y ,对它们的随机变量2K 的观测值k 来说,k 越小,则“X 与Y 有关系”的把握程度越大.其中正确命题的序号是__________.15.某大学进行自主招生时,需要进行逻辑思维和阅读表达两项能力的测试.学校对参加测试的200名学生的逻辑思维成绩、阅读表达成绩以及这两项的总成绩进行了排名.其中甲、乙、丙三位同学的排名情况如下图所示:得出下面四个结论:①甲同学的阅读表达成绩排名比他的逻辑思维成绩排名更靠前 ②乙同学的逻辑思维成绩排名比他的阅读表达成绩排名更靠前 ③甲、乙、丙三位同学的逻辑思维成绩排名中,甲同学更靠前 ④乙同学的总成绩排名比丙同学的总成绩排名更靠前 则所有正确结论的序号是_________. 16.已知x 、y 之间的一组数据如下: x 0 1 2 3 y8264则线性回归方程ˆya bx =+所表示的直线必经过点________. 17.某学生在上学路上要经过4个路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是13,那么该生在上学路上到第3个路口首次遇到红灯的概率为__________.18.关于变量,x y 的一组样本数据11()a b ,,22()a b ,,……,(),n n a b (2n ≥,12,,,n a a a ⋅⋅⋅不全相等)的散点图中,若所有样本点(,)i i a b (1,2,,i n =⋅⋅⋅)恰好都在直线21y x =-+上,则根据这组样本数据推断的变量,x y 的相关系数为_____________.19.排球比赛实行“五局三胜制”.某次比赛中,中国女排和M 国女排相遇,统计以往数据可知,每局比赛中国女排获胜的概率为23,M 国女排获胜的概率为13,则中国女排在先输一局的情况下最终获胜的概率为________.20.投到某出版社的稿件,先由两位初审专家进行评审,若能通过两位初审专家的评审,则直接予以录用,若两位初审专家都未予通过,则不予录用,若恰能通过一位初审专家的评审,则再由第三位专家进行复审,若能通过复审专家的评审,则予以录用,否则不予录用.设稿件能通过各初审专家评审的概率均为12,复审的稿件能通过评审的概率为14,各专家独立评审,则投到该出版社的1篇稿件被录用的概率为__________.三、解答题21.随着生活质量的提升,家庭轿车保有量逐年递增.方便之余却加剧了交通拥堵和环保问题.绿色出行引领时尚,共享单车进驻城市黄泽市有统计数据显示.2020年该市共享单车用户年龄等级分布如图1所示,一周内市民使用单车的频率分布扇形图如图2所示.若将共享单车用户按照年齡分为“年轻人”(20岁~391岁)和“非年轻人”( 19岁及以下或者40岁及以上)两类,将一周内使用的次数为6次或6次以上的经常使用共享单车的称为“单车族”.使用次数为5次或不足5次的称为“非单车族”.已知在“单车族”中有56是“年轻人”.(1)现对该市市民进行“经常使用共享单车与年龄关系”的调查,采用随机抽样的方法,抽取一个容量为400的样本,请你根据图表中的数据,补全下列22⨯列联表,并判断是否有95%的把握认为经常使用共享单车与年龄有关?使用共享单车情况与年龄列联表年轻人 非年轻人 合计单车族 非单车族 合计是“非年轻人”的人数为随机变量,X 求X 的分布列与期望. 参考数据:独立性检验界值表20()P K k ≥0.15 0.10 0.05 0.025 0.010k2.0722.7063.8415.0246.635其中,()()()()()2,n ad bc n a b c d K a b c d a c b d -=+++=++++(注:保留三位小数). 22.2020年10月1日既是中华人民共和国第71个国庆日,又是农历中秋节,双节同庆,很多人通过短视频APP 或微信、微博表达了对祖国的祝福.某调查机构为了解通过短视频APP 或微信、微博表达对祖国祝福的人们是否存在年龄差异,通过不同途径调查了数千个通过短视频APP 或微信、微博表达对祖国祝福的人,并从参与者中随机选出200人,经统计这200人中通过微信或微博表达对祖国祝福的有160人.将这160人按年龄分组:第1组[)15,25,第2组[)25,35,第3组[)35,45,第4组[)45,55,第5组[]55,65,得到的频率分布直方图如图所示:(1)求a 的值并估计这160人的平均年龄;(2)把年龄在第1,2,3组的居民称为青少年组,年龄在第4,5组的居民称为中老年组,选出的200人中通过短视频APP 表达对祖国祝福的中老年人有26人,问是否有99%的把握认为是否通过微信或微博表达对祖国的祝福与年龄有关? 附:()20P K k > 0.150.10 0.05 0.025 0.010 0.005 0.0010k2.072 2.7063.841 5.024 6.635 7.879 10.828()()()()()22n ad bc K a b c d a c b d -=++++23.2019年6月25日,《固体废物污染环境防治法(修订草案)》初次提请全国人大常委会审议,草案对“生活垃圾污染环境的防治”进行了专章规定.草案提出,国家推行生活垃圾分类制度.为了了解人民群众对垃圾分类的认识,某市环保部门对该市市民进行了一次垃圾分类网络知识问卷调查,每一位市民仅有一次参加机会,通过随机抽样,得到参加问卷调查的1000人(其中450人为女性)的得分(满分:100分)数据,统计结果如表所示: 得分[)30,40 [)40,50 [)50,60 [)60,70 [)70,80 [)80,90 []90,100男性人数 15 90 130 100 125 60 30 女性人数 1060701501004020(1)由频数分布表可以认为,此次问卷调查的得分Z 服从正态分布,210N ,近似为这1000人得分的平均值(同一组数据用该组区间的中点值作为代表),请利用正态分布的知识求()50.594P Z <<;(2)把市民分为对垃圾分类“比较了解”(不低于60分的)和“不太了解”(低于60分的)两类,请完成如下22⨯列联表,并判断是否有99%的把握认为市民对垃圾分类的了解程度与性10名.再从这10人中随机抽取3人,求抽取的3人中男性人数的分布列及数学期望.参考数据:14.5≈;②若()2,XN μσ,则()0.6827P X μσμσ-<<+=,()220.9545P X μσμσ-<<+=,()330.9973P X μσμσ-<<+=;③()()()()()2n ad bc K a b c d a c b d -=++++, .n a b c d =+++ 24.某种疾病可分为Ⅰ、Ⅱ两种类型.为了解该疾病类型与性别的关系,在某地区随机抽取了患该疾病的病人进行调查,其中女性是男性的2倍,男性患Ⅰ型病的人数占男性病人的56,女性患Ⅰ型病的人数占女性病人的13. (1)若在犯错误的概率不超过0.005的前提下认为“所患疾病类型”与“性别”有关,求男性患者至少有多少人?(2)某药品研发公司欲安排甲乙两个研发团队来研发此疾病的治疗药物.两个团队各至多安排2个接种周期进行试验.甲团队研发的药物每次接种后产生抗体的概率为p ,每人每次接种花费()0m m >元,每个周期至多接种3次,第一个周期连续2次出现抗体则终止本接种周期进入第二个接种周期,否则需依次接种至第一周期结束,再进入第二周期;第二接种周期连续2次出现抗体则终止试验,否则需依次接种至至试验结束;乙团队研发的药物每次接种后产生抗体的概率为q ,每人每次花费()0n n >元,每个周期接种3次,每个周期必须完成3次接种,若一个周期内至少出现2次抗体,则该周期结束后终止试验,否则进入第二个接种周期.假设两个研发团队每次接种后产生抗体与否均相互独立.①若甲团队的试验平均花费大于乙团队的试验平均花费,求p 、q 、m 、n 满足的关系式;②若m n =,2p q =,从两个团队试验的平均花费考虑,该公司应选择哪个团队进行药品附:()()()()()22n ad bc K a b c d a c b d -=++++,()20P K k ≥ 0.10 0.05 0.01 0.005 0.001 0k2.7063.8416.6357.87910.82825.某基地蔬菜大棚采用水培、无土栽培方式种植各类蔬菜.过去50周的资料显示,该地周光照量X (小时)都在30小时以上,其中不足50小时的周数有5周,不低于50小时且不超过70小时的周数有35周,超过70小时的周数有10周.根据统计,该基地的西红柿增加量y (百斤)与使用某种液体肥料x (千克)之间对应数据为如图所示的折线图.(1)依据数据的折线图,是否可用线性回归模型拟合y 与x 的关系?请计算相关系数r 并加以说明(精确到0.01).(若||0.75r >,则线性相关程度很高,可用线性回归模型拟合)(2)蔬菜大棚对光照要求较大,某光照控制仪商家为该基地提供了部分光照控制仪,但每周光照控制仪最多可运行台数受周光照量X 限制,并有如下关系: 周光照量X (单位:小时)3050X << 5070X ≤≤ 70X >光照控制仪最多可运行台数 321若某台光照控制仪运行,则该台光照控制仪周利润为3000元;若某台光照控制仪未运行,则该台光照控制仪周亏损1000元.若商家安装了3台光照控制仪,求商家在过去50周周总利润的平均值.附:相关系数公式12211()()()()niii n niii i x x y y r x x y y ===--=--∑∑∑0.30.55≈,0.90.95≈.26.某花圃为提高某品种花苗质量,开展技术创新活动,分别用甲、乙两种方法培育该品种花苗.为比较两种培育方法的效果,选取了40棵花苗,随机分成两组,每组20棵.第一组花苗用甲方法培育,第二组用乙方法培育.培育完成后,对每棵花苗进行综合评分,绘制了如图所示的茎叶图:(1)分别求两种方法培育的花苗综合评分的中位数.你认为哪一种方法培育的花苗综合评分更高?并说明理由.(2)综合评分超过80的花苗称为优质花苗,填写下面的列联表,并判断是否有99.5%的把握认为优质花苗与培育方法有关?优质花苗 非优质花苗 合计甲培育法 乙培育法 合计附:()()()()()22n ad bc K a b c d a c b d -=++++. ()20P K k ≥ 0.010 0.050 0.025 0.010 0.005 0.001 0k2.7063.8415.0246.6357.87910.828【参考答案】***试卷处理标记,请不要删除一、选择题 1.D 解析:D 【分析】首先确定是条件概率,在出现数字乘积为偶数的前提下,乘积为非零偶数的概率, 首先求两次数字乘积为偶数的概率, 然后两次为非零偶数的概率,再按照条件概率的公式求解. 【详解】两次数字乘积为偶数,可先考虑其反面——只需两次均出现1向上,概率是22169⎛⎫= ⎪⎝⎭, 所以两次数字乘积为偶数的概率P =228169⎛⎫-= ⎪⎝⎭ ; 若乘积非零且为偶数,需连续两次抛掷小正方体的情况为(1,2)或(2,1)或(2,2),P =111152366636⨯⨯+⨯=,.故所求条件概率为55368329P ==.故选:D 【点睛】本题主要考查了条件概率的计算和独立事件,考查了学生的计算能力,属于基础题.2.C解析:C 【分析】根据独立性检验、非线性回归方程以及回归直线方程相关知识进行判断. 【详解】对于命题①,根据独立性检验的性质知,两个分类变量2χ越大,说明两个分类变量相关程度越大,命题①正确;对于命题②,由kxy ce =,两边取自然对数,可得ln ln y c kx =+,令ln z y =,得ln z kx c =+,0.34z x =+,所以ln 40.3c k =⎧⎨=⎩,则40.3c e k ⎧=⎨=⎩,命题②正确;对于命题③,回归直线方程y a bx =+中,3211a y bx =-=-⨯=,命题③正确; 对于命题④,通过回归直线y bx a =+及回归系数b ,可估计和预测变量的取值和变化趋势,命题④错误.故选C. 【点睛】本题考查了回归直线方程、非线性回归方程变换以及独立性检验相关知识,考查推理能力,属于中等题.3.C解析:C若甲得冠军且丙得亚军,则甲、乙比赛甲获胜,丙、丁比赛丙获胜,决赛甲获胜. 【详解】甲、乙比赛甲获胜的概率是0.3, 丙、丁比赛丙获胜的概率是0.5, 甲、丙决赛甲获胜的概率是0.3, 根据独立事件的概率等于概率之积,所以, 甲得冠军且丙得亚军的概率:0.30.50.30.045⨯⨯=. 故选C. 【点睛】本题考查独立事件的概率,考查分析问题解决问题的能力.4.C解析:C 【解析】分析:利用公式求得观测值2K ,对照数表,即可得出正确的结论. 详解:根据列联表可得()223042168=1020101218K ⨯⨯-⨯=⨯⨯⨯,27.8791010.828K <=<,对照数表知,有99.5%的把握认为玩手机对学习有影响,故选C.点睛:本题考查了独立性检验的应用问题,是基础题目. 独立性检验的一般步骤:(1)根据样本数据制成22⨯列联表;(2)根据公式()()()()()22n ad bc K a b a d a c b d -=++++计算2K 的值;(3) 查表比较2K 与临界值的大小关系,作统计判断.5.C解析:C 【解析】分析:先求()P AB ,()P A ,再根据()(|)()P AB P B A P A =得结果. 详解:因为214421101022(),()155C C P AB P A C C ====, 所以2()115(|)2()35P AB P B A P A ===, 选C.点睛:本题考查条件概率,考查基本求解能力.6.D解析:D变量x 增加,变量y 减少,所以变量x 和y 是负相关;变量u 增加,变量v 增加,所以变量u 和v 是正相关,因此选D.7.B解析:B 【解析】因2163a +=,故42a =,又22a b +=,则64b = ,应选答案B 。
(易错题)高中数学选修1-2第三章《推理与证明》测试(含答案解析)(1)
一、选择题1.某校实行选科走班制度,张毅同学的选择是物理、生物、政治这三科,且物理在A 层班级,生物在B 层班级,该校周一上午课程安排如下表所示,张毅选择三个科目的课各上一节,另外一节上自习,则他不同的选课方法有 第一节 第二节 第三节 第四节 地理B 层2班 化学A 层3班 地理A 层1班 化学A 层4班 生物A 层1班 化学B 层2班 生物B 层2班 历史B 层1班 物理A 层1班 生物A 层3班 物理A 层2班 生物A 层4班 物理B 层2班 生物B 层1班 物理B 层1班 物理A 层4班 政治1班物理A 层3班政治2班政治3班A .8种B .10种C .12种D .14种2.正整数按下表的规律排列,则上起第2005行,左起第2006列的数应为( )A .22005B .22006C .20052006+D .20052006⨯3.下列推理过程不是演绎推理的是( )①一切奇数都不能被2整除,2019是奇数,2019不能被2整除; ②由“正方形面积为边长的平方”得到结论:正方体的体积为棱长的立方; ③在数列{}n a 中,()111,312n n a a a n -==-≥,由此归纳出{}n a 的通项公式; ④由“三角形内角和为180︒”得到结论:直角三角形内角和为180︒. A .①②B .③④C .②③D .②④4.李雷、韩梅梅、张亮、刘静四人考上大学后,就读于法学、教育学、医学和管理学四个学科,就他们分别就读于哪个学科,同学们做了如下猜测: 同学甲猜,李雷就读于管理学,张亮就读于法学; 同学乙猜,韩梅梅就读于管理学,刘静就读于医学; 同学丙猜,李雷就读于管理学,张亮就读于教育学; 同学丁猜,韩梅梅就读于法学,刘静就读于教育学.结果恰有三位同学的猜测各对一半,只有一位同学全部猜对,那么李雷、韩梅梅、张亮、刘静四人分别就读的学科是( ) A .管理学、医学、法学、教育学 B .教育学、管理学、医学、法学 C .管理学、法学、教育学、医学D .管理学、教育学、医学、法学5.如图中的三角形图案称为谢宾斯基三角形.在四个三角形图案中,着色的小三角形的个数依次构成数列{}n a 的前4项,则{}n a 的通项公式可以为( )A .21n a n =-B .21nn a =- C .3nn a =D .13-=n n a6.将正整数1,2,3,4,,,n 按第k 组含1k +个数分组:()()()1,2,3,4,5,6,7,8,9,,那么2019所在的组数为( ) A .62B .63C .64D .657.斐波纳契数列,又称黄金分割数列,指的是这样一个数列:1,1,2,3,5,8,13,21,34,55,89,⋯,在数学上,斐波纳契数列{}n a 定义为:1a 1=,2a 1=,n 2n n 1a a a ++=+,斐波纳契数列有种看起来很神奇的巧合,如根据n 2n n 1a a a ++=+可得n n 2n 1a a a ++=-,所以()()()12n 3243n 2n 1n 22n 2a a a a a a a a a a a a 1++++++⋯+=-+-+⋯+-=-=-,类比这一方法,可得2221210a a a (++⋯= )A .714B .1870C .4895D .48968.0x y =,则0x y ==,假设为( )A .,x y 都不为0B .,x y 不都为0C .,x y 都不为0,且x y ≠D .,x y 至少有一个为09.222233+=333388+=4441515+=⋅⋅⋅66n nm m+=(m 、n 均为正实数),根据以上等式,可推测m 、n 的值,则m n +等于( )A .40B .41C .42D .4310.有6名选手参加演讲比赛,观众甲猜测:1、2、6号选手中的一位获得第一名;观众乙猜测:4、5、6号选手都不可能获得第一名;观众丙猜测:4号或5号选手得第一名;观众丁猜测:3号选手不可能得第一名.比赛后发现没有并列名次,且甲、乙、丙、丁中只有1人猜对比赛结果,此人是( ) A .甲B .乙C .丙D .丁11.我国古代数学名著《九章算术》的论割圆术中有:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣.”它体现了一种无限与有限的转化过程.比如在表达式11111+++中“”即代表无限次重复,但原式却是个定值,它可以通过方程11x x +=,求得x =.=AB .3C .2D .12.“干支纪年法”是中国历法上自古以来使用的纪年方法,甲、乙、丙、丁、戊、己、庚、辛、壬、癸被称为“十天干”,子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥叫做“十二地支”.“天干”以“甲”字开始,“地支”以“子”字开始,两者按干支顺序相配,组成了干支纪年法,其相配顺序为:甲子、乙丑、丙寅…癸酉,甲戌、乙亥、丙子…癸未,甲申、乙酉、丙戌…癸巳,…,共得到60个组合,称六十甲子,周而复始,无穷无尽.2019年是“干支纪年法”中的己亥年,那么2026年是“干支纪年法”中的 A .甲辰年B .乙巳年C .丙午年D .丁未年二、填空题13.等差数列{}n a 的公差为d ,前n 项和为S n ,对于常数m ∈N *,则数列 {}(1)-+m n mn S S 为等差数列,公差为m 2d.类似地,等比数列{}n b 的公比为q ,前n 项积为T n ,则数列(1)m n mn T T +⎧⎫⎨⎬⎩⎭为等比数列,公比为____. 14.已知等差数列{}()*n a n N∈中,若10100a=,则等式()121220192019,*n n a a a a a a n n N -+++=+++<∈恒成立;运用类比思想方法,可知在等比数列{}()*n b n N ∈中,若1001b=,则与此相应的等式_________________恒成立.15.现将甲、乙、丙、丁四个人安排到座位号分别是1,2,3,4的四个座位上,他们分别有以下要求:甲:我不坐座位号为1和2的座位;乙:我不坐座位号为1和4的座位;丙:我的要求和乙一样;丁:如果乙不坐座位号为2的座位,那么我就不坐座位号为1的座位.那么坐在座位号为3的座位上的是________. 16.观察下列恒等式:12tan tan tan 2ααα=+,14tan 2tan 2tan tan 4αααα=++,18tan 2tan 24tan 4tan tan8ααααα=+++,,请你把结论推广到一般情形,则得到的第n 个等式为___________________________________.17.某班级A,B,C,D 四位学生A B C D 、、、参加了文科综合知识竞赛,在竞赛结果公布前,地理老师预测得冠军的是A 或B ;历史老师预测得冠军的是C ;政治老师预测得冠军的不可能是A 或D ;语文老师预测得冠军的是B ,而班主任老师看了竞赛结果后说以上只有两位老师都说对了,则得冠军的是_____。
【1月刊】2024年1月江苏省高三高频错题数学+答案解析
【1月刊】2024年1月江苏省高三高频错题(累计作答36425人次,平均得分率19.14%)一、单选题:本题共6小题,每小题5分,共30分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.已知双曲线C :的左,右焦点分别是,,左,右顶点分别是,,离心率为2,点P 在C 上,若直线,的斜率之和为,的面积为,则()A.1B.C.D.22.临近高考,同学们写祝福卡片许美好愿望.某寝室的5位同学每人写一张祝福卡片放在一起,打乱后每人从中随机抽取一张卡片,已知有同学拿到自己写的祝福卡,则至少有3位同学摸到自己写的祝福卡片的概率为()A.B.C.D.3.四面体ABCD 的所有棱长都是3,点M ,N ,P 分别在棱AB ,AD ,CD 上,,,,平面MNP 交BC 于点Q ,则BQ 的长为()A. B.C.D.14.若过点可以作曲线的两条切线,切点分别为,,则的取值范围是()A. B.C. D.5.若函数的值域为则实数m 的可能值共有()A.1个 B.2个C.3个D.4个6.已知函数的导函数为,且对任意的实数x 都有是自然对数的底数,且,若关于x 的不等式仅有1个整数解,则实数m 的取值范围是()A.B.C.D.二、多选题:本题共11小题,共55分。
在每小题给出的选项中,有多项符合题目要求。
全部选对的得5分,部分选对的得2分,有选错的得0分。
7.三棱柱中,,点O 是的外心,平面ABC ,,二面角为,则下列选项中正确的是()A.三棱柱的侧面积为B.与所成角的余弦值为C.点到平面的距离为D.若四棱锥各顶点都在同一球面上,则该球的半径为8.已知在三棱锥中,,,,,设二面角的大小为,M是PC的中点.当变化时,下列说法正确的是()A.存在,使得B.存在,使得平面PABC.点M在某个球面上运动D.当时,三棱锥外接球的体积为9.在三棱锥中,对棱所成角为,平面ABC和平面BCD的夹角为,直线AB与平面BCD所成角为,点P为平面ABC和平面BCD外一定点,则下列结论正确的是()A.过点P且与直线所成角都是的直线有2条B.过点P且与平面ABC和平面BCD所成角都是的直线有3条C.过点P且与平面ABC和平面BCD所成角都是的直线有3条D.过点P与平面BCD所成角为,且与直线AB成的直线有2条10.已知函数的图象是连续不间断的,函数的图象关于点对称,在区间上单调递增.若对任意恒成立,则下列选项中m 的可能取值有()A. B. C. D.11.已知函数,下列说法正确的是()A.对于都存在零点B.若恒成立,则正实数a的最小值为C.若图像与直线分别交于A,B两点,则的最小值为D.存在直线与的图像分别交于A,B两点,使得在A处的切线与在B处的切线平行12.已知函数,若,且,则()A. B.C.D.13.已知圆锥的顶点为P ,底面圆心为O ,AB 为底面直径,,点C 在底面圆周上,且二面角为,则()A.该圆锥的体积为B.该圆锥的侧面积为C.D.的面积为14.已知函数的定义域为R ,,则()A. B. C.是偶函数D.为的极小值点15.在标准温度和大气压下,人体血液中氢离子的物质的量的浓度单位,记作和氢氧根离子的物质的量的浓度单位,记作的乘积等于常数已知pH 值的定义为,健康人体血液的pH 值保持在之间,那么健康人体血液中的可以为参考数据:,()A.B.C.D.16.已知A ,B 为圆上的两点,P 为直线上一动点,则()A.直线l 与圆O 相离B.当A ,B 为两定点时,满足的点P 最多有2个C.当时,的最大值是D.当PA ,PB 为圆O 的两条切线时,直线AB 过定点17.A ,B 为随机事件,已知,,下列结论中正确的是()A.若A ,B 为互斥事件,则B.若A ,B 为互斥事件,则C.若A ,B 是相互独立事件,D.若,则三、填空题:本题共12小题,每小题5分,共60分。
苏教版高三数学选修1-2同步课堂精练:2.1.3推理案例赏析 Word版含答案
… 由以上规律,可得出 f(n+1)-f(n)=4n, 因为 f(n+1)-f(n)=4n,所以 f(n+1)=f(n)+4n.所以 f(n)=f(n-1)+4(n-1) =f(n-2)+4(n-1)+4(n-2)=f(n-3)+4(n-1)+4(n-2)+4(n-3)
=… =f+4(n-1)+4(n-2)+4(n-3)+…+4=2n2-2n+1.
=1
1 2
1
1 n
3 2
1 2n
.
2
1 2
④在数列{an}中,a1=1, an
1
2
an1
1 an1
(n≥2),由此归纳出{an}的通项公式
2.“平面内到两定点 F1,F2 的距离之和为定值的点的轨迹是椭圆(大前提),平面内动点
M 到两定点 F1(-2,0),F2(2,0)的距离之和为 4(小前提),则 M 点的轨迹是椭圆(结论).”此
“正三棱锥”形的展品,其中第 1 堆只有一层,就一个球;第 2,3,4,…堆最底层(第一层)
分别按下图所示方式固定摆放,从第二层开始,每层的小球自然垒放在下一层之上,第 n 堆
第 n 层就放一个乒乓球.以 f(n)表示第 n 堆的乒乓球总数,则 f(3)=________,f(n)
=________(答案用含 n 的式子表示).
(1)求出 f(5)的值; (2)利用合情推理的“归纳推理思想”,归纳出 f(n+1)与 f(n)之间的关系式,并根据你
2
1
得到的关系式求出 f(n)的表达式;
(3)求 1 1 1 … 1 的值.
f 1 f 2 1 f 3 1
f n 1
