常见刚体的转动惯量
转动惯量计算方法

转动惯量计算方法转动惯量是描述物体对转动运动的惯性大小的物理量,它在物理学中有着重要的应用。
在工程和科学领域中,我们经常需要计算各种物体的转动惯量,以便更好地理解它们的转动特性。
本文将介绍一些常见的转动惯量计算方法,希望能够帮助读者更好地理解和运用这一概念。
首先,我们来介绍一下关于点质点的转动惯量计算方法。
对于一个质点,其转动惯量可以通过以下公式计算:\[ I = mr^2 \]其中,m为质点的质量,r为质点到转轴的距离。
这个公式表明,转动惯量与质点的质量成正比,与质点到转轴的距离的平方成正比。
这是一个非常基础的转动惯量计算方法,适用于质点的简单情况。
接下来,我们来介绍一下关于刚体的转动惯量计算方法。
对于一个刚体,其转动惯量可以通过积分的方法计算:\[ I = \int r^2 dm \]其中,r为刚体上各个质点到转轴的距离,dm为刚体上各个质点的质量微元。
通过对整个刚体进行积分,我们可以得到刚体的转动惯量。
这个方法适用于各种形状的刚体,可以比较准确地计算出其转动惯量。
此外,对于一些特殊形状的物体,我们也可以利用一些特殊的公式来计算其转动惯量。
比如对于绕轴旋转的圆环,其转动惯量可以通过以下公式计算:\[ I = mr^2 \]其中,m为圆环的质量,r为圆环的半径。
这个公式适用于绕轴旋转的圆环,可以方便地计算出其转动惯量。
总结一下,转动惯量的计算方法有很多种,我们可以根据具体的情况选择合适的方法来计算。
对于质点,可以利用简单的公式进行计算;对于刚体,则可以通过积分的方法得到转动惯量;对于一些特殊形状的物体,也可以利用特殊的公式来计算。
希望本文介绍的内容能够对大家有所帮助,让大家对转动惯量的计算有更深入的理解。
转动惯量公式表
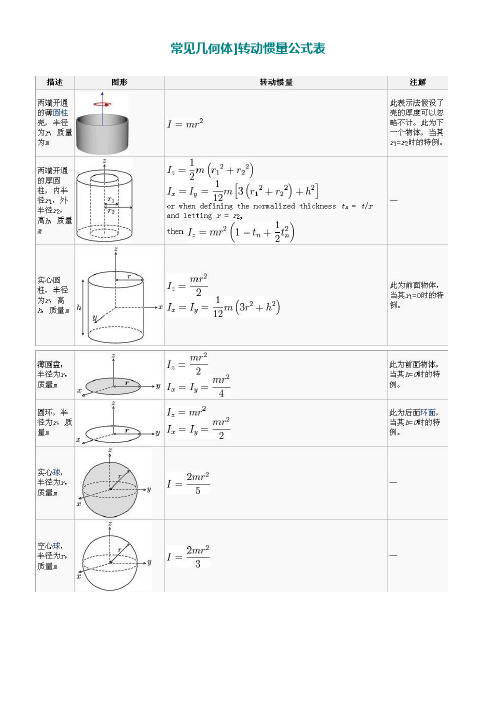
常见几何体]转动惯量公式表关于细杆当回转轴过杆的中点并垂直于杆时;J=m(L^2)/12 其中m是杆的质量,L是杆的长度。
当回转轴过杆的端点并垂直于杆时:J=m(L^2)/3 其中m是杆的质量,L是杆的长度。
关于圆柱体当回转轴是圆柱体轴线时;J=m(r^2)/2其中m是圆柱体的质量,r是圆柱体的半径。
关于细圆环当回转轴通过中心与环面垂直时,J=mR^2;当回转轴通过边缘与环面垂直时,J=2mR^2;R为其半径关于薄圆盘当回转轴通过中心与盘面垂直时,J=﹙1/2﹚mR^2;当回转轴通过边缘与盘面垂直时,J=﹙3/2﹚mR^2;R为其半径关于空心圆柱当回转轴为对称轴时,J=﹙1/2﹚m[(R1)^2+(R2)^2];R1和R2别离为其内外半径。
关于球壳当回转轴为中心轴时,J=﹙2/3﹚mR^2;当回转轴为球壳的切线时,J=﹙5/3﹚mR^2;R为球壳半径。
关于实心球体当回转轴为球体的中心轴时,J=﹙2/5﹚mR^2;当回转轴为球体的切线时,J=﹙7/5﹚mR^2;R为球体半径关于立方体当回为其中心轴时,J=﹙1/6﹚mL^2;当回转轴为其棱边时,J=﹙2/3﹚mL^2;当回转轴为其体对角线时,J=(3/16)mL^2;L为立方体边长。
只明白转动惯量的计算方式而不能利用是没成心义的。
下面给出一些(绕定轴转动时)的刚体动力学公式。
角加速度与合外力矩的关系:角加速度与合外力矩式中M为合外,β为。
能够看出那个式子与牛顿第二定律是对应的。
角动量:角动量刚体的定轴转动动能:转动动能注意这只是刚体绕定轴的转动动能,其总动能应该再加上质心动能。
只用E=(1/2)mv^2不行分析转动刚体的问题,是因为其中不包括刚体的任何转动信息,里面的速度v只代表刚体的质心运动情形。
由这一公式,能够从能量的角度分析刚体动力学的问题。
惯量(Moment of Inertia)是绕轴转动时惯性(回转物体维持其或静止的特性)的,用字母I或J表示。
转动惯量公式表
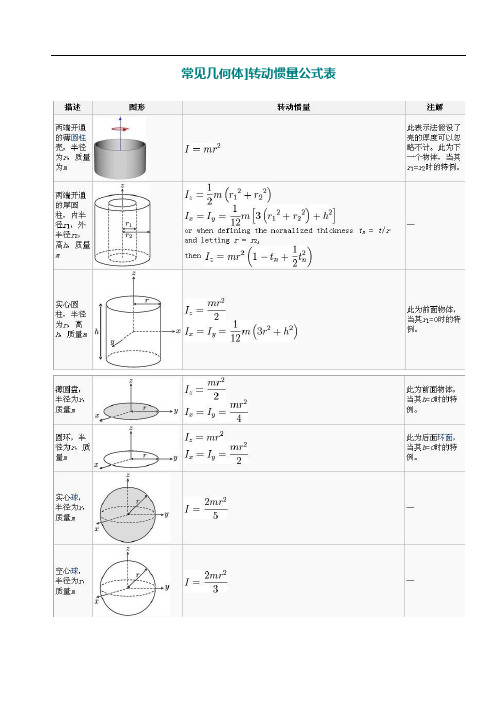
常见几何体]转动惯量公式表对于细杆当回转轴过杆的中点并垂直于杆时;J=m(L^2)/12 其中m是杆的质量,L是杆的长度。
当回转轴过杆的端点并垂直于杆时:J=m(L^2)/3 其中m是杆的质量,L是杆的长度。
对于圆柱体当回转轴是圆柱体轴线时;J=m(r^2)/2其中m是圆柱体的质量,r是圆柱体的半径。
对于细圆环当回转轴通过中心与环面垂直时,J=mR^2;当回转轴通过边缘与环面垂直时,J=2mR^2;R为其半径对于薄圆盘当回转轴通过中心与盘面垂直时,J=﹙1/2﹚mR^2;当回转轴通过边缘与盘面垂直时,J=﹙3/2﹚mR^2;R为其半径对于空心圆柱当回转轴为对称轴时,J=﹙1/2﹚m[(R1)^2+(R2)^2];R1和R2分别为其内外半径。
对于球壳当回转轴为中心轴时,J=﹙2/3﹚mR^2;当回转轴为球壳的切线时,J=﹙5/3﹚mR^2;R为球壳半径。
对于实心球体当回转轴为球体的中心轴时,J=﹙2/5﹚mR^2;当回转轴为球体的切线时,J=﹙7/5﹚mR^2;R为球体半径对于立方体当回转轴为其中心轴时,J=﹙1/6﹚mL^2;当回转轴为其棱边时,J=﹙2/3﹚mL^2;当回转轴为其体对角线时,J=(3/16)mL^2;L为立方体边长。
只知道转动惯量的计算方式而不能使用是没有意义的。
下面给出一些(绕定轴转动时)的刚体动力学公式。
角加速度与合外力矩的关系:角加速度与合外力矩式中M为合外力矩,β为角加速度。
可以看出这个式子与牛顿第二定律是对应的。
角动量:角动量刚体的定轴转动动能:转动动能注意这只是刚体绕定轴的转动动能,其总动能应该再加上质心动能。
只用E=(1/2)mv^2不好分析转动刚体的问题,是因为其中不包含刚体的任何转动信息,里面的速度v 只代表刚体的质心运动情况。
由这一公式,可以从能量的角度分析刚体动力学的问题。
转动惯量(Moment of Inertia)是刚体绕轴转动时惯性(回转物体保持其匀速圆周运动或静止的特性)的量度,用字母I或J表示。
转动惯量公式表

转动惯量公式表 Company number:【WTUT-WT88Y-W8BBGB-BWYTT-19998】常见几何体]转动惯量公式表对于细杆当回转轴过杆的中点并垂直于杆时;J=m(L^2)/12其中m是杆的质量,L是杆的长度。
当回转轴过杆的端点并垂直于杆时:J=m(L^2)/3其中m是杆的质量,L是杆的长度。
对于圆柱体当回转轴是圆柱体轴线时;J=m(r^2)/2其中m是圆柱体的质量,r是圆柱体的半径。
对于细圆环当回转轴通过中心与环面垂直时,J=mR^2;当回转轴通过边缘与环面垂直时,J=2mR^2;R为其半径对于薄圆盘当回转轴通过中心与盘面垂直时,J=﹙1/2﹚mR^2;当回转轴通过边缘与盘面垂直时,J=﹙3/2﹚mR^2;R为其半径对于空心圆柱当回转轴为对称轴时,J=﹙1/2﹚m[(R1)^2+(R2)^2];R1和R2分别为其内外半径。
对于球壳当回转轴为中心轴时,J=﹙2/3﹚mR^2;当回转轴为球壳的切线时,J=﹙5/3﹚mR^2;R为球壳半径。
对于实心球体当回转轴为球体的中心轴时,J=﹙2/5﹚mR^2;当回转轴为球体的切线时,J=﹙7/5﹚mR^2;R为球体半径对于立方体当回为其中心轴时,J=﹙1/6﹚mL^2;当回转轴为其棱边时,J=﹙2/3﹚mL^2;当回转轴为其体对角线时,J=(3/16)mL^2;L为立方体边长。
只知道转动惯量的计算方式而不能使用是没有意义的。
下面给出一些(绕定轴转动时)的刚体动力学公式。
角加速度与合外力矩的关系:角加速度与合外力矩式中M为合外,β为。
可以看出这个式子与牛顿第二定律是对应的。
角动量:角动量刚体的定轴转动动能:转动动能注意这只是刚体绕定轴的转动动能,其总动能应该再加上质心动能。
只用E=(1/2)mv^2不好分析转动刚体的问题,是因为其中不包含刚体的任何转动信息,里面的速度v只代表刚体的质心运动情况。
由这一公式,可以从能量的角度分析刚体动力学的问题。
常用转动惯量公式

常用转动惯量公式
常用转动惯量表达式:I=mr2。
其中m是其质量,r是质点和转轴的垂直距离。
转动惯量是刚体绕轴转动时惯性(回转物体保持其匀速圆周运动或静止的特性)的量度。
扩展资料
转动惯量计算公式
1、对于细杆:
当回转轴过杆的中点(质心)并垂直于杆时I=mL2/I2;其中m是杆的'质量,L是杆的长度。
当回转轴过杆的端点并垂直于杆时I=mL2/3;其中m是杆的质量,L是杆的长度。
2、对于圆柱体:
当回转轴是圆柱体轴线时I=mr2/2;其中m是圆柱体的质量,r 是圆柱体的半径。
3、对于细圆环:
当回转轴通过环心且与环面垂直时,I=mR2;当回转轴通过环边缘且与环面垂直时,I=2mR2;I=mR2/2沿环的某一直径;R为其半径。
4、对于立方体:
当回转轴为其中心轴时,I=mL2/6;当回转轴为其棱边时I=2mL2/3;当回转轴为其体对角线时,I=3mL2/16;L为立方体边长。
5、对于实心球体:
当回转轴为球体的中心轴时,I=2mR2/5;当回转轴为球体的切线时,I=7mR2/5;R为球体半径。
向你推荐的相关文章
相关文章列表
微信扫码分享。
刚体转动与转动惯量计算

刚体转动与转动惯量计算刚体转动是物体绕固定轴进行转动的运动。
在刚体转动中,关键参数是物体的转动惯量,它反映了物体对转动的惯性。
转动惯量的定义是:转动惯量(I)是刚体对轴的转动惯性的量度,它等于刚体各个微小质量元的质量乘以其到转轴的距离的平方之和,即I=Σm_i*r_i²其中,m_i是质量微元,r_i是质量微元到转轴的距离。
对于不同形状的物体,转动惯量有不同的计算方法。
我们来分别讨论以下几种常见形状的物体和它们的转动惯量计算方法。
1.球体的转动惯量:对于均匀球体来说,其转动惯量与质量和尺寸有关,可以通过以下公式计算:I=(2/5)*m*r²其中,m是球体的质量,r是球体的半径。
2.圆柱体的转动惯量:对于均匀圆柱体来说,其转动惯量与质量和尺寸有关,可以通过以下公式计算:I=(1/2)*m*r²其中,m是圆柱体的质量,r是圆柱体的半径。
3.长方体的转动惯量:对于均匀长方体来说,其转动惯量与质量和尺寸有关,可以通过以下公式计算:I=(1/12)*m*(a²+b²)其中,m是长方体的质量,a和b是长方体的两个相邻边的长度。
4.薄杆的转动惯量:对于均匀薄杆来说,其转动惯量与质量和尺寸有关,可以通过以下公式计算:I=(1/12)*m*h²其中,m是薄杆的质量,h是薄杆的长度。
5.圆环的转动惯量:对于均匀圆环来说,其转动惯量与质量和尺寸有关,可以通过以下公式计算:I=m*r²其中,m是圆环的质量,r是圆环的半径。
6.圆盘的转动惯量:对于均匀圆盘来说,其转动惯量与质量和尺寸有关,可以通过以下公式计算:I=(1/2)*m*r²其中,m是圆盘的质量,r是圆盘的半径。
需要注意的是,上述公式都是对于均匀物体的计算方法。
如果物体不均匀,转动惯量的计算将更为复杂,需要将物体分为质量微元进行积分计算。
转动惯量在物理学中有着广泛的应用,例如在机械工程中,可以用来计算机械系统的转动稳定性;在天体物理学中,可以用来描述行星、恒星等宏观物体的转动状态等等。
各类刚体转动惯量公式的推导

各类刚体转动惯量公式的推导
在物理学中,刚体转动惯量是一个非常重要的概念。它描述了一个刚体在受到外力作用时,围绕其质心旋转的难易程度。为了更好地理解这一概念,我们将从理论和实践两个方面来探讨各类刚体转动惯量的推导过程。
我们来看一下理论部分。刚体的转动惯量可以通过以下公式计算:
I = π * m2 * r2
其中,I表示刚体的转动惯量,m表示刚体的质量,r表示刚体到质心的距离,π是一个常数,约等于3.14159。从这个公式中,我们可以看出转动惯量的计算与刚体的质量和距离有关。因此,要计算一个刚体的转动惯量,我们需要知道它的质量和位置。
接下来,我们来看一下实践部分。在现实生活中,我们可以通过实验来测量刚体的转动惯量。例如,我们可以制作一个简单的实验装置,将一个质量一定的物体悬挂在一个转盘上。然后,我们可以通过改变转盘的速度和方向,观察物体的运动情况。通过测量物体在不同速度和方向下的运动时间和位移,我们可以计算出物体的转动惯量。
接下来,我们来看一下圆柱体刚体的转动惯量。对于一个圆柱体,它的转动惯量可以通过以下公式计算:
I = π * m * (R + h)2
其中,R表示圆柱体底面半径,h表示圆柱体的高。从这个公式中,我们可以看出转动惯量的计算与圆柱体的底面半径和高有关。因此,要计算一个圆柱体刚体的转动惯量,我们需要知道它的底面半径、高和质量。
我们来看一下球体刚体的转动惯量。对于一个球体,它的转动惯量可以通过以下公式计算:
转动惯量公式表
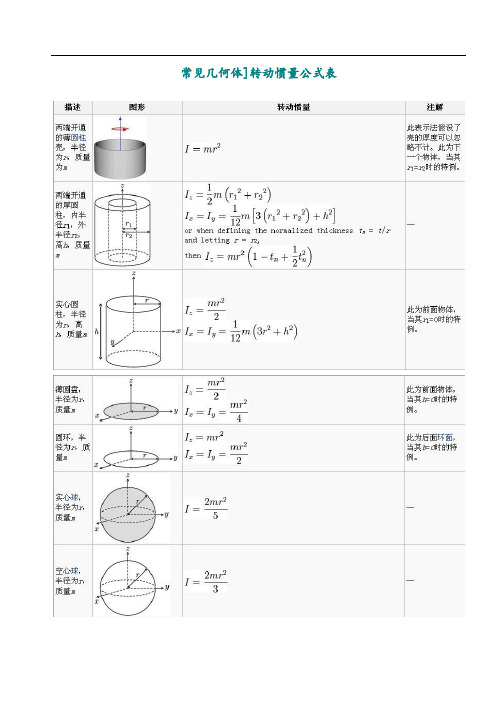
常见几何体]转动惯量公式表对于细杆当回转轴过杆的中点并垂直于杆时;J=m(L^2)/12 其中m是杆的质量,L是杆的长度。
当回转轴过杆的端点并垂直于杆时:J=m(L^2)/3 其中m是杆的质量,L是杆的长度。
对于圆柱体当回转轴是圆柱体轴线时;J=m(r^2)/2其中m是圆柱体的质量,r是圆柱体的半径。
对于细圆环当回转轴通过中心与环面垂直时,J=mR^2;当回转轴通过边缘与环面垂直时,J=2mR^2;R为其半径对于薄圆盘当回转轴通过中心与盘面垂直时,J=﹙1/2﹚mR^2;当回转轴通过边缘与盘面垂直时,J=﹙3/2﹚mR^2;R为其半径对于空心圆柱当回转轴为对称轴时,J=﹙1/2﹚m[(R1)^2+(R2)^2];R1和R2分别为其内外半径。
对于球壳当回转轴为中心轴时,J=﹙2/3﹚mR^2;当回转轴为球壳的切线时,J=﹙5/3﹚mR^2;R为球壳半径。
对于实心球体当回转轴为球体的中心轴时,J=﹙2/5﹚mR^2;当回转轴为球体的切线时,J=﹙7/5﹚mR^2;R为球体半径对于立方体当回转轴为其中心轴时,J=﹙1/6﹚mL^2;当回转轴为其棱边时,J=﹙2/3﹚mL^2;当回转轴为其体对角线时,J=(3/16)mL^2;L为立方体边长。
只知道转动惯量的计算方式而不能使用是没有意义的。
下面给出一些(绕定轴转动时)的刚体动力学公式。
角加速度与合外力矩的关系:角加速度与合外力矩式中M为合外力矩,β为角加速度。
可以看出这个式子与牛顿第二定律是对应的。
角动量:角动量刚体的定轴转动动能:转动动能注意这只是刚体绕定轴的转动动能,其总动能应该再加上质心动能。
只用E=(1/2)mv^2不好分析转动刚体的问题,是因为其中不包含刚体的任何转动信息,里面的速度v 只代表刚体的质心运动情况。
由这一公式,可以从能量的角度分析刚体动力学的问题。
转动惯量(Moment of Inertia)是刚体绕轴转动时惯性(回转物体保持其匀速圆周运动或静止的特性)的量度,用字母I或J表示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ρz =
3 r 10 3 (4r 2 + l 2 ) 80
ρx = ρy
=
圆环
3 J z = m( R 2 + r 2 ) 4
ρ z = R2 + r2
3 4
Jz =
椭圆形 薄 板
m 2 (a + b2 ) 4 m J y = a2 4 m J y = b2 4
1 2 a + b2 2 a ρx = 2 b ρy = 2
173
阅读建议
第一章 本书没有叙述“静力学公理” ,兴趣的读者可以参阅[3]上 6-13 页和[5]上 9-13 页。 第二章 主矢和主矩相同为力学等效的充分必要条件可以由动力学分析证明。 从矢量观点和能量 观点的证明分别可参阅[9]213-221 页和[12]110-111 页。 第三章 关于静定和超静定问题的深入讨论参阅[10]58-62 页和[14]47-50 页。 第四章 点的运动还可以用曲线坐标系进行描述,参阅[1]上 128-157 页和[12]15-17 页。 第五章 变矢量的时间导数与描述该矢量的变化的坐标系有关, 相对运动坐标系的矢量导数称为 相对导数。 在证明牵连运动为转动的加速度合成定理时事实上已用相对导数的概念。 关于相 对导数进一步说明,参阅[1]上 215-218 页和[8]148-151 页。牵连运动为平面运动等更复杂的 运动时,速度和加速度合成定理仍适用,证明见[1]上 218-223 页和[12]38-40 页。牵连运动 为平面运动时,复合运动分析的例题参阅[3]上 311-313 页和[11]145-147 页。 第六章 本书仅讨论刚体的平面运动。若需要继续学习刚体的空间运动,可参阅[10]153-166 页 和[14]146-163 页。 刚体的复合运动成立角速度合成定理, 证明见[1]上 199-201 页和[12]45-46 页,重要的应用是刚体绕相交轴转动的合成,参阅[11]159-161 页和[14]153-155 页。本章还 简要涉及运动分析的解析方法,引入自由度概念的阐述参阅[11]174-179 页,更系统、并程 序实现的阐述参阅[13]75-191 页。 第七章 本书仅简要地讨论了振动问题。 振动是力学中的专门研究领域。 在理论力学课程范围内 对振动问题的详细讨论可参阅[7]II44-67 页和[10]328-350 页。 第八章 应用动量定理和动量矩定理可以研究变质量系统的动力学问题, 这方面内容本书没有涉 及,可参阅页[12]236-244 和[14]215-218 页。相对于一般动点的动量矩定理及推导参阅[1]下 47-48 页 和 [10]229-235 页 。 动 量 定 理 和 动 量 矩 定 理 可 以 推 广 到 非 惯 性 参 考 系 , 参 阅 [12]225-226 页。本书对刚体动力学的讨论仅限于平面运动情形,刚体空间运动的动力学可 参阅[7]II21-40 页和[10]379-403 页。突加约束是与碰撞相关的动力学问题,本书没有涉及, 可 参 阅 [10]367-368 页 和 [8]419-422 页 ; 关 于 刚 体 系 和 空 间 运 动 刚 体 碰 撞 的 例 子 参 阅 [14]356-360 页。 第九章 本书仅考虑定常双面完整约束,关于约束及其虚位移更一般的讨论参阅[10]283-288 页 和[14]294-300 页。本书没有给出虚功原理的充分性证明,可参阅[6]110-111 页和[10]290 页。 平衡稳定性的拉格朗日定理几何解释和证明可参阅[11]68-69 页和 79 页。 第十章 关于动能计算的柯尼希定理的证明和应用可参阅[8]307-309 页和[10]248 页。动能定理 可以推广到非惯性参考系,参阅[10]261-264 页和[12]226-227 页。本书中拉格朗日方程的推 导局限于定常约束系统, 该推导也适用于非定常约束系统, 区别仅是拉格朗日关系式的证明, 可参阅[8]390-391 和[10]313 页。对于非定常约束系统,当拉格朗日函数不显含时间时,拉 格朗日方程存在广义能量积分,参阅[10]319-320 页和[12]229-230 页。能量方法也可应用于 碰撞问题的研究,参阅[10]361-366 页和[12]214-215 页。
10 刘延柱,杨海兴,朱本华(编著). 理论力学(第二版). 北京:高等教育出版社,2001 11 刘延柱(编著). 高等动力学. 北京:高等教育出版社,2001 12 李俊峰,张雄,任革学,高云峰(编著). 理论力学. 北京:清华大学出版社,2001 13 洪嘉振,杨长俊(编著). 理论力学(第二版). 北京:高等教育出版社,2002 14 贾书惠,李万琼(编著). 理论力学. 北京:高等教育出版社,2002 15 范钦珊,刘燕,王琪(编著). 理论力学. 北京:清华大学出版社,2004 16 Soutas-Little R W, Inman D J. Engineering Mechanics: Statics and Dynamics. New Jersey: Prentice Hall, 1999 17 Hibbeler R C. Engineering Mechanics: Statics & Dynamics (SI Edition). 2nd ed. Prentice Hall, 2001 18 Pytel A, Kiusalaas J. Engineering Mechanics: Statics and Dynamics. 2nd ed. 北京: 清华大学 出版社, 2001 19 Beer F P, Johnston E R. Vector Mechanics for Engineers: Statics & Dynamics. 3rd SI Metric ed. 北京:清华大学出版社, 2003
174
习题答案
第一章
F (h − 3r ), M y = 3 F (r + h ), M z = − Fr . 1-3 4 4 2 2 bc ab ca a ab M ξ = −513.36 N ⋅ m . 1-4 M x = M − F ,My = M + F ,Mz = M, k1 k1 k1 2k 2 2k 2 abc 2 2 2 2 2 2 F. 其中: k1 = (ab ) + (bc ) + (ca ) , k2 = a + b / 4 + c . 1-5 M τ = rAB b 2 + c 2
附录
物体的 形 状
常见几种均质物体的转动惯量和回转半径
简 图 转动惯量 (m 为物体的质量) 回转半径
J zC =
细直杆
m 2 l 12 m Jz = l2 3
2 3 l ρz = 3
C
ρz =
l
薄壁 圆筒
J z = mR 2
ρz = R
圆柱
1 mR 2 2 Jx = Jy Jz = = m ( 3R 2 + l 2 ) 12
ρz =
Jz =
长方体
m 2 (a + b2 ) 12 m J y = (a 2 + c2 ) 12 m J y = (b 2 + c 2 ) 12
ρz = ρx = ρy =
1 2 (a + b2 ) 12 1 2 2 (a + c ) 12 1 2 2 (b + c ) 12
Jz =
矩形 薄板
m 2 (a + b2 ) 12 m J y = a2 12 m J y = b2 12
1-1 FR=645N. 1-2
Mx =
(
)
第二章 2-1 合力大小为 2F, 方向沿对角线 DH。 2-2 a/F1+b/F2+c/F3=0, F1/(bF3)=F2/(cF1)=F3/(aF2). 2-3 合力大 小为:(a) (q1+q2)l/2; (b) qlcosθ; 过图形形心与 q 平行. 2-4 xC=1.319m, yC=3.333m, zC=1.361m. 2-5 xC=21.43mm, yC=21.43m, zC=-7.143mm. 2-6 xC=19.05mm. 2-7 重心离地面高度为 0.659 m ,离 B 端距离为 1.68 m 第三章 3-1 均 为 静 不 定 . 3-2 P>4Q=60kN. 3-3 (a) FA=-63.22kN, FB=-88.74kN, FC=30kN; (b) FB=8.42kN, FC=3.45kN, FD=57.4kN. 3-4 (a) FAx=0, FAy=6kN, MA=32kN⋅m; (b) FAx=0, FAy=-15kN, FB=40kN, FCx=0, FCy=5kN, FD=15kN. 3-5 (a) FAx=0, FAy=-F+M/a+qa/2, FB=2F-2M/a+5qa/2, FC=M/a+qa/2; (b) FAx=0, FAy=7qa/6, MA=2qa2, FC=5qa/6. 3-6 FAx=1200N, FBA=-1500N, FB=-1050N. 3-7 FEx=F, FEy=-F/3. 3-8 FAx=(2Q-P)/4, FAy=(6Q+7P)/4, FCx=(P-6Q)/4, FCy=3(P+2Q)/4, Fk=1.414P. 3-9 FAx=FBy=500N, FAB=700N, FBC=100N. 3-10 FAx=FBy=30kN, FCx=FCy=10kN, FBE=0, FCE=14.142kN. 3-11 FAx=0, FAy=M/(2a), FDx=0, FDy=M/a, FBx=0, FAy=-M/(2a) 3-12 FAx=-F, FAy=-F, FDx=2F, FDy=F, FBx=-F, FBy=0. 3-13 FAx=-120kN, FAy=-160kN, FB=226.3kN, FC=-80kN. 3-14 FAx=267kN, FAy=-87.5kN, FB=550kN, FCx=209kN, FCy=-187.5kN. 3-15 FAD=FBD=31.55kN, FCD=-1.55kN. 3-16 FN=500N, FTA=750N, FTB=433N. 3-17 F1=F2=5kN, F3=-7.07kN, F4=F5=5kN, F1=-10kN. 3-18 FNA=8.33kN, FNB=78.33kN, FNC=43.34kN. 3-19 a=35cm. 3-20 FT=707N, FAx=400kN, FAy=800kN, FAz=500kN, FBy=-500kN, FBz=0. 3-21 M=22.5N⋅m, FAx=75kN, FAy=0, FAz=50kN, Fx=75kN, Fy=0. 3-22 F=70.9N, FAx=-47.6kN, FAz=-68.8kN, FBx=-19kN, FAz=-207kN. 3-23 128.23 N. 3-24 GAmin=1.37kN. 3-25 11.55 kN. 3-26 Fmin=280N. 3-27 d≥110mm. 3-28 6.0N≤F≤46.1N. 3-29 lmin=100mm. 3-30 bmin=fh/3, 与门重无关. 3-31 M=P2(Rsinθ-r), F=P2sinθ, FN=P1-P2cosθ. 3-32 θ=1°9′. 3-33 M=1.867kN⋅m, F≥0.752. 3-34 1, 4, 7, 9, 13, 14, 11. 3-35 F1=-16.9kN, F2=3.1kN, F3=15.0kN 3-36 (a) FAB=-F/2; (b) FAB=-2kN. 3-37 F1=-5.333F(压),F2=2F (拉), F3=-1.667F (压). 3-38 FCD=-0.866F (压). 第四章 4-1Fra bibliotekρz =
