机械制造行业中的流水作业排序问题
生产作业排序

)
华中科技大学管理学院
一、基本概念
4、排序问题的假设条件
• 一个工件不能同时在几台不同的机器上加工。 • 工件在加工过程中采取平行移动方式。 • 不允许中断。 • 每道工序只在一台机器上完成。 • 每台机器同时只能加工一个工件。 • 工件数、机器数和加工时间已知,加工时间与加工
顺序无关。
)
华中科技大学管理学院
一个实例: D=
2,1,3 2,2,1 2,3,2
241
T= 345
i {Ot} Tk
T’k
T*
M*
Oj
1 1,1,1 0
2
0
M1 1,1,1
2,1,3 0
3
0
M3
2 1,2,3 2
6
2,1,3 0
3
0
M3 2,1,3
3 1,2,3
3
7
3
M3 1,2,3
2,2,1 3
7
3
M1
4 1,3,2 7 2,2,1 3
四、一般n/m/P/ Fmax问题的 启发式算法
2、关键工件法:
• 计算Pi= Pij ,找出Pi最长的工件,将之作为 关键工件C。
• 对其余工件,若Pi1≤Pim ,则按Pi1由小到大排 成序列SA。若Pi1> Pim ,则按Pim由大到小排成 序列SB。
• 顺序(SA,C,SB)即为近优解。
)
四、一般n/m/P/ Fmax问题的 启发式算法
1、Palmer法
m
• 计算工件斜度指标i : i [k (m 1) / 2]pik
m : 机器数
k 1
pik :工件i在机器k上的加工时间。 i=1,2, ,n
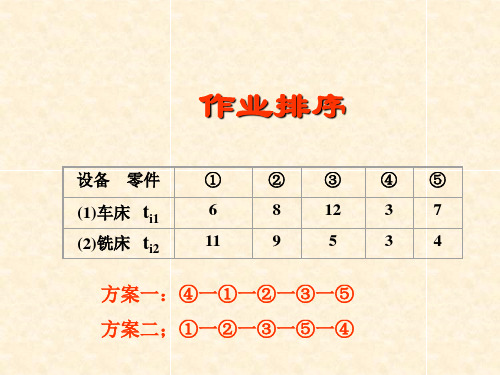
作业排序
例题:已知条件如表所示,求平均流程时间,平均等待时 间,最大交货延期.
零件号
①②③ ④ ⑤ ⑥
作业时间 4 8 2 5 9 3 预定交货期 24 23 8 6 32 13
解:列表如下
加工顺序
12
3
4
5
6
零件号
③⑥①④②
⑤
作业时间 2
3
4
5
8
9
流程时间 2
5
9
14 22
31
等待时间 0
2
5
9
14
22
预定交货期 8
13 24 6
23
32
交货延期 0
0
0
8
0
0
加工顺序
12
3
4
5
6
零件号
③⑥①④②
⑤
作业时间 2
3
4
5
8
9
流程时间 2
5
9
14 22
31
等待时间 0
2
5
9
14
22
预定交货期 8
13 24 6
23
32
交货延期 0
0
0
8
0
0
答:最大流程时间:31 最大等待时间:22 平均流程时间=(2+5+9+14+22+31)/6=13.83 平均等待时间=(0+2+5+9+1+14+22)/6=8.67 最大交货延期:8 总交货延期:( 0+0+0+8+0+0)=8
作业时间 4 8 2 5 9 3
基于遗传算法的流水车间调度问题

基于遗传算法的流水车间调度问题中文摘要流水车间调度问题是研究多个工件在若干个机器上的加工次序的问题,有效的调度算法对企业提高生产效率有着重要作用。
本文使用遗传算法求解流水车间调度问题,把一个染色体编码成若干个自然数,表示相应工件的排序权值;通过简单交换两个父代的若干相同位置的基因,产生能够继承父代优良特性的子代;并且采用均匀变异,更好地保持种群中的基因的多样性。
实验表明,该方法能取得较好的效果。
关键字:遗传算法,流水车间调度方法,实数编码,基因链码,群体,适应度。
外文摘要Abstract: Flow-shop scheduling problem study the problem the processing sequence of A plurality of workpieces on some working machine,and it makes good effects on proving production efficiency to the industries with effective methods.In the case,we deal with flow-shop scheduling problem using a algorithm,the Genetic Algorithm.There is a chromosome we've just coded into some natural numbers to represent the weight order of these workpieces; exchanging simply two fathers' places of some gene to produce new children that carried good feature on two fathers;we also use the Uniform Mutation,and it keeps its diversity of gene on the population.This experiment show this method can achieve good results.Key Words: Genetic Algorithm, Flow-shop scheduling problem,natural number coding,genic bar code,group,fitness.目录中文摘要 (1)外文摘要 (2)目录 (3)1 引言 (4)1.1 论文的发展背景及重要性 (4)1.1.1 时代背景 (4)1.1.2 论文研究的重要性 (4)1.2 论文的研究问题及解决方法 (4)2 FSP问题描述 (5)2.1 排序问题的基本概念 (5)2.1.1 名词术语 (5)2.1.2 条件假设 (5)2.2车间作业排序问题的特点 (6)2.3 车间作业排序问题 (6)2.3.1 目标函数 (6)2.3.2 车间调度问题的分类 (7)3 遗传算法理论 (7)3.1 遗传算法的产生和发展 (7)3.2 遗传算法的基本思想 (8)3.2.1 基本概念 (8)3.2.2 遗传算法的基本思想 (9)4 基于遗传算法的流水车间调度方法 (11) 4.1 问题的提出 (11)4.2 遗传算法基本步骤 (11)4.2.1 编码 (11)4.2.2 初始群体生成 (12)4.2.3 适应度计算 (12)4.2.4 选择 (14)4.2.5 交叉 (15)4.2.6 变异 (17)4.2.7 终止 (19)5. 研究成果 (20)5.1 算法求解与分析 (20)5.2 实验结果 (21)参考文献 (22)附录 (23)1 引言1.1 论文的发展背景及重要性1.1.1 时代背景从第一次工业革命起,由于科技的进步人类社会就开始了一个经济腾飞的大时代。
流水施工排序优化

流水施工排序优化工程排序优化就是加工过程和加工对象及其排列顺序的优化,也称为流程优化。
它可分为单向工程排序优化和双向工程排序优化两种;施工项目的工程排序优化属于单向工程排序优化。
这里介绍一种新而简捷的工程排序优化方法——矩阵法。
该法是在保证流水施工条件下,寻求施工项目(或施工段)最优排列顺序的优化方法,其优化目标是计算总工期最短。
故该法实质是流水施工排序优化。
1.基本概念(1)基本排序任何两个施工项目或施工段的排列顺序,均称为基本排序。
如A和B两个施工项目的基本排序有A→B和B→A两种;前者A→B称为正基本排序,后者B→A称为逆基本排序。
(2)基本排序间歇任何两个施工项目,由于排列顺序不同而造成的施工过程间歇时间的总和,均称为基本排序间歇,并以Z i,i+1表示。
如:A→B基本排序间歇记为Z A,B,B→A基本排序间歇记为Z B,A。
(3)基本排序流水步距任何两个施工项目(i)与(i+1),先后投入到第(j)个施工过程开始施工的时间间隔,均称为基本排序流水步距;即施工项目(i)与(i+1)之间的流水步距,并以K i,i+l表示。
如:A→B基本排序流水步距记为K A,B,B→A基本排序流水步距记为K B,A。
(4)施工项目排序模式在进行流水施工排序优化时,通常将若干个施工项目(或施工段)排列顺序的全部可能模式,称为施工项目排序模式。
如A、B、C、D 4个施工项目就有A →B→C→D;A→B→D→C;……;B→D→A→C等24种施工项目排序模式。
2.基本原理矩阵法是从流水施工基本原理出发,通过对工程排序优化问题深人研究之后,发现并证实影响计算总工期长短的关键是基本排序间歇(Z i,i+1)的数值大小。
这样该法首先根据分析计算法确定出施工项目基本排序流水步距,同时计算出基本排序间歇,并建立起基本排序间歇矩阵表;然后按照最优工程排序模式确定规则,由矩阵表上寻求其最优排序方案。
根据分析计算法原理,任意相邻两个施工项目基本排序流水步距,均可由公式(34-9)确定;而其基本排序间歇,可由公式(34-10)计算。
车间作业调度问题的研究与应用

管作 业计 划问 题 已进 行 了 大 量 的 研 究 并 取 得 了一 题 得 不 到较 好 的控 制 , 配 现 场停 工 等待 零 件配 齐 装 定 的成果 , 是 , 于所 有 的 生 产 作 业 问 题 都 要 得 的现 象 时有 出现 , 底 常 加 班 加 点 赶 任 务 , 产 过 但 对 月 生 到最 优 解是 困难 的 , 至是 不 可 能 的 。而启 发式算 程 不 均衡 。 甚
很 忙 , 间工 作 人 员 也 经 常 加 班 加 点 , 是 任务 完 与 “ 车 可 补缺 料 ” 现 象 , 需 零 件 难 以 及 时 赶 制 出来 , 等 急
成 得 并 不理 想 。
所有这些都会给按 时完成生产任务 、 使生产过程清 通 常 , 统 机 械 制 造 业 车 间 任 务 特 点 是 : 划 楚 、 传 计 方便在 制 品管理 和提高设 备利用 率等 带来 困 批 量 任务 、 件 小 批 任 务 和 新 产 品开 发 、 时试 制 难 。 单 临
这种 混 流生 产 情 况 , 何 充 分 利 用 现 有 设 备 资 源 。 如
车间 调 度需 要 考察 以下几 个 方 面 :
( )加工 机 器 总数 m; 1
()加 工 工 件 总数 n以 及工 件 P需 要 加 工 的 2 ;
( )工 件 的 工艺 路 线及 加 工 时 间 Xi 3 ; ]
车 间作 业调 度 问题 的研 究 与 应 用
叶何文
摘 要
饶运 清2 邓建春2 刘世平2
车间生产作业排序知识讲座

一、基本概念
排序中常用的几个概念
• 工件(Job):服务对象; • 机器(Machine、Processor):服务者。
如: • n个零件在机器上加工,则零件是工件,设备
是机器; • 工人维修设备,出故障的设备是工件,工人
是机器。
一、基本概念
所以,作业排序也就是要确定工件在机器上 的加工顺序,可用一组工件代号的一种排列 来表示。 如可用(1,6,5,4,3,2)表示加工顺序: J1—J6—J5—J4—J3—J2。
短的工件。 • MOPNR(Most Operations Remaining)法则:优先选择余下工序
数最多的工件。
五、单件车间排序问题(n/m/G/Fmax)
优选调度法则:
• 按SPT法则可使工件的平均流程时间最短,从而减少 在制品量。
• FCFS法则来自排队论,它对工件较公平。 • EDD法则可使工件最大延误时间最小。 • SCR也是保证工件延误最少的法则。 • MWKR法则使不同工作量的工件的完工时间尽量接
一、基本概念
2、作业计划(Scheduling) • 作业计划与排序不是一回事,它不仅要确定
工件的加工顺序,而且还要确定每台机器加 工每个工件的开工时间和完工时间。
• 如果按最早可能开(完)工时间来编排作业 计划,则排序完后,作业计划也就确定了。
一、基本概念
3、排序问题的分类与表示 1)单台机器与多台机器的排序问题。 2)流水车间与单件车间排序问题。
• 顺序(SA,C,SB)即为近优解。
四、一般n/m/P/ Fmax问题的 启发式算法
用关键工件法求解
i
1234
Pi1
1263
Pi2
8429
Pi3
生产作业排序
华中科技大学管理学院
三、n/2/F/Fmax问题的算法
Johnson算法的步骤: • 从加工时间矩阵中找出最短的加工时间。 • 若最短时间出现在M1上,则对应的工件尽可能
往前排。
• 若最短时间出现在M2上,则对应的工件尽可能 往后排。
一个实例: D=
2,1,3 2,2,1 2,3,2
241
T= 345
i {Ot} Tk
T’k
T*
M*
Oj
1 1,1,1 0
2
0
M1 1,1,1
2,1,3 0
3
0
M3
2 1,2,3 2
6
2,1,3 0
3
0
M3 2,1,3
3 1,2,3
3
7
3
M3 1,2,3
2,2,1 3
7
3
M1
4 1,3,2 7 2,2,1 3
• 若最短时间有多个,则任选一个。 • 划去已排序的工件。
• 若所有工件都已排序,则停止,否则重复上述 步骤。
华中科技大学管理学院
四、一般n/m/P/ Fmax问题的 启发式算法
对于一般的n/m/P/Fmax问题,可以用分支 定界法求得最优解,但计算量很大。实际 中,可以用启发式算法求近优解。
华中科技大学管理学院
华中科技大学管理学院
五、单件车间排序问题(n/m/G/Fmax)
能动作业计划的构成步骤:
①设t=1,{St}为空,{Ot}为各工件第一道工序的集合。 ②求最小的最早完工时间 T*= min{T’k },并找到出现T*
的机器M*,若有多台,任选一台。 ③从{Ot}中跳出满足以下两条件的工序Oj
C++程序-流水作业调度
一、问题描述给定n个作业,每个作业有两道工序,分别在两台机器上处理。
一台机器一次只能处理一道工序,并且一道工序一旦开始就必须进行下去直到完成。
一个作业只有在机器1上的处理完成以后才能由机器2处理。
假设已知作业i在机器j上需要的处理时间为t[i,j]。
流水作业调度问题就是要求确定一个作业的处理顺序使得尽快完成这n个作业。
二、算法分析n个作业{1,2,…,n}要在由2台机器M和2M组成的流水线上完成加工。
每1个作业加工的顺序都是先在M上加工,然后在2M上加工。
1M和2M加工作业i所1需要的时间分别为t[i,1]和t[i,2], n1.流水作业调度问题要求确定这ni≤≤个作业的最优加工顺序,使得从第一个作业在机器M上开始加工,到最后一个1作业在机器M上加工完成所需的时间最少。
2从直观上我们可以看到,一个最优调度应使机器M没有空闲时间,且机器2M1的空闲时间是最少。
在一般情况下,机器M上会有机器空闲和作业积压两种情2况。
设全部作业的集合为}N=。
N2,1{n,....,S⊆是N的作业子集。
在一般情况下,机器M开始加工S中作业时,机器2M还在加工其他作业,要等时间t后才能利1用。
将这种情况下完成S中作业所需的最短时间计为),ST。
流水作业调度问题(t的最优解为)0,T。
(N1.证明流水作业调度问题具有最优子结构设a是所给n个流水作业的一个最优调度,它所需要的加工时间为']1),1([T a t +。
其中,'T 是在机器2M 的等待时间为]2),1([a t 时,安排作业)(),......,3(),2(n a a a 所需的时间。
记)}1({a N S -=,则我们可以得到])2),1([,('a t S T T =。
事实上,有T 的定义可知])2),1([,('a t S T T ≥.若])2),1([,('a t S T T >,设'a 是作业集S 在机器2M 的等待时间为]2),1([a t 情况下的一个最优调度。
流水作业法
03
流水作业法的应用场景
制造业中的流作业法通常用于优化生产线,确保每个生产
环节都紧密衔接,从而提高生产效率。
工艺流程的改进
02
通过流水作业法,可以发现和改进工艺流程中的瓶颈,减少浪
费和提高产品质量。
生产计划的制定
03
流水作业法可以帮助企业制定更加科学和准确的生产计划,以
产效率。 • 提高产品质量:每个阶段都有专门的人员负责,可以减少错误和不良品率,提高产品质量。 • 降低成本:通过均衡生产和批量生产,可以降低单位成本和库存成本。 • 缺点 • 初始投资成本高:流水作业法需要投入大量的设备和人力,初始投资成本较高。 • 不适合小批量生产:由于流水作业法的生产效率高,不适合小批量生产,需要有一定的生产规模。 • 对设备依赖度高:流水作业法对设备的依赖度很高,一旦设备出现故障,整个生产过程都会受到影响。
04
流水作业法的案例分析
制造业流水作业法的案例分析
总结词
高效、标准化、规模化
详细描述
流水作业法在制造业中有着广泛的应用。以汽车制造为例,通过将复杂的汽车制造过程划分为一系列简单的、 重复的工序,并按照一定的顺序将各道工序链接起来,形成一条“流水线”。通过流水作业法,可以大大提高 生产效率,降低生产成本,并提高产品质量。
确定生产任务
根据市场需求和生产能力,确定生 产任务和产品品种、数量。
制定工艺流程
根据产品特点和生产任务,制定合 理的工艺流程和作业标准。
安排生产进度
根据工艺流程和作业标准,安排各 阶段的作业时间和顺序,制定生产 进度计划。
调整生产计划
根据实际生产进度和市场需求,及 时调整生产计划,确保按时交付产 品。
《流水作业法》
第十一章 作业排序
22
44
22
总数
115
118
3
36
平均数
23.0
0.6 7.2
平均在制品库存=115/44=2.61个
平均总库存=118/44=2.68个
假设:顾客不会提前取货,如果加工延迟,顾客将在加工完成后马上去走。
平均在制品库存=各工件流程时间之和/全部完工时间 平均总库存=全部在制品库存+完成品库存(等待顾客取货) 各工件的实际取货时间=等待加工时间+加工时间+等待取货时间 平均总库存=各工件实际取货时间之和/全部完工时间 排序结果比较 SPT规则排序,平均流程时间更短,在制品库存更少。 EDD规则排序,为顾客提供更好的服务,总库存水平低。
五、局部与整体优先规则及其事例
优先调度规则可以分为局部优先规则和整体优先规则两类,局 部优先规则决定工作的优先分配顺序仅以在单个工作地队列中的工 作所代表的信息为依据。例如,EDD,FCFS和SPT都是局部优先规则。 相比之下,整体优先规则决定工作地优先分配顺序不仅根据正在排 序的工作地,而且还要考虑到其他工作地的信息。SCR、MWKR、LWKR 以及MOPNR都是整体优先规则。整体优先规则可以看作是更好的选择, 但由于需要较多的信息,而信息的获取也是要付出成本的,因此在 某些情况下不一定能够提供足够的优势。
第十一章 作业排序
作业排序的基本概念 制造业中的生产作业排序 服务业中的服务作业排序
第一节 作业排序的基本概念
一、作业计划与排序
排序:只是确定工件在机器上的加工顺序。 作业计划:不仅包括确定工件的加工顺序,还包括确定机器加工每个 工件的开始时间和完成时间 工件等待:一个工件的某道工序完成之后,执行它下一道工序的机器 还在加工其他工件,这时,工件要等待一段时间才能开始加工。 机器空闲:一台机器已经完成对某个工件的加工,但随后要加工的工 件还未到达。 提供服务者:指“工作地”、“机器”、“人员”等。 接受服务者:指“工作”、“工件”、“顾客”等。 排程难点:按时间来分配特定的工作,但许多工作同时为同一资源而 竞争。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
l I f l
3 4 8 7
I l f l
4 2 7 6 ”
台设 备进行加工 ,并且每种零 部件在每 台设 备上 的加工 时间各不相
同。那么怎样编排这 n 种零部件 的加工顺序可 以使总加工时间最短 ,
这 是 排 序 要 解 决 的 问题 。 般说来 ,排序只是确定工件在机器上的加 工顺序 ,而编制生产
一
、
生产作 业计 划与流水作业排序 问题
生产作业计划是根据企业年度 、 季度计划的要求 , 来具体地安排 车 间、工段、班组乃至工作地在月 、 旬、日 以及昼夜 、 轮班和小 时的 工作任务 。 对于大型机械制造企业 , 生产作业计划 一般分 为公 司级生 产作业计划 和车 间级生产作业计划两级 。一般来说 , 公 司生产制造部 负责编制和下达公 司级生产作业计划 , 各 车间的作业计划员在接到公 司级生产作业计划 以后 ,要负责编制本 车间的生 产作业计划 , 并将车 间级生产作业计划分解落实到各个班组及各个工作地 , 将车间 的生产 任务变成各个班组 、 各个工作地的生产任务。 每个工作地生产作业计 划 的完成 ,保证了车间生产作业计划的完成 ; 每个 车间生产作业计划 的完成 ,保证 了公 司级生产计划 的完成 ;公 司级生产计划 的完成 ,保 证 了公司生产经 营计划 的完成 。 假如某个车 间需要生产 n种零部件 ,这 1 ' 1 种零部件需要经过 m
为零 。 设n 个 工 件雕 船 工 顺序为s ={ s s , … ・ s , 翼 申s t 为 第 位 抽工 的 工 件的 代 号・ 以G ±表
。
式 中,m为机器数 ;p i k为工件 i 在 Mk上的加工 时间。 按照各工件 i 不增的顺 序排列工件 ,可得出令人满 意的顺序 。 对 于本 例 中 ) L i _一P i l +P i 3
工 业 技 术
பைடு நூலகம்机械 制造行 业 中的流水作业排序 问题
马 超
黑龙江 齐齐 哈尔 1 6 1 0 0 2) ( 中国北车齐齐哈尔轨道交通装备有限责任公司生产制造部
【 摘 要 】企业要管理好 ,生产计划很重要 。保证生产交期和提高生产效率的前提条件 ,就是要 有一个完整合理的生产计划 ,制定好详细 的生产计划对生产 的顺利进行有举足轻重的作用。无论何种生产型态 ,首先要重视计划 ,实施有计划地生产 。无计划意味着无序 , 无序 的结果 便是无效率 ,最终是无效益 。而解决好生产过程中的排序问题就是 完成生 产计划 的重要保 障。 【 关键 词】排序 生产作业计划 P a l me r 法 关键工件法 C D S法 中图分 类号 :T H 文献标识码 :A 文章编号 :1 0 0 9 —9 1 4 x( 2 0 1 3 )3 5 -3 9 3 -0 1
=
二 、排 序饲题 的表示方法
通常我们用 4 个参数来表示不同的排序问题 , 4 个参数表示法为 :
r d m/ p / Fma x
其 中,n为零部件数 ,m为设 备 ( 或机器数 ) ,P表示流水作业排 列排序 问题 , F m a x则表示 目标 数 , 通 常是使其值最小 。流水作业 排序 问题 的基本特征是每个零部件 的加工路线都一致 , 并且每个零部 件在每 台设备上 的加工顺序都相 同。 我们所说 的加工路线一致 , 是指 零部件的流 向一致 , 并不要求 每个零部件必须经过加工路线上每 台设 备加工 。 如果某些零部件不经过某些设 备加工 , 则设相应 的加工时间
称之 为 P a l m e r 法 。工件 的斜度指标可按下式计算
作业计划 , 则不仅包括确定工件的加工顺 序 , 而且还包括确定机器加
=
工每个工件 的扦始时间和完工时间。 可以说解决好排序 问题是顺利完
成生产作业计划 的保障 。
∑£ 惫 一 ( 礅 手 i ) , 2 × 母 & = i 2 . n
一
我们按 照 S =( 1 、2 、3 、4)的顺序计 算了最 长加工 时间,但是 这个顺序是否是最优的顺序 , 这就涉及到我们上面提到的流水作业排 序 问题 ,找到最优 的加工顺序 ,使 目标 函数 F ma x最短。解决流水作 业排序 问题 主要有几下几种的方法 : ( 一 )P a l me r 法 1 9 6 5 年 ,D .S .P a l m e r 提 出按斜度指标排列工件的启 发式算法 ,
这样最后一行 的最后一列右上角的数字即为 F m a x 。按照 S =( 1 、2 、 3 、4 )的加工顺序 ,F  ̄= 3 3 。 表 2 加工时间矩 阵 ( 2)
i P B P ,
I l J 1
1 3 2 6 “
2 5 4 4
示工 蚌s 癌机 器蕊 上的 完工 时 间 p t 表 示工 件s 在 上的 加 工 时 间 , k : 1 , 2 , …, 珊 = I , 2
于是 , 1 = 一P1 1+P 1 3 =一3 + 6 = 3
入2= 一P 21+P 2 3 =一5+4 = 一1 3:一 P 3l+P 3 3 =一4+7 =3 ) L 4= 一P 41+P 4 3 =一2+6= 4
按照 i 不增 的顺序排列进行排列 ,得 到加工顺序 s =( 4 、3、1 、 2)或 者 s =( 4 、1 、3 、2) 。当 s :( 4 、3 、1 、2)时 ,F ma x = 3 4( 如 表 3所示 ) ,当 S =( 4 、1 、3 、2)时 ,F ma x = 3 2( 如表 4所示 ) 。所 以 本例 中 S =( 4 、1 、3 、2)为最优顺序 ,在该顺 序下 F m a x : 3 2 。 表3 S =( 4 、3 、1 、2)
