平衡二叉树构造过程
二叉排序树

②若*p结点只有左子树,或只有右子树,则可将*p的左子 树或右子树直接改为其双亲结点*f的左子树,即: f->1child=p->1child(或f->1child=p->rchild); free(p); *f
F *p P P1
*f
F
*f
F *p P
*f
F
Pr
P1
Pr
③若*p既有左子树,又有右子树。则:
-1 0
47
-1
47
47
0
31 69
69
25
0
47
0
25
0
47
-1 0
31
0
69
0
40
69
40
69
0
25 76
40
76
(a)
AL、BL、BR 都是空树
(b) AL、BL、BR 都是非空树
LR型调整操作示意图
2
A
-1
0
C
AR C BL CL CR AR
0 0
B BL CL S
B
A
CR
(a) 插入结点*s后失去平衡
31
0 0 -1
31
0 1
28
0
25
0 0
47
0
25
-1
47
0
25
0
31
0
16 0
28
16
28
0
16 30
30
47
(c) LR(R)型调整
RL型调整操作示意图
A B C A BR CR B BR
AL
C
AL
CL CR
字典的两种实现原理

字典的两种实现原理字典是一种常用的数据结构,它能够存储键值对,并且可以高效地进行插入、删除和查找操作。
在实际应用中,字典有两种常见的实现原理,分别是哈希表和平衡二叉树。
一、哈希表实现原理哈希表是一种基于哈希函数的数据结构,它通过计算键的哈希值来确定存储位置。
哈希函数将键映射为一个固定大小的整数,这个整数就是键的哈希值。
哈希表通常使用数组来存储数据,数组的下标就是键的哈希值。
在哈希表中,通过哈希函数计算得到的哈希值可以直接用作数组的下标,从而快速地定位到存储位置。
当插入或查找一个键值对时,只需要通过哈希函数计算键的哈希值,然后在数组中进行操作即可。
这种操作的时间复杂度通常是常数级别的,即O(1)。
然而,哈希函数可能会产生冲突,即不同的键可能会计算得到相同的哈希值。
为了解决冲突问题,哈希表通常使用链表或者其他数据结构来存储相同哈希值的键值对。
当发生冲突时,只需要将新的键值对插入到链表的末尾即可。
由于哈希表的插入、删除和查找操作的时间复杂度都是O(1),所以它在实际应用中具有广泛的应用。
例如,在编程语言中,字典类型通常就是基于哈希表实现的。
另外,哈希表还被用于缓存、数据库索引等领域。
二、平衡二叉树实现原理平衡二叉树是一种特殊的二叉搜索树,它的左子树和右子树的高度差不超过1。
平衡二叉树的实现通常使用红黑树或者AVL树。
在平衡二叉树中,每个节点都包含一个键值对,且节点按照键的大小进行排序。
对于任意一个节点,它的左子树中的所有键都小于该节点的键,而右子树中的所有键都大于该节点的键。
这样,在平衡二叉树中查找一个键值对的时间复杂度是O(logn),其中n是树中节点的个数。
当插入或删除一个键值对时,平衡二叉树会通过旋转操作来保持树的平衡性。
旋转操作包括左旋和右旋,通过交换节点的位置来重新调整树的结构。
在插入或删除一个节点后,如果树的平衡性被破坏,就会进行旋转操作来恢复平衡。
平衡二叉树相对于哈希表的优势在于,它可以保持键值对的有序性。
数据结构 二叉排序树

9.6.2 哈希函数的构造方法
构造哈希函数的目标:
哈希地址尽可能均匀分布在表空间上——均 匀性好; 哈希地址计算尽量简单。
考虑因素:
函数的复杂度; 关键字长度与表长的关系; 关键字分布情况; 元素的查找频率。
一、直接地址法 取关键字或关键字的某个线性函数值为哈希地址 即: H(key) = key 或: H(key) = a* key + b 其中,a, b为常数。 例:1949年后出生的人口调查表,关键字是年份 年份 1949 1950 1951 … 人数 … … … …
9.4 二叉排序树
1.定义:
二叉排序树(二叉搜索树或二叉查找树) 或者是一棵空树;或者是具有如下特性的二叉树
(1) 若它的左子树不空,则左子树上所有结点的 值均小于根结点的值;
(2) 若它的右子树不空,则右子树上所有结点 的值均大于等于根结点的值; (3) 它的左、右子树也都分别是二叉排序树。
例如:
H(key)
通常设定一个一维数组空间存储记录集合,则 H(key)指示数组中的下标。
称这个一维数组为哈希(Hash)表或散列表。 称映射函数 H 为哈希函数。 H(key)为哈希地址
例:假定一个线性表为: A = (18,75,60,43,54,90,46) 假定选取的哈希函数为
hash3(key) = key % 13
H(key) = key + (-1948) 此法仅适合于: 地址集合的大小 = = 关键字集合的大小
二、数字分析法
假设关键字集合中的每个关键字都是由 s 位数 字组成 (u1, u2, …, us),分析关键字集中的全体, 并从中提取分布均匀的若干位或它们的组合作为 地址。 例如:有若干记录,关键字为 8 位十进制数, 假设哈希表的表长为100, 对关键字进行分析, 取随机性较好的两位十进制数作为哈希地址。
2016年考研核心题型【数据结构部分】【第4章 树与二叉树】

其余的 b 和 c 结点都各有一个前驱结点和后继结点。
那么,将 d 右指针域(初始为空)调整并指向其后继结点 b。将 b 结点的左指针域调整
指向其前驱结点 d,因为 b 的右指针域不为空,所以线索化过程中不需要调整。c 的左右指
针域都为空,令其左指针域指向其前驱结点 b,右指针域指向其后继结点 a。
有在已知前序遍历序列或者后序遍历序列的情况下,又知道中序遍历序列,才能唯一确定
一棵二叉树。
遍历一棵二叉树,要使得前序遍历序列和后序遍历序列刚好相反,那么必须保证每一
个结点都只有一个孩子结点。故而,二叉树的高度为 4。那么,在前序遍历序列为 1、2、3、
4,后序遍历序列为 4、3、2、1 的情况下,该二叉树第 1、2、3、4 层的结点依次为 1、2、
【解析】对于某一种遍历顺序对应的线索化,只需写出对应的遍历序列,然后修改空
指针域分别指向该遍历序列的前驱和后继即可。例如,本题中的二叉树的后序遍历可得到
序列 d、b、c、a。那么,d 是第一个元素,没有前驱,所以其左指针域原来为空,线索化时
亦为空;a 是最后一个元素,但是其左右孩子都不为空,所以不需要考虑该结点的线索化;
24
13
53
37
90
48
图 4.4 插入新的结点 48 之后,我们沿着叶子结点 48 往根节点的路径上,查找第一个不平衡 的结点。显然,24 是第一个不平衡的结点,其左子树的高度为 1,右子树的高度为 3。图中 的粗线部分,即需要旋转的部分。 那么,造成了什么类型的不平衡呢?我们这样判断:53 是 24 右孩子(R),37 是 24 的左孩子(L),所以是 RL 型不平衡。于是,先把结点 24 的右孩子 53 的左孩子 37 向右上 方旋转到原来 53 的位置,再将 37 向左上旋转到 24 的位置,24 被旋转下来。成了如图 4.5 所示的样子。
非线性结构阶段复习 - 精简版

22
练习1
下列序列不是堆的是 D 。
A、(100,85,98,77,80,60,82,40,20,10,66)
B、(100,98,85,82,80,77,66,60,40,20,10) C、(10,20,40,60,66,77,80,82,85,98,100) D、(100,85,40,77,80,60,66,98,82,10,20)
– 注意:函数指针的定义和使用
– 一般函数指针 VS. 类成员函数指针
9
二叉树的应用
• 设置信号放大器
– 后序遍历的应用 – 设计一个算法以确定把信号放大器放在何处, 使所用的放大器数目最小并且保证信号衰减 不超过给定的容忍值
• 理解:PlaceBoosters
10
第八章作业
P252-练习4:绘制表达式的二叉树 P259-练习9:采用数组存储二叉树,实现中序遍 历(提示:递归算法) P259-练习17:使用链式堆栈方法,来实现二叉树 的前序遍历 (提示:非递归算法;在向左子树遍历 之前,先把当前右子树节点压入栈中,以便后面遍 历)
27
搜索树的应用
• 直方图问题:基于BST的改进算法
– InsertVisit:插入并统计同值元素
• 箱子装载问题:基于AVL的最优匹配
– FindGE:支持重复键值 – BestFitPack
28
平均搜索长度(ASL) ——衡量搜索算法效率的标准
指在数据表中搜索各数据元素所需进行的关键码的比较次 数的期望值。 对于具有n个数据元素的数据表,搜索某数据元素成功时的 平均搜索长度为:
11
基于数组的中序遍历算法
• P259-练习8-10
template <class T> void InOrder(T a[], int last, int i) { if (i <= last && a[i]) { InOrder(a, last, 2*i); Visit(a, i); InOrder(a, last, 2*i+1); } }
王道数据结构 第七章 查找思维导图-高清脑图模板
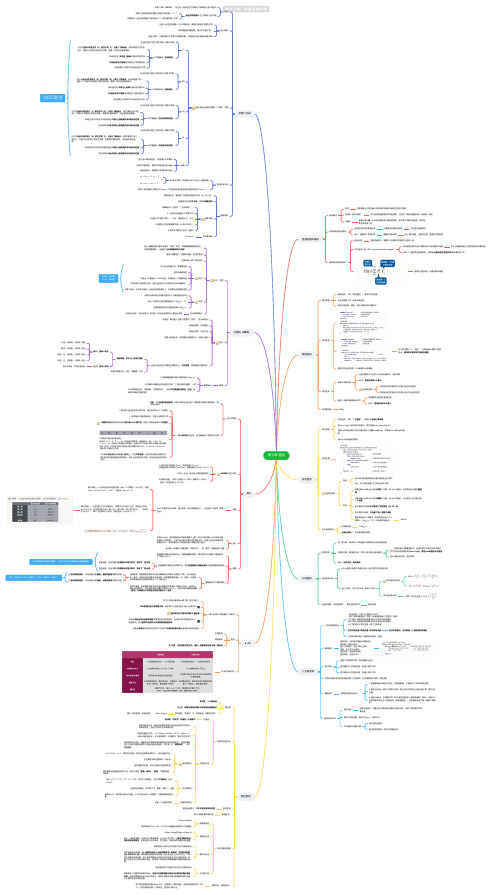
每次调整的对象都是“最小不平衡子树”
插入操作
在插入操作,只要将最小不平衡子树调整平衡,则其他祖先结点都会恢复平衡
在A的左孩子的左子树中插入导致不平衡
由于在结点A的左孩子(L)的左子树(L)上插入了新结点,A的平衡因子由1增
至2,导致以A为根的子树失去平衡,需要一次向右的旋转操作。
LL
将A的左孩子B向右上旋转代替A成为根节点 将A结点向右下旋转成为B的右子树的根结点
RR平衡旋转(左单旋转)
而B的原左子树则作为A结点的右子树
在A的左孩子的右子树中插入导致不平衡
由于在结点A的左孩子(L)的右子树(R)上插入了新结点,A的平衡因子由1增
LR
至2,导致以A为根的子树失去平衡,需要两次旋转操作,先左旋转再右旋转。
将A的左孩子B的右子树的根结点C向左上旋转提升至B结点的位置
本质:永远保证 子树0<关键字1<子树1<关键字2<子树2<...
当左兄弟很宽裕时,用当前结点的前驱、前驱的前驱来填补空缺 当右兄弟很宽裕时,用当前结点的后继、后继的后继来填补空缺
兄弟够借。若被删除关键字所在结点删除前的关键字个数低于下限,且与此结点 右(或左)兄弟结点的关键字还很宽裕,则需要调整该结点、右(或左)兄弟结 点及其双亲结点及其双亲结点(父子换位法)
LL平衡旋转(右单旋转)
而B的原右子树则作为A结点的左子树
在A的右孩子的右子树中插入导致不平衡
由于在结点A的右孩子(R)的右子树(R)上插入了新结点,A的平衡因子由-1
减至-2,导致以A为根的子树失去平衡,需要一次向左的旋转操作。
RR
将A的右孩子B向左上旋转代替A成为根节点 将A结点向左下旋转成为B的左子树的根结点
数据结构之二叉树(BinaryTree)

数据结构之⼆叉树(BinaryTree)⽬录导读 ⼆叉树是⼀种很常见的数据结构,但要注意的是,⼆叉树并不是树的特殊情况,⼆叉树与树是两种不⼀样的数据结构。
⽬录 ⼀、⼆叉树的定义 ⼆、⼆叉树为何不是特殊的树 三、⼆叉树的五种基本形态 四、⼆叉树相关术语 五、⼆叉树的主要性质(6个) 六、⼆叉树的存储结构(2种) 七、⼆叉树的遍历算法(4种) ⼋、⼆叉树的基本应⽤:⼆叉排序树、平衡⼆叉树、赫夫曼树及赫夫曼编码⼀、⼆叉树的定义 如果你知道树的定义(有限个结点组成的具有层次关系的集合),那么就很好理解⼆叉树了。
定义:⼆叉树是n(n≥0)个结点的有限集,⼆叉树是每个结点最多有两个⼦树的树结构,它由⼀个根结点及左⼦树和右⼦树组成。
(这⾥的左⼦树和右⼦树也是⼆叉树)。
值得注意的是,⼆叉树和“度⾄多为2的有序树”⼏乎⼀样,但,⼆叉树不是树的特殊情形。
具体分析如下⼆、⼆叉树为何不是特殊的树 1、⼆叉树与⽆序树不同 ⼆叉树的⼦树有左右之分,不能颠倒。
⽆序树的⼦树⽆左右之分。
2、⼆叉树与有序树也不同(关键) 当有序树有两个⼦树时,确实可以看做⼀颗⼆叉树,但当只有⼀个⼦树时,就没有了左右之分,如图所⽰:三、⼆叉树的五种基本状态四、⼆叉树相关术语是满⼆叉树;⽽国际定义为,不存在度为1的结点,即结点的度要么为2要么为0,这样的⼆叉树就称为满⼆叉树。
这两种概念完全不同,既然在国内,我们就默认第⼀种定义就好)。
完全⼆叉树:如果将⼀颗深度为K的⼆叉树按从上到下、从左到右的顺序进⾏编号,如果各结点的编号与深度为K的满⼆叉树相同位置的编号完全对应,那么这就是⼀颗完全⼆叉树。
如图所⽰:五、⼆叉树的主要性质 ⼆叉树的性质是基于它的结构⽽得来的,这些性质不必死记,使⽤到再查询或者⾃⼰根据⼆叉树结构进⾏推理即可。
性质1:⾮空⼆叉树的叶⼦结点数等于双分⽀结点数加1。
证明:设⼆叉树的叶⼦结点数为X,单分⽀结点数为Y,双分⽀结点数为Z。
数据结构二叉排序树

05
13
19
21
37
56
64
75
80
88
92
low mid high 因为r[mid].key<k,所以向右找,令low:=mid+1=4 (3) low=4;high=5;mid=(4+5) div 2=4
05
13
19
low
21
37
56
64
75
80
88
92
mid high
因为r[mid].key=k,查找成功,所查元素在表中的序号为mid 的值
平均查找长度:为确定某元素在表中某位置所进行的比 较次数的期望值。 在长度为n的表中找某一元素,查找成功的平均查找长度:
ASL=∑PiCi
Pi :为查找表中第i个元素的概率 Ci :为查到表中第i个元素时已经进行的比较次数
在顺序查找时, Ci取决于所查元素在表中的位置, Ci =i,设每个元素的查找概率相等,即Pi=1/n,则:
RL型的第一次旋转(顺时针) 以 53 为轴心,把 37 从 53 的左上转到 53 的左下,使得 53 的左 是 37 ;右是 90 ,原 53 的左变成了 37 的右。 RL型的第二次旋转(逆时针)
一般情况下,假设由于二叉排序树上插入结点而失去 平衡的最小子树的根结点指针为a(即a是离插入结点最 近,且平衡因子绝对值超过1的祖先结点),则失去平衡 后进行调整的规律可归纳为下列四种情况: ⒈RR型平衡旋转: a -2 b -1 h-1 a1
2.查找关键字k=85 的情况 (1) low=1;high=11;mid=(1+11) / 2=6
05
13
19
21
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平衡二叉树构造过程
1.插入操作:
插入新节点是平衡二叉树构造过程中的基本操作之一、首先,将新节
点插入到二叉树中的合适位置,然后检查树的平衡性。
在插入过程中,需
要更新每个节点的高度,并验证是否需要进行旋转操作,以保持树的平衡。
具体插入操作的步骤如下:
1.1在树中查找合适的位置插入新节点,按照二叉树的规则:
-如果新节点值小于当前节点值,则继续在当前节点的左子树中查找
合适位置插入新节点;
-如果新节点值大于当前节点值,则继续在当前节点的右子树中查找
合适位置插入新节点;
-如果当前节点为空,则将新节点插入到此位置。
1.2更新每个节点的高度,从插入的节点开始,向上遍历到根节点。
计算每个节点的左子树高度和右子树高度,然后取其中较大值加1作为节
点的新高度。
1.3验证平衡性。
对于每个节点,计算其左右子树高度差的绝对值,
如果超过1,则需要进行旋转操作。
2.旋转操作:
旋转是平衡二叉树构造过程中的关键步骤,用来调整树的结构,使其
保持平衡。
2.1左旋:将当前节点的右子树变为新的根节点,当前节点成为新的根节点的左子树,新的根节点的左子树成为当前节点的右子树。
2.2右旋:将当前节点的左子树变为新的根节点,当前节点成为新的根节点的右子树,新的根节点的右子树成为当前节点的左子树。
2.3左右旋:先对当前节点的左子树进行左旋操作,然后再对当前节点进行右旋操作。
2.4右左旋:先对当前节点的右子树进行右旋操作,然后再对当前节点进行左旋操作。
旋转操作的目的是调整树的结构,使得左右子树的高度差不超过1,并保持二叉树的性质。
3.删除操作:
删除节点是平衡二叉树构造过程中的另一个重要操作。
删除操作也需要更新树的高度和进行旋转操作。
删除操作的步骤如下:
3.1在树中查找要删除的节点。
如果要删除的节点是叶子节点,则直接删除即可。
3.2如果要删除的节点只有一个子节点,则将子节点替换成当前节点的位置。
3.3如果要删除的节点有两个子节点,则找到当前节点的后继节点(即比当前节点大的最小节点)或前驱节点(即比当前节点小的最大节点),将后继节点或前驱节点的值复制到当前节点,并删除后继节点或前驱节点。
3.4更新每个节点的高度,从删除的节点开始,向上遍历到根节点。
计算每个节点的左子树高度和右子树高度,然后取其中较大值加1作为节
点的新高度。
3.5验证平衡性。
对于每个节点,计算其左右子树高度差的绝对值,
如果超过1,则需要进行旋转操作。
总结:
平衡二叉树的构造过程包括插入、删除、旋转等操作。
通过插入新节点、更新树的高度和进行旋转操作,可以保持平衡二叉树的平衡性。
插入
和删除操作需要根据节点的情况选择合适的旋转操作,以调整树的结构。
通过平衡二叉树的构造过程,可以快速、高效地进行和插入、删除等操作。
