优化设计复习资料有答案
《机械优化设计》试卷及答案 新 全

《机械优化设计》复习题及答案一、选择题1、下面 方法需要求海赛矩阵。
A 、最速下降法B 、共轭梯度法C 、牛顿型法D 、DFP 法2、对于约束问题()()()()2212221122132min 44g 10g 30g 0f X x x x X x x X x X x =+-+=--≥=-≥=≥根据目标函数等值线和约束曲线,判断()1[1,1]T X =为 ,()251[,]22TX =为 。
A .内点;内点B. 外点;外点C. 内点;外点D. 外点;内点3、内点惩罚函数法可用于求解__________优化问题。
A 无约束优化问题B 只含有不等式约束的优化问题C 只含有等式的优化问题D 含有不等式和等式约束的优化问题4、对于一维搜索,搜索区间为[a ,b],中间插入两个点a 1、b 1,a 1<b 1,计算出f(a 1)<f(b 1),则缩短后的搜索区间为___________。
A [a 1,b 1]B [ b 1,b]C [a1,b]D [a,b1]5、_________不是优化设计问题数学模型的基本要素。
A设计变量B约束条件C目标函数D 最佳步长6、变尺度法的迭代公式为x k+1=x k-αk H k▽f(x k),下列不属于H k必须满足的条件的是________。
A. H k之间有简单的迭代形式B.拟牛顿条件C.与海塞矩阵正交D.对称正定7、函数)(Xf在某点的梯度方向为函数在该点的。
A、最速上升方向B、上升方向C、最速下降方向D、下降方向8、下面四种无约束优化方法中,__________在构成搜索方向时没有使用到目标函数的一阶或二阶导数。
A 梯度法B 牛顿法C 变尺度法D 坐标轮换法9、设)f在R上为凸函数的(X(Xf为定义在凸集R上且具有连续二阶导数的函数,则)充分必要条件是海塞矩阵G(X)在R上处处。
A 正定B 半正定C 负定D 半负定10、下列关于最常用的一维搜索试探方法——黄金分割法的叙述,错误的是,。
2021年高中总复习优化设计生物答案

2021年高中总复习优化设计生物答案一、选择题1.在确定DNA是遗传物质的研究过程中,艾弗里和赫尔希与蔡斯进行的实验有重要意义。
下列相关叙述错误的是()A.两个实验的设计思路共同点是将DNA与蛋白质分开B.他们都选用了结构十分简单的生物——病毒展开研究C.两个实验都应用了细菌培养技术为实验成功提供了保障D.两个实验表明:亲代的各种性状是通过DNA遗传给后代的解析:选B。
肺炎双球菌体外转化实验和噬菌体侵染细菌实验证明DNA 是遗传物质的关键是设法将DNA与其他物质分开,单独地、直接地观察它们的作用,A正确;艾弗里选用的实验材料是肺炎双球菌,赫尔希与蔡斯选用的实验材料是噬菌体和大肠杆菌,B错误;两个实验中都有细菌的培养过程,都应用了细菌培养技术,C正确;两个实验都证明了DNA是遗传物质,即亲代的各种性状是通过DNA遗传给后代的,D正确。
2.经检测得知,一双链DNA分子中鸟嘌呤的数目为x,其占碱基总数量的比例是y,以下推断正确的是()A.与鸟嘌呤互补的碱基比例是1-yB.该DNA分子中嘌呤和嘧啶的比例是x/yC.该DNA分子中碱基之间的氢键数是x(1+2/y)D.与鸟嘌呤不互补的碱基数目是x(1-2y)/y解析:选D。
由题意可知,G、C所占比例都为y,数量都为x;A、T所占比例都为1/2-y,数量都为(x/y-2x)/2=x/2y-x。
与鸟嘌呤互补的碱基比例是y;该DNA分子中嘌呤和嘧啶的比例是1;G—C碱基对中有三个氢键,A—T碱基对中有两个氢键,该DNA分子中碱基之间的氢键数是3x+2(x/2y-x)=x+x/y;腺嘌呤和胸腺嘧啶与鸟嘌呤不互补,其数目为x(1-2y)/y。
3.将全部DNA分子双链经32P标记的雄性动物细胞(染色体数2n=20)置于不含32P的培养液中培养,经过连续两次细胞分裂后产生了4个子细胞。
下列有关推断正确的是()A.第二次有丝分裂后期,1个细胞中被32P标记的染色体为40条B.减数第二次分裂后期,1个细胞中被32P标记的染色体为40条C.若进行有丝分裂,则4个子细胞中含32P染色体的子细胞比例一定为2(1)D.若进行减数分裂,则4个子细胞中含32P染色体的子细胞比例一定为1解析:选D。
优化设计复习题(原)

优化设计复习题一、单项选择题(在每小题列出的选项中只有一个选项是符合题目要求的)1.多元函数F(X)在点X *附近偏导数连续, F ’(X *)=0且H(X *)正定,则该点为F(X)的( )①极小值点 ②极大值点 ③鞍点 ④不连续点2.F(X)为定义在n 维欧氏空间中凸集D 上的具有连续二阶偏导数的函数,若H(X)正定,则称F(X)为定义在凸集D 上的( )①凸函数 ②凹函数3.黄金分割法中,每次缩短后的新区间长度与原区间长度的比值始终是一个常数,此常数是( ) ①0.382 ②0.186 ③0.618 ④0.8164.在单峰搜索区间[x 1,x 3](x 1<x 3)内,取一点x 2,用二次插值法计算得x 4(在[x 1,x 3]内),若x 2>x 4,并且其函数值F (x 4)<F(x 2),则取新区间为( )①[x 1,x 4] ②[x 2,x 3] ③[x 1,x 2] ④[x 4,x 3]5.用变尺度法求一n 元正定二次函数的极小点,理论上需进行一维搜索的次数最多为( )①n 次 ②2n 次 ③n+1次 ④2次 6.下列特性中,梯度法不具有的是( )①二次收剑性 ②要计算一阶偏导数 ③对初始点的要求不高 ④只利用目标函数的一阶偏导数值构成搜索方向 8.对于极小化F(X),而受限于约束g μ(X)≤0(μ=1,2,…,m)的优化问题,其内点罚函数表达式为( ) ① Ф(X,r (k))=F(X)-r(k)11/()gX u u m=∑② Ф(X,r (k))=F(X)+r(k)11/()g X u u m=∑③ Ф(X,r (k))=F(X)-r(k)max[,()]01gX u u m =∑④ Ф(X,r (k))=F(X)-r (k)min[,()]01g X u u m=∑9.外点罚函数法的罚因子为( ) ①递增负序列 ②递减正序列 ③递增正序列 ④递减负序列 10.函数F (X )为在区间[10,20]内有极小值的单峰函数,进行一维搜索时,取两点13和16,若F (13)<F (16),则缩小后的区间为( ) ①[10,16] ②[10,13] ③[13,16] ④[16,20]11.多元函数F (X )在X *处存在极大值的充分必要条件是:在X *处的Hesse 矩阵( )①等于零 ②大于零 ③负定 ④正定 12.对于函数F (x )=x 21+2x 22,从初始点x (0)={1,1}T 出发,沿方向s (0)={-1,-2}T进行一维搜索,最优步长因子为( )①10/16 ②5/9 ③9/34 ④1/213.目标函数F (x )=x 21+x 22-x 1x 2,具有等式约束,其等式约束条件为h(x)=x 1+x 2-1=0,则目标函数的极小值为( )①1 ②0.5 ③0.25 ④0.1 14. 优化设计的自由度是指( )① 设计空间的维数 ② 可选优化方法数 ③ 所提目标函数数 ④ 所提约束条件数15. 在无约束优化方法中,只利用目标函数值构成的搜索方法是( )①梯度法 ② Powell 法 ③共轭梯度法 ④变尺度法 17. 利用0.618法在搜索区间[a,b ]内确定两点a 1=0.382,b 1=0.618,由此可知区间[a,b ]的值是( ) ①[0,0.382] ② [0.382,1] ③ [0.618,1]④ [0,1]18. 已知函数F(X)=x 12+x 22-3x 1x 2+x 1-2x 2+1,则其Hesse 矩阵是( ) ① ⎥⎦⎤⎢⎣⎡--2332 ② ⎥⎦⎤⎢⎣⎡2332③ ⎥⎦⎤⎢⎣⎡2112 ④ ⎥⎦⎤⎢⎣⎡--322319. 对于求minF(X)受约束于g i (x)≤0(i=1,2,…,m)的约束优化设计问题,当取λi ≥0时,则约束极值点的库恩—塔克条件为( )① ()i i 1F X g (X)mi λ=∇=∇∑,其中λi 为拉格朗日乘子② ()i i 1F X =g (X)mi λ=-∇∇∑,其中λi 为拉格朗日乘子③ ()i i 1F X g (X)qi λ=∇=∇∑,其中λi 为拉格朗日乘子,q 为该设计点X 处的约束面数④()i i 1F X g (X)qi λ=-∇=∇∑,其中λi 为拉格朗日乘子,q 为该设计点X 处的约束面数20. 在共轭梯度法中,新构造的共轭方向S (k+1)为( ) ① S (k+1)= ∇F(X (k+1))+β(k)S (K),其中β(k)为共轭系数② S (k+1)=∇F(X (k+1))-β(k)S (K),其中β(k)为共轭系数 ③ S (k+1)=-∇F(X (k+1))+β(k)S (K),其中β(k)为共轭系数④ S (k+1)=-∇F(X (k+1))-β(k)S (K),其中β(k)为共轭系数 21. 用内点罚函数法求目标函数F(X)=ax+b 受约束于g(X)=c-x ≤0的约束优化设计问题,其惩罚函数表达式为( )① (k)1ax b r c-x +-,r (k)为递增正数序列 ② (k)1ax b r c-x +-,r (k)为递减正数序列 ③ (k)1ax b r c-x ++,r (k)为递增正数序列 ④ (k)1ax b r c-x ++,r (k)为递减正数序列22. f(x)在区间[x 1,x 3]上为单峰函数,x 2为区间中的一点,x 4为利用二次插值法求得的近似极值点,若x 4-x 2<0,且f(x 4)≥f(x 2),则新的搜索区间为( )① [x 1,x 4] ② [x 2,x 3] ③ [x 1,x 2] ④[x 4,x 3]23. 已知F(X)=x 1x 2+2x 22+4,则F(X)在点X (0)=⎭⎬⎫⎩⎨⎧-11的最大变化率为( )① 10 ② 4 ③ 2 ④ 1024.试判别矩阵1111⎡⎣⎢⎤⎦⎥,它是( )矩阵 ①单位 ②正定矩 ③负定 ④不定 ⑤半正定 ⑥半负定 25.约束极值点的库恩——塔克条件为:-∇=∇=∑F X g Xii qi()()**λ1,当约束函数是g i (X)≤0和λi >0时,则q 应为( )①等式约束数目 ②不等式约束数目 ③起作用的等式约束数目 ④起作用的不等式约束数目26.在图示极小化的约束优化问题中,最优点为( ) ①A ②B ③C ④D27.内点罚函数(X,r (k))=F(X)-r(k)101gX g X u u u m(),(())≤=∑,在其无约束极值点X ·(r (k))逼近原目标函数的约束最优点时,惩罚项中( ) ①r (k)趋向零,11g X u u m()=∑不趋向零 ②r (k)趋向零,11g X u u m()=∑趋向零 ③r (k)不趋向零,11g X u u m()=∑趋向零④r (k)不趋向零,11g X uu m()=∑不趋向零 29.0.618法在迭代运算的过程中,区间的缩短率是( ) ①不变的 ②任意变化的 ③逐渐变大 ④逐渐变小 30.对于目标函数F(X)受约束于g u (X) ≤0(u=1,2,…,m)的最优化设计问题,外点法惩罚函数的表达式是( ) ①()()(k)(k)2()1X,M F X M {max[(),0]},mk u u g X M =Φ=+∑为递增正数序列②()()(k)(k)2()1X,M F X M {max[(),0]},mk u u g X M =Φ=+∑为递减正数序列③()()(k)(k)2()1X,M F X M {min[(),0]},mk u u g x M =Φ=+∑为递增正数序列④()()(k)(k)2()1X,M F X M {min[(),0]},mk u u g x M =Φ=+∑为递减正数序列31.对于二次函数F(X)=12X T AX+b T X+c,若X *为其驻点,则▽F(X *)为( )①零 ②无穷大 ③正值 ④负值 32.在约束优化方法中,容易处理含等式约束条件的优化设计方法是( )①可行方向法 ②复合形法 ③内点罚函数法 ④外点罚函数法33.已知F(X)=(x 1-2)2+x 22,则在点X (0)=00⎧⎨⎩⎫⎬⎭处的梯度为( ) ①∇=⎧⎨⎩⎫⎬⎭F X()()000 ②∇=-⎧⎨⎩⎫⎬⎭F X ()()020③∇=⎧⎨⎩⎫⎬⎭F X()()040 ④∇=-⎧⎨⎩⎫⎬⎭F X ()()040 34.Powell 修正算法是一种( )①一维搜索方法②处理约束问题的优化方法③利用梯度的无约束优化方法④不利用梯度的无约束优化方法 二、多项选择题(在每小题列出的多个选项中有两个以上选项是符合题目要求的,多选、少选、错选均无分) 35.下列矢量组中,关于矩阵A=105051--⎡⎣⎢⎤⎦⎥..共轭的矢量组是( )①s 1={0 1} ,s 2={1 0}T②s 1={-1 1}T ,s 2={1 1}T③s 1={1 0}T ,s 2={1 2}T④s 1={1 1}T ,s 2={1 2}T⑤.s 1={1 2}T ,s 2={2 1}T36. 对于只含不等式约束的优化设计问题,可选用的优化方法有( )① Powell 法 ② 变尺度法 ③ 内点罚函数法 ④ 外点罚函数法 E. 混合罚函数法37. 根据无约束多元函数极值点的充分条件,已知驻点X *,下列判别正确的是( )①若Hesse矩阵H(X*)正定,则X*是极大值点②若Hesse矩阵H(X*)正定,则X*是极小值点③若Hesse矩阵H(X*)负定,则X*是极大值点④若Hesse矩阵H(X*)负定,则X*是极小值点⑤若Hesse矩阵H(X*)不定,则X*是鞍点38.下述Hesse矩阵中,正定矩阵为()①3335⎡⎣⎢⎤⎦⎥②313153337⎡⎤⎢⎥-⎢⎥-⎢⎥⎣⎦③3445⎡⎣⎢⎤⎦⎥④245434542⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦⑤523222327⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦39.F(X)在区间[a,b]上为单峰函数,区间内函数情况如图所示:F1=F2。
《机械优化设计》试卷习题及答案

精选文档你我共享《机械优化设计》复习题及答案一、填空题、用最速降落法求22212的最优解时,设X(0)=[-0.5,0.5]T,第一1)+(1-x)1f(X)=100(x-x步迭代的搜寻方向为[-47;-50]。
2、机械优化设计采纳数学规划法,其中心一是成立搜寻方向二是计算最正确步长因子。
3、当优化问题是__凸规划______的状况下,任何局部最优解就是全域最优解。
4、应用进退法来确立搜寻区间时,最后获取的三点,即为搜寻区间的始点、中间点和终点,它们的函数值形成高-低-高趋向。
5、包括n个设计变量的优化问题,称为n维优化问题。
、函数1X THX BTX C的梯度为HX+B。
627、设G为n×n对称正定矩阵,若n维空间中有两个非零向量0,d1,知足(d0T1,d)Gd=0则d0、d1之间存在_共轭_____关系。
8、设计变量、拘束条件、目标函数是优化设计问题数学模型的基本因素。
9、对于无拘束二元函数f(x1,x2),若在x0(x10,x20)点处获得极小值,其必需条件是梯度为零,充足条件是海塞矩阵正定。
10、库恩-塔克条件能够表达为在极值点处目标函数的梯度为起作用的各拘束函数梯度的非负线性组合。
11、用黄金切割法求一元函数f(x)x210x36的极小点,初始搜寻区间[a,b][10,10],经第一次区间消去后获取的新区间为[-2.36,2.36]。
12、优化设计问题的数学模型的基本因素有设计变量、拘束条件目标函数、13、牛顿法的搜寻方向d k=,其计算量大,且要求初始点在极小点迫近位置。
14、将函数f(X)=x222-10x1-4x2+60表示成1XTHXTX C的形1+x2-x1x2B式。
15、存在矩阵H,向量d,向量d,当知足(d1)TGd2=0,向量d和向量d1212是对于H共轭。
16、采纳外点法求解拘束优化问题时,将拘束优化问题转变为外点形式时引入的处罚因子r数列,拥有由小到大趋于无量特色。
高中总复习优化设计一轮用书 第3章 地表形态及其变化 含答案
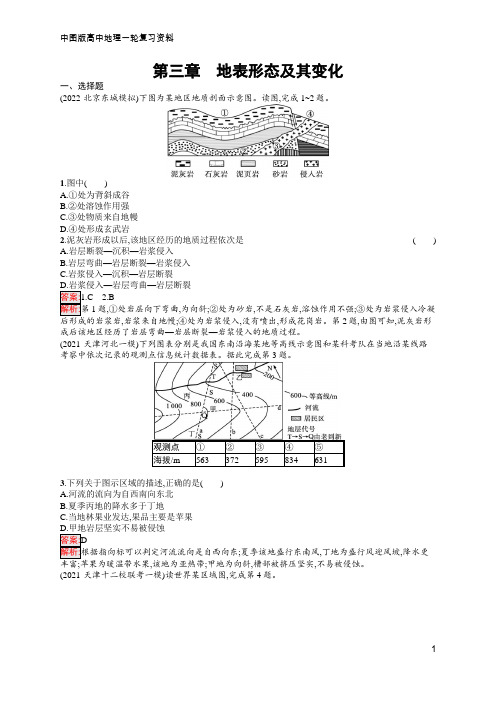
第三章地表形态及其变化一、选择题(2022·北京东城模拟)下图为某地区地质剖面示意图。
读图,完成1~2题。
1.图中()A.①处为背斜成谷B.②处溶蚀作用强C.③处物质来自地幔D.④处形成玄武岩2.泥灰岩形成以后,该地区经历的地质过程依次是()A.岩层断裂—沉积—岩浆侵入B.岩层弯曲—岩层断裂—岩浆侵入C.岩浆侵入—沉积—岩层断裂—岩层弯曲—岩层断裂2.B1题,①处岩层向下弯曲,为向斜;②处为砂岩,不是石灰岩,溶蚀作用不强;③处为岩浆侵入冷凝,岩浆来自地幔;④处为岩浆侵入,没有喷出,形成花岗岩。
第2题,由图可知,泥灰岩形成后该地区经历了岩层弯曲—岩层断裂—岩浆侵入的地质过程。
(2021·天津河北一模)下列图表分别是我国东南沿海某地等高线示意图和某科考队在当地沿某线路考察中依次记录的观测点信息统计数据表。
据此完成第3题。
3.下列关于图示区域的描述,正确的是()A.河流的流向为自西南向东北B.夏季丙地的降水多于丁地C.当地林果业发达,果品主要是苹果;夏季该地盛行东南风,丁地为盛行风迎风坡,降水更,该地为亚热带;甲地为向斜,槽部被挤压坚实,不易被侵蚀。
(2021·天津十二校联考一模)读世界某区域图,完成第4题。
4.图中乙地以南沿海地区有曲折幽深的峡湾,海岸线异常曲折、破碎的原因有()①地壳运动②流水沉积③海浪侵蚀④流水侵蚀⑤冰川侵蚀⑥风力沉积A.①②④⑥B.②③④⑤D.①③④⑤,地壳活跃,导致岩石破碎;受冰川侵蚀影响形成冰川谷,之后受海浪及(2021·湖北襄阳期末)和田玉是一种深埋在地下的白云岩变质而成的大理岩,经岩浆活动形成的岩石(石包玉的石与玉边界清楚,可以分离)。
当岩石露出地表,经风化、流水冲刷和搬运、沉积,石与玉分离,这便形成鹅卵石状的籽料。
据此完成5~6题。
5.籽料形成过程中地质作用的先后顺序是()A.岩浆侵入—变质作用—外力作用—地壳运动B.变质作用—岩浆侵入—地壳运动—外力作用C.变质作用—地壳运动—岩浆侵入—外力作用D.外力作用—变质作用—岩浆侵入—地壳运动6.根据材料和图片信息推测,图中寻找籽料的最佳地段是()B.②C.③D.④6.C5题,由材料可知,首先白云岩变质形成大理岩;然后发生岩浆侵入,且大理岩被包入岩浆中形;“岩石露出地表”说明有地壳上升运动;最后经外力作用,玉、石分离形成籽料。
高中总复习优化设计一轮用书 第13章区域发展 含答案

第十三章区域发展一、选择题都市圈(区)是指由起核心作用的中心城市和周边受到中心城市强烈辐射、有着紧密联系的城市组成的城市经济区域。
它是城镇化发展到成熟阶段的最高空间组织形式。
都市圈(区)的发育程度已成为衡量一个国家或地区社会经济发展水平的重要标志。
下图为我国山东都市圈(区)分布图。
据此完成1~2题。
1.山东省都市圈(区)的形成得益于()A.城市空间分布格局的变化B.生产要素的空间集聚C.跨区域的人口迁移D.快速化交通通信方式的兴起2.山东省六大都市圈(区)的形成,有利于()A.优化配置生产要素,形成优势互补的城市分工与协作B.加强中心城市的辐射带动作用,促进郊区城市化C.减轻大城市的土地承载压力,有效遏制环境恶化,建立多层次的城市空间网络2.A1题,据材料可知,都市圈(区)内的各个城市之间联系密切,信息、资金、人口、物质流动交换2题,通过材料可知,都市圈(区)是城镇化发展到成熟阶段的最高空间组织形式,都市圈(区)的发育程度已成为衡量一个国家或地区社会经济发展水平的重要标志,都市圈(区)的最大特点是中心城市与周边城市之间经济联系密切,生产要素优化配置,存在产业分工与合作。
(2022·山东德州模拟)西藏“一江两河”中部流域地区在地貌上属于藏南山原宽谷区,大部分谷地宽度为2~5千米,在拉萨河、年楚河等支流与干流汇合处,最宽可达10千米。
其年降水量400~550毫米,主要集中在5—9月。
受自然条件影响,河谷地带风沙地貌发育,风沙灾害严重。
下图为该区域某河段剖面示意图。
据此完成3~4题。
3.与我国西北沙漠相比,影响该地区风沙形成的主要原因是()A.年降水量小B.过度开垦C.河流水位变化D.过度放牧4.该地区风沙灾害治理面临的困难有()①沙土入渗强烈,保水能力较差②高台沙地和沙坡地的地下水位低③年降水量小,灌木不能生长④冬春季节河床和沙滩易裸露起沙A.①②③B.①②④C.①③④D.②③④4.B3题,考查风沙的成因。
高中总复习优化设计 化学 第一轮 考点规范练37 晶体结构与性质 含答案
考点规范练37 晶体结构与性质(时间:45分钟 满分:100分)非选择题(共5小题,共100分)1.(20分)磁性材料氮化铁镍合金可用Fe(NO 3)3、Ni(NO 3)2、丁二酮肟、氨气、氮气、氢氧化钠、盐酸等物质在一定条件下反应制得。
(1)Fe 3+的电子排布式是 。
(2)N O 3-和NH 3中氮原子的杂化方式分别为 。
(3)NH 3的沸点高于PH 3,其主要原因是 。
(4)与N 3-具有相同电子数的三原子分子的立体构型是 。
(5)向Ni(NO 3)2溶液中滴加氨水,刚开始时生成绿色Ni(OH)2沉淀,当氨水过量时,沉淀会溶解,生成[Ni(NH 3)6]2+蓝色溶液,则1 mol [Ni(NH 3)6]2+含有的σ键为 mol 。
图1图2(6)图1是丁二酮肟与镍形成的配合物,则分子内含有的作用力有 (填字母)。
A.氢键 B.离子键 C.共价键 D.金属键 E.配位键组成该配合物分子且同属第二周期元素的电负性由大到小的顺序是 。
(7)铁元素对应的单质在形成晶体时,采用如图2所示的堆积方式。
则这种堆积模型的配位数为 ,如果Fe 的原子半径为a cm,阿伏加德罗常数的值为N A ,则计算此单质的密度表达式为 -3(不必化简)。
22s 22p 63s 23p 63d 5或[Ar]3d 5 sp 3(3)NH 3分子间可以形成氢键 (4)V 形 (5)24(6)ACE O>N>C (7)856×2N A(4a √3)3为26号元素,则Fe 3+的电子排布式为1s 22s 22p 63s 23p 63d 5或[Ar]3d 5。
3为平面三角形,氮原子为sp 2杂化;NH 3为三角锥形,氮原子为sp 3杂化。
(4)N 3-电子数为10,与N 3-具有相同电子数的三原子分子为H 2O,分子的立体构型为V 形。
(5)在[Ni(NH 3)6]2+中,每个氮原子与3个氢原子形成σ键,同时还与镍原子形成配位键,也是σ键,因此1mol[Ni(NH 3)6]2+含有的σ键为4mol×6=24mol 。
优化设计复习二
15、梯度法属于无约束优化问题求解算法中的( )。 A直接法 B间接法 C人工智能优化法 16、一般情况下,用powell法求解无约束优化问题时,比坐标轮法求解速 度( )。 A慢 B一样 C快 17、( )属于一维优化方法。 A二次插值法 B罚函数法 C牛顿法 18、牛顿法是以( )为搜索方向的约束优化方法。 A共轭方向 B牛顿方向 C 梯度方向 19、复合形法的搜索方向一般是以( )为依据。 A最坏点 B 次坏点 C 最好点 20、Powell基本算法存在( )现象。 A 理论上不收敛 B 退化 C 共轭方向组不能保证线性独立 21、K-T”条件是( )取得极值的必要条件。 A约束优化问题 B 无约束优化问题 C 非线性规划问题
复习二
1、属于无约束优化问题求解算法中的直接法是:( )。 A 梯度法 B牛顿法 C POWELL法 D变尺度法 2. 复合形法中,映射点(迭代新点)XR需满足的条件为( ) 要求。 A适用性和可行性 B 可行性 C适用性 D映射性 3. 按类型划分,罚函数法属于( )。 A 一维优化方法 B无约束优化方法 C 直接法 D约束优化方法 4. 对于只含有不等式约束的优化问题,满足每一个设计约束的设 计点,称为( )。 A边界点 B非可行点 C 外点 D内点 5. 多元函数梯度的概念是:( ) A以其各二阶偏导数为分量的一个列向量 B以其各一阶偏导数为分量的 一个列向量 C以其各二阶偏导数为分量的一个行向量 D以其各一阶偏导数为分量的 一个行向量
8设计的发展经历了3个阶段,包 括: 、 、 。 9、提高价值可以从三个方面着手: 、 、 。 10、创造性思维的四对基本类型: 。 11、判定约束非线性规划优化问题中的某迭代点是否为约束极值 点的必要条件,一般采用 进行检验。 12、坐标轮换法若用于求解二维无约束问题,则遇到在极值点附 近等值线形状是 时,有效;是 时,显效 时,无效。 13、梯度法又称 ,其原因为梯度法以 为搜索方 向。 14、黄金分割法的区间缩短率每次都 ,大小为 。
高中总复习优化设计一轮用书 第6章 自然地理环境的整体性与地域分异规律 含答案
第六章自然地理环境的整体性与地域分异规律一、选择题富铝土是土壤形成过程中铁、铝等成分相对富集后的一类土壤的总称。
其在我国分布广泛,包含多种土壤类型,并具有下图所示的过渡关系。
读图,完成1~2题。
1.影响富铝土形成的主要自然因素是()A.成土母质B.气候C.生物D.地形2.下列土壤类型中,铁、铝相对含量最高的是()A.赤红壤B.砖红壤D.黄壤2.B1题,富铝土是土壤在湿热气候条件下,土体铝硅酸盐矿物受到分解,氧化铝在土壤中残留和,影响其形成的最主要自然因素是气候,B项正确。
第2题,湿热气候促进矿物分解,更易形成富铝土。
红壤、赤红壤分布区,热量较低,气候干燥,土壤铁、铝含量较少;南方气温较高,东部沿海气候湿润,所以铁、铝含量最高的是砖红壤;黄壤分布的纬度较高,热量较低,铁、铝含量较少。
(2021·天津高三二模)植被覆盖度是指植被(包括叶、茎、枝)在地面的垂直投影面积占统计区总面积的百分比。
气候、地形地势、人类活动等因素影响一个地区的植被覆盖度。
下图为我国某山脉4—10月南、北坡植被覆盖度在垂直方向上的变化统计示意图。
读图,完成3~4题。
3.根据图中的海拔信息,该山脉可能为()A.盘山B.天山C.秦岭D.南岭4.图中甲处南、北坡植被覆盖度基本一致,其主要原因是()A.植被类型相似B.人类活动相似C.水热条件相似4.B3题,4—10月为我国绝大部分植被的生长期,图示南、北坡植被覆盖度在海拔1000~3000米说明该山脉植被覆盖度较高。
海拔2000米以下,南坡大部分植被覆盖度比北坡高,说明在2000米以下的同海拔处,南坡水热条件好。
天山位于我国西北内陆地区,气候干旱,植被覆盖度较低,北坡受北冰洋和大西洋水汽的影响,水分条件比南坡好,所以北坡应比南坡植被覆盖度高,B项错误;盘山主峰挂月峰海拔864.4米,盘山平均海拔400~600米,不符合本山的海拔,A项错误;秦岭是我国亚热带季风气候和温带季风气候的分界线,夏季雨热同期,水热丰富,植被覆盖度高,且秦岭海拔接近4000米,南岭海拔较低,海拔仅千余米,C项正确,D项错误。
八下生物优化设计中考总复习内蒙古专版答案
八下生物优化设计中考总复习内蒙古专版答案1、下列几种说法错误的是() [单选题] *A、水螅生活在水中B、水螅身体呈左右对称(正确答案)C、水螅的体壁由两个胚层构成D、水螅有口无肛门2、下面几种动物不是腔肠动物的是() [单选题] *A、珊瑚虫B、海葵C、血吸虫(正确答案)D、水母3、下列动物中有口无肛门,食物残渣由口排出体外的是() [单选题] *A、中华鲟B、海蜇(正确答案)C、龟D、梭子蟹4、蛔虫体内最发达的器官是() [单选题] *A、感觉器官B、消化器官C、神经器官D、生殖器官(正确答案)5、蚯蚓的身体必须保持湿润的主要原因是() [单选题] *A、有利于钻洞(正确答案)B、有利于提高蠕动速度C、有利于取食D、有利于呼吸6、下列属于环节动物的一组是() [单选题] *A、沙蚕和蚯蚓(正确答案)B、水蛭和蛇C、蚯蚓和对虾D、水蛭和蜈蚣7、下列几种动物是软体动物的是() [单选题] *A、乌贼(正确答案)B、蚯蚓C、沙蚕D、青蛙8、下列几项中不是软体动物的共同特征的是() [单选题] *A、身体柔软B、有外套膜C、生活在水中D、身体外都有贝壳(正确答案)9、下列几种动物不属于节肢动物的是() [单选题] *A、蜻蜓B、蝉C、蚯蚓(正确答案)D、蜈蚣10、很多昆虫在生长发育过程中有蜕皮的现象,这是因为() [单选题] *A、昆虫的体表的外骨骼能保护和支持内脏B、外骨骼可以防止体内水分的蒸发C、外骨骼非常坚韧D、坚韧的外骨骼不能随昆虫的生长而生长(正确答案)11、关于蝗虫的外骨骼的叙述,正确的是() [单选题] *①长在身体的表面②具有支持和保护作用③防止体内水分蒸发④随蝗虫的生长而生长(正确答案)A②③④ B①③④ C①②④ D①②③12、下列属于鱼类的是() [单选题] *A、鲨鱼鳄鱼B、中华鲟鲨鱼(正确答案)C、鲸鱼鲳鱼D、鲍鱼鲤鱼13、鱼类游泳的动力来源于() [单选题] *A、尾鳍的摆动B、胸鳍和腹鳍的摆动C、各种鳍的共同作用D、躯干部和尾鳍的摆动(正确答案)14、下列动物中属于四大家鱼的有()①青鱼②草鱼③鳙鱼④鲸鱼⑤鲢鱼⑥鲫鱼⑦带鱼 [单选题] *A、①②③⑤(正确答案)B①⑤⑦C③④⑥D①②③④⑤⑦15、下列几种动物中不是两栖动物的是() [单选题] *A、青蛙(正确答案)B、蝾螈C、蜥蜴D、蟾蜍16、下列选项中全是爬行动物的是() [单选题] *A、蜥蜴蝾螈(正确答案)B、甲鱼蛇C、壁虎青蛙D、蝙蝠家猫17.青蛙的受精方式是( ) [单选题] *A、体内受精B、体外受精(正确答案)C、无性生殖D、体内受精或体外受精18.青蛙的发育过程是( ) [单选题] *A、卵细胞→蝌蚪→成蛙(正确答案)B、卵细胞→蝌蚪→幼蛙→成蛙C、受精卵→蝌蚪→成蛙D、受精卵→蝌蚪→幼蛙→成蛙19.下列动物中是两栖动物的是() [单选题] *A、蟾蜍(正确答案)B、海龟C、鳄鱼D、企鹅20.青蛙的幼体和成体的呼吸器官分别是() [单选题] *A、鰓;肺和皮肤(正确答案)B、肺;皮肤和肺C、鰓;皮肤D、鰓;气管21.与蝌蚪相比,只有成蛙才具有的结构是() [单选题] *A、鰓B、后肢C、尾巴D、肺(正确答案)22蜥蜴的皮肤干燥又粗糙,表面覆盖着角质鳞片,这样的皮肤有利于() [单选题] *A、爬行(正确答案)B、吸收营养C、辅助呼吸D、减少体内水分蒸发23.蜥蜴呼吸的特点是( )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
现代设计方法参考书目:1、陈继平. 现代设计方法,华中科技大学出版社。
2、高健. 机械设计优化基础,科学出版社,2007,93、刘惟信. 机械最优化设计,第二版,清华大学出版社。
第一章习题例2 某工厂生产甲乙两种产品。
生产每种产品所需的材料、工时、电力和可获得的利润,以及能够提供的材料、工时和电力见表。
试确定两种产品每天的产量,以使每天可能获得的利润最大。
设每天生产甲产品x1件,乙x2件,利润为f(x1,x2)f(x1,x2)=60x1+120x2每天实际消耗的材料、工时和电力分别用函数g1(x1,x2)、g2(x1,x2)、g3(x1,x2)表示:g1(x1,x2)=9x1+4x2g2(x1,x2)=3x1+10x2g3(x1,x2)=4x1+5x2于是上述问题可归结为:求变量x1,x2使函数f(x1,x2)= 60x1+120x2极大化满足条件g1(x1,x2)=9x1+4x2≤360g2(x1,x2)=3x1+10x2≤300g3(x1,x2)=4x1+5x2≤200g4(x1,x2)=x1≥0g5(x1,x2)=x2≥0例3 一种承受纯扭矩的空心传动轴,已知传递的扭矩为T,试确定此传动轴的内外径,以使其用料最省。
例: 求下列非线性规划优化问题优化设计的迭代算法1、下降迭代算法的基本格式 迭代公式基本原理:从某一初始设计开始,沿某个搜索方向以适当步长得到新的可行的设计,如此反复迭代,直到满足设计要求,迭代终止。
k k k SX X k 1α+=+S(k)——第k步的搜索方向,是一个向量; αk ——第k 步的步长因子,是一个数,它决定在方向S(k)上所取的步长大小。
简单的说:是一个搜索、迭代、逼近的过程。
最关键的是搜索的方向和步长。
迭代算法的基本步骤:1,选定初始点X(0),令k=0;2、在X(k)处选定下降方向S(k);,3、从X(k)出发沿S(k)一维搜索,找到X(k+1)=X(k)+αkS(k), 使得f(X(k+1))<f(X(k)); 令k=k+1,转(2)。
例:f (X)=x12+4x22,已知初始点X(0)=[1,1]T ,搜索方向S(o)=[-2,-4]T ,求X(1)=?迭代终止条件:迭代法收敛性1)线性收敛性(2)二次收敛性(3)超线性收敛性终止迭代收敛准则。
第二章2.1 函数的方向导数与梯度一、 函数的方向导数偏导数: 只描述函数沿特殊方向(x, y 轴)的变化情况在许多实际问题中,常常要知道函数沿其它任一方向上的变化率——引入方向导数的概念。
方向导数定义:设函数f(x1,x2)是点X(0)的某个邻域上的函数,它与x 轴夹角为θ1,与y 轴夹角θ2,设X(1)为S 上另一点,则||X(0)X(1)||=ρ=如果极限存在,则称这个极限为函数f(x1,x2)在点X(0)沿S 的方向导数。
已知F(X)=X21+X22,取 , 则在点处沿S 方向的方向导数数值为( ))41(4)21()(4121421122)1()0()0()1(αααααα-+-=⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡--+⎥⎦⎤⎢⎣⎡=+=X f S X X ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-==171178)1( 369X ααβ**1X X X X k k -=-+⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎭⎬⎫⎩⎨⎧=2/22/2cos cos 21ααS例题已知函数f(X)=则其在点X=(2,1)T处梯度的模为【】例2-1 求二元函数f(x1, x2)=x12+x22-4x1-2x2+5 在X0=[2,2]处函数下降最快的方向。
解:梯度方向是函数变化率最大的方向。
负梯度方向则是函数下降最快的方向。
例2-2 求二元函数f(x1, x2)=(x1-2)2+(x2-1)2 在点X(1)=[3,2]T和X(2)=[2,2]T的梯度,并作图表示作业:1、求函数f (X)=x12+x22-6x1在点X(1)=[1,1]T, X(2)=[1,2]T, X(3)=[-2,1]T的梯度及其模,并作图表示。
2、求例2-2 求二元函数f(x1, x2)=x12+x22-4x1-2x2+5 在X0=[2,2]T 处的海赛二阶泰勒展开式。
二次函数 B 为常数向量;H 为nxn 阶常数矩阵。
XTHX 称为二次型,H 称二次型矩阵。
1)若有XTHX>0,则称矩阵H 是正定的;(2)若有XTHX ≥0,则称矩阵H 是半正定的;(3)若有XTHX<0,则称矩阵H 是负定的;(4)若有XTHX ≤0,则称矩阵H 是半负定的;(5)若有XTHX =0,则称矩阵H 是不定的;正定二次函数的性质:1)正定二次函数的等值线或等值面是一族同心的椭圆或同心椭球。
椭圆族或椭球族的中心就是该二次函数的极小点。
2)非正定二次函数在极小点附近的等值线或等值面近似于椭圆或椭球。
例:求解等式约束问题的最优解。
解:[][]()52x 4x x x 2x 2x 20022x 2x 212x 2x 201H 212002H 2022x 42x 15222422212222T 220T 00T 0022022022022020210002201111+--+=⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛--+⎪⎪⎭⎫ ⎝⎛--+=--+-∇+≈∴⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛∂∂∂∂∂∂∂∂∂∂=⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎪⎭⎫ ⎝⎛∂∂∂∂=∇=+--+=()()()()()()()()()()()()()()(**)(11121X X X X X X X X f X f X f x X f x x X f x x X f x X f X x X f x X f X f X f C X B HX X X f T T ++=21)(1、多元函数F(X)在X*处存在极大值的必要条件是:在X*处的Hessian矩阵()A.等于零B.大于零C.负定D.正定2、在约束优化问题中,库恩—塔克条件是目标函数存在极值点的()A.充分条件B.必要条件C.充分必要条件D.不必要条件3、多元函数F(X)在点X*附近偏导数连续且H(X*)正定,则该点为F(X)的()A. 极小值点B. 极大值点 C 鞍点 D 不连续点4、F(X)为定义在n维欧氏空间中凸集D上的具有连续二阶偏导数,若H(X)正定,则称F(X)为定义在凸集D上的()A 凸函数B 凹函数C 严格凸函数D 严格凹函数5. 约束极值点的库恩—塔克条件为当约束条件gi(X)≤0(i=1,2,…,m)和λi≥0时,则q应为( )。
A. 等式约束数目B. 不等式约束数目C. 起作用的等式约束数目D. 起作用的不等式约束数目6.对于求minF(X)受约束于gi (x)≤0 (i=1,2,…,m) 的约束优化设计问题,当取λi≥0时,则约束极值点的库恩—塔克(K-T)条件为( )。
第三章例:已知目标函数f(X)=(X1-4)2+(X2-4)2。
由X(0)=[1 1]T为起点,沿S(0)=[2 1]T作一维搜索,求下一个迭代点X(1)。
例题:确定函数f(x)=3x3-4x+2的初始区间。
给定x0=0,h=1.解:x1=x0=0, f1=f(x1)=2 x2=x0+h=1, f2=f(x2)=1f1>f2, 则h=2h=2 x3=x0+h=2f3=f(x3)=18 f2<f3, 则[a b]=[0,2]1、函数F(X)为在区间[10,20]内有极小值的单峰函数,进行一维搜索时,取两点13和16,若F(13)<F(16),则缩小后的区间为()A.[10,16] B.[10,13] C.[13,16] D.[16,20]2、在用0.618法求函数极小值的迭代运算中,a1,b1为搜索区间[a,b]中的两点,函数值分别记为F1,F2。
已知F2>F1。
在下次搜索区间中,应作如下符号置换()①a1→a b1→a1 F2→F1 ②a→a1 a1→b1 F1→F2③b→b1 b1→a1 F2→F1 ④b1→b a1→b1 F1→F23、例:用黄金分割法求函数f(x)=3x3-4x+2的极小点,给定x0=0, h=1, ε=0.2。
解:1)确定初始区间x1=x0=0, f1=f(x1)=2x2=x0+h=0+1=1, f2=f(x2)=1 由于f1>f2, 应在原方向继续向前探测x3= x2+h=1+1=2, f3=f(x3)=18由于f2<f3,可知初始区间已经找到,即[a,b]=[x1,x2]=[0,2]2)用黄金分割法缩小区间第一次缩小区间:x1=0+0.382X(2-0)=0.764, f1=0.282x2=0+0.618 X(2-0)=1.236, f2=2.72f1<f2, 新区间[a,b]=[a,x2]=[0, 1.236], b-a>0.2第二次缩小区间:令x2=x1=0.764, f2=f1=0.282x1=0+0.382X(1.236-0)=0.472, f1=0.317由于f1>f2, 故新区间[a,b]=[x1,b]=[0.472, 1.236]因为b-a=1.236-0.472=0.764>0.2, 应继续缩小区间。
第三次缩小区间:令x1=x2=0.764, f1=f2=0.282x2=0.472+0.618X(1.236-0.472)=0.944, f2=0.747由于f1<f2, 故新区间[a,b]=[a, x2]=[0.472, 0.944]因为b-a=0.944-0.472=0.472>0.2, 应继续缩小区间第四次缩小区间:令x2=x1=0.764, f2=f1=0.282x1=0.472+0.382X(0.944-0.472)=0.652, f1=0.223由于f1<f2, 故新区间[a,b]=[a, x2]=[0.472, 0.764]因为b-a=0.764-0.472=0.292>0.2, 应继续缩小区间。
第五次缩小区间:令x2=x1=0.652, f2=f1=0.223x1=0.472+0.382X(0.764-0.472)=0.584, f1=0.262由于f1>f2, 故新区间[a,b]=[x1,b]=[0.584, 0.764]因为b-a=0.764-0.584=0.18<0.2, 停止迭代。
极小点与极小值:x*=0.5X(0.584+0.764)=0.674, f(x*)=0.2224、F(X)在区间[X1,X3]上为单峰函数,X2为区间中一点,X4为利用二次插值法公式求得的近似极值点。
如X4-X2>0,且F(X4)>F(X2),那么为求F(X)的极小值,X4点在下一次搜索区间内将作为()。
