高考数学一轮复习知识点总结:三角函数
高考数学一轮复习---三角函数的图象与性质---单调性

高考数学一轮复习---三角函数的图象与性质---单调性一、基础知识1.用五点法作正弦函数和余弦函数的简图 (1)“五点法”作图原理:在正弦函数y =sin x ,x ∈[0,2π]的图象上,五个关键点是:(0,0),⎪⎭⎫⎝⎛1,2π,(π,0),⎪⎭⎫⎝⎛-1,23π,(2π,0). 在余弦函数y =cos x ,x ∈[0,2π]的图象上,五个关键点是:(0,1),⎪⎭⎫⎝⎛0,2π,(π,-1),⎪⎭⎫⎝⎛0,23π,(2π,1). 函数y =sin x ,x ∈[0,2π],y =cos x ,x ∈[0,2π]的五个关键点的横坐标是零点和极值点(最值点). (2)五点法作图的三步骤:列表、描点、连线(注意光滑). 2.正弦、余弦、正切函数的图象与性质三角函数性质的注意点:(1)正、余弦函数一个完整的单调区间的长度是半个周期;y =tan x 无单调递减区间;y =tan x 在整个定义域内不单调.(2)要注意求函数y =A sin(ωx +φ)的单调区间时A 和ω的符号,尽量化成ω>0的形式,避免出现增减区间的混淆.二、常用结论 1.对称与周期的关系正弦曲线、余弦曲线相邻的两个对称中心、相邻的两条对称轴之间的距离是半个周期,相邻的对称中心与对称轴之间的距离是四分之一个周期;正切曲线相邻两个对称中心之间的距离是半个周期. 2.与三角函数的奇偶性相关的结论(1)若y =A sin(ωx +φ)为偶函数,则有φ=k π+π2(k ∈Z );若为奇函数,则有φ=k π (k ∈Z ).(2)若y =A cos(ωx +φ)为偶函数,则有φ=k π(k ∈Z );若为奇函数,则有φ=k π+π2 (k ∈Z ).(3)若y =A tan(ωx +φ)为奇函数,则有φ=k π(k ∈Z ).三、考点解析考点一 求三角函数的单调区间例、已知函数f (x )=sin 2x -cos 2x -23sin x cos x (x ∈R ). (1)求f ⎪⎭⎫⎝⎛32π的值; (2)求f (x )的最小正周期及单调递增区间.跟踪训练1.函数y =|tan x |在⎪⎭⎫⎝⎛-23,2ππ上的单调递减区间为________. 2.函数g (x )=-cos ⎪⎭⎫⎝⎛+-32πx ])2,2[(ππ-∈x 的单调递增区间为________.3.已知函数f (x )=3cos 2x -2sin 2(x -α),其中0<α<π2,且f ⎪⎭⎫⎝⎛2π=-3-1.(1)求α的值;(2)求f (x )的最小正周期和单调递减区间.考点二 求三角函数的值域(最值)例、(1)函数f (x )=3sin ⎪⎭⎫⎝⎛-62πx 在区间]2,0[π上的值域为( )A ]23,23[-. B.]3,23[- C.]233,233[- D.]3,233[- (2)函数f (x )=sin 2x +3cos x -34])2,0[(π∈x 的最大值是________.变式练习1.(变条件)若本例(1)中函数f (x )的解析式变为:f (x )=3cos ⎪⎭⎫⎝⎛-62πx ,则f (x )在区间]2,0[π上的值域为________.2.(变条件)若本例(2)中函数f (x )的解析式变为:函数f (x )=sin x +cos x +sin x cos x ,则f (x )的最大值为________.3.已知函数f (x )=sin ⎪⎭⎫⎝⎛+6πx ,其中x ∈],2[a π-,若f (x )的值域是]1,21[-,则实数a 的取值范围是________.考点三 根据三角函数单调性确定参数例、(1)若f (x )=cos x -sin x 在[-a ,a ]是减函数,则a 的最大值是( ) A.π4 B.π2 C.3π4 D .π (2)若f (x )=2sin ωx (ω>0)在区间]23,2[ππ-上是增函数,则ω的取值范围是________.[解题技法]已知三角函数的单调区间求参数范围的3种方法(1)求出原函数的相应单调区间,由所给区间是所求某区间的子集,列不等式(组)求解.(2)由所给区间求出整体角的范围,由该范围是某相应正、余弦函数的某个单调区间的子集,列不等式(组)求解.(3)由所给区间的两个端点到其相应对称中心的距离不超过14周期列不等式(组)求解.。
三角函数的概念 诱导公式(七大题型)(学生版)--2025年高考数学一轮复习

三角函数的概念 诱导公式(七大题型)目录:01任意角与弧度制02求弧长、扇形面积03求弧长、扇形面积的实际应用04三角函数的概念(求三角函数值及应用)05同角三角函数的基本关系06诱导公式07三角函数的概念诱导公式难点分析01任意角与弧度制1(2024高三·全国·专题练习)下列说法中正确的是()A.锐角是第一象限角B.终边相等的角必相等C.小于90°的角一定在第一象限D.第二象限角必大于第一象限角2(23-24高一上·湖南株洲·阶段练习)把5π4化成角度是()A.45°B.225°C.300°D.135°3(2023高三·全国·专题练习)与9π4终边相同的角的表达式中,正确的是()A.45°+2kπ,k∈ZB.k⋅360°+π4,k∈ZC.k⋅360°+315°,k∈ZD.2kπ-7π4,k∈Z4(2023高三·全国·专题练习)已知角α第二象限角,且cos α2=-cosα2,则角α2是() A.第一象限角 B.第二象限角 C.第三象限角 D.第四象限角5(2014高三·全国·专题练习)集合αkπ+π4≤α≤kπ+π2,k∈Z中的角所表示的范围(阴影部分)是()A. B.C. D.,B= 6(22-23高三上·贵州贵阳·期末)已知集合A=α 2kπ+π4≤α≤2kπ+π2,k∈Z,则()α kπ+π4≤α≤kπ+π2,k∈ZA.A⊆BB.B⊆AC.A=BD.A∩B=∅02求弧长、扇形面积7(23-24高三上·安徽铜陵·阶段练习)已知扇形的周长为30cm,圆心角为3rad,则此扇形的面积为()A.9cm2B.27cm2C.48cm2D.54cm28(23-24高三下·浙江·开学考试)半径为2的圆上长度为4的圆弧所对的圆心角是()A.1B.2C.4D.89(22-23高一下·河北张家口·期中)如图,已知扇形的周长为6,当该扇形的面积取最大值时,弦长AB=()A.3sin1B.3sin2C.3sin1°D.3sin2°10(22-23高三下·上海宝山·阶段练习)如图所示,圆心为原点O的单位圆的上半圆周上,有一动点P x,y,点B是P关于原点O的对称点.分别连结PA、PB、AB,如此形成了三个区 (y>0).设A1,0域,标记如图所示.使区域Ⅰ的面积等于区域Ⅱ、Ⅲ面积之和的点P的个数是()A.0个B.1个C.2个D.3个03求弧长、扇形面积的实际应用11(23-24高三上·广东肇庆·阶段练习)“顺德眼”是华南地区首座双立柱全拉索设计的摩天轮总共设有36个等间距座舱,其中亲子座舱4个,每2个亲子座舱之间有8个普通座舱,摩天轮上的座舱运动可以近似地看作是质点在圆周上做匀速圆周运动,质点运行轨迹为圆弧,运行距离为弧长,“顺德眼”在旋转过程中,座舱每秒运行约0.2米,转一周大约需要21分钟,则两个相邻的亲子座舱在运行一周的过程中,距离地面的高度差的最大值约为( )(参考数据:2π≈0.45,计算结果保留整数)A.40米B.50米C.57米D.63米12(23-24高三上·安徽·期中)扇子是引风用品,夏令必备之物.我国传统扇文化源远流长,是中华文化的一个组成部分.历史上最早的扇子是一种礼仪工具,后来慢慢演变为纳凉、娱乐、观赏的生活用品和工艺品.扇子的种类较多,受大众喜爱的有团扇和折扇.如图1是一把折扇,是用竹木做扇骨,用特殊纸或绫绢做扇面而制成的.完全打开后的折扇为扇形(如图2),若图2中∠ABC =θ,D ,E 分别在BA ,BC 上,AD =CE =m ,AC的长为l ,则该折扇的扇面ADEC 的面积为()图1 图2 A.m l -θ2B.m l -θm2C.m 2l -θ2D.m 2l -θm213(2024·湖南长沙·一模)“会圆术”是我国古代计算圆弧长度的方法,它是我国古代科技史上的杰作,如图所示AB是以O 为圆心,OA 为半径的圆弧,C 是AB 的中点,D 在AB上,CD ⊥AB ,则AB的弧长的近似值s 的计算公式:s =AB +CD 2OA.利用上述公式解决如下问题:现有一自动伞在空中受人的体重影响,自然缓慢下降,伞面与人体恰好可以抽象成伞面的曲线在以人体为圆心的圆上的一段圆弧,若伞打开后绳长为6米,该圆弧所对的圆心角为60°,则伞的弧长大约为( )3≈1.7A.5.3米B.6.3米C.8.3米D.11.3米04三角函数的概念(求三角函数值及应用)14(23-24高三下·重庆渝中·阶段练习)已知角α的终边经过点P 1,2sin α ,则sin α的值不可能是() A.32B.0C.-32D.1215(2024·上海松江·二模)已知点A 的坐标为12,32 ,将OA 绕坐标原点O 逆时针旋转π2至OP ,则点P 的坐标为.16(2024·全国·模拟预测)已知角θ的顶点为坐标原点,始边为x 轴的非负半轴.若P m ,2 是角θ终边上一点,且cos θ=-31010,则m =.17(2023高三·全国·专题练习)已知角α的终边经过点P -x ,-6 ,且cos α=-513,则1sin α+1tan α=.18(2024·四川成都·模拟预测)在平面直角坐标系中,角α的顶点与原点重合,始边与x 轴的非负半轴重合,终边经过点P 3,4 ,则sin α+2cos αcos α-sin α=()A.11B.-10C.10D.-1119(2024·云南昆明·一模)已知角θ的顶点为坐标原点O ,始边与x 轴的非负半轴重合,点A (1,a )(a ∈Z )在角θ终边上,且OA ≤3,则tan θ的值可以是.(写一个即可)20(2024高三·全国·专题练习)在平面直角坐标系xOy 中,角α的顶点为原点O ,以x 轴的非负半轴为始边,终边经过点P (1,m )(m <0),则下列各式的值恒大于0的有( )个.①sin αtan α;②cos α-sin α;③sin αcos α;④sin α+cos α.A.0B.1C.2D.321(21-22高三下·河南许昌·开学考试)已知某质点从平面直角坐标系xOy 中的初始位置点A 4,0 ,沿以O 为圆心,4为半径的圆周按逆时针方向匀速运动到B 点,则B 点的坐标为()A.4cos ∠AOB ,4sin ∠AOBB.4sin ∠AOB ,4cos ∠AOBC.4cos ∠AOB ,4 sin ∠AOBD.4sin ∠AOB ,4 cos ∠AOB05同角三角函数的基本关系22(21-22高一上·安徽宿州·期末)已知cos α=-513,且α为第二象限角,则sin α=()A.-1213B.-513C.1213D.12523(21-22高一上·四川遂宁·期末)已知cos x 1-sin x =3,则1+sin xcos x=()A.3B.-3C.33D.-3324(2024·河南洛阳·模拟预测)已知tan α=2,则5sin α+cos a2sin α-cos α=()A.13B.113C.53D.225(2023·全国·高考真题)若θ∈0,π2 ,tan θ=12,则sin θ-cos θ=.26(22-23高三·全国·对口高考)已知角α的终边落在直线y =-3x (x <0)上,则|sin α|sin α-|cos α|cos α=.27(2024高一上·全国·专题练习)已知tan α=12,则sin 2α+sin αcos αcos 2α+1的值为.06诱导公式28(2024·全国·模拟预测)已知sin 5π8+α =13,则cos π8+α =()A.-13B.13C.-33D.3329(2024·全国·模拟预测)已知cos θ-2π5 =23,则2sin 19π10-θ +cos θ+13π5=()A.-2B.2C.-23D.2330(23-24高一上·江苏无锡·阶段练习)已知sin α+cos α=-12,则cos π2+α 1-tan -α 的值为()A.-34B.34C.-316D.31631(23-24高一下·湖南株洲·开学考试)已知sin π3-x =13,且0<x <π2,则tan 2π3+x =.32(2023高三·全国·专题练习)已知sin 3π+θ =13,则cos π+θ cos θcos π+θ -1+cos θ-2πsin θ-3π2 cos θ-π -sin 3π2+θ的值为.07三角函数的概念诱导公式难点分析33(23-24高一上·山西运城·期末)若α,β∈0,π2 ,且4sin 2α-sin 2β+23=0,则当2sin α+cos β取最大值时,sin β的值为()A.66B.306C.33D.2634(22-23高三上·山东枣庄·阶段练习)若0<θ<π,且点P cos θ,sin θ 与点Q cos θ+π6 ,sin θ+π6关于x 轴对称,则cos θ=.35(20-21高二上·贵州铜仁·阶段练习)已知sin 5θ-cos 5θ<3cos 3θ-sin 3θ 恒成立,则θ取值范围是.36(2022·上海黄浦·二模)设a ,b ∈R ,c ∈0,4π .若对任意实数x 都有sin 2x -π3=a sin bx +c ,则满足条件的有序实数组a ,b ,c 的组数为.一、单选题1(2023·安徽·模拟预测)已知角α终边上有一点P sin 2π3,cos 2π3,则π-α为()A.第一象限角B.第二象限角C.第三象限角D.第四象限角2(2024·黑龙江·二模)已知角α的终边与单位圆的交点P 35,-45 ,则sin α-π2=()A.-45B.-35C.35D.453(2024·辽宁·三模)已知tan α=12,则sin α+π2 -cos 3π2-α cos -α -sin π-α=()A.-1 B.1 C.-3D.34(2023·海南·模拟预测)若α∈0,π ,且cos α-sin α=12,则tan α=()A.4+75B.4-75C.4+73D.4-735(2024·全国·模拟预测)石雕、木雕、砖雕被称为建筑三雕.源远流长的砖雕,由东周瓦当、汉代画像砖等发展而来,明清时代进入巅峰,形成北京、天津、山西、徽州、广东、临夏以及苏派砖雕七大主要流派.苏派砖雕被称为“南方之秀”,是南方地区砖雕艺术的典型代表,被广泛运用到墙壁、门窗、檐廊、栏槛等建筑中.图(1)是一个梅花砖雕,其正面是一个扇环ABCD ,如图(2),砖雕厚度为6cm ,AD =80cm ,CD=3AB,CD所对的圆心角为直角,则该梅花砖雕的表面积为(单位:cm 2)()A.3200πB.480π+960C.6880π+960D.3680π+9606(2023·贵州遵义·三模)已知a =sin0.1,b =10-1,c =tan0.1,则()A.c >b >aB.b >c >aC.b >a >cD.a >c >b7(2023·山西·模拟预测)已知α,β,γ均是锐角,设sin αcos β+sin βcos γ+sin γcos α的最大值为tan θ,则sin θsin θ+cos θ =()A.3B.1513C.1D.5138(2024·浙江·二模)古人把正弦函数、余弦函数、正切函数、余切函数、正割函数、余割函数、正矢函数、余矢函数这八种三角函数的函数线合称为八线.其中余切函数cot θ=1tan θ,正割函数sec θ=1cos θ,余割函数csc θ=1sin θ,正矢函数ver sin θ=1-cos θ,余矢函数ver cos θ=1-sin θ.如图角θ始边为x 轴的非负半轴,其终边与单位圆交点P ,A 、B 分别是单位圆与x 轴和y 轴正半轴的交点,过点P 作PM 垂直x 轴,作PN 垂直y 轴,垂足分别为M 、N ,过点A 作x 轴的垂线,过点B 作y 轴的垂线分别交θ的终边于T 、S ,其中AM、PS、BS、NB为有向线段,下列表示正确的是()A.ver sinθ=AMB.cscθ=PSC.cotθ=BSD.secθ=NB二、多选题9(2023·贵州遵义·模拟预测)下列说法正确的是()A.若sinα=sinβ,则α与β是终边相同的角B.若角α的终边过点P3k,4kk≠0,则sinα=4 5C.若扇形的周长为3,半径为1,则其圆心角的大小为1弧度D.若sinα⋅cosα>0,则角α的终边在第一象限或第三象限10(2023·辽宁·模拟预测)设α为第一象限角,cosα-π8=13,则()A.sin5π8-α=-13 B.cosα+7π8=-13C.sin13π8-α=-223 D.tanπ8-α=-2211(2024·全国·模拟预测)质点A和B在以坐标原点O为圆心,半径为1的圆O上逆时针做匀速圆周运动,同时出发,A的起点在射线y=3x x≥0和圆O的交点处,A的角速度为2rad/s,B的起点为圆O与x轴正半轴的交点,B的角速度为3rad/s,则下列说法正确的是()A.在1s末时,点A的坐标为cos2,sin2B.在2s 末时,点B的坐标为cos6,-sin6C.在2s末时,劣弧AB的长为2-π3D.当A与B重合时,点A的坐标可以为-1,0三、填空题12(2023·江苏苏州·模拟预测)已知x∈(0,π),若sin x1-cos x=3,则1+cos xsin x=.13(2023·四川成都·一模)函数f x =tanπ32x-1,x>012x,x≤0,则f f-3=.14(2023·江西景德镇·三模)已知直线x=a0<a<π2与函数f x =sin x和函数g x =cos x的图象分别交于P,Q两点,若PQ=14,则线段PQ中点的纵坐标为.。
高考数学三角函数的图象与性质一轮复习

答案:⑤
考点专项突破
考点一 三角函数的定义域
【例 1】 (1)函数 y=
1 的定义域为 tan x 1
在讲练中理解知识
;
tan x 1 0, 解析:(1)要使函数有意义,必须有 π x kπ, k Z, 2
x 即 x
π π ,kπ+ )k∈Z 上都是 2 2
知识梳理
正弦函数、余弦函数、正切函数的图象和性质
函数 图象 y=sin x y=cos x y=tan x
定义域 值域
R [-1,1]
R [-1,1] 在[2kπ -π ,2kπ ] (k∈Z)上单调递增; 在[2kπ ,2kπ +π ] (k∈Z)上单调递减
第 4节
三角函数的图象与性质
最新考纲
1.能画出y=sin x,y=cos x, y=tan x的图象,了解三角函 数的周期性.
2.理解正弦函数、余弦函数在[0,2π ]上 的性质(如单调性、最大值和最小值、图 π π 象与x轴的交点等),理解正切函数在 , 2 2 内的单调性.
x= 最值
2kπ
π ( k Z) 2
时,
ymax=1;
π x=2kπ - (k∈Z)时, 2
x= 2kπ (k∈Z) 时, ymax=1; x=2kπ +π (k∈Z) 时,ymin=-1 无最值
ymin=-1 奇偶性
奇函数
对称中心
偶函数
π 对称中心 k π ,0 2
{x︱x≠
π +kπ , 2
k∈Z} R
π π 在 2kπ ,2kπ 2 2
高考数学(文通用)一轮复习课件:第三章第5讲三角函数的图象与性质

第三章三角函数、解三角形第5讲三角函数的图象与性质教材回顾▼夯实基础课本温故追根求源知识梳理Aj=sinxJ =COSXj=tanxJT2k盘 ----2JJI2k Jt H—,L 23Ji"2— H——2」仇wz)为减[2 吃7T, 2航+兀]仗WZ)为减;\2kn—n92kn\(k^Z)为(一-于,仇GZ)为增2.学会求三角函数值域(最值)的两种方法(1)将所给函数化为j=Asin(ft>x+ (p)的形式,通过分析亦+卩的范围,结合图象写出函数的值域;(2)换元法:把sin x(cos劝看作一个整体,化为二次函数来解决.双基自测1. (2015•高考四川卷)下列函数中,最小正周期为兀的奇函数是(A.j=sin(2x+—B.j=cos^2r+~C.y= sin 2x+ cos 2xD.y= sin x+ cos xC 项,y=sin 2x+cos 2x=\/2sin^2x+—为非奇非偶函数,不符合题意;ink+于)最小正周期为2兀, 为非奇非偶函数,不符合题意.( JIj=sin|2x+- 为偶函数,不符合题意;解析:A 项,= cos 2x,最小正周期为n ,且y= cos^2r+_j= —sin 2x,最小正周期为 函数,符合题意;B 项, 1=/兀,且为奇,最小正周期为皿,D 项,j=sin x+ cos兀B. x=——33 x=-兀4解析:由题意得 f(x)= 2cos 2^x+~J= 2sin 2x= 1— cos 2x,函 数图象的对称轴方程为尸竺kEZ,故选D.2A • x~—4 C. 71故函数/(对=$中一了丿在区间[o,于]±的最小值为一申.3・函数/(x) = sin上的最小值为A. -1B. -申C 誓 D. 0解析:由已知xG 0, 兀 8二討得加-2兀 -eJI2在区间o,兀4所以14.(必修4 P40 练习1X2)改编)函数/(x) = 4-2cos -x, xE32,取得最小值时,X的取值集合为R的最小值是—{x\x=6kn9 kEL}(JT JI \5.(必修4 P44例6改编)函数j=tan|^-x—yJ的最小正周期是—,单调增区间是G+"扌+2”(疋牛典例剖析▼考点突破*名师导悟以例说法考点一三角函数的定义域和值域^§例1 (1)函数y= lg(2sin x—1)+*\/1 —2cosx的定义域是" 兀5兀、2k Ji +—, 2k 乳—]9 ZL 3 6 丿______ .3(2)函数j=cos 2x+ 2sin x的最大值为—132'[解析]⑴要使函数丿=lg(2sinx —1)+^/1—2cos 兀有意义,sin ,■ “Ji 5 n解得 2k Ji +_^x<2^ Ji +飞-,kEL.即函数的定义域为卜—+专,2—+寻)kE 乙3i 3所以当/=扌时,函数取得最大值字2sinx —1>0, 即1—2cosx^0, cosxWq.+WWl),(2)y=cos 2x+2sin x= —2sin 2x+2sin x+1,设 f=sin x(—12Q互动探光本例(2)变为函数y = cos 2x+ 4sin5的最大值为 _________解析:j=cos 2x+4sin x= — 2sin2x+ 4sin 兀+1,设t=sin中冬怎*),则原函数可以化为y=~li +4(+1= —2(1—1『+3,所以当1=扌时,函数取得最大值丰.⑴三角函数定义域的求法求三角函数定义域实际上是构造简单的三角不等式(组),常借助三角函数线或三角函数图象来求解.(2)三角函数值域的不同求法①利用sinx和cosx的值域直接求.②把所给的三角函数式变换成y=Asin(cox+^的形式求值域.③把sin兀或cos兀看作一个整体,转换成二次函数求值域・④利用sin兀土cos兀和sin xcos x的关系转换成二次函数求值域.壘踪i噬1・(1)函数y= /2+logjx + \/tanx的定义域为r i V 2jxIOVxV亍或Ji WxW4 »____________________________ ■7(2)函数y= (4— 3sin x)(4— 3cos兀)的最小值为xIOVxV 亍或 n4j.解析:⑴要使函数有意义, 厂2+10即亠0,2JIx^kn T —, I 2—o -------- o ——0 ?利用数轴可得函数的定义域是x>0, tan x^O, k 兀 WxVkii T 扌WZ)・-<—e---------(2)j = 16— 12(sin x+ cos x)+ 9sin xcos x,令Z=sinx+cosx,贝!1[—\[29 ^2],且sinxcosx=-------------------2『一1 ]所以y=16- 12Z+9X --------- =一(9,一24/+23)・2 2• 4 7故当时,Jmin = --考点二三角函数的奇偶性、周期性及对称性典例2 (1)(2014-高考课标全国卷I )在函数®j= cos 12x1,®y = Icos xl, (3)j=cos^x, (4)j= tan(2x—^中,最小正周期为n的所有函数为(C )A.②④C.①②③B.①③④D.①③(2)(2016-河北省五校联盟质量监测)下列函数中最小正周期为兀且图象关于直线兀=£■对称的函数是(B)[解析]⑴①yKOsMFOslx, 1- •②由图象知,函数的周期r= 31・③*兀・兀④丁=亍综上可知,最小正周期为询所有函数为①②③.⑵由函数的最小正周期为兀,可排除C •由函数图象关于直JT线*=〒对称知,该直线过函数图象的最高点或最低点,对选B.(i )三角函数的奇偶性的判断技巧于 A,因为 sin^2Xy+确・对于D, sinl2X ---------33 f) ( Tl JI 、 对于 B, sin|2X-——J=_:. =sin Ji =0,所以选项A 不正 =si 可羊所以D 不正确, 兀=sinT =h所以选项B 正确,故首先要知道基本三角函数的奇偶性,再根据题目去判断所求三角函数的奇偶性;也可以根据图象进行判断.(2)求三角函数周期的方法①利用周期函数的定义.②利用公式:y=Asin(cox+(p)和y =Acos(cyx+°)的最小正周2兀JT期为面,y=tan(cox+(/)).③利用图象.(3)三角函数的对称性正、余弦函数的图象既是中心对称图形,又是轴对称图形,正切函数的图象只是中心对称图形,应熟记它们的对称轴和对称中心,并注意数形结合思想的应用.[注意]判断函数的奇偶性时,必须先分析函数定义域是否关于原点对称.MISS] 2.(1)(2016-西安地区八校联考)若函数j = cos(ex+〒j(cyEN*)图象的一个对称中心是匕,0J,则co 的最小值为(A. 1B. 2C. 4D.(2)(2016•揭阳模拟)当心了时,函数/(gin(十)取得最小值,则函数)A.是奇函数且图象关于点仔,0)对称B.是偶函数且图象关于点(兀,0)对称C.是奇函数且图象关于直线兀=于对称D.是偶函数且图象关于直线兀=兀对称,■一JI 6; JI JI解析:(1 --------- 1=kJi ---------- (k £ Z)=>(o = 6k+ 2(kE:Z)=>(o6 6 2min =2Jl⑵因为当x=丁时,函数几兀)取得最小值,4所以sin&+J = —1,所以0=2反兀一普"(kEZ).所以/(x)=sin(+2“ 一冷9=sin|x J(k W Z).所以y=^~~x.=sin(—x)= —sin x.e 兀、JI 所以尸x)是奇函数,且图象关于直线兀=亍对称•考点三三角函数的单调性(高频考点)三角函数的单调性是每年高考命题的热点,题型既有选择题也有填空题,或解答题某一问出现,难度适中,多为中档题.高考对三角函数单调性的考查有以下四个命题角度:(1)求已知三角函数的单调区间;⑵已知三角函数的单调区间求参数;(3)利用三角函数的单调性求值域(或最值);(4)利用三角函数的单调性比较大小.⑴求心)的最小正周期和最大值;⑵讨论心)在[十,牛] 上的单调性.• sin (2015•高考重庆卷)已知函数几兀)=os 2x.[解](l)Ax)=sin 仔一Jsin x —A /§C =cos xsinx — 2 (H~cos 2x)1・,© o 並=-sm 2x — cos 2x —因此冷)的最小正周期为兀,最大值为2苫.os 2x(2)当兀丘[于,牛]时'0W2x —于W 兀,从而当弓^加一7~Wn,即弓时,/(兀)单调递减. Z Q 丄/ J调递减•J fl _ 7 y \ TL1 lz\ A A J KX& M n I y-Z z 产〒 r^Q^i 0« h P <Jlu tz 二\ J nf r/7 J? ryj n r^z^C 77 f r三角函数单调性问题解题策略.兀 兀 当0»亍亏, JI 5 JT . 即訐Tr 时' 的单调递增, 综上可知,几r )在单调递增; 刊上单(1)已知三角函数解析式求单调区间.①求函数的单调区间应遵循简单化原则,将解析式先化简,并注意复合函数单调性规律"同增异减”:②求形如j=Asin(ft)x+^)或y=Acos(ov +卩)(其中少>0)的单调区间时,要视“ov+卩”为一个整体, 通过解不等式求解.但如果evO,那么一定先借助诱导公式将少化为正数,防止把单调性弄错.(2)已知三角函数的单调区间求参数.先求出函数的单调区间,然后利用集合间的关系求解.⑶利用三角函数的单调性求值域(或最值).形如j=Asin(ft>x +°)+〃或可化为y=4sin@v+°)+〃的三角函数的值域(或最值)问题常利用三角函数的单调性解决.通关练习3.(1)已知函数/(x)=2sinC+亍) ,则a9 b9 c的大小关系是(BB. c<a<bD. b<c<aA. a<c<bC. b<a<c减,则 少的取值范围是(A54-(2)已知 ft»O,函数 f(x)=sirA. 12-D. (0, 2]10 —n 21兀因为j=sinx 在0,—上递增,——= 2sin 解:⑴选Ra兀= 2sin所以c<a<b.6>>0,JlJTJIH < 3X ---- < 3 兀 H - ,44 4G JI 3131〒+亡'313 JI3 JI H —W —4 2又 j=sinx所以6) JI3 31"T解得詳。
高考数学一轮单元复习 三角函数课件

│ 考纲要求
• (2)简单的三角恒等变换能运用上述公式进行 简单的恒等变换(包括导出积化和差、和差化积、 半角公式,但对这三组公式不要求记忆). • 3.解三角形 • (1)正弦定理和余弦定理掌握正弦定理、余弦 定理,并能解决一些简单的三角形度量问题. • (2)应用能够运用正弦定理、余弦定理等知识 和方法解决一些与测量和几何计算有关的实际问 题.
第三单元 第三单元 三角函数 三角函数
│ 知识框架 知识框架
│ 考纲要求
考纲要求
• • • •
1.基本初等函数Ⅱ(三角函数) (1)任意角的概念、弧度制 ①了解任意角的概念. ②了解弧度制的概念,能进行弧度与角度 的互化.
│ 考纲要求
• (2)三角函数 • ①理解任意角三角函数(正弦、余弦、正切)的 定义. • ②能利用单位圆中的三角函数线推导出 ±α,π±α的正弦、余弦、正切的诱导公式, 能画出y=sinx,y=cosx,y=tanx的图象, 了解三角函数的周期性. • ③理解正弦函数、余弦函数在区间[0,2π] 上的性质(如单调性、最大值和最小值以及与x 轴的交点等),理解正切函数在区间 内的单调性.
│ 命题趋势
• 3.更加强调三角函数的工具性,加强了 三角函数与其他知识的结合,如在解三角 形、导数、立体几何、平面解析几何中考 查三角函数的知识. • 4.预测2011年考题还会符合以上特点, 在与向量、解析几何、数列等知识的交汇 处命题.
│ 使用建议使用建议 源自 1.本单元知识是对教材中的三角函数、三角恒 等变形、解三角形知识的整合.在整合过程中, 遵循研究一般函数的规律:从定义到图象,到性 使用建议 质,再到应用,总体上由浅入深,由简单到复杂, 逐步提高综合能力.本单元编写中注意体现“变 换为主线,统一为目标”的思想:角的变换,三 角函数名称的变换,三角函数次数的变换,三角 函数式表达形式的变换等;但变换的目标是“统 一”:如角的统一,名称的统一,运算的统一, 形式的统一等.
新高考三角函数知识点归纳总结

新高考三角函数知识点归纳总结三角函数在新高考数学考试中扮演着重要的角色。
掌握三角函数的相关知识点,不仅可以帮助我们解决各类与角度、长度及图形性质相关的问题,还能够为以后的高等数学学习打下坚实的基础。
本文将对新高考中的三角函数知识点进行归纳总结,以帮助同学们更好地复习和应对考试。
一、三角函数的基本概念和性质三角函数包括正弦函数、余弦函数和正切函数,它们都是角的函数,表示角与某一边的长度的比值。
1. 正弦函数(sin):在直角三角形中,正弦值等于对边与斜边的比值,即sin(A) = a/c。
2. 余弦函数(cos):在直角三角形中,余弦值等于邻边与斜边的比值,即cos(A) = b/c。
3. 正切函数(tan):在直角三角形中,正切值等于对边与邻边的比值,即tan(A) = a/b。
此外,我们还需了解三角函数在单位圆上的定义和性质:4. 单位圆的角度:单位圆的半径为1,角度以弧度制表示,其中360°等于2π弧度。
5. 弧度与角度的转换关系:1弧度约等于57.3°,即1弧度≈ 57.3°。
6. 三角函数的周期性:正弦函数和余弦函数的周期为2π,而正切函数的周期为π。
二、三角函数的基本关系及推导1. 三角函数之间的基本关系:根据三角恒等式,我们可以推导出三角函数之间的基本关系。
例如,sin²A + cos²A = 1,tanA = sinA/cosA等。
2. 三角函数的和差化积公式:通过和差化积公式,我们可以将两个三角函数的和差表示为一个三角函数的乘积。
三、三角函数的图像和性质1. 正弦函数的图像和性质:正弦函数的图像是一条连续的波浪线,振幅为1,在0~2π的区间内周期性重复。
2. 余弦函数的图像和性质:余弦函数的图像也是一条连续的波浪线,振幅为1,在0~2π的区间内周期性重复,与正弦函数的图像相位差90°。
3. 正切函数的图像和性质:正切函数的图像有无数个渐近线,它在每个π的整数倍处有一个垂直渐近线,且在每个π/2的整数倍处有一个水平渐近线。
2023年高考数学一轮复习讲义——同角三角函数基本关系式及诱导公式
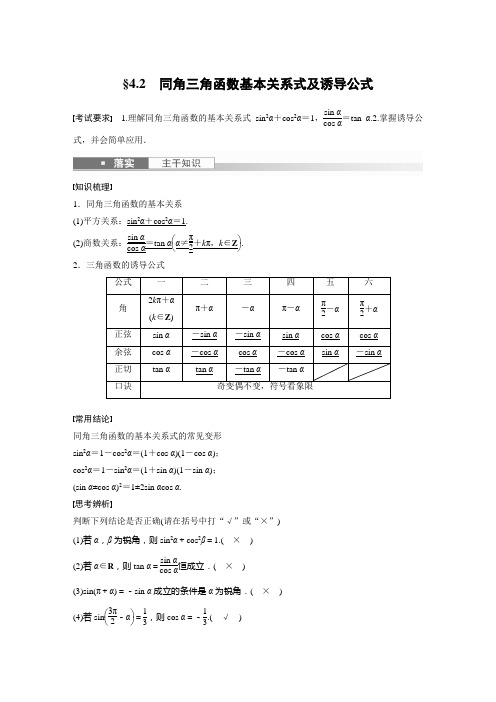
§4.2 同角三角函数基本关系式及诱导公式考试要求 1.理解同角三角函数的基本关系式sin 2α+cos 2α=1,sin αcos α=tan α.2.掌握诱导公式,并会简单应用.知识梳理1.同角三角函数的基本关系 (1)平方关系:sin 2α+cos 2α=1.(2)商数关系:sin αcos α=tan α⎝⎛⎭⎫α≠π2+k π,k ∈Z . 2.三角函数的诱导公式公式 一 二 三 四 五 六 角 2k π+α (k ∈Z ) π+α -α π-α π2-α π2+α 正弦 sin α -sin α -sin α sin α cos α cos α 余弦 cos α -cos α cos α -cos α sin α -sin α 正切 tan αtan α-tan α-tan α口诀奇变偶不变,符号看象限常用结论同角三角函数的基本关系式的常见变形 sin 2α=1-cos 2α=(1+cos α)(1-cos α); cos 2α=1-sin 2α=(1+sin α)(1-sin α); (sin α±cos α)2=1±2sin αcos α. 思考辨析判断下列结论是否正确(请在括号中打“√”或“×”) (1)若α,β为锐角,则sin 2α+cos 2β=1.( × ) (2)若α∈R ,则tan α=sin αcos α恒成立.( × )(3)sin(π+α)=-sin α成立的条件是α为锐角.( × ) (4)若sin ⎝⎛⎭⎫3π2-α=13,则cos α=-13.( √ )教材改编题1.已知α是第二象限角,sin α=55,则cos α的值为 . 答案 -255解析 ∵sin α=55,α是第二象限角, ∴cos α=-1-sin 2α=-255.2.已知sin α-2cos α3sin α+5cos α=-5,那么tan α的值为 .答案 -2316解析 由sin α-2cos α3sin α+5cos α=-5,知cos α≠0,等式左边分子、分母同时除以cos α,可得tan α-23tan α+5=-5,解得tan α=-2316.3.化简cos ⎝⎛⎭⎫α-π2sin ⎝⎛⎭⎫5π2+α·sin(α-π)·cos(2π-α)的结果为 . 答案 -sin 2α解析 原式=sin αcos α·(-sin α)·cos α=-sin 2α.题型一 同角三角函数基本关系例1 (1)已知cos α=-513,则13sin α+5tan α= .答案 0解析 ∵cos α=-513<0且cos α≠-1,∴α是第二或第三象限角. ①若α是第二象限角,则sin α=1-cos 2α=1-⎝⎛⎭⎫-5132=1213, ∴tan α=sin αcos α=1213-513=-125.此时13sin α+5tan α=13×1213+5×⎝⎛⎭⎫-125=0. ②若α是第三象限角, 则sin α=-1-cos 2α=-1-⎝⎛⎭⎫-5132 =-1213,∴tan α=sin αcos α=-1213-513=125,此时,13sin α+5tan α=13×⎝⎛⎭⎫-1213+5×125=0. 综上,13sin α+5tan α=0.(2)已知tan α=12,则sin α-3cos αsin α+cos α= ;sin 2α+sin αcos α+2= .答案 -53 135解析 已知tan α=12,所以sin α-3cos αsin α+cos α=tan α-3tan α+1=-53.sin 2α+sin αcos α+2 =sin 2α+sin αcos αsin 2α+cos 2α+2=tan 2α+tan αtan 2α+1+2=⎝⎛⎭⎫122+12⎝⎛⎭⎫122+1+2=135.(3)已知sin θ+cos θ=713,θ∈(0,π),则tan θ= .答案 -125解析 由sin θ+cos θ=713,得sin θcos θ=-60169,因为θ∈(0,π),所以sin θ>0,cos θ<0, 所以sin θ-cos θ=1-2sin θcos θ=1713, 联立⎩⎨⎧sin θ+cos θ=713,sin θ-cos θ=1713,解得⎩⎨⎧sin θ=1213,cos θ=-513,所以tan θ=-125.教师备选1.(2022·锦州联考)已知sin α+3cos α3cos α-sin α=5,则cos 2α+12sin 2α等于( )A.35 B .-35C .-3D .3答案 A解析 由sin α+3cos α3cos α-sin α=5,得tan α+33-tan α=5,可得tan α=2,则cos 2α+12sin 2α=cos 2α+sin αcos α=cos 2α+sin αcos αcos 2α+sin 2α=1+tan α1+tan 2α=35. 2.若α∈(0,π),sin(π-α)+cos α=23,则sin α-cos α的值为( ) A.23B .-23 C.43 D .-43答案 C解析 由诱导公式得sin(π-α)+cos α=sin α+cos α=23, 所以(sin α+cos α)2=1+2sin αcos α=29,则2sin αcos α=-79<0,因为α∈(0,π),所以sin α>0, 所以cos α<0,所以sin α-cos α>0, 因为(sin α-cos α)2=1-2sin αcos α=169,所以sin α-cos α=43.思维升华 (1)应用公式时注意方程思想的应用:对于sin α+cos α,sin αcos α,sin α-cos α这三个式子,利用(sin α±cos α)2=1±2sin αcos α,可以知一求二.(2)注意公式逆用及变形应用:1=sin 2α+cos 2α,sin 2α=1-cos 2α,cos 2α=1-sin 2α. 跟踪训练1 (1)(2021·新高考全国Ⅰ)若tan θ=-2,则sin θ(1+sin 2θ)sin θ+cos θ等于( )A .-65B .-25 C.25 D.65答案 C解析 方法一 因为tan θ=-2, 所以角θ的终边在第二或第四象限,所以⎩⎨⎧sin θ=25,cos θ=-15或⎩⎨⎧sin θ=-25,cos θ=15,所以sin θ(1+sin 2θ)sin θ+cos θ=sin θ(sin θ+cos θ)2sin θ+cos θ=sin θ(sin θ+cos θ) =sin 2θ+sin θcos θ =45-25=25.方法二 (弦化切法)因为tan θ=-2, 所以sin θ(1+sin 2θ)sin θ+cos θ=sin θ(sin θ+cos θ)2sin θ+cos θ=sin θ(sin θ+cos θ) =sin 2θ+sin θcos θsin 2θ+cos 2θ=tan 2θ+tan θ1+tan 2θ=4-21+4=25.(2)已知α是三角形的内角,且tan α=-13,则sin α+cos α的值为 .答案 -105解析 由tan α=-13,得sin α=-13cos α,将其代入sin 2α+cos 2α=1,得109cos 2α=1,所以cos 2α=910,易知cos α<0,所以cos α=-31010,sin α=1010,故sin α+cos α=-105. 题型二 诱导公式例2 (1)已知sin ⎝⎛⎭⎫α-π4=13,则cos ⎝⎛⎭⎫π4+α的值为( ) A.223B .-223C.13 D .-13答案 D解析 cos ⎝⎛⎭⎫π4+α=cos ⎣⎡⎦⎤π2+⎝⎛⎭⎫α-π4 =-sin ⎝⎛⎭⎫α-π4=-13.延伸探究 本例(1)改为已知θ是第二象限角,且sin ⎝⎛⎭⎫θ+π4=45,则tan ⎝⎛⎭⎫θ-π4= . 答案 34解析 ∵θ是第二象限角,且sin ⎝⎛⎭⎫θ+π4=45, ∴θ+π4为第二象限角,∴cos ⎝⎛⎭⎫θ+π4=-35, ∴tan ⎝⎛⎭⎫θ-π4=sin ⎝⎛⎭⎫θ-π4cos ⎝⎛⎭⎫θ-π4 =sin ⎣⎡⎦⎤⎝⎛⎭⎫θ+π4-π2cos ⎣⎡⎦⎤⎝⎛⎭⎫θ+π4-π2 =-cos ⎝⎛⎭⎫θ+π4sin ⎝⎛⎭⎫θ+π4=-⎝⎛⎭⎫-3545=34. (2)tan (π-α)cos (2π-α)sin ⎝⎛⎭⎫-α+3π2cos (-α-π)sin (-π-α)的值为( )A .-2B .-1C .1D .2 答案 B解析 原式=-tan α·cos α·(-cos α)cos (π+α)·[-sin (π+α)]=tan α·cos 2α-cos α·sin α =-sin αcos α·cos αsin α=-1.教师备选1.已知函数f (x )=a x -2+2(a >0且a ≠1)的图象过定点P ,且角α的始边与x 轴的正半轴重合,终边过点P ,则cos ⎝⎛⎭⎫11π2-αsin ⎝⎛⎭⎫9π2+α+sin 2αcos ⎝⎛⎭⎫π2+αsin (-π-α)等于( )A.23 B .-23C.32 D .-32答案 B解析 易知函数f (x )=a x -2+2(a >0且a ≠1)的图象过定点P (2,3), 故tan α=32,则cos ⎝⎛⎭⎫11π2-αsin ⎝⎛⎭⎫9π2+α+sin 2αcos ⎝⎛⎭⎫π2+αsin (-π-α)=cos ⎝⎛⎭⎫3π2-αsin ⎝⎛⎭⎫π2+α+sin 2αcos ⎝⎛⎭⎫π2+αsin α=-sin αcos α+2sin αcos α-sin αsin α=-cos αsin α=-1tan α=-23.2.若sin x =3sin ⎝⎛⎭⎫x -π2,则cos x ·cos ⎝⎛⎭⎫x +π2等于( ) A.310 B .-310C.34 D .-34答案 A解析 易知sin x =3sin ⎝⎛⎭⎫x -π2=-3cos x , 所以tan x =-3, 所以cos x cos ⎝⎛⎭⎫x +π2 =-sin x cos x =-sin x cos xsin 2x +cos 2xtan 2x +110思维升华 (1)诱导公式的两个应用①求值:负化正,大化小,化到锐角为终了; ②化简:统一角,统一名,同角名少为终了. (2)诱导公式的应用步骤任意负角的三角函数――――――→利用诱导公式三或一任意正角的三角函数――――――→利用诱导公式一0~2π内的角的三角函数――――――→利用诱导公式二或四或五或六锐角三角函数. 跟踪训练2 (1)已知cos(75°+α)=13,求cos(105°-α)+sin(15°-α)= .答案 0解析 因为(105°-α)+(75°+α)=180°, (15°-α)+(α+75°)=90°,所以cos(105°-α)=cos[180°-(75°+α)] =-cos(75°+α)=-13,sin(15°-α)=sin[90°-(α+75°)] =cos(75°+α)=13.所以cos(105°-α)+sin(15°-α)=-13+13=0.(2)(2022·盐城南阳中学月考)设tan(5π+α)=2,则sin (-3π+α)+cos (α-π)cos ⎝⎛⎭⎫α-112π+sin ⎝⎛⎭⎫9π2+α= .答案 3解析 由已知tan(5π+α)=tan α=2, sin (-3π+α)+cos (α-π)cos ⎝⎛⎭⎫α-112π+sin ⎝⎛⎭⎫9π2+α=sin (π+α)+cos (π-α)cos ⎝⎛⎭⎫α+π2+sin ⎝⎛⎭⎫π2+α-sin α+cos α=sin α+cos αsin α-cos α=tan α+1tan α-1=3. 题型三 同角三角函数基本关系式和诱导公式的综合应用 例3 已知f (α)=sin (α-3π)cos (2π-α)sin ⎝⎛⎭⎫-α+3π2cos (-π-α)sin (-π-α).(1)化简f (α);(2)若α=-31π3,求f (α)的值;(3)若cos ⎝⎛⎭⎫-α-π2=15,α∈⎣⎡⎦⎤π,3π2,求f (α)的值. 解 (1)f (α)=sin (α-3π)cos (2π-α)sin ⎝⎛⎭⎫-α+3π2cos (-π-α)sin (-π-α)=-sin α×cos α×(-cos α)-cos α×sin α=-cos α. (2)若α=-31π3,则f (α)=-cos ⎝⎛⎭⎫-31π3=-cos π3=-12. (3)由cos ⎝⎛⎭⎫-α-π2=15, 可得sin α=-15,因为α∈⎣⎡⎦⎤π,3π2, 所以cos α=-265,所以f (α)=-cos α=265.教师备选设f (α)=2sin (π+α)cos (π-α)-cos (π+α)1+sin 2α+cos ⎝⎛⎭⎫3π2+α-sin 2⎝⎛⎭⎫π2+α(1+2sin α≠0). (1)化简f (α);(2)若α=-23π6,求f (α)的值. 解 (1)f (α)=(-2sin α)·(-cos α)-(-cos α)1+sin 2α+sin α-cos 2α=2sin αcos α+cos α2sin 2α+sin α=cos α(2sin α+1)sin α(2sin α+1)=cos αsin α=1tan α. (2)当α=-23π6时, f (α)=f ⎝⎛⎭⎫-23π6=1tan ⎝⎛⎭⎫-23π6 =1tan ⎝⎛⎭⎫-4π+π6 =1tan π6=133= 3. 思维升华 (1)利用同角三角函数关系式和诱导公式求值或化简时,关键是寻求条件、结论间的联系,灵活使用公式进行变形.(2)注意角的范围对三角函数符号的影响.跟踪训练3 (1)(2022·聊城模拟)已知α为锐角,且2tan(π-α)-3cos ⎝⎛⎭⎫π2+β+5=0,tan(π+α)+6sin(π+β)-1=0,则sin α的值是( )A.355B.377C.31010D.13答案 C解析 由已知得⎩⎪⎨⎪⎧3sin β-2tan α+5=0,tan α-6sin β-1=0. 消去sin β,得tan α=3,∴sin α=3cos α,代入sin 2α+cos 2α=1,化简得sin 2α=910,则sin α=31010(α为锐角). (2)已知-π<x <0,sin(π+x )-cos x =-15,则sin 2x +2sin 2x 1-tan x= . 答案 -24175解析 由已知,得sin x +cos x =15, 两边平方得sin 2x +2sin x cos x +cos 2x =125, 整理得2sin x cos x =-2425. ∴(sin x -cos x )2=1-2sin x cos x =4925, 由-π<x <0知,sin x <0,又sin x cos x =-1225<0, ∴cos x >0,∴sin x -cos x <0,故sin x -cos x =-75. ∴sin 2x +2sin 2x 1-tan x =2sin x (cos x +sin x )1-sin x cos x=2sin x cos x (cos x +sin x )cos x -sin x=-2425×1575=-24175.课时精练1.cos ⎝⎛⎭⎫-19π3等于( ) A .-32 B .-12 C.12D.32 答案 C解析 cos ⎝⎛⎭⎫-19π3=cos 19π3=cos ⎝⎛⎭⎫6π+π3=cos π3=12. 2.若cos 165°=a ,则tan 195°等于( )A.1-a 2B.1-a 2aC .-1-a 2aD .-a 1-a 2 答案 C解析 若cos 165°=a ,则cos 15°=cos(180°-165°)=-cos 165°=-a ,sin 15°=1-a 2,所以tan 195°=tan(180°+15°)=tan 15°=sin 15°cos 15°=-1-a 2a. 3.若cos ⎝⎛⎭⎫α-π5=513,则sin ⎝⎛⎭⎫7π10-α等于( ) A .-513B .-1213 C.1213 D.513答案 D解析 因为7π10-α+⎝⎛⎭⎫α-π5=π2,所以7π10-α=π2-⎝⎛⎭⎫α-π5,所以sin ⎝⎛⎭⎫7π10-α=cos ⎝⎛⎭⎫α-π5=513.4.(2022·天津西青区模拟)已知sin α+cos α=-2,则tan α+1tan α等于() A .2 B.12 C .-2 D .-12答案 A解析 由已知得1+2sin αcos α=2,∴sin αcos α=12,∴tan α+1tan α=sin αcos α+cos αsin α=sin 2α+cos 2αsin αcos α=112=2.5.(多选)在△ABC 中,下列结论正确的是( )A .sin(A +B )=sin CB .sin B +C 2=cos A 2C .tan(A +B )=-tan C ⎝⎛⎭⎫C ≠π2D .cos(A +B )=cos C答案 ABC解析 在△ABC 中,有A +B +C =π,则sin(A +B )=sin(π-C )=sin C ,A 正确.sin B +C 2=sin ⎝⎛⎭⎫π2-A 2=cos A 2,B 正确.tan(A +B )=tan(π-C )=-tan C ⎝⎛⎭⎫C ≠π2,C 正确.cos(A +B )=cos(π-C )=-cos C ,D 错误.6.(多选)已知α∈(0,π),且sin α+cos α=15,则( ) A.π2<α<π B .sin αcos α=-1225C .cos α-sin α=75D .cos α-sin α=-75答案 ABD解析 ∵sin α+cos α=15, 等式两边平方得(sin α+cos α)2=1+2sin αcos α=125, 解得sin αcos α=-1225,故B 正确; ∵α∈(0,π),sin αcos α=-1225<0, ∴α∈⎝⎛⎭⎫π2,π,故A 正确;cos α-sin α<0,且(cos α-sin α)2=1-2sin αcos α=1-2×⎝⎛⎭⎫-1225=4925, 解得cos α-sin α=-75,故D 正确. 7.cos 1°+cos 2°+cos 3°+…+cos 177°+cos 178°+cos 179°= .答案 0解析 因为cos(180°-α)=-cos α,于是得cos 1°+cos 2°+cos 3°+…+cos 89°+cos 90°+cos 91°+…+cos 177°+cos 178°+cos 179° =cos 1°+cos 2°+cos 3°+…+cos 89°+cos 90°-cos 89°-…-cos 3°-cos 2°-cos 1° =cos 90°=0.8.设f (θ)=2cos 2θ+sin 2(2π-θ)+sin ⎝⎛⎭⎫π2+θ-32+2cos 2(π+θ)+cos (-θ),则f ⎝⎛⎭⎫17π3= . 答案 -512解析 ∵f (θ)=2cos 2θ+sin 2θ+cos θ-32+2cos 2θ+cos θ=cos 2θ+cos θ-22cos 2θ+cos θ+2,又cos 17π3=cos ⎝⎛⎭⎫6π-π3=cos π3=12,∴f ⎝⎛⎭⎫17π3=14+12-212+12+2=-512.9.(1)已知cos α是方程3x 2-x -2=0的根,且α是第三象限角,求sin ⎝⎛⎭⎫-α+3π2cos ⎝⎛⎭⎫3π2+αtan 2(π-α)cos ⎝⎛⎭⎫π2+αsin ⎝⎛⎭⎫π2-α的值;(2)已知sin x +cos x =-713(0<x <π),求cos x -2sin x 的值.解 (1)因为方程3x 2-x -2=0的根为x 1=1,x 2=-23,又α是第三象限角,所以cos α=-23,所以sin α=-53,tan α=52.所以原式=-cos αsin αtan 2α-sin αcos α=tan 2α=54.(2)∵sin x +cos x =-713(0<x <π),∴cos x <0,sin x >0,即sin x -cos x >0,把sin x +cos x =-713,两边平方得1+2sin x cos x =49169, 即2sin x cos x =-120169, ∴(sin x -cos x )2=1-2sin x cos x =289169, 即sin x -cos x =1713, 联立⎩⎨⎧ sin x +cos x =-713,sin x -cos x =1713,解得sin x =513,cos x =-1213, ∴cos x -2sin x =-2213. 10.(2022·衡水模拟)已知角α的终边经过点P (3m ,-6m )(m ≠0).(1)求sin (α+π)+cos (α-π)sin ⎝⎛⎭⎫α+π2+2cos ⎝⎛⎭⎫α-π2的值; (2)若α是第二象限角,求sin 2⎝⎛⎭⎫α+3π2+sin(π-α)cos α-cos ⎝⎛⎭⎫π2+α的值. 解 (1)∵m ≠0,∴cos α≠0,即sin (α+π)+cos (α-π)sin ⎝⎛⎭⎫α+π2+2cos ⎝⎛⎭⎫α-π2 =-sin α-cos αcos α+2sin α=-tan α-11+2tan α. 又∵角α的终边经过点P (3m ,-6m )(m ≠0),∴tan α=-6m 3m=-2, 故sin (α+π)+cos (α-π)sin ⎝⎛⎭⎫α+π2+2cos ⎝⎛⎭⎫α-π2=-tan α-11+2tan α =2-11+2×(-2)=-13. (2)∵α是第二象限角,∴m <0,则sin α=-6m (3m )2+(-6m )2 =-6m 35|m | =255, cos α=3m(3m )2+(-6m )2 =3m 35|m | =-55, ∴sin 2⎝⎛⎭⎫α+3π2+sin(π-α)cos α-cos ⎝⎛⎭⎫π2+α =cos 2α+sin αcos α+sin α=⎝⎛⎭⎫-552+255×⎝⎛⎭⎫-55+255=-1+255.11.(多选)已知角α满足sin α·cos α≠0,则表达式sin (α+k π)sin α+cos (α+k π)cos α(k ∈Z )的取值可能为( )A .-2B .-1或1C .2D .-2或2或0答案 AC解析 当k 为奇数时,原式=-sin αsin α+-cos αcos α=(-1)+(-1)=-2;当k 为偶数时,原式=sin αsin α+cos αcos α=1+1=2. ∴原表达式的取值可能为-2或2.12.(2022·河北六校联考)若sin α是方程5x 2-7x -6=0的根,则sin ⎝⎛⎭⎫-α-3π2sin ⎝⎛⎭⎫3π2-αtan 2(2π-α)cos ⎝⎛⎭⎫π2-αcos ⎝⎛⎭⎫π2+αsin (π+α)等于( )A.35B.53C.45D.54答案 B解析 方程5x 2-7x -6=0的两根为x 1=-35,x 2=2,则sin α=-35. 原式=cos α(-cos α)tan 2αsin α(-sin α)(-sin α)=-1sin α=53. 13.曲线y =e x +x 2-23x 在x =0处的切线的倾斜角为α,则sin ⎝⎛⎭⎫2α+π2= . 答案 45解析 由题意得y ′=f ′(x )=e x +2x -23, 所以f ′(0)=e 0-23=13, 所以tan α=13, 所以α∈⎝⎛⎭⎫0,π2, 所以cos α=310, 所以sin ⎝⎛⎭⎫2α+π2 =cos 2α=2cos 2α-1=2×910-1=45. 14.函数y =log a (x -3)+2(a >0且a ≠1)的图象过定点Q ,且角α的终边也过点Q ,则3sin 2α+2sin αcos α= .答案 75解析 由题意可知点Q (4,2),所以tan α=12, 所以3sin 2α+2sin αcos α=3sin 2α+2sin αcos αsin 2α+cos 2α =3tan 2α+2tan α1+tan 2α=3×14+2×121+14=75.15.(多选)已知f (α)=2sin αcos α-2sin α+cos α+1⎝⎛⎭⎫0≤α≤π2,则下列说法正确的是() A .f (α)的最小值为- 2B .f (α)的最小值为-1C .f (α)的最大值为2-1D .f (α)的最大值为1- 2答案 BD解析 设t =sin α+cos α=2sin ⎝⎛⎭⎫α+π4,由0≤α≤π2,得π4≤α+π4≤3π4,则1≤t ≤2,又由(sin α+cos α)2=t 2,得2sin αcos α=t 2-1,所以f (α)=g (t )=t 2-1-2t +1=t -1-2t +1,又因为函数y =t -1和y =-2t +1在[1,2]上单调递增,所以g (t )=t -1-2t +1在[1,2]上单调递增, g (t )min =g (1)=-1,g (t )max =g (2)=1- 2.16.已知关于x 的方程2x 2-(3+1)x +m =0的两根分别是sin θ和cos θ,θ∈(0,2π),求:(1)sin 2θsin θ-cos θ+cos θ1-tan θ的值; (2)m 的值;(3)方程的两根及此时θ的值.解 (1)原式=sin 2θsin θ-cos θ+cos θ1-sin θcos θ=sin 2θsin θ-cos θ+cos 2θcos θ-sin θ=sin 2θ-cos 2θsin θ-cos θ=sin θ+cos θ.由已知得sin θ+cos θ=3+12, 所以sin 2θsin θ-cos θ+cos θ1-tan θ=3+12. (2)由已知得sin θcos θ=m 2, 因为1+2sin θcos θ=(sin θ+cos θ)2,所以1+m =⎝⎛⎭⎪⎫3+122, 解得m =32. (3)联立⎩⎪⎨⎪⎧ sin θ+cos θ=3+12,sin θcos θ=34,解得⎩⎨⎧ sin θ=32,cos θ=12 或⎩⎨⎧ sin θ=12,cos θ=32.因为θ∈(0,2π),所以θ=π3或π6.。
高考第一轮复习数学三角函数的图象与性质三

9.已知P1,cosx,Qcosx,1,x∈- , .
1求向量 和 的夹角θ的余弦用x表示的函数fx;
2求θ的最值.
解:1∵ · =2cosx,
| |·| |=1+cos2x,
∴fx=cosθ= .
2cosθ= = ,
x∈- , ,cosx∈ ,1.
∴2≤cosx+ ≤ , ≤fx≤1,即 ≤cosθ≤1.
解:定义域为R,又fx+f-x=lg1=0,
即f-x=-fx,∴fx为奇函数.
评述:定义域关于原点对称是函数具有奇偶性的必要但不充分条件.
例2求下列函数的单调区间:
1y= sin - ;2y=-|sinx+ |.
剖析:1要将原函数化为y=- sin x- 再求之.2可画出y=-|sinx+ |的图象.
3.判断y=-Asinωx+ ω>0的单调区间,只需求y=Asinωx+ 的相反区间即可,一般常用数形结合.而求y=Asin-ωx+ -ω<0单调区间时,则需要先将x的系数变为正的,再设法求之.读者考虑为什么
●教师下载中心
教学点睛
本节是图象和性质的综合应用的内容,例题讲解要突出数形结合思想、化归转化思想、分类讨论等数学思想方法,并注意三角知识的载体作用,注意和其他知识间的关联.
解析:显然fx为偶函数,结论①错.
对于结论②,当x=1000π时,x>2003,sin21000π=0,∴f1000π= - 1000π< ,因此结论②错.
又fx= - |x|+ =1- cos2x- |x|,-1≤cos2x≤1,
∴- ≤1- cos2x≤ .
故1- cos2x- |x|< ,即结论③错.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高考数学一轮复习知识点总结:三角函数
高考第一轮复习既以教材为基本内容,又以教学大纲以及当年的考试说明为依据,做到知识点的全面涉及与提高巩固。
查字典数学网整理了高考数学一轮复习知识点总结:三角函数,供参考。
高中数学三角函数知识点总结:锐角三角函数公式
sin =的对边 / 斜边
cos =的邻边 / 斜边
tan =的对边 / 的邻边
cot =的邻边 / 的对边
倍角公式
Sin2A=2SinA?CosA
Cos2A=CosA^2-SinA^2=1-2SinA^2=2CosA^2-1
tan2A=(2tanA)/(1-tanA^2)
(注:SinA^2 是sinA的平方 sin2(A) )
高中数学三角函数知识点总结:三倍角公式
sin3=4sinsin(/3+)sin(/3-)
cos3=4coscos(/3+)cos(/3-)
tan3a = tan a tan(/3+a) tan(/3-a)
高中数学三角函数知识点总结:三倍角公式推导
sin3a
=sin(2a+a)
=sin2acosa+cos2asina
高中数学三角函数知识点总结:辅助角公式
Asin+Bcos=(A^2+B^2)^(1/2)sin(+t),其中
sint=B/(A^2+B^2)^(1/2)
cost=A/(A^2+B^2)^(1/2)
tant=B/A
Asin+Bcos=(A^2+B^2)^(1/2)cos(-t),tant=A/B降幂公式sin^2()=(1-cos(2))/2=versin(2)/2
cos^2()=(1+cos(2))/2=covers(2)/2
tan^2()=(1-cos(2))/(1+cos(2))
高中数学三角函数知识点总结:推导公式
tan+cot=2/sin2
tan-cot=-2cot2
1+cos2=2cos^2
1-cos2=2sin^2
1+sin=(sin/2+cos/2)^2
=2sina(1-sin2a)+(1-2sin2a)sina
=3sina-4sin3a
cos3a
=cos(2a+a)
=cos2acosa-sin2asina
=(2cos2a-1)cosa-2(1-sin2a)cosa
=4cos3a-3cosa
sin3a=3sina-4sin3a
=4sina(3/4-sin2a)
=4sina[(3/2)2-sin2a]
=4sina(sin260-sin2a)
=4sina(sin60+sina)(sin60-sina)
=4sina*2sin[(60+a)/2]cos[(60-a)/2]*2sin[(60-a)/2]co s[(60-a)/2]
=4sinasin(60+a)sin(60-a)
cos3a=4cos3a-3cosa
=4cosa(cos2a-3/4)
=4cosa[cos2a-(3/2)2]
=4cosa(cos2a-cos230)
=4cosa(cosa+cos30)(cosa-cos30)
=4cosa*2cos[(a+30)/2]cos[(a-30)/2]*{-2sin[(a+30)/2] sin[(a-30)/2]}
=-4cosasin(a+30)sin(a-30)
=-4cosasin[90-(60-a)]sin[-90+(60+a)]
=-4cosacos(60-a)[-cos(60+a)]
=4cosacos(60-a)cos(60+a)
上述两式相比可得
tan3a=tanatan(60-a)tan(60+a)
高中数学三角函数知识点总结:半角公式
tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA);
cot(A/2)=sinA/(1-cosA)=(1+cosA)/sinA.
sin^2(a/2)=(1-cos(a))/2
cos^2(a/2)=(1+cos(a))/2
tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))三角和sin(++)=sincoscos+cossincos+coscossin-sinsinsin cos(++)=coscoscos-cossinsin-sincossin-sinsincos tan(++)=(tan+tan+tan-tantantan)/(1-tantan-tantan-ta ntan)
高中数学三角函数知识点总结:两角和差
cos(+)=coscos-sinsin
cos(-)=coscos+sinsin
sin()=sincoscossin
tan(+)=(tan+tan)/(1-tantan)
tan(-)=(tan-tan)/(1+tantan)
高中数学三角函数知识点总结:和差化积
sin+sin = 2 sin[(+)/2] cos[(-)/2]
sin-sin = 2 cos[(+)/2] sin[(-)/2]
cos+cos = 2 cos[(+)/2] cos[(-)/2]
cos-cos = -2 sin[(+)/2] sin[(-)/2]
tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB)
tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB) 高中数学三角函数知识点总结:积化和差
sinsin = [cos(-)-cos(+)] /2
coscos = [cos(+)+cos(-)]/2
sincos = [sin(+)+sin(-)]/2
cossin = [sin(+)-sin(-)]/2
高中数学三角函数知识点总结:诱导公式
sin(-) = -sin
cos(-) = cos
tan (a)=-tan
sin(/2-) = cos
cos(/2-) = sin
sin(/2+) = cos
cos(/2+) = -sin
sin() = sin
cos() = -cos
sin() = -sin
cos() = -cos
tanA= sinA/cosA
tan(/2+)=-cot
tan(/2-)=cot
tan()=-tan
tan()=tan
诱导公式记背诀窍:奇变偶不变,符号看象限
万能公式
sin=2tan(/2)/[1+tan^(/2)]
cos=[1-tan^(/2)]/1+tan^(/2)]
tan=2tan(/2)/[1-tan^(/2)]
高中数学三角函数知识点总结:其它公式
(1)(sin)^2+(cos)^2=1
(2)1+(tan)^2=(sec)^2
(3)1+(cot)^2=(csc)^2
证明下面两式,只需将一式,左右同除(sin)^2,第二个除(cos)^2即可
(4)对于任意非直角三角形,总有
tanA+tanB+tanC=tanAtanBtanC
证:
A+B=-C
tan(A+B)=tan(-C)
(tanA+tanB)/(1-tanAtanB)=(tan-tanC)/(1+tantanC) 整理可得
tanA+tanB+tanC=tanAtanBtanC
得证
同样可以得证,当x+y+z=nZ)时,该关系式也成立
由tanA+tanB+tanC=tanAtanBtanC可得出以下结论
(5)cotAcotB+cotAcotC+cotBcotC=1
(6)cot(A/2)+cot(B/2)+cot(C/2)=cot(A/2)cot(B/2)cot(C /2)
(7)(cosA)^2+(cosB)^2+(cosC)^2=1-2cosAcosBcosC
(8)(sinA)^2+(sinB)^2+(sinC)^2=2+2cosAcosBcosC
(9)sin+sin(+2/n)+sin(+2*2/n)+sin(+2*3/n)++sin[+2*(n -1)/n]=0
cos+cos(+2/n)+cos(+2*2/n)+cos(+2*3/n)++cos[+2*(n-1) /n]=0 以及
sin^2()+sin^2(-2/3)+sin^2(+2/3)=3/2
tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0
高考数学一轮复习知识点总结:三角函数就分享到这里了,更多高考备考信息请继续关注查字典数学网高考频道!。
