电路第六章储能元件
合集下载
电路 第五版 邱关源 第6章(新版)

3.并联的等效电感 并联的等效电感
串联的等效电感等于各个电感之和; 串联的等效电感等于各个电感之和; 并联等效电感的倒数等于各个电感倒数之和
本章小结
• 电容和电感元件的性质,作用 电容和电感元件的性质, • 电容和电感元件特性(库伏特性和伏安特 电容和电感元件特性( 性) • 电容和电感元件的功率及能量 • 电容和电感串并联的等效电容
• 关于电感元件的结论: 关于电感元件的结论:
(1)电感元件是一个无源元件,动态元件,具有 )电感元件是一个无源元件,动态元件, 记忆”功能的元件, “记忆”功能的元件, 短路直流的作用 (2)能储存和释放能量。具有短路直流的作用 )能储存和释放能量。具有短路直流
( ) 注: 1)实际的电感线圈的模型可用线性电感元件和电阻元 件串联组合。 件串联组合。 (2)非线性电感元件韦安特性不是直线 )非线性电感元件韦安特性不是直线, 电感元件 (3)L ) 元件的参数
第六章: 第六章:储能元件
• 本章的重点: 1.电容和电感元件的特性和伏安关系 2.电容和电感的串并联的等效参数 • 本章难点: 对电容和电感元件特性的理解
§6-1 电容元件
一、电容元件符号: 电容元件符号: 二、电容元件特性(库伏特性) 电容元件特性(库伏特性)
任何时刻, 任何时刻 , 当电压的参考方向 与电容元件极板上存储电荷的方向 一致时,电荷q与电压 成正比。 一致时,电荷 与电压 u 成正比。 C
分部电容,三极管极间存在的杂散电容。 分部电容,三极管极间存在的杂散电容。 (2)实际电容元件的模型是电容和电阻元件的并联组合。 实际电容元件的模型是电容和电阻元件的并联组合。 实际电容元件的模型是电容和电阻元件的并联组合
(3)非线性电容元件库伏特性不是直线,如变容 非线性电容元件库伏特性不是直线,
(播放版12)第6章储能元件

釉、聚碳酸脂、金属化纸介、
空气等;还有铝电解、钽电解、
U
合金电解电容等。
2020年3月25日星期三
2
各种类型的电容器(1)
电解电容 (有极性)
2020年3月25日星期三
3
各种类型的电容器(2)
高压陶瓷电容器 多层陶瓷电容器 金属膜电容器
可控硅专用吸收电容器 2020年3月25日(内星期置三 电阻)
2020年3月25日星期三
11
伏安关系的积分形式
由
i
=
dq dt
得
t
t0
t
q(t) = i(x) dx = i(x) dx + i(x) dx
-∞
-∞
t0
t
以t0为计时起点
q(t) = q(t0) +
i(x) dx
t0
将q = C u 代入得
u(t)
=
u(t0) +
1 C
t
i(x) dx
t0
表明
①某一时刻的电容电压值与 - 到该时刻的所有电
其它类型线性电容元件的图形符号:
+
有极性的 微调 电解电容 电容
可变 电容
同轴双连 可变电容
2020年3月25日星期三
9
2.电容元件的定义
+q C -q
任何时刻其储存的电荷 q 与其两端 的电压 u 能用 q~u 平面上的一条 曲线来描述,称库伏特性。
+uq
对于线性时不变电容元件,任 何时刻,电容元件极板上的电
29
积分表达式
i
=
i(t0)
+
1 L
两边乘以 L得
6储能元件

并且 u(3s) (30 + 25 3)V 105V
画出电容电压波形
-2A
o
u
3s
7s
105V 30V
o
3s
7s
t
(2)3s≤t<7s, i= -2A 电容放电
1 t u u (3) + i ( )d C 3 1 t 105 + 3 (-2)d 0.2
135 - 10t
i
Ceq
u (t ) u1 (t ) + u2 (t ) + .... +u n (t )
1 C1 1 - i( )d + C2
t
n 1 1 Ceq k 1 Ck
t
-
1 i ( )d + ... + Cn
t
-
i ( )d
1 u1 (t0 ) + C1
1 u (t0 ) + Ceq
4s
6s
t
di u L 0.15V dt
0.45W
(c)
0.15V
u 2s 4s 6s
p ui 0.225t W
O
t
(2) 2s t 4s : i 3 A
di uL 0 dt
i
p ui 0
(3) 4s t 6s : i -1.5t + 9
di u L -0.15V dt
t
-
i ( )d
物理意义:t 时刻电容上的电荷量(电压)是 t 时刻之前 由充电、放电而积累起来的。 ——记忆元件。
讨论:
1 2 (三) WC (t ) Cu(t ) 2
画出电容电压波形
-2A
o
u
3s
7s
105V 30V
o
3s
7s
t
(2)3s≤t<7s, i= -2A 电容放电
1 t u u (3) + i ( )d C 3 1 t 105 + 3 (-2)d 0.2
135 - 10t
i
Ceq
u (t ) u1 (t ) + u2 (t ) + .... +u n (t )
1 C1 1 - i( )d + C2
t
n 1 1 Ceq k 1 Ck
t
-
1 i ( )d + ... + Cn
t
-
i ( )d
1 u1 (t0 ) + C1
1 u (t0 ) + Ceq
4s
6s
t
di u L 0.15V dt
0.45W
(c)
0.15V
u 2s 4s 6s
p ui 0.225t W
O
t
(2) 2s t 4s : i 3 A
di uL 0 dt
i
p ui 0
(3) 4s t 6s : i -1.5t + 9
di u L -0.15V dt
t
-
i ( )d
物理意义:t 时刻电容上的电荷量(电压)是 t 时刻之前 由充电、放电而积累起来的。 ——记忆元件。
讨论:
1 2 (三) WC (t ) Cu(t ) 2
chapter06储能元件.
t0
udξ
1 L
t
t0
udξ
i(t
)0
1 L
tt0udξ
ψ(t
)
ψ( t
)0
t
t0
udξ
讨论:
(1) u的大小取决与 i 的变化率,与 i 的大小无关; (微分形式)
(2) 电感元件是一种记忆元件;(积分形式)
i 1
t
ud
1
0
ud
1
t
ud
i(0)
的方程得到电感元件的方程;
(3) C 和 L称为对偶元件, 、q等称为对偶元素。
* 显然,R、G也是一对对偶元素: U=RI I=GU I=U/R U=I/G
电感和电容的串并联
电感的串联 电感的并联
n
Leq Lk k 1
1
n
1
Leq k1 Lk
电容的串联 电容的并联
1 n 1 Ceq k1 Ck
q =Cu
def q C
u
C 称为电容器的电容
电容 C 的单位:F (法) (Farad,法拉) F= C/V = A•s/V = s/
常用F,nF,pF等表示。
线性电容的q~u 特性是过原点的直线 q
Ou
C= q/u tg
线性电容的电压、电流关系: u, i 取关联参考方向
i
i dq C du dt dt
电容元件与电感元件的比较:
变量
电容 C 电压 u
电荷 q
电感 L 电流 i
磁链
关系式
q Cu
6、储能元件

i
L
+ uL
伏安关系
u L di dt
只有电感上的电流变化时,电感两端才有电压。 在直流电路中,电感上即使有电流通过, 但 u = 0,相当于短路
Ψ= L i
磁化曲线
Ψ
线圈在铁磁材料的非饱和状 态下工作,L近似不变
饱和区
线性区,磁导 率大且不变
起始段,磁导率较小
i
磁滞现象与磁滞回线
Ψ
• 电流强度i缓慢地
i dq (单位时间内通过的电荷量) dt
ቤተ መጻሕፍቲ ባይዱ
电路符号:
+i uC
−
伏安关系 i C du dt
i du /dt。只有电容上的电压变化
时,电容两端才有电流。 在直流电路中,电容上即使有电压,
但 i = 0,相当于开路,即 电容具有 隔直作用。
实际电容器示例
链接 RC动画
电解电容器
瓷质电容器
固定电容器
聚丙烯膜电容器
管式空气可调电容器
可变电容器
片式空气可调电容器
伏安关系
i C du dt
uC
1 C
t
i
d
UC 0
1 C
t
0
i
d
UC(0)为初始时刻t=0时电容的初始电压,反映t=0前 “历史”中电容电流的积累效应——电容对它的电 流具有记忆能力,
Ψr
循环变化, Ψ-i曲
线是一封闭曲线:
磁滞回线
剩磁Ψr
i
电容元件中的电场能量
Wc
t
uidt
u(t )
Cudu
1Cu2
6 储能元件

Li
i1
1 L1
t
u
(ξ
)dξ
L L1
i
L2i L1 L2
i2
1 L2
t
u
(ξ
)dξ
L L2
i
L1i L1 L2
注意
以上虽然是关于两个电容或两个电感
的串联和并联等效,但其结论可以推广到
n 个电容或 n 个电感的串联和并联等效。
2
2C
从t0到 t 电容储能的变化量:
WC
1 2
Cu2
(t)
1 2
Cu2
(t0
)
1 2C
q2(t) 1 2C
q2 (t0 )
表 (1)电容的储能只与当时的电压值有关,电容
明
电压不能跃变,反映了储能不能跃变;
(2)电容储存的能量一定大于或等于零。
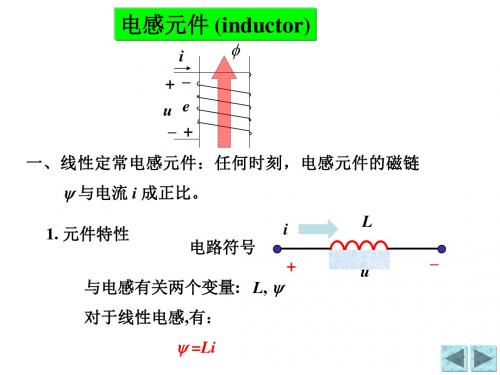
§6.2 电感元件
电感器
(t)=N (t)
L dt
L L1 L2
串联电感的分压
u1
L1
di dt
L1 L
u
L1
L1 L2
u
u2
L2
di dt
L2 L
u
L1
L2 L2
u
i
+
L1 u
L2
+
u1
+-
等效
u2
-
+i
uL
-
4.电感的并联
等效电感
+ i1 i2
+i
电路PPT课件:储能元件

0
1
2 t /s
返回 上頁 下頁
若已知電流求電容電壓,有 i/A 1
0
i(t)
1 1
0
t 0 0 t 1s 1 t 2s t 2s
0 -1
1
2 t /s
0t 1s
1 t 2s
uc(t)
1 C
00dξ
1 C
0t1dξ
02t
2t
uC (t)
u(1)
1 0.5
t
1
(1)d
4
2t
2t
uC (t)
u(2)
1 0.5
t
2
0d
0
返回 上頁 下頁
實際電容器的模型
C i
+
-
u
C
qi +
_q
C
+
G
-+
u
G
-
u
返回 上頁 下頁
實際電容器
返回 上頁 下頁
電力電容
返回 上頁 下頁
衝擊電壓發生器
返回 上頁 下頁
6.2 電感元件
電感線圈把金屬導線繞在一骨架上構成一實際電感 線圈,當電流通過線圈時,將產生磁通,是一種 抵抗電流變化、儲存磁能的部件。
WL
t
Li
di dξ
dξ
1 2
Li2 (ξ)
t
1 Li2(t) 1 Li2() 1 Li2(t)
2
2
2
從t0到 t 電感儲能的變化量:
WL
1 2
Li2 (t )
1 2
Li2 (t0 )
返回 上頁 下頁
WL
1 2
Li2 (t )
0
第六章-储能元件

),与线圈交链成磁链ψ
把金属导线绕在一骨架上 构成一实际电感线圈,当电 流通过线圈时,将产生磁通 ,是一种抵抗电流变化、储
i
i
+–
ue
–+
存磁能的部件。
电感线圈原理示意图
几种实际电感线圈示例
贴片型空心线圈
可调式电感
环形线圈
立式功率型电感
一、定义
任意时刻,能用Ψ-i平面内一条曲线来描述的二端元件→ 韦-安曲线
d(12 2t) 1 106 dt
1μA
例2 : C=0.5F的电容电流波形如图 (b)所示,求电容电压uC(t)。
解:根据图(b)波形的情况,按照时间分段来进行计算
1.当t0时,iC(t)=0,得
uC
(t)
1 C
t
iC ( )d
2 106
t
0d 0
2.当0t<1s时,iC(t)=1A,得
i +– ue L –+
对于线性电感,有: =Li =N 为电感线圈的磁链(韦伯)
L
def
ψ
i
L 称为自感系数,也代表 电感元件本身
线性电感的 ~i 特性(韦-安特性)是过原点的直线
i
L= /i tg + –
Oi
六、线性电感电压、电流关系→伏安关系:
ue L –+
u, i 取关联参考方向:根据电磁感应定律与 楞次定律
i
u, i 取关联参考方向
+ +
i dq C du dt dt
u
C
u, i 取非关联参考方向
–
–
i dq C du
dt
dt
电容充放电形成电流: u, i 取关联参考方向
