《电路》第六章储能元件
合集下载
储能元件的电路

(t ) Li(t )
L
i
tan
o i
建筑电气系
电路符号 i + L u (t) 电感 器的 自感
单位
H (亨利),常用H,mH表示。
1H=103 mH 1 mH =103 H
建筑电气系
3.线性电感的电压、电流关系
i + L u (t) u、i 取关联 参考方向
C C2 u1 u u C1 C1 C2
C C1 u2 u u C2 C1 C2
建筑电气系
2.电容的并联
i
+
u
等效电容
i1
i2
du i1 C1 dt
du i2 C2 dt
C1
C2
等效
du du C i i1 i2 (C1 C2 ) dt dt
+
u
i
C C1 C2
C
建筑电气系
-
并联电容的分流
i
+
u
du i1 C1 dt
i1
C1
i2
C2
du i2 C2 dt
+
u i C
du i C dt
C1 i1 i C
C2 i2 i C
建筑电气系
3. 电感的串联
等效电感
i
+
u
di u1 L1 dt
L1 L2
+
+
-
u1 u2
建筑电气系
电感的储能
di 1 2 WL Li dξ Li (ξ) dξ 2
邱关源《电路》第五版 第六章 储能元件

u(t0 ) u1 (t0 ) u2 (t0 ) ...... un (t0 )
§6-3 电容、电感元件的串联与并联
2) 并联
i i1 u
i2 C1 (a) C2
in Cn
i u
Ceq (b)
等效电容
Ceq C1 C2 ...... Cn
初始条件
u1 (t0 ) u2 (t0 ) ...... un (t0 ) u(t0 )
WL
t2
t1
di 1 2 1 2 Li dt Li (t 2 ) Li (t1 ) dt 2 2
* 在t1到t2期间供给电感的能量只与时间端点的电感电 流值有关。
* 电感在某一时刻的储能只与该时刻的电流有关。
1 2 WL Li (t ) 2
§6-2 电感元件
5. 电感元件的应用
uic61电容元件uic0011ddtttiicc?令t00则?00d1d1ticictuti0cud1061电容元件1dtutic?ti0cutud10当选定一个研究问题的起点后如t0就没有必要去了解t0以前电流的情况它对t0的电容电压的影响可用电容的初始电压u0来反映
第六章 储能元件
电容元件 电感元件 电容、电感元件的串联与并联
§6-2 电感元件
1 t i (t ) i (0) u ( )d L 0
* 当选定一个研究问题的起点后(如 t = 0),就没
有必要去了解 t = 0以前电压的情况,它对 t >0 的
电感电流的影响可用电感的初始电流i (0)来反映。
即:知道了初始电流i (0)及t 0的u (t),就能确定
i
u
+
u
V
§6-3 电容、电感元件的串联与并联
2) 并联
i i1 u
i2 C1 (a) C2
in Cn
i u
Ceq (b)
等效电容
Ceq C1 C2 ...... Cn
初始条件
u1 (t0 ) u2 (t0 ) ...... un (t0 ) u(t0 )
WL
t2
t1
di 1 2 1 2 Li dt Li (t 2 ) Li (t1 ) dt 2 2
* 在t1到t2期间供给电感的能量只与时间端点的电感电 流值有关。
* 电感在某一时刻的储能只与该时刻的电流有关。
1 2 WL Li (t ) 2
§6-2 电感元件
5. 电感元件的应用
uic61电容元件uic0011ddtttiicc?令t00则?00d1d1ticictuti0cud1061电容元件1dtutic?ti0cutud10当选定一个研究问题的起点后如t0就没有必要去了解t0以前电流的情况它对t0的电容电压的影响可用电容的初始电压u0来反映
第六章 储能元件
电容元件 电感元件 电容、电感元件的串联与并联
§6-2 电感元件
1 t i (t ) i (0) u ( )d L 0
* 当选定一个研究问题的起点后(如 t = 0),就没
有必要去了解 t = 0以前电压的情况,它对 t >0 的
电感电流的影响可用电感的初始电流i (0)来反映。
即:知道了初始电流i (0)及t 0的u (t),就能确定
i
u
+
u
V
《电路》第六章储能元件

与 N匝全部交链,则磁通链 Ψ =NΦ Φ ,Ψ —自感磁通,自感磁 通链(由自身电流产生,或用 Φ L ,Ψ L表示)单位:韦伯Wb
规定Φ L(Ψ L )与i的参考方向满足右螺旋关系。
当电感元件上电流的参考方向与磁通成右螺旋关系时,则任何 时刻线性电感元件的自感磁通链Ψ与流过的电流i 之间有以下 关系:
2. 线性定常电感元件
任何时刻,通过电感元件的电流i与其磁链 成正比。
~ i 特性是过原点的直线
(t) Li(t) or L tan
i
电路符号
i
L
Oi
单位
+
u (t)
-
L 称为电感器的自感系数, L的单位:H (亨) (Henry,亨利),常用H,m H表示。
R2 R1 R2
US
例电路如图所示。已知两个电容在开关闭合前一瞬间的电压分 别为uC1(0-)=0V,uC2(0-)=6V,试求在开关闭合后一瞬间,电容 电压uC1(0+),uC2(0+) 。
解: 开关闭合后,两个电容并联,按照KVL的约束,两个 电容电压必须相等,得到以下方程
uC1(0 ) uC2 (0 )
实际电路中使用的电容器类型很多,电容的范围
变化很大,大多数电容器漏电很小,在工作电压低的 情况下,可以用一个电容作为它的电路模型。当其漏 电不能忽略,则需要用一个电阻与电容的并联作为它 的电路模型。
在工作频率很高的情况下,还需要增加一个电感 来构成电容器的电路模型.
线性电容的电压、电流关系 电容元件VCR
1.定义
电容元件
储存电能的元件。其
特性可用u~q 平面
上的一条曲线来描述
q
+
规定Φ L(Ψ L )与i的参考方向满足右螺旋关系。
当电感元件上电流的参考方向与磁通成右螺旋关系时,则任何 时刻线性电感元件的自感磁通链Ψ与流过的电流i 之间有以下 关系:
2. 线性定常电感元件
任何时刻,通过电感元件的电流i与其磁链 成正比。
~ i 特性是过原点的直线
(t) Li(t) or L tan
i
电路符号
i
L
Oi
单位
+
u (t)
-
L 称为电感器的自感系数, L的单位:H (亨) (Henry,亨利),常用H,m H表示。
R2 R1 R2
US
例电路如图所示。已知两个电容在开关闭合前一瞬间的电压分 别为uC1(0-)=0V,uC2(0-)=6V,试求在开关闭合后一瞬间,电容 电压uC1(0+),uC2(0+) 。
解: 开关闭合后,两个电容并联,按照KVL的约束,两个 电容电压必须相等,得到以下方程
uC1(0 ) uC2 (0 )
实际电路中使用的电容器类型很多,电容的范围
变化很大,大多数电容器漏电很小,在工作电压低的 情况下,可以用一个电容作为它的电路模型。当其漏 电不能忽略,则需要用一个电阻与电容的并联作为它 的电路模型。
在工作频率很高的情况下,还需要增加一个电感 来构成电容器的电路模型.
线性电容的电压、电流关系 电容元件VCR
1.定义
电容元件
储存电能的元件。其
特性可用u~q 平面
上的一条曲线来描述
q
+
062第六章储能元件PPT课件

第六章 储能元件
重点: 1. 电容元件 2. 电感元件 3. 电容、电感元件的串联与并联
1
标题添加
点击此处输入相 关文本内容
前言
点击此处输入 相关文本内容
标题添加
点击此处输入相 关文本内容
点击此处输入 相关文本内容
2
§ 6.1 电容元件 (capacitor)
电容器
+
+ +
+
+q
–
– –
–
–q
由两块金属板间隔以不同的 介质(如云母、绝缘纸、电解质 等)所组成。
若: i(t2)i(t1) 则: W L(t2)W L(t1)
电感在此时间内释放能量。
电感元件不把吸收的能量消耗掉,而是以磁场能量的 形式储存在磁场中。
电感元件是一种储能元件,同时它也不会释放出多于它吸收或 储存的能量,因此它又是无源元件。
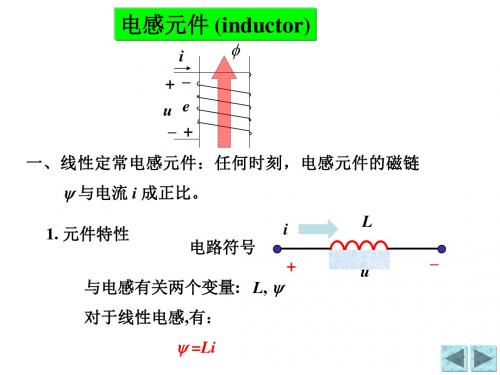
任何时刻,电感元件的磁链 与电流 i 成正比。
1. 元件特性
iL
电路符号
u
对于线性电感,有: =Li
def ψ L
i
=N 为电感线圈的磁链
N为电感线圈的匝数。
单位:Wb (韦伯)
L 称为自感系数或电感,L是一个正实常数。
13
电感 L 的单位:H(亨) (Henry,亨利)
def ψ L
i
H=Wb/A=V•s/A=•s
uu(t0)C 1tt0idξ
(2) 电容元件是一种记忆元件;(积分形式)
(3) 当 u 为常数(直流)时,du/dt =0 i=0。电容在直流电路
中相当于开路,电容有隔直作用;
(4) 表达式前的正、负号与u,i 的参考方向有关。
重点: 1. 电容元件 2. 电感元件 3. 电容、电感元件的串联与并联
1
标题添加
点击此处输入相 关文本内容
前言
点击此处输入 相关文本内容
标题添加
点击此处输入相 关文本内容
点击此处输入 相关文本内容
2
§ 6.1 电容元件 (capacitor)
电容器
+
+ +
+
+q
–
– –
–
–q
由两块金属板间隔以不同的 介质(如云母、绝缘纸、电解质 等)所组成。
若: i(t2)i(t1) 则: W L(t2)W L(t1)
电感在此时间内释放能量。
电感元件不把吸收的能量消耗掉,而是以磁场能量的 形式储存在磁场中。
电感元件是一种储能元件,同时它也不会释放出多于它吸收或 储存的能量,因此它又是无源元件。
任何时刻,电感元件的磁链 与电流 i 成正比。
1. 元件特性
iL
电路符号
u
对于线性电感,有: =Li
def ψ L
i
=N 为电感线圈的磁链
N为电感线圈的匝数。
单位:Wb (韦伯)
L 称为自感系数或电感,L是一个正实常数。
13
电感 L 的单位:H(亨) (Henry,亨利)
def ψ L
i
H=Wb/A=V•s/A=•s
uu(t0)C 1tt0idξ
(2) 电容元件是一种记忆元件;(积分形式)
(3) 当 u 为常数(直流)时,du/dt =0 i=0。电容在直流电路
中相当于开路,电容有隔直作用;
(4) 表达式前的正、负号与u,i 的参考方向有关。
【人大名师精品课件】电路第6讲储能元件

i ++
u
L1
u1 -
L2
+ u2 -
-
Ln
+ un -
i
+
u
Leq
-
根据电感的伏安关系,第k个(k=1,2,3,…,n)电感
的端电压
uk
Lkdi dt和KVL,可求得n个电感相
串联的等效电感
n
Leq
Lk
k 1
4、电感的并联
Leq的倒数表示式为
1
n
1
Leq
L k 1 k
i
+
i1
二、电容上 u ~ i关系——表示为微分关系
i(t) dq(t) C du
dt
dt
i C du dt
u(t) u(0) 1
t
i( )d
C0
动态元件, 又是记忆元件
故电容在直流时相当于“开路”, 即电容元件有隔直通交的作用
四、电容元件储存的能量
p吸
ui
uC
du dt
Ceq C1 C2
Cn C k 1 k
2、电容的并联
n个电容相并联的电路,各电容的端电压是同 一电压 u。
i
i
+
i1
i2
in +
u C1
C2
Cn
u
Ceq
-
-
n
其中 Ceq C1 C2 ... Cn Ck k 1
例: 如图所示电路,各个电容器的初始电压均为零,
给值定电容CC1 1F,C2 2F,C3 3F,C4 4F 试求ab间的等
储能元件的电路.

q Cu
电容器的 电容
q
q C tan u
o u
建筑电气系
建筑电气系
电路符号
C +q -q
+
u
-
单位
F (法拉), 常用F,pF等表示。
1F=106 F 1 F =106pF
建筑电气系
3. 电容的电压电流关系
i C u 电容元件VCR 的微分形式
+
-
u、i 取关联 参考方向
建筑电气系
电容的储能
t t
du 1 2 WC Cu dξ Cu (ξ ) dξ 2
1 2 1 2 1 2 Cu (t ) Cu ( ) Cu (t ) 2 2 2
从t0到 t 电容储能的变化量:
1 2 1 2 WC Cu (t ) Cu (t0 ) 2 2
(t ) Li(t )
L
i
tan
o i
建筑电气系
电路符号 i + L u ( t) 电感 器的 自感
单位
H (亨利),常用H,mH表示。
1H=103 mH 1 mH =103 H
建筑电气系
3.线性电感的电压、电流关系
i + L u ( t) u、i 取关联 参考方向
功率
di p ui L i dt
u、 i 取关联 参考方向
①当电流增大,p>0, 电感吸收功率。 ②当电流减小,p<0, 电感发出功率。
表明 电感能在一段时间内吸收外部供给的
能量转化为磁场能量储存起来,在另一段时间 内又把能量释放回电路,因此电感元件是无源 元件、是储能元件,它本身不消耗能量。
chapter06储能元件.
t0
udξ
1 L
t
t0
udξ
i(t
)0
1 L
tt0udξ
ψ(t
)
ψ( t
)0
t
t0
udξ
讨论:
(1) u的大小取决与 i 的变化率,与 i 的大小无关; (微分形式)
(2) 电感元件是一种记忆元件;(积分形式)
i 1
t
ud
1
0
ud
1
t
ud
i(0)
的方程得到电感元件的方程;
(3) C 和 L称为对偶元件, 、q等称为对偶元素。
* 显然,R、G也是一对对偶元素: U=RI I=GU I=U/R U=I/G
电感和电容的串并联
电感的串联 电感的并联
n
Leq Lk k 1
1
n
1
Leq k1 Lk
电容的串联 电容的并联
1 n 1 Ceq k1 Ck
q =Cu
def q C
u
C 称为电容器的电容
电容 C 的单位:F (法) (Farad,法拉) F= C/V = A•s/V = s/
常用F,nF,pF等表示。
线性电容的q~u 特性是过原点的直线 q
Ou
C= q/u tg
线性电容的电压、电流关系: u, i 取关联参考方向
i
i dq C du dt dt
电容元件与电感元件的比较:
变量
电容 C 电压 u
电荷 q
电感 L 电流 i
磁链
关系式
q Cu
完整版邱关源电路第六章ppt课件

i C du dt
u(t
)
(u(t)01 C源自tt 0idξ
)
②上式中u(t0)称为电容电压的初始值,它反 映电容初始时刻的储能状况,也称为初始 状态。
返 回 上 页 1下1 页
4.电容的功率和储能
功率 p ui u C du dt
u、 i 取关
联参考方向
①当电容充电, p >0, 电容吸收功率。
1
0 t 0
i(t)
C
duS dt
1 1
0 t 1s 1 t 2s
0 t 2s
2 t /s
返 回 上 页 1下6 页
0
p(t)
u(t
)i(t
)
2t 2t
4
0
p/W 2
t0
0 t 1s
1 t 2s
t 2s
吸收功 率
0
1
2 t /s
-2
发出功率
返 回 上 页 1下7 页
0
t0
返 回 上 页 3下0 页
注意
①当电感的 u,i 为非关联方向时,上述微分 和积分表达式前要冠以负号 ;
u L di dt
i(t
)
(i(t
)0
1 L
t
t 0
udξ
)
②上式中 i(t0)称为电感电压的初始值,它反映电 感初始时刻的储能状况,也称为初始状态。
返 回 上 页 3下1 页
4.电感的功率和储能
6.3 电容、电感元件的串联与并联
1.电容的串联
i
等效电容
u1
1 C1
t
i(ξ )dξ
+
+
C1
u1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实际电路中使用的电容器类型很多,电容的范围
变化很大,大多数电容器漏电很小,在工作电压低的 情况下,可以用一个电容作为它的电路模型。当其漏 电不能忽略,则需要用一个电阻与电容的并联作为它 的电路模型。
在工作频率很高的情况下,还需要增加一个电感 来构成电容器的电路模型.
线性电容的电压、电流关系 电容元件VCR
d(8 2t) dt
1106 A
1A
4.当5st时,uC(t)=12-2t,可以得到
iC (t)
C
duC dt
0.5 106
d(12 2t) dt
1106 A
1A
根据以上计算结果,画出图(b)所示的矩形波形。
例电路如图(a)所示,已知电容电流波形如图(b)所示,试求 电容电压uC(t),并画波形图。
t 106 d 0 2t 2t
0
当 t 1s 时 uC (1s) 2V
3.当1st<3s时,iC(t)=0,可以得到
uC
(t
)
1 C
t
iC ( )d
uC (1)
2 106
t
0d 2V+0=2V
1
当 t 3s 时 uC (3s) 2V
4.当3st<5s时,iC(t)=1A,可以得到
在已知电容电压u(t)的条件下,用式(6-2)容易求出其电流 i(t)。例如已知C=1F电容上的电压为u(t)=10sin(5t)V,其波 形如图7-3(a)所示,与电压参考方向关联的电容电流为
i(t) C du dt
106 d[10sin(5t)] dt
50 106 cos(5t) A
当电容元件上电压的参考方向规定由正极板指向负极板, 则任何时刻正极板上的电荷q与其端电压u之间的关系有:
q(t) =Cu(t)
式中C——元件的电容Capacitance, 单位:法拉F, 微法(F), 皮法(pF)
法拉第
电容器
在外电源作用下,
两极板上分别带上等量异号电荷,撤去 电源,板上电荷仍可长久地集聚下去, 是一种储存电能的部件。
1.定义
电容元件
储存电能的元件。其
特性可用u~q 平面
上的一条曲线来描述
q
+
_q
u q
f (u, q) 0
2. 线性定常电容元件
任何时刻,电容元件极板上的电荷q与电压 u 成正比。q ~ u
特性是过原点的直线
q Cu or C q tan
u
电路符号
C
+q -q
+
-
u
q
Ou
解:开关闭合已久,各电压电流均为不随时间变化的恒定 值,造成电容电流等于零,即
iC (t)
C
duC dt
0
电容相当于开路。此时电容电压为
uC (0 )
R2 R1 R2
US
当开关断开时,在电阻R2和R3不为零的情况下,电容 电流为有限值,电容电压不能跃变,由此得到
uC (0 )
uC (0 )
C
的微分关系
i
+
u
u、i 取关
联参考方向
-
表明:
i dq C du dt dt
(1) i 的大小取决于 u 的变化率, 与 u 的大小无关, 电容是动态元件;
(2) 当 u 为常数(直流)时,i =0。电容相当于开路,电容 有隔断直流作用;
(3)实际电路中通过电容的电流 i为有限值,则电容电压u
d(2t) dt
1106 A=1A
2.当1st3s时,uC(t)=4-2t,可以得到
iC (t) C
duC dt
0.5106
d(4 2t) dt
1106 A
1A
3.当3st5s时,uC(t)=-8+2t,可以得到
iC (t) C
duC dt
0.5106
t
0d 6V+0 6V
5
根据以上计算结果,可 以画出电容电压的波形如图(c) 所示,由此可见任意时刻电 容电压的数值与此时刻以前 的全部电容电流均有关系。
例如,当1s<t<3s时,电 容电流iC(t)=0,但是电容电压 并不等于零,电容上的2V电 压是0<t<1s时间内电流作用的 结果。
例图所示电路的开关闭合已久,求开关在t=0时刻 断开瞬间电容电压的初始值uC(0+)。
50 cos(5t) A
图7-3
例 已知C=0.5F电容上的电压波形如图(a)所示,
试求电压电流采用关联参考方向时的电流iC(t),并画 出波形图。
解:根据图7-4(a)波形,按照时间分段来进行计算
1.当0t1s 时,uC(t)=2t,可以得到
iC (t)
C
duC dt
0.5 106
uC
(t)
1 C
t
iC ( )d
uC (3)
2 106
t106 d 2+2(t 3)
3
当 t 5s 时 uC (5s) 2V+4V=6V
5.当5st时,iC(t)=0,可以得到
uC
(t)
1 C
t
iC ( )d
uC (5)
2 106
解:根据图(b)波形的情况,按照时间分段来进行计算
1.当t0时,iC(t)=0,可以得到
uC
(t)
1 C
t
iC ( )d
2 106
t
0d 0
2.当0t<1s时,iC(t)=1A,可以得到
uC
(t)
1 C
t
iC ( )d
uC (0)
2 106
R2 R1 R2
US
例电路如图所示。已知两个电容在开关闭合前一瞬间的电压分 别为uC1(0-)=0V,uC2(0-)=6V,试求在开关闭合后一瞬间,电容 电压u续函数.
u(t) 1 C
t
id ξ
1 C
t0
idξ
1 C
tt0idξ
表明
u(t
)0
1 C
t
t 0
idξ
电容元件VCR 的积分关系
电容元件有记忆电流的作用,故称电容为记忆元件
注 (1)当 u,i为非关联方向时,上述微分和积分表达
式前要冠以负号 ; (2)上式中u(t0)称为电容电压的初始值,它反映电 容初始时刻的储能状况,也称为初始状态。
6. 储能元件
主要内容 • 电容元件 • 电感元件 重点难点
掌握这两类器件的工作原理、电流电压特 性、储能性能以及串并联
6.1 电容元件
实际电容器
管式空气可调电容器
片式空气可调电容器
电解电容器
瓷质电容器 聚丙烯膜电容器
电容元件介绍
i +q
-q
+ u -
介质(云母、绝缘纸、电解质等) 建立电场 储存电场能量
