方差分析与相关性分析
相关性分析操作方法

相关性分析操作方法相关性分析是指通过统计方法或机器学习算法,研究两个或多个变量之间的关系或相互依赖程度。
这个分析方法可以帮助人们理解不同变量之间的关联程度,并据此进行预测和决策。
相关性分析在各个领域都有广泛的应用,如经济学、市场营销、社会学、生物学等。
在进行相关性分析时,可采用以下几种方法:1. 相关系数分析相关系数可以衡量两个变量之间的线性关系程度。
常用的相关系数有Pearson相关系数、Spearman相关系数和Kendall相关系数。
Pearson相关系数适用于线性关系,Spearman和Kendall相关系数适用于非线性关系。
相关系数的值介于-1和1之间,接近于-1表示负相关,接近于1表示正相关,接近于0表示无线性关系。
2. 散点图散点图是展示两个变量之间关系的图形。
横坐标表示一个变量的值,纵坐标表示另一个变量的值,每个点代表一个数据。
通过观察点的分布趋势,可以初步了解变量之间的关系。
通常,正相关变量的散点图呈现上升的趋势,负相关变量的散点图呈现下降的趋势。
3. 回归分析回归分析可以用来建立两个或多个变量之间的函数关系。
线性回归是最常见的回归分析方法,通过拟合一条直线来描述两个变量之间的线性关系。
回归分析可以进一步确定相关系数,并用于预测和解释数据。
4. 协方差分析协方差可以度量两个随机变量之间的关系强度。
协方差大于0表示正相关,小于0表示负相关,等于0表示无关。
但由于协方差的取值范围较大,难以比较不同变量之间的关联程度。
因此,常常使用标准化的相关系数来进行分析。
5. 因果关系分析因果关系分析是指通过实验或观察,确定某个变量对另一个变量的影响程度。
因果关系分析的方法包括实验设计、处理效果分析、回归分析等。
通过因果关系分析,可以得出变量之间的因果关系,并据此做出相应的决策。
以上是常见的相关性分析方法,不同方法适用于不同的情况。
在实际应用过程中,需要根据数据类型、变量之间的关系以及研究目的选择适当的方法。
相关性分析

相关性分析相关性分析是指对两个或多个具备相关性的变量元素进行分析,从而衡量两个变量因素的相关密切程度。
相关性的元素之间需要存在一定的联系或者概率才可以进行相关性分析。
相关性不等于因果性,也不是简单的个性化,相关性所涵盖的范围和领域几乎覆盖了我们所见到的方方面面,相关性在不同的学科里面的定义也有很大的差异。
差时,他们的相关性就会受到削弱。
世界上的任何事物之间存在的关系无非三种:1、函数关系,如时间和距离,2、没有关系,如你老婆的头发颜色和目前的房价3、相关关系,两者之间有一定的关系,但不是函数关系。
这种密切程度可以用一个数值来表示,|1|表示相关关系达到了函数关系,从1到-1之间表示两者之间关系的密切程度,例如0.8。
相关分析用excel可以实现说判定有些严格,其实就是观察一下各个指标的相关程度。
一般来说相关性越是高,做主成分分析就越是成功。
主成分分析是通过降低空间维度来体现所有变量的特征使得样本点分散程度极大,说得直观一点就是寻找多个变量的一个加权平均来反映所有变量的一个整体性特征。
评价相关性的方法就是相关系数,由于是多变量的判定,则引出相关系数矩阵。
评价主成分分析的关键不在于相关系数的情况,而在于贡献率,也就是根据主成分分析的原理,计算相关系数矩阵的特征值和特征向量。
相关系数越是高,计算出来的特征值差距就越大,贡献率等于前n个大的特征值除以全部特征值之和,贡献率越是大说明主成分分析的效果越好。
反之,变量之间相关性越差。
举个例子来说,在二维平面内,我们的目的就是把它映射(加权)到一条直线上并使得他们分散的最开(方差最大)达到降低维度的目的,如果所有样本点都在一条直线上(也就是相关系数等于1或者-1),这样的效果是最好的。
再假设样本点呈现两条垂直的形状(相关系数等于零),你要找到一条直线来做映射就很难了。
SPSS软件的特点一、集数据录入、资料编辑、数据管理、统计分析、报表制作、图形绘制为一体。
从理论上说,只要计算机硬盘和内存足够大,SPSS可以处理任意大小的数据文件,无论文件中包含多少个变量,也不论数据中包含多少个案例。
报告中数据统计和结果显著性的分析方法

报告中数据统计和结果显著性的分析方法概述:在各个领域的研究中,数据统计和结果的显著性分析是非常重要的,它们能够帮助我们了解数据的特性以及结果的可靠性。
本文将介绍几种常用的数据统计和结果显著性的分析方法,它们分别是:描述性统计分析、t检验、方差分析、相关分析、回归分析和卡方检验。
这些方法在实际应用中具有一定的灵活性和适应性,可以根据研究的特点和目标进行选择和使用。
一、描述性统计分析描述性统计分析是研究数据的基本特征和分布情况的方法,通过统计指标来对数据进行整体的概述。
常用的描述性统计指标包括均值、中位数、众数、标准差和四分位数等。
这些统计指标能够帮助我们了解数据的集中趋势、离散程度以及分布的形状,从而为进一步的数据分析提供基础。
二、t检验t检验是用于比较两个样本均值是否有显著差异的方法。
它常用于研究中对照组和实验组之间的差异,以验证研究假设的成立。
t检验的基本原理是通过计算两组样本均值之间的偏差是否显著大于随机误差来判断两组样本的差异是否显著。
当样本量较小或总体标准差未知时,可以使用学生t检验;当样本量较大且总体标准差已知时,可以使用z检验。
三、方差分析方差分析是用于比较多个样本均值是否有显著差异的方法。
它常用于研究中对多个处理组之间的差异,以确定是否存在处理效应。
方差分析的基本原理是通过将总体方差分解为组间方差和组内方差来判断组间差异是否显著。
方差分析可以帮助我们了解各个处理组之间是否存在显著差异,以及不同处理组的均值差异程度。
四、相关分析相关分析是用于探索两个变量之间关系的方法。
它可以帮助我们了解两个变量之间是否存在相关性以及相关性的强度和方向。
常用的相关系数有皮尔逊相关系数、斯皮尔曼等级相关系数和判定系数等。
相关分析的结果可以帮助我们判断两个变量之间的相关性是否显著,并根据相关系数的数值来评估相关性的强度。
五、回归分析回归分析是用于建立变量之间关系模型的方法。
它可以帮助我们预测和解释一个变量对另一个变量的影响。
生物学科实验数据分析方法总结

生物学科实验数据分析方法总结在生物学科实验中,数据分析是一项至关重要的任务,它帮助我们理解实验结果、发现规律并得出科学结论。
本文将总结一些生物学科实验数据分析的方法,旨在帮助读者更好地处理和解释生物学实验中的数据。
一、描述性统计分析描述性统计分析是数据分析的起点,它提供了对实验结果的概括性描述。
以下是一些常见的描述性统计方法:1. 平均值:计算数据的平均值可以帮助我们了解实验结果的中心趋势。
平均值等于所有数据值的总和除以观测次数。
2. 中位数:中位数是将数据按升序排列后,位于中间位置的数值。
它可以有效地反映数据的中心趋势,特别是当有异常值存在时。
3. 众数:众数表示出现次数最多的数值。
在分析一组离散数据时,众数能够快速帮助我们找到最常见的数值。
4. 方差:方差反映了数据的离散程度,即数据分散在平均值附近的程度。
方差越大,数据越分散。
二、推断统计分析推断统计分析是通过分析样本数据来推断总体特征的方法。
以下是一些常见的推断统计方法:1. 方差分析:方差分析用于比较两个或更多个样本的均值是否存在显著差异。
通过计算F值和p值,我们可以确定不同样本组之间是否存在显著差异。
2. t检验:t检验用于比较两个样本的均值是否存在显著差异。
它可以应用于独立样本和相关样本的数据分析。
3. 相关分析:相关分析用于衡量两个变量之间的相关性。
通过计算相关系数,我们可以了解两个变量之间的线性关系强弱。
4. 回归分析:回归分析用于建立自变量和因变量之间的数学关系。
通过回归模型,我们可以预测因变量在给定自变量条件下的取值。
三、图表分析图表是数据分析中重要的可视化工具,它们可以清晰地展示实验数据的分布和趋势。
以下是一些常用的图表分析方式:1. 条形图:条形图适用于展示不同类别之间的比较。
它可以直观地比较不同类别的数据差异。
2. 折线图:折线图可以展示数据随时间或其他连续变量的变化趋势。
它可以帮助我们观察到实验数据的走势和规律。
3. 散点图:散点图用于展示两个变量之间的关系。
分类变量的统计分析

分类变量的统计分析分类变量是指由有限个离散数值所组成的变量,例如性别、年级、职业等。
在统计学中,分类变量的统计分析可以帮助我们了解变量的分布、比较不同组之间的差异以及预测未来的趋势。
下面将详细介绍分类变量的统计分析方法。
1.描述统计:描述统计是对分类变量的基本统计特征进行描述和总结,包括频数、百分比和图表等。
频数是指每个类别出现的次数,百分比是指每个类别所占的比例。
通过频数和百分比可以直观地了解各个类别的分布情况,从而对整体的情况有一个直观的了解。
图表可以用来更直观地展示分类变量的分布情况,常用的图表包括饼图、柱状图和条形图等。
2.独立性检验:独立性检验用于判断两个或多个分类变量之间是否存在关联。
通常使用卡方检验进行独立性检验。
卡方检验的原假设是两个变量之间是独立的,备择假设则是两个变量之间存在关联。
通过卡方检验的结果可以判断两个变量之间是否存在显著性差异。
3.方差分析:方差分析用于比较多个分类变量之间的均值是否存在显著性差异。
方差分析将总体的方差分解为组内方差和组间方差,通过比较组间方差与组内方差的大小来判断不同组之间的均值是否显著不同。
方差分析常用于比较多个类别的平均值,例如不同年级学生的成绩差异、不同岗位员工的工资差异等。
4. 相关分析:相关分析用于判断两个分类变量之间的关系强度和方向。
常用的相关分析方法有Spearman秩相关系数和Kendall秩相关系数。
相关系数的取值范围为-1到1,当相关系数接近于1时,说明两个变量之间存在正相关关系;当相关系数接近于-1时,说明两个变量之间存在负相关关系;当相关系数接近于0时,说明两个变量之间不存在线性相关关系。
5.预测模型:分类变量的统计分析还可以用于建立预测模型,例如逻辑回归模型和决策树模型。
逻辑回归模型可以用来预测二分类变量的概率,例如预测一些人是否患有其中一种疾病。
决策树模型可以用来预测多分类变量的类别,例如预测一些植物的品种。
总之,分类变量的统计分析方法包括描述统计、独立性检验、方差分析、相关分析和预测模型等。
第七章 SPSS的相关分析

单因素方差分析
当一个变量为定类变量,另一变量为定距 变量时,两变量间是否有关,通常以分组 平均数比较的方法来考察。即按照定类变 量的不同取值来分组,看每个分组的定距 变量的平均数是否有差异。不同组间的平 均数差异越小,两个变量间的关系越弱; 相反,平均数差异越大,变量间关系越强。
单因素方差分析的基本步骤
最后,对不同看法进行分析。如果显著性 水平设为0.05,则概率值小于0.05,拒绝原 假设,认为本市户口和外地户口对未来三 年是否打算买房的看法是不一致的。
在列联表中,这一定理就具体转化为:若 两变量无关,则两变量中条件概率应等于 各自边缘的概率乘积。反之,则两变量有 关,或称两变量不独立。
由此可见,期望值(独立模型)与观察值 的差距越大,说明两变量越不独立,也就 越有相关。因此,卡方的表达式如下:
X
2
j i
( O ij E ij ) 2 E ij
第七章
相关分析与检验
主要内容
方差分析回顾 相关分析的概念
列联分析
简单相关分析
偏相关分析
方差分析回顾
概念:方差分析是从因变量的方差入手,研究诸 多自变量中哪些变量是对因变量有显著影响的变 量,对因变量有显著影响的各个自变量其不同水 平以及各水平的交互搭配是如何影响因变量的。 方差分析认为因变量的变化受两类因素的影响: 第一,自变量不同水平所产生的影响; 第二,随机变量所产生的影响。这里的随机变量指 那些人为很难控制的因素,主要指试验过程中的 抽样误差。
卡方的取值在0~∞之间。卡方值越大,关 联性越强。在SPSS中,有Pearson X2和 相似比卡方(Likelihood Ratio X2 )两种。
spss相关分析案例多因素方差分析
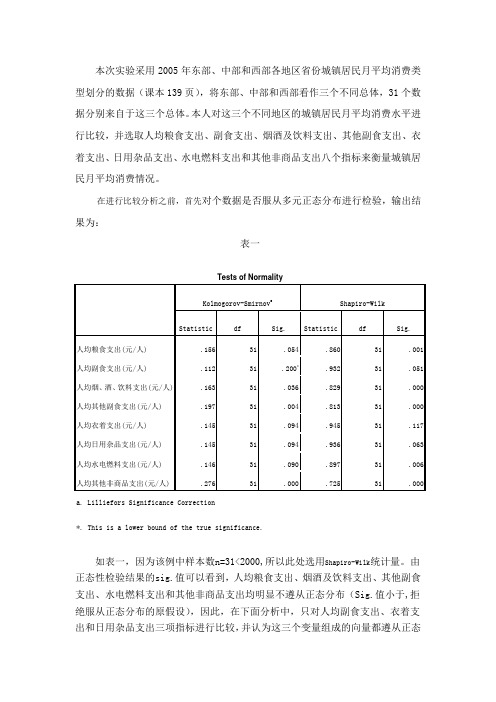
本次实验采用2005年东部、中部和西部各地区省份城镇居民月平均消费类型划分的数据(课本139页),将东部、中部和西部看作三个不同总体,31个数据分别来自于这三个总体。
本人对这三个不同地区的城镇居民月平均消费水平进行比较,并选取人均粮食支出、副食支出、烟酒及饮料支出、其他副食支出、衣着支出、日用杂品支出、水电燃料支出和其他非商品支出八个指标来衡量城镇居民月平均消费情况。
在进行比较分析之前,首先对个数据是否服从多元正态分布进行检验,输出结果为:表一如表一,因为该例中样本数n=31<2000,所以此处选用Shapiro-Wilk统计量。
由正态性检验结果的sig.值可以看到,人均粮食支出、烟酒及饮料支出、其他副食支出、水电燃料支出和其他非商品支出均明显不遵从正态分布(Sig.值小于,拒绝服从正态分布的原假设),因此,在下面分析中,只对人均副食支出、衣着支出和日用杂品支出三项指标进行比较,并认为这三个变量组成的向量都遵从正态分布,并对城镇居民月平均消费状况做出近似的度量。
另外,正态性的检验还可以通过Q-Q图来实现,此时应判别数据点是否与已知直线拟合得好。
如果数据点均落在直线附近,说明拟合得好,服从正态分布,反之,不服从。
具体情况这里不再赘述。
下面进行多因素方差分析:一、多变量检验表二由地区一栏的(即第二栏)所列几个统计量的Sig.值可以看到,无论从那个统计量来看,三个地区的城镇居民月平均消费水平都是有显著差别的(Sig.值小于,拒绝地区取值不同,对Y,即城镇居民月平均消费水平的取值没有显著影响的原假设)。
二、主体间效应检验表三如表三,可以看到三个指标地区一栏的(即第三栏)Sig.值分别为、、,说明三个地区在人均衣着支出指标上没有明显的差别(Sig.值大于,不拒绝地区取值不同,对指标的取值没有显著影响的原假设),反之,而在人均副食支出和日用杂品支出指标上有显著差别。
三、多重比较表四Contrast Results (K Matrix)地区 Simple Contrast aDependent Variable 人均副食支出(元/人)人均日用杂品支出(元/人)人均衣着支出(元/人)Level 1 vs. Level 3 Contrast EstimateHypothesized Value0 0 0 Difference (Estimate - Hypothesized) Std. Error Sig..001.036.51795% Confidence Interval for DifferenceLower Bound.173Upper BoundLevel 2 vs. Level 3 Contrast EstimateHypothesized Value0 0 0 Difference (Estimate - Hypothesized) Std. Error Sig..668.343.63895% Confidence Interval for DifferenceLower BoundUpper Bound表四Contrast Results (K Matrix)地区 Simple Contrast aDependent Variable 人均副食支出(元/人)人均日用杂品支出(元/人)人均衣着支出(元/人)Level 1 vs. Level 3 Contrast EstimateHypothesized Value0 0 0 Difference (Estimate - Hypothesized) Std. Error Sig..001.036.51795% Confidence Interval for DifferenceLower Bound.173Upper BoundLevel 2 vs. Level 3 Contrast EstimateHypothesized Value0 0 0 Difference (Estimate - Hypothesized) Std. Error Sig..668.343.63895% Confidence Interval for DifferenceLower BoundUpper Bounda. Reference category = 3如表四,在显著水平下,东部和西部的人均副食支出(Sig.值为)和日用杂品支出(Sig.值为)指标有明显差别(小于,拒绝原假设),而在人均衣着支出(Sig.值为)指标上没有明显的差别。
统计学专业学生成绩的相关性分析

安徽建筑大学毕业设计 (论文)题目统计学专业学生成绩的相关性分析专业统计学姓名王志海班级1班学号*********** 指导教师宫珊珊提交时间2016.6.6统计学专业学生成绩的相关性分析摘要:当代大学教育逐渐普及,在某种程度上已经失去了精英教育的定位.且随着时代的不同,大学生活变得丰富起来.由此引起的一个问题就是当代许多的大学生对学习失去了兴趣.在这样的背景之下,我们有必要探讨究竟有哪些因素会影响学生的学习成绩.因此本文在已有的大学生成绩的基础上,通过SPSS软件,采用统计学里的方差分析、相关分析与回归分析理论,对影响学生学习成绩的因素进行研究.由于收集的数据所限,本文只对影响学生成绩的课程种类、选课数目、挂科数量、班级四个因素进行相关的分析.首先,整合数据,采用以上提到的统计方法,对相关的因素进行显著性检验,其次,对于SPSS所生成的结果去进行统计分析,判断哪些因素对学生学习成绩产生了显著的影响,影响的程度又如何.研究结果表明:上面的四个因素中,课程种类、挂科数量对2015级统计学专业学生学习成绩的影响是显著的.而对于选课数目、班级这两个因素,通过检验我们发现它们对成绩有极弱的影响,在统计学上,我们可以认为它们与学生成绩之间没有显著的关系.该研究结果可以给教师们一些参考,以便于及时的调整授课方法,也便于教材的筛选.对于学生而言则可以了解自身的不足并加以改正,利于成绩的提高.关键词:成绩影响因素、相关分析、回归分析、方差分析Abstract: the increasing popularity of contemporary university education, in a certain extent has lost the positioning of the elite education. And as the different times, the university life becomes enriched. Caused by a problem is the contemporary many college students to learn lost interest. Under such a background, it is necessary for us to explore how factors which will affect the students' learning achievement. The in based on the existing student achievement, through the SPSS software by statistical variance analysis, correlation analysis and regression analysis theory, the impact on the students learning results were studied. Due to the limitation of the collected data. In this paper, to learn Types of courses grades, the number of course, hanging branches number and class four factors for analysis. First of all, data integration, using the above mentioned statistical methods, on related factors were significant test. Secondly, for the results generated by the SPSS to carry out statistical analysis, judge what factors on students' academic performance had a significant impact, influence and how. The results of the study show that: the above four factors, the types of courses, hanging branches number for the class of 2015 statistics majors learning achievement effect is significant. And for enrollment number, class of this two factors by inspection, we found them on the results Very weak influence, in statistics, we can think their relationship between student achievement and no significant. The research results can give some reference to the teachers, in order to facilitate the timely adjustment of teaching methods, textbook for screening. For students can understand self defects and corrected, conducive to performance improved.Key words: achievement influence factor, correlation analysis, regression analysis, variance analysis目录摘要 (2)Abstract (3)目录 (4)第一章绪论 (6)1.1研究综述 (6)1.2 主要研究内容 (7)第二章方差分析、相关分析与回归分析理论 (8)2.1相关关系的描述与测度 (8)2.1.1相关系数 (8)2.1.2相关关系的显著性检验 (8)2.2线性回归 (8)2.2.1 多元回归模型 (8)2.2.4 参数的最小二乘估计 (9)2.2.5 回归方程的拟合优度 (9)2.2.6 显著性检验 (10)2.2.7回归系数检验 (10)2.2.8多重共线性 (11)2.3 方差分析 (11)2.3.1 方差分析中的基本假定 (11)2.3.2 单因素方差分析 (11)第三章数据分析 (14)3.1 实例基础数据 (14)3.2 基于SPSS的方差分析 (14)3.2.1学生考试成绩与课程种类的单因素方差分析 (14)3.2.1为待分析数据的部分例举 (15)3.2.2 学生考试成绩加权平均数与挂科数目的单因素方差分析 (16)该分析包括如下的过程 (16)3.2.3 学生考试成绩加权平均数与班级的单因素方差分析 (18)该分析包括如下的过程 (18)3.2.4 学生考试成绩加权平均数与学生选课数量的单因素方差分析.. 19该分析包括如下的过程 (19)3.3 基于SPSS的相关性分析 (21)3.3.1 学生考试分数与课程种类的相关性分析 (21)3.3.2 学生考试成绩加权平均数与挂科数目的相关性分析 (22)3.3.3学生考试成绩加权平均数与班级的相关性分析 (23)3.3.4 学生考试成绩加权平均数与学生选课数目的相关性分析 (24)3.4 基于SPSS的线性回归分析 (25)3.4.1 学生成绩与课程种类的一元线性回归分析 (25)3.4.2 学生考试成绩加权平均数与选课数量、挂科数目、班级的多元线性回归模型 (29)第四章总结与展望 (31)参考文献 (32)致谢 (33)第一章绪论1.1研究综述大学教育不仅对大学生个人前途具有重大影响而且也关系到祖国未来的繁荣发展,所以对于大学生的教育我们必须给予极大的重视.然而经过多年的扩招,且本科院校的教学质量水平参差不齐,现在的大学相比于以往教学质量有所下降.而且随着科学的进步,越来越多的高科技产品受到了大学生的青睐,就智能手机来说,我们大学课堂的学生都变成了低头党,这严重的影响了课堂的纪律和氛围.另外,五花八门的电脑游戏,深深的毒害着学生的身心健康,包夜打游戏、逃课打游戏等等已经成了大学生的“大学生活”.所以现在的一部分大学生在某种程度上可以说早已对学习失去了激情.那么最直接的影响就是导致高的失业率.大学成绩的优秀与否对一个学生的影响是非常重要的.因此,对学生学习成绩影响因素的研究不仅对大学生的发展与成才具有重要的指引作用,而且有助于提高高校的教学质量和培养高素质人才.学术界对影响大学生的学习因素也是非常关注:张志红,耿兴芳[1]对学习态度对大学生学习成绩的影响进行了实证分析.该文以问卷调查的形式,将学习态度分为平时的学习表现、对自己专业的偏好程度、考试态度以及对课堂交流或讨论的学习方式的看法等4 个子系统,进一步建立带有虚拟变量的4 个模型,逐一分析子系统内部因素对学习成绩的影响.结果表明,科学的学习态度能够有效提高学习成绩,采用课堂交流或讨论的学习方式是最有效的提高学习成绩的途径,通过积极、主动、认真学习也能较大程度上促进学习成绩的飞跃.文献[2]指出:大学生的学习与成长过程, 是一个智力与非智力因素交互作用的过程, 在这一过程中, 非智力因素起着重要的作用.培养大学生非智力因素的途径是: 加强对入学新生的始业教育; 大力加强校园文化建设, 发挥校园文化在非智力建设中的载体作用; 为大学生非智力因素的培养构筑一个全体教育者共同参与的平台.河北农业大学与河北师范大学[2]对大学生学习成绩规律进行了研究,通过对各学期间成绩的相关性得出结论:相邻学期间在高年级中表现出强相关性;大学第一学期对各个学期的影响显著,非相邻学期间的影响随时间间隔的加大在减弱;不同类别相同学期间的相关性存在差异.哈尔滨理工大学理学院和哈尔滨师范大学经管学院[2]对大学生成绩影响因素进行了分析,该文运用主成分分析方法,对学生的基础课成绩进行分析,最终得出第一主成分是学生的学习兴趣和态度,第二主成分是家庭文化背景,第三主成分是学习动机和学习焦虑.中北大学数学系孔慧华和潘晋孝[2]对大学生的学习成绩进行了研究.该文对中北大学毕业生的32门必修课成绩进行分析,通过主成分分析找出第一二三主成分并排序,通过聚类分析将按中北大学毕业生学习成绩,将学生分为四类即综合成绩优秀,综合成绩,计算机成绩不太好但体育成绩良好,和综合成绩良好.1.2 主要研究内容(1)对现有的数据经过加之后,本文首先对影响学生成绩的四个因素进行单因素方差分析,以此来判断哪些因素对学生成绩是否产生了显著的影响.(2)其次,本文对以上所列出的四个因素进行相关性分析,来推断哪些因素与学生成绩之间具有线性关系,且会具有怎样的线性性态.(3)最后,本文所进行的是回归分析,通过回归分析我们可以进一步的判断出与因变量具有线性关系的自变量,且可以给出回归方程.(4)通过对影响学生成绩因素所进行的以上三种分析,我们将可以综合来判断哪些因素对学生成绩产生了影响,从而达到研究目的.第二章 方差分析、相关分析与回归分析理论2.1相关关系的描述与测度2.1.1相关系数相关系数是根据样本数据计算的度量两个变量之间线性关系强度的统计量.若相关系数是根据总体全部数据计算的,称为总体相关系数;若是根据样本数据计算的,则称为样本相关系数.样本相关系数的计算公式为: r=∑∑∑∑∑∑∑-•--2222)()(y y n x x n yx xy n为解释相关系数各数值的含义,首先对相关系数的性质总结如下.(1)r 的取值范围是[-1,1].若0<r ≤1,表明x 与y 之间存在正线性相关系;有-1≤r<0,表明x 与y 之间存在负线性相关关系;若r =1,表明x 与y 之间为函数关系,y 的取值完全依赖于x ;当r=0时,二者之间不存在线性相关关系.(2)r 仅仅是x 与y 之间线性关系的一个度量,它不能用于描述非线性关系.这意味着,r=0只表示两个变量之间不存在线性相关关系,并不说明变量之间没有任何关系,它们之间可能存在非线性相关关系,当r=0或很小时,应该结合散点图做出合理的解释(3)R 虽然是两个变量之间线性关系的一个度量,却不一定意味着x 与y 一定有因果关系.当r ≥0.8时,可视为高度相关;0.5≤r <0.8时,可视为中度相关;0.3≦r <0.5时,视为低度相关.2.1.2相关关系的显著性检验费希尔提出的t 检验:第一步:提出假设.第二步:计算检验的统计量. t=212rn r --~)2(-n t 第三步:进行决策.根据显著性水平α和自由度2-=n df 查t 分布表,得出)2(2-n t α的临界值.若αt t >,则拒绝原假设0H ,表明总体的两个变量之间存在显著的线性关系.2.2线性回归2.2.1 多元回归模型:设因变量y ,k 个自变量为x 1,x 2,x 3,…x k ,描述因变量如何依赖于自变量x 1,x 2,x 3,…x k 和误差项ε的方程称为多元回归模型.其一般形式可表示为:εββββ+++++=k k x x x y 22110式中,k ββββ,,,,210 是模型的参数;ε为误差项.2.2.2 多元回归方程:根据回归模型的假定有()k k x x x y ββββ++++=E 22110,该式称为多元回归方程,它描述了因变量y 的期望值与自变量k x x x ,,,21 之间的关系.2.2.3 估计的回归方程:回归方程中的参数是未知的,需要利用样本数据取估计它们.当用样本统计量∧∧∧∧k ββββ,,,,210 去估计回归方程中的未知参数k ββββ,,,,210 时,就得到了估计的多元回归方程,其一般形式为: k x x x y∧∧∧∧∧++++=ββββ 22110 2.2.4 参数的最小二乘估计回归方程中的k ∧∧∧∧ββββ,,,,210 是根据最小二乘法求得,也就是使残差平方和 21102∑∑⎪⎭⎫ ⎝⎛----=⎪⎭⎫ ⎝⎛-=∧∧∧∧k k i i i x x y y y Q βββ 最小.由此可以得到求解k ∧∧∧∧ββββ,,,,210 的标准方程组为:⎪⎪⎩⎪⎪⎨⎧=∂∂=∂∂∧∧==00000ββββββQQ i i i k i ,2,1= 求解上述方程组,可得到回归结果. 2.2.5 回归方程的拟合优度多重判定系数:多重判定系数是多元回归中的回归平方和占总平方和的比例,它是度量多元回归方程拟合优度的一个统计量,它反映了在因变量y 的变差中被估计的回归方程所解释的比例.多从判定系数如下: SSTSSR SST SSR R -==12 调整的多重判定系数为:⎪⎭⎫ ⎝⎛-----=11)1(122k n n R R a 在多元回归分析中,通常用调整的多重判定系数.(SSR SSE SST +=;2)(y y SST i -=∑为总平方和;2)(y y SSR i -=∧∑为回归平方和;2)(i i y y SSE ∧-=∑为残差平方和.)2.2.6 显著性检验线性关系检验:线性关系检验是检验因变量y 与k 个自变量之间的关系是否显著,也成为总体显著性检验.检验的具体步骤如下.第一步:提出假设. 0:210====k H βββk H βββ,,,:211 至少有一个不等于0第二步:计算检验的统计量F )1(--=k n SSE k SSR F ~)1,(--k n k F 第三步:作出统计决策.给定显著性水平α,根据分子自由度=k ,分母自由度=1--k n 查F 分布表得αF .若αF F >,则拒绝原假设;若αF F <,则不拒绝原假设.根据计算机输出的结果,克直接利用P 值作出决策:α<P ,则拒绝原假设;若α>P ,则不拒绝原假设.2.2.7回归系数检验在回归方程通过线性关系检验后,就可以对各个回归系数i β有选择的进行一次货多次的检验.但究竟要对那几个回归系数进行检验,通常在建立模型之前作出决策,此外,还应对回归系数的个数进行限制,一面犯过多的第I 类错误. 回归系数检验的具体步骤如下:第一步:提出假设.对于任意参数i β(i=1,2,…k ),有0H :0=i β1H :0≠i β第二步:计算检验的统计量t . ∧∧=ββs i i t ~)1(--k n t式中,∧βs 是回归系数∧i β的抽样分布的标准差,即∑-=∧22)(1i i x n x s s τβ第三步:做出统计决策.给定显著性水平α,根据自由度1--=k n 查t 分布表,得2αt 的值,若2αt t >,则拒绝原假设;若2αt t <,则不拒绝原假设. 2.2.8多重共线性(1)多重共线性及其所产生的问题:当回归模型中两个货两个以上的自变量彼此相关时,则称回归模型中存在多重共线性.而回归模型中使用两个或两个以上的自变量时,这些自变量往往会提供多余的信息.在实际问题中,所使用的自变量之间存在相关是比较常见的,但是在回归分析中存在多重共线性时将会产生某些问题.首先,变量之间高度相关时,可能会使回归的结果混乱,甚至会把分析引入歧途;其次多重共线性可能对参数估计值的正负号产生影响,特别是i β的正负号有可能同预期的正负号相反.(2)多重共线性的判别:具体来说,如果出现以下情况,表示可能存在多重共线性:①模型中各对自变量之间显著相关②当模型的线性关系检验(F 检验)显著时,几乎所有回归系数i β的t 检验却不显著.③回归系数的正负号与预期的相反.④容忍度与发叉扩大因子.容忍度越小,多重共线性月严重;方差扩大因子越大,(3)多重共线性问题的处理下面给出多重共线性问题的解决办法:①将一个或多个相关的自变量从模型中剔除,使保留的自变量尽量不相关. ②如果要在模型中保留所有的自变量,那就应该: ·避免根据t 统计量对单个参数β进行检验·对因变量y 值的推断(估计或预测)限定在自变量样本值的范围内. 2.3 方差分析2.3.1 方差分析中的基本假定 方差分析中有三个基本假定: (1)每个总体都应服从正态分布. (2) 各个总体的方差2σ必须相同. (3) 观测值是独立的 2.3.2 单因素方差分析(1)提出假设在方差分析中,原假设所描述的是在按照自变量的取值分成的类中,因变量的均值相等 .因此检验因素的k 个水平(总体)上午均值是否相等,需要提出如下形式的假设:k i H μμμμ===== 210: 自变量对因变量没有影响 ),,2,1(:1k i H i =μ 自变量对因变量有显著影响 式中,i μ为第i 个总体的均值.如果拒绝原假设0H ,则意味着自变量对因变量有显著影响;如果不拒绝原假设0H ,则没有证据表明自变量对因变量有显著影响,也就是说,不能认为自变量与因变量之间有显著关系. (2)构造检验的统计量 总平方和:211)(∑∑==-=k i n j ij ix x SST ;组间平方和:21)(x x n SSA i ki i -=∑=组内平方和:211)(∑∑==-=ki n j i ij ix x SSE ;组间方差:1-=k SSAMSA ; 组内方差:kn SSEMSE -=; 将上述MSE 和MSA 进行对比,即得到所需要的检验统计量F : MSEMSAF =~),1(k n k F -- (3)统计决策根据给定的显著性水平α,在F 分布表中查找与分子自由度1df 1-=k 、分母自由度k n df -=2相应的临界值),1(k n k F --α.若αF F >,则拒绝原假设k H μμμ=== 210:, 表明),2,1(k i i =μ之间有显著差异;若αF F <,则不拒绝原假设0H ,没有证据表明),,2,1(k i i =μ之间有显著差异;基于上述理论基础,结合我们自己的分析,在对学生成绩相关性进行分析主要有如下几点考虑:首先,通过大量的文献比较后了解到,大部分的学者所应用的方法为因子分析、聚类分析、主成分分析,对于应用方差分析、相关分析及回归分析的研究方法并不很广泛,本文希望在这方面进行一些尝试.其次,如何把该方法运用于成绩分析呢?一是要做好数据的修改,使得所修改的数据满足该方法,例如应用方差分析,数据必须满足因变量是数值型,自变量是分类型这个条件.二是要严格按照所选方法的要求在SPSS中组织数据,正确的组织数据,才能够得到准确的结果.最后,该方法的不足之处是不能够把因变量统一化.如在研究学生考试成绩与课程种类的单因素方差分析中,因变量是学生的各科考试成绩,研究学生考试成绩加权平均数与挂科数目的单因素方差分析中,因变量是成绩的加权平均数.但是这也是改进之处,虽然因变量不能够统一化,但都能够客观的反应学生考试成绩.第三章数据分析3.1 实例基础数据附件:15统计学最终成绩排名.xls3.2 基于SPSS的方差分析本文所采用的方差分析主要为单因素方差分析.首先,方差分析是通过检验各总体的均值是否相等来判断分类型自变量对数值型因变量是否有显著影响,而本文所研究的目的就是去判别课程种类、挂科数目、班级、选课数目着四个因素对学生成绩是否有显著影响,所以方差分析适用于本文的研究.其次,由于研究的侧重点不同,单因素方差分析相较于多因素方差分析更易于操作,目的性更加的明确,且相较于多因素方差分析,不用考虑有各个因素有无交互作用.在单因素方差分析中我们关键的一步为方差齐性检验,只有通过该检验,单因素的方差分析才具有意义.3.2.1学生考试成绩与课程种类的单因素方差分析该分析包括如下的过程(1)插入数据,如下图所示图3.1 不同课程分数在SPSS中的组织形式表3.2.1不同课程部分成绩举例学生考试成绩与课程种类的单因素方差分析的数据在SPSS中的组织形式如图3.1;表3.2.1为待分析数据的部分例举.(2)进行分析,实验结果如下表3.2.2 不同课程下学生考试分数的基本描述统计量及95%置信区间表3.2.3 不同课程的方差齐性检验结果表3.2.4 课程种类对学生考试分数的单因素方差分析结果ANOVA学生考试分数平方和df 均方 F 显著性组间3172.967 3 1057.656 37.153 .000组内3302.200 116 28.467总数6475.167 119表3.2.3为方差齐性检验,该检验主要的目的在于验证所选的数据是否满足2.3.2中所提到的基本假定.如果检验通过,该单因素方差分析才有实际意义.表3.2.4是课程种类与学生考试成绩的单因素方差分析结果,依据该表所给出的信息,可以得出相应的结论.(3)对以上的结果进行分析由表3.2.3可知,不同课程下的学生成绩的方差齐性检验值为0.257,概率值P-值为0.856,在显著性水平α为0.05下,由于概率P-值大于显著性水平,因此不应拒绝原假设,认为不同课程下的学生成绩总体方差无显著差异,满足方差分析的前提要求.由表3.2.4知,因变量学生考试分数的离差总平方和为6475.167;如果仅考虑课程种类单个因素的影响,则学生考试分数总变差中,课程种类的不同可解释的变差为3172.967,抽样误差引起的变差为3302.200,它们的方差分别为1057.656和28.467,相除所得的F统计量的观测值为37.153,对应的概率P-值近似为0.因此在显著性水平α为0.05下,由于概率P-值小于显著性水平α的值,因此应拒绝原假设,认为课程种类的不同对学生考试分数产生了显著的影响.3.2.2 学生考试成绩加权平均数与挂科数目的单因素方差分析该分析包括如下的过程(1)插入数据,如下图所示表3.2.5 不同挂科数下学生考试成绩加权平均数的部分举例表3.2.5为样本数据的部分例举.(2)进行分析,实验结果如下表3.2.6 不同挂科数下学生考试成绩加权平均数的基本描述统计量及95%置信区 间描述学生考试成绩加权平均数N均值 标准差 标准误 均值的 95% 置信区间极小值 极大值 下限 上限 .00 71 82.4211 3.59243 .42634 81.5708 83.2714 72.3889.85 1.00 8 75.5100 3.050851.0786472.959478.060671.91 80.33 2.00 1 70.7300 . . . . 70.73 70.73 总数8081.58394.25642.4758880.636782.531170.7389.85表3.2.7不同挂科数的方差齐性检验结果表3.2.8 挂科数对学生考试成绩加权平均数的 单因素方差分析结果数据分析操作过程如3.2.1节所述,以下的单因素方差分析在此不再进行赘述. (3)对以上的结果进行分析如同3.2.1节的分析一样,我们通过表3.2.7可知不同的挂科数目下,学生考试成绩加权平均数的方差齐性检验值为0.189,概率P-值为0.665.在显著性水平 为ANOVA学生考试成绩加权平均数平方和 df均方 F 显著性组间 462.713 2 231.356 18.393.000组内 968.541 77 12.578总数 1431.253790.05下,由于概率P-值大于显著性水平,因此不应拒绝原假设,认为不同挂科数目下的学生考试成绩的加权平均数的总体方差无显著差异,满足方差分析的前提条件.根据表3.2.8可知,因变量学生考试成绩加权平均数的离差平方总和为1431.253;如果仅考虑挂科数目单个因素的影响,则考试成绩的加权平均数的总变差中,不同的挂科数目可解释的变差为462.713;抽样误差引起的变差为968.541,它们的方差分别为231.356和12.578,相除所得的F统计量的观测值为18.393,对应的P-值近似为0,在显著性水平 为0.05下,由于概率P-值小于显著性水平,因此拒绝原假设,认为挂科数目的不同对学生考试成绩产生了显著的影响.3.2.3 学生考试成绩加权平均数与班级的单因素方差分析该分析包括如下的过程(1)插入数据,如下图所示表3.2.9 不同班级下学生考试成绩加权平均数的部分举例表3.2.9为样本数据的部分例举(2)进行分析,实验结果如下表3.2.10不同班级下学生考试成绩加权平均数的基本描述统计量及95%置信间表3.2.11 不同班级的方差齐性检验结果方差齐性检验学生考试成绩加权平均数Levene 统计量df1 df2 显著性.455 1 78 .502表3.2.12 班级对学生考试成绩加权平均数的单因素方差分析结果ANOVA学生考试成绩加权平均数平方和df 均方 F 显著性组间 6.956 1 6.956 .381 .539组内1424.297 78 18.260总数1431.253 79(3)对以上的结果进行分析如同3.2.1、中的分析,我们通过表3.2.111可知不同的班级下,学生考试成绩加权平均数的方差齐性检验值为0.455,概率P-值为0.502.在显著性水平α为0.05下,由于概率P-值大于显著性水平,因此不应拒绝原假设,认为不同的班级下的学生考试成绩的加权平均数的总体方差无显著差异,满足方差分析的前提要求.根据表3.2.12的结果我们可知,因变量学生考试成绩加权平均数的离差平方总和为1431.253;如果仅考虑班级单个因素的影响,则考试成绩的加权平均数的总变差中,班级的不同可解释的变差为6.956;抽样误差引起的变差为1424.297,它们的方差分别为6.956和18.260,相除所得的F统计量的观测值为0.381,对应的P-值近似为0.539,在显著性水平α为0.05下,由于概率P-值大于显著性水平,因此不应拒绝原假设,认为班级的不同对学生考试成绩没有产生显著的影响.3.2.4 学生考试成绩加权平均数与学生选课数量的单因素方差分析该分析包括如下的过程(1)插入数据,如下图所示表3.2.13不同选课数量数下学生考试成绩加权平均数的部分举例表3.2.13为样本数据的部分例举.(2)进行分析,实验结果如下表3.2.14 不同选课数量下学生考试成绩加权平均数的基本描述统计量及95%置表3.2.15不同选课数量的方差齐性检验结果表3.2.16 选课数量对学生考试成绩加权平均数的单因素方差分析结果(3)对以上的结果进行分析如同以上的分析,由表3.2.19可知选课数不同的情况下的学生考试成绩的加权平均数的方差检验值为0.362,概率P-值为0.549.在显著性水平α为0.05时,由于概率P-值大于显著性水平,因此不应拒绝原假设,认为不同的选课数下的学生考试成绩的加权平均数的总体方差无显著差异,满足方差分析的前提要求.由表3.2.20可知,因变量学生考试成绩分数的加权平均数的离差平方总和为1431.253;如果仅考虑选课数单个因素的影响,则因变量总变差中,不同选课数可解释的变差为20.395,抽样误差引起的变差为1410.859,它们的方差分别为20.395和18.088,相除所得的F统计量的观测值为1.128,对应的概率P-值为0.292.在显著性水平α为0.05时,由于概率P-值大于显著性水平α,因此不能拒绝原假设,认为不同的选课数目对学生考试成绩没有产生显著地影响.3.3 基于SPSS的相关性分析相关性分析是对两个变量之间线性关系的描述与度量.通过单因素方差分析我们可以初步的确定哪些因素对学生成绩产生了影响.为了排除偶然性,我们进行相关分析,目的在于进一步的确定哪些因素对学生成绩产生了显著地影响并判断它们之间呈现怎样的性态.所以在以下的分析中,本文用到了相关性分析.在该方法运用之前,我们首先进行的是在SPSS中组织数据.经过研究发现,相关性分析与以上进行的单因素方差分析的数据组织形式完全相同,所以在以下的相关性分析中,插入数据这一步中本文没有再进一步的给出数据.3.3.1 学生考试分数与课程种类的相关性分析该分析包括如下的过程(1)插入数据如图3.1 不同课程分数在SPSS中的组织形式,表3.2.1 不同课程部分成绩举例(2)进行分析,实验结果如下。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
方差分析与相关性分析
方差分析和相关性分析都是统计学中常用的数据分析方法,用于探究
不同变量之间的关系以及其显著性。
它们在不同的研究领域和实际问题中
具有广泛的应用。
本文将详细介绍方差分析和相关性分析的概念、原理以
及应用。
一、方差分析:
1.概念:
方差分析(Analysis of Variance, ANOVA)是一种用于比较两个或
多个组均值之间差异的统计方法。
它通过分析组间差异与组内差异的相对
贡献,来判断不同因素对总体均值的影响是否显著。
2.原理:
方差分析的原理基于样本均值之间的差异分解。
它将总体均值的差异
分解为组间差异和组内差异两部分。
组间差异反映了不同因素对总体均值
的影响,而组内差异则反映了个体间的随机误差。
3.应用:
方差分析广泛应用于实验设计和质量管理等领域。
例如,在医学研究中,研究人员可以使用方差分析来比较不同治疗方法的疗效;在工程领域,可以利用方差分析来评估不同生产批次之间的差异性;在社会科学研究中,可以使用方差分析来分析不同教育水平对工资的影响等。
二、相关性分析:
1.概念:
2.原理:
相关性分析的原理基于协方差和标准差的计算。
它衡量了两个变量之间的线性关系程度。
相关性系数的取值范围是-1到1,其中-1表示完全负相关,1表示完全正相关,0表示无相关关系。
3.应用:
相关性分析广泛应用于经济学、社会科学和自然科学等领域。
例如,在经济学中,研究人员可以使用相关性分析来分析不同经济指标之间的关系,如GDP与通货膨胀率的相关性;在社会科学研究中,可以使用相关性分析来分析不同个体之间的关系,如年龄与收入的相关性等。
总结:
方差分析和相关性分析是统计学中常用的数据分析方法。
方差分析主要用于比较两个或多个组均值之间的差异,通过分析组间差异和组内差异的相对贡献,来判断不同因素对总体均值的影响是否显著。
相关性分析则用于研究变量之间的关系强度和方向,通过计算相关性系数来量化变量之间的相关程度。
这两种分析方法在不同领域和实际问题中都具有重要的应用价值,可以帮助研究人员深入探索数据背后的关系,并为决策提供科学依据。
