2018-2019学年高中数学第二章圆锥曲线与方程2-4-2抛物线的几何性质作业苏教版选修1-1
2019高中数学 第2章 圆锥曲线与方程 2.3.2 双曲线的几何性质作业 苏教版选修2-1

2.3.2 双曲线的几何性质[基础达标]1.双曲线x 216-y 29=1的两条渐近线的方程为________.解析:由双曲线方程可知a =4,b =3,所以两条渐近线方程为y =±34x .答案:y =±34x2.已知双曲线C 1:x 2a 2-y 2b 2=1(a >0,b >0)与双曲线C 2:x 24-y 216=1有相同的渐近线,且C 1的右焦点为F (5,0),则a =________,b =________.解析:双曲线x 24-y 216=1的渐近线为y =±2x ,则b a=2,即b =2a ,又c =5,a 2+b 2=c 2,所以a =1,b =2.答案:1 23.双曲线的实轴长与虚轴长之和等于其焦距的2倍,且一个顶点的坐标为(0,2),则双曲线的标准方程是________.解析:由题意得2a +2b =22c ,即a +b =2c ,又因为a =2,所以b =2c -2,所以c 2=a 2+b 2=4+b 2=4+(2c -2)2,即c 2-42c +8=0,所以c =22,b =2,所求的双曲线的标准方程是y 24-x 24=1.答案:y 24-x 24=14.设双曲线x 2a 2-y 29=1(a >0)的渐近线方程为3x ±2y =0,则a 的值为________.解析:渐近线方程可化为y =±32x .∵双曲线的焦点在x 轴上,∴9a 2=(±32)2,解得a =±2,由题意知a >0,∴a =2.答案:25.已知双曲线C 经过点(1,1),它的一条渐近线方程为y =3x ,则双曲线C 的标准方程是________.解析:设双曲线的方程为y 2-3x 2=λ(λ≠0),将点(1,1)代入可得λ=-2,故双曲线C 的标准方程是x 223-y 22=1.答案:x 223-y 22=16.已知双曲线x 29-y 216=1的右顶点为A ,右焦点为F .过点F 作平行于双曲线的一条渐近线的直线与双曲线交于点B ,则△AFB 的面积为________.解析:由题意求出双曲线中a =3,b =4,c =5,则双曲线渐近线方程为y =±43x ,不妨设直线BF 斜率为43,可求出直线BF 的方程为4x -3y -20=0①,将①式代入双曲线方程解得y B =-3215,则S △AFB =12AF ·|y B |=12(c -a )·3215=3215.答案:32157.已知双曲线x 2a 2-y 2b2=1(a >0,b >0)的两条渐近线均和圆C :x 2+y 2-6x +5=0相切,且双曲线的右焦点为圆C 的圆心,则该双曲线的方程为________.解析:双曲线的渐近线方程为bx +ay =0和bx -ay =0,圆心为(3,0),半径r =2.由圆心到直线的距离为r =|3b |a 2+b2=2,所以4a 2=5b 2,又双曲线的右焦点为圆C 的圆心,所以c =3,即9=a 2+b 2,a 2=5,b 2=4.故所求双曲线的方程为x 25-y 24=1.答案:x 25-y 24=18.如图,双曲线x 2a 2-y 2b2=1(a ,b >0)的两顶点为A 1,A 2,虚轴两端点为B 1,B 2,两焦点为F 1,F 2.若以A 1A 2为直径的圆内切于菱形F 1B 1F 2B 2,切点分别为A ,B ,C ,D .则(1)双曲线的离心率e =________;(2)菱形F 1B 1F 2B 2的面积S 1与矩形ABCD 的面积S 2的比值S 1S 2=________.解析:(1)由题意可得a b 2+c 2=bc ,∴a 4-3a 2c 2+c 4=0,∴e 4-3e 2+1=0,∴e 2=3+52,∴e =1+52. (2)设sin θ=b b 2+c 2,cos θ=c b 2+c 2,S 1S 2=2bc 4a 2sin θcos θ=2bc 4a 2·bc b 2+c 2=b 2+c 22a 2=e 2-12=2+52.答案:(1)1+52 (2)2+529.已知F 1、F 2是双曲线x 2a 2-y 2b2=1(a >0,b >0)的左、右焦点,过F 1且垂直于x 轴的直线与双曲线的左支交于A ,B 两点,若△ABF 2是正三角形,试求该双曲线的离心率.解:由△ABF 2是正三角形,则在Rt △AF 1F 2中,有∠AF 2F 1=30°,∴AF 1=12AF 2,又AF 2-AF 1=2a ,∴AF 2=4a ,AF 1=2a ,又F 1F 2=2c ,又在Rt △AF 1F 2中有AF 21+F 1F 22=AF 22,即4a 2+4c 2=16a 2,∴e = 3.10.设双曲线x 2a 2-y 2b2=1(a >1,b >0)的焦距为2c ,直线l 过(a ,0)、(0,b )两点,且点(1,0)到直线l 的距离与点(-1,0)到直线l 的距离之和s ≥45c ,求双曲线的离心率e 的取值范围.解:直线l 过(a ,0)、(0,b )两点,得到直线方程为bx +ay -ab =0.由点到直线的距离公式,且a >1,得点(1,0)到直线l 的距离为d 1=(a -1)ba 2+b2, 同理得到点(-1,0)到直线l 的距离为d 2=(a +1)b a 2+b 2,由s ≥45c 得到2ab c ≥45c ①.将b 2=c 2-a 2代入①式的平方,整理得4c 4-25a 2c 2+25a 4≤0,两边同除以a 4后令c 2a2=x ,得到4x 2-25x +25≤0,解得54≤x ≤5,又e =c a =x ,故52≤e ≤ 5.[能力提升]1.设直线l 过双曲线C 的一个焦点,且与C 的一条对称轴垂直,l 与C 交于A ,B 两点,AB 为C 的实轴长的2倍,则C 的离心率为________.解析:设双曲线的标准方程为x 2a 2-y 2b2=1(a >0,b >0),由于直线l 过双曲线的焦点且与对称轴垂直,因此直线l 的方程为l :x =c 或x =-c ,代入x 2a 2-y 2b 2=1得y 2=b 2⎝ ⎛⎭⎪⎫c 2a 2-1=b 4a2,∴y =±b 2a ,故AB =2b2a,依题意2b 2a =4a ,∴b 2a 2=2,∴c 2-a 2a2=e 2-1=2,∴e = 3.答案: 32.已知椭圆C 1:x 2a 2+y 2b 2=1(a >b >0)与双曲线C 2:x 2-y 24=1有公共的焦点,C 2的一条渐近线与以C 1的长轴为直径的圆相交于A ,B 两点,若C 1恰好将线段AB 三等分,则b 2=________.解析:C 2的一条渐近线为y =2x ,设渐近线与椭圆C 1:x 2a 2+y2b 2=1(a >b >0)的交点分别为C (x 1,2x 1),D (x 2,2x 2),则OC 2=x 21+4x 21=⎝ ⎛⎭⎪⎫a 32,即x 21=a 245,又由C (x 1,2x 1)在C 1:x 2a 2+y 2b 2=1上,所以有145+4a245b2=1,①又由椭圆C 1:x 2a 2+y 2b 2=1(a >b >0)与双曲线C 2:x 2-y 24=1有公共的焦点可得a 2-b 2=5,②由①②可得b 2=12.答案:123.已知双曲线的中心在原点,焦点F 1、F 2在坐标轴上,离心率为2,且过点M (4,-10). (1)求双曲线方程;(2)若点N (3,m )在双曲线上,求证:NF 1→·NF 2→=0; (3)求△F 1NF 2的面积.解:(1)∵e =2,故可设等轴双曲线的方程为x 2-y 2=λ(λ≠0), ∵过点M (4,-10),∴16-10=λ,∴λ=6. ∴双曲线方程为x 26-y 26=1.(2)证明:由(1)可知:在双曲线中,a =b =6,∴c =2 3. ∴F 1(-23,0),F 2(23,0). ∴NF 1→=(-23-3,-m ),NF 2→=(23-3,-m ). ∴NF 1→·NF 2→=[(-23-3)·(23-3)]+m 2=-3+m 2.∵点N (3,m )在双曲线上,∴9-m 2=6,∴m 2=3. ∴NF 1→·NF 2→=0.(3)∵△F 1NF 2的底F 1F 2=43,高h =|m |=3,∴△F 1NF 2的面积S =6.4.P (x 0,y 0)(x 0≠±a )是双曲线E :x 2a 2-y 2b2=1(a >0,b >0)上一点,M ,N 分别是双曲线E的左,右顶点,直线PM ,PN 的斜率之积为15.(1)求双曲线的离心率;(2)过双曲线E 的右焦点且斜率为1的直线交双曲线于A ,B 两点,O 为坐标原点,C 为双曲线上一点,满足OC →=λOA →+OB →,求λ的值.解:(1)由点P (x 0,y 0)(x 0≠±a )在双曲线x 2a 2-y 2b 2=1上,有x 20a 2-y 20b2=1.由题意有y 0x 0-a ·y 0x 0+a =15,可得a 2=5b 2,c 2=a 2+b 2=6b 2,e =c a =305.(2)联立⎩⎪⎨⎪⎧x 2-5y 2=5b 2,y =x -c ,得4x 2-10cx +35b 2=0.设A (x 1,y 1),B (x 2,y 2),则⎩⎪⎨⎪⎧x 1+x 2=5c2,x 1x 2=35b 24.① 设OC →=(x 3,y 3),OC →=λOA →+OB →,即⎩⎪⎨⎪⎧x 3=λx 1+x 2,y 3=λy 1+y 2.又C 为双曲线上一点,即x 23-5y 23=5b 2,有(λx 1+x 2)2-5(λy 1+y 2)2=5b 2.化简得λ2(x 21-5y 21)+(x 22-5y 22)+2λ(x 1x 2-5y 1y 2)=5b 2.② 又A (x 1,y 1),B (x 2,y 2)在双曲线上,所以x 21-5y 21=5b 2,x 22-5y 22=5b 2.由①式又有x 1x 2-5y 1y 2=x 1x 2-5(x 1-c )(x 2-c )=-4x 1x 2+5c (x 1+x 2)-5c 2=10b 2, ②式可化为λ2+4λ=0,解得λ=0或λ=-4.。
2019_2020学年高中数学第2章圆锥曲线与方程2.4.2抛物线的几何性质讲义苏教版选修2_1
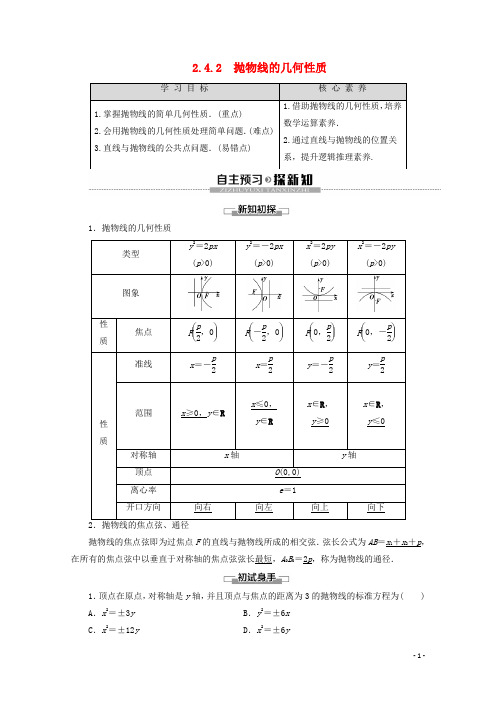
2.4.2 抛物线的几何性质学习目标核心素养1.掌握抛物线的简单几何性质.(重点)2.会用抛物线的几何性质处理简单问题.(难点)3.直线与抛物线的公共点问题.(易错点)1.借助抛物线的几何性质,培养数学运算素养.2.通过直线与抛物线的位置关系,提升逻辑推理素养.1.抛物线的几何性质类型y2=2px(p>0)y2=-2px(p>0)x2=2py(p>0)x2=-2py(p>0)图象性质焦点F⎝⎛⎭⎪⎫p2,0F⎝⎛⎭⎪⎫-p2,0F⎝⎛⎭⎪⎫0,p2F⎝⎛⎭⎪⎫0,-p2性质准线x=-p2x=p2y=-p2y=p2范围x≥0,y∈Rx≤0,y∈Rx∈R,y≥0x∈R,y≤0对称轴x轴y轴顶点O(0,0)离心率e=1开口方向向右向左向上向下抛物线的焦点弦即为过焦点F的直线与抛物线所成的相交弦.弦长公式为AB=x1+x2+p,在所有的焦点弦中以垂直于对称轴的焦点弦弦长最短,A0B0=2p,称为抛物线的通径.1.顶点在原点,对称轴是y轴,并且顶点与焦点的距离为3的抛物线的标准方程为( ) A.x2=±3y B.y2=±6xC.x2=±12y D.x2=±6yC [由题意知抛物线方程为x 2=±2py ,且p2=3,即p =6,因此抛物线方程为x 2=±12y .]2.过抛物线y 2=4x 的焦点作直线交抛物线于A (x 1,y 1),B (x 2,y 2)两点,若x 1+x 2=6,则|AB |=( )A .10B .8C .6D .4 B [|AB |=x 1+x 2+p =6+2=8.]3.过抛物线y 2=4x 的焦点F 做垂直于抛物线对称轴的直线,交抛物线于A ,B 两点,则线段AB 的长为________.4 [易知线段AB 为抛物线的通径,所以AB =4.]4.已知过抛物线y 2=4x 的焦点F 的直线交该抛物线于A ,B 两点,|AF |=2,则|BF |=________.2 [F (1,0),由抛物线定义得A 点横坐标为1. ∴AF ⊥x 轴,∴|BF |=|AF |=2.]依据性质求抛物线标准方程【例1】 (1)已知双曲线C 1:a 2-b2=1(a >0,b >0)的离心率为2.若抛物线C 2:x 2=2py (p >0)的焦点到双曲线C 1的渐近线的距离为2,则抛物线C 2的方程为________.(2)已知抛物线的焦点F 在x 轴正半轴上,直线l 过F 且垂直于x 轴,l 与抛物线交于A ,B 两点,O 是坐标原点,若△OAB 的面积等于4,则此抛物线的标准方程为________.(1)x 2=16y (2)y 2=42x [(1)∵双曲线C 1:x 2a 2-y 2b 2=1(a >0,b >0)的离心率为2,∴ca=a 2+b 2a=2,∴b =3a ,∴双曲线的渐近线方程为3x ±y =0,∴抛物线C 2:x 2=2py (p >0)的焦点⎝ ⎛⎭⎪⎫0,p 2到双曲线的渐近线的距离为⎪⎪⎪⎪⎪⎪3×0±p 22=2,∴p =8.∴所求的抛物线方程为x 2=16y .(2)不妨设抛物线的方程为y 2=2px ,如图所示,AB 是抛物线的通径,∴AB =2p ,又OF =12p ,∴S △OAB =12·AB ·OF =12·2p ·12p =12p 2=4,故p =2 2. ∴所求抛物线方程为y 2=42x .]利用抛物线几何性质可以解决的问题1.对称性:解决抛物线的内接三角形问题. 2.焦点、准线:解决与抛物线的定义有关的问题. 3.范围:解决与抛物线有关的最值问题. 4.焦点:解决焦点弦问题.1.抛物线的顶点在原点,对称轴重合于椭圆9x 2+16y 2=144的短轴所在的直线,抛物线焦点到顶点的距离为3,则抛物线的标准方程为________.x 2=12y 或x 2=-12y [椭圆的方程可化为x 216+y 29=1,其短轴在y 轴上,∴抛物线的对称轴为y 轴,设抛物线的标准方程为x 2=2py 或x 2=-2py (p >0),由抛物线焦点到顶点的距离为3得p2=3,∴p =6.∴抛物线的标准方程为x 2=12y 或x 2=-12y .]与抛物线有关的最值问题【例2[思路探究] 本题的解法有两种:法一,设P (t ,-t 2)为抛物线上一点,点P 到直线的距离为d =|4t -3t 2-8|5,再利用二次函数求最小距离;法二,设直线4x +3y +m =0与直线4x +3y -8=0平行且与抛物线相切,求出m 的值后,再利用两平行线间的距离公式求最小距离.[解] 法一:设P (t ,-t 2)为抛物线上的点, 它到直线4x +3y -8=0的距离 d =|4t -3t 2-8|5=|3t 2-4t +8|5=15⎪⎪⎪⎪⎪⎪3⎝ ⎛⎭⎪⎫t -232-43+8 =15⎪⎪⎪⎪⎪⎪3⎝ ⎛⎭⎪⎫t -232+203=35⎝ ⎛⎭⎪⎫t -232+43.∴当t=23时,d 有最小值43.法二:如图,设与直线4x +3y -8=0平行的抛物线的切线方程为4x +3y +m =0,由⎩⎪⎨⎪⎧y =-x 2,4x +3y +m =0,消去y 得3x 2-4x -m =0, ∴Δ=16+12m =0,∴m =-43.∴最小距离为⎪⎪⎪⎪⎪⎪-8+435=2035=43.抛物线中最值的求解策略1.可借助于抛物线的有关知识转化为函数的最值求解,但要注意抛物线的范围. 2.当条件中有关于抛物线上的点P 到焦点F 的距离问题,一定要考虑抛物线的定义,注意点P 到F 的距离与点P 到准线距离的转化.2.已知直线l 1:4x -3y +6=0和直线l 2:x =-1,抛物线y 2=4x 上一动点P 到直线l 1和直线l 2的距离之和的最小值是________.2 [因为抛物线的方程为y 2=4x ,所以焦点坐标F (1,0),准线方程为x =-1,所以设P 到准线的距离为PB ,则PB =PF ,P 到直线l 1:4x -3y +6=0的距离为PA ,所以PA +PB =PA +PF ≥FD ,其中FD 为焦点到直线4x -3y +6=0的距离,所以FD =|4-0+6|32+42=105=2,所以距离之和最小值是2.]直线和抛物线的位置关系[1.直线与抛物线有哪几种位置关系? [提示] 相离,相切,相交 2.如何认识抛物线的焦点弦?[提示] 如图,AB 是抛物线y 2=2px (p >0)过焦点F 的一条弦,设A (x 1,y 1),B (x 2,y 2),AB 的中点M (x 0,y 0),相应的准线为l .(1)以AB 为直径的圆必与准线l 相切; (2)AB =2⎝ ⎛⎭⎪⎫x 0+p 2(焦点弦长与中点关系);(3)AB =x 1+x 2+p ;(4)若直线AB 的倾斜角为α,则AB =2psin 2α;如当α=90°时,AB 叫抛物线的通径,是焦点弦中最短的;(5)A ,B 两点的横坐标之积、纵坐标之积为定值,即x 1·x 2=p 24,y 1·y 2=-p 2;(6)1AF +1BF =2p.【例3】 已知过抛物线y 2=2px (p >0)的焦点F 的直线交抛物线于A ,B 两点,且AB =52p ,求AB 所在的直线方程.[思路探究] 求AB 所在直线的方程的关键是确定直线的斜率k ,利用直线AB 过焦点F ,AB =x 1+x 2+p =52p 求解.[解] 由题意可知,抛物线y 2=2px (p >0)的准线为x =-p2.设A (x 1,y 1),B (x 2,y 2),A ,B 到抛物线准线的距离分别为d A ,d B . 由抛物线的定义,知AF =d A =x 1+p 2,BF =d B =x 2+p2,于是AB =x 1+x 2+p =52p ,∴x 1+x 2=32p .当x 1=x 2=p 2时,AB =2p <52p ,故直线AB 与x 轴不垂直. 设直线AB 的方程为y =k ⎝ ⎛⎭⎪⎫x -p 2.由⎩⎪⎨⎪⎧y =k ⎝ ⎛⎭⎪⎫x -p 2,y 2=2px ,得k 2x 2-p (k 2+2)x +14k 2p 2=0,∴x 1+x 2=p (k 2+2)k 2,即p (k 2+2)k 2=32p ,解得k =±2.故直线AB 的方程为y =2⎝⎛⎭⎪⎫x -p 2或y =-2⎝ ⎛⎭⎪⎫x -p 2.1.直线与抛物线交点问题的解题思路判断直线与抛物线的交点个数时,一般是将直线与抛物线的方程联立消元,转化为形如一元二次方程的形式,注意讨论二次项系数是否为0.若该方程为一元二次方程,则利用判别式判断方程解的个数.2.抛物线的弦长求解思路当直线的斜率k 存在且k ≠0时,弦长公式为|AB |=1+k 2|x 1-x 2|=1+1k2|y 1-y 2|;当直线的斜率k =0时,只有抛物线的对称轴是y 轴时弦长存在,弦长公式为|AB |=|x 1-x 2|;当直线的斜率k 不存在时,只有抛物线的对称轴是x 轴时弦长存在,弦长公式为|AB |=|y 1-y 2|.3.斜率为1的直线经过抛物线y 2=4x 的焦点,与抛物线相交于A ,B 两点,求线段AB 的长.[解] 由题意知抛物线焦点为F (1,0),k AB =1,所以AB 的方程为y =x -1,代入y 2=4x 得(x -1)2=4x ,即x 2-6x +1=0,Δ=32>0,∴设A (x 1,y 1),B (x 2,y 2),则x 1+x 2=6,AB =AF +FB =x 1+x 2+2=8,∴线段AB 的长为8.1.讨论抛物线的几何性质,一定要利用抛物线的标准方程;利用几何性质,也可以根据待定系数法求抛物线的方程.2.直线与抛物线的相交弦问题共有两类,一类是过焦点的弦,一类是不过焦点的弦.解决弦的问题,大多涉及到抛物线的弦长、弦的中点、弦的斜率.常用的办法是将直线方程与抛物线方程联立,转化为关于x 或y 的一元二次方程,然后利用根与系数的关系,这样避免求交点,尤其是弦的中点问题,还应注意“点差法”的运用.1.判断(正确的打“√”,错误的打“×”) (1)抛物线关于顶点对称.( )(2)抛物线只有一个焦点,一条对称轴,无对称中心.( )(3)抛物线的标准方程虽然各不相同,但是其离心率都相同.( ) [答案] (1)× (2)√ (3)√2.若抛物线y 2=2x 上有两点A ,B 且AB 垂直于x 轴,若|AB |=22,则抛物线的焦点到直线AB 的距离为( )A.12B.14C.16D.18A [线段AB 所在的直线的方程为x =1,抛物线的焦点坐标为⎝ ⎛⎭⎪⎫12,0,则焦点到直线AB的距离为1-12=12.]3.若直线x -y =2与抛物线y 2=4x 交于A ,B 两点,则线段AB 的中点坐标是________. (4,2) [由⎩⎪⎨⎪⎧x -y =2y 2=4x得x 2-8x +4=0,设A (x 1,y 1),B (x 2,y 2),则x 1+x 2=8,y 1+y 2=x 1+x 2-4=4,故线段AB 的中点坐标为(4,2).]4.设直线y =2x +b 与抛物线y 2=4x 交于A ,B 两点,已知弦AB 的长为35,求b 的值.[解] 由⎩⎪⎨⎪⎧y =2x +b ,y 2=4x ,消去y ,得4x 2+4(b -1)x +b 2=0.由Δ>0,得b <12.设A (x 1,y 1),B (x 2,y 2).则x 1+x 2=1-b ,x 1x 2=b 24.∴|x 1-x 2|=(x 1+x 2)2-4x 1x 2=1-2b . ∴|AB |=1+22|x 1-x 2|=5·1-2b =35,∴1-2b =9,即b =-4.。
2018-2019学年高中数学第2章圆锥曲线与方程2.6.2求曲线的方程作业苏教版选修2-

课时作业在学生用书中,此内客单独成丘@262求曲线的方程[基础达标]1. _________ 已知椭圆的焦点是F i、F2, P是椭圆的一个动点,如果M是线段F i P的中点,则动点M 的轨迹是 ____ .解析:由图知PF + PF2= 2a.连结MO贝y F i M^ M@= a( a>F i C) •故M的轨迹是以F i、O为焦点的椭圆.答案:椭圆2. 已知动点M到A(2 , 0)的距离等于它到直线x=- i的距离的2倍,则点M的轨迹方程为________ •____________解析:设M(x, y),由题意,得(x —2) 2+ y2= 2| x+ i|.化简,得—3x2—i2x + y2= 0.答案:y2= 3x2+ i2x3. 已知动抛物线以y轴为准线,且过点(i , 0),则抛物线焦点的轨迹方程为_______________ •解析:设焦点坐标为(x, y),因动抛物线以y轴为准线,且过点(i , 0),根据抛物线的定义得:(x—i) 2+ y2= i(x>0),即(x —i)2+ y2= i(x> 0) •■ 2 2答案:(x—i) + y = i(x>0)4. 设圆C与圆x2+ (y —3)2= i外切,与直线y= 0相切,则C的圆心轨迹为____________ •解析:设圆C的半径为r,则圆心C到直线y= 0的距离为r.由两圆外切可得,圆心C到点(0 , 3)的距离为r + i,也就是说,圆心C到点(0 , 3)的距离比到直线y = 0的距离大i, 故点C到点(0 , 3)的距离和它到直线y =—i的距离相等,符合抛物线的特征,故点C的轨迹为抛物线.答案:抛物线5. 设动点P在直线x = i 上, O为坐标原点,以OP为直角边,点O为直角顶点作等腰Rt△ OPQ则动点Q的轨迹是 _______ •解析:设Qx, y), F(1 , y o),由OQ O R= 0 知y o y = —x.① 又由OQ= OP 得寸x2+ y2= 1 + y2,即x2+ y2= i + y0.② 由①②消去y°,得点Q的轨迹方程为y = i或y =—i.故动点Q的轨迹是两条平行线.答案:两条平行线6. 在平面直角坐标系中,A为平面内一个动点,B(2 , 0),若OA- B A= | 6»甲O为坐标原点),则动点A的轨迹是__________ •解析:设A(x, y),则OA= (x, y), B A= (x —2, y),因为6A B A= | O B,所以x(x—2)2 2 2+ y = 2,即(x—i) + y = 3,所以动点A的轨迹是圆.答案:圆7. 长度为i的线段AB在x轴上运动,点P(0 , i)与点A连结成直线PA点Q i , 2)与点B连结成直线QB则直线PA与QB交点的轨迹方程为______________ •解析:如图所示,设直线 PA 与QB 的交点为Mx , y ) • 再设 A (a , 0)( a z 0),贝U B (a + 1, 0) •由截距式得直线 PA 的方程为X + y = 1,即x + ay = a . a 1 3即 2x + ay - 2a - 2= 0.X + ay = a故点M 的坐标是方程组£ 的解,2x + ay - 2a - 2 = 0 消去参数a 得(2 - x ) y = 2, 故点M 的轨迹方程为(2 -x )y = 2. 答案:(2 - x ) y = 28. 曲线C 是平面内与两个定点 F( - 1, 0)和F 2(1 , 0)的距离的积等于常数 a 2( a > 1)的点 的轨迹.给出下列三个结论:① 曲线C 过坐标原点;② 曲线C 关于坐标原点对称;③ 若点P 在曲线C 上,则△ F 1PB 的面积不大于歹2. 其中,所有正确结论的序号是 __________ •解析:设曲线 C 上任一点 P (x ,y),由 PF PF = a 2,可得 7 (x + 1) 2+ y 2 • (x -1) 2 + y 2 =a 2(a > 1),将原点(0 , 0)代入等式不成立,故①不正确.•••点Rx , y )在曲线C 上,点P 关于原点的对称点 P' ( -x ,- y ),将P'代入曲线 C 一 … 1 1 2的方程等式成立,故②正确.设/ FPF = 0,贝U S A RPF = §PF - PR sin 0 =歹sin 0 1 2W j a ,故③正确.答案:②③9. △ ABC 勺顶点A 固定,点A 的对边BC 的长是2a ,边BC 上的高的长是b ,边BC 沿一 条定直线移动,求△ ABC 外心的轨迹方程.:B VC *解:如图所示,以 BC 所在的定直线为x 轴,以过A 点与x 轴垂直的直线为y 轴,建立 直角坐标系,则 A 点的坐标为(0 , b ).设厶ABC 的外心为Mx , y ),作MN L BC 于N,贝U MN 是 BC 的垂直平分线. BC= 2a ,— BN= a , MN= | y |. 又 皿是厶ABC 的外心,••• MA= MB 而 MA= ,x 2+( y - b ) 2,由两点式得直线QB 的方程为 y - 2= 0— 2= x - 1a +1 — 1,MB= - MN+ BN= - a2+ y2,• 一x2+( y - b) 2= ’ a2+ y2.化简,得所求轨迹方程为x2- 2by+ b2- a2= 0.解:设P 点坐标为(x ,y ),双曲线上点 Q 的坐标为(x o ,y o ),因为点P 是线段QN 勺中点, 所以N 点的坐标为(2x -X o , 2y — y o ).又点N 在直线x + y = 2上,所以2x — x o + 2y — y o = 2, 即 X o + y o = 2x + 2y — 2.①2y — 2y ok QN = 2x — 2xo = 1,即 x o — y o = x — y .②1 1由①②,得 x o = 2(3X + y — 2), y o = ^(x + 3y — 2). 又因为点Q 在双曲线上,1 2 1 2 所以 4(3X + y — 2) — 4(x + 3y — 2) = 1.1 2 1 2 1化简,得(x — 2 — (y —2 = 2 所以线段QN 的中点P 的轨迹方程为 1 2 1 2 1(x — 2) — (y — 2)= 2.[能力提升]1.设向量i ,j 为平面直角坐标系的x 轴、y 轴正方向上的单位向量, 若向量a = (x + 3) i + yj , b = (x — 3)i + yj ,且| a | — | b | = 2,则满足上述条件的点P (x , y )的轨迹方程是解析:因为| a | — | b | = 2,所以”F (x + 3) + y — '.」(x — 3) + y = 2,其几何意义是动点 Rx,' y )到定点(一3, 0) , (3 , 0)的距离之差为2,由双曲线定义可 知点Rx , y )的轨迹是以点(一3, o)和(3 , o)为焦点,且2a = 2的双曲线的一支,由c = 3,a = 1,解得b =c — a = 8,2故点F (x , y )的轨迹方程是x 2— y = 1( x >o)或(x > 1).2答案:x 2— y = 1(x >o )或(x > 1)82.如图,半径为 其中RP 为圆C 在x 轴上方的一条切线,当圆心解析:设圆心 C 的坐标为(x o , y o )( x o M 0),则点Q P 的坐标分别为(2x o , 0)、(x o , y o3^Co ^#o + 1 + 1),得PQ 的中点M 的坐标为(三2,竺厂),因为OQR 为平行四边形,PQ 的中点M 也是OR10.如图,从双曲线 的中点P 的轨迹方程. x 2 - y =i 上一点 Q 引直线x + y = 2的垂线,垂足为 N,求线段QN又 QNL l ,个交点,OQR 为平行四边形, C 运动时,则点 R 的轨迹方程为 _________ .xX o = T 即3, [yo = y— 1x = 3x 0 的中点,所以可得R 点坐标为(3 X 0, y o + 1),令R 点坐标为(x , y ),则 y = y o + 1 2 22 2 ^x 2 ^x 2 又x o + y o = 1,代入得—+ (y — 1) = 1,故点R 的轨迹方程为—+ (y — 1) = 1(x 丰0, x 丰2). 2“宀 x 2答案:9 + (y — 1) = 1(x 丰0, X M 2) 3.已知动点 A B 分别在x 轴、y 轴上,且满足 AB= 2,点P 在线段AB 上,且AP= tPB (t 是不为零的常数)•设点P 的轨迹方程为C (1) 求点P 的轨迹方程C; (2) 若t = 2,点M N 是C 上关于原点对称的两个动点 (M N 不在坐标轴上),点Q 坐标 3 为(㊁,3),求△ QM 的面积S 的最大值. 解:(1)设 A (a , 0) , B (0 , b ), P (x , 因为云P=tPB ,即(x — a , y ) = t ( — x , a=(1+t ) ,则](1 +1)[b=— , , 2 2 2 2 1 I t 2 2因为 AB= 2, a + b = 4,即(1 +1) x + (-j ) y = 4,2 2xy4+4f =1.2 2(1 + t ) ( 1 + t )、 9x 2 9 2(2) t =2 时,轨迹方程 C 为 ~4- + 1^y = 1,设 Mx 1, y",x — a — tx 所以iy = t (b — y ) 所以点P 的轨迹方程为:则 N ( — x i , —yd , MN= 2=j x i + y i ,y ), b — y ),xy ,由题意知t >0, 3y i — 3x i2设直线MN 的方程为:y =y :x (x i *0),点Q 到直线MN 的距离为:d =2 2,xiyj xi + y i32yi — 3xiH 22\ x i + y i所以 &MNQ =2#X 2+ y i x 3 =蓉—3X 1 ,2 2 29x 1 9y 1 2 9y 1又〒 + 7= 1,所以 9x 1+ -= 4.4 16 4 所以出 MN = 4 — 9X 1 y 1, 2 2十9X 1 9y 1 3X 1而 1 = + — > — 2 - 4 16 2 所以一9x i y i W 4,当且仅当 3y 1 9x 1 y 14 =— 4 , 3x 1 3y 12 =— 4,1即x i = —尹时,取等号. 所以& MNC 的面积最大值为2 2.4.(创新题)已知点 M 4 , 0) , N (1 , 0),若动点P 满足MN- M P= 6|PN. (1)求动点P 的轨迹C 的方程;d o d n⑵设过点N的直线l交轨迹C于A, B两点,若—可w S•辰—-r,求直线I的斜率7 5的取值范围.解:⑴设动点P(x, y),则M P= (x—4, y), M N= ( —3, 0) , PN= (1 —x,—y).由已知得一3( x—4) = 6 (1—x) 2+(—y) 2,2 2化简得3x2+ 4y2= 12, 即x + 刍=1.2 2所以点P的轨迹C的方程为x+ y= 1.4 3(2)由题意知,直线I的斜率必存在,不妨设过N的直线I的方程为y= k(x—1), 设A, B两点的坐标分别为A(X1, y1) , 0X2, y2).y=k(x—1)由x2 y2_+ 乙=1 4十3 1(■8 k2! x1+ x2= 3 + 4k2, 因为N在椭圆内,所以△ >0.所以<_24k—12x1x2=芥盲.因为NB= (x1—1)( X2 —1) + yy2=(1 + k)( X1—1)( X2—1)2=(1 + k )[ X1X2—(X1 + X2) + 1]2 2 22 4k —12—8k +3 + 4k=(1+ k)3T4T—9 (1 + k )= 23 + 4k .18 —9 (1 + k2) 12 2所以—7w3+厂消去y 得(4 k2+ 3)x2—8k2x+ 4k2—12= 0.所以一3 w k w — 1 或 1 w k w 3.。
2018-2019学年高中数学 第二章 圆锥曲线与方程 2.4.1 抛物线的标准方程作业 苏教版选修1-1

2.4.1 抛物线的标准方程[基础达标]1.已知抛物线的准线方程是x =-7,则抛物线的标准方程是________.解析:由题意,设抛物线的标准方程为y 2=2px (p >0),准线方程是x =-p 2,则-p2=-7,解得p =14,故所求抛物线的标准方程为y 2=28x .答案:y 2=28x2.已知抛物线y 2=2px (p >0)的准线与圆x 2+y 2-6x -7=0相切,则p 的值为________.解析:抛物线的准线为x =-p2,将圆的方程化简得到(x -3)2+y 2=16,准线与圆相切,则-p2=-1⇒p =2.答案:23.以双曲线x 216-y 29=1的右顶点为焦点的抛物线的标准方程为________.解析:∵双曲线的方程为x 216-y 29=1,∴右顶点为(4,0).设抛物线的标准方程为y 2=2px (p >0),则p2=4,即p =8, ∴抛物线的标准方程为y 2=16x .故填y 2=16x .答案:y 2=16x4.抛物线x 2=4ay (a ≠0)的准线方程为________. 解析:∵抛物线的焦点在y 轴上,∴准线方程为y =-4a4,即y =-a .答案:y =-a5.过抛物线y 2=4x 的焦点F 的直线交该抛物线于A ,B 两点.若AF =3,则BF =________.解析:抛物线y 2=4x 的准线为x =-1,焦点为F (1,0),设A (x 1,y 1),B (x 2,y 2).由抛物线的定义可知AF =x 1+1=3,所以x 1=2,所以y 1=±22,由抛物线关于x 轴对称,假设A (2,22).由A ,F ,B 三点共线可知直线AB 的方程为y -0=22(x -1),代入抛物线方程消去y 得2x 2-5x +2=0,求得x =2或12,所以x 2=12,故BF =32.答案:326.已知F 是拋物线y 2=x 的焦点,A ,B 是该抛物线上的两点,AF +BF =3,则线段AB 的中点到y 轴的距离为________.解析:过A ,B 分别作准线l 的垂线AD ,BC ,垂足分别为D ,C ,M 是线段AB 的中点,MN 垂直准线l 于N ,由于MN 是梯形ABCD 的中位线.所以MN =AD +BC2.由抛物线的定义知AD +BC =AF +BF =3,所以MN =32,又由于准线l 的方程为x =-14,所以线段AB 中点到y 轴的距离为32-14=54,故填54.答案:547.平面上动点P 到定点F (1,0)的距离比P 到y 轴的距离大1,求动点P 的轨迹方程. 解:设P (x ,y ),则有x -2+y 2=|x |+1,两边平方并化简得y 2=2x +2|x |.∴y 2=⎩⎪⎨⎪⎧4x ,x ≥0,0, x <0.故点P 的轨迹方程为y 2=4x (x ≥0)或y =0(x <0).8.(1)抛物线的顶点为坐标原点,对称轴为坐标轴,又知抛物线经过点P (4,2),求抛物线的方程;(2)已知抛物线C :x 2=2py (p >0)上一点A (m,4)到其焦点的距离为174,求p 与m 的值.解:(1)∵抛物线的顶点为坐标原点,对称轴为坐标轴, ∴抛物线的方程为标准方程. 又∵点P (4,2)在第一象限,∴抛物线的方程设为y 2=2px ,x 2=2py (p >0).当抛物线为y 2=2px 时,则有22=2p ×4,故2p =1,y 2=x ;当抛物线为x 2=2py 时,则有42=2p ×2,故2p =8,x 2=8y .综上,所求的抛物线的方程为y 2=x 或x 2=8y .(2)由抛物线方程得其准线方程y =-p2,根据抛物线定义,点A (m,4)到焦点的距离等于它到准线的距离,即4+p 2=174,解得p =12;∴抛物线方程为:x 2=y ,将A (m ,4)代入抛物线方程,解得m =±2.[能力提升]1.在直角坐标系xOy 中,直线l 过抛物线y 2=4x 的焦点F ,且与该抛物线相交于A ,B 两点.其中点A 在x 轴上方,若直线l 的倾斜角为60°,则△OAF 的面积为________.解析:直线l 的方程为y =3(x -1),即x =33y +1,代入抛物线方程得y 2-433y -4=0,解得y A =433+ 163+162=23(y B <0,舍去),故△OAF 的面积为12×1×23= 3.答案: 32.若双曲线x 23-16y 2p2=1的左焦点在抛物线y 2=2px 的准线上,则p 的值为________.解析:把双曲线x 23-16y 2p 2=1化为标准形式x 23-y 2p 216=1,故c 2=3+p 216,c = 3+p 216=48+p 24,左焦点⎝ ⎛⎭⎪⎫-48+p 24,0,由题意知,抛物线的准线方程为x =-48+p 24,又抛物线y 2=2px 的准线方程为x =-p2,所以-48+p 24=-p 2,解得,p =4或p =-4(舍去).故p =4.答案:43.抛物线顶点在原点,它的准线过双曲线x 2a 2-y 2b2=1(a >0,b >0)的一个焦点,并与双曲线实轴垂直,已知抛物线与双曲线的一个交点为⎝ ⎛⎭⎪⎫32,6,求抛物线与双曲线的方程. 解:由题设知,抛物线以双曲线的右焦点为焦点,准线过双曲线的左焦点,∴p =2c .设抛物线方程为y 2=4cx ,∵抛物线过点⎝ ⎛⎭⎪⎫32,6,∴6=4c ·32.∴c =1, 故抛物线方程为y 2=4x .又双曲线x 2a 2-y 2b 2=1过点⎝ ⎛⎭⎪⎫32,6, ∴94a 2-6b 2=1.又a 2+b 2=c 2=1,∴94a 2-61-a2=1. ∴a 2=14或a 2=9(舍去).∴b 2=34,故双曲线方程为:4x 2-4y 23=1.4.设抛物线C :x 2=2py (p >0)的焦点为F ,准线为l ,A 为C 上一点,已知以F 为圆心,FA 为半径的圆F 交l 于B ,D 两点.(1)若∠BFD =90°,△ABD 的面积为42,求p 的值及圆F 的方程;(2)若A ,B ,F 三点在同一直线m 上,直线n 与m 平行,且n 与C 只有一个公共点,求坐标原点到m ,n 距离的比值.解:(1)由已知可得△BFD 为等腰直角三角形,BD =2p ,圆F 的半径FA =2p . 由抛物线定义可知A 到l 的距离d =FA =2p .因为△ABD 的面积为42,所以12BD ·d =42,即12·2p ·2p =42,解得p =-2(舍去)或p =2. 所以F (0,1),圆F 的方程为x 2+(y -1)2=8.(2)因为A 、B 、F 三点在同一直线m 上,所以AB 为圆F 的直径,∠ADB =90°.由抛物线定义知AD =FA =12AB ,所以∠ABD =30°,m 的斜率为33或-33. 当m 的斜率为33时,由已知可设n :y =33x +b ,代入x 2= 2py 得x 2-233px -2pb =0.由于n 与C 只有一个公共点,故Δ=43p 2+8pb =0,解得b =-p6.因为m 的截距b 1=p 2,|b 1||b |=3,所以坐标原点到m ,n 距离的比值为3.当m 的斜率为-33时,由图形对称性可知,坐标原点到m 、n 距离的比值为3.综上,坐标原点到m,n距离的比值为3.本文档仅供文库使用。
20182019学年高中数学第1部分第2章圆锥曲线与方程2.3双曲线2.3.2双曲线的几何性质讲义含解析苏教版选修2120

2.3.2 双曲线的几何性质双曲线的简单几何性质歌曲《悲伤双曲线》的歌词如下:如果我是双曲线,你就是那渐近线,如果我是反比例函数,你就是那坐标轴,虽然我们有缘,能够坐在同一平面,然而我们又无缘,漫漫长路无交点.问题1:双曲线的对称轴、对称中心是什么?提示:坐标轴;原点.问题2:过双曲线的某个焦点且平行于渐近线的直线与双曲线有交点吗?提示:有一个交点.双曲线的几何性质标准方程-=1(a>0,b>0) -=1(a>0,b>0)图形性质焦点 (±c,0) (0,±c)焦距 2c范围 x≥a或x≤-a,y∈R y≥a或y≤-a,x∈R顶点 (±a,0) (0,±a)对称性关于x轴、y轴、坐标原点对称轴长实轴长=2a,虚轴长=2b离心率e=∈(1,+∞)渐近线y=±x y=±x等轴双曲线观察所给两个双曲线方程.(1)-=1;(2)x2-y2=9.问题1:两个双曲线方程有何共同特点?提示:所给的两个双曲线方程的实轴长和虚轴长相等.问题2:两个双曲线的离心率是多少?提示:.问题3:两双曲线的渐近线方程是什么?提示:渐近线方程y=±x.实轴长和虚轴长相等的双曲线叫做等轴双曲线.1.离心率e反映了双曲线开口的大小,e越大,双曲线的开口就越大.2.双曲线有两条渐近线,渐近线与双曲线没有交点.渐近线方程用a,b表示时,受焦点所在坐标轴的影响.双曲线的几何性质[例1] 求双曲线9y2-4x2=-36的顶点坐标、焦点坐标、实轴长、虚轴长、离心率和渐近线方程.[思路点拨] 先化方程为标准形式,然后根据标准方程求出基本量a,b,c即可得解,但要注意焦点在哪条坐标轴上.[精解详析] 由9y2-4x2=-36得-=1,∴a2=9,b2=4.c2=a2+b2=13.∴c=.∴顶点坐标为(-3,0),(3,0)焦点坐标为(-,0),(,0),实轴长为2a=6,虚轴长为2b=4,离心率为e==,渐近线方程为y=±x.[一点通] 求解双曲线的几何性质问题时,首先将方程化为标准方程,分清焦点所在的轴,写出a与b的值,进而求出c,即可求得双曲线的性质.1.(湖北高考改编)已知0<θ<,则双曲线C1:-=1与C2:-=1,下列说法正确的个数为________.①实轴长相等;②虚轴长相等;③离心率相等;④焦距相等.解析:双曲线C1和C2的实轴长分别是2sin θ和2cos θ,虚轴长分别为2cos θ和2sin θ,则焦距都等于2,相等,离心率不相等,只有④正确.答案:12.(福建高考改编)双曲线x2-y2=1的顶点到其渐近线的距离等于________.解析:双曲线x2-y2=1的顶点坐标为(±1,0),渐近线为y=±x,∴顶点到渐近线的距离为=.答案:3.求双曲线16x2-9y2=-144的实半轴长、虚半轴长、焦点坐标、离心率和渐近线方程.解:把方程化为-=1,∴a=4,b=3,c=5.∴实半轴长a=4,虚半轴长b=3,焦点坐标(0,-5),(0,5),离心率e==,渐近线方程为y=±x.根据几何性质求双曲线的标准方程[例2] 求适合下列条件的双曲线标准方程:(1)虚轴长为12,离心率为;(2)顶点间距离为6,渐近线方程为y=±x;(3)求与双曲线x2-2y2=2有公共渐近线,且过点M(2,-2)的双曲线方程.[思路点拨] 分析双曲线的几何性质,求出a,b,c的值,再确定(讨论)焦点位置,写出双曲线的标准方程.[精解详析] (1)设双曲线的标准方程为-=1或-=1(a>0,b>0).由题知2b=12,=,且c2=a2+b2,∴b=6,c=10,a=8.∴所求双曲线的标准方程为-=1或-=1.(2)当焦点在x轴上时,由=且a=3,得b=.∴所求双曲线的标准方程为-=1.当焦点在y轴上时,由=且a=3,得b=2.∴所求双曲线的标准方程为-=1.(3)设与双曲线-y2=1有公共渐近线的双曲线方程为-y2=k,将点(2,-2)代入,得k=-(-2)2=-2,∴双曲线的标准方程为-=1.[一点通]由双曲线的性质求双曲线的标准方程,一般用待定系数法,其步骤为:(1)判断:利用条件判断焦点的位置;(2)设:设出双曲线的标准方程;(3)列:利用已知条件构造关于参数的方程;(4)求:解参数方程,进而得标准方程.4.(广东高考改编)已知中心在原点的双曲线C的右焦点为F(3,0),离心率为,则C的方程是________.解析:由题意可知c=3,a=2,b===,故双曲线的方程为-=1.答案:-=15.已知双曲线中心在原点,一个顶点的坐标为(3,0),且焦距与虚轴长之比为5∶4,则双曲线的标准方程是______________.解析:双曲线中心在原点,一个顶点的坐标为(3,0),则焦点在x轴上,且a=3,焦距与虚轴长之比为5∶4,即c∶b=5∶4,解得c=5,b=4,则双曲线的标准方程是-=1.答案:-=16.求中心在原点,焦点在坐标轴上,过点M(3,4)且虚轴长是实轴长的2倍的双曲线方程.解:①若焦点在x轴上,则双曲线方程为-=1.∵M(3,4)在双曲线上,∴-=1.又∵b=2a,∴9×4-16=4a2,解得a2=5,b2=20,∴双曲线方程为-=1.②若焦点在y轴上,则双曲线方程为-=1.∵M(3,4)在双曲线上,∴-=1,又∵b=2a,∴16×4-9=4a2,解得a2=,b2=55,∴双曲线方程为-=1.综上可知,双曲线方程为-=1或-=1.求双曲线的离心率及其范围[例3] (1)设△ABC是等腰三角形,∠ABC=120°,则以A,B为焦点且过点C的双曲线的离心率为________.(2)已知双曲线-=1(a>0,b>0)的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则双曲线离心率的范围是________.[思路点拨] (1)根据图形并由双曲线的定义确定a与c的关系,求出离心率,对于问题(2)可以通过图形借助直线与双曲线的关系,因为过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则必有≥tan 60°.[精解详析] (1)由题意2c=AB=BC,∴AC=2×2c×sin 60°=2 c,由双曲线的定义,有2a=AC-BC=2 c-2c ?a=(-1)c,∴e===.(2)因为双曲线渐近线的斜率为k=,直线的斜率为k=tan 60°=,故有≥,所以e==≥=2,所以所求离心率的取值范围是e≥2.[答案] (1) (2)e≥2[一点通]1.求双曲线离心率的常见方法:(1)依据条件求出a,c,利用e=;(2)利用e=;(3)依据条件,建立关于a,b,c的齐次关系式,消去b,转化为离心率e的方程求解.2.求离心率的范围,常结合已知条件构建关于a、b、c的不等关系.7.(湖南高考)设F1,F2是双曲线C:-=1(a>0,b>0)的两个焦点.若在C上存在一点P,使PF1⊥PF2,且∠PF1F2=30°,则C的离心率为________.解析:如图,由已知可得,PF1=2ccos 30°=c,PF2=2csin 30°=c,由双曲线的定义,可得c-c=2a,则e===+1.答案:+18.双曲线-=1(a>0,b>0)的两个焦点为F1、F2,若P为其上一点,且PF1=2PF2,则双曲线离心率的取值范围为________.解析:如图,设PF2=m,∠F1PF2=θ(0<θ≤π),当P在右顶点处θ=π,e===.∵-1≤cos θ<1,又∵e>1,∴e∈(1,3].答案:(1,3]1.双曲线离心率及其范围的求法.(1)双曲线离心率的求解,一般可采用定义法、直接法等方法.(2)双曲线离心率范围的求解,涉及解析几何中“范围”问题的解法.在解析几何中,求“范围”问题,一般可从以下几个方面考虑:与已知范围联系,通过求值域或解不等式来完成;通过判别式Δ>0;利用点在曲线内部形成的不等式关系;利用解析式的结构特点,如a,,|a|等非负性.2.求双曲线的标准方程,当焦点不明确时,方程可能有两种形式,为了避免讨论,也可设双曲线方程为mx2-ny2=1(mn>0),从而直接求得;若已知双曲线的渐近线方程为y=±x,还可以将方程设为-=λ(λ≠0)避免焦点的讨论.[对应课时跟踪训练(十一)]1.(陕西高考)双曲线-=1的离心率为.则m=________.解析:∵a=4,b=,∴c2=16+m,e===,∴m=9.答案:92.已知双曲线-=1(a>0,b>0),两条渐近线的夹角为60°,则双曲线的离心率为________.解析:根据题意,由于双曲线-=1(a>0,b>0),两条渐近线的夹角为60°,则可知=或=,那么可知双曲线的离心率为e=,所以结果为2或.答案:2或3.焦点为(0,6),且与双曲线-y2=1有相同的渐近线的双曲线方程是________.解析:由-y2=1,得双曲线的渐近线为y=±x.设双曲线方程为:-y2=λ(λ<0),∴-=1.∴-λ-2λ=36,∴λ=-12.故双曲线方程为-=1.答案:-=14.(新课标全国卷Ⅰ改编)已知双曲线C:-=1(a>0,b>0)的离心率为,则C的渐近线方程为________.解析:∵e2===1+=,∴=,∴=,∴y=±x.答案:y=±x5.若双曲线-=1(a>0,b>0)的两个焦点分别为F1、F2,P为双曲线上一点,且|PF1|=3|PF2|,则该双曲线离心率e的取值范围是________.解析:依题意得由此解得|PF2|=a,|PF1|=3a,∵|PF1|+|PF2|≥|F1F2|,即c≤2a,e =≤2.又e>1,∴离心率e的取值范围是(1,2].答案:(1,2]6.根据下列条件求双曲线的标准方程:(1)经过点,且一条渐近线方程为4x+3y=0.(2)P(0,6)与两个焦点的连线互相垂直,与两个顶点连线的夹角为.解:(1)∵双曲线的一条渐近线方程为4x+3y=0,∴可设双曲线方程为-=λ(λ≠0).∵双曲线经过点,∴×-=λ.即λ=1.∴所求双曲线的标准方程为-=1.(2)设F1、F2为双曲线的两个焦点,依题意,它的焦点在x轴上,∵PF1⊥PF2,且OP=6,∴2c=F1F2=2OP=12,∴c=6.又P与两顶点连线夹角为,∴a=|OP|·tan=2 ,∴b2=c2-a2=24.故所求双曲线的标准方程为-=1.7.已知F1,F2是双曲线-=1(a>0,b>0)的两个焦点,PQ是经过F1且垂直于x轴的双曲线的弦,如果∠PF2Q=90°,求双曲线的离心率.解:设F1(c,0),将x=c代入双曲线的方程得-=1,那么y=±.由PF2=QF2,∠PF2Q=90°,知|PF1|=|F1F2|,∴=2c,∴b2=2ac.由a2+b2=c2,得c2-2ac-a2=0,∴2-2×-1=0.即e2-2e-1=0.∴e=1+或e=1-(舍去).所以所求双曲线的离心率为1+.8.已知双曲线的中心在原点,焦点F1、F2在坐标轴上,离心率为且过点(4,-).(1)求双曲线方程;(2)若点M(3,m)在双曲线上,求证:点M在以F1F2为直径的圆上;(3)求△F1MF2的面积.解:(1)∵离心率e=,∴设所求双曲线方程为x2-y2=λ(λ≠0),则由点(4,-)在双曲线上,知λ=42-(-)2=6,∴双曲线方程为x2-y2=6,即-=1.(2)若点M(3,m)在双曲线上,则32-m2=6,∴m2=3.由双曲线x2-y2=6知,F1(2 ,0),F2(-2 ,0),∴·=(2 -3,-m)·(-2 -3,-m)=9-(2 )2+m2=0.∴⊥,∴点M在以F1F2为直径的圆上.(3)S△F1MF2=×2c×|m|=c|m|=2 ×=6.。
苏教版高中数学选修2-1第2章圆锥曲线与方程2.1含答案

§2.1圆锥曲线学习目标 1.了解当一个平面截一个圆锥面时,所截得的图形的各种情况.2.初步掌握椭圆、双曲线、抛物线的定义及其几何特征.3.通过平面截圆锥面的实验和对有关天体运动轨道的了解,知道圆锥曲线在我们身边广泛存在.知识点一椭圆的定义观察图形,思考下列问题:思考1如图,把细绳两端拉开一段距离,分别固定在图板上的两点F1,F2处,套上铅笔,拉紧绳子,移动笔尖,画出的轨迹是什么图形?答案椭圆思考2图中移动的笔尖始终满足怎样的几何条件?答案PF1+PF2是常数(大于F1F2).梳理平面内到两个定点F1,F2的距离的和等于常数(大于F1F2)的点的轨迹叫做椭圆,两个定点F1,F2叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距.知识点二双曲线的定义观察图示,若固定拉链上一点F1或F2,拉开或闭拢拉链,拉链头M经过的点可画出一条曲线,思考下列问题:思考1图中动点M的几何性质是什么?答案|MF1-MF2|为一个正常数.思考2若MF1-MF2=F1F2,则动点M的轨迹是什么?答案以F2为端点,向F2右边延伸的射线.梳理平面内到两个定点F1,F2的距离的差的绝对值等于常数(小于F1F2的正数)的点的轨迹叫做双曲线,两个定点F1,F2叫做双曲线的焦点,两焦点间的距离叫做双曲线的焦距.知识点三抛物线的定义观察图形,思考下列问题:思考如图,定点C和定直线EF,用三角板画出到定点的距离等于到定直线的距离的动点D的轨迹.则动点D的轨迹是什么?其满足什么条件?答案抛物线,动点D到定点C和定直线EF距离相等,且C不在EF上.梳理平面内到一个定点F和一条定直线l(F不在l上)的距离相等的点的轨迹叫做抛物线,定点F叫做抛物线的焦点,定直线l叫做抛物线的准线.椭圆、双曲线、抛物线统称为圆锥曲线.1.平面内到两定点的距离之和为常数的点的轨迹是椭圆.(×)2.平面内到两定点的距离之差的绝对值为常数的点的轨迹是双曲线.(×)3.抛物线上的点到焦点的距离与到准线的距离相等.(√)类型一 圆锥曲线定义的理解例 1 平面内动点 M 到两点 F 1(-3,0),F 2(3,0)的距离之和为 3m ,问 m 取何值时 M 的轨迹 是椭圆?解 ∵MF 1+MF 2=3m ,∴M 到两定点的距离之和为常数,当 3m 大于 F 1F 2 时,由椭圆定义知,M 的轨迹为椭圆, ∴3m >F 1F 2=3-(-3)=6,∴m >2,∴当 m >2 时,M 的轨迹是椭圆.反思与感悟 在深刻理解圆锥曲线的定义的过程中,一定要注意定义中的约束条件(1)在椭圆中,和为定值且大于 F 1F 2.(2)在双曲线中,差的绝对值为定值且小于 F 1F 2. (3)在抛物线中,点 F 不在定直线上.跟踪训练 1 (1)命题甲:动点 P 到两定点 A ,B 的距离之和 P A +PB =2a (a >0,a 为常数);命题乙:P 点轨迹是椭圆,则命题甲是命题乙的________条件.(2)动点 P 到两个定点 A (-2,0),B(2,0)构成的三角形的周长是 10,则点 P 的轨迹是________. 答案 (1)必要不充分 (2)椭圆解析 (1)若 P 点轨迹是椭圆,则 PA +PB =2a (a >0,且为常数),∴甲是乙的必要条件.反之,若 P A +PB =2a (a >0,且是常数),不能推出 P 点轨迹是椭圆.因为仅当 2a >AB 时,P 点轨迹才是椭圆;而当 2a =AB 时,P 点轨迹是线段 AB ;当 2a <AB时,P 点无轨迹,∴甲不是乙的充分条件.综上,甲是乙的必要不充分条件.(2)由题意知 P A +PB +AB =10,又 AB =4,∴PA +PB =6>4.∴点 P 的轨迹是椭圆.类型二 圆锥曲线轨迹的探究例 2 如图,已知动圆 C 与圆 F 1,F 2 均外切(圆 F 1 与圆 F 2 相离),试问:动点 C 的轨迹是什 么曲线?解 设动圆 C 的半径为 R ,圆 F 1,F 2 的半径分别为 r 1,r 2,则 CF 1=R +r 1,CF 2=R +r 2. 所以 CF 1-CF 2=r 1-r 2.跟踪训练 3 在△ABC 中,BC 固定,顶点 A 移动.设 BC =m ,且|sin C -sin B |= sin A ,则解 因为|sin C -sin B |= sin A ,由正弦定理可得|AB -AC |= BC = m ,且 m <BC ,又 CF 1-CF 2=r 1-r 2<F 1F 2,故动圆圆心 C 的轨迹是以 F 1,F 2 为焦点的双曲线靠近 F 2 的一支. 引申探究若把原题中“外切”换成“内切”再求解,结论如何?解 动点 C 的轨迹是以 F 1,F 2 为焦点的双曲线靠近 F 1 的一支.反思与感悟 紧扣圆锥曲线的定义,写出动点满足的条件,然后得到相应的轨迹.跟踪训练 2 已知动点 P 到点 A (-3,0)的距离比它到直线 x =1 的距离大 2,试判断动点 P 的轨迹.解 因点 P 到 A 的距离比它到直线 x =1 的距离大 2,所以点 P 到点 A 的距离等于它到直线 x =3 的距离.因为点 A 不在直线 x =3 上,所以点 P 的轨迹是抛物线.类型三 圆锥曲线定义的应用例 3 在△ABC 中,B (-6,0),C (0,8),且 sin B ,sin A ,sin C 成等差数列.(1)顶点 A 的轨迹是什么? (2)指出轨迹的焦点和焦距.解 (1)由 sin B ,sin A ,sin C 成等差数列,得 sin B +sin C =2sin A .由正弦定理可得 AB +AC=2BC .又 BC =10,所以 AB +AC =20,且 20>BC ,所以点 A 的轨迹是椭圆(除去直线 BC 与椭圆的交点).(2)椭圆的焦点为 B ,C ,焦距为 10.反思与感悟 利用圆锥曲线的定义可以判定动点的轨迹,在判定时要注意定义本身的限制条件,如得到 MF 1+MF 2=2a (a 为大于零的常数)时,还需要看 2a 与 F 1F 2 的大小,只有 2a >F 1F 2 时,所求轨迹才是椭圆.若得到MF 1-MF 2=2a (0<2a <F 1F 2),轨迹仅为双曲线的一支.除了 圆锥曲线定义本身的限制条件外,还要注意题目中的隐含条件.12顶点 A 的轨迹是什么?121 1 12 2 2所以点 A 的轨迹是双曲线(除去双曲线与 BC 的两交点).F FF1.设F1,2是两个定点,1F2=6,动点M满足MF1+MF2=10,则动点M的轨迹是________.答案椭圆解析因MF1+MF2=10>F1F2=6,由椭圆的定义得动点的轨迹是椭圆.2.若F1,2是两个定点且动点P1满足PF1-PF2=1,又F1F2=3,则动点P的轨迹是________.答案双曲线靠近点F2的一支解析因PF1-PF2=1<F1F2=3,故由双曲线定义判断,动点P的轨迹是双曲线靠近点F2的一支.3.到定点(1,0)和定直线x=-1距离相等的点的轨迹是________.答案抛物线解析依据抛物线定义可得.4.到两定点F1(-3,0),F2(3,0)的距离之差的绝对值等于6的点M的轨迹是________.答案两条射线解析据题|MF1-MF2|=F1F2,得动点M的轨迹是两条射线.5.如图,在正方体ABCD-A1B1C1D1中,P是侧面BB1C1C内一动点,若点P到直线BC与直线C1D1的距离相等,则动点P的轨迹是________.答案抛物线解析由正方体的性质可知,点P到C1D1的距离为PC1,故动点P到定点C1和到定直线BC的距离相等,且点C1不在直线BC上,符合抛物线的定义,所以动点P的轨迹是抛物线.1.若MF1+MF2=2a(2a>F1F2),则动点M的轨迹是椭圆.若点M在椭圆上,则MF1+MF2=2a.2.若|MF1-MF2|=2a(0<2a<F1F2),则动点M的轨迹为双曲线.若动点M在双曲线上,则|MF1-MF2|=2a.3.抛物线定义中包含三个定值,分别为一个定点,一条定直线及一个确定的比值.2”一、填空题1.平面内到两定点F1(-3,0),F2(3,0)的距离的和等于6的点P的轨迹是________.答案线段F1F2解析依题意得PF1+PF2=6=F1F2,故动点P的轨迹是线段F1F2.2.到定点(0,7)和到定直线y=7的距离相等的点的轨迹是________.答案直线解析因定点(0,7)在定直线y=7上,故符合条件的点的轨迹是直线.3.已知定点F1(-2,0),F2(2,0),在满足下列条件的平面内,动点P的轨迹为双曲线的是________.(填序号)①|PF1-PF2|=3;②|PF1-PF2|=4;③|PF1-PF2|=5;④PF1-PF2=±4.答案①解析根据双曲线定义知P到F1,F2的距离之差的绝对值要小于F1F2.4.到定点A(2,0)和B(4,0)的距离之差为2的点的轨迹是________.答案一条射线解析要注意两点:一是“差”而不是“差的绝对值;二是“常数”等于两定点间的距离.5.已知△ABC的顶点A(-5,0),B(5,0),△ABC的内切圆圆心在直线x=3上,则顶点C的轨迹是____________.答案以A,B为焦点的双曲线的右支(除去点(3,0))解析如图,AD=AE=8.BF=BE=2,CD=CF,所以CA-CB=8-2=6<AB=10.根据双曲线定义,所求轨迹是以A,B为焦点的双曲线的右支(除去点(3,0)).6.已知点M(x,y)的坐标满足(x-1)2+(y-1)2-(x+3)2+(y+3)2=±4,则动点M的轨迹是________.答案双曲线解析点(x,y)到(1,1)点及到(-3,-3)点的距离之差的绝对值为4,而(1,1)与(-3,-3)距3 10.已知点 A (-1,0),B (1,0).曲线 C 上任意一点 P 满足P A 2-PB 2=4(|P A |-|PB |)≠0.则曲线解析 由P A 2-PB 2=4(|P A |-|PB |)≠0,得|P A |+|PB |=4,且 4>AB .| 离为 4 2,由定义知动点 M 的轨迹是双曲线.7.下列说法中正确的有________.(填序号)①已知 F 1(-6,0),F 2(6,0),到 F 1,F 2 两点的距离之和等于 12 的点的轨迹是椭圆; ②已知 F 1(-6,0),F 2(6,0),到 F 1,F 2 两点的距离之和等于 8 的点的轨迹是椭圆;③到点 F 1(-6,0),F 2(6,0)两点的距离之和等于点 M (10,0)到 F 1,F 2 的距离之和的点的轨迹 是椭圆;④到点 F 1(-6,0),F 2(6,0)距离相等的点的轨迹是椭圆. 答案 ③解析 椭圆是到两个定点 F 1,F 2 的距离之和等于常数(大于 F 1F 2)的点的轨迹,应特别注意 椭圆的定义的应用.①中 F 1F 2=12,故到 F 1,F 2 两点的距离之和为常数 12 的点的轨迹是线段 F 1F 2. ②中点到 F 1,F 2 两点的距离之和 8 小于 F 1F 2,故这样的点不存在.③中点 M (10,0)到 F 1,F 2 两点的距离之和为 (10+6)2+02+ (10-6)2+02=20>F 1F 2=12, 故③中点的轨迹是椭圆.④中点的轨迹是线段 F 1F 2 的垂直平分线. 故正确的是③.8.若动点 P 到定点 F (1,1)和到直线 l :x +y -4=0 的距离相等,则动点 P 的轨迹是________. 答案 直线解析设动点 P 的坐标为(x ,y ),则 (x -1)2+(y -1)2=|3x +y -4|.整理,得 x -3y +2=0,10所以动点 P 的轨迹为直线.9.平面内有两个定点 F 1,F 2 及动点 P ,设命题甲:PF 1-PF 2|是非零常数,命题乙:动点P 的轨迹是以 F 1,F 2 为焦点的双曲线,则甲是乙的________条件.(“充分不必要”“必要不 充分”“充要”“既不充分又不必要”)答案 必要不充分解析 由双曲线的定义可知,若动点 P 的轨迹是以 F 1,F 2 为焦点的双曲线,则|PF 1-PF 2| 是非零常数,反之则不成立.→ → → →C 的轨迹是______.答案 椭圆→ → → →→ →故曲线 C 的轨迹是椭圆.(解析把轨迹方程5x2+y2=|3x+4y-12|写成x2+y2=,∴动点M到原点的=BD,MC=CE,于是MB+MC=BD+CE=(BD+CE)=×39=26>24=BC. 11.已知动圆M过定点A(-3,0),并且在定圆B:(x-3)2+y2=64的内部与其相内切,则动圆圆心M的轨迹为________.答案椭圆解析设动圆M的半径为r.因为动圆M与定圆B内切,所以MB=8-r.又动圆M过定点A,MA=r,所以MA+MB=8>AB=6,故动圆圆心M的轨迹是椭圆.二、解答题12.点M到点F(0,-2)的距离比它到直线l:y-3=0的距离小1,试确定点M的轨迹.解由题意得点M与点F的距离等于它到直线y-2=0的距离,且点F不在直线l上,所以点M的轨迹是抛物线.13.如图所示,已知点P为圆R:x+c)2+y2=4a2上一动点,Q(c,0)为定点(c>a>0,为常数),O为坐标原点,求线段PQ的垂直平分线与直线RP的交点M的轨迹.解由题意,得MP=MQ,RP=2a.MR-MQ=MR-MP=RP=2a<RQ=2c.∴点M的轨迹是以R,Q为两焦点,2a为实轴长的双曲线的右支.三、探究与拓展14.已知动点M的坐标满足方程5x2+y2=|3x+4y-12|,则动点M的轨迹是__________.答案抛物线|3x+4y-12|5距离与到直线3x+4y-12=0的距离相等.∵原点不在直线3x+4y-12=0上,∴点M的轨迹是以原点为焦点,直线3x+4y-12=0为准线的抛物线.△15.在ABC中,BC=24,AC,AB边上的中线长之和等于△39,求ABC的重心的轨迹.解如图所示,以BC的中点O为坐标原点,线段BC所在直线为x轴,线段BC的中垂线为y轴建立平面直角坐标系xOy.设M为△ABC的重心,BD是AC边上的中线,CE是AB边上的中线,由重心的性质知M B 222222333333根据椭圆的定义知,点M的轨迹是以B,C为两焦点,26为实轴长的椭圆去掉点(-13,0),(13,0).。
圆锥曲线(2018-2)
(3)已知双曲线xa22-by22=1 的左、右焦点分别为 F1、F2,过 F1 作圆 x2+y2=a2 的
切线分别交双曲线的左、右两支于点 B、C,
且|BC|=|CF2|,则双曲线的渐近线方程为( )
A.y=±3x
B.y=±2 2x
C.y=±( 3+1)x D.y=±( 3-1)x
热点二 圆锥曲线的几何性质
直
相切
只有一个交点且 0
线 与
椭圆 两个交点 0
圆
锥
交于两点 0
曲 线
相交
双曲线 交于一点(直线与渐近线平行)
的
位
交于两点 0
置 关 系
抛物线 交于一点(直线平行于抛物线的对称轴)
相离
无公共点 0
热点三 直线与圆锥曲线
例 3. 椭圆 C:xa22+by22=1(a>b>0)的离心率为12,其左焦点到点 P(2,1)的距离为 10.
(3)在平面直角坐标系中,已知△ABC 的顶点 A(-4,0)和 C(4,0),顶点 B
在椭圆2x52 +y92=1
上,则sin
A+sin sin B
C=________.
解析
热点二 圆锥曲线的几何性质
1.椭圆、双曲线中,a,b,c 之间的关系
(1)在椭圆中:a2=b2+c2,离心率为 e=ac=
例 2(4) 如图,过抛物线 y2=2px(p>0)的焦点 F 的直线 交抛物线于点 A,B,交其准线 l 于点 C,若|BC|=2|BF|, 且|AF|=3,则此抛物线的方程为( )
A.y2=9x B.y2=6x C.y2=3x D.y2= 3x
抛物线的标准方程与几何性质解题方略 (1)求抛物线的标准方程的方法及流程 ①方法:求抛物线的标准方程常用待定系数法,
高中数学第二章圆锥曲线与方程2
法二:设动点 M(x,y), 则点 M 的轨迹是集合:P={M||MA|=|MN|}, 即: (x-3)2+y2=|x+3|, 化简得:y2=12x. ∴点 M 的轨迹方程为 y2=12x.
1.若抛物线y2=8x上一点P到其焦点的距离为10,
则点P的坐标为( C )
A.(8,8)
B.(8,-8)
∵p2=4,∴p=8, ∴抛物线方程为 y2=16x;
当焦点为(0,-2)时, 设抛物线方程为 x2=-2py(p>0), ∵- p2=-2,∴p=4, ∴抛物线方程为 x2=-8y, 综上,所求抛物线方程为 y2=16x 或 x2=-8y.
【点评】 避免讨论,如焦点在x轴 上 的 抛 物 线 标 准 方 程 可 设 为 y2 = 2mx(m≠0) , 焦 点 在 y 轴 上 的 抛 物 线 标准方程可设为x2=2my(m≠0).
F (0, -
p )
2
p y=
2
抛物线的标准方程
怎样把抛物线的位置特 想 征(标准位置)和方程特征
一
想 (标准方程)统一起来?
?
抛物线的标准方程
标准方程为
左右型
y2 =+ 2px
抛
(p>0)
物
线
方
程
标准方程为
上下型
x2 =+ 2py
(p>0)
开口向右: y2 =2px(x≥ 0) 开口向左: y2 = -2p8y.
【变式练习】
1.根据下列条件写出抛物线的标准方程.
(1)焦点是(0,-3);
x2=-12y
(2)准线是 x 1 .
2
y2=2x
2.求下列抛物线的焦点坐标与准线方程.
20182019学年高中数学第2章圆锥曲线与方程263曲线的交点作业苏教版选修21
宝宝宝宝嘻嘻嘻曲线的交点[ 基础达标 ]1. 若直线 l 过点 (3 , 0) 且与双曲线 4x 2-9y 2= 36 只有一个公共点,则这样的直线共有 ________条.2分析:有两条与渐近线平行的直线: y =± 3( x - 3) ,此外,还有一条切线 x =3.答案: 32. 抛物线 y 2= 2px 与直线 ax + y - 4= 0 的一个交点为 (1 ,2) ,则抛物线的焦点到该直线的距离是 ________.分析:由交点坐标为 (1 ,2) ,求得 a 、p 的值,利用点到直线距离求得焦点到该直线的2 5距离为5.25 答案:3. 曲线 x 2+ y 2= 9 与曲线 x 2= 8y 的交点坐标是 ________.x 2+ y 2= 9 y = 1 分析:由,得,x 2 = 8yx =±2 2∴交点为 ( ±2 2, 1) . 答案: ( ±2 2, 1)4. 过点 (0 , 1) 且与抛物线 y 2= x 只有一个公共点的直线有 ________条.分析:一条与抛物线的对称轴平行,两条相切,共 3 条.答案: 35. 已知直线 x - y - 1= 0 与抛物线 y = ax 2 相切,则 a = ________.x -y - 1= 02-x + 1= 0.分析:由, 消去 y 得方程 axy =ax 21令 = 1- 4a =0,得 a = 4.1答案: 4x 2 y 26.若直线 y = kx +1 与椭圆 5 + m = 1 恒有公共点,则 m 的取值范围是 ________.分析:由于直线过定点 (0 ,1) 恒在椭圆上或在椭圆内,因此 1≤ 1. 又 m ≠5,因此 m ≥1m且 m ≠5.答案: m ≥1且 m ≠57.过抛物线 2= 4x 的焦点作直线交抛物线于 1122) 两点,若 AB =10,那yA ( x ,y ) ,B ( x ,y 么 x 1+ x 2= ________.分析:由于 p =2, AB = x 1+x 2+ p = 10,因此 x 1+ x 2=8. 答案: 88. 抛物线 y = 4x 2 上一点到直线 y = 4x -5 的距离最短,则该点坐标为 ________. 分析:由于 y =4 x 2 与 y = 4 - 5 不订交,设与 y = 4 x - 5 平行的直线方程为 = 4 x + .xy m2y = 4x2则 ? 4x - 4x - m =0. ①1设此直线与抛物线相切,则有 = 0, 即 = 16+ 16m = 0,∴ m =- 1.1 将 m =- 1 代入①式, x = 2, y = 1,1 所求点的坐标为, 1 .1答案: 2, 19.如图,斜率为 1 的直线 l 过椭圆 x2+y 2= 1 的右焦点,交椭圆于 A 、B 两点,求弦 AB 的4长.2= 4, 2= 1, 2解:设 、两点的坐标分别为( 1, y 1)、 (2, 2) ,由椭圆方程知aA BA xB xybc=3,因此 ( 3, 0) ,直线l 的方程为 y = - 3. 将其代入 x2+ 4 2=4,化简整理,得 5x 2Fxy8 38-8 3x +8= 0. 因此 x 1+ x 2= 5 , x 1x 2 =5.因此 AB = 1+k 2| x 1- x 2|= 1+k 2· ( x 1+ x 2) 2- 4x 1x 2( 8 3) 2-4×5×8 8= 2× 5= 5. 10. 已知抛物线 C :y =2x 2,直线 y =kx + 2 交 C 于 A ,B 两点, M 是线段 AB 的中点,过 M 作 x 轴的垂线交抛物线 C 于点 N .(1) 证明:抛物线 C 在点 N 处的切线与 AB 平行;→ →(2) 能否存在实数 k 使 NA · NB = 0?若存在,求 k 的值;若不存在,说明原因.解:(1) 证明:如下图,设22A( x , 2x ) ,B( x , 2x ) ,1122把 y =kx + 2 代入 y = 2x 2,得 2x 2- kx - 2= 0, 由根与系数的关系得 x 1+ 2= k,12=- 1,x x2x 1+ x 2 kk k 2∴ x = x = 2=4,∴ N 点的坐标为 ( 4, 8) .NM设抛物线在点 N 处的切线 l 的方程为k 2ky - 8 = m ( x - 4) ,k 222mk将 y =2x 代入上式得 2x - mx + 4 - 8 = 0.∵直线 l 与抛物线 C 相切,22mk k 22 22∴ =m - 8( 4 - 8 ) = m - 2mk + k = ( m -k ) = 0,∴ m = k ,即 l ∥AB .故抛物线 C 在点 N 处的切线与 AB 平行.→ →(2) 假定存在实数 k ,使 NA · NB = 0,则 NA ⊥ NB .1 又∵ M 是 AB 的中点,∴ MN = 2AB .1 1由 (1) 知 y M = 2( y 1+ y 2) = 2( kx 1+ 2+ kx 2+ 2)1 1 k2 k 2= 2[ k ( x 1+ x 2) + 4] =2( 2 + 4) = 4 +2.∵ MN ⊥x 轴,k 2 k 2 k 2+ 16∴ MN =| y M - y N | = +2- =.4 8 8又 AB = 1+ k 2· | x 1- x 2|= 1+k 2· ( x 1+ x 2) 2- 4x 1x 2=1+k 2·( k) 2-4×(- 1)2= 1 k 2+ 1· k 2+ 16. 2 ∴ k 2+ 16 1 2 +1· 2+16,8 = k k4解得 k =± 2.→ →即存在 k =± 2,使 NA · NB = 0.[ 能力提高 ]1. 直线 y = x + 1 被椭圆 x 2 y 2+ =1 所截得的弦的中点坐标是 ________.4 2y = x +1分析:由 x 2 y 2,消去 y 得 3x 2+ 4x - 2= 0,4+ 2=1因此 x 1+x 2=- 4,因此弦的中点的横坐标为- 2, 332 1代入 y = x + 1,得中点坐标是 ( - 3, 3) .2 1 答案: ( -3, 3)2. y x 2x已知抛物线 =-+ 3 上存在对于直线+ = 0对称的相异两点、 ,则 =yA BAB________.22分析:设 AB 的方程为 y =x + b ,与 y =- x +3 联立得: x + x + b - 3= 0,11∴ AB 的中点 C -2, b - 2 在 x + y =0 上;1 1 即- 2+ b - 2= 0 解得 b = 1 切合 >0, ∴弦长 AB = 1+ 1· 1-4×(- 2)= 3 2. 答案: 32 23. yFAOB过抛物线 = 2 (> 0) 的焦点作倾斜角为 θ 的直线交抛物线于、 两点.设△px pA B的面积为 S ( O 为原点 ) ,若 S 的最小值为 8,求此时的抛物线方程.3宝宝宝宝嘻嘻嘻解:如图,设 (1, 1), (2, 2) ,直线 的方程为 x = +p ,代入 y 2= 2 ,得 y 2- 2 pmyA x yB x yAB my 2px 2,∴ y y2-p = 01 =- p .2又1 p y1 p · | y p y 1| +|p |yp 2△AOB= △OAF + △ OBF = · · |1|+ ·2|= (| 2|)≥ ·2 12|=.SS S 22 2 2 4 y 4y2p2p2当且仅当 | y 1| = | y 2 | = p 时等号建立.故 S min = 2 . 由题意有 2 = 8,∴ p = 4. 故所求的抛物线方程为 y 2=8x . 4.( 创新题 ) 已知抛物线 C : y =- x 2+mx - 1,点 A (3 , 0) 、 B (0 , 3) ,求 C 与线段 AB 有两个不一样交点时 m 的取值范围.解:线段 AB : x + y - 3=0(0 ≤ x ≤3) .x + y - 3= 0,由 y =- x 2+ mx -1. 消去 y ,得 x 2-( m + 1) x + 4= 0. 令 f( ) = x 2- ( +1) x + 4,x m则方程 f ( x ) = 0 在 [0 , 3] 内有两个不一样实数根的充要条件是2=( m + 1) -4×1×4> 0,m + 10<2<3,f ( 0)= 4> 0,f ( 3)= 32- 3( m + 1)+ 4≥0,10解得 3< m ≤ 3 .10故所求 m 的取值范围为 { m |3 < m ≤ 3 } .4。
2019高中数学 第2章 圆锥曲线与方程 2.2.2 椭圆的几何性质作业 苏教版选修2-1
2.2.2 椭圆的几何性质[基础达标]1.椭圆x 2+my 2=1的焦点在y 轴上,长轴长是短轴长的两倍,则m 的值为________.解析:把椭圆的方程化为标准形式y 21m+x 21=1⎝ ⎛⎭⎪⎫1m >1,故a 2=1m ,b 2=1,所以a =1m ,b=1,21m =4,解得,m =14,符合题意. 答案:142.已知椭圆的中心在原点,焦点在x 轴上,且长轴长为12,离心率为13,则椭圆的方程是________.解析:由题意,知2a =12,c a =13,故a =6,c =2,∴b 2=a 2-c 2=32,故所求椭圆的方程为x 236+y 232=1.答案:x 236+y 232=13.已知椭圆的短半轴长为1,离心率e 满足0<e ≤32,则长轴的最大值是________. 解析:由e 2=c 2a 2=a 2-b 2a 2=a 2-1a 2,得0<a 2-1a 2≤34,解得1<a 2≤4.故1<a ≤2,2<2a ≤4.即长轴的最大值是4.答案:44.若一个椭圆长轴的长度、短轴的长度和焦距成等差数列,则该椭圆的离心率是________.解析:由题意知2b =a +c ,又b 2=a 2-c 2,∴4(a 2-c 2)=a 2+c 2+2ac .∴3a 2-2ac -5c 2=0,∴5c 2+2ac -3a 2=0.∴5e 2+2e -3=0,∴e =35或e =-1(舍去).答案:355.若椭圆x 216+y 2m =1的离心率为13,则m 的值为________.解析:由已知得1-m 16=19或1-16m =19,∴m =1289或18.答案:1289或186.已知F 1、F 2是椭圆的两个焦点,满足MF 1→·MF 2→=0的点M 总在椭圆内部,则椭圆离心率的取值范围是________.解析:结合图形(图略),转化为c <b .答案:⎝ ⎛⎭⎪⎫0,22 7.设P 为椭圆x 2a 2+y 2b2=1(a >b >0)上一点,F 1,F 2是椭圆的两个焦点,如果∠PF 1F 2=75°,∠PF 2F 1=15°,则椭圆的离心率是________.解析:在Rt △PF 1F 2中,由正弦定理,得PF 1sin 15°=PF 2sin 75°=F 1F 2sin 90°=2c ,∴PF 1+PF 2sin 15°+sin 75°=2c . 由椭圆的定义,知PF 1+PF 2=2a .代入上式,有e =c a =1sin 75°+sin 15°=63.答案:638.在平面直角坐标系xOy 中,以椭圆x 2a 2+y 2b2=1(a >b >0)上的一点A 为圆心的圆与x 轴相切于椭圆的一个焦点,与y 轴相交于B 、C 两点,若△ABC 是锐角三角形,则该椭圆的率心率的取值范围是________.解析:由题意得,圆半径r =b 2a ,因为△ABC 是锐角三角形,所以cos 0>cos A 2=c r >cos π4,即22<c r <1,所以22<ac a 2-c 2<1,即22<e 1-e 2<1,解得e ∈⎝ ⎛⎭⎪⎫6-22,5-12. 答案:⎝⎛⎭⎪⎫6-22,5-129.已知椭圆的中心在原点,对称轴为坐标轴,焦点在x 轴上,短轴的一个顶点B 与两个焦点F 1,F 2组成的三角形的周长为4+23,且∠F 1BF 2=2π3,求椭圆的标准方程.解:设长轴长为2a ,焦距为2c ,则在△F 2OB 中,由∠F 2BO =π3得:c =32a ,所以△F 2BF 1的周长为2a +2c =2a +3a =4+23,∴a =2,c =3,∴b 2=1;故所求椭圆的标准方程为x 24+y 2=1.10.已知椭圆C 1:x 24+y 2=1,椭圆C 2以C 1的长轴为短轴,且与C 1有相同的离心率.(1)求椭圆C 2的方程;(2)设O 为坐标原点,点A ,B 分别在椭圆C 1和C 2上, OB →=2OA →,求直线AB 的方程.解:(1)由已知可设椭圆C 2的方程为y 2a 2+x 24=1(a >2),其离心率为32,故a 2-4a =32,则a =4,故椭圆C 2的方程为y 216+x24=1.(2)法一:A ,B 两点的坐标分别记为(x A ,y A ),(x B ,y B ),由OB →=2OA →及(1)知,O ,A ,B 三点共线且点A ,B 不在y 轴上,因此可设直线AB 的方程为y =kx .将y =kx 代入x 24+y 2=1中,得(1+4k 2)x 2=4,所以x 2A =41+4k2,将y =kx 代入y 216+x 24=1中,得(4+k 2)x 2=16,所以x 2B =164+k2,又由OB →=2OA →,得x 2B =4x 2A ,即164+k 2=161+4k2,解得k =±1,故直线AB 的方程为y =x 或y =-x . 法二:A ,B 两点的坐标分别记为(x A ,y A ),(x B ,y B ), 由OB →=2OA →及(1)知,O ,A ,B 三点共线且点A ,B 不在y 轴上,因此可设直线AB 的方程为y =kx .将y =kx 代入x 24+y 2=1中,得(1+4k 2)x 2=4,所以x 2A =41+4k2,由OB →=2OA →,得x 2B =161+4k 2,y 2B =16k 21+4k2,将x 2B ,y 2B 代入y 216+x 24=1中,得4+k 21+4k 2=1,即4+k 2=1+4k 2,解得k =±1,故直线AB 的方程为y =x 或y =-x .[能力提升] 1.过椭圆x 25+y 24=1的右焦点作一条斜率为2的直线与椭圆交于A ,B 两点,O 为坐标原点,则△OAB 的面积为________.解析:椭圆x 25+y 24=1的右焦点F 2(1,0),故直线AB 的方程y =2(x -1),由⎩⎪⎨⎪⎧x 25+y 24=1y =2(x -1),消去y ,整理得3x 2-5x =0,设A (x 1,y 1),B (x 2,y 2),x 1<x 2,则x 1,x 2是方程3x 2-5x =0的两个实根,解得x 1=0,x 2=53,故A (0,-2),B ⎝ ⎛⎭⎪⎫53,43,故S △OAB =S △OFA +S △OFB =12×⎝ ⎛⎭⎪⎫|-2|+43×1=53.答案:532.设F 1、F 2是椭圆E :x 2a 2+y 2b 2=1(a >b >0)的左、右焦点,P 为直线x =3a2上一点,△F 2PF 1是底角为30°的等腰三角形,则E 的离心率为________.解析:由题意,知∠F 2F 1P =∠F 2PF 1=30°, ∴∠PF 2x =60°.∴PF 2=2×⎝ ⎛⎭⎪⎫32a -c =3a -2c . ∵F 1F 2=2c ,F 1F 2=PF 2,∴3a -2c =2c ,∴e =c a =34.答案:343.椭圆x 29+y 24=1的焦点为F 1,F 2,点P 为其上的动点,当∠F 1PF 2为钝角时,求点P 的横坐标的取值范围.解:设点P 的坐标为(x ,y ),F 1(-5,0),F 2(5,0), 在三角形PF 1F 2中,由余弦定理得:cos ∠F 1PF 2=PF 21+PF 22-F 1F 222PF 1·PF 2,因为PF 1+PF 2=6,F 1F 2=25,故cos ∠F 1PF 2=36-2PF 1·PF 2-202PF 1·PF 2=162PF 1·PF 2-1≥162⎝ ⎛⎭⎪⎫PF 1+PF 222-1=-19,当且仅当PF 1=PF 2时取等号,即-19≤cos ∠F 1PF 2≤1.所以当-19≤cos ∠F 1PF 2<0时,∠F 1PF 2为钝角.令PF 1→·PF 2→=0,因为PF 1→=(-5-x ,-y ), PF 2→=(5-x ,-y ),则x 2-5+y 2=0,y 2=-x 2+5,代入椭圆方程得:x 2=95,x =±355,所以点P 的横坐标的取值范围是-355<x <355.4.如图,在平面直角坐标系xOy 中,椭圆x 2a 2+y 2b 2=1(a >b >0)的左、右焦点分别为F 1(-c ,0)、F 2(c ,0).已知点(1,e )和⎝ ⎛⎭⎪⎫e ,32都在椭圆上,其中e 为椭圆的离心率.(1)求椭圆的方程;(2)设A ,B 是椭圆上位于x 轴上方的两点,且直线AF 1与直线BF 2平行,AF 2与BF 1交于点P .(ⅰ)若AF 1-BF 2=62,求直线AF 1的斜率;(ⅱ)求证:PF 1+PF 2是定值.解:(1)由题设知a 2=b 2+c 2,e =c a.由点(1,e )在椭圆上,得1a 2+c 2a 2b2=1,解得b 2=1,于是c 2=a 2-1.又点⎝⎛⎭⎪⎫e ,32在椭圆上,所以e 2a 2+34b 2=1,即a 2-1a 4+34=1,解得a 2=2.因此,所求椭圆的方程是x 22+y 2=1. (2)由(1)知F 1(-1,0),F 2(1,0),又直线AF 1与BF 2平行,所以可设直线AF 1的方程为x +1=my ,直线BF 2的方程为x -1=my .设A (x 1,y 1),B (x 2,y 2),y 1>0,y 2>0.由⎩⎪⎨⎪⎧x 212+y 21=1,x 1+1=my 1,得(m 2+2)y 21-2my 1-1=0, 解得y 1=m +2m 2+2m 2+2,故AF 1=(x 1+1)2+(y 1-0)2=(my 1)2+y 21=2(m 2+1)+m m 2+1m 2+2.①同理,BF 2=2(m 2+1)-m m 2+1m 2+2.②(ⅰ)由①②得AF 1-BF 2=2m m 2+1m +2,解2m m 2+1m 2+2=62得m 2=2,注意到m >0,故m = 2.所以直线AF 1的斜率为1m =22.(ⅱ)证明:因为直线AF 1与BF 2平行,所以PB PF 1=BF 2AF 1, 于是PB +PF 1PF 1=BF 2+AF 1AF 1, 故PF 1=AF 1AF 1+BF 2BF 1.由B 点在椭圆上知BF 1+BF 2=22,从而PF 1=AF 1AF 1+BF 2(22-BF 2).同理,PF 2=BF 2AF 1+BF 2(22-AF 1).因此PF 1+PF 2=AF 1AF 1+BF 2(22-BF 2)+BF 2AF 1+BF 2·()22-AF 1=22-2AF 1·BF 2AF 1+BF 2.由①②得,AF 1+BF 2=22(m 2+1)m 2+2,AF 1·BF 2=m 2+1m 2+2,∴PF 1+PF 2=22-22=322,∴PF 1+PF 2是定值.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019年精心整理试题、试卷、学案、教案
You and your family are invited to join the YMCA for a Halloween hike up Badger Mountain! Make sure to wear your Hallowee
1 / 4
2018-2019学年高中数学第二章圆锥曲线与方程2-4-2抛物
线的几何性质作业苏教版选修1-1
[基础达标]
1.设抛物线y2=mx的准线与直线x=1的距离为3,则抛物线的
方程为________.
解析:当m>0时,准线方程为x=-=-2,
∴m=8,此时抛物线方程为y2=8x;
当m<0时,准线方程为x=-=4,
∴m=-16,此时抛物线方程为y2=-16x.
∴所求抛物线方程为y2=8x或y2=-16x.
答案:y2=8x或y2=-16x
2.已知抛物线C的顶点为坐标原点,焦点在x轴上,直线y=x
与抛物线C交于A,B两点.若P(2,2)为AB的中点,则抛物线C的方
程为________.
解析:设抛物线方程为y2=2px,A(x1,y1),B(x2,y2),则⇒y
-y=2p(x1-x2),
即·(y1+y2)=2p⇒2p=1×4⇒p=2.
故y2=4x.
答案:y2=4x
3.设O是坐标原点,F是抛物线y2=2px(p>0)的焦点,A是抛物
线上的一点,与x轴正向的夹角为60°,则||=________.
解析:如图,过A作AD⊥x轴于D.
在Rt△AFD中,∠AFD=60°.
令FD=m,则FA=2m.
AD=m.
根据抛物线的定义可知.
p+m=2m.∴m=p.
∴||== =p.
答案:p
4.若抛物线y2=2x上的一点M到坐标原点O的距离为,则M到
该抛物线焦点的距离为________.
解析:依题意,设点M(x,y),其中x>0,则有,由此解得x=1,
又该抛物线的准线方程为x=-,结合抛物线的定义,点M到该抛物
2019年精心整理试题、试卷、学案、教案
You and your family are invited to join the YMCA for a Halloween hike up Badger Mountain! Make sure to wear your Hallowee
2 / 4
线的焦点的距离等于1+=.
答案:
3
2
5.直线y=x-3与抛物线y2=4x交于A,B两点,过A,B两点
向抛物线的准线作垂线,垂足分别为P,Q,则梯形APQB的面积为
________.
解析:直线y=x-3与抛物线y2=4x交于A,B两点,过A,B两
点向抛物线的准线作垂线,垂足分别为P,Q,联立方程组得,消元得
x2-10x+9=0,
解得,和,∴AP=10,BQ=2,PQ=8,
∴梯形APQB的面积为48.
答案:48
6. 如图,圆形花坛水池中央有一喷泉,水管OP=1 m,水从喷头
P喷出后呈抛物线状,先向上至最高点后落下,若最高点距水面2 m,
P距抛物线对称轴1 m,则为使水不落到池外,水池直径最小为
________m.
解析:如图,建立平面直角坐标系,设抛物线方程为x2=-
2py(p>0),则P(-1,-1),代入抛物线方程得p=,抛物线x2=-
y,代入点(x,-2),得x=,即水池半径最小为r=(1+)m,水池直
径最小为2r=(2+2)m.
答案:2+2
2
7.已知抛物线的焦点F在x轴上,直线l过点F且垂直于x轴,
l与抛物线交于A、B两点,O为坐标原点,若△OAB的面积等于4,求
此抛物线的标准方程.
解:由题意,抛物线方程为y2=2px(p≠0),
焦点F,直线l:x=,
∴A、B两点坐标为,,
∴AB=2|p|.
∵△OAB的面积为4,
∴··2|p|=4,∴p=±2.
∴抛物线的标准方程为y2=±4x.
8. 如图,过抛物线y2=x上一点A(4,2)作倾斜角互补的两条直
线AB,AC交抛物线于B,C两点,求证:直线BC的斜率是定值.
证明:设kAB=k(k≠0),
∵直线AB,AC的倾斜角互补,
∴kAC=-k(k≠0),
∵直线AB的方程是y=k(x-4)+2.
由方程组消去y后,整理得
