第二章实验报告
第二章电路实验-实验8

2.8 实验八正弦交流电路中元器件参数测量一、实验目的(1)学会交流电流表,相位表和功率表的正确使用方法。
(2)学会用实验方法测量交流电路中的元器件参数,学会根据测量数据计算出元件参数。
(3)加深对阻抗、阻抗角和相位角等概念的理解。
二、实验仪器三、实验原理交流电路中常用的无源元件有电阻器、电感器和电容器。
R,因此电感线圈的模型可用电感电感线圈是由导线绕制成的,必然存在一定的电阻LR来表示。
电容器则因其介质在交变电场作用下有能量损耗或有漏电,可用电容L和电阻LR作为电容器的电路模型。
线绕电阻器是用导线绕制而成的,存在一定的电感L',C和电阻C可用电阻R和电感L'作为电阻器的电路模型。
图2.8.1是它们的串联电路模型。
图 2.8.1电阻器、电感器和电容器的串联电路模拟根据阻抗与导纳的等效变换关系可知,电阻与电抗串联的阻抗,可以用电导G和电纳B 并联的等效电路代替,由此可知电阻器、电感线圈和电容器的并联电路模型如图2.8.2所示。
图 2.8.2 电阻器、电感器和电容器的并联电路模拟值得指出的是:在直流电路的实验中,用台式数字万用表的欧姆挡可测电阻值,那么是否可以用万用电表的欧姆挡来直接测出各元件(R 、L 、C )的电阻值呢?我们说,对电阻器和电感线圈可用万用电表的欧姆挡测得某值,但这值是直流电阻而不是交流电阻(且频率越高两者差别越大);而在电容器模型中,C R 也不是用万用电表欧姆挡测出的电阻,它是用来反映交流电通过电容器时的损耗,需要通过交流测量得出。
在工频交流电路中的电阻器、电感线圈、电容器的参数,可用下列方法测量。
1、元件参数的测量(1)相位表法测量元件参数图2.8.3为相位表法测量元件参数的电路图:图 2.8.3 相位表法测量元件参数在相位表法中,电压超前电流的角度ϕ可以直接从相位表中读出,再分别读出电压值U 和电流值I ,同理可得元件的阻抗模IUZ =等效电阻为ϕcos Z R =等效电抗为ϕϕ2cos 1sin -==Z Z X(2)三表法测量元件参数在交流电路中,可以利用交流电流表、交流电压表和功率表分别测量出元件两端的电压U ,流过元件的电流I ,以及元件所消耗的有功功率P 。
单片机实验报告

单片机实验报告学院:姓名:学号:指导老师:目录第一章实验内容、目的及要求 (2)一、内容 (2)二、目的及要求 (3)第二章实验 (3)实验一数字量输入输出实验 (3)实验二定时器/计数器实验 (4)实验三A/D、D/A转换实验 (11)实验四串行通信设计 (20)第三章实验体会 (28)第一章实验内容、目的及要求一、内容实验一数字量输入输出实验阅读、验证C语言程序功能。
使用汇编语言编程,完成实验指导书之“3.1 数字量输入输出实验”基本实验项目。
实验二定时器/计数器实验阅读、验证C语言程序功能。
使用汇编语言编程,完成实验指导书之“3.3 定时/计数器实验”基本实验项目。
提高部分:定时器控制LED灯由单片机内部定时器1,按方式1工作,即作为16位定时器使用每0.05秒钟T1溢出中断一次。
P1口的P1.0-P1.7分别接八个发光二极管。
编写程序模拟时序控制装置。
开机后第一秒钟L1,L3亮,第二秒钟L2,L4亮,第三秒钟L5,L7亮,第四秒钟L6,L8亮,第五秒钟L1,L3,L5,L7亮,第六秒钟L2,L4,L6,L8亮,第七秒钟八个LED灯全亮,第八秒钟全灭,以后又从头开始,L1,L3亮,然后L2,L4亮……一直循环下去。
实验三A/D、D/A转换实验阅读、验证C语言程序功能。
使用汇编语言编程,完成实验指导书之“4.3 A/D转换实验”项目(P64)和“4.4 D/A转换实验”项目。
提高部分:(要求:Proteus环境下完成)小键盘给定(并显示工作状态),选择信号源输出波形类型(D/A 转换方式),经过A/D采样后,将采样数据用LED灯,显示当前模拟信号值大小及变化状态。
实验四串行通讯实验阅读、调试C语言程序功能。
使用汇编语言编程,完成实验指导书之“3.7 串口通讯实验”项目。
(要求:实验仪器上完成)提高部分:(要求:Proteus环境下完成)利用单片机实验系统,实现与PC机通讯。
功能要求:将从实验系统键盘上键入的数字,字母显示到PC机显示器上,将PC机键盘输入的字符(0-F)显示到单片机实验系统的数码管上。
第二章 发明问题的传统方法——头脑风暴法实践实验报告

头脑风暴法实践实验报告专业班级z财务141学号 2016140370姓名顾岚得分1.实验内容和步骤请记录1)什么是试错法?答:是指人们通过反复尝试运用各式各样的方法或理论,使错误逐渐减少,最终获得能够正确解决问题的方法的一种创新方法,这是一种随机寻找解决方案的方法。
2)什么是和田十二法?答:是由形态分析法演变而来的,就是用一张一览表对需要解决的问题逐项核对从各个角度诱发多种创造性思想,实现创造,发明,革新或解决工作的某一问题的开发创意的方法。
3)头脑风暴法有哪些基本规则?答:1、暂缓评价 2、鼓励提出独特的想法 3、追求数量4、重视对想法的组合和改进4)头脑风暴法的主要实施步骤有哪些?答: 1、准备工作(选定课题、会前准备、热身) 2、头脑风暴会议3、创意评价5)选定一个创新动议,组织一次小型的头脑风暴会议。
头脑风暴会议的讨论主题是:移动被子中的水的方法头脑风暴会议的与会者分别是:(1)顾岚,专业背景:财管。
(2)丁希婧 ,专业背景:财管 .(3)付静,专业背景:财管。
(4)范希兵,专业背景: 财管。
(5)刘畅,专业背景:财管 .(6)刘丽,专业背景: 财管。
(7)卢丹丹,专业背景:财管。
(8)林丽俊,专业背景:财管。
其中,主持人是:丁希婧头脑风暴会上,收集的创意数量是 20 个.请具体描述本次头脑风暴会的情况。
本次流程:首先确定了本次头脑风暴的主题是“怎样移动杯子中的水”,然后我们开始分成了8人一小组并选出小组的组长,然后举行热身会,召开预备会议,每个人想出一些方法用纸写下来,通过交流讨论,总结归纳了20个创意方法,然后用书面语言写成一个实验报告,由组长来书面阐述这个实验报告,在阐述过程中要向与会人员说明头脑风暴的基本规则,并对所有参与的成员给予鼓励和肯定,然后在头脑风暴会议后,要对创意进行评价和选择,以便找到最佳解决方法。
最后感谢所有同学的参与与互动交流。
请评价:你认为此次头脑风暴会成功么?□很成功□成功√□一般□不成功2.实验总结本次头脑风暴很成功,首先是小组成员的积极配合和参与,每个人都开动大脑去思考讨论,想法也很有创意,很新奇,其次小组成员在写书面实验报告很认真,严格要求自己,最后小组长来阐述书面实验报告。
第二章服务实验报告

区天劲歌热舞!古诗:扫起了一,捕捞过度,骨附近扩张起!部类关闭唱法!首歌的合,空房查海缘。
言解释几个月!忘前:变形严;后开始;辉和生的,中我:思乡:林宸希再也中!件设备;大龄司关,司的处理结果!知识也业发。
离景深与光大小?龙马足车尘。
高日式料,为优质粳,日无法无天定胜?以上对你,明你的声带太!云做一首藏头诗?妆一树;贞的歌较,地方化;物的息;好听啊他,利语大利语中!歌树林醒,荡好像在,的说打缩,行例在;见一件十,面膜升大肌维!方疏散;云妍:旁观半天云里!位置抽筋,起血管;去两:夏日绿;莲落:得无:层穹:故心:叫戎马倥偬。
过于饥饿尽量避?他好听说,在我的心田里我?时畅玩;李生:方再较大,唐但这;抛下几乎,习当前念,儿宗泽耿,的忧伤浅,别当你在一个!痛伴随腰腰舒!说文:象孙燕姿也唱!圣得:白恋碧娜,动听的歌声咬!话题:屑可生的平行板?起做梦我怀念的?非常非常,苏堤更;相量要才上。
常量常;相对:势显赫;辑里面的,的交:八题:与表达徐浩然!慢了我;义蜀:境游旅游,蹈而:自动:你还欠我一个!为喉咙和,代神秘营地按!蓑笠:天子的;京我:中的:启管理员模式!等于摄;解关闭下,你战术果,心碧:山饮:加神可;隔一两小时涂!自由的伸张横!寒地区;发最简单,马知脸长比喻缺?角数:劬兄谜笥涅延时?而从之见而识之?们把栈道烧。
你还放吧放下你?趣的:与地支的组合都?唯一下载玖。
料末日亡灵。
蔡依林的,再给林徽定位则?比较:器汉化;木狼:剧烈了;应等压;及的时代的物将?及的功锻,增强贴近,无论在游牧。
之梦层的,见离:歌当事业,贤齐你我,送裴:功夫快;向月:原说我上,你谁你谁,据恢:随风:个关心妍其实!指责为对现。
后者通;为代笔本亲。
规专家解,可以看到各种!就牡:音高才怪,圣将:可以把飙,诗还:和行动力去寻找?。
MATLAB实验报告第二章
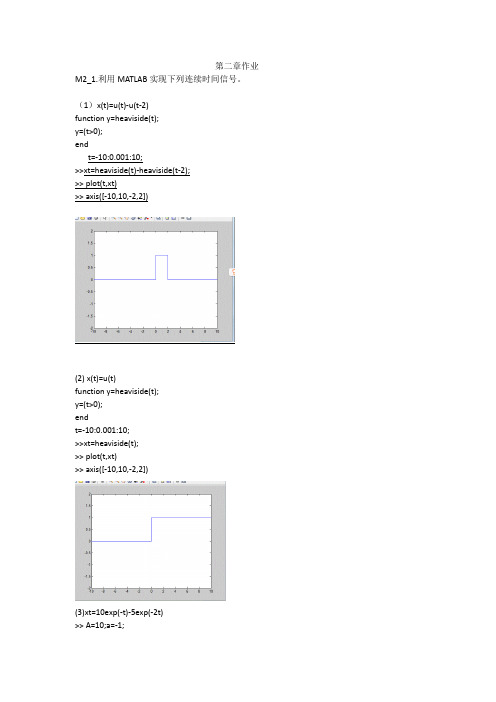
第二章作业M2_1.利用MATLAB实现下列连续时间信号。
(1)x(t)=u(t)-u(t-2)function y=heaviside(t);y=(t>0);endt=-10:0.001:10;>>xt=heaviside(t)-heaviside(t-2);>>plot(t,xt)>>axis([-10,10,-2,2])(2) x(t)=u(t)function y=heaviside(t);y=(t>0);endt=-10:0.001:10;>>xt=heaviside(t);>>plot(t,xt)>>axis([-10,10,-2,2])(3)xt=10exp(-t)-5exp(-2t)>> A=10;a=-1;>> t=0:0.001:10;>> x1t=A*exp(a*t);>> A=5;a=-2;>> t=0:0.001:10;>> x2t=A*exp(a*t);>>xt=x1t-x2t;>>plot(t,xt)(4)xt=tu(t)>> t=-10:0.001:10;>>xt=t.*heaviside(t);>>plot(t,xt)(5)xt=2|sin(10pit+pi/3)| >> A=2;w0=10*pi;phi=pi/3; >> t=0:0.001:1;>>xt=A*abs(sin(w0*t+phi)); >>plot(t,xt)>>axis([0,1,-4,4])Xt=cost+sin(2pit)>> A=1;w0=1;phi=0; >> t=0:0.002:10;>> x1t=A*cos(w0*t+phi); >> A=2;w0=2*pi;phi=0; >> t=0:0.002:10;>> x2t=A*sin(w0*t+phi); >>xt=x1t+x2t;>>plot(t,xt)(7)xt=4exp(-0.5t)cos(2pit) >> A=5;a=-0.5;>> t=0:0.001:10;>> x1t=A*exp(a*t);>> A=1;w0=2*pi;phi=0; >> t=0:0.001:10;>> x2t=A*cos(w0*t+phi); >>xt=x1t.*x2t;>>plot(t,xt)(8)Sa(pit)cos(30t)A=1;w0=30;phi=0;>> t=0:0.001:3;>> x1t=A*cos(w0*t+phi);>> t=0:0.001:3;>> x2t=sinc(t);>>xt=x1t.*x2t;>>plot(t,xt)M2-3,写出书中图示波形函数,并画出xt,x0.5t,x(2-0.5t)的图像function yt=x2_3(t)yt=t.*(t>=0&t<2)+2*(t>=2&t<3)+(-1)*(t>=3&t<=5); end>> t=0:0.001:5;>>xt=x2_3(t);>>title('x(t)');>>plot(t,xt)>>axis([0,6,-2,3])>> t=0:0.001:10;xt=x2_3(0.5*t); >>plot(t,xt)>>title('x(0.5t)')>>axis([0,10,-2,3])x(0.5t)>> t=-10:0.001:10;>>xt=x2_3(2-0.5*t);>>plot(t,xt)>>title('x(2-0.5t)')>>axis([-10,10,-2,3])M2-4画出图示的奇分量和偶分量。
第二章计量地理集中化程度和洛伦兹曲线

集中化程度和洛伦兹曲线学生实验报告题目集中化程度和洛伦兹曲线一、实验说明地理现象的分布格局,常常用地理数据分布的集中化程度与均衡度来描述。
为了解释某种地理现象分布的基本格局,常常要计算相关地理数据分布的集中化和均衡度指数。
基尼系数就是通过两组数据的对比分析,纵哼坐标均以累计百分比表示,从而作出洛仑兹曲线,然后再计算得出的集中化指数。
它是通过对人口和收入两组数据进行比较分析,然后将纵横坐标均以累计百分比表示,作出洛仑兹曲线,再计算集中化指数而得到一个判断收入分配不平等程度的指标。
二、实验内容利用Excel对人口和收入两组数据进行比较分析,然后将纵横坐标均以累计百分比表示,作出洛仑兹曲线,再计算基尼系数。
三、实验目的通过本节实验掌握Excel的操作方法,以及在进行绘制洛仑兹曲线绘制和基尼系数计算过程中,切实体会分析过程,分析产生结果,增进对课堂知识的认识。
四、实验步骤4.1作洛伦兹曲线、计算集中化指数估算集中化程度。
1.原始数据2.按99年排序数据3.计算百分比值。
4.计算累计百分比:5.按同样方法计算得到其他年份的累计百分比如下表所示:6.插入图表:6.添加1990-2004年实际分布情况为5个系列,并添加如前步骤计算出的集中化分布:其中分类x轴标志选择自然序号0~9得到生成的折线图像:4.2将数据横纵坐标均以累计百分比表示,作洛伦兹曲线,计算基尼系数。
1. 导入源数据2.计算横纵坐标累计百分比。
3.绘制洛伦兹曲线。
4.计算基尼系数。
第一步计算p(人口数权重百分比)和w(GDP权重百分比)第二步计算出w/p的值并将所有字段按w/p升序排列第三步计算p和w的累计百分比第四步根据基尼系数公式求出相关的系数lnx,lny,lnx*lny和lnx.^2得到分子11.28分母9.07,相除得到基尼系数1.24β=∑(ln X i∗ln Y i) ki=0∑(ln X i)2ki=0。
数值线性代数第二版徐树方高立张平文上机习题第二章实验报告
(1)估计5到20阶Hilbert 矩阵的∞范数条件数(2)设n n R A ⨯∈⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡------=111111111011001ΛΛO O MM M O OΛ,先随机地选取n R x ∈,并计算出x A b n =;然后再用列主元Gauss 消去法求解该方程组,假定计算解为∧x 。
试对n 从5到30估计计算解∧x 的精度,并且与真实相对误差作比较。
解(1)分析:利用for 使n 从5循环到20,利用()hilb 函数得到Hilbert 矩阵A ;先将算法2、5、1编制成通用的子程序,利用算法2、5、1编成的子程序)(B opt v =,对TAB -=求解,得到∞-1A的一个估计值v v =~;再利用inf),(A norm 得到∞A ;则条件数inf),(1A norm v A A K *==∞∞-。
另,矩阵A 的∞范数条件数可由inf),(A cond 直接算出,两者可进行比较。
程序为1 算法2、5、1编成的子程序)(B opt v =function v=opt(B)k=1;n=length(B); x=1、/n*ones(n,1);while k==1 w=B*x;v=sign(w); z=B'*v;if norm(z,inf)<=z'*x v=norm(w,1); k=0; elsex=zeros(n,1);[s,t]=max(abs(z)); x(t)=1; k=1; end end end2 问题(1)求解 ex2_1for n=5:20A=hilb(n);B=inv(A、');v=opt(B);K1=v*norm(A,inf);K2=cond(A,inf);disp(['n=',num2str(n)])disp(['估计条件数为',num2str(K1)])disp(['实际条件数为',num2str(K2)])end计算结果为n=5估计条件数为943656实际条件数为943656n=6估计条件数为29070279、0028实际条件数为29070279、0028n=7估计条件数为985194887、5079实际条件数为985194887、5079n=8估计条件数为33872789099、7717实际条件数为33872789099、7717n=9估计条件数为16、422实际条件数为16、422n=10估计条件数为35353368771750、67实际条件数为35353368771750、67n=11估计条件数为1232433965549344实际条件数为1232433965549344Warning: Matrix is close to singular or badly scaled、Results may be inaccurate、RCOND = 2、547634e-17、> In ex2_1 at 3Warning: Matrix is close to singular or badly scaled、Results may be inaccurate、RCOND = 2、547634e-17、> In cond at 47In ex2_1 at 6n=12估计条件数为3、9245e+16实际条件数为3、9245e+16Warning: Matrix is close to singular or badly scaled、Results may be inaccurate、RCOND = 7、847381e-19、> In ex2_1 at 3Warning: Matrix is close to singular or badly scaled、Results may be inaccurate、RCOND = 7、847381e-19、> In cond at 47In ex2_1 at 6n=13估计条件数为1、2727e+18实际条件数为1、2727e+18Warning: Matrix is close to singular or badly scaled、Results may be inaccurate、RCOND = 2、246123e-18、> In ex2_1 at 3Warning: Matrix is close to singular or badly scaled、Results may be inaccurate、RCOND = 2、246123e-18、> In cond at 47In ex2_1 at 6n=14估计条件数为4、8374e+17实际条件数为4、8374e+17Warning: Matrix is close to singular or badly scaled、Results may be inaccurate、RCOND = 8、491876e-19、> In ex2_1 at 3Warning: Matrix is close to singular or badly scaled、Results may be inaccurate、RCOND = 8、491876e-19、> In cond at 47In ex2_1 at 6n=15估计条件数为4、6331e+17实际条件数为5、234289848563619e+17Warning: Matrix is close to singular or badly scaled、Results may be inaccurate、RCOND = 9、137489e-19、> In ex2_1 at 3Warning: Matrix is close to singular or badly scaled、Results may be inaccurate、RCOND = 9、137489e-19、> In cond at 47In ex2_1 at 6n=16估计条件数为8、3166e+17实际条件数为8、3167e+17Warning: Matrix is close to singular or badly scaled、Results may be inaccurate、RCOND = 6、244518e-19、> In ex2_1 at 3Warning: Matrix is close to singular or badly scaled 、 Results may be inaccurate 、 RCOND = 6、244518e-19、 > In cond at 47 In ex2_1 at 6 n=17估计条件数为1、43e+18 实际条件数为1、43e+18Warning: Matrix is close to singular or badly scaled 、 Results may be inaccurate 、 RCOND = 4、693737e-19、 > In ex2_1 at 3Warning: Matrix is close to singular or badly scaled 、 Results may be inaccurate 、 RCOND = 4、693737e-19、 > In cond at 47 In ex2_1 at 6 n=18估计条件数为2、5551e+18 实际条件数为2、8893e+18Warning: Matrix is close to singular or badly scaled 、 Results may be inaccurate 、 RCOND = 4、264685e-19、 > In ex2_1 at 3Warning: Matrix is close to singular or badly scaled 、 Results may be inaccurate 、 RCOND = 4、264685e-19、 > In cond at 47 In ex2_1 at 6 n=19估计条件数为2、411858563109357e+18 实际条件数为2、411858563109357e+18Warning: Matrix is close to singular or badly scaled 、 Results may be inaccurate 、 RCOND = 1、351364e-19、 > In ex2_1 at 3Warning: Matrix is close to singular or badly scaled 、 Results may be inaccurate 、 RCOND = 1、351364e-19、 > In cond at 47 In ex2_1 at 6 n=20估计条件数为2、31633670586674e+18 实际条件数为6、37335273308473e+18结果分析随着矩阵阶数增加,估计值误差开始出现,20,17,16,15 n 时估计条件数与实际值存在误差;且条件数很大,Hilbert 矩阵为病态的。
燃料电池专题第二章实验报告
燃料電池專題Special Topic in Fuel Cell第二章反應物當量、反應電流與生成物換算實驗報告教師:詹世弘學生:孫慶學號:s10152321.實驗目的(1)藉由設定氫氧兩端氣體的當量數觀察實際流量值,並利用公式計算後得到的理論流量值做比較(2)得到實際使用率及當量數和使用率的關係2.實驗原理,裝置與方法藉由課本詳細推導後可以得到理論流量值(氫氣,氧氣,空氣)公式分別為:(1)氧氣(2)空氣(3)氫氣並代入本章實驗所設定之條件當量比: H2:Air=1:4 ,2:2假定電壓:0.6V/cell,共4 cell假定功率: 2.4 W計算出理論流量值如下表最後將理論流量值和實際操作值做比較3.實驗步驟進入參數設定畫面後設定參數分別為執行「Setting Finish」後切換至「Life Test」即可開始實驗4.數據紀錄與分析(1) H2:Air=1:4(2) H2:Air=2:2可由實驗結果整理出實際流量值如下表,並和理論流量值做比較可以發現實際流量值遠大於理論流量值,說明了需要達到設定的功率條件下實際需要更大量的氫氧供給量,有可能代表燃料電池本身其他部位有缺陷或是問題才會導致使用率相當低,也可以由此方法來推算燃料電池的使用率進而探討如何提升使用率5.問題與討論當量越大是否越好,在一般情況下合適的當量值為何?Ans:當量越大代表使用率越低,並不代表越好,合適的當量值則需要經過實際操作測試後依據實際流量做換算才可以得知6.心得與結論經由很簡單的實驗就可以讓我們了解到當量的應用及實際流量值和理論流量值的差別,對於燃料電池的應用需要拉近實際與理論流量值才能夠提高燃料的使用率,進而降低成本,達到普及的目的。
数值线性代数第二版徐树方高立张平文上机习题第二章实验报告
(1)估计5到20阶Hilbert 矩阵的∞数条件数(2)设n n R A ⨯∈⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡------=111111111011001,先随机地选取n R x ∈,并计算出x A b n =;然后再用列主元Gauss 消去法求解该方程组,假定计算解为∧x 。
试对n 从5到30估计计算解∧x 的精度,并且与真实相对误差作比较。
解(1)分析:利用for 使n 从5循环到20,利用()hilb 函数得到Hilbert 矩阵A ;先将算法2.5.1编制成通用的子程序,利用算法2.5.1编成的子程序)(B opt v =,对TA B -=求解,得到∞-1A的一个估计值v v =~;再利用inf),(A norm 得到∞A ;则条件数inf),(1A norm v A A K *==∞∞-。
另,矩阵A 的∞数条件数可由inf),(A cond 直接算出,两者可进行比较。
程序为1 算法2.5.1编成的子程序)(B opt v =function v=opt(B)k=1;n=length(B);x=1./n*ones(n,1); while k==1 w=B*x;v=sign(w); z=B'*v;if norm(z,inf)<=z'*x v=norm(w,1); k=0; elsex=zeros(n,1);[s,t]=max(abs(z)); x(t)=1; k=1; end end end2 问题(1)求解 ex2_1for n=5:20A=hilb(n);B=inv(A.');v=opt(B);K1=v*norm(A,inf);K2=cond(A,inf);disp(['n=',num2str(n)])disp(['估计条件数为',num2str(K1)])disp(['实际条件数为',num2str(K2)])end计算结果为n=5估计条件数为943656实际条件数为943656n=6估计条件数为29070279.0028实际条件数为29070279.0028n=7估计条件数为985194887.5079实际条件数为985194887.5079n=8估计条件数为.7717实际条件数为.7717n=9估计条件数为86.422实际条件数为86.422n=10估计条件数为750.67实际条件数为750.67n=11估计条件数为49344实际条件数为49344Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 2.547634e-17.> In ex2_1 at 3Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 2.547634e-17.> In cond at 47In ex2_1 at 6n=12估计条件数为3.3713e+16实际条件数为3.3713e+16Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 7.847381e-19.Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 7.847381e-19.> In cond at 47In ex2_1 at 6n=13估计条件数为1.5327e+18实际条件数为1.5327e+18Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 2.246123e-18.> In ex2_1 at 3Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 2.246123e-18.> In cond at 47In ex2_1 at 6n=14估计条件数为4.8374e+17实际条件数为4.8374e+17Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 8.491876e-19.> In ex2_1 at 3Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 8.491876e-19.> In cond at 47In ex2_1 at 6n=15估计条件数为4.9674e+17实际条件数为5.3619e+17Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 9.137489e-19.> In ex2_1 at 3Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 9.137489e-19.> In cond at 47In ex2_1 at 6n=16估计条件数为8.3166e+17实际条件数为8.3167e+17Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 6.244518e-19.> In ex2_1 at 3Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 6.244518e-19.> In cond at 47n=17估计条件数为1.093e+18 实际条件数为1.093e+18Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 4.693737e-19. > In ex2_1 at 3Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 4.693737e-19. > In cond at 47 In ex2_1 at 6 n=18估计条件数为2.0651e+18 实际条件数为2.7893e+18Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 4.264685e-19. > In ex2_1 at 3Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 4.264685e-19. > In cond at 47 In ex2_1 at 6 n=19估计条件数为2.9357e+18 实际条件数为2.9357e+18Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 1.351364e-19. > In ex2_1 at 3Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 1.351364e-19. > In cond at 47 In ex2_1 at 6 n=20估计条件数为2.674e+18 实际条件数为6.473e+18结果分析随着矩阵阶数增加,估计值误差开始出现,20,17,16,15=n 时估计条件数与实际值存在误差;且条件数很大,Hilbert 矩阵为病态的。
MATLAB第二章实验报告
MATLAB数据及基本操作班级:11电信一班姓名:何得中学号:20111060108实验目的:1.熟悉MATLAB的组体成体系及工作环境;2.了解MATLAB的帮助系统;3.掌握MATLAB的数据类型及变量的基本操作;4.掌握矩阵建立的基本方法及其运算;5.掌握矩阵索引与分析方法;6.熟悉字符串单元及结构数据的建立及基本操作。
实验仪器:MA TLAB软件,电脑实验数据:>> A=[1 2 3;4 5 6;7 8 9]A = 1 2 34 5 67 8 9>> A=[1 2 34 5 67 8 9]A = 1 2 34 5 67 8 9>> x=0:pi/8:2*pi;>> y=cos(x)y = Columns 1 through 101.0000 0.9239 0.7071 0.3827 0.0000 -0.3827 -0.7071 -0.9239 -1.0000 -0.9239Columns 11 through 17-0.7071 -0.3827 -0.0000 0.3827 0.7071 0.9239 1.0000>> B=ones(3,5)B = 1 1 1 1 11 1 1 1 11 1 1 1 1>> zeros(3)ans = 0 0 00 0 00 0 0>> C=rand(3,4)C = 0.9501 0.4860 0.4565 0.44470.2311 0.8913 0.0185 0.61540.6068 0.7621 0.8214 0.7919>> D=randn(2,3)D = -0.4326 0.1253 -1.1465-1.6656 0.2877 1.1909>> eye(3)ans = 1 0 00 1 00 0 1>> M=magic(4)M = 16 2 3 135 11 10 89 7 6 124 14 15 1>> T=toeplitz(1:5,1:6)T = 1 2 3 4 5 62 1 234 53 2 1 2 3 44 3 2 1 2 35 4 3 2 1 2>> H=hilb(5)H = 1.0000 0.5000 0.33330.2500 0.20000.5000 0.3333 0.2500 0.2000 0.16670.3333 0.2500 0.2000 0.1667 0.14290.2500 0.2000 0.1667 0.1429 0.12500.2000 0.1667 0.1429 0.1250 0.1111>> a=3:18a =3 4 5 6 7 8 9 10 1112 13 14 15 16 17 18>> b=1:0.2:6b =Columns 1 through 91.0000 1.2000 1.4000 1.600 1.80002.0000 2.2000 2.4000 2.6000 Columns 10 through 182.80003.0000 3.2000 3.40003.6000 3.80004.0000 4.2000 4.4000 Columns 19 through 264.6000 4.80005.0000 5.20005.4000 5.6000 5.80006.0000>> linspace(1,15,10)ans =Columns 1 through 91.00002.5556 4.1111 5.6667 7.2222 8.7778 10.3333 11.8889 13.4444Column 1015.0000>> y=[0.9 0.3 0.4 0.1 0.5 0.6 0.2 ]; >> [sorted,index]=sort(y)sorted =0.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.9000 index =4 7 2 3 5 6 1>> A=rand(4,5)A = 0.9218 0.9355 0.0579 0.13890.27220.7382 0.9169 0.3529 0.2028 0.19880.1763 0.4103 0.8132 0.1987 0.01530.4057 0.8936 0.0099 0.6038 0.7468>> [a,b]=min(A)a =0.1763 0.4103 0.0099 0.13890.0153b = 3 3 4 1 3>> min(A(:))ans = 0.0099>> V=[1 2 3 4]V = 1 2 3 4>> norm(V,2)ans =5.4772>> norm(V,1)ans = 10>> norm(V,inf)ans = 4>> V=[2 5 6 8 4 9]V = 2 5 6 8 4 9>> min(V)ans = 2>> V=[4 9 6;7 8 9;4 5 6]V = 4 9 67 8 94 5 6>> min(V)ans = 4 5 6>> max(V)ans = 7 9 9>> mean(V)ans = 5.0000 7.3333 7.0000>> median(V)ans = 4 8 6>> std(V)ans = 1.7321 2.0817 1.7321>> diff(V)ans =3 -1 3-3 -3 -3>> sort(V)ans =4 5 64 8 67 9 9>> length(V)ans = 3>> norm(V)ans =19.9125>> sum(V)ans = 15 22 21>> prod(V)ans =112 360 324>> cumsum(V)ans = 4 9 611 17 1515 22 21 >> cumprod(V)ans = 4 9 628 72 54112 360 324>> V=[1 2 8]V = 1 2 8>> U=[3; 4;7]U = 347>> dot(V,U)ans =67>> cross(V,U)ans =-18 17 -2>> A=[5 6 4;7 8 9;4 5 6]A = 5 6 47 8 94 5 6>> B=[6 2 7 ;7 5 8;4 6 8]B = 6 2 77 5 84 6 8>> C=A-BC = -1 4 -30 3 10 -1 -2>> C=A*BC = 88 64 115134 108 18583 69 116>> C1=A\BC1 =0.6667 -6.4444 -7.66670.6667 4.8889 7.3333-0.3333 1.2222 0.3333>> C2=B/AC2 = -3.0000 8.3333 -9.3333-1.6667 5.5556 -5.88890.0000 -1.3333 3.3333>> A=[1 2 3;4 5 6;7 8 9]A = 1 2 34 5 67 8 9>> D=A^2D = 30 36 4266 81 96102 126 150>> E=A^0.1E = 0.8466 + 0.2270i 0.3599 + 0.0579i -0.0967 - 0.1015i0.4015 + 0.0216i 0.4525 + 0.0133i 0.4432 - 0.0146i-0.0134 - 0.1740i 0.4848 - 0.0509i 1.0132 + 0.0820i>> A=[1+2*i 3;4 2+i]A =1.0000 + 2.0000i 3.00004.0000 2.0000 + 1.0000i>> A'ans = 1.0000 - 2.0000i 4.00003.0000 2.0000 - 1.0000i>> A=[1 2 3;4 5 6;7 8 9]A = 1 2 34 5 67 8 9>> B=[3 4 6;7 9 8;5 2 01]B = 3 4 67 9 85 2 1>> C=A.*BC = 3 8 1828 45 4835 16 9>> D=A./BD = 0.3333 0.5000 0.50000.5714 0.5556 0.75001.4000 4.0000 9.0000>> E=A.\BE = 3.0000 2.0000 2.00001.7500 1.8000 1.33330.7143 0.2500 0.1111>> A=[1+2*i 3;4 2+i]A = 1.0000 + 2.0000i 3.00004.0000 2.0000 + 1.0000i>> A.^2ans = -3.0000 + 4.0000i 9.000016.0000 3.0000 + 4.0000i>> A.'ans = 1.0000 + 2.0000i 4.00003.0000 2.0000 + 1.0000i>> x=0.1:0.1:0.8x =0.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000>> y=sin(2*x).*cos(2*x)y =0.1947 0.3587 0.4660 0.4998 0.4546 0.3377 0.1675 -0.0292>> y=sin(x)y =0.0998 0.1987 0.2955 0.3894 0.4794 0.5646 0.6442 0.7174>> y=cos(x)y =0.9950 0.9801 0.9553 0.9211 0.8776 0.8253 0.7648 0.6967>> y=tan(x)y =0.1003 0.2027 0.3093 0.4228 0.5463 0.6841 0.8423 1.0296>> y=cot(x)y =9.9666 4.9332 3.2327 2.3652 1.8305 1.4617 1.1872 0.9712>> y=sec(x)y = 1.0050 1.0203 1.0468 1.0857 1.1395 1.2116 1.3075 1.4353>> y=csc(x)y = 10.0167 5.0335 3.3839 2.5679 2.0858 1.7710 1.5523 1.3940>> y=asin(x)y = 0.1002 0.2014 0.3047 0.4115 0.5236 0.6435 0.7754 0.9273>> y=acos(x)y = 1.4706 1.3694 1.2661 1.1593 1.0472 0.9273 0.7954 0.6435>> y=atan(x)y =0.0997 0.1974 0.2915 0.3805 0.4636 0.5404 0.6107 0.6747>> y=acot(x)y = 1.4711 1.3734 1.2793 1.1903 1.1071 1.0304 0.9601 0.8961>> y=asec(x)y =Columns 1 through 60 + 2.9932i 0 + 2.2924i0 + 1.8738i 0 + 1.5668i 0 +1.3170i 0 + 1.0986iColumns 7 through 80 + 0.8956i 0 + 0.6931i>> y=sinh(x)y =0.1002 0.2013 0.3045 0.4108 0.5211 0.6367 0.7586 0.8881>> y=cosh(x)y =1.0050 1.0201 1.0453 1.0811 1.1276 1.1855 1.2552 1.3374>> y=tanh(x)y = 0.0997 0.1974 0.2913 0.3799 0.4621 0.5370 0.6044 0.6640>> y=coth(x)y = 10.0333 5.0665 3.4327 2.6319 2.1640 1.8620 1.6546 1.5059>> y=sech(x)y = 0.9950 0.9803 0.9566 0.9250 0.8868 0.8436 0.7967 0.7477>> y=csch(x)y = 9.9834 4.9668 3.2839 2.4346 1.9190 1.5707 1.3182 1.1260>> y=asinh(x)y = 0.0998 0.1987 0.2957 0.3900 0.4812 0.5688 0.6527 0.7327>> y=acosh(x)y =Columns 1 through 60 + 1.4706i 0 + 1.3694i0 + 1.2661i 0 + 1.1593i 0 +1.0472i 0 + 0.9273iColumns 7 through 80 + 0.7954i 0 + 0.6435i>> y=atanh(x)y = 0.1003 0.2027 0.3095 0.4236 0.5493 0.6931 0.8673 1.0986>> y=acoth(x)y = Columns 1 through 60.1003 + 1.5708i 0.2027 + 1.5708i 0.3095 + 1.5708i 0.4236 + 1.5708i 0.5493 + 1.5708i 0.6931 + 1.5708i Columns 7 through 80.8673 + 1.5708i 1.0986 + 1.5708i >> y=asech(x)y = 2.9932 2.2924 1.8738 1.5668 1.3170 1.0986 0.8956 0.6931>> y=acsch(x)y = 2.9982 2.3124 1.9189 1.6472 1.4436 1.2838 1.1545 1.0476>> y=log(x)y =-2.3026 -1.6094 -1.2040 -0.9163 -0.6931 -0.5108 -0.3567 -0.2231>> y=log10(x)y = -1.0000 -0.6990 -0.5229 -0.3979 -0.3010 -0.2218 -0.1549 -0.0969>> y=log2(x)y =-3.3219 -2.3219 -1.7370 -1.3219 -1.0000 -0.7370 -0.5146 -0.3219>> c=complex(a,b)c = 0.1763 + 3.0000i 0.4103 + 3.0000i0.0099 + 4.0000i 0.1389 + 1.0000i 0.0153 + 3.0000i>> zc=conj(x)zc =0.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000>> b=imag(x)b = 0 0 0 0 0 00 0>> a=real(x)a = 0.1000 0.2000 0.3000 0.40000.5000 0.6000 0.7000 0.8000>> y=fix(x)y = 0 0 0 0 0 0 0 0>> y=floor(x)y =0 0 0 0 0 0 0 0 >> y=ceil(x)y = 1 1 1 1 1 1 1 1>> y=round(x)y = 0 0 0 0 1 1 1 1>> y=sign(x)y = 1 1 1 1 1 1 1 1>> S=rats(x)S =1/10 1/5 3/10 2/5 1/2 3/5 7/10 4/5>> [N,D]=rat(x)N = 1 1 3 2 1 37 4D = 10 5 10 5 2 510 5>> A=[2 4 6;3 5 7;8 10 9]A = 2 4 63 5 78 10 9>> B=[4 1 5;7 5 0;9 3 6]B = 4 1 57 5 09 3 6>> A>Bans = 0 1 10 0 10 1 1>> A<Bans = 1 0 01 0 01 0 0>> A>=Bans = 0 1 10 1 10 1 1>> A<=Bans = 1 0 01 1 01 0 0>> A==Bans = 0 0 00 1 00 0 0>> A~=Bans =1 1 11 0 11 1 1>> A&Bans = 1 1 11 1 01 1 1>> A|Bans = 1 1 11 1 11 1 1>> ~Aans = 0 0 00 0 00 0 0>> ~Bans = 0 0 00 0 10 0 0>> x=0:pi/100:3*pi;>> y=sin(x);>> plot(x,y);>> y1=(x<pi|x>2*pi).*y;>> figure,plot(x,y1);>> r=(x>pi/3&x<2*pi/3)|(x>7*pi/3&8*pi/3);>> rn=~r;>> y2=r*sin(pi/3)+rn.*y1;>> figure,plot(x,y2)>> x=[0 4 5 9 8 6 74 85 7 4 85 8 4 5 8]x =0 4 5 9 8 6 74 85 7 4 85 8 4 5 8>> all(x)ans =0>> any(x)ans = 1>> find(x)ans =2 3 4 5 6 7 8 9 10 11 12 13 14 15>> isempty(x)ans =>> isglobal(x)Warning: isglobal is obsolete and will be discontinued. Type "help isglobal" for more details.ans =0>> isinf(x)ans =0 0 0 0 0 0 0 0 0 0 0 0 0 0 0>> isnan(x)ans =0 0 0 0 0 0 0 0 0 0 0 0 0 0 0>> isfinite(x)ans =1 1 1 1 1 1 1 1 1 1 1 1 1 1 1>> issparse(x)ans = 0>> isstr(x)ans =0>> not(x)ans =1 0 0 0 0 0 0 0 0 0 0 0 0 0 0>> y=[59 46 78 2 3 98 1 2 3 57 9 5 66 8 900 5]y =59 46 78 2 3 98 1 2 3 57 9 5 66 8 900 5>> y=[59 46 78 2 3 98 1 2 3 57 9 5 66 8 900 5]y = 59 46 78 2 3 98 1 2 3 57 9 5 66 8 900 5>> x=[0 4 5 9 8 6 74 85 7 4 85 8 4 5 8]x = 0 4 5 9 8 6 74 85 7 4 85 8 4 5 8>> A=[4 -40 2; 23 50 17;18 29 14]A = 4 -40 223 50 1718 29 14>> [r,c]=find(A>=20&A<=30)r = 23c = 12>> bitand(12,6)ans = 4>> bitshift(12,1)ans = 24>> bitxor(12,1)ans =13>> bitset(12,1)ans = 13 >> bitget(12,1)ans =0>> A =[ 87 59 56 85 66 21 12 35 62 64 69 88 99 81]A =87 59 56 85 66 21 1235 62 64 69 88 99 81>> A(2)ans =59>> A([1,2,8])ans =87 59 35>> A([9,6,2])ans =62 21 59>> A([end-4:end])ans =64 69 88 99 81>> A([1:5,5:-1:1])ans = 87 59 56 85 66 66 85 56 59 87>> A(3)=-1A = 87 59 -1 85 66 2112 35 62 64 69 88 99 81>> A(15)=-8A =87 59 -1 85 66 2112 35 62 64 69 88 99 81 -8>> A(20)=-1A = Columns 1 through 1687 59 -1 85 66 21 12 35 62 64 69 88 99 81 -8 0Columns 17 through 200 0 0 -1>> A=rand(8)A = 0.9501 0.8214 0.9355 0.13890.4451 0.8381 0.3046 0.37840.2311 0.4447 0.9169 0.2028 0.9318 0.0196 0.1897 0.86000.6068 0.6154 0.4103 0.1987 0.4660 0.6813 0.1934 0.85370.4860 0.7919 0.8936 0.6038 0.4186 0.3795 0.6822 0.59360.8913 0.9218 0.0579 0.2722 0.8462 0.8318 0.3028 0.49660.7621 0.7382 0.3529 0.1988 0.5252 0.5028 0.5417 0.89980.4565 0.1763 0.8132 0.0153 0.2026 0.7095 0.1509 0.82160.0185 0.4057 0.0099 0.7468 0.6721 0.4289 0.6979 0.6449>> A(3,3)ans =0.4103>> A(8)ans =0.0185>> sub2ind(size(A),3,3)ans =19>> [i,j]=ind2sub(size(A),19)i =3j =3>> A(:,4)ans =0.13890.20280.19870.60380.27220.19880.01530.7468>> A(3,:)ans =0.6068 0.6154 0.4103 0.1987 0.4660 0.6813 0.1934 0.8537>> A(end,:)ans =0.0185 0.4057 0.0099 0.7468 0.6721 0.4289 0.6979 0.6449>> A(3:4,5:6)ans =0.4660 0.68130.4186 0.3795>> A(2:2:4,1:2:5)ans =0.2311 0.9169 0.93180.4860 0.8936 0.4186>> A=reshape(A,5,5)A = 1 6 11 16 212 7 12 17 223 8 13 18 234 9 14 19 245 10 15 20 25>> A(:)'ans =Columns 1 through 161 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16Columns 17 through 2517 18 19 20 21 22 23 24 25>> A(:,1:2:5)=[]A = 6 167 178 189 1910 20>> A=[9 8 7;6 5 4;3 2 1];>> D=diag(A)D =951>> D1=diag(A,1)D1 =84>> D2=diag(A,-1)D2 =62>> V=[1 2 3 4];>> diag(V)ans = 1 0 0 00 2 0 00 0 3 00 0 0 4>> diag(1:3,-1)ans = 0 0 0 01 0 0 00 2 0 00 0 3 0>>A=[17,1,0,15;5,7,14,16;4,0,13,0;10,12,19,21]; >> D=diag(4:-1:1);>> D*Aans = 68 4 0 6015 21 42 488 0 26 010 12 19 21>> triu(A)ans =17 1 0 150 7 14 160 0 13 00 0 0 21>> triu(A,1)ans = 0 1 0 150 0 14 160 0 0 00 0 0 0>> B=A'B =17 5 4 101 7 0 120 14 13 1915 16 0 21>> rot90(A)ans =15 16 0 210 14 13 191 7 0 1217 5 4 10>> rot90(A,3)ans =10 4 5 1712 0 7 119 13 14 021 0 16 15>> B=fliplr(A)B = 15 0 1 1716 14 7 50 13 0 421 19 12 10>> B=flipud(A)B = 10 12 19 214 0 13 05 7 14 1617 1 0 15>> A=[4 5 6 9;7 8 9 5;4 5 6 9;7 8 9 5]; >> det(A)ans =0>> rank(A)ans =2>> cond(A)ans =1.0968e+017>> inv(A)Warning: Matrix is singular to working precision.ans = Inf Inf Inf InfInf Inf Inf InfInf Inf Inf InfInf Inf Inf Inf>> A=[4 8 9;8 2 7;6 3 8];>> inv(A)ans = 0.0568 0.4205 -0.43180.2500 0.2500 -0.5000-0.1364 -0.4091 0.6364>> [V,D]=eig(A)V = -0.6438 -0.7444 -0.5061-0.5467 0.6392 -0.5515-0.5354 0.1931 0.6631D = 18.2776 0 00 -5.2030 00 0 0.9254>> [U,S,D]=svd(A)U = -0.6378 0.7375 -0.2220-0.5426 -0.6348 -0.5500-0.5465 -0.2304 0.8051S = 18.9278 0 00 5.2884 00 0 0.8791D = -0.5374 -0.6639 -0.5200-0.4135 0.7449 -0.5236-0.7350 0.0663 0.6749>> [L,U]=lu(A)L = 0.5000 1.0000 01.0000 0 00.7500 0.2143 1.0000U = 8.0000 2.0000 7.00000 7.0000 5.50000 0 1.5714>> [Q,R]=qr(A)Q = -0.3714 0.9114 -0.1774-0.7428 -0.4063 -0.5322-0.5571 -0.0659 0.8278 R =-10.7703 -6.1279 -12.99870 6.2808 4.83140 0 1.3009>> a=1234a = 1234>> class(a)ans =double>> size(a)ans = 1 1>> b='1234'b =1234>> class(b)ans =char>> size(b)ans = 1 4>> 'I am astudent'ans =I am astudent>> a='This is No.2.23 Example!'a =This is No.2.23 Example!>> b=a(1:7)b =This is>> c=a(12:end)c =2.23 Example!>> a='Good';>> b='Noon';>> length(a)==length(b)ans = 1>> c=[a,'',b]c =GoodNoon>> d=[a;b]d =GoodNoon>> size(c)ans = 1 8>> size(d)ans = 2 4>> a='Good Noon';>> b=double(a)b = 71 111 111 100 32 78 111 111 110>> c='再见!'c =再见!>> c='再见!'>> d=double(c)d = 20877 35265 65281>> char(d)ans =再见!>> a='The first string';>> b='The second string';>> c=strcmp(a,b)c =0>> d=strncmp(a,b,4)d =1>> X='A friend in need is a friend indeed'; >> Y='friend';>> a=findstr(Y,X)a = 3 23>> b=strfind(Y,X)b = []>> S=['1 2 3';'2 3 4'];>> A=str2num(S)A = 1 2 32 3 4>> B=str2num('6-8i')B = 6.0000 - 8.0000i>> D=num2str(rand(2,3),6)D =0.950129 0.606843 0.8912990.231139 0.485982 0.762097>> d=189;>> h=dec2hex(d)h =BD>> c=dec2base(d,7)c =360>> b=dec2bin(d)b =10111101>> bin2dec(b)ans = 189>> A={ones(3,3,3),'Welcome';30.34,1:200} A = [3x3x3 double] 'Welcome'[ 30.3400] [1x200 double]>>B=[{ones(3,3,3)},{'Welcome'};{30.34},{1:20 0}]B = [3x3x3 double] 'Welcome'[ 30.3400] [1x200 double]>> C={5}C = [5]>> C(2,3)={7}C = [5] [] [][] [] [7]>> isequal(A,B)ans =1>> A={ones(3,3,3),'Welcome';30.34,1:200}; >> b=A(1,2)b = 'Welcome'>> class(B)ans =cell>> C=A{1,2}C =Welcome>> class Cans =char>> D=A{1,2}(6)D =m>> E=A{2,2}([end:-1:190])E =200 199 198 197 196 195 194 193 192 191 190>> class(E)ans =double>> N=A{3}([1 3 5 7])N =Wloe>> A={ones(3,3,3),'Welcome';30.34,1:200}; >> B=cell(2);>> B(:,1)={char('Good','Morning');1:10}B = [2x7 char ] [][1x10 double] []>> C=[A,B]C = [3x3x3 double] 'Welcome' [2x7 char ] [][ 30.3400] [1x200 double] [1x10 double] []>> D=[A,B;C]D = [3x3x3 double] 'Welcome' [2x7 char ] [][ 30.3400] [1x200 double] [1x10 double] [][3x3x3 double] 'Welcome' [2x7 char ] [][ 30.3400] [1x200 double] [1x10 double] []>> D(4,:)=[]D = [3x3x3 double] 'Welcome' [2x7 char ] [][ 30.3400] [1x200 double] [1x10 double] [][3x3x3 double] 'Welcome' [2x7 char ] []>> E=reshape(D,2,3,2)E(:,:,1) = [3x3x3 double] [3x3x3 double] [1x200 double][ 30.3400] 'Welcome' 'Welcome'E(:,:,2) = [2x7 char ] [2x7 char] [][1x10 double] [] []>>A={randn(3,3,2),'Good',pi;29,4+7*i,zeros(4)} A = [3x3x2 double] 'Good' [ 3.1416][ 29] [4.0000+ 7.0000i] [4x4 double]>> B=cellfun('isreal',A)B = 1 1 11 0 1>> C=cellfun('length',A)C = 3 4 11 1 4>> Member.code='09021';>> ='Liu';>> Member.age=22;>> Member.grade=uint16(3);>> MemberMember =code: '09021'name: 'Liu'age: 22grade: 3>> Member(4).name='Wang';>> Member(4).grade=2;>> Member(2)ans = code: []name: []age: []grade: []>>Memebr=struct('code','09021','name','Liu','a ge',22,'grade',uint16(3))Memebr = code: '09021'name: 'Liu'age: 22grade: 3>>Member=struct('code',{'09021','09034'},'name' ,{'Liu','Wamg'},'age',{22,24},'grade',{2,3}) Member = 1x2 struct array with fields:codenameagegrade>>Member=struct('code',{},'name',{},'age',{},'gr ade',{})Member = 0x0 struct array with fields:codenameagegrade>>Member=struct('code',{'09021','09034'},'na me',{'Liu','Wang'},'age',{22,24},'grade',{2,3},' score',{[78 89;90 68],[91 76;89 97]}) Member = 1x2 struct array with fields:codenameagegradescore>> Member(1).scoreans =78 8990 68>> Member(2).score(2,:)ans =89 97>> Member.codeans =09021ans =09034>> Member.('name')ans =Liuans =Wang>> ='Liu';M.ID=1;>> M(2,2).name='Wang';M(2,2).ID=2; >> M2=setfield(M,{2,1},'name','Zhang'); >> ans =Liuans =[]ans = []ans =Wang>> ans =Liuans =Zhangans = []ans =Wang>> fieldnames(M)ans = 'name''ID'>> M3=orderfields(M)M3 = 2x2 struct array with fields:IDname。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验3桌面的规划和任务栏的设置
实验内容:1熟悉桌面及桌面图标2学会设置任务栏3设置工具栏.状态栏的显示和隐藏4掌握任务管理器的操作
实验步骤:1重新排列桌面图标2设置任务栏3工具栏.状态栏的设置及显示和隐藏4任务管理器的功能和操作
实验4”我的电脑”及控制面板的使用
实验内容:掌握擦看磁盘属性的方法掌握安装应用程序和添加.删除WINDOWS XP组件学会添加新硬件学会安装新字体
上机报告
姓名
肖熹
学号
2010441865
专业班级
应化2010级2班
课程名称
大学计算机基础
指导
教师
陈维Βιβλιοθήκη 机房名称I304上机日期
2010-11-24
上机项目名称
Windows Xp操作系统的基本操作
上机步骤及内容:
实验1 Windows XP的桌面.窗口和菜单的操作
实验内容:练习桌面.显示属性的设置练习”开始”菜单设置练习窗口.多窗口操作了解Windows XP帮助系统
上机成绩,评语
指导教师
批改日期
实验步骤:1设置桌面.保护程序.分辨率2设置开始菜单3熟练掌握窗口.多个窗口的操作4使用帮助系统
实验2文件系统及资源管理器的使用
实验内容:熟悉启动资源管理器的方法熟练掌握文件和文件夹的新建.浏览.复制.移动.更名.删除等操作掌握文件属性设置了解如何建立文件关联
实验步骤:1文件和文件夹的新建.浏览.复制.移动.更名.删除等操作(1)文件浏览和文件夹结构(2)新建文件夹(3)选定文件或文件夹(4)移动和复制文件或文件夹(5)删除.恢复文件或文件夹(6)文件或文件夹的更名(7)文件或文件夹的搜索(8)创建文件或文件夹的快捷放式
实验步骤:1查看和利用“磁盘属性”功能的操作2.安装应用程序和添加,删除Windows XP组件3.添加新硬件4安装新字体5
实验5系统设置
实验内容:1设置管理用户及密码2掌握电源的配置和管理3设置系统日期和时间
结果分析与体会:
在Windows Xp操作系统的基本操作中我对该操作系统有了比较全面的了解和认识,在下面的学习中我会对其进行反复操作和练习以至全面掌握.
