用Nullor构建理想电压源模型求解符号传递函数的方法
buck电路的传递函数

buck电路的传递函数Buck电路是一种最常用的DC-DC降压转换器,可以将输入电压转换为输出电压,因此在实际应用中得到广泛应用。
在Buck电路中,传递函数是电路的重要参数之一,它描述了输入电压和输出电压之间的关系,因此是设计Buck电路的关键之一。
在讨论Buck电路的传递函数之前,首先需要了解Buck电路的基本工作原理。
Buck电路工作时,由开关管进行开关操作,通过控制开关管的通断,变换电源的等效电阻,从而达到输入电压变换输出电压的目的。
开关管的通断实际上就是决定了电路的整体状态,它可以采用脉冲宽度调制(PWM)的方式来进行控制,从而改变输出电压。
了解了Buck电路的基本工作原理之后,接下来我们来研究Buck 电路的传递函数。
传递函数也叫传输函数,是指一个系统的输出与输入的比例关系。
在Buck电路中,传递函数是指输出电压与输入电压之间的关系。
传递函数可以用数学公式表示为Vout/Vin,其中Vout是输出电压,Vin是输入电压。
具体计算Buck电路的传递函数需要进行以下步骤:第一步:从Buck电路中取得原理图第二步:利用基尔霍夫第二定律来求出输出电压与电感电流之间的关系。
第三步:根据电感电流和电容电压之间的关系,求出均值并带入公式中。
第四步:用基尔霍夫第一定律来计算输出电压和输入电压之间的比例关系,即求出传递函数的公式。
Buck电路的传递函数可以表示为D/(1-D),其中D是PWM的占空比,也是控制开关管通断的参数。
通过以上步骤,就可以得出Buck电路的传递函数公式。
不过需要注意的是,传递函数是数学模型,与实际情况可能略有偏差,需要通过实验进行验证。
总之,Buck电路是电子电路中非常重要的一种降压转换器,其传递函数描述了输入电压和输出电压之间的关系,是设计Buck电路的关键之一。
通过对传递函数的计算及验证,可以更好地了解Buck电路工作的原理,并进一步优化Buck电路的性能,从而满足具体的应用需求。
戴维南等效电压的求法

戴维南等效电压的求法戴维南等效电压的求法,是一种在电路分析中常用的方法,旨在简化复杂电路的分析和计算。
戴维南等效电压是指由于电路中含有多个电源或电阻,我们将其转换为一个等效的电源和电阻,从而方便求解和分析电路。
戴维南等效电压的求法方法主要有以下几个步骤:1.找出要求等效电压的两个节点,并将它们标记为a和b。
2.将所有的电源和电阻连接到这两个节点上,形成一个戴维南等效电路。
这就是将原来的电路转换为等效电路的关键步骤。
3.计算戴维南等效电路的等效电阻。
这可以通过以下步骤进行:(1)将所有其他电源和电阻从原来的电路中去掉;(2)用一个测试电源(如电压源或电流源)施加在a和b节点上,并测量在a和b节点之间的电压和电流;(3)根据欧姆定律和基尔霍夫定律,计算测试电源施加的电压和电流。
4.计算戴维南等效电路的等效电压。
这可以通过以下步骤进行:(1)利用戴维南定理,将等效电阻和测试电源施加的电压和电流关联起来;(2)根据之前测量的电压和电流,计算得到等效电压。
需要注意的是,在进行戴维南等效电压的求法时,我们通常需要根据具体的电路特点选择合适的测试电源和测量方法。
例如,当我们要求一个电路中某两个节点之间的等效电压时,我们可以选择将一个电压源或电流源连接到这两个节点上,并测量在这两个节点之间的电压或电流。
这样可以根据欧姆定律和基尔霍夫定律,方便地计算等效电压。
总之,戴维南等效电压的求法是一种常用的简化电路分析和计算的方法。
通过将复杂的电路转换为等效电路,并利用戴维南定理和基本电路定律进行计算,可以方便地求解和分析复杂电路中的等效电压。
这种方法在电子电路设计和故障排除中具有重要的应用价值。
(NEW)邱关源《电路》(第5版)配套题库【名校考研真题+课后习题+章节题库+模拟试题】(上册)

图1-9 【答案】30W,-10W 【解析】电压源发出的功率PV=15×2=30W,电流源发出的功率PI =-2×(15-5×2)=-10W。 三、计算题 1.计算图1-10中A点的电位 。[西南大学电工技术2012研]
图1-10 解:由串联分压原理有:
故A点的电位为 。
2.如图1-11(a)所示的为某电路的部分电路。各已知的电流及元 件值已标在图中,求I1,US。[北京航空航天大学2002研]
( )W。[北京交通大学2009研]
图2-2 A.80/9 B.20 C.80 D.40/3 【答案】A 【解析】设有源线性网络等效电压源电压为Uo,等效电阻为Ro 已知短路电流为6A,则有 ;
已知R=5Ω时,R消耗的功率为20W,则有
;
两式联立解得:
V。
当R=20Ω时,R消耗的功率为:
。
3.如图2-3所示电路,等效电阻 为( )。[西安电子科技大 学2010研]
3.欲使如图1-12所示电路中的2Ω电阻的功率为4Ω电阻功率的2 倍,求电压源E的值。[华南理工大学2003研]
图1-12 解:给出电路中各有关电流、电压的参考方向,如图1-13所示。
图1-13 根据题意可得:2 =2×4 ,则有I1= 2I2 由KCL得: 由KVL得: 联立上述五个方程,可得:
图3-6 解:如图3-7所示,对电路节点进行编号。
列写节点电压方程为:
图3-7
补充方程: 联立解得: 受控电流源发出的平均功率为:
2.在图3-8所示直流电路中,已知:
,
,
,
,
,试求流过支路 的电流 。[南京航空航天大学2012
研]
图3-8
解:取下端节点为参考节点,对节点a、b列写节点电压方程:
等效电源定理
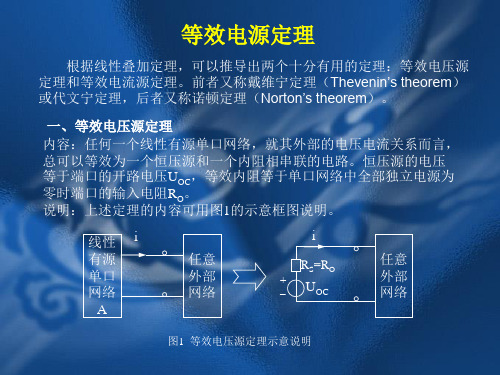
由此也可推知:理想电压源和理想电流源并联的电路可等效为一个 理想电压源。
习题:
1、如图题1所示单口网络,求其戴维宁等效电路。 2、如图题2所示电路中的i5和U1。
题1图
题2图
3、如图题3所示含独立电源的单口网络N,其断口ab间外接 一个电阻R。当R=10 Ω时,u=8V;当R=5 Ω时,u=6V,求网 络N的诺顿等效电路。 4、求图题4所示电路等效电压源模型 。
(b)
(1)求单口网络的开路电压UOC,如图2(c)所示:
(c)
(d)
U OC
R2 R1 R 2
US
2 22
12 6 (V )
(2)再求单口网络的等效内阻RO,这是要令网络内所有独立电源为零 (及恒压源短路,恒流源开路),如图2(d)所示,可得
R O R1 // R 2 R 3 2 // 2 1 2 ( )
由图3(b),U’=UOC 所以
U”= –iRO
U=U’+U”=UOC–iRO
对应的等效电路如图3(c)。最后把恒流源变会为原来的任意外部 网络,如图3(d)
应用: 在有些电路计算中,有时只要求出某一支路的电流或电压,这时如果 用基尔霍夫定律求解一般要列多个联立方程,计算过程比较麻烦。如 果多用戴维宁定理,计算则要简单一些,特别是分析某支路电阻的变 化对该支路电流或电压的影响时,用戴维宁定理更为方便。下边举例 加以说明。 [例1] 电路如图4所示,已知直流电源US,电阻R1、R2、R3、R4和检 流计G的内阻RG之值,求流过G的电流iG。 解:本图如果采用基尔霍夫定 律求 解,由于电路有6条支路,则需列出 6个独立方程。但因为只要求求一个 支路的电流,用等效电压源定理就 方便得多。为清楚起见,可将待求 支路(G)拉出,如图5(a)所示, 这是a,b端向左看是一个线性有源单 口网络。
multisim传递函数分析

(1)Parameter Type窗口 在Parameter Type窗口可以选择所要设定的元 件模型参数(Model Parameter选项)或器件参 数 ( Device Parameter 选 项 ) , 其 下 的 Parameter区将随之改变,说明如下:
multisim传递函数分析
(2)Parameter区 ①在Parameter区中的Device Type窗口可以选 择需要设定参数的器件种类,其中包括电路图中 所使用到的元件种类,例如 BJT(双极性晶体管 类)、 Capacitor(电容器类)、 Diode(二极管 类)、 Resistor(电阻器类)及Vsource(电压 源类)等。
multisim传递函数分析
在Function窗口中,可以选择分析方式。其中: MAX最大值分析,仅在 DC operating point选项 时选用。MIN 最小值分析,仅在 DC operating point选项时选用。RISE EDGE上升沿分析,其 右边的Threshold窗口用来输入其门限值。 FALL EDGE 下 降 沿 分 析 , 其 右 边 的 Threshold 窗 口 用 来输入其门限值。
multisim传递函数分析
பைடு நூலகம்
2. Analysis Parameters对话框 Analysis Parameters对话框如图1.6.22所示。
multisim传递函数分析
图1.6.22 Worst Case Analyses Parameters对话框
multisim传递函数分析
在Analysis Parameters对话框中: 在Analysis窗口中,可以选择所要进行的分析 ,有 AC analysis(交流分析)及 DC Operating point(直流工作点分析)两个选项。 在Output variable窗口中,可以选择所要分析 的输出节点。
求运放传递函数

求运放传递函数
运放传递函数指的是输出电压与输入电压之间的关系。
由于不同类型的运放具有不同的传递函数,因此没有一个通用的运放传递函数。
以下是常用的几种运放传递函数:
1. 非反馈运放传递函数:Vout = A*(V+ - V-)。
其中,V+和V-分别是运放的正输入和负输入,A是运放的开环增益。
该传递函数适用于非反馈运放,即没有反馈电阻的运放电路。
2. 反馈运放传递函数(非 inverting 模式):Vout =
(1+R2/R1)*Vin。
其中,R1 和 R2 是反馈电阻,Vin 是输入电压,Vout 是输出电压。
该传递函数适用于非反馈运放,即没有反馈电阻的运放电路。
3. 反馈运放传递函数(inverting 模式):Vout = -R2/R1*Vin。
其中,R1 和 R2 是反馈电阻,Vin 是输入电压,Vout 是输出电压。
该传递函数适用于反馈运放的 inverting 模式,即反馈电阻连接在运放的负输入端。
4.带通、带阻等滤波器的传递函数:根据具体电路而定,可以采用传统网络分析方法或者基于运放的滤波器设计方法来求解。
需要注意的是,运放传递函数是基于线性电路理论推导出来的,只在一定范围内有效,超出范围后就不能保证精度和可靠性。
因此,在实际应用中,需要根据具体电路参数和条件来选择合适的运放和电路,以获得最佳的性能和稳定性。
[工学]第2章 电路的基本分析方法
I2 I2 I2
U1 U1 U1
R1 I S E I2 R1 R2 R1 R2
I2
E R1 R2
R1 I2 IS R1 R2
R1 R2 U 1 IS R1 R2
R1 U 1 E R1 R2
R1 R1 R2 U1 US IS R1 R2 R1 R2
电路的基本分析方法
结论: 1. 当电压源等效变换为电流源时,电流源的电激流应等于电压源 的源电压US除以电压源的内电阻Rou;
2. 当电流源等效变换为电压源时,电压源的源电压应等于电流源 的电激流IS与其内电阻R0的乘积;
3. 等效前后两电源的电压和电流的参考方向(极性)应保持一致, 内电阻应相等。
I5
电压方程:取网孔I和网孔II
d
I : I1R1 I 2 R2 I 5 R5 E
II : I 4 R4 I 6 R6 I5 R5 0
联立5个方程求解
第2章
电路的基本分析方法
2.3 结点电压法
结点电压的概念 任选电路中某一结点为零电位参考点(用 表示) 结点电压是指该结点与参考点之间的电压 参考方向从该结点指向参考结点。 图中C为参考结点,则“UA‖―UB‖为A、B结点电压
E E Ro 0
(不存在)
例如:理想电压源短路电流I无穷大 理想电流源短路电流I=IS
第2章
电路的基本分析方法
注意
(2)与恒压源并联的元件,对外电路可看成断路 。 (3)与恒流源串联的元件,对外电路可看成短路。
I
I
+
10V -
U
2
Is
U
2
不影响对外电路的作用,I、U不变 但会影响电源内部的电压或电流
配套课件 电路分析基础(第二版)--李实秋
§1.3 基尔霍夫定律
基尔霍夫电流定律(KCL): Kirchhoff’s Current Law 基尔霍夫电压定律(KVL): Kirchhoff’s Voltage Law
1.电路术语:
➢ 支路branch :没有分支的一段电路叫支路。 b 6 ➢ 节点node :三条或三条以上支路的汇接点。 n 4
i1
i2
i3
8 10 i1 10 0.2A
i2
10 4
5
1.25A
i3 i1 i2 0.2 1.25 1.45A
注:电路图中所标方向均为参考方向。 参考方向一经选定,不再改变。
2.电压:
➢ 定义:电路中 a 、b 两点间的电压表明了单位正电 荷由 a 点转移到 b 点能量的改变量。
equivalent analysis method 重点:
• 等效的定义 • 两种实际电源的等效互换 • 无源和含源单口网络的等效化简
§2.1 单口电路等效的概念
The equivalent condition of one-port networks
如果一个单口电路N1和另一个单口电路 N2 端口 的VAR完全相同,则这两个单口电路对端口以外的电 路而言是等效的,可进行等效互换。
i1 +
u1 _
i2 +
b i1
u2
_
i2=b i1
CCCS
➢受控源在电路中的一般画法 :
§1.7 电位的计算
电路中某点的电位就是该点对参考点的电压。 参考点:电位为零的点,用“⊥”表示。
例 : 电路如图,求A点电位 UA 。
例 : 电路如图,求A点电位 U A和B点电位 UB 。
电子电路中的一种常用画法:
电工电子技术基础知识点详解2-4-电源的两种模型及其等效变换
电源的两种模型及其等效变换
理想电压源(恒压源) I
+
E
_
特点:(1)内阻R0 = 0
+
U
E
U
RL
_
O 外特性曲线 I
(2) 输出电压是一定值,恒等于电动势。
对直流电压,有 U E。
(3)恒压源中的电流由外电路决定。
例1:设 E = 10 V,接上RL 后,恒压源对外输出电流。
当 RL= 1 时, U = 10 V,I = 10A;
电压恒定,电
当 RL = 10 时, U = 10 V,I = 1A。 流随负载变化。
电源的两种模型及其等效变换
2. 电流源模型
I
电流源是由电流 IS 和内阻 R0 并联的电源的电路模型。
+
U
IS
R0 R0 U
RL
_
U
理
U0=ISR0
想 电流源 电
流
O
IS 源I
电流源的外特性
电流源模型
由图可得: U
I IS R0 若 R0 =
理想电流源 : I IS
若 R0 >>RL ,I IS ,可近似认为是理想电流源。
电源的两种模型及其等效变换
理想电流源(恒流源)
I U
+
IS
U
RL
_
特点: (1)内阻R0 = ;
O
IS
I
外特性曲线
(2)输出电流是一定值,恒等于电流 IS ;
(3)恒流源两端的电压 U 由外电路决定。
电压源 由图a: U = E- IR0
等效变换条件:
E = ISR0 E
IS R0
控制系统仿真实验六simulink
实验六:Simulin建模与仿真一、实验目的1、掌握Simulink建模与仿真的基本方法。
2、熟悉Simulink基本模块库及主要元件的使用方法。
二、实验学时:4学时三、实验原理:1、Simulink 仿真过程在已知系统数学模型或系统框图的情况下,利用Simulink进行建模仿真的基本步骤如下。
(1)启动Simulink,打开Simulink库浏览器。
(2)建立空白模型窗口。
(3)由控制系统数学模型或结构框图建立Simulink仿真模型。
(4)设置仿真参数,运行仿真。
(5)输出仿真结果。
2、Simulink建模与仿真基本方法根据给定的数学模型或控制系统框图,可建立Simulink仿真模型。
下面以图3-1所示的控制系统框图为例,说明Simulink建模与仿真的基本方法。
图中R 是单位阶跃输入信号,Y为系统输出响应。
建立图6-3所示系统框图的Simulink仿真模型的基本方法如下。
1.启动MATLAB/Simulink工具箱依次启动MATLAB软件、Simulink模块库浏览器后,如图6-1所示。
2.建立Simulink空白模型Simulink空白模型的建立可通过如下方法进行。
1、在MATLAB主窗口中选择【File】→【New】→【Model】命令。
2、在Simulink模块库浏览器窗口中选择【File】→【New】→【Model】命令。
3、单击Simulink模块库浏览器工具栏中的(New model)工具。
图6-1 闭环控制系统框图通过上述方法可以打开Simulink空白模型,如图6-2所示。
并可将其保存为后缀是mdl的文件(Simulink仿真模型的文件存储格式),例如Example_Model.mdl。
在保存Simulink模型文件的时候,为了实现向下兼容,MATLAB R2008/Simulink 7.1允许将模型保存为其他版本的Simulink模型。
图6-2 空白模型窗口3.根据系统框图选择模块构建Simulink仿真模型,首先需要知道所需模块所属的子模块库名称。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
号 传 递 函数 求 解过 程 中抵 销 掉 。
23 非独 立 源和 放 大器 的模 型 -
丁一 莩] 上
递 函数 一 般 采 用节 点分 析 法 求解 。节 点 分 析法 在 电路 分 析 和计 算 机 辅 助 网络 分 析 中应 用 非 常广 泛 ,但 其 缺 点是 对 独 立 电压 源 要 做 特 殊 的处 理 。文 献 [] 出 了节 点 问含 有独 立 源 的 分 析 方法 。其 基 本 思想 是 2提 将 原 电路 转 换 为 去源 电路 ( ecie i ut d at d cr i)和 强 制 电路 (ocd crut, 分 别 获得 节 点 导纳 矩 阵 和 v c fre i i c ) 节 点 电流 向量 ,求 解 后 可得 到 各 节 点 电压 。文 献 [] 这 个方 法 扩 展 到 含 受控 电压 源 的 电路 。这些 方 法 3将
其 等 效性 如 下 :根 据 Nulr的特 点 ,i / 点之 间 的 电压 通 l o ,_节
i j
[匾
图 2 独 立 电 压 源
收稿 日期 t 0 50 -2 20 —42
修 订 日期 :2 0 -30 0 60 ・9ຫໍສະໝຸດ 维普资讯 第 4期
含 有 理想 电压 源 的 电路 进 行 节 点 分析 ,借 助 于 Mah mai te t a软 件 c . i
的 强 大 的符 号 处 理 能 力 ,扩 展 了节 点分 析 法 的 应用 范 围 。利 用 该
v
- =
二
各递的表r 大化路与过 fT Tv。_卜 种函符达 地了分设程 (=88I 传数号式 简电析计。 Y lY , 极 }=r U ) v 【 2 电 和 件的N l 模型 源 器 uo l 01 一 r ( 。
22 理 想 电压源 的 Nulr . l 模型 o
0N l tr 约 束条 件 ulo 是 a () abt r 单 口网络 。 riay的 r
为 了 能够 直 接 对位 于节 点 i 节 点 之 问的 理 想 电压 源 和 列 写 导纳 矩 阵 , Nulr 建 的理 想 电压源 模 型 如 图 2所 示 。 用 l 构 o
V O .2 11
No. 4
Aug t 2 7 us , 00
用 N l r 建理想 电压 源模 型求解符 号传递 函数 的方法 ul 构 o
滕建 辅 , 董健 , 史斌 , 马杰
( 津 大学 电 子信 息 工 程 学 院 ,天津 3 0 7 ) 天 0 0 2
摘 要 :电路 网络 的符号 传递 函数分析 技术在 电路 分析与 设计 中起 着重 要 的作 用 。本 文利用 Nulr l 元件 ,构建 了理 o
21 N l r 型 . ul 模 o 图 1 N lr ul 的表不 o
Nulr是 一 种 重 要 的双 口网络 ,其 性质 适 合 应 用 于 R 有 源 网络 的分 析 与 综 合 ,并 且可 以建立 各 l o C 种 RC有源 网络 的 内在 联系 ,如 图 l 示 L。 所 4 J 定义 :Nulr l 是具 有 零 传 输 矩 阵 的两 端 口网络 , o 为 () I ) =,( =0的单 I 网络 。Noao S l rtr是约 束条 件 为 ( abt r ria ) r y,
对 于 电路 的手 工计 算 ,可 以极 大地 简化 分 析 过程 ,但 对 于 计 算 机 辅助 网络 符 号 传 递 函数 分 析 ,其 优 势 并 不 明显 。为此 ,本文 提 出 了一 种 用 N I r 建 的 理 想 电压 源 模 型 。利 用 该 模 型 ,可 以直 接对 节 点 问 ul 构 o
令参考节点的节点电压为零删除式中的第行和第列简化如下引入模型将独立电压源受控源等元件用和表示使节点分析法适用于更广泛的网莩丁一乃儿乃儿理想运算放大器曲图理想运放和四种受控源的模型图一般网络的表示络再利用式求出然后求出相应的支路电流从而求出网络的各种传递函数如下砌器驰揣即焉驰怒啪篇从基于数学平台的实现基于强大的符号处理能力可以方便地实现电路的符号传递函数求解其流程如下嵌入和模型
滕建辅等:用 Nulr l 构建理想 电压源模型求解符号传递函数的方法 o
15 2
过 Nultr 住 ,与 并 联 电阻 R上 的 电压 相 同 即 ,而 两 节 点 问 l o钳 a
的 电流 只通 过 No a r即为 abt r 。 中 的并 联 电阻 R可 以在 符 rt o r iay 其 r
的有 利助手 。 关键词 :符号 电路分析 :Nulr l ;Mah mai :C o te t a AD c
中图分 类号 ;T l N7 3
文献标识 码 ;A
1 引 言
在 电路 分 析 与 设计 中 , 电路 符 号 传递 函数 分 析 的 作 用 非 常重 要 [。运 用 网络 参数 的 符 号表 达 式 , 1 】
想 电压 源 的模 型 ,扩 展 了节点 分析法 的应用 范围 ,并且基 于 Mah maia强大 的符 号处理 能力 ,设计 出一种求 解 网络 te t c
符号传 递 函数的节 点分析法 。该方 法可 以求解 节点 问含 有理想 电压 源 的线 性时 不变 ( T )系统 中各种 电路参 数 的符 号 、 LI 传递 函数 。 电路分 析与设 计实例 表 明,利用 本文给 出 的方 法所 开发 的符号传 递函数 求解程 序 ,是 电路 分析和 电路设 计
可 以方 便 地 分 析频 率 响 应 ,计 算灵 敏 度 和 进 行故 障 诊 断 。在 有源 滤 波 器 的 设计 过 程 中 ,将 要 实现 的数
值 传递 函数 的 系数 与 电路 的 符 号传 递 函数 的 系数 相 匹配 ,就 可 以计 算 出 电路 的元 件 值 。 电路 的符 号 传
维普资讯
第l 2卷 第 4期
20 年 8月 07
文章 编 号 : 1 0 -2 9( 0 7 0 - 1 4 0 0 70 4 2 0 ) 4 0 2 -4
电路与系统学报
J RNAL OF CI OU RCUI S AND YS EM S T S T
