电阻串联和并联的计算
电阻在串联和并联中的规律和公式

电阻在串联和并联中的规律和公式
(实用版)
目录
1.串联电路的电阻规律和公式
2.并联电路的电阻规律和公式
3.电阻串联和并联的实际应用
正文
一、串联电路的电阻规律和公式
串联电路是指多个电阻依次排列在同一电路中,电流在各个电阻之间是相等的。
根据欧姆定律,电阻的计算公式为 R=U/I,其中 R 代表电阻,U 代表电压,I 代表电流。
在串联电路中,总电阻等于各电阻之和,即R_total=R1+R2+R3+...+Rn。
二、并联电路的电阻规律和公式
并联电路是指多个电阻同时连接在电路的两个分支上,电压在各个电阻之间是相等的。
根据基尔霍夫定律,并联电路的总电阻公式为
1/R_total=1/R1+1/R2+1/R3+...+1/Rn。
化简后得到
R_total=R1*R2*R3*...*Rn/(R1+R2+R3+...+Rn)。
三、电阻串联和并联的实际应用
电阻串联和并联在实际电路中应用广泛,例如在家庭用电、工业生产等领域。
在串联电路中,电阻值越大,电流越小,总电阻等于各电阻之和。
在并联电路中,电阻值越小,电流越大,总电阻的倒数等于各电阻阻值的倒数之和。
第1页共1页。
串联并联中电阻的关系

串并联电路中电阻的关系如下:
串联电路的总电阻等于各串联导体电阻之和,即R串=R1+R2+-+Rn。
并联电路的总电阻的倒数等于各并联电阻的倒数和,即1/R并=1/R1+1/R2+--+1/Rn。
串联电路的电阻和功率的关系
在串联电路中,由P=UI=I²R,I相同时,R越大,P越大。
即在串联电路中,电阻越大,实际电功率越大。
在并联电路中,P=UI=U²/R,U相同时,R越大,P越小。
所以在并联电路中,电阻越大,实际电功率越小。
电功率是作为表示电流做功快慢的物理量,一个用电器功率的大小数值上等于它在1秒内所消耗的电能。
如果在t(SI单位为J)这么长的时间内消耗的电能W(SI单位为J),那么这个用电器的电功率就是P=W/t。
电功率还等于导体两端电压与通过导体电流的乘积。
串联和并联电路的总电阻推导公式
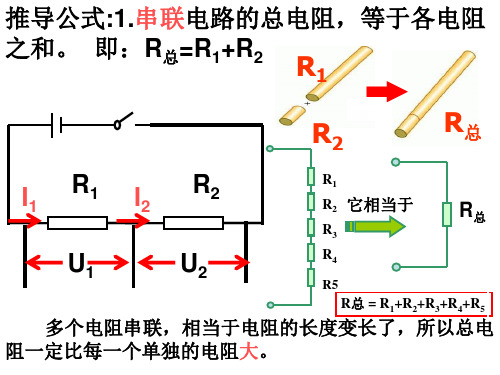
R总
多个电阻并联,相当于总的 横截面积变粗了,所以总电阻一
定比每个电阻都小。
它相当于
R总
R1 R2 R3 R4 R5
推导过程:
并联电路的特点:I = I1+ I2
U = U1=U2
欧姆定律: I = U
所以
I1=
U1 R1
R
I2=
U2 R2
由于I=I1十I2
所以:U/R=U1/R1+U2/R2
由此得出: 1 R
U = U1+U2 欧姆定律:I = U 得U=IR
R 所以:U1=IR1,U2=IR2 由于U=U1+U2 因此IR=I1R1+I2R2
所以:R=R1十R2
推导公式:2.并联电路中并联电路的总电阻的倒数, 等于各并联电阻的倒数之和。即:1 1 1
R总 R1 R2
I1
R1
U1
I2
R2
U2
R1
R2
=
1 R1
+
1 R2
分流关系 与分压关系
分压关系
电流
电压
电阻
分配关系
串 联
I=I1=I2
U=U1+U2
R=R1+R2
U1 R1 U 2 R2
并 联
I=I1+I2
11 1 U=U1=U2 R R1 R2
I1 R2 I 2 R1
分流关系
推导公式:1.#43;R2 R1
R2
R总
I1 R1 I2 R2
R1
R2 它相当于
R总
R3
U1
U2
R4
R5
R总 = R1+R2+R3+R4+R5
多个电阻串联,相当于电阻的长度变长了,所以总电
初中物理:电阻的串并联等效电阻计算

初中物理:电阻的串并联等效电阻计算电阻是初中物理中一个非常重要的概念,它是构成电路的基本元件之一,用于控制电流的强度和电压。
在电路中,电阻可以起到能量转换、分压限流、以及热效应等作用。
而串并联等效电阻计算则是电阻连接中常见的问题,对于理解电路的工作原理具有重要意义。
一、电阻的基本概念电阻器是一种电子元件,它通过电子流动时产生的阻碍作用来消耗电能。
电阻器的符号通常用字母“R”表示,其大小由元件自身的材料和尺寸决定。
电阻器的主要参数包括阻值、额定电压和功率等。
二、串联电阻在电路中,两个或多个电阻元件连接在一起,形成串联关系,此时每个电阻器对电流的阻碍作用增加,总电压等于各电阻器额定电压之和。
根据欧姆定律,串联电阻的计算公式为:R总=R1+R2+...+Rn。
三、并联电阻在另一个极端,我们将电阻器并联在一起,形成并联关系。
此时每个电阻器对电流的阻碍作用减小,总电流是所有并联电阻允许电流之和。
根据欧姆定律,并联电阻的计算公式为:1/R总=1/R1+1/R2+...+1/Rn。
四、串并联组合的等效电阻在现实电路中,电阻常常是串联和并联的组合。
这种组合方式改变了电路的总电阻值,进而影响了电路的工作特性。
当有两个或更多电阻元件串联或并联时,我们需要计算它们的等效电阻。
计算等效电阻的方法通常是根据串并联电路定律进行。
五、分流和分压原理在串并联电路中,电流和电压的分配规律有着一定的规律。
这就是欧姆定律的延伸——分流和分压原理。
根据这个原理,我们可以根据电路的总电阻和总电流来计算各个电阻上的电压或电流。
六、应用举例让我们通过一个具体的例子来应用上述知识。
假设我们有三个相同大小的电阻器A、B、C,阻值分别为R1、R2、R3,现在我们将其中的两个并联后再与第三个串联,求此时的等效电阻。
根据并联和串联的关系,我们可以列出以下公式:(R1+R2) / (R1+R2+R3) = R' (等效电阻)通过简单的数学运算,我们可以得到 R' = R1 + R2 - R1 * R2 / (R3 + R1 + R2)这就是我们要求的等效电阻。
电阻在串联和并联中的规律和公式

电阻在串联和并联中的规律和公式
(实用版)
目录
1.串联电路的电阻规律和公式
2.并联电路的电阻规律和公式
3.电阻在串联和并联中的实际应用
正文
一、串联电路的电阻规律和公式
串联电路是指多个电阻依次排列在同一电路中,电流在各个电阻之间是相同的。
根据欧姆定律,电阻的计算公式为 R=U/I,其中 R 代表电阻,U 代表电压,I 代表电流。
在串联电路中,总电阻等于各部分电路电阻之和,即 R_total=R1+R2+R3+...+Rn。
二、并联电路的电阻规律和公式
并联电路是指多个电阻同时连接在电路的两个分支上,电压在各个电阻之间是相同的。
根据基尔霍夫定律,电阻的计算公式为
1/R_total=1/R1+1/R2+1/R3+...+1/Rn,即
R_total=1/(1/R1+1/R2+1/R3+...+1/Rn)。
三、电阻在串联和并联中的实际应用
在实际应用中,串联电路和并联电路有着不同的特点。
串联电路中,电阻值相加,总电阻随着电阻值的增加而增加;并联电路中,电阻值相乘,总电阻随着电阻值的减小而减小。
因此,在需要限制电流的场合,通常采用串联电路;在需要提高电压的场合,通常采用并联电路。
总之,电阻在串联和并联电路中的规律和公式分别为:串联电路中,总电阻等于各部分电路电阻之和;并联电路中,总电阻的倒数等于各电阻阻值的倒数之和。
电阻并联 串联

电阻并联串联电阻是电路中常用的元件之一,它是在电路中提供电阻力的元件。
在电路中,电阻可以进行串联和并联,这是电路设计中的基本元素。
串联和并联的组合方式不同,会影响电路的性质和使用。
一、串联电阻的概念和计算方法串联电阻是指将电路中的电阻依次排列在同一电路路径上,串联在一起,形成一个串联电路回路。
串联电路的电阻值相当于所有电阻值之和。
例如:我们将三个电阻A、B、C依次串联在一起,电阻值分别为10Ω、20Ω、30Ω,则串联电路的总电阻为:10Ω+20Ω+30Ω=60Ω。
串联电路的电阻值计算公式为:总电阻= R1 + R2 + R3 + … + Rn其中,R1、R2、R3、…、Rn分别为电路中的每个电阻的电阻值。
串联电路的特点是电流能够依次通过每个电阻,并且若一个电阻损耗或故障,其他电阻也会受到影响,整个电路将被中断。
二、并联电阻的概念和计算方法并联电阻是指将电路中的电阻分别连到同一电路节点上,使它们形成一个并联电路回路。
并联电路的电阻值相当于所有电阻值的倒数之和的倒数。
例如:我们将三个电阻A、B、C连接在同一电路节点上,电阻值分别为10Ω、20Ω、30Ω,则并联电路的总电阻为:1/(1/10Ω + 1/20Ω + 1/30Ω) = 5.45Ω。
并联电路的电阻值计算公式为:总电阻 = 1 / (1/ R1 + 1/ R2 + 1/ R3 + … + 1/ Rn)其中,R1、R2、R3、…、Rn分别为电路中的每个电阻的电阻值。
并联电路的特点是电流能够分流,每个电阻上的电流相等,而总电流等于各个分流电流的和。
三、串联和并联的应用串联电阻可以用于电路的调节和控制。
例如电子电路中的电压调节器(如调整LED灯亮度的明亮度调节器),就是通过改变串联电阻的电阻值,从而调节电路的电压大小,实现电路的控制。
并联电阻可以用于电路中的负载匹配和检测。
例如,在音频放大器电路中,使用并联电阻作为负载匹配器,调整输入和输出电阻之间的阻抗匹配。
串并联电路的电阻和电功率计算

串并联电路的电阻和电功率计算电阻和电功率是串并联电路中重要的计算参数。
串联电路是指电器或电子元件按照一条路径连接起来,电流在其中的大小相同;而并联电路是指电器或电子元件按照多条路径连接起来,电压在其中的大小相同。
本文将介绍串并联电路中电阻和电功率的计算方法。
一、串联电路中电阻的计算在串联电路中,电器或电子元件依次连接,电流在其中的大小保持一致。
串联电路中总电阻(Rt)等于各个电阻(R1、R2、R3…)的累加。
即:Rt = R1 + R2 + R3 + ...例如,串联电路中有三个电阻,分别为10欧姆、15欧姆和20欧姆,则串联电路的总电阻为:Rt = 10Ω + 15Ω + 20Ω = 45Ω二、并联电路中电阻的计算在并联电路中,电器或电子元件按照多条路径连接,电压在其中的大小保持一致。
并联电路中总电阻(Rt)等于各个电阻(R1、R2、R3…)的倒数之和的倒数。
即:1/Rt = 1/R1 + 1/R2 + 1/R3 + ...例如,并联电路中有三个电阻,分别为10欧姆、15欧姆和20欧姆,则并联电路的总电阻为:1/Rt = 1/10Ω + 1/15Ω + 1/20Ω = 0.1 + 0.0667 + 0.05 = 0.2167ΩRt = 1/0.2167 = 4.61Ω三、串并联电路中电功率的计算串并联电路中,电功率的计算可以使用以下公式:P = V^2 / R其中,P表示电功率(单位为瓦特W),V表示电压(单位为伏特V),R表示电阻(单位为欧姆Ω)。
在串联电路中,总电阻Rt已经计算得到,电流I和电压V之间的关系为:V = I * Rt。
因此,串联电路中的电功率可以用以下公式计算:P = (I * Rt)^2 / Rt = I^2 * Rt在并联电路中,总电阻Rt已经计算得到,电流I和电压V之间的关系为:I = V / Rt。
因此,并联电路中的电功率可以用以下公式计算:P = V^2 / Rt四、串并联电路中的实例计算为了更好的理解串并联电路中电阻和电功率的计算方法,下面通过一个实例进行计算。
电路分析串联与并联电阻的计算方法

电路分析串联与并联电阻的计算方法电路分析是电子工程领域中的关键技能之一。
在电路设计和故障排除中,理解串联与并联电阻的计算方法至关重要。
本文将介绍串联与并联电阻的概念以及相应的计算方法。
一、串联电阻的概念与计算方法串联电阻是指将多个电阻按照一定的顺序连接在一起,电流依次通过每个电阻,总电流等于各个电阻上的电流之和。
串联电阻的计算方法如下:假设有n个电阻R1、R2、...、Rn依次串联连接,总电阻记为RT。
根据欧姆定律,电流在串联电路中保持不变,因此可以通过计算总电压与总电流的比值来求得总电阻:RT = V / I其中V为电路上的总电压,I为电路中的总电流。
若各个电阻的阻值分别为R1、R2、...、Rn,则总电阻RT可以表示为:RT = R1 + R2 + ... + Rn这意味着将各个电阻的阻值相加即可得到串联电路的总阻值。
二、并联电阻的概念与计算方法并联电阻是指将多个电阻同时连接在一起,电压相同,总电流等于各个电阻上的电流之和。
并联电阻的计算方法如下:假设有n个电阻R1、R2、...、Rn同时并联连接,总电阻记为RP。
根据欧姆定律,总电流等于各个电阻上的电流之和,即:I = I1 + I2 + ... + In又根据电流与电阻的关系,即I = V / R,可以得到:1 / RP = 1 / R1 + 1 / R2 + ... + 1 / Rn这就是并联电阻的计算公式。
三、串联与并联电阻的应用举例为了更好地理解串联与并联电阻的计算方法,以下举例说明:1. 串联电阻应用举例:假设有三个串联电阻,阻值分别为R1 = 10Ω,R2 = 20Ω,R3 = 30Ω。
如果电路上的总电压V为5V,求总电流和总电阻。
根据串联电阻的计算方法,总电阻RT = R1 + R2 + R3 = 60Ω。
总电流I = V / RT = 5V / 60Ω = 0.083A。
2. 并联电阻应用举例:假设有三个并联电阻,阻值分别为R1 = 10Ω,R2 = 20Ω,R3 = 30Ω。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电阻串联和并联的计算
电阻是电路中常见的元件之一,用于控制电流的流动和电压的大小。
在电路中,电阻可以串联或并联连接,以满足不同的电路要求和应用场景。
我们来看电阻的串联连接。
串联连接是指将多个电阻依次连接起来,电流依次通过每个电阻,形成电流的连续路径。
在串联连接中,电阻的总阻值等于各个电阻阻值之和。
假设有两个电阻R1和R2串联连接在一起,其总电阻记为RT,那么有如下关系式:RT = R1 + R2。
以一个简单的例子来说明串联连接的计算方法。
假设有两个电阻,一个阻值为10欧姆,另一个阻值为20欧姆,它们串联连接在一起。
根据串联连接的定义,总电阻等于两个电阻阻值之和,即RT = 10 + 20 = 30欧姆。
因此,串联连接后的电阻为30欧姆。
接下来,我们来看电阻的并联连接。
并联连接是指将多个电阻同时连接在电路中,形成电流分流的路径。
在并联连接中,电阻的总阻值等于各个电阻阻值的倒数之和再取倒数。
假设有两个电阻R1和R2并联连接在一起,其总电阻记为RT,那么有如下关系式:1/RT = 1/R1 + 1/R2。
同样以一个简单的例子来说明并联连接的计算方法。
假设有两个电阻,一个阻值为10欧姆,另一个阻值为20欧姆,它们并联连接在
一起。
根据并联连接的定义,总电阻等于两个电阻阻值的倒数之和再取倒数,即1/RT = 1/10 + 1/20 = 3/20。
将等式两边取倒数,得到RT = 20/3 = 6.67欧姆。
因此,并联连接后的电阻为6.67欧姆。
在实际应用中,串联和并联连接常常被用于电路设计和电路分析中。
串联连接可以增加电路的总阻值,降低电流的流动,起到限流的作用。
而并联连接可以降低电路的总阻值,增大电流的流动,起到增流的作用。
这些特性使得串联和并联连接在电路中有着不同的应用。
总结起来,电阻的串联和并联连接是电路中常见的连接方式。
串联连接的总电阻等于各个电阻阻值之和,而并联连接的总电阻等于各个电阻阻值的倒数之和再取倒数。
通过合理选择和组合电阻的串联和并联连接,可以满足不同的电路需求,实现精确的电流和电压控制。
在电路设计和分析中,熟练掌握串联和并联连接的计算方法,对于解决电路中的问题和优化电路性能都具有重要的意义。
